| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 11 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201016201 | |
| Published online | 03 August 2011 | |
The influence of radio-extended structures on offsets between the optical and VLBI positions of sources in the ICRF2⋆,⋆⋆
1
Observatório Nacional/MCT, R. Gal. José Cristino 77, CEP 20921-400, RJ, Brasil
e-mail: camargo@on.br
2
Observatório do Valongo/UFRJ, Ladeira do Pedro Antônio 43, CEP 20080-090, RJ, Brasil
3
Centro Universitário Estadual da Zona Oeste, Av. Manuel Caldeira de Alvarenga 1203, CEP 23070-200, RJ, Brasil
Received: 25 November 2010
Accepted: 3 May 2011
Context. We investigate the differences between positions as determined by optical (direct imaging) and Very Long Baseline Interferometry (VLBI) techniques of extragalactic sources listed in the second realization of the International Celestial Reference Frame (ICRF2).
Aims. We aim to verify the influence of the source’s intrinsic structure on these differences.
Methods. Instruments with mosaics of CCDs were used to acquire the optical positions presented here, which lead us to opt for overlapping techniques to build a virtual, continuous CCD over the whole angular size of the respective fields of view, whose translation of the resulting intrumental positions into positions that are consistent with those in the ICRF2 was obtained with the help of the UCAC2.
Results. The differences obtained between the optical and VLBI positions of the observed sources can reach more than 80 milliarsec for some measurements and, considering that they can hardly be explained by statistical fluctuations or systematic errors in the optical reference frame used here only, we argue that these differences can be related to the sources’ X-band structure index (8.4 GHz).
Conclusions. In this context, the presence of the intrinsic structure should be considered when comparing the optical and VLBI positions of ICRF2 sources in the future.
Key words: astrometry / reference systems / quasars: general
© ESO, 2011
1. Introduction
Fixed (non-rotating) directions on the celestial sphere can be kinematically defined by the positions of very distant objects. This concept has been the basis of the fundamental celestial frames adopted by the International Astronomical Union (IAU) since 1998, starting with the first realization of the International Celestial Reference Frame (ICRF1; Ma et al. 1998). The main conceptual difference between the ICRF1 and its predecessor, the Fifth Fundamental Catalogue (FK5; Fricke et al. 1988), is that the first had the directions of its coordinate axes defined kinematically by the positions of very distant (and therefore fixed) objects, whereas fixed directions in the latter were given by stellar positions and proper motions based on the mean equator and equinox of a reference epoch – J2000 (Feissel & Mignard 1998).
The current IAU’s fundamental celestial frame, effective as of 1st January 2010, is the second realization of the International Celestial Reference Frame (ICRF2; for a detailed description, see Fey et al. 2009). The ICRF2 contains the positions of 3414 extragalactic sources as determined by Very Long Baseline Interferometry (VLBI), but only the most accurate (<0.4 milliarsec) positions of 295 sources, selected on the basis of positional stability and the lack of extensive intrinsic source structure, are effectively used to define the frame axes. The remaining 3119 sources have positions consistent with the defining ones and help to densify the frame. The ICRF2 is now the prime realization of the IAU’s International Celestial Reference System (ICRS; Arias et al. 1995).
In contrast with the advantage of being a natural choice to the kinematical definition of fixed directions, extragalactic sources may present spatially extended structures at radio wavelengths. In fact, the sources’ intrinsic radio structure is one of the limiting factors in defining the celestial frame (Charlot et al. 2008) and may also be associated to differences between the orientation of the respective optical and radio frames (da Silva Neto et al. 2002).
The instrinsic structure of the extragalactic sources may also present temporal evolution. Therefore, monitoring this evolution is of great importance to maintain and improve the frame. Information about the structure of sources in the ICRF2 can be found at the Radio Reference Frame Image Database1 (RRFID) and the Bordeaux VLBI Image Database2 (BVID). Along with the high-resolution images available therein, the X- and S-band structure indices (8.4 and 2.3 GHz, respectively) are of particular interest. This index quantifies the VLBI astrometric quality of the sources with integer numbers ranging from 1 (best case – most compact sources) to 4 (worst case – most extended sources). Details about the determination of these indices are found in Fey & Charlot (1997) and Fey & Charlot (2000). Because the intrinsic structure may affect the alignment between the optical and radio frames, as mentioned above, the structure index is also relevant considering the extragalactic frame as seen from optical wavelengths. At this point, it is just as well to say that this is the part of the spectrum most frequently used by astronomers to access the axes materialized by the ICRF2. It is also relevant to mention that the Gaia mission (Perryman et al. 2001; Mignard 2005a; Perryman 2005) is expected to bring the prime materialization of the celestial coordinate axes back to optical wavelengths and the best alignment of the future Gaia optical frame with the current radio one is very important. For some astrometric and reference frame topics related to Gaia, see Mignard (2002), Lindegren (2005), Mignard (2005b), Lindegren et al. (2008), Andrei et al. (2009), Bourda et al. (2008), Bourda et al. (2010), Bourda et al. (2011). For a broader variety of topics related to Gaia, see also Turon et al. (2005).
In this context, the accurate optical positions of ICRF sources have been determined (see, for instance, Assafin et al. 2003; Camargo et al. 2005; Assafin et al. 2007; Aslan et al. 2010) and provided numbers about the alignment between the optical and radio frames. This work focuses on statistically significant optical to radio positional differences and aims at investigating them.
ICRF2 sources that were observed with WFI and SOI: physical characteristics and astrometric results.
Here, we determine accurate optical positions of 22 sources listed in the ICRF2 with the SOAR Optical Imager (SOI; Schwarz et al. 2004), mounted at the 4.2 m aperture SOAR (SOuthern Astrophysical Research) telescope, and the Wide Field Imager (WFI; Baade et al. 1999) mounted at the ESO/MPG 2.2 m aperture telescope. We find that statistically significant optical to VLBI differences in a given position are most frequently associated to sources with a large (3–4) X-band structure index. These significant differences may reach beyond 80 mas and can hardly be explained only by systematic errors affecting the astrometric reference catalogue used here, the Second US Naval Observatory CCD Astrograph Catalog (UCAC2; Zacharias et al. 2004), or by statistical fluctuations. These results not only agree with the conclusion of da Silva Neto et al. (2002), where a smaller mean difference was found from their statistic study of a larger sample, but also indicate that significant differences between the optical and VLBI positions of reference frame sources, associated to the presence of spatially extended structure, may be found on an individual basis. In Sect. 2 we present the targets and observational procedures. In Sect. 3 we describe the data reduction. The error budget can be found in Sect. 4. Discussion and conclusions are presented in Sects. 5 and 6, respectively.
2. Targets and observational procedures
The 22 extragalactic sources (see Table 1) observed in this work were selected according to their X-band structure index, as provided by the BVID, and to the presence of extended structure, as given by high angular resolution maps at the BVID and RRFID. The structure indices shown in Table 1 were selected by considering that the dates of the VLBI experiments should be the closest to those of the respective optical observations presented here (see also Tables 2 and 3). Further considerations were their magnitudes and their observability by two southern telescopes. These telescopes were the SOAR (Cerro Pachón) and the ESO/MPG 2.2 m (La Silla), both in Chile. Imagers on both telescopes are mosaics of CCDs.
ICRF2 sources that were observed with WFI and SOI: observational information and astrometric results.
2.1. SOAR Optical Imager
The SOI is a mosaic of two 2 k × 4 k CCDs separated by a gap of 7.8′′ along the largest dimension. This covers a total field of view of 5.3′ × 5.3′ with a scale of 0.077′′ per pixel. A linear atmospheric dispersion corrector actuated to deliver images with improved seeing. The filter used throughout the observations with SOI was a R Bessel (see Table 2).
Overlapping images were acquired in such a way to cover these gaps and, as a consequence, to allow for an optical materialization of the ICRF2 axes given by the largest number of UCAC2 stars available over the area covered by a given mosaic. To the SOI images, the overlap could be accomplished by a rotation of the imager, by pointing offsets, or by a combination of these two. These pointing offsets were in some cases applied in such a way to drive the telescope towards nearby reference stars.
2.2. Wide-Field Imager
The WFI is a mosaic of 4 × 2 2 k × 4 k CCDs. A gap of 14.3′′ along the right ascension axis separates the two rows of four CCDs, running along their shortest dimension. Three gaps of 22.9′′, perpendicular to the one mentioned above, separate the four rows of two CCDs, each gap running then along the CCD longest dimension. This mosaic covers a total field of view of 33′ × 33′ with a scale of 0.238′′ per pixel. Again, a red filter (ESO844) was used throughout the observations (see Table 2).
As for the SOI, overlapping images were acquired to cover the gaps. To the WFI, the overlapping procedure was the same to all acquisitions and consisted of two sets of dithered images. An offset applied between these two sets displaced the targets symetrically with respect to the optical axis of the imager. As a consequence, the targets were imaged in two different CCDs and close to the centre of the mosaic.
3. Data reduction
In a first step, bias and flatfield corrections were applied to all images from both telescopes through IRAF3 (Tody 1993). In addition, a bad pixel mask was applied to the WFI data only.
In a second step, astrometric and photometric measurements to all objects on the SOI and WFI images were obtained with the software PRAIA (Assafin 2006) to each CCD, individually. A mask to correct for the field distortion pattern (FDP) was previously applied to the WFI observations only. The mask itself, as well as procedures and data used to build it, are all described in Assafin et al. (2010). That paper is also based on WFI data and the respective observation dates are close to those shown here from this same imager. No FDP mask was used on the SOI images because no evidence was found to justify its use.
The UCAC3 (Zacharias et al. 2010) was released during the IAU General Assembly in Rio de Janeiro, Brazil, and is supposed to supersede the UCAC2. Our option for this latter as reference for astrometry, however, is based on the following three reasons: Roeser et al. (2010) reports problems in the proper motion system of the UCAC3; the UCAC2 was released in mid 2003 and since then has been widely used and analysed by a large number of works (up to date, more than 370 citations4); the observational data presented in Table 1 were almost all achieved and reduced before the release of the UCAC3.
3.1. Overlapping technique
Final positions to the targets listed in Table 1 were obtained by means of a global reduction procedure to combine all astrometric information from the individual CCDs associated to the observations of a given object with a given telescope. This procedure was discussed in detail by many authors (Eichhorn 1960; Googe et al. 1970; Benevides-Soares & Teixeira 1992; Teixeira et al. 1992, 1998)5, so that we will give only a brief description of the calculations made here.
The basic equation in right ascension (declination) to an individual CCD of a given mosaic is as follows:  (1)where
(1)where
 In Eq. (1), the unknowns are a, b, c, DXR, and the coefficients of PX,Y. This polynomial is an incomplete second degree one in the sense that it contains only the terms x2, xy, and y2. This choice was made after several tests involving polynomials up to the third degree.
In Eq. (1), the unknowns are a, b, c, DXR, and the coefficients of PX,Y. This polynomial is an incomplete second degree one in the sense that it contains only the terms x2, xy, and y2. This choice was made after several tests involving polynomials up to the third degree.
The unknown parameters are determined from a Gauss-Seidel iteration, where unknowns a, b, and c are determined by setting DXR and the coefficients of PX,Y equal to zero in the first run of the iteration. In the second run, DXR is determined from the updated values of a, b, and c. In the third run, the coefficients of PX,Y are determined from updated values of a, b, c, and DXR. The iteration is then implemented by going back to run one again with the updated values of DXR and PX,Y. This procedure was shown to be convergent (Benevides-Soares & Teixeira 1992). It should be noticed that the term DXR is the responsible for interchanging information through a given mosaic, because this correction is obtained from averaging positional information from stars that may be found in different CCDs.
The presence of the terms c and DXR in Eq. (1) gives rise to a rank deficiency, so that the results delivered by the iterations described above are just a particular solution of the problem. Strictly speaking, this rank deficiency reflects an origin indetermination so that a simple translation of the whole instrumental system, as obtained from the iterations decribed above, suffices to provide a general solution. One way to determine this translation is to elect a privileged group of stars (UCAC2 ones, for instance) and force the sum of their respective final (global) corrections DXR to be equal to zero.
Instead of a simple translation, however, we opted for a higher order polynomial to serve as boundary condition to the iterative process described above and to consequently derive the results shown in Table 1. This aimed at taking into account any remaining systematic trend of the residuals for the reference stars as a function of the position on the mosaic. For the WFI, a complete third degree polynomial was employed and a complete first degree polynomial for the SOI. In both cases, the respective coefficients were determined from an iterative process that eliminated at each iteration the reference star with the largest arc length between the observed and catalogue positions. This star was selected among those whose absolute value of the “observed minus calculated” (O–C) either in right ascension or in declination was greater than 100 mas.
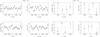 |
Fig. 1 Mean values of the differences in the sense O–C in right ascension and declination for the reference stars, as a function of the position on the whole acquired field as given by the overlapping images. Bins along the X and Y directions encompass an arc of 2.3′ for the WFI (left panels) and 1.8′ for the SOI (right panels). Each dot represents the mean of at least 100 points for the WFI and 9 points for the SOI. The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. In these plots, the targets are always found on X = Y = 0. |
4. Error budget
The positional accuracy of each of the observed targets was determined by taking into account three sources of uncertainty on their astrometric measurements: the FDP, the precision of the target position on the detector system, and the accuracy of the astrometric reference catalogue (UCAC2) as an optical extension of the ICRF. If we call σD the uncertainty from the FDP, σI the internal precision of the target (that is, the precision with which the position is measured within the detector system), and σE the accuracy that the optical reference catalogue materializes the coordinate axes of the ICRF, then the final uncertainty (at 1σ level) of the positions of the sources in Table 1 can be given by 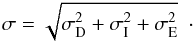 (2)These three quantities, σD, σI, and σE, are evaluated next.
(2)These three quantities, σD, σI, and σE, are evaluated next.
4.1. σ D
Figure 1 shows the differences, in the sense O–C, in right ascension and declination for the reference stars as a function of the position on both imagers. These differences indicate how well positions were corrected for the FDP. The results shown in this figure are typically smaller than 10 mas to the SOI and 5 mas to the WFI so that no systematic effects larger than these values, as a function of the position on a given imager, are to be expected. It is important to notice that the error bars in this figure are given by the standard deviation of the mean, and the similar size of the error bars comes from the uniformly distributed number of used reference stars over the mosaics. For the WFI, this feature would not be verified without an efficient FDP model. The value adopted to σD is 10 mas for both imagers.
4.2. σ I
Because each source had its position measured multiple times (see Table 2, last column), it is natural to obtain the internal precision of this position by means of Eq. (3) 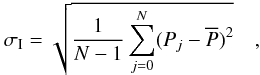 (3)where, to a given source, N is the total number of frames that contributed to the measurement of both its equatorial coordinates, Pj is one of its equatorial coordinates as measured from frame j, and
(3)where, to a given source, N is the total number of frames that contributed to the measurement of both its equatorial coordinates, Pj is one of its equatorial coordinates as measured from frame j, and 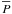 is the respective mean value of Pj, j = 1...N. The value of σI (or internal precision) of the observed sources is given by Table 1, Cols. 13 and 14, in right ascension and declination respectively.
is the respective mean value of Pj, j = 1...N. The value of σI (or internal precision) of the observed sources is given by Table 1, Cols. 13 and 14, in right ascension and declination respectively.
4.3. σ E
The accuracy of the UCAC2 as an optical representation of the ICRF can be directly obtained from Zacharias et al. (2010). From that paper, one finds that 20 mas is a good estimate of the systematic errors in the UCAC2 positions. Therefore, 20 mas is the adopted value of σE for all observed targets.
4.4. Quantifying significant offsets
As a consequence, the confidence level as given by Cols. 15 and 16 in Table 1 is 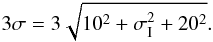 (4)We call offsets either in right ascension or declination as shown in Cols. 11 and 12 of Table 1 “significant offset”, those whose absolute values are higher than the respective 3σ level values (Eq. (4)) given by the last two columns of the same table.
(4)We call offsets either in right ascension or declination as shown in Cols. 11 and 12 of Table 1 “significant offset”, those whose absolute values are higher than the respective 3σ level values (Eq. (4)) given by the last two columns of the same table.
The uncertainties of the VLBI positions to the sources concerned here are smaller than 1 mas, which makes their contribution to the error budget negligible.
 |
Fig. 2 Mean values of the differences in the sense O–C in right ascension and declination for the reference stars as a function of the magnitude. Each dot represents the mean of at least 100 points in the case of the WFI (left panels) and 14 points in the case of the SOI (right panels). The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. The difference between the magnitudes of the points associated to a given dot do not exceed one. The corresponding magnitude in the X-axis is the respective mean magnitude. |
4.5. Further considerations on errors
The magnitudes of the reference stars used in this work are typically within the range 13.0 < R < 16.0. Figure 2 shows that systematic errors as a function of the magnitude are not expected for these stars. From Fig. 3 (four upper panels) one notices that the internal precision within this same range of magnitude is about 10 mas for the astrometric measurements from the WFI and about 5 mas for those from the SOI. On the other hand, Table 2 shows (Cols. 9 and 10) that the standard deviation of the differences between the observed and catalogue positions for the UCAC2 stars is on average 41 mas and 39 mas for the right ascension and declination respectively. Considering that the observed positions of the reference stars present no systematic effects as a function of the magnitude and that the FDP correction was conducted properly (Fig. 1), it is possible to conclude that the observed positions of the reference stars are more precise than their catalogue counterparts at the date of the observations studied here. This is reasonable considering the error propagation from the proper motions on the UCAC2 positions.
In this work, the SNR was constrained by an exposure time (see Table 2) that was supposed to not saturate the UCAC2 stars as from R ~ 13.5 to neither of the telescopes. This constraint is reflected in Fig. 3 (four upper panels), which shows the limiting best internal precision achieved by each imager as well as the magnitude from which this precision begins to degrade. This degradation is mostly a consequence of lower signal-to-noise ratios rather than effects on position caused by undersampling. Indeed, acquisition on a dither and/or offset basis of a number of images of both instruments renders the resulting averaged (see Sect. 3) positions less affected by pixel phase effects (see, for instance, Zacharias et al. (2004) for a brief characterization of the problem). This is strengthened by the results shown by the four lower panels of Fig. 3, from which no (or negligible) systematic effects on the observed positions as a function of the magnitude are expected.
Another source of systematic errors on positions is related to the differential chromatic refraction (DCR). Figure 4 shows the DRC on the positions from the WFI and SOI. The results shown in this figure were derived from the second step described in Sect. 3 and point out that the final positions of the reference stars as obtained from the overlapping technique do not (or only negligibly) depend on colour. Here, we used the J − Ks colour index. These near infrared magnitudes are from the 2MASS (Skrutskie et al. 2006) and were directly obtained from the UCAC2. They are considerably more precise than the visible magnitudes obtained from our observations or from the observations made by UCAC2.
We point out that the reference stars are mostly main-sequence objects and their average colour is different from that of the quasars (compare the range of colours shown in Fig. 4 to Col. 9 of Table 1 and also to the range of colours in Fig. 5).
Figure 5 plots the optical minus radio offsets in position of the observed sources as a function of the respective J − Ks colour indices. In this case, however, each dot in the figure represents the offset of a single source (instead of a mean offset). It is important to notice that Fig. 5 shows no evidence of increasing or decreasing trend of the offset values as a function of the colour index as one would expect (see, for instance, Zacharias et al. 2004; Ducourant et al. 2006). This feature agrees with the study presented by Stone (2002) and profited from the red filters used in the observations as well as the moderate zenith distances involved. In most cases, the observations were also performed not far from the local meridian (see Table 2, Cols. 7 and 8).
5. Discussion
From Table 1 one notices that four sources present significant offsets. They are 0237 − 233, 0430 + 052, 0440 − 003, and 0920 − 397. In Fig. 6 the angular distance (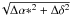 ) between the respective optical and VLBI positions of the observed sources is given as a function of the X-band structure index, where Δα ∗ and Δδ are given by Cols. 11 and 12 of Table 1. These four sources are indicated with a circle in Fig. 6. The other sources are indicated with a cross.
) between the respective optical and VLBI positions of the observed sources is given as a function of the X-band structure index, where Δα ∗ and Δδ are given by Cols. 11 and 12 of Table 1. These four sources are indicated with a circle in Fig. 6. The other sources are indicated with a cross.
 |
Fig. 3 Mean values of the internal precision to all objects (four upper panels) and mean values of the residuals from the iterative process (four lower panels) as described in Sect. 3 as a function of the magnitude. Each dot represents the mean of at least 13 000 points for the WFI (left panels) and 190 points for the SOI (right panels). The difference between the magnitudes of the points associated to a given dot do not exceed one. The corresponding magnitude in the X-axis is the respective mean magnitude. |
 |
Fig. 4 Mean values of the differences in position in the sense O–C to the reference stars as a function of the J − Ks colour index. Bins along the X-axis encompass an interval of 0.05 mag for the WFI (left panels) and 0.2 mag for the SOI (right panels). Each dot represents the mean of at least 12 points for the WFI and 13 points for the SOI. The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. |
Figure 6 also shows that the structure index 4 hosts the majority of the sources with significant offsets, which are indicated by a circle.
We can set a conservative average threshold of 80 mas from Cols. 15 and 16 in Table 1 from which optical to radio offsets are considered to be significant in this work. This value is higher than the positional accuracy of 60 mas presented by Assafin et al. (2010), from where candidate stars to be occulted by Pluto and its satellites were determined, also based on data obtained with the WFI and at dates close to those of the observations presented here. The analysis of the position of one of these candidates, as derived from a real occultation (Sicardy et al. 2011), gives support to that value of 60 mas. This reinforces that the levels of significance given by Cols. 15 and 16 in Table 1 are not overestimating the accuracy of the observed ICRF sources’ positions.
Assafin et al. (2003) report accurate optical positions of 172 ICRF sources using a preliminary version of the UCAC2 as astrometric reference. We selected from that paper all those sources with a significant optical minus radio positional offset with existing structure information in the BVID. By significant we mean an offset whose absolute value in either right ascension or declination is greater than 3σ , where σ was defined in Sect. 4 making σD equal to zero. Table 4 presents data about these sources. The structure indices of the sources shown in Table 4 are from the BVID and were selected by considering that the dates of the VLBI experiments should be closest to those of the optical observations given by Assafin et al. (2003).
 |
Fig. 5 Optical (observed) minus radio positions of the sources listed in Table 1 (both imagers) as a function of their J − Ks colour index (Col. 9 of the same table). The error bars are given by the two last columns of Table 1. For the sources 0743 − 673 and 0754 + 100 only the results from the WFI are considered. |
 |
Fig. 6 Angular distance (see Sect. 5) between the VLBI positions and the respective optical ones determined here as a function of the X-band structure index. Circles: sources where at least one of the offsets, Δα ∗ or Δδ (Table 1, Cols. 11 and 12), were significant (Table 1, Cols. 15 and 16 and Sect. 4). Crosses are given otherwise. |
Evidently, three sources of the seven shown in Table 4 have X-band structure indices of 3 or 4.
These mean epochs range from 1999 to 2001. Source 1548 + 056 has a mean epoch of observation of 2000.20 and an X-band structure index of 2 in 1997 and of 3 in 2005. In this context one could argue that four (instead of three) sources of the seven shown in Table 4 have X-band structure indices of 3 or 4.
Therefore, as far as those sources (Tables 1 and 4) with significant offsets are concerned, we can share the conclusions from Zacharias & Zacharias (2010)6: there is either a problem in the optical representation of the radio frame (case one) or we are dealing with a real offset between the optical and radio positions of the ICRF2 sources (case two).
5.1. First case
As mentioned above, a value of 20 mas was adopted for the systematic errors in the UCAC2, which also agrees with a previous estimate from an independent work (Assafin et al. 2003). If we trust this value, the significant offsets would then result mostly from systematic effects present in the Tycho-2 catalogue (Høg et al. 2000b,a), the astrometric reference for the UCAC series.
Systematic errors in positions and proper motions in the Tycho–2 were studied with the help of common stars with the Hipparcos (Perryman & ESA 1997) in cells of 6° × 6°. Høg et al. (2000a) show that these systematic errors are below 1 mas and 0.5 mas/yr, for positions and proper motions respectively, on angular scales of 6° × 6° or more. Interesting though, the field of view for the UCAC observations was of about 1° × 1°, much smaller than the areas used to check the Tycho–2 for systematic errors.
It is through catalogues like the UCAC2 that most of the astronomical community has access in optical wavelengths to the coordinate axes materialized by the ICRF. If it contains systematic errors, no matter the origin, this is clearly of great relevance. The errors could mimic a physical effect for instance, where it in fact does not exist.
5.2. Second case
On the other hand, Fig. 6 shows that significant offsets are most frequently associated with sources that have large (3 and 4) X-band structure indices. This is reinforced by the gof values presented in Table 1 and would suggest a case of a real non-coincidence between the optical and radio centres of the concerned sources.
Indeed, optical and radio positions may differ when the emission is not core-dominated (Daigne et al. 2003). Most of the radio flux emission is associated to non-thermal emission from jets, while the bulk of the optical emission is associated to the central engine7. This must imply a parsec scale separation between the two emitting regions. Adopting the Standard Model, this translates into a floor of sub mas angular distances (Feissel et al. 2000). Accordingly, Kovalev et al. (2008) estimate an average shift between the radio and optical cores of 0.1 mas from theoretical assumptions on the optical emission. This value is two to three orders of magnitude lower than the significant offsets shown in Tables 1 and 4. In this context, our results (and those of Table 4, to some extent) are relevant material to better understand the origin of optical emission in quasars.
The investigation of a larger number of sources would certainly help to decide which case most contributes to the significant offsets found here.
5.3. The time dependence of the structure index
Another factor is that the structure indices of the sources may change as a function of time and that not all sources were observed close to the dates when these indices were determined (see Tables 2 and 3). Table 3 reports data from the three most recent years of experiments obtained from the BVID (when available). Obviously, the time variation of these indices, as far as the sources studied here are concerned, typically do not exceed one. This is often true also when we consider dates older than those from the three most recent years in the BVID when they are available for the same experiments. One clear exception is the source 0440 − 003. A. Collioud (2011, pers. comm.) determined the continuous X-band structure index (Bourda et al. 2011) of this source and found the value of 1.83 for the experiment of 1995. This indicates, therefore, a variation from about 2 to 4, which is less pronounced than that of 1 to 4. In general, it is then reasonable to assume that the results shown in by Fig. 6 remain the same although observation dates are not always close to those of the respective VLBI experiments.
Results from Assafin et al. (2003).
5.4. Comments on individual sources
Source 0743 − 673 has its position given by both SOAR and ESO/MPG telescopes, where a difference of 43 mas and 30 mas is seen, respectively, between the right ascension and declination as determined from both instruments. The number of reference stars used to obtain the final position of this source from the ESO/MPG is 380, whereas only 8 were used to obtain the final position from the SOAR. It is just as well to remember that the area on the sky covered by the WFI is about 30 times that of the SOI. In this context, a possible important contribution for the above difference comes from the materialization of the celestial frame as given by two different sets of reference stars, the smallest one giving rise to statistical fluctuations.
Source 0754 + 100 was also observed by both telescopes. In this case, there are differences of 46 mas and 22 mas, respectively, between the right ascension and declination as determined from both instruments. The number of reference stars used to obtain the source’s position from the WFI (408) and that from the SOI (9) leads to the same rationale presented for 0743 − 673 to explain the differences. Furthermore, from the observations of 0754 + 100 made with SOI only, this source should appear in Fig. 6 as a circle. The results from the WFI, however, come from a much larger number of reference stars spread on a larger area of the sky. Therefore, we preferred the offsets and respective significance levels obtained from this last imager.
For both sources (0743 − 673 and 0754 + 100), the values of Δα ∗ and Δδ obtained from the positions given by the SOAR and the ESO/MPG telescopes are within their respective uncertainties at the 1σ level.
A well known strategy in astrometry, aimed at avoiding systematic errors in the determination of positions of celestial bodies, is to observe (and link) objects separated by large angles on the sky. This is by far not the case for any of the two imagers considered in this work. It is reasonable at least to expect that the larger the number of reference stars on the image, the better the celestial frame can be represented. A large number of reference stars was always available on the WFI frames, which is not verified for the SOI. This was not considered when we determined the significant thresholds (last two columns of Table 1) for the offsets of each source. The offsets obtained for sources 0743 − 673 and 0754 + 100 given by the SOI and the WFI, provide a rough indication of how different results can be. In any case, as mentioned above, these differences are within the uncertainties at the 1σ level.
6. Conclusion
We have determined accurate positions for 22 ICRF2 sources in optical wavelengths with the SOAR and the ESO/MPG telescopes. A conservative level of significance for the optical to radio offsets in position was determined for each source, as given by Table 1. Four sources presented significant offsets.
In our opinion, as also suggested by Zacharias & Zacharias (2010), these significant offsets indicate either a problem with the optical representation of the ICRF or a real offset between the respective optical and radio positions.
In the first case, the UCAC2 is directly addressed. Assuming that this catalogue represents the IAU’s celestial frame as materialized by the Tycho–2 catalogue within the claimed accuracy (see Zacharias et al. 2004, 2010), then it is the Tycho–2 that presents systematic errors.
In the second case, we can suppose that the results outlined by Fig. 6 are not just a coincidence and that significant optical to radio offsets in position are related to high (3 and 4) X-band structure indices. In this context, the results presented here would be of interest for studying the origin of optical emission in quasars.
Whatever the reason, the consequences are important. It is through catalogues like the UCAC2 that most of the astronomical community has access in optical wavelengths to the coordinate axes materialized by the ICRF. The existence of systematic errors may lead, for instance, to erroneous conclusions about the physics of a given object. On the other hand, assuming that the significant offsets found here are definitely connected to the X-band structure index, the relation between optical and radio frames in the future must consider spatially extended structure effects.
A larger number of accurate optical positions of reference frame sources would greatly help to pinpoint the reason for the results presented here.
The paper by Eichhorn (1960) is written in German and only the very enlightening English abstract is accessible to the author. However, in the context of the overlapping technique, this is an important reference and should not be omitted.
See Johnston et al. (2009) for a brief enumeration of potential sources of optical emission in quasars.
Acknowledgments
J.I.B.C., A.H.A., M.A. and R.V.M. acknowledge CNPq grants 151392/2005-6, 477943/2007-1, 478318/2007-3, 306028/2005-0, 304124/2007-9 and 307126/2006-4. J.I.B.C., M.A., and D.N.S.N. thank FAPERJ for grants E-26/170.686/2004, E-26/100.229/2008 and E-26/110.177/2009. A.H.A. acknowledges Marie Curie fellowship grant PIIF-GA-2009-236735. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This research has made use of the VizieR catalogue access tool, CDS, Strasbourg, France. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. The authors acknowledge the anonymous referee for fruitful discussions and suggestions.
References
- Andrei, A. H., Souchay, J., Zacharias, N., et al. 2009, A&A, 505, 385 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Arias, E. F., Charlot, P., Feissel, M., & Lestrade, J. 1995, A&A, 303, 604 [NASA ADS] [Google Scholar]
- Aslan, Z., Gumerov, R., Jin, W., et al. 2010, A&A, 510, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Assafin, M. 2006, Bull. Astron. Soc. Braz., 26, 189 [Google Scholar]
- Assafin, M., Zacharias, N., Rafferty, T. J., et al. 2003, AJ, 125, 2728 [NASA ADS] [CrossRef] [Google Scholar]
- Assafin, M., Nedelcu, D. A., Badescu, O., et al. 2007, A&A, 476, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Assafin, M., Camargo, J. I. B., Vieira Martins, R., et al. 2010, A&A, 515, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baade, D., Meisenheimer, K., Iwert, O., et al. 1999, The Messenger, 95, 15 [NASA ADS] [Google Scholar]
- Benevides-Soares, P., & Teixeira, R. 1992, A&A, 253, 307 [NASA ADS] [Google Scholar]
- Bourda, G., Charlot, P., & Le Campion, J. 2008, A&A, 490, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourda, G., Charlot, P., Porcas, R. W., & Garrington, S. T. 2010, A&A, 520, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourda, G., Collioud, A., Charlot, P., Porcas, R., & Garrington, S. 2011, A&A, 526, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Camargo, J. I. B., Daigne, G., Ducourant, C., & Charlot, P. 2005, A&A, 437, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Fey, A. L., Collioud, A., et al. 2008, in IAU Symp. ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 248, 344 [Google Scholar]
- da Silva Neto, D. N., Andrei, A. H., Vieira Martins, R., & Assafin, M. 2002, AJ, 124, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Daigne, G., Charlot, P., Ducourant, C., & Lestrade, J. 2003, Ap&SS, 286, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Ducourant, C., Le Campion, J. F., Rapaport, M., et al. 2006, A&A, 448, 1235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichhorn, H. 1960, Astron. Nachr., 285, 233 [Google Scholar]
- Feissel, M., & Mignard, F. 1998, A&A, 331, L33 [Google Scholar]
- Feissel, M., Gontier, A., & Eubanks, T. M. 2000, A&A, 359, 1201 [NASA ADS] [Google Scholar]
- Fey, A. L., & Charlot, P. 1997, ApJS, 111, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Fey, A. L., & Charlot, P. 2000, ApJS, 128, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Fey, A. L., Gordon, D., Jacobs, C. S., et al. 2009, IERS Technical Note, 35, 1 [Google Scholar]
- Fricke, W., Schwan, H., Lederle, T., et al. 1988, Veroeffentlichungen des Astronomischen Rechen-Instituts Heidelberg, 32, 1 [NASA ADS] [Google Scholar]
- Gontier, A., Le Bail, K., Feissel, M., & Eubanks, T. M. 2001, A&A, 375, 661 [Google Scholar]
- Googe, W. D., Eichhorn, H., & Luckac, C. F. 1970, MNRAS, 150, 35 [NASA ADS] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000a, A&A, 357, 367 [NASA ADS] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000b, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Johnston, K., Wehrle, A. E., Makarov, V., et al. 2009, in Astronomy, 2010, astro2010: The Astronomy and Astrophysics Decadal Survey, 143 [Google Scholar]
- Kovalev, Y. Y., Lobanov, A. P., Pushkarev, A. B., & Zensus, J. A. 2008, A&A, 483, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 29 [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, in IAU Symp. 248, ed. W. J. Jin, I. Platais, & M. A. C. Perryman, 217 [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 2002, in EAS Publications Series, ed. O. Bienayme, & C. Turon, 2, 327 [Google Scholar]
- Mignard, F. 2005a, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA Special Publication, 576, 5 [Google Scholar]
- Mignard, F. 2005b, in Journées 2004 – systèmes de référence spatio-temporels, ed. N. Capitaine, 196 [Google Scholar]
- Perryman, M. A. C. 2005, in The Three-Dimensional Universe with Gaia, ed. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 15 [Google Scholar]
- Perryman, M. A. C., & ESA, 1997, The HIPPARCOS and TYCHO catalogues, Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, H. E., Ashe, M. C., & Boccas, M. 2004, in SPIE 5492, ed. A. F. M. Moorwood, & M. Iye, 564 [Google Scholar]
- Sicardy, B., Bolt, G., Broughton, J., et al. 2011, AJ, 141, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, R. C. 2002, PASP, 114, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- Teixeira, R., Requieme, Y., Benevides-Soares, P., & Rapaport, M. 1992, A&A, 264, 307 [NASA ADS] [Google Scholar]
- Teixeira, R., Camargo, J. I. B., Benevides-Soares, P., & Requieme, Y. 1998, A&A, 333, 1107 [NASA ADS] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, ed. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 5252, 173 [Google Scholar]
- Turon, C., O’Flaherty, K. S., & Perryman, M. A. C. 2005, The Three-Dimensional Universe with Gaia, ESA SP, 576 [Google Scholar]
- Zacharias, M., & Zacharias, N. 2010, XXVII IAU-GA – Commission 8, homepage of the work – http://www.ast.cam.ac.uk/iau_comm8/iau27/ [Google Scholar]
- Zacharias, N., Urban, S. E., Zacharias, M. I., et al. 2004, AJ, 127, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
ICRF2 sources that were observed with WFI and SOI: physical characteristics and astrometric results.
ICRF2 sources that were observed with WFI and SOI: observational information and astrometric results.
All Figures
 |
Fig. 1 Mean values of the differences in the sense O–C in right ascension and declination for the reference stars, as a function of the position on the whole acquired field as given by the overlapping images. Bins along the X and Y directions encompass an arc of 2.3′ for the WFI (left panels) and 1.8′ for the SOI (right panels). Each dot represents the mean of at least 100 points for the WFI and 9 points for the SOI. The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. In these plots, the targets are always found on X = Y = 0. |
| In the text | |
 |
Fig. 2 Mean values of the differences in the sense O–C in right ascension and declination for the reference stars as a function of the magnitude. Each dot represents the mean of at least 100 points in the case of the WFI (left panels) and 14 points in the case of the SOI (right panels). The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. The difference between the magnitudes of the points associated to a given dot do not exceed one. The corresponding magnitude in the X-axis is the respective mean magnitude. |
| In the text | |
 |
Fig. 3 Mean values of the internal precision to all objects (four upper panels) and mean values of the residuals from the iterative process (four lower panels) as described in Sect. 3 as a function of the magnitude. Each dot represents the mean of at least 13 000 points for the WFI (left panels) and 190 points for the SOI (right panels). The difference between the magnitudes of the points associated to a given dot do not exceed one. The corresponding magnitude in the X-axis is the respective mean magnitude. |
| In the text | |
 |
Fig. 4 Mean values of the differences in position in the sense O–C to the reference stars as a function of the J − Ks colour index. Bins along the X-axis encompass an interval of 0.05 mag for the WFI (left panels) and 0.2 mag for the SOI (right panels). Each dot represents the mean of at least 12 points for the WFI and 13 points for the SOI. The error bars are standard deviations of the mean and are plotted 1σ above and below the corresponding dot. |
| In the text | |
 |
Fig. 5 Optical (observed) minus radio positions of the sources listed in Table 1 (both imagers) as a function of their J − Ks colour index (Col. 9 of the same table). The error bars are given by the two last columns of Table 1. For the sources 0743 − 673 and 0754 + 100 only the results from the WFI are considered. |
| In the text | |
 |
Fig. 6 Angular distance (see Sect. 5) between the VLBI positions and the respective optical ones determined here as a function of the X-band structure index. Circles: sources where at least one of the offsets, Δα ∗ or Δδ (Table 1, Cols. 11 and 12), were significant (Table 1, Cols. 15 and 16 and Sect. 4). Crosses are given otherwise. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


