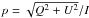| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014988 | |
| Published online | 22 July 2011 | |
The height of chromospheric loops in an emerging flux region
1 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Straße 2, Katlenburg-Lindau, Germany
e-mail: merenda@mps.mpg.de
2 School of Space Research, Kyung Hee University, Yongin, Gyeonggi, 446-701 Korea
Received: 14 May 2010
Accepted: 1 June 2011
Context. The chromospheric layer observable with the He i 10 830 Å triplet is strongly warped. The analysis of the magnetic morphology of this layer therefore requires a reliable technique to determine the height at which the He i absorption takes place.
Aims. The He i absorption signature connecting two pores of opposite polarity in an emerging flux region is investigated. This signature is suggestive of a loop system connecting the two pores. We aim to show that limits can be set on the height of this chromospheric loop system.
Methods. The increasing anisotropy in the illumination of a thin, magnetic structure intensifies the linear polarization signal observed in the He i triplet with height. This signal is altered by the Hanle effect. We apply an inversion technique incorporating the joint action of the Hanle and Zeeman effects, with the absorption layer height being one of the free parameters.
Results. The observed linear polarization signal can be explained only if the loop apex is higher than ≈ 5 Mm. Best agreement with the observations is achieved for a height of 6.3 Mm.
Conclusions. The strength of the linear polarization signal in the loop apex is inconsistent with the assumption of a He i absorption layer at a constant height level. The determined height supports the earlier conclusion that dark He 10 830 Å filaments in emerging flux regions trace emerging loops.
Key words: Sun: chromosphere / magnetic fields / polarization
© ESO, 2011
1. Introduction
The magnetic field is commonly measured in the solar photosphere, while measurements of the chromospheric and coronal field are rarer (see, e.g., Solanki et al. 2006 for an overview). Whereas photospheric magnetic field measurements dominantly employ the Zeeman effect, in higher layers of the solar atmosphere other methods come increasingly into play (see Lagg 2005 for a review), in particular also the Hanle effect. One of the most used diagnostics of the magnetic field in the upper chromosphere is the 10 830 Å He i multiplet. For this multiplet the Zeeman effect is sensitive to magnetic fields above ≈ 50 Gauss, well suited to study magnetic fields of active regions (e.g. Harvey & Hall 1971; Rüedi et al. 1995; Penn & Kuhn 1995). The Hanle effect is sensitive to weaker fields (1–100 Gauss) and has been used to measure the magnetic fields of prominences and spicules observed off-limb (e.g. Trujillo Bueno et al. 2005; Merenda et al. 2006) and of filaments and emerging flux regions observed on-disk (e.g. Trujillo Bueno et al. 2005; Lagg et al. 2004). Unlike the level of polarization produced by the Zeeman effect, the polarization produced by scattering and then modified by the Hanle effect (in both 90° and forward scattering) depends on the anisotropy of the radiation field exciting the scattering atoms.
This anisotropy increases with the height of the observed structure above the solar surface (Sahal-Brechot et al. 1977). Therefore, this effect can in principle be used to determine at what height in the chromosphere or corona the observed magnetic structures are located. Since the He i lines are optically thin in some locations, notably in the quite Sun (e.g. Giovanelli & Hall 1977), but optically thick at others, in particular in young active regions (Xu et al. 2010), its formation could vary considerably, making such an independent determination of the height an interesting addition to the diagnostic capabilities of the He multiplet.
Solanki et al. (2003) proposed an interpretation of spectropolarimetric observations of an emerging flux region based on the assumption that the He 10 830 Å line is formed along the freshly emerged magnetic field lines, which in this case reached ≈ 10 Mm. Recently, Judge (2009) has proposed a different interpretation of these observations according to which the magnetic field sampled by the observations is located in a thin layer at a constant height (≈2.4 Mm) near the top of the chromosphere. This controversy lends an even stronger need for an independent diagnostic of the height of the magnetic features sampled by the He i 10 830 triplet. In this paper we develop the height diagnostic further, first considering the influence of the height on the strength of the Stokes Q and U profiles. Then, exploiting the sensitivity of the Hanle effect to the height of the observed structure, we have analyzed again the data of May 13, 2003, in order to independently estimate the height to which these data refer to, particularly at the location interpreted by Solanki et al. (2003) to be the apex of the highest reconstructed loop.
In Sect. 2 we summarize the data we analyze in this paper and introduce the codes we use to synthesize and invert the Stokes profiles. In Sect. 3 we present results of a parameter study of the strength of the linear polarization signal. We also compare the observed with the theoretical profiles in order to fix a minimum height and perform inversions with HeLIx+, which allow the field strength, direction and the height to be determined.
2. Observational data and codes
2.1. Data
Spectropolarimetric maps of the emerging flux region NOAA 9451 were recorded on 13 May 2001 using the Tenerife Infrared Polarimeter (TIP, Martínez Pillet et al. 1999). The covered wavelength range contains the 10 830 Å multiplet. The active region was located near disk center at μ = cosΘ = 0.8. These observations have been analyzed in several papers (Solanki et al. 2003; Lagg et al. 2004, 2007) which emphasize different aspects of this rich data set. In the present paper we focus on one spatial pixel of the observed map situated in the central part of the active region (pixel x = 72, y = 43 of Fig. 1 in Lagg et al. 2004).
The Stokes profiles at this pixel are also displayed in Fig. 3 of Lagg et al. (2004). This point is within the area of few pixels where the Hanle effect in forward scattering is most prominent in the Stokes profiles. Around this area the linear polarization rapidly falls below the noise level. This pixel also displays the largest linear polarization signal in the entire map and, importantly, it corresponds to the apex of the highest loop reconstructed by Solanki et al. (2003). We refer to this pixel as the loop apex. It makes sense to concentrate on this loop-top pixel since it displays the largest discrepancy between the interpretations of Solanki et al. (2003) and Judge (2009) and the large linear polarization also makes this pixel the best location to demonstrate the new technique.
The degree of linear polarization reaches 0.45% of the continuum intensity in the center of the red component of the multiplet (see Fig. 3 of Lagg et al. 2004). The observed polarization is approximately parallel to the dark lines visible in the core of the red He i component which connect the footpoints of the reconstructed loop spanning the emerging flux region. These elongated absorption structures (see Fig. 1 of Solanki et al. 2003; Lagg et al. 2004) are reminiscent of Hα arch filament systems. The Stokes V signal in this region is comparable to the noise level of 10-3 of the continuum intensity. The surrounding pixels show similar Stokes spectra with slightly lower linear polarization signal, but enhanced circular polarization signal.
2.2. Synthesis code
The Hanle profiles observed on disk are produced by the presence of atomic polarization (i.e. population imbalances and quantum coherences between the magnetic sublevels pertaining to the upper and lower term of the 10 830 Å multiplet; i.e.  and
and 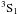 respectively), generated proportionally to the degree of anisotropy of the unpolarized radiation field coming from the underlying layers of the solar atmosphere. This atomic polarization, modified in the presence of a magnetic field by the Hanle effect in forward scattering (Trujillo Bueno et al. 2002), selectively absorbs and re-emits the unpolarized light coming from solar disk center, acting as sinks and sources of linear polarization.
respectively), generated proportionally to the degree of anisotropy of the unpolarized radiation field coming from the underlying layers of the solar atmosphere. This atomic polarization, modified in the presence of a magnetic field by the Hanle effect in forward scattering (Trujillo Bueno et al. 2002), selectively absorbs and re-emits the unpolarized light coming from solar disk center, acting as sinks and sources of linear polarization.
To reproduce these observed Hanle profiles we use a synthesis code with the same forward calculation module as described in Landi Degl’Innocenti (1982), Landi Degl’Innocenti & Landolfi (2004) and Asensio Ramos et al. (2008).
The helium absorption is modeled to take place in a constant-property slab located at a given height h above the solar surface and illuminated from the underlying solar photosphere. In this situation the degree of atomic polarization of the helium atoms is a function of (1) the anisotropic illumination that produces this population imbalance, and (2) the presence of a magnetic field that modifies it. In a plane parallel atmosphere the anisotropy of the radiation at a given λ depends basically on the height of the scattering atom.
In order to quantify the atomic polarization we solve the statistical equilibrium equations for the multipole components 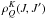 of the atomic density matrix for a multi-term atom. We take into account coherences between different J-levels (see Chap. 7 in Landi Degl’Innocenti & Landolfi 2004), the anisotropy of the radiation field for a given height (computed for the center-to-limb variation tabulated in Pierce 2000) and the presence of a magnetic field. Note that the sophistication with which the polarization produced by the Hanle effect is computed here is considerably greater than in the analysis of Solanki et al. (2003). From the calculated density matrix elements it is possible to compute the emission coefficients (ϵI,ϵX with X = Q,U,V) and the absorption coefficients (ηI,ηX) for polarized light. To calculate the emergent Stokes parameters we use the solution of the radiative equations for a slab of constant properties (see, e.g., Asensio Ramos et al. 2008) taken to lie in the upper chromosphere
of the atomic density matrix for a multi-term atom. We take into account coherences between different J-levels (see Chap. 7 in Landi Degl’Innocenti & Landolfi 2004), the anisotropy of the radiation field for a given height (computed for the center-to-limb variation tabulated in Pierce 2000) and the presence of a magnetic field. Note that the sophistication with which the polarization produced by the Hanle effect is computed here is considerably greater than in the analysis of Solanki et al. (2003). From the calculated density matrix elements it is possible to compute the emission coefficients (ϵI,ϵX with X = Q,U,V) and the absorption coefficients (ηI,ηX) for polarized light. To calculate the emergent Stokes parameters we use the solution of the radiative equations for a slab of constant properties (see, e.g., Asensio Ramos et al. 2008) taken to lie in the upper chromosphere ![\begin{eqnarray} I(\tau) &=& I_0 {\rm e}^{-\tau} + \frac{\epsilon_I}{\eta_I}\left(1 - {\rm e}^{-\tau}\right), \\[1.5mm] X(\tau) &=& X_0 {\rm e}^{-\tau} + \frac{\epsilon_X}{\eta_I}\left(1 - {\rm e}^{-\tau}\right) - \frac{\epsilon_I \eta_X}{\eta^2_I}\left(1 - {\rm e}^{-\tau}\right)\notag\\[1.5mm] && + \frac{\eta_X}{\eta_I}\tau {\rm e}^{-\tau} \left(\frac{\epsilon_I}{\eta_I}-I_0\right), \end{eqnarray}](/articles/aa/full_html/2011/08/aa14988-10/aa14988-10-eq25.png) where I0 and X0 are the boundary conditions representing the radiation entering the slab from below. We take I0 to be the photospheric continuum at μ = 0.8 as tabulated by Pierce (2000) and X0 = 0. This solution differs from the Milne-Eddington solution employed in earlier analysis of the observed Stokes profiles considered here. The slab geometry has the advantage that it allows a unique height to be assigned to the center of the absorption region. It may also be closer to the case of He i formation in an emerging flux region.
where I0 and X0 are the boundary conditions representing the radiation entering the slab from below. We take I0 to be the photospheric continuum at μ = 0.8 as tabulated by Pierce (2000) and X0 = 0. This solution differs from the Milne-Eddington solution employed in earlier analysis of the observed Stokes profiles considered here. The slab geometry has the advantage that it allows a unique height to be assigned to the center of the absorption region. It may also be closer to the case of He i formation in an emerging flux region.
 |
Fig. 1 Polarization diagrams computed for different heights above the solar surface (from 1 Mm in the leftmost frame to 9 Mm in the rightmost frame). In every diagram, the y-axis gives the degree of linear polarization |
2.3. Inversion code H eLIX+
The forward model described in the previous section is implemented in the inversion code HeLIx+ (Lagg et al. 2010). The free parameters of the constant-property slab model are the magnetic field strength, inclination and azimuth, B, γ and χ (in the solar reference frame), the line of sight velocity, vLOS, the damping parameter a, the thermal broadening of the line, vDopp, the optical thickness of the slab, d, and the height of the slab above the solar surface, h. Following the analysis of Solanki et al. (2003) we assume the filling factor to be unity. The Pikaia genetic algorithm (Charbonneau 1995) was used to maximize the fitness function f, defined as the reciprocal of the squared difference between the measured and the observed Stokes vector P (P = I, Q, U, or V) over a wavelength window of ( − 1.8, + 0.9) Å centered at the red lines of the He i triplet, divided by the strength s of the observed profiles (sI = ∑ λ|I(λ) − 1| and sQ,U,V = ∑ λ|(Q,U,V)(λ)|) and the number of free parameters Nfree: ![\begin{equation} \frac{1}{f} = \sum\limits_{P}\frac{1}{N_{\rm free}} \sum\limits_\lambda \frac{w_P(\lambda)}{s_P} \, \left[P_{\rm fit}(\lambda) - P_{\rm obs}(\lambda)\right]^2 \end{equation}](/articles/aa/full_html/2011/08/aa14988-10/aa14988-10-eq55.png) (3)The weighting functions wP were chosen to be unity within ± 0.6 Å around the core of the red component of the He i triplet, and was set to 0.6 outside this range. To take into account the reduction of the intensity level caused by the wings of the photospheric Si i at 10 827 Å we fit this line with a Voigt function. The parameters of this Voigt function are determined from an average of 100 Stokes I profiles centered around the loop apex.
(3)The weighting functions wP were chosen to be unity within ± 0.6 Å around the core of the red component of the He i triplet, and was set to 0.6 outside this range. To take into account the reduction of the intensity level caused by the wings of the photospheric Si i at 10 827 Å we fit this line with a Voigt function. The parameters of this Voigt function are determined from an average of 100 Stokes I profiles centered around the loop apex.
In extensive tests we found the Pikaia algorithm to be the most reliable technique to determine the global minimum within the considered parameter space independently of the choice of the initial guess values. Additionally, the random walk convergence of the Pikaia algorithm allows for a comprehensive error analysis in a statistical sense. The fluctuation of the retrieved parameters for individual, independent inversions of the same Stokes vector naturally delivers a measure for the reliability and robustness of the retrieved parameters.
 |
Fig. 2 Observed Stokes U/Ic profile (points) of Fig. 3 of Lagg et al. (2004) compared with the maximum U/Ic profiles computed for each height (solid line). At each height the observed and computed profile is plotted vs. λ. The same observed profile is repeated for comparison at each height. The computed Stokes I profile (not shown here) fits the observed intensity. The reference direction for positive Stokes Q forms an angle 12° with the nearest solar limb. This reference direction gives Q/Ic ≈ 0. The horizontal bar indicates the wavelength range, 10827.9–10831.6 Å of the leftmost profile. |
3. Results
We have performed computations with both codes introduced in Sects. 2.2 and 2.3. These computations have different aims. In a first step, described in Sect. 3.1, we obtain an idea of the dependence of the linear polarization in the He i triplet on the components of the magnetic vector and the height of the slab. Then, in Sect. 3.2 we test whether this technique can be employed to set lower or upper limits on the height of the scattering atoms by comparing with a given observed profile. Finally, in Sect. 3.3, we obtain a best estimate of the height of the sampled field using an inversion technique.
3.1. Dependence of the computed polarization on height and magnetic field
The way in which the presence of a magnetic field modifies the emitted polarization signal depends on its direction and on the position of the observed point on the solar disk. For example, off-limb linear polarization emission is maximum in the absence of a magnetic field, or for a vertical magnetic field (with respect to the solar surface). Its value decreases for increasingly horizontal magnetic fields. For observations at solar disk center, on the contrary, the He atoms do not emit linear polarization in the absence of a magnetic field or for a vertical magnetic field. Here the intensity of linearly polarized radiation increases for increasingly horizontal magnetic fields. For observations at other locations of the solar disk a behavior somewhere in between these two extremes is present. Figure 1 displays the results of an extensive parameter survey, which aims to determine the dependence of properties of the linear polarization on the parameters of the magnetic vector and the height of the slab. The computed examples refer to μ = 0.8, which corresponds to the location of NOAA 9451 at the time it was observed in He i. Each dot represents the degree of linear polarization  plotted versus the polarization angle α = 0.5 tan-1(U/Q) (both at the λ of maximum p) for profiles computed for all possible orientations of the magnetic field. The inclination angle with respect to the local solar vertical, θB, is varied from 0° to 180° in steps of 2° (θB = 0° for a magnetic field vector pointing outward from the Sun) and the azimuth angle in the plane parallel to the solar surface, χB, is varied from −90° to 90° in steps of 4° (χB = 0° for a magnetic field vector lying in the plane of the local solar vertical and the observer direction). At every distance above the solar surface there is a maximum polarization, corresponding to “vertical” magnetic fields (less inclined than Van Vleck’s angle 54.7° to the solar surface normal, red points in the figure). This maximum increases with height. The same increase occurs for the “horizontal” field (more inclined than Van Vleck’s angle, black points in the figure), although in this case the maximum reached is lower. Note that irrespective of the height there is no minimum polarization. This behavior implies that for a given measured linear polarization magnitude a lower limit on the height of scattering atoms can be placed, but no upper limit (just based on the degree of linear polarization). Furthermore, this lower limit is higher for a horizontal magnetic field than for a vertical field.
plotted versus the polarization angle α = 0.5 tan-1(U/Q) (both at the λ of maximum p) for profiles computed for all possible orientations of the magnetic field. The inclination angle with respect to the local solar vertical, θB, is varied from 0° to 180° in steps of 2° (θB = 0° for a magnetic field vector pointing outward from the Sun) and the azimuth angle in the plane parallel to the solar surface, χB, is varied from −90° to 90° in steps of 4° (χB = 0° for a magnetic field vector lying in the plane of the local solar vertical and the observer direction). At every distance above the solar surface there is a maximum polarization, corresponding to “vertical” magnetic fields (less inclined than Van Vleck’s angle 54.7° to the solar surface normal, red points in the figure). This maximum increases with height. The same increase occurs for the “horizontal” field (more inclined than Van Vleck’s angle, black points in the figure), although in this case the maximum reached is lower. Note that irrespective of the height there is no minimum polarization. This behavior implies that for a given measured linear polarization magnitude a lower limit on the height of scattering atoms can be placed, but no upper limit (just based on the degree of linear polarization). Furthermore, this lower limit is higher for a horizontal magnetic field than for a vertical field.
3.2. Comparing observed with synthetic profiles for different heights
In Fig. 2 we compare the linear polarization profile of Fig. 3 of Lagg et al. (2004), pixel x = 72, y = 43 in their Fig. 1, (points) with the computed profile displaying the maximum linear polarization for a set of heights between 1 and 10 Mm above the solar surface. Each solid profile is plotted versus wavelength and corresponds to the height given on the horizontal axis. Each synthetic profile is the one showing the largest U/Ic among all profiles in the “horizontal” range, i.e., more inclined to the vertical than 54.7°, formed at that height (for both synthetic and observed profile the reference direction for positive Stokes Q form an angle of 12° with the nearest solar limb, resulting in Q/Ic ≈ 0). The requirement that the magnetic field is in the “horizontal” range is driven by the fact that the Stokes V signal is comparable to the noise level. Additionally, the Stokes V spectra along the loop structure change polarity close to the loop apex. It is also consistent with the finding of Solanki et al. (2003) that this location corresponds to the top of a loop. Clearly, for heights lower than 5 Mm the anisotropy of the radiation field that excites the helium atoms is not able to produce sufficient atomic polarization to reproduce the observed U profile. In particular, a slab at a constant height of 2.4 Mm, as proposed by Judge (2009), does not provide a satisfactory description, since even the strongest U profile from that slab fails to achieve the polarization level of the observed profile. It falls well short of the polarization in the 5 most strongly polarized points of the observed profile.
3.3. Results of inversions
We carried out a series of inversions (see Sect. 2.3 for a description of the code and setup) in order to determine the atmospheric parameters which best describe the observed Stokes profiles shown in Fig. 3 of Lagg et al. (2004). The minimization technique used for the inversions with HeLIx+ involves the genetic algorithm PIKAIA (Charbonneau 1995). This algorithm has the advantage of finding the global minimum (i.e. the synthetic Stokes profile best matching the observed one) within the considered parameter space completely independent of any initial guess values. However, the path of convergence to this global minimum is random and may require an infinite number of iterations. To overcome this problem we repeated the inversions 100 times, each with a sufficiently high number of iterations (n = 500). The result of the inversion run with the best fitness out of the 100 independent runs was considered to be the solution closest to the global minimum.
 |
Fig. 3 Best fitness out of 100 individual inversion runs for fixed height values from 0.7 Mm to 17.5 Mm. The optimum fit to the observed Stokes vector is achieved for a height of the He slab of ≈ 6.3 Mm. The diamond and the rectangular symbol indicate the fitness at a height of 2.4 Mm and 10.5 Mm. |
Ranges for the atmospheric parameters.
The allowed range for the values of the the atmospheric parameters for the individual inversion runs is presented in Table 1. These ranges represent a carefully selected compromise between, on the one hand, stability and speed of the inversions and, on the other hand, the full coverage of expected values for the atmospheric parameters at the loop top. We carried out 100 independent inversion runs on the loop top pixel for each fixed He slab height ranging from 0.7 Mm to 17.5 Mm. The best fitness of the 100 inversions at each height is plotted as a function of height in Fig. 3. The figure clearly shows that a global maximum of the fitness is achieved for a height of the He slab at the loop top of ≈ 6.3 Mm. Note that a higher fitness corresponds to a better fit. The smoothness of the maximum fitness curve in Fig. 3 indicates that even relatively small fitness differences are significant. The fitness at the height of 2.4 Mm, proposed by Judge (2009) is marked in Fig. 3 by a diamond. It is significantly lower than the best fitness. Additionally we marked the fitness corresponding to height of 10.5 Mm as retrieved by Solanki et al. (2003).
Figure 4 shows the fit obtained from the best inversion run for a slab centered on a height of 6.3 Mm. Lower height values fail to produce a sufficiently strong linear polarization signal. If the absorbing helium slab is located higher than 6.3 Mm, the linear polarization signal resulting from scattering would be larger than the observed one. The inversion procedure compensates these strong signal by increasing the magnetic field strength, since a stronger magnetic field leads to depolarization of the scattering polarization. However, with increasing magnetic field strength the Zeeman signal increases, resulting in a mismatch for the Stokes V signal and consequently in a reduction of the fitness. The atmospheric parameters from the best inversion run are displayed in the fourth column of Table 1. The magnetic field strength at the loop top is 311 G, the field is nearly parallel to the solar surface (inclination angle γ = 95°), and the azimuth angle confirms the orientation of the field along the visible structures in the He equivalent width image in Fig. 1 of Solanki et al. (2003). The up-flow of 1.3 km s-1 at the loop top confirms the rising flux tube scenario presented in that paper.
 |
Fig. 4 The observed Stokes profile analyzed in this paper (solid black curves; left vertical scale; same reference direction as Fig. 2). The horizontal dashed line in the top panel corresponds to the adopted continuum level. Also plotted (red solid lines) are best fit profiles for a height of 6.3 Mm, obtained for a magnetic field of 320 G, with an inclination of 95° with respect to the local solar vertical, and an azimuth of − 86° (see Sect. 3.3). |
The simpler analysis of Solanki et al. (2003) provided a field strength that dropped to around 50 G at the loop apex, while here we obtain 320 G. The higher value lies considerably closer to the field strength that Wiegelmann et al. (2005) retrieved at the apex of the loops closest to the one whose apex we study in this paper using a force-free extrapolation from the photospheric magnetic field map (305–615 G). This illustrates the importance of using the more realistic treatment of the Hanle effect employed here compared to that employed by Solanki et al. (2003) and Lagg et al. (2004).
We also have inverted the few pixels showing linear polarization located near this one, finding comparable values of magnetic field and slightly lower heights, consistently with the fact that the pixel discussed here in detail was located at the loop apex.
4. Discussion and conclusions
We have shown that an analysis of the linear polarization of the He i 10 830 Å triplet using an atomic polarization interpretation can be used to estimate the height at which the triplet is formed and hence the height at which it samples the local magnetic and velocity field. Lower limits on this height are more straightforward to obtain than upper limits. Because the lower limit is tighter for larger polarizations, this technique works best for profiles displaying large-amplitude Hanle-like Q or U signals.
Solanki et al. (2003) have proposed a reconstruction technique to obtain the 3D magnetic field structure of an emerging flux region observed near the disk center. This technique is based on the assumption that the He 10 830 Å line is formed along the magnetic flux tube as it emerges through the chromosphere into the corona. The reconstruction was constrained by requiring the physical quantities in the loops to be smoothly varying and for both footpoints of the loops to lie at the same height. They found that the tallest reconstructed loop reached in its central part a height of ≈ 10 Mm over the solar surface. Recently Judge (2009) has proposed an alternative interpretation of this observation. He argues that the observed magnetic fields are located in a thin layer at a constant height ( ≈ 2.4 Mm) at the top of the basically plane-parallel chromosphere.
In the present paper we have analyzed the most critical pixel in the observation of Solanki et al. (2003), namely that at the apex of the highest loop, with the help of HeLIx+, an inversion code incorporating both Hanle and Zeeman effects. We found the best inversion fit for an height of ≈ 6.3 Mm. This value is lower that the value found by Solanki et al. (2003), but the inversions favor the interpretation of the 3D loop reconstruction of Solanki et al. (2003) over the interpretation proposed by Judge (2009) because the fitness of the results (a measure of the goodness of the fit) displays an asymmetric behavior, dropping rapidly towards lower heights, but comparatively gently towards greater heights.
Further support for the above conclusion is provided by an inversion using HeLIx+ of a profile at the apex of emerging loops in AR NOAA 10917 presented by Xu et al. (2010). For that active region the inversion including atomic polarization returns a height of 7.1 ± 2″ (5.0 ± 1.4 Mm), which is not only higher than the formation height of 2.4 Mm favored by Judge (2009), but also higher than the reconstructed looptops at 4 Mm. Consequently, there is some discrepancy between the heights obtained from magnetic field reconstructions and from the Hanle effect, but in the two cases studied so far the difference has opposite sign, which suggest that it is due to statistical errors. From the present analysis we cannot judge if the error is larger in the heights of the reconstructed loops or in the heights deduced from the Hanle effect. In both studied cases, however, the height deduced from the Hanle effect is higher than that proposed by Judge (2009).
The interpretation put forward by Judge (2009) is probably valid in the quiet Sun, where under “normal conditions” the He i 10 830 Å multiplet tends to form in a thin layer at the top of the chromosphere. As Judge himself pointed out, the He triplet is formed over “a broad distribution of heights owing to the corrugated nature of the chromosphere”. An example of a structure in which He i 10 830 forms well above its quiet Sun formation level are filaments or prominences. Thus, in prominences He 10 830 Å has been observed up to several tens of Mm above the limb. The reason is the much higher density of material at chromospheric temperatures inside prominences and filaments than in the surrounding corona. The density is sufficient to make the line optically thick. Our result suggests that the line forms at much greater heights than usual in an EFR, just as it does in filaments. Young, recently emerged loops in EFR, are often referred to as arch filament systems (AFS) when observed in Hα (see, e.g., the review by Chou 1993) due to their arch-like shape and their high density of chromospheric material, which leads to enhanced absorption, giving them a filament-like appearance. The He triplet similarly displays enhanced absorption in both EFRs studied to date, displaying dark filaments that look very similar to the ones seen in Hα (Xu et al. 2010). These dark filaments lie parallel to the magnetic field azimuth and are the locations at which loops can be reconstructed. They do not show interruptions or inhomogeneities along their long axes as one would expect in the interpretation favoured by Judge, but rather a smooth change in brightness. The chromospheric magnetic field changes equally smoothly along these filaments, in stark contrast to the photospheric field, which displays a very much higher level of inhomogeneity, including the presence of opposite polarities below the loop tops (see Fig. 1 of Solanki et al.2003; Fig. 5 of Xu et al.2010). Thus, the magnetic field structure in an EFR is rather different from the simple potential field model used by Judge (2009), in which the photospheric and chromospheric fields are basically identical. These points also favor the interpretation of Solanki et al. (2003) and lend support to the reconstructed loops.
Finally, in his paper Judge (2009) did not put any emphasis on the fact that the 3-D structure of the reconstructed loops agrees rather well with a non-linear force-free (NLFF) extrapolation starting from a map of the photospheric vector magnetic field. This was derived from an independent inversion of simultaneously recorded spectropolarimetric measurements of the photospheric Si i 10 827 Å line. Since NLFF extrapolations have no free parameter and take into account electric currents, this agreement is quite remarkable. Interestingly the work of Wiegelmann et al. (2005) also showed that a potential field is a very poor representation of the chromospheric field, giving a completely different azimuth. Hence, even if ignoring the problem that photospheric magnetic structure is far more complex than the chromospheric one, it is unclear if conclusions based on a (extremely simple) potential field computation (Judge 2009) have any validity for AR 9451.
In summary, a state-of-art treatment of the Hanle effect suggests that the interpretation of Solanki et al. (2003) is to be preferred over that of Judge (2009). More importantly, this paper has demonstrated the value of treating the Hanle effect more completely than the simple approximation employed by Solanki et al. (2003). This more complete treatment leads not only to the possibility of estimating the height of formation of the He triplet, but also results in improved retrieved values of the magnetic vector. The effect of the height on the line profiles is rather small, however, and thus requires observations with extremely low noise levels.
Acknowledgments
We thank E. Landi Degl’Innocenti for helpful discussions, and P. Judge for his comments on the manuscript. This work was supported by the EU through the EC FP7 Marie-Curie European Reintegration Grant (contract no. MERG-CT-2007-211048, “ChroMag”). This work was partly supported by the WCU grant No. R31-10016 of the Korean Ministry of Education, Science and Technology.
References
- Asensio Ramos, A., Trujillo Bueno, J., & Landi Degl’Innocenti, E. 2008, ApJ, 683, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Chou, D.-Y. 1993, in The Magnetic and Velocity Fields of Solar Active Regions, ed. H. Zirin, G. Ai, & H. Wang, IAU Colloq., 141, ASP Conf. Ser., 46, 471 [Google Scholar]
- Giovanelli, R. G., & Hall, D. 1977, Sol. Phys., 52, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J., & Hall, D. 1971, in Solar Magnetic Fields, ed. R. Howard, IAU Symp., 43, 279 [NASA ADS] [Google Scholar]
- Judge, P. G. 2009, A&A, 493, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A. 2005, in Chromospheric and Coronal Magnetic Fields, ed. D. E. Innes, A. Lagg, & S. A. Solanki, ESA SP, 596 [Google Scholar]
- Lagg, A., Woch, J., Krupp, N., & Solanki, S. K. 2004, A&A, 414, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Woch, J., Solanki, S. K., & Krupp, N. 2007, A&A, 462, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagg, A., Ishikawa, R., Merenda, L., et al. 2010, in ASP Conf. Ser. 415, ed. M. Cheung, B. Lites, T. Magara, J. Mariska, & K. Reeves, 327 [Google Scholar]
- Landi Degl’Innocenti, E. 1982, Sol. Phys., 79, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophys. Space Sci. Lib., 307 [Google Scholar]
- Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, ed. T. R. Rimmele, K. S. Balasubramaniam, & R. R. Radick, ASP Conf. Ser., 183, 264 [Google Scholar]
- Merenda, L., Trujillo Bueno, J., Landi Degl’Innocenti, E., & Collados, M. 2006, ApJ, 642, 554 [Google Scholar]
- Penn, M. J., & Kuhn, J. R. 1995, ApJ, 441, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Pierce, K. 2000, in Allen’s Astrophysical Quantities, ed. A. N. Cox (Springer) [Google Scholar]
- Rüedi, I., Solanki, S. K., & Livingston, W. C. 1995, A&A, 293, 252 [NASA ADS] [Google Scholar]
- Sahal-Brechot, S., Bommier, V., & Leroy, J. L. 1977, A&A, 59, 223 [NASA ADS] [Google Scholar]
- Solanki, S. K., Lagg, A., Woch, J., Krupp, N., & Collados, M. 2003, Nature, 425, 692 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Solanki, S. K., Inhester, B., & Schüssler, M. 2006, Rep. Prog. Phys., 69, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Landi Degl’Innocenti, E., Collados, M., Merenda, L., & Manso Sainz, R. 2002, Nature, 415, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Trujillo Bueno, J., Merenda, L., Centeno, R., Collados, M., & Landi Degl’Innocenti, E. 2005, ApJ, 619, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Lagg, A., Solanki, S. K., Inhester, B., & Woch, J. 2005, A&A, 433, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, Z., Lagg, A., & Solanki, S. K. 2010, A&A, 520, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Polarization diagrams computed for different heights above the solar surface (from 1 Mm in the leftmost frame to 9 Mm in the rightmost frame). In every diagram, the y-axis gives the degree of linear polarization |
| In the text | |
 |
Fig. 2 Observed Stokes U/Ic profile (points) of Fig. 3 of Lagg et al. (2004) compared with the maximum U/Ic profiles computed for each height (solid line). At each height the observed and computed profile is plotted vs. λ. The same observed profile is repeated for comparison at each height. The computed Stokes I profile (not shown here) fits the observed intensity. The reference direction for positive Stokes Q forms an angle 12° with the nearest solar limb. This reference direction gives Q/Ic ≈ 0. The horizontal bar indicates the wavelength range, 10827.9–10831.6 Å of the leftmost profile. |
| In the text | |
 |
Fig. 3 Best fitness out of 100 individual inversion runs for fixed height values from 0.7 Mm to 17.5 Mm. The optimum fit to the observed Stokes vector is achieved for a height of the He slab of ≈ 6.3 Mm. The diamond and the rectangular symbol indicate the fitness at a height of 2.4 Mm and 10.5 Mm. |
| In the text | |
 |
Fig. 4 The observed Stokes profile analyzed in this paper (solid black curves; left vertical scale; same reference direction as Fig. 2). The horizontal dashed line in the top panel corresponds to the adopted continuum level. Also plotted (red solid lines) are best fit profiles for a height of 6.3 Mm, obtained for a magnetic field of 320 G, with an inclination of 95° with respect to the local solar vertical, and an azimuth of − 86° (see Sect. 3.3). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.