EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 531 (July 2011) A&A, 531 (2011) L20 Full HTML
Free Access
Issue
A&A
Volume 531, July 2011
Article Number L20
Number of page(s) 5
Section Letters
DOI https://doi.org/10.1051/0004-6361/201117261
Published online 08 July 2011

© ESO, 2011

1. Introduction

Before the CoRoT mission, the B1.5 II-III star V1449 Aql (=HD 180642) was known as a β   Cephei pulsator with a high-amplitude radial mode of frequency 5.487 d-1 (Waelkens et al. 1998). White light photometry from space revealed the rich frequency spectrum of this target (Degroote et al. 2009) with the first detection of solar-like oscillations in a massive star (Belkacem et al. 2009). Additional ground-based, multi-colour photometry and high-resolution spectroscopy were used to put constraints on the atmospheric parameters and the chemical abundances, and to identify three modes of low amplitudes (Briquet et al. 2009). Notably, the dominant mode does not behave sinusoidally, and the first velocity moment  ⟨ v1 ⟩  has a peak-to-peak amplitude of about 90 km s-1. This is the third largest peak-to-peak radial-velocity amplitude measured among β   Cephei stars, after BW Vul (e.g. Crowe & Gillet 1989) and σ Sco (Mathias et al. 1991). A detailed NLTE abundance analysis showed a nitrogen excess of  ~0.3 dex with respect to the average nitrogen abundance in B-type stars in the solar neighbourhood. Previous abundance studies of hot stars indicate that the appearance of such an excess may be linked to the presence of a magnetic field (e.g., Morel et al. 2006; 2008; Przybilla & Nieva 2010).

The first spectropolarimetric observations of V1449 Aql were obtained with the multi-mode instrument FORS 1 at the VLT on two consecutive nights in 2007 and revealed a change in polarity from one night to the next and the presence of a weak magnetic field on the second night of observations (Hubrig et al. 2009). In the present work we discuss 13 new spectropolarimetric observations acquired during the last two years at the 2.56 m Nordic Optical Telescope using the SOFIN echelle spectrograph. The new longitudinal magnetic field measurements are used to determine the stellar rotation period and to put constraints on the magnetic field geometry.

2. Magnetic field measurements and period determination

Multi-epoch series of polarimetric spectra of V1449 Aql with S/N ≥ 200 were obtained with the low-resolution camera (R = λ/Δλ ≈ 30   000) of the high-resolution echelle spectrograph SOFIN (Tuominen et al. 1999) mounted at the Cassegrain focus of the Nordic Optical Telescope (NOT) in 2009 August–September and in 2010 July. We used a 2 K Loral CCD detector to register 40 echelle orders partially covering the range from 3500 to 10 000 Å with a length of the spectral orders of about 140 Å at 5500 Å. Two exposures with the quarter-wave plate angles separated by 90° are necessary to derive circularly polarized spectra. The spectra are reduced with the 4A software package (Ilyin 2000). Wavelength shifts between the right- and left-hand side circularly polarized spectra were interpreted in terms of a longitudinal magnetic field ⟨Bz⟩, using the moment technique described by Mathys (1994).

Table 1

Magnetic field measurements of V1449 Aql with SOFIN.

The magnetic field measurements with SOFIN and FORS 1 are presented in Table 1. In the first column we list the heliocentric Julian dates for the middle of the spectropolarimetric observations. The phases of the measurements of the magnetic field are shown in Col. 2, and in Col. 3 we present the mean longitudinal magnetic field ⟨Bz⟩. An example of Stokes I and Stokes V profiles of N ii in the wavelength region λλ 4775–4800 is presented in Fig. A.1.

thumbnail Fig. 1

The periodogram of V1449 Aql built from the longitudinal magnetic field measurements with the most prominent frequency at f = 0.0720 d-1, corresponding to a period of 13.893 days. The lower thin line presents the window function.

thumbnail Fig. 2

Phase diagram with the best sinusoidal fit for the longitudinal magnetic field measurements with a reduced χ2 = 0.46. The residuals (Observed – Calculated) are shown in the lower panel. The two FORS 1 measurements appear in green.

The frequency analysis was performed on the 13 SOFIN longitudinal magnetic field measurements and two previous FORS 1 measurements using a non-linear least-squares fit of the multiple harmonics utilising the Levenberg-Marquardt method (Press et al. 1992) with an optional possibility of pre-whitening the trial harmonics. To detect the most probable period, we calculated the frequency spectrum and for each trial frequency we performed a statistical F-test of the null hypothesis for the absence of periodicity (Seber 1977). The resulting periodogram displays three dominant peaks with the highest peak at f = 0.0720 d-1 corresponding to a period P = 13ḍ893. In the framework of the rigid rotator model usually assumed for magnetic stars on the upper main-sequence, the period of the magnetic field variation corresponds to the stellar rotation period. In Fig. 1 we show that two lower peaks appear at f = 0.069162 d-1 and f = 0.059689 d-1 with equivalent periods of P = 14ḍ459 and P = 16ḍ753, respectively. Since two measurements in our data set were obtained with the low-resolution FORS 1 spectrograph, we carried out a few tests to evaluate the significance of these measurements for the period determination. We find that omitting the FORS 1 measurements from the period search leads to the dominance of a frequency peak corresponding to a period of 14ḍ496. On the other hand, the period search without weighting tied to the measurement accuracies leads to a much stronger dominance of the frequency peak f = 0.0720 d-1 with the equivalent period of P = 13ḍ893. The referee of this paper informed us that his implementation of a CLEAN analysis leads to a detection of the same periods, but favors the period of P = 14ḍ459. These results show that the periodicity determination may depend on the technique used and that the relevance of the frequencies f = 0.069162 d-1 and f = 0.059689 d-1 is difficult to ascertain at the present stage without additional magnetic data. The derived ephemeris for the detected period corresponding to the highest frequency peak is 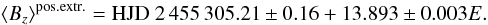(1)The phase diagram of the magnetic field measurements for the determined period is presented in Fig. 2.

thumbnail Fig. 3

Variability of the output spectra in two SOFIN subexposures taken with the quarter-wave plate angles separated by 90° taken around HJD 2 455 398.530. The lower two spectra, (I + V)0 and (I − V)0, correspond to the first subexposure, while the upper spectra, (I − V)90 and (I + V)90, correspond to the second subexposure. The strong effect of pulsations on the line profile shapes and the line positions is clearly visible between the spectra of the first subexposure with a duration of 20 min and the spectra of the second subexposure with the same duration.

The measurements of the longitudinal magnetic field in V1449 Aql require, however, special care in treating the data, as the timescale of a complete single observation of the length of  ~ 40 min with SOFIN, including two subexposures, is comparable to the timescale of the pulsation variability. As we mention above, two subexposures with the quarter-wave plate angles separated by 90° are needed to derive circularly polarized spectra. To remove the instrumental effects of small misalignments, differences in transmission, etc., the complete observation of a star usually consists of at least two successive subexposures with the waveplate rotated by 90° to exchange the positions of the two spectra on the CCD. The final Stokes I and V spectra are then calculated from the polarized spectra by taking the respective averages. To obtain Stokes I, the two average corresponding spectra, in our case the average of (I + V)0 and (I + V)90 are added with the average of (I − V)0 and (I − V)90, while Stokes V is calculated from the difference of the two spectra, the average of (I + V)0 and (I + V)90 and of (I − V)0 and (I − V)90. However, owing to very strong changes in the line profile positions and shapes in the strongly pulsating V1449 Aql, the method of using respective average spectra would lead to erroneous wavelength shifts and thus to wrong values of the longitudinal magnetic field. The behaviour of all four spectra in both subexposures taken around HJD 2 455 398.530 is illustrated in Fig. 3. To remedy this situation, we decided to carry out the measurements of the line shifts between the spectra (I + V)0 and (I − V)0 in the first subexposure and the spectra (I − V)90 and (I + V)90 in the second subexposure separately. The final longitudinal magnetic field value was then calculated as an average of the measurements for each subexposure.

thumbnail Fig. 4

Time series of FEROS spectra showing pulsational line profile variability in the spectral region 4590–4615 Å. The pulsation phase zero is at the bottom.

thumbnail Fig. 5

Velocity moments of line profiles: equivalent width (m0), radial velocity (m1), line width (m2), asymmetry (m3), and kurtosis (m4). In each panel five curves are plotted corresponding to five spectral lines of various elements: He i 4713.1, C ii 5133.1, N ii 5667.6, O ii 4592.0, and Si iii 4553.6, shown from bottom to top.

The line profiles undergo very significant pulsational variability, and any rotational modulation of the observed profiles is completely masked by the pulsational modulation. In Fig. A.2 we demonstrate the behaviour of the O ii and He i line profiles in SOFIN spectra in the spectral region 4695–4715 Å over the rotation cycle. The inspection of 224 FEROS spectra used in the study of Briquet et al. (2009) reveals that all lines behave in a rather similar way. In Fig. 4 we present a clear pulsation pattern in the spectral region 4590–4615 Å. The moment variations for five lines belonging to different elements, namely He i 4713.1, C ii 5133.1, N ii 5667.6, O ii 4592.0, and Si iii 4553.6, shown in Fig. 5, however, exhibit slight differences between the elements. The equivalent widths of O ii and Si iii are larger at the phase of minimum radius, while C ii and N ii are larger at the maximum radius. The equivalent width of He i is almost constant. At minimum radius the elements N, C, and O show line profiles narrower than those of Si and He. Also the amplitude of the radial velocity curve of the He i line is about 4 km s-1 greater than for the C ii line and 2 km s-1 more than for the N ii line.

Table 2

Magnetic field model for V1449 Aql.

The longitudinal field of V1449 Aql can be adequately represented by a single-wave variation curve during the stellar rotation cycle (see Fig. 2), indicating a dominant dipolar contribution to the magnetic field topology. Assuming that V1449 Aql is an oblique dipole rotator, the magnetic dipole axis tilt β is constrained by ⟨Bz⟩max/⟨Bz⟩min = cos(i + β)/cos(i − β). In Table 2 we show the mean value 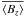and the semi-amplitude of the field variation A⟨Bz⟩ for V1449 Aql in rows 1 and 2. Values for vt = 44 km s-1, which is the total line broadening, and veq = 38 ± 15 km s-1 were published by Briquet et al. (2009). The stellar radius, R = 11.2 ± 1.4 R⊙, was calculated using main-sequence evolutionary CLÉS models (Scuflaire et al. 2008). Obviously, the accuracy of the determination of veq from the best-fit-solutions of the spectroscopic mode identification described in the work of Briquet et al. (2009) is rather low. However, the equatorial rotation velocity can also be calculated using the relation veq = 50.6 R/P, where R = 11.2 ± 1.4 R⊙ is the stellar radius in solar units and P = 13.893 d the period in days. Using this formula, we obtain veq = 41 ± 5 km s-1. On the other hand, Lefever (private communication) obtained v sin i = 24 km s-1, using the different procedure described in Lefever et al. (2010), which takes macroturbulent broadening into account. Our own estimate of the v sin i value, v sin i = 23.5 km s-1 using the technique of Díaz et al. (2011) fully agrees with that of Lefever. The combination of v sin i = 24 km s-1 with a typical estimation error of 2 km s-1 and veq = 41 ± 5 km s-1 leads to the inclination angle i = 36 ± 6°. In the last two rows, we list the parameters of the magnetic field dipole model.

thumbnail Fig. 6

The position of the β Cephei and candidate β Cephei stars in the H-R diagram. Upper panel: the boundaries of the theoretical instability strips are calculated using the OP opacities. Lower panel: boundaries are calculated using OPAL opacities. Full lines correspond to strips for metallicity Z = 0.01 and dotted lines to strips with metallicity Z = 0.02. The thick and thin lines correspond to the boundaries of the β Cephei and SPB instability regions, respectively.

3. Discussion

Using FORS 1/2 and SOFIN longitudinal magnetic field measurements collected in our recent studies, we were able to detect a weak mean longitudinal magnetic field of a few hundred Gauss in four β Cephei stars, δ Cet, ξ1 CMa, 15 CMa, and V1449 Aql, and in two candidate β Cephei stars, α Pyx and ϵ Lup (Hubrig et al. 2006; 2009; 2011). Before we started our systematic search for magnetic fields in pulsating B-type stars, a weak magnetic field was detected in two other β Cephei stars, in the prototype of the class, β Cep itself, by Henrichs et al. (2000) and in V2052 Oph by Neiner et al. (2003). The strongest longitudinal magnetic fields were detected in the two β Cephei stars with the large radial velocity amplitudes, namely in V1449 Aql and ξ1 CMa, for which peak-to-peak amplitudes reach  ~ 90 km s-1 and  ~ 33 km s-1, respectively. The rather strong magnetic field in the atmosphere of these two stars and the rather low v sin i values, certainly make these stars the most suitable targets for studying the impact of magnetic fields on stellar rotation, pulsations, element diffusion, and frequency patterns.

In the frequency analysis of the CoRoT data obtained for V1449 Aql (Degroote et al. 2009), the frequency f = 0.068790 ± 0.000393 d-1 is, within the errors, close to the frequency f = 0.069162 d-1 detected in our study of the periodicity using magnetic field measurements. Additional magnetic field measurements will be worthwhile for proving whether this photometric frequency corresponds to the rotation/magnetic period of this star.

Our studies indicate that dipole models provide a satisfactory fit to the magnetic data and among the presently known

magnetic β Cephei stars, ξ1 CMa and V1449 Aql, possess the largest magnetic fields, with a dipole strength of several kG. The position of the currently known eight magnetic β Cephei and candidate β Cephei stars in the log Teff − log    g diagram is presented in Fig. 6 together with the boundaries of the theoretical instability strips calculated for different metallicities (Z = 0.01 and Z = 0.02) and using the OP opacities (http://cdsweb.u-strasbg.fr/topbase/op.html, see also Miglio et al. 2007) and OPAL opacities (http://opalopacity.llnl.gov/opal.html). The stellar fundamental parameters and their literature sources are compiled in Table A.1. We give in the same table the information on the dominant mode and the radial velocity amplitude, if known. The extent and the position of the instability strip are highly dependent on the opacities used and on the metallicity adopted. Recent studies indicate, however, a lower metallicity than Z = 0.02 for early B-type stars in the solar neighbourhood with Z = 0.014 (e.g. Przybilla et al. 2008). Although the sample of magnetic pulsating stars is still very small, and it is difficult to determine any trend in the distribution of the stars in the H-R diagram, it might seem that magnetic stars are clustered rather close to the instability strip boundaries (full lines in left panel of Fig. 6). Certainly, additional future magnetic field studies of a larger sample of β Cephei stars are needed to study the indicated trend.

Online material

Appendix A: Additional material

Table A.1

Fundamental parameters of β Cephei and candidate β Cephei stars with detected magnetic fields.

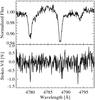thumbnail Fig. A.1

An example of Stokes I and Stokes V spectra observed at phase 0.648 in the wavelength region λλ 4775–4800 containing several N ii spectral lines.

thumbnail Fig. A.2

Line profile variability of O ii λλ4699, 4705, 4710, and He i λ4713 over the rotation cycle on SOFIN spectra. The spectra are presented with phases increasing from bottom to top and offset in the vertical direction for clarity.

Acknowledgments

M.B. acknowledges the Fund for Scientific Research, Flanders, for a grant for a long stay abroad. T.M. acknowledges financial support from Belspo for contract PRODEX-GAIA DPAC. We thank the anonymous referee for useful comments and suggestions.

References

  1. Aerts, C., de Pauw, M., & Waelkens, C. 1992, A&A, 266, 294 [NASA ADS] [Google Scholar]
  2. Aerts, C., Mathias, P., Gillet, D., & Waelkens, C. 1994, A&A, 286, 109 [Google Scholar]
  3. Belkacem, K., Samadi, R., Goupil, M.-J., et al. 2009, Science, 324, 1540 [NASA ADS] [CrossRef] [Google Scholar]
  4. Briquet, M., Uytterhoeven, K., Morel, T., et al. 2009, A&A, 506, 269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Crowe, R., & Gillet, D. 1989, A&A, 211, 365 [NASA ADS] [Google Scholar]
  6. Degroote, P., Briquet, M., Catala, C., et al. 2009, A&A, 506, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Díaz, C. G., González, J. F., Levato, H., & Grosso, M. 2011, A&A, 531, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Henrichs, H. F., Neiner, C., Hubert, A. M., et al. 2000, ASPC, 214, 372 [NASA ADS] [Google Scholar]
  9. Heynderickx, D. 1992, A&AS, 96, 207 [NASA ADS] [Google Scholar]
  10. Heynderickx, D., Waelkens, C., & Smeyers, P. 1994, A&AS, 105, 447 [NASA ADS] [Google Scholar]
  11. Hubrig, S., Briquet, M., Schöller, M., et al. 2006, MNRAS, 369, L61 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hubrig, S., Briquet, M., De Cat, P., et al. 2009, AN, 330, 317 [Google Scholar]
  13. Hubrig, S., Ilyin, I., Schöller, M., et al. 2011, ApJ, 726, L5 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ilyin, I. 2000, Ph.D. Thesis, University of Oulu, Finland [Google Scholar]
  15. Lefever, K., Puls, J., Morel, T., et al. 2010, A&A, 515, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Mathias, P., Gillet, D., & Crowe, R. 1991, A&A, 252, 245 [NASA ADS] [Google Scholar]
  17. Mathys, G. 1994, A&AS, 108, 547 [NASA ADS] [Google Scholar]
  18. Miglio, A., Montalbán, J., & Dupret, M.-A. 2007, Comm. in Asteroseismology, 151, 48 [NASA ADS] [CrossRef] [Google Scholar]
  19. Morel, T., Butler, K., Aerts, C., et al. 2006, A&A, 457, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Morel, T., Hubrig, S., & Briquet, M. 2008, A&A, 481, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Neiner, C., Henrichs, H. F., Floquet, M., et al. 2003, A&A, 411, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes, 2nd edn. (Cambridge: Cambridge University Press) [Google Scholar]
  23. Przybilla, N., & Nieva, M. F. 2010, in Active OB stars – structure, evolution, mass loss, and critical limits, ed. C. Neiner, G. Wade, G. Meynet, & G. Peter, IAU Symp., 272, in press [arXiv:1011.5977] [Google Scholar]
  24. Przybilla, N., Nieva, M.-F., & Butler, K. 2008, ApJ, 688, L103 [NASA ADS] [CrossRef] [Google Scholar]
  25. Przybilla, N., Firnstein, M., Nieva, M. F., et al. 2010, A&A, 517, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Saesen, S., Briquet, M., & Aerts, C. 2006, Comm. in Asteroseismology, 147, 109 [Google Scholar]
  27. Scuflaire, R., Théado, S., Montalbán, J., et al. 2008, Ap&SS, 316, 83 [NASA ADS] [CrossRef] [Google Scholar]
  28. Seber, G. A. F. 1977, Linear Regression Analysis (New York: Wiley) [Google Scholar]
  29. Telting, J. H., Schrijvers, C., Ilyin, I. V., et al. 2006, A&A, 452, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Tuominen, I., Ilyin, I., & Petrov, P. 1999, in Astrophysics with the NOT, ed. H. Karttunen, & V. Piirola, University of Turku, Tuorla Observatory, 47 [Google Scholar]
  31. Waelkens, C., Aerts, C., Kestens, E., et al. 1998, A&A, 330, 215 [NASA ADS] [Google Scholar]

All Tables

Table 1

Magnetic field measurements of V1449 Aql with SOFIN.

In the text
Table 2

Magnetic field model for V1449 Aql.

In the text
Table A.1

Fundamental parameters of β Cephei and candidate β Cephei stars with detected magnetic fields.

In the text

All Figures

thumbnail Fig. 1

The periodogram of V1449 Aql built from the longitudinal magnetic field measurements with the most prominent frequency at f = 0.0720 d-1, corresponding to a period of 13.893 days. The lower thin line presents the window function.

In the text
thumbnail Fig. 2

Phase diagram with the best sinusoidal fit for the longitudinal magnetic field measurements with a reduced χ2 = 0.46. The residuals (Observed – Calculated) are shown in the lower panel. The two FORS 1 measurements appear in green.

In the text
thumbnail Fig. 3

Variability of the output spectra in two SOFIN subexposures taken with the quarter-wave plate angles separated by 90° taken around HJD 2 455 398.530. The lower two spectra, (I + V)0 and (I − V)0, correspond to the first subexposure, while the upper spectra, (I − V)90 and (I + V)90, correspond to the second subexposure. The strong effect of pulsations on the line profile shapes and the line positions is clearly visible between the spectra of the first subexposure with a duration of 20 min and the spectra of the second subexposure with the same duration.

In the text
thumbnail Fig. 4

Time series of FEROS spectra showing pulsational line profile variability in the spectral region 4590–4615 Å. The pulsation phase zero is at the bottom.

In the text
thumbnail Fig. 5

Velocity moments of line profiles: equivalent width (m0), radial velocity (m1), line width (m2), asymmetry (m3), and kurtosis (m4). In each panel five curves are plotted corresponding to five spectral lines of various elements: He i 4713.1, C ii 5133.1, N ii 5667.6, O ii 4592.0, and Si iii 4553.6, shown from bottom to top.

In the text
thumbnail Fig. 6

The position of the β Cephei and candidate β Cephei stars in the H-R diagram. Upper panel: the boundaries of the theoretical instability strips are calculated using the OP opacities. Lower panel: boundaries are calculated using OPAL opacities. Full lines correspond to strips for metallicity Z = 0.01 and dotted lines to strips with metallicity Z = 0.02. The thick and thin lines correspond to the boundaries of the β Cephei and SPB instability regions, respectively.

In the text
thumbnail Fig. A.1

An example of Stokes I and Stokes V spectra observed at phase 0.648 in the wavelength region λλ 4775–4800 containing several N ii spectral lines.
In the text
thumbnail Fig. A.2

Line profile variability of O ii λλ4699, 4705, 4710, and He i λ4713 over the rotation cycle on SOFIN spectra. The spectra are presented with phases increasing from bottom to top and offset in the vertical direction for clarity.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.