| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 5 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201117065 | |
| Published online | 22 June 2011 | |
The ionization equilibrium and flare line spectra for the electron distribution with a power-law tail
1
Astronomical Institute of the Academy of Sciences of the Czech
Republic,
Fričova 298,
251 65
Ondřejov,
Czech Republic
e-mail: elena@asu.cas.cz
2
Faculty of Mathematics Physics and Informatics, Comenius
University, Mlynská dolina
F2, 842 48
Bratislava,
Slovakia
e-mail: homola@fmph.uniba.sk, dudik@fmph.uniba.sk
Received: 12 April 2011
Accepted: 1 June 2011
Context. Electron energy spectra exhibiting a high-energy tail are commonly observed during solar flares.
Aims. We investigate the influence of the high-energy tail and thermal or nonthermal plasma bulk on the ionization equilibrium of Si and Si flare line spectra.
Methods. We construct a realistically composed distribution that reflects the fits to RHESSI observations. We describe the high-energy tail by a power-law distribution and the bulk of the electron distribution by either the Maxwellian or n-distribution. The shape of this composed distribution is described by three parameters: the ratio of the plasma bulk density to the density of the high-energy tail, the power-law index of the high-energy tail, and the parameter n, which describes the bulk of the distribution.
Results. Both the plasma bulk and the high-energy tail change the ionization equilibrium. The relative ion abundances are sensitive to the shape of the plasma bulk, but are much less sensitive to the high-energy tail. The high-energy tail increases the ratio of temperature-sensitive lines Si XIV λ5.22/Si XIII λ5.68. Because this ratio can be fitted with a thermal distribution with higher temperature, the high-energy tail influences the temperature diagnostics from flare lines. The high-energy tail has only a small effect on the ratio of the satellite-to-allowed Si XIId/Si XIII lines, which are dominantly sensitive on the shape of the plasma bulk. This enables us to perform an accurate diagnostic of the parameter n describing the plasma bulk.
Conclusions. The realistically composed distribution is able to explain the observed features of the RESIK X-ray flare line spectra.
Key words: atomic processes / radiation mechanisms: non-thermal / Sun: flares / Sun: X-rays, gamma rays
© ESO, 2011
1. Introduction
X-ray observations with, e.g., RHESSI (Lin et al. 2002) show that the flare electron distribution is composed of a plasma bulk, which is usually considered to be Maxwellian, and a high-energy tail, approximated with a power-law distribution (e.g., Brown 1971; Lin & Hudson 1971; Holman et al. 2003; Brown et al. 2008; Krucker & Lin 2008; Krucker et al. 2008; Asai et al. 2009; Warmuth et al. 2009; Veronig et al. 2010; Kurt et al. 2010; Zharkova et al. 2010; Guo et al. 2011). The ionization equilibrium and synthetic spectra for the Maxwellian electron distribution are widely known (e.g., CHIANTI, Landi et al. 2006; Dere et al. 2009), but there are only few papers on the influence of the high-energy tail on the ionization equilibrium and the line spectra.
Porquet et al. (2001) studied the impact of the nonthermal power-law electron tail on the ionization and recombination rates. The authors used a hybrid distribution, which was Maxwellian for energies lower than a break energy, and power-law for higher energies, to describe the distribution function in supernova remnants. This hybrid distribution is described by the median energy and by the power-law index of the high-energy tail. To ensure the continuity of the hybrid distribution, the authors had to apply normalization constants to both parts of this distribution. They found a significant increase in the ionization rates due to the high-energy tail. The recombination rates were much less affected. However, this kind of distribution does not reflect the fits to the RHESSI observations.
Gabriel & Phillips (1979) studied the impact of the high-energy power-law tail on the Fe XXIVd/Fe XXV line ratios. These authors used a Maxwellian electron distribution with an added high-energy tail. They found that the high-energy tail increases the total excitation rate of the Fe XXV resonance line, but does not influence the excitation of the Fe XXIVd dielectronic satellites. This is because the excitation of the dielectronic satellites is a resonant process with lower excitation energies than the high-energy tail cutoff. The Fe XXV resonance line has a higher excitation treshhold, and thus its intensity increases if the high-energy tail is present. As a result, the Fe XXIVd / Fe XXV line ratios decrease. For two hypotetical flare events with temperatures of 15 and 20 MK, the decrease is about 40% with respect to the purely thermal case. This prediction contradicts the observed increase of satellite lines emitted by Li-like ions with respect to the He-like resonance lines (e.g., Seely et al. 1987; Phillips et al. 2006; Dzifčáková et al. 2008; Kulinová et al. 2011).
In addition, the plasma bulk can have a shape different from the Maxwellian one. The return current with a drift velocity changes the shape of the plasma bulk distribution. The resulting space-angle integrated distribution can be described by the n-distribution (Dzifčáková & Karlický 2008). Its deviation from the Maxwellian distribution depends on the ratio of the electron drift velocity to the electron thermal velocity and can be expessed by a free parameter n. The possible presence of n-distributions during impusive phase of the flare was first shown by Seely et al. (1987) and their effect on the ionization equilibrium and line spectra was subsequently studied by, e.g., Dzifčáková (1998, 2000) and Dzifčáková & Tóthová (2007). Dzifčáková et al. (2008) analyzed the X-ray line spectra observed by CORONAS-F/RESIK (Sylwester et al. 2005). The authors proposed diagnostics of the n-distribution, which uses the Si XIId satellite line together with the allowed Si XIII and Si XIV lines. The n-distribution was able to explain the observed enhancement of the ratio of the Si XIId satellite lines to Si XIII allowed lines. The thermal and multi-thermal synthetic spectra did not show this enhacement. However, the authors did not include the presence of the high-energy tail into their analysis. Kulinová et al. (2011) showed that observed RHESSI X-ray spectrum for two flares corresponds to the n-distribution in the low energy range, to the power-law tail in the high energy range, plus a significant thermal (Maxwellian) component present below 12 keV. Despite this, the authors argued that the thermal component does not originate in the same volume as the nonthermal bulk and the high-energy tail.
Kašparová & Karlický (2009) tried to interpret the RHESSI X-ray spectra of several flares using the κ-distributions, which also exhibit a power-law tail. These authors found that some of the studied loop-top X-ray sources can be described by this type of the electron distribution. The effect of the κ-distribution on the ionization equilibrium has been analyzed by, e.g., Dzifčáková (2002) and Wannawichian et al. (2003), and on the EUV line spectra by Dzifčáková (2006a). A rewiev on κ-distributions can be found in Pierrard & Lazar (2010) and Pierrard (2011).
In this paper, we calculate the Si ionization equilibrium and synthetic spectra for the electron distribution composed from the Maxwellian or n-distribution and a high-energy power-law tail. The composed distribution is constructed in a realistic manner to reflect the fits to the RHESSI observations. The effect of the power-law tail together with the plasma bulk on the ionization equilibrium is examined in Sect. 3 and on the Si X-ray line intensities in Sect. 4.
2. Composed electron distribution
We assume that the distribution function in solar flares can be composed from a Maxwellian or n-distribution together with a power-law distribution. The expression for the n-distribution function is (e.g., Seely et al. 1987; Dzifčáková 1998) 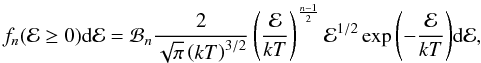 (1)where n ∈ ⟨1,∞) is a parameter and ℬn =
(1)where n ∈ ⟨1,∞) is a parameter and ℬn = 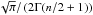 is the normalization constant. The n-distribution becomes Maxwellian one for n = 1 and its deviation from the Maxwellian distribution increases with the increase of n. The mean energy of the n-distribution is ⟨ En ⟩ = (n/2 + 1)kT. Because the mean energy of the distribution depends on both n and T, a new parameter, the pseudo-temperature τ has been introduced by Dzifčáková (1998). Pseudo-temperature is the temperature of the Maxwellian distribution with the same mean energy as the mean energy of the n-distribution:
is the normalization constant. The n-distribution becomes Maxwellian one for n = 1 and its deviation from the Maxwellian distribution increases with the increase of n. The mean energy of the n-distribution is ⟨ En ⟩ = (n/2 + 1)kT. Because the mean energy of the distribution depends on both n and T, a new parameter, the pseudo-temperature τ has been introduced by Dzifčáková (1998). Pseudo-temperature is the temperature of the Maxwellian distribution with the same mean energy as the mean energy of the n-distribution: 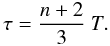 (2)The pseudo-temperature has a similar physical meaning as T for Maxwellian distribution (for which τ ≡ T), and can be used for computation of all quantities depending on the mean energy of the distribution (Dzifčáková 1998).
(2)The pseudo-temperature has a similar physical meaning as T for Maxwellian distribution (for which τ ≡ T), and can be used for computation of all quantities depending on the mean energy of the distribution (Dzifčáková 1998).
The normalized power-law distribution can be expressed by (e.g., Brown et al. 2008; Saint-Hilaire et al. 2009) 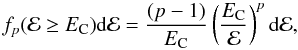 (3)where p is a power-law index and EC is the low-energy cutoff. The mean energy of this distribution is ⟨ Ep ⟩ = EC(p − 1)/(p − 2). The condition p > 2 must thus be fulfilled for the existence of a finite positive mean energy.
(3)where p is a power-law index and EC is the low-energy cutoff. The mean energy of this distribution is ⟨ Ep ⟩ = EC(p − 1)/(p − 2). The condition p > 2 must thus be fulfilled for the existence of a finite positive mean energy.
 |
Fig. 1 Dependence of EC/kτ on the value of the power-law index p for the Maxwellian distribution (n = 1, left) and n-distribution with n = 7 (right). The curves are labeled with the values of a/b. |
 |
Fig. 2 Composed np-distribution with the values of a/b = 20, 200, and 1000 (top), and p = 2.1, 3−5 (bottom). The bulk of the distribution is Maxwellian (n = 1, left column) and an n-distribution with n = 7 (right column). |
We define the composed np-distribution as 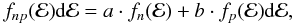 (4)where a/b is the bulk/tail ratio, and a + b = 1. We impose following conditions for the values of EC, a/b, n, and p:
(4)where a/b is the bulk/tail ratio, and a + b = 1. We impose following conditions for the values of EC, a/b, n, and p:
-
the power-law distribution does not affect the shape of the plasmabulk;
-
the discontinuity, fnp(EC)/fn(EC) − 1, in the composed electron distribution at ℰ = EC must be smaller than 1/10.
These conditions restrict the values of a/b, p, and n, for which a suitable EC can be found (Fig. 1). The suitable value of EC decreases with increasing p and increases with increasing a/b or n. The lowest suitable bulk/tail ratio is a/b ≈ 20. The observed ratios are much higher (e.g., Kulinová et al. 2011). An example of the composed np-distributions is shown in Fig. 2.
We tested that adding electrons below the EC has a negligible effect on the ionization and excitation equilibrium. Thus the EC shown in Fig. 1 are the upper limit values.
We note that the construction of the composed np-distribution in Eq. (4) is different from the one of Porquet et al. (2001), who use a break energy and multiplication factors to ensure the continuosness of their distribution. The composed np-distribution is designed to reflect the fits to the RHESSI observations.
 |
Fig. 3 Direct ionization rates (left column) and the recombination rates (right column) for the composed np-distribution with n = 1, p = 2.1 and different a/b (top row), with n = 1, a/b = 50 and different p (middle row), and with a/b = 50, p = 2.1 and diffent n (bottom row). |
 |
Fig. 4 Ionization equilibrium for Si for the composed np-distribution with various values of n, p, and a/b. Left column: Maxwellian bulk (n = 1), right column: bulk with n > 1. For comparison, the dashed lines representing the ionization equilibrium for the Maxwellian distribution are plotted in each figure. |
3. Ionization equilibrium
In the coronal approximation, the ionization equilibrium depends on the rates of the direct ionization, autoionization, and radiative and dielectronic recombination. To obtain these rates, we used the atomic data from the works of Arnaud & Rothenflug (1985), Arnaud & Raymond (1992), Shull & Van Steenberg (1982), Verner & Ferland (1996), Mazzotta et al. (1998), and Pequignot et al. (1991).
We demonstrate here the effect of the composed np-distribution on the rates for Si (Fig. 3). This choice is made is because the Si flare X-ray spectra observed by RESIK were used to diagnose the shape of the plasma bulk (Dzifčáková et al. 2008; Kulinová et al. 2011). However, the results obtained in this section are also valid for other elements, e.g., Fe and Ni.
The high-energy tail in the composed np-distribution increases the direct ionization rates for low τ (Fig. 3left). This effect is greatest for small a/b and p. The behavior is similar for each ion, with details depending on the ratio χ/kT, where χ is the ionization potential. The changes in the shape of plasma bulk, i.e., in n, influence the direct ionization rates in the entire range of τ (Fig. 3bottom left). The autoionization rates show a very similar behavior.
 |
Fig. 5 Observed and synthetic spectra. Left: spectrum observed by RESIK (full line) together with a synthetic isothermal Maxwellian spectrum (dash-dotted line) with log(T/K) = 7.01. Middle: synthetic spectrum for the composed np-distribution with n = 1, p = 2.1, a/b = 20, and log(τ/K) = 7.0 and the Maxwellian spectrum with the same log(T/K) = 7.0. Right: synthetic spectrum for the composed np-distribution with n = 11, p = 2.1, a/b = 20, and log(τ/K) = 7.1 compared to the Maxwellian spectrum with log(T/K) = 7.02. |
If the bulk of the distribution is Maxellian, there are no significant changes in either the radiative recombination or the total recombination rates owing to the high-energy tail (Fig. 3right). This is because the low-energy bulk electrons are the main contributors to the radiative recombination rates, and their number is the same for the composed np-distribution with n = 1 (Maxellian bulk) compared to the Maxwellian distribution itself. The recombination rates are sensitive only to the changes in the plasma bulk shape, i.e., to the changes of n (Fig. 3bottom right).
The power-law high-energy tail shifts the abundance peaks of all Si ions to lower τ independently of n (Fig. 4top). The changes are again greatest for low values of a/b and/or p, i.e., a strong high-energy tail. If n = 1, a weaker tail has only a small effect (Fig. 4, left column), and its effect is completely negligible for a/b ≥ 500. Furthermore, for n = 1, the changes in the ratios of ion abundances are small even for a strong tail because all ions are shifted to lower τ. Thus, it is impossible to diagnose the presence of the high-energy tail from the ionization equilibrium, if the plasma bulk is Maxwellian and τ is not a priori known.
If the composed np-distribution has a bulk with higher n, the behavior of the ionization equilibrium is more complicated. The high-energy tail shifts the Si ionization peaks to lower τ (Fig. 4top right), but the increased n shifts the ion abundance peaks in the opposite direction, i.e., to higher τ (Fig. 4bottom right). Thus, the ionization equilibrium can be shifted to either lower or higher τ depending on values of n, a/b and p. Therefore, it is possible to find a composed np-distribution with nonthermal bulk (n > 1) and a high-energy tail, for which the ion abundance peaks are located near the same τ as for the Maxwellian distribution (e.g., Fig. 4middle right). However, the nonthermal bulk modifies the relative ion abundances significantly (Fig. 4middle right, bottom right), thus allowing for the diagnostic of the shape of the plasma bulk.
4. Synthetic spectra
The CHIANTI atomic database and software (Landi et al. 2006; Dere et al. 2009) allows a calculation of the synthetic spectra for the Maxwellian distribution. The original modification of CHIANTI 5.2 developed by Dzifčáková (2006b) was used previously for computation of line intensities for the nonthermal κ- and n-distributions (e.g., Dzifčáková & Tóthová 2007; Dzifčáková & Mason 2008). This modification can be used for computation of line intensities for any kind of distribution, i.e., also for the composed np-distributions.
We studied the influence of the plasma bulk and high-energy tail on the Si flare spectrum observed by RESIK in the 5−6 Å channel (Fig. 5left). The observed transitions, according to CHIANTI, are summarized in Table 1. For Si XIId, only the strongest of the several tens of transitions are listed. A more complete list can be found in Phillips et al. (2006). However, all the intensities of the dielectronic satellite lines listed in CHIANTI were used to calculate the synthetic spectra in Fig. 5.
Si lines and corresponding transitions observed in the fourth channel of RESIK.
The high-energy tail increases the ratio of the allowed Si XIV λ5.22/Si XIII λ5.68 lines (Fig. 5middle). A given value of this ratio for a composed np-distribution with n = 1 can be fitted with a Maxwellian spectrum corresponding to higher T. This is because the high-energy tail increases the ionization and also excitation of both lines. The shift in temperature is higher for low values of p and/or a/b. E.g., the Si XIV λ5.22/Si XIII λ5.68 line ratio in Fig. 5middle corresponding to log(τ/K) = 7 could be fitted with a Maxwellian with log(T/K) ≈ 7.05, which is ≈10% higher. The changes in the Si XIII λ5.28/Si XIII λ5.68 and Si XIII λ5.40/Si XIII λ5.68 line ratios are almost negligible (Fig. 5middle). This is because these ratios have only a low sensitivity to τ, while the Si XIV λ5.22/Si XIII λ5.68 is very sensitive to τ.
The high-energy tail decreases the ratios Si XIId λ5.56/ Si XIII λ5.68 and Si XIId λ5.82/Si XIII λ5.68 involving the Si XIId dielectronic satellite lines. This decrease is quite small (Fig. 5middle). The behavior of the Fe XXIVd/Fe XXV ratios is much more affected by the high-energy tail (Gabriel & Phillips 1979). This can be because of the higher excitation treshhold of the Fe XXV resonance line, which is therefore more affected by the high-energy tail. Note again that the observations show an increase of the the Si XIId/Si XIII ratios in comparison with the thermal case, not a decrease.
However, these ratios are sensitive to the shape of the plasma bulk. If the ratio Si XIV λ5.22/Si XIII λ5.68 is held fixed, the ratios Si XIId λ5.56 or λ5.82 / Si XIII λ5.68 increase with n (Fig. 5right). In this figure, the full line corresponds to the np-distribution with n = 11 and log(τ/K) = 7.1, while the dash-dotted thermal spectrum corresponds to a Maxwellian with log(T/K) ≈ 7.02 giving the same ratio of Si XIV λ5.22/Si XIII λ5.68. The increase of the Si XIId/Si XIII ratio for n > 1 comes from the increase of the slope of the distribution for energies above the excitation energy for the Si XIId double excited state. This steeper slope lowers the intensitiy of the Si XIII line and thus increases the Si XIId/Si XIII ratio. In our case, the effect of the slope of the bulk of the distribution dominates over the effect of the high-energy tail.
Because the Si XIId / Si XIII ratios dominantly depend on n and only slightly on p, they allow us to diagnose n (Dzifčáková et al. 2008; Kulinová et al. 2011). For the large observed a/b (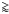 103, Kulinová et al. 2011, Table 4 therein), neglecting the effect of the high-energy tail only leads to negligible error in the diagnosed n. Under these conditions, the diagnostics of p from line spectra is not possible. For small a/b, i.e., large tails, simultaneous diagnostics of n and the parameters of the high-energy tail from the RESIK Si spectra must be done by fitting the whole spectrum. However, the parameters of the high-energy tail can also be diagnosed from RHESSI observations.
103, Kulinová et al. 2011, Table 4 therein), neglecting the effect of the high-energy tail only leads to negligible error in the diagnosed n. Under these conditions, the diagnostics of p from line spectra is not possible. For small a/b, i.e., large tails, simultaneous diagnostics of n and the parameters of the high-energy tail from the RESIK Si spectra must be done by fitting the whole spectrum. However, the parameters of the high-energy tail can also be diagnosed from RHESSI observations.
5. Conclusions
We constructed a composed distribution consisting of the plasma bulk, described by the Maxwellian or n-distribution, and a high-energy power-law tail with the slope p. The bulk/tail density ratio a/b represents a third parameter of the composed distribution. The values of these three parameters are restricted by the condition of finite mean energy and a low-energy cutoff. The composed np-distribution offers an easy parametrization of the observed distribution of electron energies in flare plasma.
We studied the influence of the plasma bulk and high-energy tail of the composed np-distribution on the Si ionization equilibrium and flare line spectra. Both the plasma bulk and the nonthermal tail significantly influence the ionization equilibrium. However, only the value of n related to the shape of the plasma bulk has a significant effect on the relative ion abundances.
The composed np-distribution is able to form a spectrum that has enhanced intensities of the Si XIId dielectronic satellite lines, a feature observed in the RESIK flare spectra. This enhancement occurs because the value of n > 1 and is almost independent of the slope p of the high-energy tail. The Si XIId/Si XIII ratio can thus be used to diagnose n, i.e., the shape of plasma bulk.
If n is held fixed, the ratio of the two strongest lines, Si XIV λ5.22/Si XIII λ5.68 highly depends on p for any n. This ratio can be fitted with a thermal spectrum (Maxwellian) with higher T. Thus, the presence of the nonthermal, high-energy tail can influence the temperature diagnostics from flare line spectra.
Acknowledgments
This work was supported by Grant No. 205/09/1705 of the Grant Agency of the Czech Republic, grant No. 1/0240/11 of the Scientific Grant Agency VEGA, Slovakia, and the Comenius University Grant No. UK/57/2011. The authors are very grateful for the existence and availability of the CHIANTI database. CHIANTI is a collaborative project involving the Naval Research Observatory and George Mason University (USA), the Rutherford Appleton Laboratory, the Mullard Space Science Laboratory and University of Cambridge (UK) and the University of Florence (Italy).
References
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Asai, A., Nakajima, H., Shimojo, M., et al. 2009, ApJ, 695, 1623 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C. 1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, C. M., Kašparová, J., Massone, A. M., & Piana, M. 2008, A&A, 486, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dzifčáková, E. 1998, Sol. Phys., 178, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E. 2000, Sol. Phys., 196, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E. 2002, Sol. Phys., 208, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E. 2006a, Sol. Phys., 234, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E. 2006b, in Proc. SOHO-17, 10 Years of SOHO and Beyond, ed. H. Lacoste, & L. Ouwehand, ESA SP-617, 89.1 [Google Scholar]
- Dzifčáková, E., & Karlický, M. 2008, Sol. Phys., 250, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E., & Mason, H. 2008, Sol. Phys., 247, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E., & Tóthová, D. 2007, Sol. Phys., 240, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Dzifčáková, E., Kulinová, A., Chifor, C., et al. 2008, A&A, 488, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabriel, A. H., & Phillips, K. J. H. 1979, MNRAS, 189, 319 [NASA ADS] [Google Scholar]
- Guo, J., Liu, S., Fletcher, L., & Kontar, E. P. 2011, ApJ, 728, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, G. D., Sui, L., Schwartz, R. A., & Emslie, A. G. 2003, ApJ, 595, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Kašparová, J., & Karlický, M. 2009, A&A, 497, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krucker, S., & Lin, R. P. 2008, ApJ, 673, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Battaglia, M., & Cargill, J. P. 2008, A&ARv, 16, 155 [Google Scholar]
- Kulinová, A., Kašparová, J., Dzifčáková, E., et al. 2011, A&A, submitted [Google Scholar]
- Kurt, V. G., Svertilov, S. I., Yuskov, B. Yu., et al. 2010, Astron. Lett., 36, 4 [Google Scholar]
- Lin, R. P., & Hudson, H. S. 1971, Sol. Phys., 17, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pequignot, D., Petitjean, P., & Boisson, C. 1991, A&A, 251, 680 [NASA ADS] [Google Scholar]
- Pierrard, V. 2011, Space Sci. Rev., in press [Google Scholar]
- Pierrard, V., & Lazar, M. 2010, Sol. Phys., 267, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, K. J. H., Dubau, J., Sylwester, J., & Sylwester, B. 2006, ApJ, 638, 1154 [NASA ADS] [CrossRef] [Google Scholar]
- Porquet, D., Arnaud, M., & Decourchelle, A. 2001, A&A, 373, 1110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saint-Hilaire, P., Krucker, S., Christe, S., & Lin, R. P. 2009, ApJ, 696, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Seely, J. F., Feldman, U., & Doschek, G. A. 1987, ApJ, 319, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Shoub, E. C. 1983, ApJ, 266, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Shull, J. M., & Van Steenberg, M. 1982, ApJS, 48, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Sylwester, J., Gaicki, I., Kordylewski, Z., et al. 2005, Sol. Phys., 226, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Veronig, A. M., Rybák, J., Gömöry, P., et al. 2010, ApJ, 719, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Wannawichian, S. S., Ruffolo, D., & Kartavykh, Yu. Yu. 2003, ApJS, 146, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Warmuth, A., Holman, G. D., Dennis, B. R., et al. 2009, ApJ, 699, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Kuznetsov, A. A., & Siversky, T. V. 2010, A&A, 512, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Dependence of EC/kτ on the value of the power-law index p for the Maxwellian distribution (n = 1, left) and n-distribution with n = 7 (right). The curves are labeled with the values of a/b. |
| In the text | |
 |
Fig. 2 Composed np-distribution with the values of a/b = 20, 200, and 1000 (top), and p = 2.1, 3−5 (bottom). The bulk of the distribution is Maxwellian (n = 1, left column) and an n-distribution with n = 7 (right column). |
| In the text | |
 |
Fig. 3 Direct ionization rates (left column) and the recombination rates (right column) for the composed np-distribution with n = 1, p = 2.1 and different a/b (top row), with n = 1, a/b = 50 and different p (middle row), and with a/b = 50, p = 2.1 and diffent n (bottom row). |
| In the text | |
 |
Fig. 4 Ionization equilibrium for Si for the composed np-distribution with various values of n, p, and a/b. Left column: Maxwellian bulk (n = 1), right column: bulk with n > 1. For comparison, the dashed lines representing the ionization equilibrium for the Maxwellian distribution are plotted in each figure. |
| In the text | |
 |
Fig. 5 Observed and synthetic spectra. Left: spectrum observed by RESIK (full line) together with a synthetic isothermal Maxwellian spectrum (dash-dotted line) with log(T/K) = 7.01. Middle: synthetic spectrum for the composed np-distribution with n = 1, p = 2.1, a/b = 20, and log(τ/K) = 7.0 and the Maxwellian spectrum with the same log(T/K) = 7.0. Right: synthetic spectrum for the composed np-distribution with n = 11, p = 2.1, a/b = 20, and log(τ/K) = 7.1 compared to the Maxwellian spectrum with log(T/K) = 7.02. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


