| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A3 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201116779 | |
| Published online | 30 May 2011 | |
The multiple planets transiting Kepler-9
I. Inferring stellar properties and planetary compositions⋆
1
Université de Nice-Sophia Antipolis, CNRS UMR 6202, Observatoire de la Côte d’Azur, BP 4229, 06304 Nice Cedex 4, France
e-mail: mathieu.havel@oca.eu
2
Earth, Atmospheric and Planetary Sciences, MIT, 77 Massachusetts Ave, Cambridge, MA, 02139, USA
Received: 25 February 2011
Accepted: 30 March 2011
The discovery of multiple transiting planetary systems offers new possibilities for characterising exoplanets and understanding their formation. The Kepler-9 system contains two Saturn-mass planets, Kepler-9b and 9c. Using evolution models of gas giants that reproduce the sizes of known transiting planets and accounting for all sources of uncertainties, we show that Kepler-9b (respectively 9c) contains 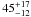 M⊕ (resp.
M⊕ (resp. 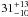 M⊕) of hydrogen and helium and
M⊕) of hydrogen and helium and 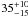 M⊕ (resp.
M⊕ (resp. 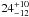 M⊕) of heavy elements. More accurate constraints are obtained when comparing planets 9b and 9c: the ratio of the total mass fractions of heavy elements are Zb/Zc = 1.02 ± 0.14, indicating that, although the masses of the planets differ, their global composition is very similar, an unexpected result for formation models. Using evolution models for super-Earths, we find that Kepler-9d must contain less than 0.1% of its mass in hydrogen and helium and predict a mostly rocky structure with a total mass between 4 and 16 M⊕.
M⊕) of heavy elements. More accurate constraints are obtained when comparing planets 9b and 9c: the ratio of the total mass fractions of heavy elements are Zb/Zc = 1.02 ± 0.14, indicating that, although the masses of the planets differ, their global composition is very similar, an unexpected result for formation models. Using evolution models for super-Earths, we find that Kepler-9d must contain less than 0.1% of its mass in hydrogen and helium and predict a mostly rocky structure with a total mass between 4 and 16 M⊕.
Key words: star: individual: Kepler-9 / planetary systems / planets and satellites: physical evolution
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
Although much progress has been made since the discovery of the first transiting exoplanet, understanding their composition, evolution, and formation has remained elusive. One longstanding problem has been that a significant fraction of close-in exoplanets are inflated compared to what theoretical models predict (Bodenheimer et al. 2001; Guillot & Showman 2002; Baraffe et al. 2003; Guillot et al. 2006; Burrows et al. 2007; Guillot 2008; Miller et al. 2009). As a consequence, the global composition that may be derived from size and mass measurements of a given planet is intrinsically model-dependent. This implies that, thus far, constraints from the compositions and their consequences in terms of planet formation models have only been grasped in a statistical way (e.g. Ida & Lin 2008; Mordasini et al. 2009), not from any analysis of individual planetary systems.
The discovery of the multiple system of transiting planets around Kepler-9 (Holman et al. 2010) opens a new window on characterisation of exoplanets and on understanding their formation. The system consists of two Saturn-size planets with 19.2 and 38.9 day orbital periods and a likely super-Earth candidate with a 1.6 day orbit (Torres et al. 2011). The advantage of this system is that the planets and the star share the same age within a few million years, therefore we can constrain the composition of one giant planet much more accurately relative to the other. These two planets are also in a 2:1 mean motion resonance, which means that their dynamical history is strongly constrained. Altogether, this implies that a detailed scenario of the formation and the dynamical and physical evolution of the complete system may be obtained. In this first article, we focus on the compositional constraints obtained for the three planets in the system.
Given that the largest uncertainties in the parameters of transiting planets arise from the uncertainties in the star (e.g. Sozzetti et al. 2007; Torres et al. 2008), we first derive the stellar properties (Sect. 2). We subsequently infer the compositions of the two confirmed giant planets (Sect. 3) and model the possible composition for the small planet candidate, Kepler-9d in Sect. 4. We finish by discussing the implications of our results.
2. Kepler-9a, a solar-like star
 |
Fig. 1 Constraints derived from stellar evolution models on the mass of Kepler-9a as a function of its age. The dots correspond to solutions that fit the input constraints at the 68.3%, 95.4% (blue), and 99.7% levels (purple). The upper panel uses Teff and log g as inputs constraints. The lower panel in addition uses the constraint on the stellar mean density. |
According to Holman et al. (2010), Kepler-9a, the host star of the system is a solar-like star, with an estimated mass of 1.0 ± 0.1 M⊙ and radius of 1.1 ± 0.09 R⊙. Spectroscopic measurements give a Teff of 5777 ± 61 K and a super-solar metallicity [Fe/H] of 0.12 ± 0.04 dex. The star is slightly more active than our Sun, with a rotation period of 16.7 days, implying an age of 2 to 4 Ga from gyrochronology (Barnes 2007; Holman et al. 2010).
We chose to re-examine the constraints on the stellar parameters with the approach described in Guillot & Havel (2011). We used the measured effective temperature and surface gravity as constraints for the evolution models. Alone, these constraints are relatively weak compared to what is achieved for other stars with transiting systems, because the stellar density obtained from photometric measurement is not provided directly by Holman et al. (2010), probably because the analysis is complex. However, it may be obtained from the estimate of the planetary semi-major axis, orbital period, and the inferred stellar radius (e.g. see Beatty et al. 2007). Our adopted final value for the density of Kepler-9a, ρ ⋆ = 0.79 ± 0.19ρ⊙ was obtained from the constraints provided by the two giant planets, with the error estimated as the quadratic mean of the two values.
Using a grid of stellar evolution models calculated with CESAM (Morel & Lebreton 2008), we determined all combinations of stellar mass, age, and metallicity that match the constraints. We first calculated solutions using only the constraints obtained from effective temperature and gravity. Assuming Gaussian errors for both quantities, we derived three ellipses corresponding to probabilities of occurrence of 68.3% (1σ), 95.4% (2σ), and 99.7% (3σ), respectively. The ensemble of solutions that fall within these values is represented with colour-coded dots in Fig. 1 (top panel). After restricting ourselves to the “2σ” solutions, we see that the stellar mass is constrained to lie within 1.0 and 1.1 M⊙, but that the age constraint is extremely weak (only ages > 8 Ga are excluded). Adding the stellar density constraints (Fig. 1, bottom panel) yields a tighter constraint on the stellar age, but very similar results in mass.The corresponding stellar parameters of this case are summarised as a function of age in Table 1. With the 2–4 Ga age range obtained from gyrochronology, we obtain a stellar mass M ⋆ = 1.05 ± 0.03 M⊙ and radius R ⋆ = 1.05 ± 0.06 R⊙, in good agreement with Holman et al. (2010).
Derived stellar parameters at 68.3% and 95.4% level of confidence.
3. Modelling the giant planets Kepler-9b and Kepler-9c
3.1. Methodology
The characteristics of the two giant planets derived by Holman et al. (2010) are Mp = 80.1 ± 4.1 M⊕, Rp = 9.44 ± 0.77 R⊕ for Kepler-9b, and Mp = 54.7 ± 4.1 M⊕, Rp = 9.22 ± 0.75 R⊕ for Kepler-9c. We derived zero-albedo equilibrium temperatures (see Saumon et al. 1996) of Teq= 780 K and Teq= 620 K for the two planets, respectively1.
Since the semi-amplitude of the radial velocity measurements is not provided by Holman et al. (2010), and the eccentricity of the planet’s orbits is not well constrained, we choose to not derive the planetary mass again and use the above-mentioned values. We note that a 10–15% change in the total mass (equivalent to ~2σ of the quoted error) of the planet induces an uncertainty on the modelled radius of 3–4%, a relatively significant value. Further analysis of photometric and radial-velocity measurements should therefore allow the derivation of tighter constraints on the planetary mass and therefore planetary composition than possible with the data at our disposal.
On the other hand, we do use the known radii ratios provided by transit light curves (kb = Rp, b/R ⋆ = 0.07885 ± 0.00081 and kc = Rp, c/R ⋆ = 0.07708 ± 0.00080, respectively for Kepler-9b and Kepler-9c) and our results for the stellar radius (with the constraint on the stellar density) to compute the radius of each planet as a function of the age, propagating all sources of uncertainties. In the 2–4 Ga age range, we find that the two planets have radii  km and
km and 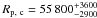 km, respectively (see Fig. 2).
km, respectively (see Fig. 2).
 |
Fig. 2 Constraints derived from stellar evolution models on the radius of Kepler-9b (upper panel) and Kepler-9c (lower panel) as a function of its age. We use 1 Rjup = 71 492 km. See Fig. 1 for colour coding. These results use solutions presented in lower panel of Fig. 1, i.e. with the constraint on the stellar density. |
In principle, the knowledge of both mass and size should allow a direct determination of the planetary compositions. However, several additional uncertainties have to be taken into account. A first uncertainty in the modelling concerns the atmospheric boundary condition to be used. In particular, the temperature of the deep atmosphere that is used as a boundary condition for the interior models depends on the greenhouse factor γ-1, i.e. the ratio between infrared and visible mean opacities that will depend on unknown factors such as precise composition, cloud coverage and atmospheric dynamics (Hansen 2008; Guillot 2010). On the basis of detailed radiative transfer calculations (Fortney et al. 2008; Spiegel et al. 2009), we adopt two extreme possibilities that are scaled as a function of Teq, the zero-albedo equilibrium temperature of the planet: either a low value γ-1 = 1.7(Teq/2000 K) − 1/2 or a much higher one γ-1 = 2.5(Teq/2000 K)-2. Another significant source of uncertainty is related to the inflation of close-in exoplanets over what standard models predict, for which several explanations have been put forward (e.g. Bodenheimer et al. 2001; Guillot & Showman 2002; Guillot et al. 2006; Chabrier & Baraffe 2007; Burrows et al. 2007; Guillot 2008; Laine et al. 2008; Miller et al. 2009; Ibgui et al. 2010; Batygin & Stevenson 2010; Perna et al. 2010). On the basis of both attempts to fit the ensemble of known transiting planets (Guillot et al. 2006; Guillot 2008) and models for the generation and dissipation of atmospheric kinetic energy generated by the stellar heating (Guillot & Showman 2002; Showman & Guillot 2002; Batygin & Stevenson 2010; Perna et al. 2010), we assume that heat is dissipated in the planet proportionally to its irradiation level. We choose two models: either no heat is dissipated or a fraction (0.25%) of the incoming stellar heat is dissipated at the centre of the planet, as required to reproduce the sizes of known transiting exoplanets (Guillot et al. 2006; Guillot 2008). When doing so, we assume equilibrium temperatures are fixed, and thus do not propagate the uncertainties on the stellar parameters to the irradiation levels of the planets, but this is clearly a weaker effect compared to uncertainties e.g. on the atmospheric models. Then, using the same approach as in Guillot & Havel (2011), we calculate grids of evolution models for Kepler-9b and 9c (using CEPAM Guillot & Morel 1995) for hydrogen-helium planets with various core masses for all relevant total masses, atmospheric boundary conditions and assumptions regarding heat dissipation. Although the core hypothesis is used for simplicity, we cannot distinguish between heavy elements embedded in a central core or mixed throughout the envelope. The difference is expected to be smaller than other sources of uncertainty considered here (Baraffe et al. 2008).
The ensemble of possible compositions is obtained from a comparison between model results and constraints on inferred planetary sizes and ages (Guillot & Havel 2011): with a given set of assumptions for the Mb, Mc, atmospheric model and dissipation value, we obtain values of MZ,b and MZ,c matching the age and Rb, Rc values (when a solution exists). Overall, we associate values of MZ,b, MZ,c, Zb, Zc, MZ,b/MZ,c, Zb/Zc to each solution of the stellar evolution (given observational constraints), for the given choices of kb, kc, Mb, Mc, atmospheric model, or dissipation value.
To assess the quality of the solutions, we first identify which stellar models match the stellar constraints within 1, 2, and 3σ by assuming independent Gaussian errors for the stellar density and effective temperature. We calculate planetary solutions for the different extreme atmospheric boundary conditions and dissipation rates using fiducial values for the planetary masses and photometric k values. We then account for the uncertainty on the planetary masses and photometric k values by adding models in which these quantities have been modified by 1, 2, and 3σ from their mean value, respectively. Therefore, to estimate the uncertainties, we consider that 1σ solutions are obtained from the ensemble of points including 1σ stellar evolution solutions with mean values of (kb, kc, Mb, Mc) and 1σ stellar evolution solutions, which in turn (kb, kc, Mb, Mc) has been changed by ± 1σ. Solutions at 2σ (resp. 3σ) are obtained from the ensemble of points including 2σ (resp. 3σ) stellar evolution solutions with mean values of (kb, kc, Mb, Mc) and 1σ stellar evolution solutions in which (kb, kc, Mb, Mc) have been changed by ± 2σ (resp. ± 3σ). We always consider the two possibilities for the atmospheric models and for the dissipation value.
To assess the magnitude of the different contributions to the global uncertainty in the solutions, we compared the range of solutions 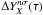 obtained for each given age τ when only one given parameter X (stellar parameters, kb, kc, Mb, Mc, atmospheric model, dissipation value) is changed by ± nσ to the total nσ uncertainty ΔYnσ(τ). We note
obtained for each given age τ when only one given parameter X (stellar parameters, kb, kc, Mb, Mc, atmospheric model, dissipation value) is changed by ± nσ to the total nσ uncertainty ΔYnσ(τ). We note
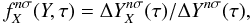 where Y is any of MZ,b, MZ,c, Zb, Zc, MZ,b/MZ,c, Zb/Zc.
where Y is any of MZ,b, MZ,c, Zb, Zc, MZ,b/MZ,c, Zb/Zc.
3.2. Results
The overall results are presented for representative age values and for each of MZ,b, MZ,c, Zb, Zc, MZ,b/MZ,c, Zb/Zc, in Tables A.1 to A.6 (Appendix). The fraction (in percent) of the uncertainty on the stellar parameters is denoted f ⋆ . The uncertainties on both kb and kc have been combined into a value fk and similarly for those on Mb and Mc, denoted fMtot. The two atmospheric models and two dissipation models are treated like the other errors (fatm and fdiss, respectively), but of course their contribution 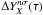 is always the same regardless of nσ. The values of fatm and fdiss in Tables A.1–A.6 thus become progressively lower from 1σ, to 2σ, and to 3σ solutions.
is always the same regardless of nσ. The values of fatm and fdiss in Tables A.1–A.6 thus become progressively lower from 1σ, to 2σ, and to 3σ solutions.
Tables A.1 to A.6 show that, in the 2–4 Ga age range, the solutions are generally well behaved. When adding the f values linearly, we obtain on average 77% of the total error. When summing them quadratically, this mean value is 44%. This indicates that our method probably overestimates the errors, but we believe that the treatment is adequate given the intrinsic difficulty in combining observational uncertainties to model uncertainties.
One can note that, for ages beyond 4 Ga, the solutions for the planet parameters become less constrained. This is due both to the increased number of solutions for the stellar parameters and to the existence of solutions matching the planetary constraints with very low MZ values, particularly when considering the ratios MZ,b/MZ,c and Zb/Zc.
 |
Fig. 3 Constraints derived from stellar and planetary evolution models on the mass of heavy elements present in planets Kepler-9b (top) and Kepler-9c (bottom) as a function of their age. The areas correspond to the ensemble of models that fit the constraints within 1σ (green), 2σ (blue), and 3σ (purple). The 2–4 Ga age range is highlighted because it is strongly favoured by gyrochronology. The error bar on each panel represents the total mass of the corresponding planet and its 1σ uncertainty. |
shows the resulting heavy elements content in Kepler-9b and 9c as a function of age. The two planets are found to be made of hydrogen and helium and heavy elements in relatively similar proportions. The total masses of heavy elements needed to reproduce the observed planetary sizes depend on the assumed age: higher masses are required in younger systems, while pure hydrogen-helium solutions are possible for older ages and no heat dissipation assumed. Given the 2–4 Ga age constraint, however, the ensemble of possibilities is limited to values of 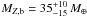 and
and  when considering 1σ solutions. The constraints must be taken with care because the ensemble of solutions has a non-Gaussian behaviour. The values provided here overestimate slightly the ensemble of solutions at 3σ (see Appendix for complete solutions).
when considering 1σ solutions. The constraints must be taken with care because the ensemble of solutions has a non-Gaussian behaviour. The values provided here overestimate slightly the ensemble of solutions at 3σ (see Appendix for complete solutions).
When considering the planets independently, the ratio of heavy elements to total mass of the planets are loosely bounded (Zb/Zc = 0.67 to 1.81 for 1σ solutions). However, much tighter constraints are obtained when comparing the two planets because the solutions are less sensitive to errors on the stellar radius and mass. Given the similarity in mass, irradiation level, and composition of the two planets, we also assume that the same class of model holds and that the two planets are affected in the same way by heat dissipation mechanisms. As shown in Fig. 4, we thus find that Kepler-9b contains 1.50 ± 0.24 times more heavy elements in mass than Kepler-9c. Strikingly, the two planets appear to have the same global composition as indicated by a similar ratio of mass of heavy elements to total planetary mass Zb/Zc = 1.02 ± 0.14.
To assess the importance of the different measurements/modelling hypotheses, we compare results obtained by assuming only one source of uncertainty at a time to the global results. We find that the present uncertainties on MZ and Z for both planets mostly stem from uncertainties on the stellar parameters (~50% of the total error) and assumed dissipation rates (~30%). When considering the ratios of these quantities, i.e. MZ,b/MZ,c and Zb/Zc, the contribution by the stellar parameters’ uncertainties is strongly suppressed (to less than ~10%). In the case of MZ,b/MZ,c, the dominant uncertainties are then those on the planetary masses (~60%), on the k values (~30%), and on dissipation (~30%). In the case of Zb/Zc, the dominant uncertainties are due to the k values (~40%), dissipation (~30%), with less of an effect on the planetary masses (~10%). Further measurements from Kepler and from ground-based radial velocimetry will be extremely valuable in reducing the uncertainties on the stellar density, planetary masses, and k values.
 |
Fig. 4 Constraints on the ratios of the masses of heavy elements MZ,b/MZ,c (top) and of the total mass fractions of heavy elements Zb/Zc (bottom) in Kepler-9b versus Kepler-9c. The colours have the same meaning as in Fig. 3. |
4. Modelling the possible super-Earth Kepler-9d (KOI-377)
Kepler-9d cannot be compared with the same method as its sister planets b and c, both because of its different nature and because of its undetermined mass. For this planet, we combined internal structure models developed for solid planets to models of gaseous models (Valencia et al. 2010). We considered two types of planets: rocky planets with different amounts of iron and volatile planets. For the latter we assumed the planets to be differentiated into a solid nucleus of terrestrial composition (a silicate mantle above an iron core), overlaid by a gaseous envelope composed of either hydrogen and helium, or water. Because the equilibrium temperature we estimate for Kepler-9d (Teq ~ 1800 − 2200 K) is well above the critical temperature of water, the water in the envelope is in a fluid form.
shows the results. Given the size of Kepler-9d, the amount of hydrogen and helium present would be less than 0.1% by mass. Owing to the proximity to the star, this atmosphere would be very vulnerable to escape, thus yielding a scenario for only hydrogen and helium that is practically unfeasible, as obtained for CoRoT-7b (Valencia et al. 2010). On the other hand, this can be a water-vapour planet with volatiles making up less than 50% by mass.
Alternatively, the composition may be rocky, for which the mass range corresponding to the radius will depend on the amount of iron. The values are 4 − 7 M⊕ for a planet with little or no iron (i.e. a super-Moon), 5−11 M⊕ for a terrestrial composition (iron core is 33% by mass), 7−16 M⊕ for a super-Mercury composition (iron core is 65% by mass), and up to 30 M⊕ if made of pure iron. While it is quite unlikely for a planet to be composed only of iron, the precise amount is unknown. If Mercury’s high iron content is used as a proxy, a reasonable upper limit to the mass of Kepler-9d is 16 M⊕.
 |
Fig. 5 Mass-radius relations for different compositions of Kepler-9d. For the rocky scenarios: a pure iron planet (dashed black), a mercury-like planet – 35% silicate mantle above a 65% iron core (thin black), an earth-like planet – 63% silicate mantle above a 33% iron core (thick black). For the gaseous compositions: an earth-like nucleus covered by an H-He envelope of 0.01% (dotted brown), 0.1% (dotted orange), and 1% (dotted red) by mass; or covered by a water envelope of 5% (solid purple) and 50% (solid dark blue) by mass, or a pure 100% water-vapor planet (solid light blue). The radius range for Kepler-9d (grey band) suggests the planet has no considerable H-He. A physically plausible upper limit for the mass is 16 M⊕. Transiting exoplanets in a similar mass-radius range, as well as Uranus and Neptune, are shown for reference. |
5. Conclusion
In this paper, we combined stellar and planetary evolution models to constrain the star and planets in the Kepler-9 system
in a homogeneous way. We showed that the two Saturn-like gas giants contain a relatively significant fraction of heavy elements in their interior (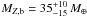 and
and  ) and that the close-in super-Earth most probably contains no hydrogen and helium, because the low allowed mass fraction (<0.01%) would have been rapidly blown away.
) and that the close-in super-Earth most probably contains no hydrogen and helium, because the low allowed mass fraction (<0.01%) would have been rapidly blown away.
Comparing the two planets Kepler-9b and 9c led us to derive tight constraints on the ratios of heavy elements in these planets, i.e. Zb/Zc = 1.02 ± 0.14. This is surprising because accretion models predict a faster accretion of hydrogen and helium and thus a lower Z value for the first formed, most massive planet (e.g. Hori & Ikoma 2010). These two planets are also highly interesting because they are in a 2:1 mean motion resonance, as are several other known exoplanetary planets. Their orbital properties generally imply an early migration in the presence of an inner-gas disc to damp any eccentricities (Crida et al. 2008).
Detailed studies of the formation and migration of the entire Kepler-9 planetary system thus should shed light on the mechanisms responsible for planetary formation.
Online material
Appendix A: Planetary parameters and main uncertainties for Kepler-9b and 9c
Constraints obtained on MZ,b as a function of age and sources of uncertainties.
Constraints obtained on MZ,c as a function of age and sources of uncertainties.
Constraints obtained on Zb as a function of age and sources of uncertainties.
Constraints obtained on Zc as a function of age and sources of uncertainties.
Constraints obtained on MZ,b/MZ,c as a function of age and sources of uncertainties.
Constraints obtained on Zb/Zc as a function of age and sources of uncertainties.
Acknowledgments
We acknowledge the support of the Programme National de Planétologie and of CNES. Computations have been done on the Mesocentre SIGAMM machine, hosted by the Observatoire de la Côte d’Azur.
References
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., & Barman, T. 2008, A&A, 482, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
- Beatty, T. G., Fernandez, J. M., Latham, D. W., et al. 2007, ApJ, 663, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Bodenheimer, P., Lin, D. N. C., & Mardling, R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2007, ApJ, 661, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Crida, A., Sándor, Z., & Kley, W. 2008, A&A, 483, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortney, J. J., Lodders, K., Marley, M. S., & Freedman, R. S. 2008, ApJ, 678, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2008, Phys. Scripta T, 130, 014023 [Google Scholar]
- Guillot, T. 2010, A&A, 520, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Havel, M. 2011, A&A, 527, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., & Morel, P. 1995, A&AS, 109, 109 [NASA ADS] [Google Scholar]
- Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, B. M. S. 2008, ApJS, 179, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hori, Y., & Ikoma, M. 2010, ApJ, 714, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Ibgui, L., Burrows, A., & Spiegel, D. S. 2010, ApJ, 713, 751 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2008, ApJ, 673, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Laine, R. O., Lin, D. N. C., & Dong, S. 2008, ApJ, 685, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N., Fortney, J., & Jackson, B. 2009, ApJ, 702, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, P., & Lebreton, Y. 2008, Ap&SS, 316, 61 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 724, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Hubbard, W. B., Burrows, A., et al. 1996, ApJ, 460, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Showman, A. P., & Guillot, T. 2002, A&A, 385, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Torres, G., Charbonneau, D., et al. 2007, ApJ, 664, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Spiegel, D. S., Silverio, K., & Burrows, A. 2009, ApJ, 699, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Winn, J. N., & Holman, M. J. 2008, ApJ, 677, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fressin, F., Batalha, N. M., et al. 2011, ApJ, 727, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Ikoma, M., Guillot, T., & Nettelmann, N. 2010, A&A, 516, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Constraints obtained on MZ,b as a function of age and sources of uncertainties.
Constraints obtained on MZ,c as a function of age and sources of uncertainties.
Constraints obtained on MZ,b/MZ,c as a function of age and sources of uncertainties.
Constraints obtained on Zb/Zc as a function of age and sources of uncertainties.
All Figures
 |
Fig. 1 Constraints derived from stellar evolution models on the mass of Kepler-9a as a function of its age. The dots correspond to solutions that fit the input constraints at the 68.3%, 95.4% (blue), and 99.7% levels (purple). The upper panel uses Teff and log g as inputs constraints. The lower panel in addition uses the constraint on the stellar mean density. |
| In the text | |
 |
Fig. 2 Constraints derived from stellar evolution models on the radius of Kepler-9b (upper panel) and Kepler-9c (lower panel) as a function of its age. We use 1 Rjup = 71 492 km. See Fig. 1 for colour coding. These results use solutions presented in lower panel of Fig. 1, i.e. with the constraint on the stellar density. |
| In the text | |
 |
Fig. 3 Constraints derived from stellar and planetary evolution models on the mass of heavy elements present in planets Kepler-9b (top) and Kepler-9c (bottom) as a function of their age. The areas correspond to the ensemble of models that fit the constraints within 1σ (green), 2σ (blue), and 3σ (purple). The 2–4 Ga age range is highlighted because it is strongly favoured by gyrochronology. The error bar on each panel represents the total mass of the corresponding planet and its 1σ uncertainty. |
| In the text | |
 |
Fig. 4 Constraints on the ratios of the masses of heavy elements MZ,b/MZ,c (top) and of the total mass fractions of heavy elements Zb/Zc (bottom) in Kepler-9b versus Kepler-9c. The colours have the same meaning as in Fig. 3. |
| In the text | |
 |
Fig. 5 Mass-radius relations for different compositions of Kepler-9d. For the rocky scenarios: a pure iron planet (dashed black), a mercury-like planet – 35% silicate mantle above a 65% iron core (thin black), an earth-like planet – 63% silicate mantle above a 33% iron core (thick black). For the gaseous compositions: an earth-like nucleus covered by an H-He envelope of 0.01% (dotted brown), 0.1% (dotted orange), and 1% (dotted red) by mass; or covered by a water envelope of 5% (solid purple) and 50% (solid dark blue) by mass, or a pure 100% water-vapor planet (solid light blue). The radius range for Kepler-9d (grey band) suggests the planet has no considerable H-He. A physically plausible upper limit for the mass is 16 M⊕. Transiting exoplanets in a similar mass-radius range, as well as Uranus and Neptune, are shown for reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


