| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 4 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201116689 | |
| Published online | 01 June 2011 | |
Evolution of the progenitor binary of V1309 Scorpii before merger
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warsaw, Poland
e-mail: kst@astrouw.edu.pl
Received: 10 February 2011
Accepted: 30 April 2011
Context. It was recently demonstrated that the eruption of V1309 Sco was a result of a merger of the components of a cool contact binary.
Aims. We computed a set of evolutionary models of the detached binaries with different initial parameters to compare it with pre-burst observations of V1309 Sco.
Methods. The models are based on our recently developed evolutionary model of the formation of cool contact binaries.
Results. The best agreement with observations was obtained for binaries with initial masses of 1.8–2.0 M⊙ and initial periods of 2.5–3.1 d. The evolution of these binaries consists of three phases: at first the binary is detached and both components lose mass and angular momentum through a magnetized wind. This takes almost two thirds of the total evolutionary lifetime. The remaining third is spent in a semi-detached configuration of the Algol-type, following the Roche-lobe overflow by the initially more massive component. When the other component leaves the main sequence and moves toward the giant branch, a contact configuration is formed for a short time, followed by the coalescence of both components.
Key words: stars: individual: V1309 Sco / binaries: close / stars: late-type / stars: evolution
© ESO, 2011
1. Introduction
V1309 Sco erupted in 2008, which increased its brightness by about 10 mag. The discussion of spectral and photometric observations obtained after the eruption showed a close resemblance of the outburst of V1309 Sco to that of V838 Mon and outbursts of a few other variables classified as “red novae” (Mason et al. 2010). Several explanations of these unusual eruptions have been offered (Mason et al. 2010; Tylenda et al. 2011, and references therein). In particular, Soker & Tylenda (2003) and Tylenda & Soker (2006) suggested that a collision of two stars (or a star and a substellar object) best reproduces the observed characteristics of the red novae outbursts, however, till recently, other mechanisms were considered as well. Fortuitously, V1309 Sco lies in one of the stellar fields observed by the OGLE team, so several years of precise photometric monitoring preceding the eruption of the variable exist. These data are analyzed by Tylenda et al. (2011). The observations clearly show that the progenitor of V1309 Sco was an eclipsing contact binary with a period of about 1.4 d, which rapidly shortened its period and substantially changed the light curve just before the eruption. The observations obtained after the outburst show no trace of periodicity. That leaves no doubt that the outburst of V1309 Sco was the result of a violent collision of the binary components.
The purpose of the present paper is to model the evolution of the progenitor of V1309 Sco from zero age main sequence (ZAMS) to the eruption.
2. Model
2.1. Description of the model
Recently we developed new model of the formation of cool contact binaries (Stȩpień 2004, 2006a,b, 2009). The model assumes that contact binaries emerge from cool detached binaries with initial orbital periods of a few days. Both components possess subphotospheric convective zones that are necessary for generating surface magnetic fields. This limits the mass of each component to values less than or equal to 1.3 M⊙. For more massive stars the coronal X-ray surface flux decreases so rapidly with increasing mass (Schmitt 1997) that they are not expected to possess significant magnetized winds, which originate in hot coronae. The magnetic activity level of a cool star increases with the increase of its rotational angular velocity (e.g. Pizzolato et al. 2003). Assuming the spin-orbit synchronization of rotation, the activity of both components of a short-period binary is very high, at the so-called “saturation” level. The magnetic activity drives stellar winds, carrying away mass and spin angular momentum (AM). Because of synchronization, the AM loss (AML) results in a decrease of the orbital AM, a shortening of the orbital period, and an actual spin-up of both components.
Neglecting the spin AM of the components we have 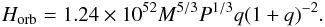 (1)The AML rate of a close binary is given by (Gazeas & Stȩpień 2008)
(1)The AML rate of a close binary is given by (Gazeas & Stȩpień 2008) 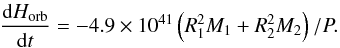 (2)Here Horb is orbital AM in cgs units, P – period in days, M = M1 + M2, M1,2 and R1,2 are masses and radii of the components in solar units and t is time in years. The formula is based on the semi-empirically determined AML rate of single, cool stars (Stȩpień 2006b). The uncertainty of the numerical coefficient is about 30%.
(2)Here Horb is orbital AM in cgs units, P – period in days, M = M1 + M2, M1,2 and R1,2 are masses and radii of the components in solar units and t is time in years. The formula is based on the semi-empirically determined AML rate of single, cool stars (Stȩpień 2006b). The uncertainty of the numerical coefficient is about 30%.
The mass loss rate due to the wind at its highest, saturated strength, adopted here for each component, is based on the empirical determination by Wood et al. (2002)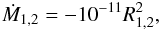 (3)where mass loss rates are in M⊙/year and radii in solar units. This relation applies to stars with M1,2 ≤ 1 M⊙. For stars with higher masses R1, 2 ≡ 1 is adopted.
(3)where mass loss rates are in M⊙/year and radii in solar units. This relation applies to stars with M1,2 ≤ 1 M⊙. For stars with higher masses R1, 2 ≡ 1 is adopted.
Mass loss rates of cool active MS stars belong to the least known parameters. The values from 1.3 × 10-10 M⊙/year (Demircan et al. 2006) down to 2 × 10-13 M⊙/year (Holzwarth & Jardine 2007) can be found in the literature. Equation (3) results from a relation between the directly observed mass loss rate per unit surface area and X-ray surface flux, see Fig. 7 in Wood et al. (2002) and Fig. 3 in Wood et al. (2005). The latter authors published measurements of three additional solar type stars. They included 70 Oph with a very high value of the mass loss rate into a final fit, but rejected ξ Boo, considering it as an outlier whose value of this rate is too low. If, however, both stars are included, one obtains the relation log ṁ ∝ (1.01 ± 0.24)log Fx, where ṁ is the stellar mass loss per unit surface area, expressed in the units of the solar mass loss rate. Deviations of 70 Oph and ξ Boo from the line described by this relation are roughly the same. The relation suggests a strict proportionality of mass loss rate and X-ray flux, both per unit surface area. For the saturated state Fx = 1−2 × 107 (in cgs units), hence ṁ ≈ 300−700 ṁ(Sun). We adopt 500 for this coefficient and with Ṁ(Sun) = 2 × 10-14 M⊙/year we obtain Eq. (3). The estimated uncertainty of the numerical factor in it is of order a factor of two.
Two more, albeit indirect, estimates give similar values for the mass loss rate. From a linear relation between mass loss rate and X-ray flux an upper limit for this rate can be found, applying the so-called, Reimers formula to rapidly rotating, solar type stars. The value 1.5 × 10-11 M⊙/year is obtained (Lednicka & Stȩpień 2008). Another rough estimate of the mass loss rate of these stars results from an observation that for magnetized winds the Alfvén radius is close to 10 stellar radii and varies little from star to star (Shore 1992). Taking Eq. (2) for one component with solar values of parameters and remembering that AML rate equals to (RA)2ωṀ, where RA is the Alfvén radius and ω – stellar angular velocity, we obtain after simple calculations, Ṁ = 0.8 × 10-11 M⊙/year. Both results are close to the value appearing in Eq. (3).
We assign the subscript “1” to the initially more massive stars and keep it this way also after mass ratio reversal, when this subscript denotes the less massive star. The mass ratio q ≡ M1/M2 so initially q > 1 and after the mass reversal q < 1.
The equations are combined with the third Kepler law and the approximations for Roche lobe sizes given by Eggleton (1983). The set of equations is integrated in time to follow the evolution of binaries with various initial masses and periods. We assume that the evolution of internal structure of each component can be approximated by the single star evolution. Models obtained by Girardi et al. (2000) and a set of low-mass models calculated for us by Dr. Sienkiewicz were used1. We also assume that both components independently lose AM through the magnetized wind, i.e. any interaction between them is neglected. The calculations start when the binary is on the ZAMS. It is detached at that time and AML results in shrinking of the orbit accompanied by the slow mass loss of the components. At the same time the components expand because of their internal evolution. At one point the shrinking Roche lobe of star “1” descends onto its surface and the (first) Roche lobe overflow (RLOF) occurs. This is followed by fast mass transfer from star “1” to star “2”. This process has not yet been satisfactorily modeled. The existing models suggest that the rapid transfer of a small amount of mass results in an expansion of star “2” followed by filling of its Roche lobe (Webbink 1976). A contact binary is formed. Following the idea put forward by Lucy (1968, 1976) and Flannery (1976), many authors assume that the expanded component does not relax thermally and stays oversized, transferring mass back to its more massive companion on the evolutionary time scale. It was, however, demonstrated by Stȩpień (2009) that the energy transfer between components of a contact binary takes place in the form of a large-scale circulation bound to the equatorial region of the less massive component. The core energy of that component can be freely radiated by the polar regions and the star remains in thermal equilibrium. This result indicates that star “2” will relax thermally when the fast mass transfer is stopped. In other words, it is assumed that mass transfer in cool close binaries is conceptually similar to the process taking place during the formation of semi-detached Algols. This process results in mass ratio reversal. Some amount of mass and AM may likely be lost during the common envelope phase but without reliable models of this phase, two additional free parameters would have to be introduced to allow for the losses. To avoid that, we assume conservative mass transfer during the RLOF – an assumption commonly accepted when modeling the formation of Algols.
For Pinit ≈ 2 d the time scale for AML is roughly equal to the evolutionary time scale of star “1” (Stȩpień 2006a; Gazeas & Stȩpień 2008) and varies with period as P4/3. Shorter initial periods result in early mass transfer when both components are still on the MS, whereas in binaries with initial periods exceeding 2 d mass transfer takes place when star “1” is depleted of hydrogen in the center or even possesses a small helium core. After the fast mass exchange the mass continues to flow from star “1” to star “2” at the much lower rate owing to the slow evolutionary expansion of star “1” accompanied by AML through the magnetized wind. Mass transfer lengthens the orbital period, whereas AML acts in the opposite direction. Time evolution of the orbital period and mass ratio is governed by interplay between these two processes. The instantaneous mass transfer is usually computed from a parametric formula (e.g. Eggleton & Kiseleva-Eggleton 2002), relating it to the amount by which the star overflows its Roche lobe. Instead of calculating that rate at each time step, an average (constant) mass transfer rate can be used. Its value results from the condition that the star fits into the Roche lobe at the beginning and at the end of the considered time interval (Gazeas & Stȩpień 2008). This is the approach we applied here.
Note that the above model does not contain any free parameters. The only adjustable parameter is the average mass transfer rate in the phase of slow mass transfer past fast mass exchange. Once the value of this parameter is found, the model is fully determined, which means that a binary with specified values of the initial orbital period and component masses evolves up to the final stage along a unique track.
2.2. Observational constraints and evolutionary scenario
The main constraints on the parameters of the progenitor of V1309 result from its photometric observations prior to the outburst (Tylenda et al. 2011). The first useful observations from 2002 show a regular light curve corresponding to a cool contact binary with an orbital period of 1.438 d. From two-color observations Tylenda et al. (2011) estimate the effective temperature of the binary at 4500 K. The uncertainty of this value can be estimated at 500 K.
Based on the red color of the binary, massive hot components are excluded. Because the components fill their Roche lobes, they must both be substantially oversized with respect to their expected MS sizes. This is true for any mass ratio and consequently both stars must be evolutionary advanced.
The observational constraints require that the initial orbital period should be longer than 2 days and the initial mass of star “1” should be higher than 1 M⊙, because this component must complete its MS evolution within the age of the binary. Indeed, its MS life time should be appropriately shorter than that because star “2” also needs time to complete its MS evolution prior to the eruption. The latter condition means that the initial mass of star “2” cannot be too low.
We assume that the outburst was triggered by an instability resulting from a rapid increase of the spin AM of the more massive component above the limiting value of about a third of the orbital spin AM (Rasio & Shapiro 1995; Eggleton & Kiseleva-Eggleton 2001), following its evolutionary expansion and filling the Roche lobe. The transfer of orbital AM into spin AM brings both components closer to one another so that they overflow the outer critical Roche surface and mass and AM are lost very efficiently through the L2 point (Webbink 1976). The process results in a rapid merging of the components. In contact binaries the instability sets in when the mass ratio reaches a critical value q ≈ 0.07−0.10 (the exact value depends on the detailed structure of the binary).
We calculated the evolution of binaries with initial masses between 1.1 and 1.3 M⊙ for star “1” and the initial masses between 0.5 and 1.1 for star “2” from the ZAMS to the pre-burst stage. We did not consider binaries with two identical components (qinit = 1).
3. Results and conclusions
As the detailed calculations show, very few models from the considered set lead to the binary with the observed pre-burst properties. The majority of the considered binaries end their evolution either as W UMa-type stars with periods of a fraction of a day if they lost too much AM, or as Algols with periods of several days if they lost too little AM. This divergence of the period is mostly due to the period dependence of the AML rate (Eq. (2)): the shorter the period, the higher the AML rate, and vice versa. The initial parameters must have just the right values so that with a specified AML rate, star “1” has enough time to complete its MS evolution and the mass exchange takes place in the AB case. The following evolutionary phase of the binary must take just so much time that star “2” completes its MS evolution and migrates to the base of the red giant branch.
 |
Fig. 1 Variations in time of the orbital period (top) and geometrical parameters of the binary with initial masses 1.2 + 0.6 M⊙ and initial period of 2.8 d. Short vertical bars denote: 1 – beginning of the fast mass transfer phase from star “1” to star “2”, 2 – end of the fast mass transfer phase, 3 – rapid increase of radius and moment of inertia of star “2” resulting in instability. |
Three models from the considered set fulfill all the requirements and reproduce the observations of V1309 Sco correctly. Their evolutionary parameters are given in Table 1 (the first three models). Figure 1 shows the time evolution of the orbital period (top) and the geometrical parameters (bottom) of one of the models. The time behavior of all three models is similar, although the total time scales are different. In particular, the total age of the first models exceeds 11 Gyr, which is rather long for a star from the galactic disk. Note a rapid increase of the radius of star “1” shortly before phase 1 and of star “2” at phase 3. The stellar radii are plotted very approximately in Fig. 1 between phases 1 and 2 because both stars are out of thermal equilibrium. In the final stage both components possess small helium cores with a mass of 0.10–0.15 M⊙.
We provide here a more detailed description of the evolutionary models. The initial period of each binary is long enough that star “1” reaches TAMS still in the detached phase but its Roche lobe has a size just slightly larger than the TAMS radius. The star expands while it builds a small helium core, and fills its lobe (phase 1 in Fig. 1). Fast mass transfer follows. When both components reach thermal equilibrium, an Algol is formed with a period between 1.2 and 1.6 d (phase 2 in Fig. 1). Between phases 2 and 3 mass transfer continues at a very low rate while the helium core of star “1” slowly grows. At the same time star “2” evolves across MS. After a few Gyr it reaches the TAMS and moves toward the red giant region. It fills its Roche lobe when it is at the bottom of the red giant branch (phase 3). It possesses a helium core at that time with a mass of about 0.15–0.16 M⊙. All three binaries look very similar just before the eruption: star “2” has a mass of about 1.5 M⊙ the mass ratio q ≈ 0.1 and the orbital period is about 1.43 d. These values of the binary parameters, in particular the extreme mass ratio, were not assumed in the modeling procedure. On the contrary, they result from the calculations. The mass transfer rate in the semi-detached phase is uniquely determined by the rate of evolution of star “1” together with the influence of the wind removing mass and AM from the system. The resulting values of mass transfer rate were between 0.8 − 1.3 × 10-10 M⊙/year, depending on the binary. Altogether, about 0.3 M⊙ were transferred in 2.5–3 Gyr – the time needed to finish the MS evolution by star “2” (between phases 2 and 3 in Fig. 1).
Main properties of the evolutionary models of the possible progenitors of V1309 Sco.
Table 1 shows that V1309 Sco might have been produced from a binary with the following initial parameters: more and less massive components from the range of 1.1–1.3 M⊙ and 0.9–0.5 M⊙, respectively and the orbital period from the range 2.5–3.1 d with the additional condition that the total mass should not exceed 2 M⊙. The pre-burst contact binary V1309 is different from W UMa-type stars. These stars have their primaries on the MS and stay in contact for a long time, on the order of Gyr (Stȩpień 2006a). The primary of V1309 Sco is a giant that recently filled its Roche lobe and the contact phase is very short, ending with coalescence.
The luminosity and the effective temperature of star “2” just before the outburst is equal to 7.5 L⊙ and 5000 K, respectively. With this luminosity the distance to the star is equal to 3700 pc. Assuming that star “2” transfers a fraction of its luminosity to star “1”, which is observed in contact binaries (Stȩpień 2009), the effective temperature of the whole binary is equal to about 4840 K, which is close to the temperature estimated by Tylenda et al. (2011). If the eruption resulted in merging of both components, the post-eruption star has a mass of about 1.7 M⊙ with a helium core of about 0.2–0.3 M⊙. The star will relax to the red giant stage.
The instability resulting in the merging of both components was triggered by a dramatic increase of the moment of inertia of star “2” when it approached the base of the red giant branch. It increased by a factor of several, up to the value of 1.8 × 1055 in cgs units (Rutten & Pylyser 1988). The migration time to the red giant region is on the order of 108 years, which is slow enough to keep the synchronization of its rotation with orbital period. As a result the spin AM of star “2” reaches 9 × 1050 in cgs units compared to about 3 × 1051 for orbital AM. The ratio of the spin AM to the orbital AM approaches 1/3, which is a sufficient condition for the occurrence of instability.
The uncertainties of the computed models come mostly from the uncertainty of the coefficients in Eqs. (2)–(3) and the accuracy of the evolutionary models of both components. An increase/decrease of the efficiency of AML via the wind by 30% requires an increase/decrease of the initial period by about 0.2 d to preserve the required amount of AM in the final, pre-burst model. A change of the mass loss rate by a factor of two requires a corresponding change of the initial masses by about 0.1 M⊙. Of particular importance is the case of a lower mass loss rate than resulting from Eq. (3). Let us take an example of the first model in Table 1. For the mass loss rate decreased by a factor of two, the initial mass of each component would have to be decreased by 0.1 M⊙ to obtain nearly identical pre-burst model as listed at the top of Table 1. However, the total age of this model would be higher by about 10%. To see the effect of a substantial decrease of the mass loss rate (beyond our estimated uncertainty), a series of models with the same initial masses as the first one in Table 1 were computed but with different initial orbital periods. The employed mass loss rate was five times lower than resulting from Eq. (3) i.e. at the level of the highest directly measured rate (Wood et al. 2005). The model that best reproduced the pre-burst binary was selected and is shown at the bottom of Table 1. The reduced mass loss rate influences the final model in several ways. The masses of both components are higher, which shortens the evolutionary time scales. A low mass loss rate accelerates the orbit tightening compared to the high rate. This is why the initial period had to be lengthened to a value 2.9 d, compared to 2.5 d in the first model in Table 1. Moreover, the final mass ratio has not reached a critical value for the Darwin instability to occur. Nevertheless, after star “2” left MS and approached the giant branch, a common envelope should develop, which may also result in a merging of both components.
An estimate of the uncertainties connected with the evolutionary models of the components is more difficult. Even the models of single stars differ significantly among different authors. In particular, time scales of the consecutive evolutionary stages and radii of the models may differ by several percent – compare, e.g., Schaller et al. (1992) and Girardi et al. (2000) (see also Torres et al. 2010). The differences result from different input physics, methods of computation, additional effects such as overshooting, the presence of magnetic fields, etc. The uncertainties resulting from interpolation in the existing sets of models or from differences between single star models and interacting binary component models are also difficult to assess. We assume that all those uncertainties amount to ± 10% on the input parameters and the final parameters of the pre-burst binary. The generous estimate of all uncertainties indicates that the ZAMS progenitor of V1309 Sco was a binary with the period between 2.3–3.3 d, the total mass between 1.7 and 2.2 M⊙ and the mass of the more massive component between 1.1 and 1.3 M⊙.
A description of the models is given in Stȩpień (2006a) and the details of the modeling program are given in Paczyński et al. (2007).
References
- Demircan, O., Eker, Z., Karataş, Y., & Bilir, S. 2006, MNRAS, 366, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2001, ApJ, 562, 1012 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P., & Kiseleva-Eggleton, L. 2002, ApJ, 575, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Flannery, B. P. 1976, ApJ, 205, 217 [Google Scholar]
- Gazeas, K., & Stȩpień, K. 2008, MNRAS, 390, 1577 [NASA ADS] [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, G., & Chiosi, C. 2000, A&AS, 141, 371 [Google Scholar]
- Holzwarth, V., & Jardine, M. 2007, A&A, 463, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lednicka, A., & Stȩpień, K. 2008, Astron. Nachr., 329, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1968, ApJ, 151, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1976, ApJ, 205, 208 [Google Scholar]
- Mason, E., Diaz, M., Williams, R. E., Preston, G., & Bensby, T. 2010, A&A, 516, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczyński, B., Sienkiewicz, R., & Szczygieł, D. M. 2007, MNRAS, 378, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasio, F. A., & Shapiro, S. L. 1995, ApJ, 438, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. G. M., & Pylyser, E. 1988, A&A, 191, 227 [NASA ADS] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schmitt, J. H. M. M. 1997, A&A, 318, 215 [NASA ADS] [Google Scholar]
- Shore, S. N. 1992, An Introduction to Astrophysical Hydrodynamics (Academic Press), 280 [Google Scholar]
- Soker, N,. & Tylenda, R. 2003, ApJ, 582, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Stȩpień, K. 2004, in Stars as Suns: Activity, Evolution and Planets, ed. A. K. Dupree, & A. O. Benz, ASP, IAU Symp., 219, 967 [Google Scholar]
- Stȩpień, K. 2006a, Acta Astron., 56, 199 [NASA ADS] [Google Scholar]
- Stȩpień, K. 2006b, Acta Astron., 56, 347 [NASA ADS] [Google Scholar]
- Stȩpień, K. 2009, MNRAS, 397, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Tylenda, R., & Soker, N. 2006, A&A, 451, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tylenda, R., Hajduk, M., Kamiński, T., et al. 2011, A&A, 528, A114 [Google Scholar]
- Webbink, R. F. 1976, ApJS, 32, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H. R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, B. E., Müller, H. R., Zank, G. P., Linsky, J. L., & Redfield, S. 2005, ApJ, 628, L143 [Google Scholar]
All Tables
Main properties of the evolutionary models of the possible progenitors of V1309 Sco.
All Figures
 |
Fig. 1 Variations in time of the orbital period (top) and geometrical parameters of the binary with initial masses 1.2 + 0.6 M⊙ and initial period of 2.8 d. Short vertical bars denote: 1 – beginning of the fast mass transfer phase from star “1” to star “2”, 2 – end of the fast mass transfer phase, 3 – rapid increase of radius and moment of inertia of star “2” resulting in instability. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


