| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201116531 | |
| Published online | 21 June 2011 | |
Research Note
Remarks on the properties of elliptical galaxies in modified Newtonian dynamics
1
Universidad de Concepción, Departamento de Astronomia, Concepción, Chile
e-mail: tom@astro-udec.cl
2
Argelander Institut für Astronomie, Universität Bonn, Bonn, Germany
3
Observatoire Astronomique de Strasbourg, CNRS, Strasbourg, France
4
Sterrenkundig Observatorium, Universiteit Gent, Gent, Belgium
Received: 17 January 2011
Accepted: 9 March 2011
Context. Two incorrect arguments against MOND in elliptical galaxies could be that the equivalent circular velocity curves tend to become flat at much larger accelerations than in spiral galaxies, and that the Newtonian dark matter halos are more concentrated than in spirals.
Aims. We compare published scaling relations for the dark halos of elliptical galaxies to the scaling relations expected for MONDian phantom halos.
Methods. We represent the baryonic content of galaxies by spherical profiles, and their corresponding MONDian phantom halos by logarithmic halos. We then derive the surface densities, central densities, and phase space densities and compare them with published scaling relations.
Results. We conclude that it is possible to recreate flat circular velocity curves at high acceleration in MOND, and that this happens for baryonic distributions described by Jaffe profiles in the region where the circular velocity curve is flat. Moreover, the scaling relations of the dark halos of ellipticals are remarkably similar to the scaling relations of phantom halos of MOND.
Key words: galaxies: elliptical and lenticular, cD / galaxies: kinematics and dynamics / gravitation
© ESO, 2011
1. Introduction
While data on large-scale structures point toward a Universe dominated by dark matter and dark energy (e.g. Komatsu et al. 2011), the nature of these remains a deep mystery (e.g. Frieman et al. 2008; Wiltshire 2008; Bertone 2010; Kroupa et al. 2010). In this context, it is good to keep in mind that this conclusion relies on the assumption that gravity is correctly described by Einstein’s general relativity in the extreme weak-field limit, a regime where the need for dark matter itself prevents the theory from being tested. Until this double dark mystery is solved, it is thus worth investigating alternative paradigms and their implications.
For instance, modified Newtonian dynamics (Milgrom 1983, MOND) naturally explains various spiral galaxy scaling relations (Tully & Fisher 1977; McGaugh et al. 2000; McGaugh 2004). The existence of a very tight baryonic Tully-Fisher relation for disk galaxies (McGaugh 2005; Trachternach et al. 2009) is for instance one of the remarkable predictions of MOND. The corresponding relation for early-type galaxies is much more difficult to investigate because they are pressure-supported systems, and the equivalent circular velocity curves determined from the velocity dispersion profiles suffer from the well-known degeneracy with anisotropy. However, some studies circumvented this problem: for instance, Kronawitter et al. (2000) used data on 21 elliptical galaxies to construct non-parametric models from which circular velocity curves, radial profiles of mass-to-light ratio, and anisotropy profiles as well as high-order moments could be computed. This led Gerhard et al. (2001, hereafter G01) to publish benchmark scaling relations for ellipticals. It was e.g. shown for the first time that circular velocity curves tend to become flat at much larger accelerations than in spiral galaxies. This would seem to contradict the MOND prescriptions, for which flat circular velocities typically occur well below the acceleration threshold a0 ~ 10-8 cm s-2, but not at accelerations of the order of a few times a0 as in ellipticals. In addition, Thomas et al. (2009, hereafter T09) published scaling relations for dark matter halos of 18 Coma galaxies, using similar prescriptions as G01. We note that G01 employed spherical models, while the models of T09 are axisymmetric.
Not many studies have considered the predictions of MOND in elliptical galaxies. Milgrom (1984) showed that pressure-supported isothermal systems have finite mass in MOND with the density at large radii falling approximately as r-4. It was also shown that MOND predicts a mass-velocity dispersion relation of the form (M/1011 M⊙) ≈ (σr/100 km s-1)4, which is similar to the observed Faber-Jackson relation (Sanders 2000, 2010), and that, in order to match the fundamental plane, MOND models must deviate from being strictly isothermal and isotropic: a radial orbit anisotropy in the outer regions is needed (Sanders 2000; Cardone et al. 2011). Tiret et al. (2007) and Angus et al. (2008) also analyzed the distribution of the velocity dispersions of PNe on scales of 20 kpc, and of satellites on very large scales of the order of 400 kpc around red isolated ellipticals, showing that MOND was able to reproduce both scales successfully.
Hereafter, we make general remarks about the properties of spherical galaxies within MOND, and their scaling relations. We first point out a remarkable property of elliptical galaxies exhibiting a flattening of their circular velocity curve at small radii: this flattening in the intermediate gravity regime is generated by a baryonic density distribution following a Jaffe profile in these parts of the galaxies. We then show that the observational scaling relations for the dark halos of the elliptical galaxy sample by G01 are strikingly similar to the theoretical “phantom” halos of MOND (i.e. the halo that would produce in Newtonian gravity the same additional gravity as MOND), with one remarkable exception: MOND predicts that the product of the central density with the core radius should be constant, as observed for spiral galaxies (Donato et al. 2009; Gentile et al. 2009).
2. Flat circular velocity curves and the Jaffe profile
Although it has been argued that some ellipticals do not need any dark matter or enhancement of gravity (Romanowsky et al. 2003), there are many counter-examples (Magorrian & Ballantyne 2001; Richtler et al. 2004; Schuberth et al. 2006; Kumar et al. 2007). An example is the elliptical galaxy NGC 2974 where the presence of an HI disk allowed a more or less direct measurement of circular velocities (Weijmans et al. 2008). There is also evidence that elliptical galaxies exhibit flat circular velocity curves, but that, in contrast to spiral galaxies, this happens in the inner regions where g > a0 (e.g., G01, Weijmans et al. 2008). This flattening of circular velocities is a priori not expected in the strong to intermediate gravity regime in MOND, and poses the question of how to analytically interpret it.
In the intermediate gravity regime, the transition from Newtonian to MONDian dynamics is described by the μ-function of MOND. Many concordant studies have recently shown that, in spiral galaxies, the “simple” transition of Famaey & Binney (2005) is a good representation of the data (Gentile et al. 2011, for an extensive discussion). In a spherical system, with this simple transition, the enclosed (baryonic) mass MM(r) needed to produce the same gravitational potential in MOND as the (baryonic+dark) mass MN(r) in Newtonian gravity is 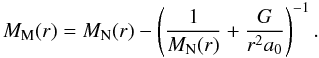 (1)In a region where the circular velocity is constant vc = V (even if g > a0), one can write MN(r) = V2r/G, thus after some algebra
(1)In a region where the circular velocity is constant vc = V (even if g > a0), one can write MN(r) = V2r/G, thus after some algebra 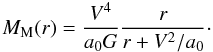 (2)Remarkably, this enclosed mass profile corresponds precisely to a Jaffe profile (Jaffe 1983) of scale-radius rj = V2/a0 (meaning that the acceleration is a0 at rj), and with total mass Mtot = V4/(a0G). Indeed, as the enclosed mass
(2)Remarkably, this enclosed mass profile corresponds precisely to a Jaffe profile (Jaffe 1983) of scale-radius rj = V2/a0 (meaning that the acceleration is a0 at rj), and with total mass Mtot = V4/(a0G). Indeed, as the enclosed mass 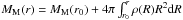 , this enclosed mass profile corresponds locally to the density profile:
, this enclosed mass profile corresponds locally to the density profile: 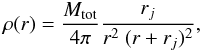 (3)with the characteristic surface density (see also Milgrom 1984)
(3)with the characteristic surface density (see also Milgrom 1984) 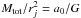 . This profile is of course invalid for the very inner parts of an elliptical galaxy, where V is not constant. We also note that (i) it was already known that a Jaffe profile produces a flat circular velocity curve at r ≪ rj in Newtonian gravity, which MOND generalizes to radii r ~ rj; (ii) Mtot does not necessarily have to be the true total mass of the galaxy, as the Jaffe profile fit to the density distribution could have a cut-off in the outer parts. In that case, the constant circular velocity V would fall slightly above the prediction from the baryonic Tully-Fisher relation of spiral galaxies. Interestingly, this is precisely what is observed for the G01 sample of ellipticals.
. This profile is of course invalid for the very inner parts of an elliptical galaxy, where V is not constant. We also note that (i) it was already known that a Jaffe profile produces a flat circular velocity curve at r ≪ rj in Newtonian gravity, which MOND generalizes to radii r ~ rj; (ii) Mtot does not necessarily have to be the true total mass of the galaxy, as the Jaffe profile fit to the density distribution could have a cut-off in the outer parts. In that case, the constant circular velocity V would fall slightly above the prediction from the baryonic Tully-Fisher relation of spiral galaxies. Interestingly, this is precisely what is observed for the G01 sample of ellipticals.
That elliptical galaxies can exhibit (equivalent) circular velocity curves that are flat in the intermediate gravity regime is thus analytically understood in MOND from the finding that the outer regions of ellipticals can be approximated by a Jaffe profile with a large scale-radius, i.e. in regions well within the intermediate gravity regime rather than in the deep-MOND regime. These flat circular velocity curves would have been impossible with exponential density profiles (as encountered in spiral galaxies), meaning that circular velocity curves becoming flat quicker in ellipticals does not come as a surprise in the context of MOND.
This looks like an interesting possibility to devise new tests of MOND based on photometry. However, in reality it might be difficult: not many spherical galaxies with a precisely measured density profile are dynamically investigated out to large radii, and have enough tracers to measure the higher order moments and constrain the anisotropy. Moreover, light might not trace the baryonic mass precisely. As an example, the circular velocity in NGC 2974, which can be traced by an HI disk, becomes constant at around 5 kpc and has the value 300 km s-1, which would correspond to a Jaffe scale radius of 23 kpc. Unfortunately, NGC 2974 is neither spherical nor the subject of photometry reaching large radii, so it does not serve well as a test object. In any case, Weijmans et al. (2008, their Fig. 20) showed that the reverse procedure (going from the density to the circular velocity curve) leads to a very good fit.
3. Dark matter scaling relations for phantom halos of ellipticals
Parameters of MONDian phantom halos represented by logarithmic potentials.
We now apply the reverse procedure, and check whether the phantom halos predicted by the simple transition of MOND (Famaey & Binney 2005) comply with the observational scaling relations of dark halos of ellipticals. As stated above, Jaffe profiles are not good descriptions of the very inner parts of ellipticals. We hereafter choose Hernquist profiles (Hernquist 1990) instead to represent the baryonic content of ellipticals: these are realistic enough and allow for an exhaustive exploration of their properties without varying too many free parameters. This Hernquist model is described by its total mass M and scale radius rH. The profile of the Newtonian circular velocity curve is then given by 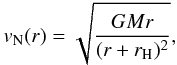 (4)where the scale radius rH of the Hernquist-model is related to the effective (half-light) radius by Reff = 1.815 rH.
(4)where the scale radius rH of the Hernquist-model is related to the effective (half-light) radius by Reff = 1.815 rH.
Adopting the simple transition formula between the Newtonian and the MONDian regime, one finds for the MOND circular velocity that 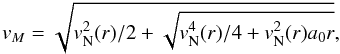 (5)and the MONDian phantom halo has the circular velocity
(5)and the MONDian phantom halo has the circular velocity 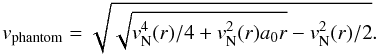 (6)To enable a comparison with the scaling relations of G01, where the dark matter halos are adopted as logarithmic halos, we fit vphantom(r) to the circular velocity vlog (r) of a logarithmic halo with asymptotic circular velocity v0 and core radius r0, given by
(6)To enable a comparison with the scaling relations of G01, where the dark matter halos are adopted as logarithmic halos, we fit vphantom(r) to the circular velocity vlog (r) of a logarithmic halo with asymptotic circular velocity v0 and core radius r0, given by 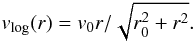 (7)The fits are performed within the inner two effective radii1. The fitted central dark matter density is then given by
(7)The fits are performed within the inner two effective radii1. The fitted central dark matter density is then given by 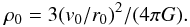 (8)The central phase space density is defined (see G01) as
(8)The central phase space density is defined (see G01) as 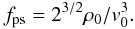 (9)The characteristic surface density within r0 is then also defined as (see also Donato et al. 2009)
(9)The characteristic surface density within r0 is then also defined as (see also Donato et al. 2009) 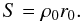 (10)Table 1 lists these fitted parameters for six baryonic Hernquist masses over a large mass range. The combinations of the masses and effective radii in Table 1 follow Eq. (5) of G01 (in accordance with the fundamental plane), where we transformed their luminosities into masses by using M/LB = 8 for all galaxy baryonic masses.
(10)Table 1 lists these fitted parameters for six baryonic Hernquist masses over a large mass range. The combinations of the masses and effective radii in Table 1 follow Eq. (5) of G01 (in accordance with the fundamental plane), where we transformed their luminosities into masses by using M/LB = 8 for all galaxy baryonic masses.
 |
Fig. 1 The figure shows the surface density, central density, and the central phase space density logarithmically (see the text for more explanation) of the phantom dark halos for different baryonic Hernquist masses from Table 1 together with the relations given by G01 (dotted lines) and T09 (dashed lines). Note that these parameters observationally exhibit a very large scatter around the mean relations. Note also that the relations of T09 are not given explicitly in their paper but have been constructed from their Table 3 omitting galaxies with young stellar cores. |
Figure 1 shows the values of the fitted dark halo parameters derived by applying MOND to the baryonic Hernquist profiles, together with the observational scaling relations given by G01 (dotted lines) and T09 (dashed lines). The upper panel shows the characteristic phase space density, the middle panel the central volume density, and the lower panel the characteristic surface density. We note that the plotted relations are only indicative, since the data (Fig. 18 of G01 and Figs. 1 and 4 of T09) show a very large scatter even when logarithmically displayed. However, within this observational uncertainty, it is remarkable that some features are perfectly reproduced, particularly the slopes of the phase space density and the central volume density as a function of baryonic mass (given the observational scatter, the almost perfect reproduction of the central volume density of G01 might of course be partly coincidental).
As first emphasized by G01, the phase-space density values at a given mass are higher than in spirals, which means that under the Λ Cold Dark Matter paradigm, dark halos of ellipticals cannot be the result of collisionless mergers of present-day spirals, but must have been assembled at a very early time, when the cosmological density was higher. In MOND, this is of course not necessarily the case, as the phase-space argument does not apply to phantom halos.
One also notes a remarkable exception to the scaling relations: the fitted characteristic dark matter surface density S is fully independent of the Hernquist parameters, and is systematically lower than in G01 and T09. We emphasize that this constancy is not related to the special relation of mass and effective radius. Varying Reff by a factor of two at a given mass does not change the constant surface density significantly. This prediction of MOND thus brings the value closer to the (also constant) value of S observed in spiral galaxies, log S = 2.1 (Donato et al. 2009). We note that MOND also predicts the observed constant value of S in spirals, which is somewhat lower because (i) spirals are a bit deeper into the MOND regime (Milgrom 2009) and (ii) their flattened baryonic profiles lead to a somewhat higher Newtonian gravity at a given mass, and in turn a somewhat lower MOND contribution to the phantom halo.
At the first glance, one might interpret this constancy and the other scaling relations as a clear signature of MOND in ellipticals; however, CDM may also predict that the surface density within the scale radius of NFW halos weakly depends on dark matter total mass (Boyarsky et al. 2010). For spiral galaxies, this is of little interest as it is known that cuspy profiles often do not fit rotation curves (Famaey & Binney 2005; de Blok 2010; Gentile et al. 2005), the mystery then being how to erase the cusp by the feedback from the baryons while keeping the product ρ0r0 constant. In elliptical galaxies, the situation is less clear as NFW profiles often reproduce the data equally well as cored profiles (Schuberth et al. 2010). We thus fitted NFW profiles to the same MONDian phantom halos and found perfect agreement. The question remains of whether these NFW-halos are “cosmological” or in other words, fulfill the relation between virial mass and concentration predicted by cosmological simulations. For our Hernquist masses, Fig. 2 displays the resulting concentrations of the NFW-halos (open circles) corresponding to the MONDian phantom halos, while the triangles show the concentration values expected from Eq. (9) of Macciò et al. (2008), where the mean density within the virial radius is defined to be 200 times the critical density for a standard cosmology: h = 0.7, Ωm = 0.3, ΩΛ = 0.7. One concludes that for high masses the MONDian phantom halos are indistinguishable from cosmological NFW halos, given also that the simulations predict that there is considerable scatter. For lower masses, the difference between MONDian phantom halos and NFW cosmological halos is larger.
 |
Fig. 2 The figure shows for our 6 Hernquist masses the concentration parameters of the associated NFW-halos, if the MONDian phantom halos are fitted by NFW profiles (open circles). The triangles are the concentration parameters expected from the relation quoted by Macciò et al. (2008) |
4. External field effect
Owing to the non-linearity of MOND and its associated breaking of the strong equivalence principle, a MONDian stellar system embedded in an external gravitational field (EF) stronger than its own internal field behaves in a quasi-Newtonian way, with an effectively higher gravitational constant (Milgrom 1983; Famaey et al. 2007). Most of the sample galaxies are located in clusters or groups where the EF might have an influence. Wu et al. (2010), for instance, showed how the EF can lead to the lopsidedness of an originally axisymmetric non-isolated galaxy.
While it is beyond the scope of this research note to evaluate in detail the EF in the present sample, a very rough estimation is presented in Fig. 3, which plots for the Virgo and Coma clusters the accelerations based on the mass models cited in the figure caption (the extrapolation for Virgo is only meant to give an order of magnitude estimate, but should not be taken as a rigorous model). This can be compared with the internal accelerations at 2 Reff for the Hernquist models in Table 1. Indicated are the projected distances of galaxies in the Virgo and Coma region. The positions of the Virgo galaxies correspond to the middle points of their NGC numbers, while the Coma galaxies are plotted as small open circles. One concludes that the EF should have no influence in the two samples at the galactocentric distances that we consider.
 |
Fig. 3 This plot estimates the external field for Virgo and Coma galaxies. Abscissa is the projected distance in Mpc from M 87 and NGC 4874, respectively. Ordinate is the acceleration in units of a0. The adopted distances for Virgo and Coma are 15 Mpc and 100 Mpc, respectively. The values for Virgo are generated by an extrapolation of the M 87 mass model of McLaughlin (1999). Some G01 galaxies are indicated by their NGC numbers. The values for Coma are generated by using the NFW dark halo of Łokas & Mamon (2003). Small open circles are the 18 T09 galaxies whose projected distances are taken from Godwin et al. (1983). The comparison with Table 1 shows that the EF is small. |
5. Conclusion
We have demonstrated that (i) in MOND, galaxies exhibit a flattening of their circular velocity curve at high gravities (g > a0) if they are described by a Jaffe profile with characteristic surface density a0/G in the region where the circular velocity is constant (since this is impossible for exponential profiles, it is remarkable that these flattenings of circular velocity curves at high accelerations are only observed in elliptical galaxies); (ii) the phantom halos of ellipticals predicted by MOND (i.e., the dark halos that in Newtonian gravity would produce the same additional gravity as MOND) can be fitted by logarithmic halos that perfectly reproduce the observed scaling relations of ellipticals for phase-space densities and central volume densities ρ0; (iii) these halos have a constant characteristic surface density ρ0r0; (iv) in contrast to spirals (for which there are more data in the very central parts), the phantom halos of ellipticals can also be fitted by cuspy NFW halos, the concentration of which is in accordance with the theoretical predictions of ΛCDM for the highest masses, but in slight disagreement for baryonic masses smaller than 1011M⊙: a modern, large, sample of elliptical galaxies, which are dynamically studied well to large radii and cover a large range of masses, will thus be required. In any case, regardless of the true physical reason, it is remarkable that a recipe (MOND) known to fit rotation curves of spiral galaxies with remarkable accuracy also apparently predicts the observed distribution of “dark matter” in elliptical galaxies.
Acknowledgments
We thank the anonymous referee for a thoughtful report. T.R. acknowledges financial support from the Chilean Center for Astrophysics, FONDAP Nr. 15010003, from FONDECYT project Nr. 1100620, and from the BASAL Centro de Astrofisica y Tecnologias Afines (CATA) PFB-06/2007. B.F. acknowledges the support of the Humboldt foundation. GG is a postdoctoral researcher of the FWO-Vlaanderen (Belgium).
References
- Angus, G. W., Famaey, B., Tiret, O., Combes, F., & Zhao, H. S. 2008, MNRAS, 383, L1 [NASA ADS] [Google Scholar]
- Bertone, G. 2010, Nature, 468, 389 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyarsky, A., Neronov, A., Ruchayskiy, O., & Tkachev, I. 2010, Phys. Rev. Lett., 104, 191301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cardone, V. F., Angus, G., Diaferio, A., Tortora, C., & Molinaro, R. 2011, MNRAS, 412, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G. 2010, Adv. Astron., 2010, 789293 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, F., Gentile, G., Salucci, P., et al. 2009, MNRAS, 397, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., & Binney, J. 2005, MNRAS, 363, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Bruneton, J., & Zhao, H. 2007, MNRAS, 377, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Frieman, J. A., Turner, M. S., & Huterer, D. 2008, ARA&A, 46, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Burkert, A., Salucci, P., Klein, U., & Walter, F. 2005, ApJ, 634, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile, G., Famaey, B., Zhao, H., & Salucci, P. 2009, Nature, 461, 627 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gentile, G., Famaey, B., & de Blok, W. J. G. 2011, A&A, 527, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerhard, O., Kronawitter, A., Saglia, R. P., & Bender, R. 2001, AJ, 121, 1936 [NASA ADS] [CrossRef] [Google Scholar]
- Godwin, J. G., Metcalfe, N., & Peach, J. V. 1983, MNRAS, 202, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, W. 1983, MNRAS, 202, 995 [NASA ADS] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kronawitter, A., Saglia, R. P., Gerhard, O., & Bender, R. 2000, A&AS, 144, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P., Famaey, B., de Boer, K. S., et al. 2010, A&A, 523, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kumar, B., Romanowsky, A. J., Richtler, T., et al. 2007, in VI Reunion Anual Sociedad Chilena de Astronomia (SOCHIAS), 27 [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2003, MNRAS, 343, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Dutton, A. A., & van den Bosch, F. C. 2008, MNRAS, 391, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., & Ballantyne, D. 2001, MNRAS, 322, 702 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2004, ApJ, 609, 652 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S. 2005, ApJ, 632, 859 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., Bothun, G. D., & de Blok, W. J. G. 2000, ApJ, 533, L99 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McLaughlin, D. E. 1999, ApJ, 512, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 371 [Google Scholar]
- Milgrom, M. 1984, ApJ, 287, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2009, MNRAS, 398, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Richtler, T., Dirsch, B., Gebhardt, K., et al. 2004, AJ, 127, 2094 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Douglas, N. G., Arnaboldi, M., et al. 2003, Science, 301, 1696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sanders, R. H. 2000, MNRAS, 313, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H. 2010, MNRAS, 407, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Dirsch, B., et al. 2006, A&A, 459, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thomas, J., Saglia, R. P., Bender, R., et al. 2009, ApJ, 691, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Tiret, O., Combes, F., Angus, G. W., Famaey, B., & Zhao, H. S. 2007, A&A, 476, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trachternach, C., de Blok, W. J. G., McGaugh, S. S., van der Hulst, J. M., & Dettmar, R. 2009, A&A, 505, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B., & Fisher, J. R. 1977, A&A, 54, 661 [NASA ADS] [Google Scholar]
- Weijmans, A., Krajnović, D., van de Ven, G., et al. 2008, MNRAS, 383, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Wiltshire, D. L. 2008, Int. J. Mod. Phys. D, 17, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, X., Zhao, H., & Famaey, B. 2010, J. Cosmology Astropart. Phys., 6, 10 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The figure shows the surface density, central density, and the central phase space density logarithmically (see the text for more explanation) of the phantom dark halos for different baryonic Hernquist masses from Table 1 together with the relations given by G01 (dotted lines) and T09 (dashed lines). Note that these parameters observationally exhibit a very large scatter around the mean relations. Note also that the relations of T09 are not given explicitly in their paper but have been constructed from their Table 3 omitting galaxies with young stellar cores. |
| In the text | |
 |
Fig. 2 The figure shows for our 6 Hernquist masses the concentration parameters of the associated NFW-halos, if the MONDian phantom halos are fitted by NFW profiles (open circles). The triangles are the concentration parameters expected from the relation quoted by Macciò et al. (2008) |
| In the text | |
 |
Fig. 3 This plot estimates the external field for Virgo and Coma galaxies. Abscissa is the projected distance in Mpc from M 87 and NGC 4874, respectively. Ordinate is the acceleration in units of a0. The adopted distances for Virgo and Coma are 15 Mpc and 100 Mpc, respectively. The values for Virgo are generated by an extrapolation of the M 87 mass model of McLaughlin (1999). Some G01 galaxies are indicated by their NGC numbers. The values for Coma are generated by using the NFW dark halo of Łokas & Mamon (2003). Small open circles are the 18 T09 galaxies whose projected distances are taken from Godwin et al. (1983). The comparison with Table 1 shows that the EF is small. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


