| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201116513 | |
| Published online | 15 June 2011 | |
The inner heliospheric source for keV-energetic IBEX ENAs
The anomalous cosmic ray-induced component
1
Argelander Institut für Astronomie der Universität Bonn, Abteilung f. Astrophysik und Extraterrestrische Forschung, Auf dem Huegel 71, 53121 Bonn, Germany
e-mail: hfahr@astro.uni-bonn.de
2
Southwest Research Institute, San Antonio, TX USA and University of Texas, San Antonio, San Antonio, TX, USA
3
Department of Astronomy, University of New Hampshire, Durham, NH, USA
Received: 14 January 2011
Accepted: 11 May 2011
Context. Up to now, three succesive full-sky maps of heliospheric fluxes of KeV-energetic neutral H-atoms have been registered with the satellite IBEX. The most outstanding feature persisting in these maps is the so-called ribbon which appears as an arc around the upwind direction with unexpectedly high fluxes. This radiation feature was not predicted by models, but at present is tentatively explained as due to energetic plasma sites outside the heliosphere in regions beyond the heliopause.
Aims. Since all these proposed explanations, however, need to rely on unproven energizing ion processes, we shall investigate in this article alternative ion sources of keV-ENAs that in contrast appear much closer to the sun, but are based on a clear concept of ion energization to KeV energies, namely suprathermal pick-up ions at a few AU inside and outside of the solar wind termination shock.
Methods. Using well-established models for the solar wind magnetic field and the heliospheric TS surface, we derive skymaps of the magnetic field tilt angle, the resulting injection efficiency and the resulting ENA flows. The results are normalised to the ion flux observations made by Voyager-1. We also discuss basic modifications of the TS geometry within the framework of the model.
Results. We calculate ENA fluxes of these pick-up ions and show that they, due to their sensitivities to magnetic tilt angles at the termination shock surface, reveal a radiative sickle feature around the upwind direction which in many of its properties resembles the ENA ribbon feature seen by IBEX, although the highest IBEX intensities do not seem to be quantitatively representable by our calculations.
Key words: shock waves / plasmas / solar wind / Sun: heliosphere
© ESO, 2011
1. Introduction
Plasma regions in the heliosphere are, unfortunately, not remotely observable from the earth, since they generally do not emit electromagnetic radiation. For that reason, until recently, no direct information existed about the actual physics going on at and beyond the border of the solar system and the heliosphere. Instead, all our knowledge was derived from magnetohydrodynamical speculations and theoretical simulations trying to anticipate the transheliospheric plasma states, the accuracy of which, however, depends on the specific microphysics implemented numerically. In the past several years in situ observations have also become available from the Voyager 1 and then 2 spacecraft as they each crossed the Termination Shock and began making observations at two unique locations in the inner heliosheath (Stone et al. 2005, 2008; Decker et al. 2005, 2008).
Most recently, a new, global window on these systems was opened thanks to newly developed detectors specifically targeting the observation of energetic neutral atoms (ENAs) coming from distant plasma sites (McComas et al. 2006, 2009a,b). Such ENAs are produced at the distant plasma sites by charge exchange collisions of ions with H-atoms which, maintain the thermodynamical state of their parent ions, and are able to transport this information directly to an earth-orbiting detector, without being deflected by heliospheric electromagnetic fields (for a review, see Fahr et al. 2007).
Two of the most technologically advanced ENA detectors were put into a highly elliptical earthbound orbit onboard of the IBEX satellite in the end of 2008 (see McComas et al. 2006, 2009b), and from the beginning of 2009 accumulated unique ENA data from all directions of the sky. The unique mission design provides one full sky coverage in just half a year of observation time, and towards the end of 2009 the first IBEX full-sky ENA maps at various energies were published (McComas et al. 2009a). The IBEX-Hi ENA detector, which covers the range of ENA energies from 0.6 up to 6 keV, discovered an outstanding and exciting feature prevalent through all energy channels; the same feature was observed with poorer statistics by IBEX-Lo at energies down to 100 eV. This feature, which was completely unexpected and still provides a major challenge to all theoreticians, consists of an enhanced ENA emissive region (dubbed the “ribbon” in present literature) running in an angle of 30 degrees around the inflow direction of the local interstellar medium (LISM), i.e. the heliospheric nose. While all theoretical calculations up to 2009 predicted a diffuse ENA emissivity pattern extending from the nose (i.e. the apex of the solar system) to the tail of the heliosphere, which is also observed by IBEX, the ribbon in contrast not only shows higher than expected ENA fluxes, but also appearing in a spatially strongly limited region (see McComas et al. 2009a; Schwadron et al. 2009). At present many efforts are undertaken to interpret this extraordinary emission feature. One leading concept to explain the Ribbon is the idea of an emission region outside of the heliopause (i.e. at solar distances larger than 150 AU), where interstellar magnetic fields could pile up due to magnetic draping effects. These ideas were initially proposed by McComas et al. (2009a) and are shown as processes 2 and 3 in Fig. 1. Since then, several additional papers have examined these possibilities in more detail Schwadron et al. (2009); Grzedzielski et al. (2010); Heerikhuisen et al. (2010); Chalov et al. (2010).
In this paper we investigate an alternative source which in contrast to the others is located inside the solar wind termination shock and is explained by neutralization of keV-energetic ions in the region upstream of this shock, i.e. at distances smaller than 90 AU from IBEX, with some continuation downstream of the shock, communicating plasma source conditions in less than one year. This process, complementing the above mentioned ones, was qualitatively mentioned as process (5) in the original Science paper McComas et al. (2009a) and followup study McComas et al. (2010) (see illustrative Fig. 1). In this study, we present quantitative calculations of possible ENA intensity patterns arising from this inner heliospheric source.
 |
Fig. 1 Schematic representation of ENA generation processes appearing in current discussions of the IBEX ribbon. Taken from McComas (2010); see also McComas et al. (2009a, 2010). |
2. Sources of keV ENAs in the inner heliosphere
2.1. Injection to PUIs from the ACR-regime
In the paper by Fahr et al. (2009), the authors considered how shock-generated anomalous cosmic ray particles (ACRs) behave when diffusing inwards from the shock and getting modulated in energy due to adiabatic cooling processes. These authors showed that with the loss of particle energy and the associated decrease of the spatial diffusion coefficient, these ions eventually lose their diffusive mobility while propagating inwards and then are again convected outward with the bulk of the solar wind to increasing solar distances. In principle, GCRs need to be taken into account as well. However, ignoring this contribution by only taking into account ACRs is justified by the observational fact that, especially during solar minimum and at energies below 1 MeV/nucleon, ACRs are the dominant contribution (see e.g. Christian et al. 1995), providing the dominant contribution to our term. ACR/GCR modulation theory then leads to an expression for the distribution function f(r,p) which is constant at low momenta p, respectively low energies E = p2/2m, and at small solar distances r. This result, however, is solidly connected with the fact that the ACR/GCR streaming S(f) has a negative spatial divergence (i.e. ions are lost). One thus can cut off the ACR/GCR spectrum at some lower border ppui, where ions are reconvected radially outwards with the solar wind, and instead calculate the local losses due to this integrated S-divergence, which one can then take as source to the pick-up ion regime. As shown by Fahr et al. (2009), the integrated losses only depend on the lower cut-off border ppui and lead to a constant and ubiquitous injection rate of ions at the energy  keV. If this injection rate is now added to a pick-up ion transport equation, solving this equation, together with convective changes and cooling, leads to power law PUI spectra which are independent on r, behaving exclusively like v-4.
keV. If this injection rate is now added to a pick-up ion transport equation, solving this equation, together with convective changes and cooling, leads to power law PUI spectra which are independent on r, behaving exclusively like v-4.
Additional diffusion processes may result in a modified distribution function. In addition to diffusion due to conventional nonlinear wave-particle interactions with Alfven waves, which however were shown to be too inefficient by Chalov et al. (2004) and Fahr et al. (2009), a further mechanism of transit time damping was proposed by Fisk (1976), which described stochastic ion interactions with local field compressions. Energy diffusion by this transit time-damping mechanism was compared in its efficiency with acceleration due to nonlinear interaction with Alfvenic turbulences by Fichtner et al. (1996) and Chalov et al. (1997), who found that due to the rapid decrease of the field compression amplitude with distance, transit time damping in the pick-up ion regime can also not be efficient at distances beyond 10 AU. On the other hand, the compressional pumping mechanism proposed more recently by Fisk & Gloeckler (2008) works for the higher-energetic (i.e. > 100 keV) diffusive ion population, but again, not for the adiabatically reacting core population.
Therefore, sinks in the ACR population are transformed as sources for the pick-up ion population. With this additional ACR-induced pick-up ion injection term, and without need of any energy-diffusion process, the resulting pick-up ion distribution function was derived in an analytic form by solving an adequate Boltzmann-Vlasow transport equation for this scenario. The resulting solution is given by  (1)with Λ = σexnH,s rE, where the charge exchange cross section is given by σex ≃ 2 × 10-15 cm2 and the interstellar hydrogen density near the upwind termination shock is given by 0.03 ≤ nH, s ≤ 0.1 cm-3. In addition, np, E is the solar wind proton density at r = rE = 1 AU, U is the solar wind bulk velocity, and ppui, respectively vpui, are the critical momentum and velocity of ions injected from the ACR regime. The quantity
(1)with Λ = σexnH,s rE, where the charge exchange cross section is given by σex ≃ 2 × 10-15 cm2 and the interstellar hydrogen density near the upwind termination shock is given by 0.03 ≤ nH, s ≤ 0.1 cm-3. In addition, np, E is the solar wind proton density at r = rE = 1 AU, U is the solar wind bulk velocity, and ppui, respectively vpui, are the critical momentum and velocity of ions injected from the ACR regime. The quantity  is the constant value of the ACR distribution function at p = ppui. The function H(x) is the Heaviside step function with H(x ≤ 0) = 0 and H(x > 0) = 1.
is the constant value of the ACR distribution function at p = ppui. The function H(x) is the Heaviside step function with H(x ≤ 0) = 0 and H(x > 0) = 1.
The assumption that f(v) does not depend upon distance can, unfortunately, not be derived from experimental data, since even ULYSSES, the mission covering the greatest distances while providing significant PUI-data related to this point, did not provide data at solar distances of 5 AU ≤ r ≤ 90 AU. Especially the core region of this interval, between 10 and 80 AU, is unfortunately “uncharted territory” what concerns ion spectra in the energy range between a few to a few 100 keV. The lower energetic particle detectors on the Voyagers (see Lanzerotti et al. 2001; Krimigis et al. 2004) start with energies of about 0.5 MeV/nuc, thus not covering the range below 100 keV. Describing spectra to be expected in this range of energies and distances hence is exclusively a matter of theoretical speculations.
In addition, it is possible to assume that the form of the PUI distribution function can be separated into an r-dependent and a longitude-dependent function. Fahr et al. (1992) have shown that, under axial symmetry conditions, the ACR transport equation can be solved by a separation ansatz for the distribution function, i.e. in the form f ∝ g(β,v)·h(r,v), where β is the longitude angle measured from the upwind direction. This result suggests that a similar approach is possible in this study.
Before examining the magnitude of this quantity  , we would like to clarify the following point: in the following we are looking exclusively for ion sources in the inner heliosphere that can produce ENAs seen by IBEX in the range of energies higher than several hundred eV (say 0.6–6.0 keV). Since the pick-up ions described by the above distribution function are all moving with the solar wind bulk flow, one can easily see that the first term of Eq. (1) does not contain ions that can contribute to this kind of ENAs (i.e. ions with v ≤ U). In the following we shall thus only examine ENAs produced from ions described by the second term of this equation, which is why we now study the most essential quantity of this term,
, we would like to clarify the following point: in the following we are looking exclusively for ion sources in the inner heliosphere that can produce ENAs seen by IBEX in the range of energies higher than several hundred eV (say 0.6–6.0 keV). Since the pick-up ions described by the above distribution function are all moving with the solar wind bulk flow, one can easily see that the first term of Eq. (1) does not contain ions that can contribute to this kind of ENAs (i.e. ions with v ≤ U). In the following we shall thus only examine ENAs produced from ions described by the second term of this equation, which is why we now study the most essential quantity of this term,  . At this point, we would like to emphasize that the first term – after passing the termination shock from the upstream to the downstream side – does result in a distribution function that is able to generate observable ENA flows. This term will be studied in a separate puplication which is currently under preparation.
. At this point, we would like to emphasize that the first term – after passing the termination shock from the upstream to the downstream side – does result in a distribution function that is able to generate observable ENA flows. This term will be studied in a separate puplication which is currently under preparation.
In the earlier approach (Fahr et al. 2009), this quantity was taken as a constant which is reasonable in a radially symmetric approach to the problem. However, since the termination shock is not expected to be spherical, but instead to vary in a characteristic way with larger heliocentric distances at larger angles from the nose of the heliosphere (McComas & Schwadron 2006),  , which is closely connected with the ion injection rate to the ACR regime at the termination shock must also vary with longitude and latitude. Here we investigate the variation of this injection rate with the angle θ between the upstream magnetic field and the shock normal. The connection of
, which is closely connected with the ion injection rate to the ACR regime at the termination shock must also vary with longitude and latitude. Here we investigate the variation of this injection rate with the angle θ between the upstream magnetic field and the shock normal. The connection of  with the injection of pick-up ions to the ACR regime becomes evident from the following expression derived in Fahr et al. (2009), where the differential ACR intensity is defined by
with the injection of pick-up ions to the ACR regime becomes evident from the following expression derived in Fahr et al. (2009), where the differential ACR intensity is defined by  (2)with fACR(r,p) as the ACR distribution function. Then the differential streaming is given by (Gleeson & Axford 1967)
(2)with fACR(r,p) as the ACR distribution function. Then the differential streaming is given by (Gleeson & Axford 1967)  (3)which, considering the local spatial divergence of this streaming at the critical momentum border p = ppui, i and using Eq. (55) of Fahr et al. (2009), gives us the upper source to the pick-up ion regime in the form
(3)which, considering the local spatial divergence of this streaming at the critical momentum border p = ppui, i and using Eq. (55) of Fahr et al. (2009), gives us the upper source to the pick-up ion regime in the form  (4)where
(4)where  is the ACR ion injection at the termination shock which is directly proportional to the distribution function
is the ACR ion injection at the termination shock which is directly proportional to the distribution function  .
.
Next, we assume that this injection is dependant on two physical processes. First, there is the local ion injection efficiency ϵ describing the percentage of pick-up ions locally entering into the Fermi-1 shock acceleration process due to repeated back- and forth-scatterings between upstream and downstream flow conditions at the shock. (see Kucharek & Scholer 1995; Chalov & Fahr 1996; Giacalone & Jokipii 1999; McComas & Schwadron 2006; Kallenbach et al. 2009), and second, we also consider the total local upstream pick-up ion flux Φi, s arriving at the shock. This finally results in  (5)As discussed in the following sections, both these quantities vary as function of the conditions of the specific shock position r = rs(α,δ) in the celestial position defined by the ecliptic coordinates α and δ. Since the IBEX project is using a different orientation of the coordinate system, namely one with the nose centered at (α,δ) = (0,0), we will use a similar coordinate system, i.e. an ecliptic system rotated to a nose/upstream direction fixed at (0,0). In the following part of the study, we will call this the “IBEX coordinate system”.
(5)As discussed in the following sections, both these quantities vary as function of the conditions of the specific shock position r = rs(α,δ) in the celestial position defined by the ecliptic coordinates α and δ. Since the IBEX project is using a different orientation of the coordinate system, namely one with the nose centered at (α,δ) = (0,0), we will use a similar coordinate system, i.e. an ecliptic system rotated to a nose/upstream direction fixed at (0,0). In the following part of the study, we will call this the “IBEX coordinate system”.
2.2. The injection efficiency
Fahr et al. (2008) derived the expression for the injection efficiency ϵ = ϵ(θ) as function of the local magnetic tilt angle θ = θ(α,δ), i.e. the angles between the upstream magnetic field and the shock normal vector. This efficiency for average interplanetary Alfvenic turbulence levels is given by Chalov & Fahr (1996) and is best-fitted by the expression (Fahr et al. 2008) ![\begin{equation} \epsilon (\theta) = \epsilon_{0}\left( (1-\gamma )\exp [-k\times \theta^{n}]+\gamma \right) \label{eq-epsilon} \end{equation}](/articles/aa/full_html/2011/07/aa16513-11/aa16513-11-eq48.png) (6)with k = 2 × 10-20 and n = 10.9. This clearly shows a plateau with ϵ ≃ ϵ0 = 10-2 for tilt angles θ ≤ 60° and a strong fall-off of ϵ at tilt angles θ ≥ 65° (see Sect. 2.4 for a more detailed study of this function). At these large tilt angles the quantity γ, which is the ratio of periods of a magnetic current sheath passage over the shock and the full solar rotation period, becomes important (see Fahr et al. 2008) and also ensures that ϵ(θ) does not drop to zero. Estimating a realistic value of γ, however, is not trivial; the parameter γ is the relative length of the period during which, at current sheet crossings of the termination shock due to the turning of the magnetic field vector, the magnetic field angle θ is much smaller than the normal angle for monodirectional Archimedian fields. On the basis of Voyager-1 magnetic field data (see Burlaga et al. 2003), the value for γ can be estimated between 0.1 ≲ γ ≲ 0.5. We study the impact of this parameter in Sect. 2.4.
(6)with k = 2 × 10-20 and n = 10.9. This clearly shows a plateau with ϵ ≃ ϵ0 = 10-2 for tilt angles θ ≤ 60° and a strong fall-off of ϵ at tilt angles θ ≥ 65° (see Sect. 2.4 for a more detailed study of this function). At these large tilt angles the quantity γ, which is the ratio of periods of a magnetic current sheath passage over the shock and the full solar rotation period, becomes important (see Fahr et al. 2008) and also ensures that ϵ(θ) does not drop to zero. Estimating a realistic value of γ, however, is not trivial; the parameter γ is the relative length of the period during which, at current sheet crossings of the termination shock due to the turning of the magnetic field vector, the magnetic field angle θ is much smaller than the normal angle for monodirectional Archimedian fields. On the basis of Voyager-1 magnetic field data (see Burlaga et al. 2003), the value for γ can be estimated between 0.1 ≲ γ ≲ 0.5. We study the impact of this parameter in Sect. 2.4.
Introducing the pick-up ion abundance by ξ = npui/np which is independent on the solar wind velocity U as derived by Fahr & Ruciński (1999), one obtains ![\begin{equation} \xi (r,\beta ) = 1-\exp [-\int_{r_{0}}^{r}\sigma _{\rm ex}n_{\rm H}(r',\beta ){\rm d}r'], \end{equation}](/articles/aa/full_html/2011/07/aa16513-11/aa16513-11-eq60.png) (7)where β is the angle between the position vector r⊙(α,δ) and the upwind nose direction, from where interstellar H-atoms are flowing into the solar system (using cosβ = cosδcosα). The H-atom density profiles may be taken from Fahr & Ruciński (1999).
(7)where β is the angle between the position vector r⊙(α,δ) and the upwind nose direction, from where interstellar H-atoms are flowing into the solar system (using cosβ = cosδcosα). The H-atom density profiles may be taken from Fahr & Ruciński (1999).
Taking everything together, we find the ACR ion injection  (8)with rE = 1 AU and np, E = np(rE). Due to the fact that, for nH, ∞ = 0.1 cm-3, the abundance at the termination shock as modeled by Fahr & Ruciński (1999) in fact turns out to be independent of β, i.e. ξ(rs(α,δ),β) ≃ const. = 0.15, this simplifies the above expression to
(8)with rE = 1 AU and np, E = np(rE). Due to the fact that, for nH, ∞ = 0.1 cm-3, the abundance at the termination shock as modeled by Fahr & Ruciński (1999) in fact turns out to be independent of β, i.e. ξ(rs(α,δ),β) ≃ const. = 0.15, this simplifies the above expression to  (9)On the basis of this relation we thus obtain the distribution function of energetic pick-up ions (i.e. v ≥ U)
(9)On the basis of this relation we thus obtain the distribution function of energetic pick-up ions (i.e. v ≥ U)  (10)
(10)
2.3. Inner heliospheric sources for IBEX ENA fluxes between 0.6 and 6.0 keV
The above derived PUI distribution function fpui(v,r,α,δ) contains several poorly defined quantities like the injection threshold ppui from ACRs to PUIs and the injection efficiency ϵ. Therefore, in the following we fix the absolute value of fpui(v,r,α,δ) at a specific reference velocity v0, reference distance r = rs(α0,δ0) (which is the distance from the sun to the termination shock in the nose region) and reference position α0,δ0 by a fit to observational data in the form:  . Then, we can close the observational gap between a few keV and a few 102 keV with the spectral feature of the above distribution fpui(v,r,α,δ) (see Eq. (10)).
. Then, we can close the observational gap between a few keV and a few 102 keV with the spectral feature of the above distribution fpui(v,r,α,δ) (see Eq. (10)).
Assuming a line of sight, directed from the upwind-positioned earth towards the nose of the heliosphere, one can calculate the following ENA flux originating from charge-exchange reactions of upstream energetic ions as they have been detected by Voyager-1/-2 (Decker et al. 2005, 2008). Based on Voyager-1/-2 observational data, the fairly constant flux level of low-energy ions (40–53 keV) in regions far ahead of the shock according to Decker et al. (2008) can be given by  (11)at an average energy of 45 keV where the differential energy flux j(E) is defined as (e.g. see Lee et al. 2009)
(11)at an average energy of 45 keV where the differential energy flux j(E) is defined as (e.g. see Lee et al. 2009)  (12)with f(E) being the ion energy distribution function normalised by
(12)with f(E) being the ion energy distribution function normalised by  .
.
The above estimate of the upstream ion intensity, though derived from noisy data, can also be supported starting out from the less noisy, better identified downstream fluxes measured by Voyager-1 and then calculating from the data for the nearly perpendicular shock the associated upstream fluxes on the basis of kinetic relations developed by Siewert & Fahr (2007), delivering the relation between the near upstream (subscript 1) and near downstream (subscript 2) ion distribution functions  (13)where the individual ion velocities v1 and v2 are associated by v1 = v2/s and the actual compression ratio at the Voyager-1 shock crossing found by s = 2.6 (see Stone et al. 2005).
(13)where the individual ion velocities v1 and v2 are associated by v1 = v2/s and the actual compression ratio at the Voyager-1 shock crossing found by s = 2.6 (see Stone et al. 2005).
Assuming in addition that in the energy range below this boundary, i.e. E ≤ E0 = 45 keV, the ions at solar distances between 5 and 90 AU are distributed by a distance-independent power law according to f(v) = fpui(v) ~ v-4 or f(E) ~ E-2 (see formula given in Eq. (10)) one would arrive at an isotropic differential ion flux at 4.5 keV upstream of the shock of  (14)with the relations already mentioned above one can derive a flux on the downstream side given by
(14)with the relations already mentioned above one can derive a flux on the downstream side given by 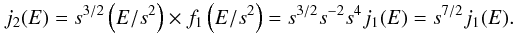 (15)Letting these ions locally undergo charge exchange reactions with the locally present neutral H-atoms of density nH ≃ nH, ∞ = 0.1 cm-3, one calculates a local 4.5 keV ENA production rate per energy increment dE in the wind frame of
(15)Letting these ions locally undergo charge exchange reactions with the locally present neutral H-atoms of density nH ≃ nH, ∞ = 0.1 cm-3, one calculates a local 4.5 keV ENA production rate per energy increment dE in the wind frame of  (16)Ions with a random velocity of
(16)Ions with a random velocity of  and with orientation towards the earth (i.e. roughly the sun), when neutralized have a solar velocity vENA in the solar rest frame which depends on the solar wind bulk velocity U. Adopting a bulk velocity of U = 450 km s-1 with 1 keV = (m/2)U2 leads to
and with orientation towards the earth (i.e. roughly the sun), when neutralized have a solar velocity vENA in the solar rest frame which depends on the solar wind bulk velocity U. Adopting a bulk velocity of U = 450 km s-1 with 1 keV = (m/2)U2 leads to  (17)and thus to ENAs that hit the detector with an energy of EENA = 1.26 keV. Nevertheless, we would like to mention that, most probably, the typical speed over this epoch for low to mid latitudes is more like 350–400 km s-1 at 1 AU (McComas et al. 2008) and 300–350 measured at V2 upstream of the TS (after mass loading of the SW by PUIs). We now calculate the total ENA flux of such ENAs per unit of detector surface and per steradian generated along a radian pointing to a direction {α,δ} and find
(17)and thus to ENAs that hit the detector with an energy of EENA = 1.26 keV. Nevertheless, we would like to mention that, most probably, the typical speed over this epoch for low to mid latitudes is more like 350–400 km s-1 at 1 AU (McComas et al. 2008) and 300–350 measured at V2 upstream of the TS (after mass loading of the SW by PUIs). We now calculate the total ENA flux of such ENAs per unit of detector surface and per steradian generated along a radian pointing to a direction {α,δ} and find  (18)Keeping in mind now that both the differential ion fluxes and the H-atom density in this calculation are assumed to be constant along the line of sight then directly gives us the following result:
(18)Keeping in mind now that both the differential ion fluxes and the H-atom density in this calculation are assumed to be constant along the line of sight then directly gives us the following result:  (19)With the assumption that the upwind shock distance is given by rs(α = 0,δ = 0) = 90 AU one obtains an upstream (subscript 1) ENA flux of
(19)With the assumption that the upwind shock distance is given by rs(α = 0,δ = 0) = 90 AU one obtains an upstream (subscript 1) ENA flux of ![\begin{eqnarray} \Phi _{\rm ENA,\,1}(0,0) &\simeq& j_{1}(E_{4.5})\sigma _{\rm ex}(E_{4.5})\times n_{\rm H}\times r_{\rm s}(0,0) \nonumber\\ &=& 5\times 10^{-1}10^{-15}10^{-1}90\times 1.5\times 10^{13} \nonumber\\ &=& 6.75\times 10^{-2}[{\rm cm^{-2}\,s\, keV\, ster}]. \end{eqnarray}](/articles/aa/full_html/2011/07/aa16513-11/aa16513-11-eq111.png) (20)This flux is enhanced by ENAs produced on the downstream side, denoted by Φ2, where a differential flux j2(E) = s7/2j1(E) prevails (see Eq. (15)). To select ENAs with the same velocity as considered before with
(20)This flux is enhanced by ENAs produced on the downstream side, denoted by Φ2, where a differential flux j2(E) = s7/2j1(E) prevails (see Eq. (15)). To select ENAs with the same velocity as considered before with  keV in the solar rest frame, in view of the reduced downstream bulk velocity of U2 = U1/s, have to have a smaller wind-frame energy of only 0.84E0. For the differential flux due to Eq. (1) this means an enhancement by a factor 1.2 = 1/0.84. Thus taking things together one arrives at a downstream ENA flux contribution of:
keV in the solar rest frame, in view of the reduced downstream bulk velocity of U2 = U1/s, have to have a smaller wind-frame energy of only 0.84E0. For the differential flux due to Eq. (1) this means an enhancement by a factor 1.2 = 1/0.84. Thus taking things together one arrives at a downstream ENA flux contribution of: ![\begin{eqnarray} \Phi_{\rm ENA,\,2}(0,0) &\simeq& j_{2}(E_{4.5})\sigma _{\rm ex}(E_{4.5})\times n_{\rm H}\times (r_{\rm hp}(0,0)-r_{\rm s}(0,0)) \nonumber\\ & = &1.2s^{7/2}j_{1}(E_{4.5})\sigma _{\rm ex}(E_{4.5}) n_{\rm H} (r_{\rm hp}(0,0)-r_{\rm s}(0,0)) \nonumber\\ & = &\Phi _{\rm ENA,\,1}(0,0)\times \lbrack 1.2s^{7/2}(r_{\rm hp}/r_{\rm s}-1)] \nonumber\\ & = &\Phi _{\rm ENA,\,1}(0,0)\times (1.2\times 28.4\times 1.66) \nonumber\\ & = &56.8\times \Phi_{\rm ENA,\,1}(0,0), \end{eqnarray}](/articles/aa/full_html/2011/07/aa16513-11/aa16513-11-eq118.png) (21)where it has been assumed that the ratio between heliopause and shock distance is given by rhp/rs = 5/3.
(21)where it has been assumed that the ratio between heliopause and shock distance is given by rhp/rs = 5/3.
All together this means that at an energy of 1.12 keV an ENA flux of ![\begin{eqnarray} \Phi_{\rm ENA}(0,0) &=& \Phi _{\rm ENA,\,1}(0,0)+\Phi _{\rm ENA,\,2}(0,0) \nonumber\\ &=& 58\times 6.75\times 10^{-2}[{\rm cm^{-2}\,s\, keV\, ster}] \nonumber\\ &=& 3.92[{\rm cm^{-2}\,s\, keV\, ster}] \label{eq-reference} \end{eqnarray}](/articles/aa/full_html/2011/07/aa16513-11/aa16513-11-eq120.png) (22)can be expected.
(22)can be expected.
This now is taken as a data-based reference value for the nose region and now the variation of this ENA-flux with the look-direction {α,δ} is studied. For that purpose we use Eqs. (19) and (22) and thus can write the following relation  (23)where the last factor is taking into account that the ENA fluxes are proportional to the TS distance (i.e. a line-of-sight integral), which needs to be corrected for the different TS distances in the flanks and the tail. Using the recognition of the solar wind mass flow is largely independent of latitude (and fast vs slow solar winds) (McComas et al. 2000) with U(α,δ) × np, E(α,δ) = U(0,0) × np, E(0,0) simplifies to the following form:
(23)where the last factor is taking into account that the ENA fluxes are proportional to the TS distance (i.e. a line-of-sight integral), which needs to be corrected for the different TS distances in the flanks and the tail. Using the recognition of the solar wind mass flow is largely independent of latitude (and fast vs slow solar winds) (McComas et al. 2000) with U(α,δ) × np, E(α,δ) = U(0,0) × np, E(0,0) simplifies to the following form:  (24)
(24)
2.4. Models for the solar magnetic field and the TS geometry
We now examine which conditions are required for this approach to produce the actually observed ENA flux enhancements; this analysis requires a careful evaluation of multiple competing contributions. To simplify the calculations, and also to make the results more easily comparable, we introduce the relative ENA flux rate (see also Eq. (24))  (25)This expression corresponds to the total ENA flux enhancement with respect to a reference point taken at the heliospheric nose, i.e. it is completely independent of the actually observed absolute values.
(25)This expression corresponds to the total ENA flux enhancement with respect to a reference point taken at the heliospheric nose, i.e. it is completely independent of the actually observed absolute values.
From the earlier study of Eq. (6), we know that the ratio of injection efficiencies is almost unity for mostly perpendicular shocks, which are most commonly found in the nose (and tail) regions (see also Fig. 3 for the behaviour of the TS angle). Even without going into details, on the other hand the TS distance reaches a minimum here, which results in Eq. (25) to exhibit, due to the second factor, a local maximum (with  ). In other words, the ENA emission fluxes around the nose are actually a little weaker, than the reference value in the direct nose region. To produce a significant enhancement, this reduction now needs to be overcompensated by the ratio of injection efficiencies, i.e. ϵ(α,δ)/ϵ(0,0), which, depending on the model parameter γ and the lowest magnetic field tilt angle θBn appearing at the 3d-TS, may grow sufficiently large to result in a visible feature.
). In other words, the ENA emission fluxes around the nose are actually a little weaker, than the reference value in the direct nose region. To produce a significant enhancement, this reduction now needs to be overcompensated by the ratio of injection efficiencies, i.e. ϵ(α,δ)/ϵ(0,0), which, depending on the model parameter γ and the lowest magnetic field tilt angle θBn appearing at the 3d-TS, may grow sufficiently large to result in a visible feature.
Obviously, since the heliosphere is a complicated system, the TS geometry and the resulting angles θBn are not well predicted from theoretical and numerical considerations alone. Unfortunately, due to a lack of observational data, we are restricted to magneto-kinetic/-hydrodynamic models based on varying degree of physical sophistications. One of the most recent theoretical models for the geometry of the TS has been derived by Borrmann & Fichtner (2005); in this study, we make, however, use of the analytic approximation by Fahr et al. (2008), who describe the TS as an ellipsoid with two identical short (104.7 AU) and one long (133.5 AU) semi-major axes, which best-fits the shape of the termination shock obtained by Borrmann & Fichtner (2005).
 |
Fig. 2 The injection rate enhancement function |
In this respect, also a so-called “blunt”-helioshock (discussed by McComas & Schwadron 2006) could be represented by a prolate ellipsoid, simply by selecting appropriate semimajor axes values perpendicular to the LISM inflow direction, different from the ones used here. Since the blunt-shaped shock fitted by McComas & Schwadron (2006) can only be expected if the LISM is fully ionized, i.e. if LISM H-atom density vanishes (see e.g. Izmodenov & Baranov 2006), while actually LISM neutral H-atoms in fact have to be considered with densities of the order of 0.1 cm-3, we prefer to use here mainly the ellipsoidal best-fit to the kinetic/hydrodynamical simulation delivered by Borrmann & Fichtner (2005).
In addition, we adopt the standard Parker model for the solar magnetic field (Parker 1958), which describes the field as frozen into the plasma and convected outward with the solar wind plasma, producing a spiral pattern. It turns out from a numerical study (reproduced in Fig. 3), the magnetic field tilt angle θBn(α,δ) varies between 65° in the rear flanks and 90° in the nose and tail regions. Interestingly enough, the lower limit of 65° quite coincides with the region where the PUI injection starts to become pronounced (see Fig. 2), offering a qualitative mechanism to generate a strongly localized emission region.
 |
Fig. 3 The magnetic field tilt angle θBn for the default model of the heliospheric termination shock surface discussed in Sect. 2.4, using a Mollweide projection for greater compatibility with IBEX data. |
2.5. Relative ENA flux predictions
After the foregoing theoretical preparation, we are now able to derive the relative (i.e. normalised to the observed reference value at the nose, Eq. (22)) ENA production rates and fluxes. The resulting ENA flux rate accumulated between the Heliopause and the observer due to energetic ACR-induced PUIs is presented in Fig. 4. This image demonstrates the following properties of the ENA sky. First, qualitatively, the flux from the tail is much weaker than the flux from the nose, which is mainly due to the r-2 factor in Eq. (24), which is simply a result of the spherical expansion of the solar wind plasma flow. In the flanks (i.e. between the tail-minimum and the nose-maximum), another interesting feature emerges, namely a (weaker) second maximum, which has a ribbon-like structure. This result is directly correlated to the relatively small magnetic field tilt angles in this region, and correlated to the ENA flux enhancement due to an increased injection efficiency (see Eq. (6)) emerging (see Fig. 2) around θBn ≲ 65°.
These basic properties are quantitatively modified significantly by variations of the injection model parameter γ. First, we study the behavior of the ENA production rate as a function of this injection parameter γ. Adopting smaller values of this parameter results in a weaker production rate in the nose region as compared to more favorable regions in the flanks (due to  , see Eq. (25), which however is used as reference by the normalisation to Voyager data), while at the same time enhancing the ribbon-like emission feature in the flanks of the heliosphere. The ribbon-like feature appearing in this model unfortunately is not well coinciding with the ribbon feature observed by IBEX, which is most prominently featured at polar angles below 90° around the nose. This is at least partly due to the fact that the idealized heliospheric model applied here – and especially the representation of the TS surface as a prolate ellipsoid – is not appropriate to describe the IBEX observations, although it does, in fact, result in a qualitatively similar feature.
, see Eq. (25), which however is used as reference by the normalisation to Voyager data), while at the same time enhancing the ribbon-like emission feature in the flanks of the heliosphere. The ribbon-like feature appearing in this model unfortunately is not well coinciding with the ribbon feature observed by IBEX, which is most prominently featured at polar angles below 90° around the nose. This is at least partly due to the fact that the idealized heliospheric model applied here – and especially the representation of the TS surface as a prolate ellipsoid – is not appropriate to describe the IBEX observations, although it does, in fact, result in a qualitatively similar feature.
 |
Fig. 4 Relative ENA flux enhancements according to Eq. (25) as a function of the direction (α,δ) in a Mollweide projection for different values of γ. |
We will not study more realistic heliospheric models in detail in this initial study, but we summarize what kinds of physical modifications may result in a closer match between the model and observations in the framework of an ellipsoid model of the TS. First, the Voyagers discovered a significant difference in the TS distance in the near-nose region of the order of 10 AU (with Voyager 1 encountering the TS at 94 AU and Voyager 2 at 84 AU, see Fisk 2005; and Jokipii 2008). This discrepancy likely has some component related to dynamic behavior, however, the majority of the difference is more likely due to a spatial asymmetry, showing that the heliosphere is considerably more complex than the basic model used here. One possible explanation without replacing the model by something much more complicated would be to assume a more realistic TS ellipsoid that is not co-aligned with the upwind LISM direction; that is to assume the heliospheric nose is actually different from the TS nose. This idea may be added to our model by simply carrying out a turn-transformation of the main axis of the ellipsoid, i.e. modifying the angles according to φhelio = φTS + α and a similar modification for the azimuthal angle. In the framework of the ACR injection process discussed here, this results in a shift in the skymaps, i.e. the prominent ENA generation feature is shifted to different positions, potentially closer to the observed features. The IBEX ribbon is located approximately between 0° and 30° to the left of the heliospheric nose, while the feature emerging in this study is found near α ≃ 130°; in other words, there is a difference of Δα = o(100 AU) between the predicted and the observed positions of the IBEX ENA ribbon. If the IBEX ribbon is at least partially emerging due to ACR injection processes, then the geometry of the heliospheric TS must differ significantly from the simplest approximation used here, e.g. due to local nonlinear processes causing “ripples” on the TS geometry. Taking the Voyager observations into account, a much more complicated geometry seems highly likely.
 |
Fig. 5 Relative ENA flux enhancements according to Eq. (25) as a function of the direction (α,δ) in a Mollweide projection, using γ = 0.02 and different values of the numerical eccentricity e of the ellipsodial termination shock surface. |
Also, a more realistic ellipsoid is likely more elongated compared to what is assumed in our present calculations, transforming the TS in a more cigar-shaped surface. The default values adopted in this study are based on a theoretical, hydrodynamical model by Borrmann & Fichtner (2005), while the Voyagers demonstrate a possible difference of 10 AU in the TS distance near the nose. Therefore, we now study variations of the two ellipsoid semi-major axes a and b (or, equivalently, the parameters  and the nose TS distance (the shortest TS distance)
and the nose TS distance (the shortest TS distance)  . In addition, only the eccentricity e will result in a modification of the TS normal angles, and therefore, the ACR injection efficiency, since r0 does not modify the form of the TS. Therefore, we restrict our study to varying the eccentricity e. Figure 5 demonstrates that, in this case, increasing the eccentricity (i.e. e → 1) results in a broadening of the emission feature, and a greatly increased maximum near its central region. This is a direct result of a reduced minimal magnetic field tilt angle (θBn ≪ 65°), resulting in a significant enhancement of the ENA emission ratio due to the strong slope in the injection function (see Fig. 2).
. In addition, only the eccentricity e will result in a modification of the TS normal angles, and therefore, the ACR injection efficiency, since r0 does not modify the form of the TS. Therefore, we restrict our study to varying the eccentricity e. Figure 5 demonstrates that, in this case, increasing the eccentricity (i.e. e → 1) results in a broadening of the emission feature, and a greatly increased maximum near its central region. This is a direct result of a reduced minimal magnetic field tilt angle (θBn ≪ 65°), resulting in a significant enhancement of the ENA emission ratio due to the strong slope in the injection function (see Fig. 2).
Finally, we study the impact of the precise position of the normalising Voyager-1 data derived above. Voyager-1 did not encounter the TS precisely at the nose, but at (α,δ) = (250°,34°) (Fichtner & Scherer 2000) in ecliptic coordinates instead of IBEX coordinates, which do not have their angular coordinates co-aligned with those used in this study, i.e.  with Δφ ≃ 250 (i.e. Voyager-1 crossed the TS just a little bit over the nose). We are able, however, to estimate the impact of modifying the reference point from (0,0) to (α0,δ0). Using Eq. (24), we obtain
with Δφ ≃ 250 (i.e. Voyager-1 crossed the TS just a little bit over the nose). We are able, however, to estimate the impact of modifying the reference point from (0,0) to (α0,δ0). Using Eq. (24), we obtain  (26)i.e. the main difference between a nose-normalised model and an (α0,δ0)-normalised model is the constant factor
(26)i.e. the main difference between a nose-normalised model and an (α0,δ0)-normalised model is the constant factor  (27)Using this factor, Eq. (24) transforms into
(27)Using this factor, Eq. (24) transforms into  (28)For the actually observed Voyager-1 TS crossing, this factor turns out as Cpos ≃ 1.006, with the main contribution following from the different TS distances (the magnetic field tilt angle is still much larger than 65° around the nose region). This factor is negligibly small and our results are, to a good approximation, not modified.
(28)For the actually observed Voyager-1 TS crossing, this factor turns out as Cpos ≃ 1.006, with the main contribution following from the different TS distances (the magnetic field tilt angle is still much larger than 65° around the nose region). This factor is negligibly small and our results are, to a good approximation, not modified.
 |
Fig. 6 Magnetic field tilt angle differences |θ − θ′| in degrees between a solar wind model with constant speed and a model with altitude-dependent speed as observed by McComas et al. (2000); Fahr & Scherer (2004). The narrow line in the center results from numerical instabilities near |Δθ| = 0, where the difference switches signs. |
Another possible contribution to the emergence of a more intense ENA emission region would be to take into account another property of the solar wind under solar minimum conditions. Observations (McComas et al. 2000) demonstrate that during a solar minimum, the solar wind speed is much higher at high latitudes than near the ecliptical plane, being a factor of about 2 faster near the poles, and resulting in a more radial magnetic field. We have studied this contribution by deriving the differences in the magnetic field tilt angle with a constant solar wind speed (θ) and the same angle using the latitude-dependent solar wind speed (θ′). Studying the absolute difference between these values (|θ − θ′|) demonstrates that the main difference is smaller than 1° and therefore negligiby small (see Fig. 6).
3. Conclusions
In this paper we have investigated suprathermal pick-up ions upstream and downstream of the solar wind termination shock as potential sources of KeV-energetic H-atom ENAs. We have started from an injection mechanism at high energies (about 102 keV) coupling low energy ACR protons diffusing inwards to high energy pick-up protons convected outwards with the solar wind bulk flow. As shown in Fahr et al. (2009) this mechanism leads to pick-up ion power spectra with a velocity power index of γv = −4. Since the ACR intensities are connected with the injection rate to the Fermi-1 acceleration process at the termination shock, and the latter is related both to the total pick-up ion flux into the termination shock and the local magnetic tilt angle between the shock normal and the upstream magnetic field, one arrives at power law spectra of suprathermal pick-up protons with spectral intensities varying in a complicated way with the angle of the look direction relative to the upwind direction (i.e. LISM inflow direction = solar apex).
We then examined KeV-energetic ENA fluxes originating as charge transfer products from these suprathermal pick-up protons. We showed this leads to a radiative sickle structure of enhanced ENA fluxes around the nose region (solar apex). The intensity amplitude from the nose to the sickle and its angular separation from the nose are variable over a relatively broad range connected with theoretical input parameters which are quantitatively not well determined. Though it seems that with the radiation mechanism presented here one is not fully able – a factor of about 5 to low – to represent the maximum intensities seen with IBEX in the ribbon region (250 cm-2 s-1 sr-1 keV-1 at 1.1 keV!), one can nevertheless understand that some of the basic features of this structure can be reasonably well reproduced. In any case the ENA radiation pattern calculated here should appear in the IBEX data; even if not the dominant radiation feature, it should still be present as one of the residual contributions in the observed globally distributed ENA flux.
One specific uncertainty in our models, namely the form of the heliospheric TS, might be reduced by trying to fit the TS locations observed by the Voyagers to the model. While different approaches to this problem exist, most papers actually favor a spatial rather than a temporal reason for the oberved asymmetry (see e.g. Opher et al. 2007). Considering that both Voyager TS transitions happened during the same solar minimum, it is quite probable that the TS geometry, probed by these two events, is not largely related to dynamical processes, but importantly to specific details of the heliospheric shock asymmetry, i.e. the local orientation and the spatial extensions, on which we do not have sufficient experimental data to create a definite model.
Acknowledgments
One of the authors, M. Siewert, is grateful to the Deutsche Forschungsgemeinschaft for financial support granted to him in the frame of the project Si-1550/2-1. D. J. McComas and N. A. Schwadron were supported by NASAs Explorers Program as a part of the IBEX mission. This research benefited greatly from discussions that were held at the meetings of the International Team devoted to understanding the v-5-tails and ACRs that has been sponsored by the International Space Sciences Institute (ISSI) in Bern, Switzerland.
References
- Borrmann, T., & Fichtner, H. 2005, Adv. Space Res., 35, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Burlaga, L. F., Ness, N. F., & Richardson, J. D. 2003, J. Geophys. Res. (Space Phys.), 108, 8028 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., & Fahr, H.-J. 1996, A&A, 311, 317 [NASA ADS] [Google Scholar]
- Chalov, S. V., Fahr, H.-J., & Izmodenov, V. 1997, A&A, 320, 659 [NASA ADS] [Google Scholar]
- Chalov, S. V., Alexashov, D. B., & Fahr, H. J. 2004, A&A, 416, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chalov, S. V., Alexashov, D. B., McComas, D., et al. 2010, ApJ, 716, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Christian, E. R., Cummings, A. C., & Stone, E. C. 1995, ApJ, 446, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B., Krimigis, S. M., Roelof, E. C., et al. 2005, Science, 309, 2020 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Decker, R. B., Krimigus, S. M., Roelof, E. C., et al. 2008, Nature, 454, 67 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fahr, H. J., & Ruciński, D. 1999, A&A, 350, 1071 [NASA ADS] [Google Scholar]
- Fahr, H., & Scherer, K. 2004, Ann. Geophys., 22, 2229 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H., Fichtner, H., & Grzedzielski, S. 1992, Sol. Phys., 137, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., Fichtner, H., & Scherer, K. 2007, Rev. Geophys., 45, 4003 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H. J., Scherer, K., Potgieter, M. S., & Ferreira, S. E. S. 2008, A&A, 486, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H., Chashei, I. V., & Verscharen, D. 2009, A&A, 505, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fichtner, H., & Scherer, K. 2000, in The Outer Heliosphere: Beyond the Planets, ed. K. Scherer, H. Fichtner, & E. Marsch, 1 [Google Scholar]
- Fichtner, H., Le Roux, J. A., Mall, U., & Rucinski, D. 1996, A&A, 314, 650 [NASA ADS] [Google Scholar]
- Fisk, L. A. 1976, J. Geophys. Res., 81, 4633 [Google Scholar]
- Fisk, L. A. 2005, Science, 309, 2016 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fisk, L. A., & Gloeckler, G. 2008, ApJ, 686, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Gleeson, L. J., & Axford, W. I. 1967, ApJ, 149, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Grzedzielski, S., Bzowski, M., Czechowski, A., et al. 2010, ApJ, 715, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Zank, G. P., et al. 2010, ApJ, 708, L126 [NASA ADS] [CrossRef] [Google Scholar]
- Izmodenov, V. V., & Baranov, V. B. 2006, ISSI Sci. Rep. Ser., 5, 67 [Google Scholar]
- Jokipii, J. R. 2008, Nature, 454, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kallenbach, R., Bamert, K., & Hilchenbach, M. 2009, Astrophys. Space Sci. Trans., 5, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Krimigis, S. M., Decker, R. B., Roelof, E. C., & Hill, M. E. 2004, in Physics of the Outer Heliosphere, ed. V. Florinski, N. V. Pogorelov, & G. P. Zank, AIP Conf. Ser., 719, 133 [Google Scholar]
- Kucharek, H., & Scholer, M. 1995, J. Geophys. Res., 100, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzerotti, L. J., Krimigis, S. M., Decker, R. B., et al. 2001, Space Sci. Rev., 97, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. A., Fahr, H. J., Kucharek, H., et al. 2009, Space Sci. Rev., 146, 275 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J. 2010, IBEX web site, http://www.ibex.swri.edu/archive/2010.01.29.shtml [Google Scholar]
- McComas, D. J., & Schwadron, N. A. 2006, Geophys. Res. Lett., 33, 4102 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Barraclough, B. L., Funsten, H. O., et al. 2000, J. Geophys. Res., 105, 10419 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Allegrini, F., Bartolone, L., et al. 2006, in Physics of the Inner Heliosheath, ed. J. Heerikhuisen, V. Florinski, G. P. Zank, & N. V. Pogorelov, AIP Conf. Ser., 858, 241 [Google Scholar]
- McComas, D. J., Ebert, R. W., Elliott, H. A., et al. 2008, Geophys. Res. Lett., 35, 18103 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009a, Science, 326, 959 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McComas, D. J., Allegrini, F., Bochsler, P., et al. 2009b, Space Sci. Rev., 146, 11 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Elliott, H. A., & Schwadron, N. A. 2010, J. Geophys. Res. (Space Phys.), 115, 3102 [NASA ADS] [CrossRef] [Google Scholar]
- Opher, M., Stone, E. C., & Gombosi, T. I. 2007, Science, 316, 875 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Schwadron, N. A., Bzowski, M., Crew, G. B., et al. 2009, Science, 326, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Siewert, M., & Fahr, H.-J. 2007, A&A, 463, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2005, Science, 309, 2017 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2008, Nature, 454, 71 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Figures
 |
Fig. 1 Schematic representation of ENA generation processes appearing in current discussions of the IBEX ribbon. Taken from McComas (2010); see also McComas et al. (2009a, 2010). |
| In the text | |
 |
Fig. 2 The injection rate enhancement function |
| In the text | |
 |
Fig. 3 The magnetic field tilt angle θBn for the default model of the heliospheric termination shock surface discussed in Sect. 2.4, using a Mollweide projection for greater compatibility with IBEX data. |
| In the text | |
 |
Fig. 4 Relative ENA flux enhancements according to Eq. (25) as a function of the direction (α,δ) in a Mollweide projection for different values of γ. |
| In the text | |
 |
Fig. 5 Relative ENA flux enhancements according to Eq. (25) as a function of the direction (α,δ) in a Mollweide projection, using γ = 0.02 and different values of the numerical eccentricity e of the ellipsodial termination shock surface. |
| In the text | |
 |
Fig. 6 Magnetic field tilt angle differences |θ − θ′| in degrees between a solar wind model with constant speed and a model with altitude-dependent speed as observed by McComas et al. (2000); Fahr & Scherer (2004). The narrow line in the center results from numerical instabilities near |Δθ| = 0, where the difference switches signs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



