| Issue |
A&A
Volume 531, July 2011
|
|
|---|---|---|
| Article Number | A163 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201016314 | |
| Published online | 07 July 2011 | |
An investigation of magnetic field distortions in accretion discs around neutron stars
II. Analysis of the toroidal field component
1
Key Laboratory of Solar Activity, National Astronomical Observatories, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, Beijing 100012, PR China
e-mail: luca.naso@gmail.com
2
SISSA and INFN, via Bonomea 265, 34136 Trieste, Italy
3
Department of Physics (Astrophysics), University of Oxford, Keble Road, Oxford OX1 3RH, UK
Received: 14 December 2010
Accepted: 4 April 2011
Millisecond pulsars are believed to be old pulsars spun up by a surrounding accretion disc. Magnetic fields are thought to play a leading role in this, both by determining the location of the inner edge of the disc and by exerting an additional torque on the star (as a result of the interaction between the stellar magnetic field and the disc plasma motion, which creates a toroidal component Bφ). In some well-known analytic models, developed in the 1980s, the Bφ profile was taken to be proportional to the relative angular velocity between the disc plasma and the neutron star, multiplied by a vertical dipolar field. The present work stands in the line of improving those models, suggesting a new profile for B. In a previous paper, we discussed the poloidal component of the magnetic field and here we consider the toroidal component, again making the kinematic approximation and looking for steady solutions of the induction equation for axisymmetric models. The poloidal magnetic field is not assumed to be dipolar and the poloidal velocity field is not taken to be zero everywhere. We also do not use the thin disc approximation to simplify the induction equation but instead solve it numerically in full 2D. The profile obtained in the earlier analytic models is shown to have very limited validity and a more general semi-analytic solution is proposed.
Key words: accretion, accretion disks / magnetic fields / magnetohydrodynamics (MHD) / turbulence / methods: numerical / X-rays: binaries
© ESO, 2011
1. Introduction
In the present work we study the deformation caused in a neutron star’s magnetic field because of the interaction with the matter in a surrounding accretion disc. A basic description for this kind of system was given by Ghosh and Lamb in 1979, with the model subsequently being improved by Wang (1987) and Campbell (1987), who suggested an analytic expression for the toroidal component of the field. This expression has been widely used since then, on account of it being both simple and physically plausible.
In these analytic models, the authors made the kinematic approximation, looking for an axisymmetric stationary solution of the induction equation with a given unchanging structure for the fluid in the disc. They further took the disc to be thin, the poloidal component of the magnetic field to be exactly dipolar, and the velocity field to have zero poloidal component, with its azimuthal component being Keplerian inside the disc1 and corotating at the top of the disc. Using cylindrical coordinates (ϖ, φ, z), they found 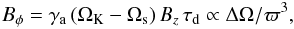 (1)where γa is the amplification factor, ΩK and Ωs are the Keplerian and stellar angular velocities, respectively, and τd is the dissipation time scale. The amplification factor γa was taken to be a constant not much greater than 1 (it depends on the steepness of the transition – in the z-direction – between Keplerian motion inside the disc and corotation with the star at the top of the disc). The precise profile of τd depends on what is the dominant mechanism for dissipating the magnetic field. Wang (1995) considered three different cases, with τd being dominated by the Alfven velocity, turbulent diffusion and magnetic reconnection, respectively.
(1)where γa is the amplification factor, ΩK and Ωs are the Keplerian and stellar angular velocities, respectively, and τd is the dissipation time scale. The amplification factor γa was taken to be a constant not much greater than 1 (it depends on the steepness of the transition – in the z-direction – between Keplerian motion inside the disc and corotation with the star at the top of the disc). The precise profile of τd depends on what is the dominant mechanism for dissipating the magnetic field. Wang (1995) considered three different cases, with τd being dominated by the Alfven velocity, turbulent diffusion and magnetic reconnection, respectively.
Equation (1) was then used for calculating the net magnetic torque exerted on the neutron star. The vertically averaged torque can be written as 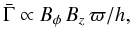 (2)where h is the semi-thickness of the disc. Regions of the disc inward of the corotation point therefore give positive contributions to the torque (because Bφ > 0), while the remainder of the disc gives negative contributions (because Bφ < 0). The total magnetic torque is obtained by integrating the local values from the inner edge to the outer boundary, and it can be either positive or negative depending on the location of the inner edge of the disc with respect to the corotation point.
(2)where h is the semi-thickness of the disc. Regions of the disc inward of the corotation point therefore give positive contributions to the torque (because Bφ > 0), while the remainder of the disc gives negative contributions (because Bφ < 0). The total magnetic torque is obtained by integrating the local values from the inner edge to the outer boundary, and it can be either positive or negative depending on the location of the inner edge of the disc with respect to the corotation point.
The aim of the present paper is to develop a semi-analytic model that can improve on those of Wang and Campbell, while remaining simple enough to be useful for people discussing the behaviour of astrophysical sources, giving a conceptual picture to go alongside results from large numerical calculations where the full set of the MHD equations is solved.
Our approach, for the time being, is to continue to retain axisymmetry and the kinematic approximation but to calculate a consistent steady-state solution for the magnetic field, relaxing the assumptions on the poloidal components of the magnetic and velocity fields and using a 2D model without any vertical averaging of the Taylor expansion of the induction equation. In the main region of the outer disc (see Fig. 1) we use a simple Keplerian velocity profile, but this is something that will be improved on later. In a previous paper (Naso & Miller 2010, hereafter Paper I) we analysed the distortion of the poloidal component of the magnetic field using a similar approach, and found that deviations away from a dipole field can be quite significant. Here we focus on the toroidal component and use the results of the previous model to solve the φ component of the induction equation. We find that in general Bφ follows a profile different from that of the analytic models, i.e. Eq. (1), and reduces to that only in a very particular case.
Following this introduction, in Sect. 2 we briefly describe our model, which is the same as that of Paper I; in Sect. 3 we recall the equations used (obtained from the induction equation), give expressions for the velocity and diffusivity profiles and outline our solution method (details of tests made on the code are given in an Appendix); in Sect. 4 we present our numerical results; in Sect. 5 we comment on these, comparing them with those of the earlier analytic models, and develop our new suggestion for the Bφ profile. Section 6 contains conclusions.
2. Model
In this study, we are considering disc accretion by a neutron star having a dipolar magnetic field. The model is the same as that of Paper I. For a detailed description of it, see Sect. 2 of that paper; here we recall the main points.
 |
Fig. 1 Schematic representation of our model (not to scale). We use rin = 10 rg, rtr ~ 22 rg and rlc ~ 115 rg. The opening angles are 8° for the disc alone and 10° for the disc plus corona. The outer disc extends much further out than the main region shown here: the grid continues until rout = 380 rg. |
We are assuming that the star is rotating about its magnetic axis, and that this axis is perpendicular to the plane of the disc; also, we assume that the fluid flow is steady and has axial symmetry everywhere. We use the kinematic approximation and do not consider any dynamo action, but turbulent diffusivity is included. The velocity field is not constrained to be purely azimuthal but is allowed to have non-zero components also in the other directions. We use spherical coordinates (r, θ, φ), with the origin being at the centre of the neutron star. Boundary conditions are imposed at the inner and outer radial edges of the disc (rin is at the Alfven radius, and rout is at 38 rin), on top of the corona (taken as being a layer above and below the disc) and on the equatorial plane. Having the inner edge of the disc at the Alfven radius justifies the kinematic approximation to some extent, since in this configuration the magnetic pressure is smaller than the gas pressure within the region that we are considering, and so the effects of the plasma on the magnetic field should be larger than the magnetic feedback on the plasma flow. The ratio h/r is taken to be constant, with the opening angle being 8° for the disc (measuring from the equatorial plane to the top of the disc), and 10° for the disc plus corona.
The inner disc region (r < rtr ~ 2 rin) and the corona are modelled with a larger value of η than the other parts. In these regions, the kinematic approximation does not provide a good description of the system for two different reasons: in the corona this is because of the low density of the plasma (which therefore tends to follow the magnetic field behaviour rather than being followed by it); in the inner region, it is because the magnetic field intensity is still quite large – although the magnetic pressure is smaller than the gas pressure, it is not yet negligible. Using a larger value for η in these regions makes the magnetic field less sensitive to the plasma motion; a somewhat similar approach was used by Kueker et al. (2000). We recall that the present knowledge of the turbulent magnetic diffusivity is quite poor and it is not a simple task to obtain a reliable expression for the η profile.
As regards the velocity field: for vr we use the expression given for the “middle region” of α-discs by Shakura & Sunyaev (1973). For Ω we take Keplerian rotation in the disc and corotation at the top of the corona and at the inner edge of the disc, giving a maximum for Ω between rin and rtr. These different parts are smoothly connected using error functions. Regarding vθ: we put it to zero in the disc but near to the boundaries we are forced to have a non-zero value in order to be consistent with the dipolar boundary conditions (as shown in Sect. 3.2 of Paper I) and so we use a non-zero profile in the corona. In this way we are including in the model an outflow from the surface of the corona, and this is in agreement with recent hydrodynamic simulations of accretion flows (Jiao & Wu 2011).
Summarising, we divide the surroundings of the central object into four parts (see Fig. 1, which is repeated from Paper I): (1) the inner disc, extending from rin out to a transition radius rtr ~ 2 rin (where the diffusivity changes); (2) the outer disc, extending from rtr to an outer radius rout = 38 rin; (3) a corona, above and below the disc; and (4) everything else, which we take here to be vacuum. As a unit for radial distances, we use the Schwarzschild radius rg. Within the outer disc, we focus on what we call the main region, extending from rtr out to the light cylinder at rlc ~ 11 rin.
3. Equations
In the kinematic approximation, one assumes that the velocity field remains fixed as specified, and the interaction between the magnetic field and the plasma is then described by the induction equation alone. In the presence of turbulence, it is more convenient to write this equation for mean fields rather than for the actual fields (which contain fluctuating parts as well).
The time dependence of the mean field is given by 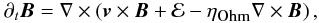 (3)where ηOhm = c2/4πσ is the Ohmic diffusivity and ℰ is the turbulent electromotive force. A common procedure is to expand ℰ in terms of the mean field and its derivatives and within the first order smoothing approximation one has ℰ = αTB − ηT∇ × B, where the αTB term generates the so-called α-effect. As in Paper I, we are neglecting this effect here and the induction equation then reduces to
(3)where ηOhm = c2/4πσ is the Ohmic diffusivity and ℰ is the turbulent electromotive force. A common procedure is to expand ℰ in terms of the mean field and its derivatives and within the first order smoothing approximation one has ℰ = αTB − ηT∇ × B, where the αTB term generates the so-called α-effect. As in Paper I, we are neglecting this effect here and the induction equation then reduces to 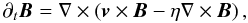 (4)where η = ηOhm + ηT and is ~ ηT, because the turbulent diffusivity is much stronger than the Ohmic one.
(4)where η = ηOhm + ηT and is ~ ηT, because the turbulent diffusivity is much stronger than the Ohmic one.
We note that the effects of a dynamo action on the disc structure have recently been studied by Tessema & Torkelsson (2010a,b), who estimated the toroidal magnetic field generated by the dynamo to be about an order of magnitude larger than the Bφ calculated according to the early models. Here we show that the profile of the toroidal field can be very different from the one suggested by those models, if the poloidal component is not forced to be a dipole, but is instead calculated self-consistently.
As described in Paper I, our strategy consists of writing Eq. (4) in spherical coordinates, applying the axisymmetry and stationarity assumptions (i.e. putting ∂φ [... ] = ∂t [... ] = 0) and then solving the final equations with the velocity field and magnetic turbulence profile given by the model. The three components of the induction equation are ![\begin{eqnarray} 0 &=& \partial_\theta \left\{ \sin\theta \left[ v_r B_\theta - v_\theta B_r - \frac{\eta}{r}[\partial_r(rB_\theta) - \partial_\theta B_r]\right] \right\} \label{eq:ind_r} , \\ 0 &=& \partial_r \left\{ r \hspace{0.5cm}\left[ v_r B_\theta - v_\theta B_r - \frac{\eta}{r}[\partial_r(rB_\theta) - \partial_\theta B_r] \right] \right\}\label{eq:ind_t} , \\ 0 &=& \partial_r \left\{ r \left[ v_\phi B_r - v_rB_\phi + \frac{\eta}{r} \partial_r(rB_\phi) \right] \right\} \nonumber\\ &&-\partial_\theta \left\{ v_\theta B_\phi - v_\phi B_\theta - \frac{\eta}{r\sin\theta}\partial_\theta (B_\phi \sin\theta) \right\} . \label{eq:ind_p} \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq51.png) The first two equations contain only poloidal quantities and have been solved in Paper I (making use of the magnetic stream function). Here we focus on the third equation and solve it using the results for Br and Bθ from the previous analysis.
The first two equations contain only poloidal quantities and have been solved in Paper I (making use of the magnetic stream function). Here we focus on the third equation and solve it using the results for Br and Bθ from the previous analysis.
We rewrite Eq. (7) in the following dimensionless way: 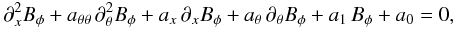 (8)where x = r/rg (not to be confused with the Cartesian coordinate x used for the plots), Bφ is the toroidal field in units of a reference field (as described in Sect. 3.4 below) and the dimensionless a coefficients are
(8)where x = r/rg (not to be confused with the Cartesian coordinate x used for the plots), Bφ is the toroidal field in units of a reference field (as described in Sect. 3.4 below) and the dimensionless a coefficients are ![\begin{eqnarray} \label{eq:att} a_{\theta\theta} & = & \frac{1}{x^2} \\ \label{eq:at} a_\theta & = & \frac{\partial_\theta \eta}{x^2\eta} + \frac{1}{x^2} \frac{\cos\theta}{\sin\theta} - \frac{v_\theta r_{\rm g}}{x\eta} = \frac{1}{x} \left[ \frac{\partial_\theta \eta}{x\eta} + \frac{1}{x} \frac{\cos\theta}{\sin\theta} - \frac{v_\theta r_{\rm g}}{\eta} \right]\\ \label{eq:ax} a_x & = & \frac{ \partial_x \eta}{\eta} + \frac{2}{x} - \frac{v_r r_{\rm g}}{\eta} \\ \nonumber a_1 & = & \frac{ \partial_x \eta }{x\eta} - \frac{ r_{\rm g} \partial_x (xv_r)} {x\eta} + \frac{\partial_\theta\eta} {x^2\eta}\frac{\cos\theta}{\sin\theta} \\ \nonumber &&-\frac{1}{x^2} \frac{\cos^2\theta}{\sin^2\theta} - \frac{r_{\rm g} \partial_\theta v_\theta}{x\eta} -\frac{1}{x^2} \\ \label{eq:a1} & = & \frac{1}{x} \left[ \frac{ \partial_x \eta }{\eta} - \frac{ r_{\rm g}\partial_x(xv_r)} {\eta} + \frac{\partial_\theta\eta} {x\eta}\frac{\cos\theta}{\sin\theta} \right.\\ \nonumber && -\left. \frac{1}{x} \frac{\cos^2\theta}{\sin^2\theta} - \frac{r_{\rm g} \partial_\theta v_\theta}{\eta} -\frac{1}{x} \right] \\ \nonumber a_0 & = & \frac{r_{\rm g}\partial_x(x v_\phi B_r)}{x\eta} + \frac{r_{\rm g} \partial_\theta(v_\phi B_\theta)}{x \eta} \\ \label{eq:a0} & = &\frac{r_{\rm g}}{x\eta} \left[ \partial_x(x v_\phi B_r) + \partial_\theta(v_\phi B_\theta) \right]. \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq58.png) All of these coefficients have direct analytic expressions, except for the last one (a0) which contains Br and Bθ, whose values are taken from the previous numerical calculations. Note that the magnetic field components appearing in Eq. (13) are dimensionless.
All of these coefficients have direct analytic expressions, except for the last one (a0) which contains Br and Bθ, whose values are taken from the previous numerical calculations. Note that the magnetic field components appearing in Eq. (13) are dimensionless.
3.1. Poloidal velocity and diffusivity
The poloidal components of the velocity field and the diffusivity have already been discussed in Paper I. Here we use the same profiles as before; for the sake of clarity, we give the expressions again below.
For vr, we use ![\begin{eqnarray} \label{eq:vr} \nonumber v_r(x)&=&2 \times 10^6 \, \alpha^{4/5} \, \dot{m}^{2/5} \, m^{-1/5}\\ && \times \, (3/x)^{2/5} \left[ 1-(3/x)^{0.5} \right]^{-3/5} \hspace{0.5cm}[\rm{cm}\,\rm{s}^{-1}] , \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq60.png) (14)where m is the stellar mass in solar mass units, ṁ is the accretion flux in units of the critical Eddington rate and α is the standard Shakura-Sunyaev viscosity coefficient. Using typical values (α = 0.1, ṁ = 0.03 and m = 1.4) this gives
(14)where m is the stellar mass in solar mass units, ṁ is the accretion flux in units of the critical Eddington rate and α is the standard Shakura-Sunyaev viscosity coefficient. Using typical values (α = 0.1, ṁ = 0.03 and m = 1.4) this gives ![\begin{equation} v_r(x)\approx7.3\times 10^4 \cdot (3/x)^{2/5} \left[ 1-(3/x)^{0.5} \right]^{-3/5} \rm{cm}\,\rm{s}^{-1}. \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq66.png) (15)For vθ, we use
(15)For vθ, we use 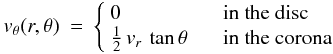 (16)where the transition in vθ between the two regions is made using
(16)where the transition in vθ between the two regions is made using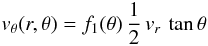 (17)with
(17)with ![\begin{equation} f_1(\theta) = \frac{1}{2} \left[ 1 + \rm{erf}\left(\frac{- \theta + \theta_{\rm D}} {d} \right) \right] , \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq69.png) (18)where θD is at the upper surface of the disc (i.e. 82°) and d = 10-3 radians (i.e. 0.057°).
(18)where θD is at the upper surface of the disc (i.e. 82°) and d = 10-3 radians (i.e. 0.057°).
For the diffusivity, we use ![\begin{eqnarray} \label{eq:eta} \eta(r,\theta) &=& \eta_0 \, \left\{1 + \big[ \eta_\theta(\theta) + \eta_r(r) \big] \, \left[ \frac{\eta_{\rm c}}{\eta_0} - 1 \right] \right\} , \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq74.png) (19)where η0 and ηc are the values in the main disc region and the corona (see Fig. 1), for which we use the values 1010 cm2 s-1 and 1012 cm2 s-1 respectively (we also use other values to study the impact on the results of varying η). For ηθ(θ) and ηr(r) we use joining functions of the form
(19)where η0 and ηc are the values in the main disc region and the corona (see Fig. 1), for which we use the values 1010 cm2 s-1 and 1012 cm2 s-1 respectively (we also use other values to study the impact on the results of varying η). For ηθ(θ) and ηr(r) we use joining functions of the form ![\begin{equation} f(x) = \frac{1}{2}\left[1 + {\rm erf}\left(\frac{- x + x_{\rm c}} {d} \right) \right] , \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq83.png) (20)with xc = θD and rtr for ηθ and ηr, respectively, and with d being the width of the transition in the error function, for which we use d = 5 rg in the radial direction and d = 2° in the θ direction2.
(20)with xc = θD and rtr for ηθ and ηr, respectively, and with d being the width of the transition in the error function, for which we use d = 5 rg in the radial direction and d = 2° in the θ direction2.
3.2. Azimuthal velocity
We are modelling the main disc region as rotating with Keplerian velocity, with the corona being taken as a transition layer where the velocity goes from Keplerian to corotation. In the inner region, we join the Keplerian flow to corotation at the radial inner edge, again using an error function. We recall that in Paper I we showed that a strictly dipolar field, without distortions, can in principle be a stationary solution of the induction equation provided that the velocity field fulfils the two conditions: 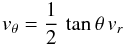 (21)and
(21)and 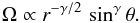 (22)From Eq. (22) one sees that corotation, which is obtained by choosing γ = 0, is consistent with having dipolar conditions (which is what we are using here).
(22)From Eq. (22) one sees that corotation, which is obtained by choosing γ = 0, is consistent with having dipolar conditions (which is what we are using here).
For the magnetic field intensities and neutron star spin rates which we are using as standards (B ~ 108 G and P ~ 10 ms), the corotation point is outward of the inner edge of the disc (which is the standard condition required for being in the accretion regime) and therefore Ω should reach a maximum at some location and then decrease again, as one moves inwards. Summarising, we use the following profile: ![\begin{equation} \label{eq:omega} \Omega(r,\theta) = \left\{ \begin{array}{cll} \Omega_{\rm K}(r) & & \mbox{in the main region:}\\ & & \theta\in[\theta_{\rm D},\pi/2], r\in[r_{\rm tr}, r_{\rm lc}]\\%[1mm] % & \\ \mbox{smooth join in }\theta & & \mbox{in the corona:}\\ & & \theta\in[\theta_{\rm C}, \theta_{\rm D}]\\%[1mm] % & \\ \mbox{smooth join in }r & & \mbox{in the inner disc:}\\ & & r\in[r_{\rm in}, r_{\rm tr}]\\%[1mm] % & \\ \Omega_{\rm s} & & \mbox{at ghost zones: } \theta = \theta_{\rm C} - \Delta \theta\\ & & \mbox{at inner edge: } r = r_{\rm in} \end{array} \right. \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq95.png) (23)where θC is the upper surface of the corona, Δθ is the angular resolution, Ωs is the stellar spin rate, ΩK is the Keplerian angular velocity
(23)where θC is the upper surface of the corona, Δθ is the angular resolution, Ωs is the stellar spin rate, ΩK is the Keplerian angular velocity 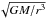 and the two smooth connections are made using the error functions given in Eqs. (25) and (27) below.
and the two smooth connections are made using the error functions given in Eqs. (25) and (27) below.
As regards the smooth joins, in the θ direction we write ![\begin{eqnarray} \nonumber \tilde{\Omega}(r,\theta) &=& \Omega_{\rm K}(r) \, f_1(\theta) + \Omega_{\rm s} \, [1-f_1(\theta)]\\ &=&[ \Omega_{\rm K}(r) - \Omega_{\rm s}] \, f_1(\theta) + \Omega_{\rm s} \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq99.png) (24)where:
(24)where: ![\begin{equation} \label{eq:erf_t} f_1(\theta) = \frac{1}{2}\left[ 1 + {\rm erf} \left( \frac{\theta-\theta_{\rm D}}{d} \right) \right] \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq100.png) (25)with d = 10-2 radians (i.e. 0.57°), and we then have a modification in the radial direction giving
(25)with d = 10-2 radians (i.e. 0.57°), and we then have a modification in the radial direction giving ![\begin{eqnarray} \nonumber \Omega(r,\theta) &=& \tilde{\Omega}(r,\theta)\,f_2(r)+\Omega_{\rm s}\,[1-f_2(r)]\\ &=&[ \tilde{\Omega}(r,\theta) - \Omega_{\rm s}] \, f_2(r) + \Omega_{\rm s} , \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq103.png) (26)where
(26)where ![\begin{equation} \label{eq:erf_r} f_2(r) = \frac{1}{2}\left[ 1 + {\rm erf} \left( \frac{x-x_{\rm c}}{d} \right) \right] \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq104.png) (27)with d = 2 rg. See Fig. 2 for a contour plot of Ω(r,θ) (made in terms of Cartesian coordinates x and z).
(27)with d = 2 rg. See Fig. 2 for a contour plot of Ω(r,θ) (made in terms of Cartesian coordinates x and z).
 |
Fig. 2 Contour plot of Ω(r,θ). This is the same for all of the configurations. The straight white line indicates the boundary between the disc and the corona. The corotation point is at r = 18.8 rg. |
3.3. Boundary conditions for Bφ
In our model we take the region outside of the disc and its associated corona to be vacuum, and suppose that there is no toroidal component of the magnetic field there (i.e. Bφ = 0). We impose the same condition also at the equatorial plane because Bφ has to be antisymmetric across it.
When Bφ = 0, Eq. (7) reduces to a0 = 0, i.e. 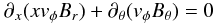 (28)at the top of the corona, at the inner edge of the disc and on the equatorial plane. We need our choice of the boundary conditions (i.e. purely dipolar field and corotation) to represent a solution of this equation. In Paper I, we showed that corotation is consistent with a pure dipolar field, as already mentioned in the previous subsection (see Eq. (22)). In addition we note here that, on the equatorial plane, Eq. (28) is trivially satisfied because Br = 0 and both vφ and Bθ are symmetric with respect to this plane.
(28)at the top of the corona, at the inner edge of the disc and on the equatorial plane. We need our choice of the boundary conditions (i.e. purely dipolar field and corotation) to represent a solution of this equation. In Paper I, we showed that corotation is consistent with a pure dipolar field, as already mentioned in the previous subsection (see Eq. (22)). In addition we note here that, on the equatorial plane, Eq. (28) is trivially satisfied because Br = 0 and both vφ and Bθ are symmetric with respect to this plane.
3.4. Solution method
In order to get to Eq. (8) we first expanded out all of the derivatives present in Eq. (7) and then put the result into a dimensionless form using x = r/rg as the radial coordinate and measuring Bφ in units of 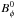 , which is a reference value for the magnetic field, taken to be
, which is a reference value for the magnetic field, taken to be 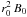 , where B0 is the magnitude of the dipolar field at the stellar equator and r0 is the dimensionless neutron-star radius. As in Paper I, we use canonical values for the mass and radius of the neutron star, 1.4 M⊙ and 10 km respectively, and take B0 = 3 × 108 G, as typical for a millisecond pulsar.
, where B0 is the magnitude of the dipolar field at the stellar equator and r0 is the dimensionless neutron-star radius. As in Paper I, we use canonical values for the mass and radius of the neutron star, 1.4 M⊙ and 10 km respectively, and take B0 = 3 × 108 G, as typical for a millisecond pulsar.
Equation (8) is a non-homogeneous elliptic partial differential equation for Bφ and we have solved it using the Gauss-Seidel relaxation method which uses a finite-difference technique, approximating the operators by discretizing the functions over a grid. At any given iteration step, the values of Bφ at the various grid points are written in terms of values at the previous step, or at the present step in the case of locations where it has already been updated. Details of the numerical scheme are given in the Appendix of Paper I, where we used the same method to solve the elliptic partial differential equation for the magnetic stream function.
Before applying the numerical scheme to the actual problem that we want to solve, we performed a series of tests on the code, which are described in detail in the Appendix. We used several configurations, with many different numbers of grid points, profiles of the turbulent diffusivity, initial estimates for the toroidal field, locations for the outer radial boundary of the grid and values for the iteration time step. In this way we have checked the code stability and convergence, have optimised the iteration procedure and have determined where best to place the outer radial boundary of the grid (so that the outer boundary conditions do not significantly influence the solution in our region of interest).
All of the results presented in this paper have been obtained using a grid spacing of Δr = 0.74 rg and Δθ = 0.125°. The final maximum residual was of the order of 10-13 and saturation was reached after about 4 × 106 iterations, the iteration time step being 4.46 × 10-4 (about 95% of the critical one, beyond which the method gives a divergent solution). As a first estimate for the profile of the magnetic field we have used a Gaussian. The numerical domain was x ∈ [10,380] , θ ∈ [80,90] (in degrees), which we covered with a homogeneous grid of 501 × 81 points. The profile of the poloidal field (which is present in the expression for the coefficient a0) was calculated by running the code used in Paper I with the same profile of η and v and the same resolutions as used in this analysis. However, since for the poloidal calculation there is a stronger dependence on the outer radial boundary conditions, we have placed rout at 750 rg and used a 1001 × 81 grid. In general the number of radial points used in the poloidal calculation (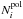 ) and in the toroidal one (
) and in the toroidal one (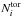 ) are related through the following condition (which comes from equating the spatial resolutions):
) are related through the following condition (which comes from equating the spatial resolutions): 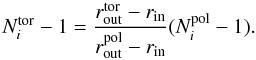 (29)For the poloidal calculation the final maximum residual was of the order of 10-9 and was reached after about 7 × 107 iterations. The iteration time step was the same as for the toroidal calculation.
(29)For the poloidal calculation the final maximum residual was of the order of 10-9 and was reached after about 7 × 107 iterations. The iteration time step was the same as for the toroidal calculation.
4. Results
4.1. Reference configuration
As mentioned in Sect. 3, we have used a slightly different configuration from that considered in Paper I (the transition in the η profile is wider and the resolution in the angular direction is increased). The poloidal field for the new configuration, resulting from solving Eqs. (5) and (6), is shown in Fig. 3. If we additionally assume a profile for the angular velocity, we can then solve Eq. (8). The result, for the profile given by Eq. (23), is shown in Fig. 4 as a contour plot of Bφ, for all of the region of interest (i.e. for r ∈ [10,115] rg and including the corona). Contours for positive values of Bφ, representing toroidal field lines rotating in the same direction as the neutron star, are shown with black solid lines; while those for negative values of Bφ (rotating in the opposite direction) are shown with black dashed lines. Triple dotted-dashed white lines show where Bφ = 0.
 |
Fig. 3 Poloidal field lines from the numerical solution (solid) and those for a dipole (dotted). In this configuration, v0 = 105 cm s-1 while the diffusivity η0 = 1010 cm2 s-1 with a transition width in θ direction of 2° (3.5 × 10-2 radians). Straight lines indicate the top surface of the corona (solid) and the boundary between disc and corona (dashed). |
 |
Fig. 4 Contour plot of the toroidal field in Cartesian coordinates, in the region r = [10−115] rg and θ = 80°−90°. The black solid lines are lines of positive Bφ, while black dashed lines are used for negative Bφ. Bφ = 0 is shown with triple dotted-dashed white lines. The straight white line indicates the boundary between disc and corona. |
 |
Fig. 5 The same as in Fig. 4 but showing an expanded view of the region r = [10−35] rg. The corotation point is at r = 18.8 rg. |
The toroidal field shows a quite structured profile, with two (positive) maxima and two (negative) minima. Surprisingly, the global maximum is located outward of the corotation point and is positive, in contrast to the standard picture according to which the sign of Bφ is the same as that of the relative angular velocity between the disc matter and the star. There is also a quite striking vertical structure, the global minimum being located just above and to the left of the global maximum. As in the analytic models, Bφ becomes zero near to the corotation point (rcor = 18.8 rg), but here one sees that for almost every value of r > rcor there is a value of θ where the field is zero, so that there are places with zero Bφ throughout all of the main disc region.
In Fig. 5 we show the Bφ contour plot in the region r ∈ [10,35] rg, so that the structure of the magnetic field in this part can be seen more clearly. In Table 1 we give the coordinates of the minima and maxima and the magnitude of the toroidal field at those locations, measured in units of the stellar field strength B0 (which is taken to be 3 × 108 G). All of these main features are located in the region r ∈ [10,55] rg; the remainder of the disc can be divided into two zones: one where Bφ > 0 (in Figs. 4 and 5 this is below the long white triple dotted-dashed curve that crosses the equatorial plane at x = 23 and x = 110), and the other where, instead, it is negative. The minimum latitude of the region with positive Bφ is about 84°.
 |
Fig. 6 Toroidal field strength plotted against r at different values of θ, in the region r = [10−50] rg (it is equal to zero on the equatorial plane). Negative values mean that Bφ is pointing backwards with respect to the disc rotation. The thick solid line is the shell average of Bφ. |
Locations of extrema of the toroidal field.
Radial profiles of Bφ are shown in Fig. 6 for several values of the latitude and for the shell average. We show the profiles for θ = 87.1° (where the global maximum is), θ = 83.6° (where the local minimum is, and which is very close also to the local maximum and the global minimum) and for an intermediate value θ = 85°. The curves all pass through zero at the corotation point (r = 18.8 rg), at least to within the accuracy of the calculation. The large positive Bφ peak at about 30 rg is progressively reduced as one moves from the mid plane of the disc towards the corona, and eventually becomes a negative local maximum. One can calculate the shell average of the radial profile, i.e. an average of Bφ over θ for each r, and this is also shown in Fig. 6 as a thick solid line. This average reproduces quite well the general behaviour of the toroidal field and shows all of its main features.
The θ dependence of the sign of Bφ is a key result, that can have quite dramatic consequences for the calculation of the magnetic torque exerted on the neutron star. In fact, it is usually assumed that the torque depends only on r, being positive inside the corotation radius and negative outside it (see Eqs. (1) and (2)), whereas we now see regions of positive Bφ even outward of the corotation point. Therefore we need to rethink the discussion of which regions in the disc tend to spin the star up or down. An appropriate approach for calculating the torque requires integration in both directions: we plan to perform this analysis in a future work.
Finally, we note here that the magnitude of the toroidal component of the magnetic field is typically larger than that of the poloidal component. For example, the maximum of the shell average of the poloidal component 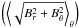 is ~ 3.6 × 10-3, while the maximum of ⟨ Bφ ⟩ θ is ~ 2.3 × 10-1. In terms of energy conservation, one has to bear in mind that any change in the magnetic energy has to be compensated by a corresponding opposite change in the plasma energy, while in the present model we are taking the flow pattern to be fixed. It is important for the back-reaction to be consistently taken into account and this will be done in subsequent work. Also, the distortions of the toroidal field will be limited by magnetic reconnection.
is ~ 3.6 × 10-3, while the maximum of ⟨ Bφ ⟩ θ is ~ 2.3 × 10-1. In terms of energy conservation, one has to bear in mind that any change in the magnetic energy has to be compensated by a corresponding opposite change in the plasma energy, while in the present model we are taking the flow pattern to be fixed. It is important for the back-reaction to be consistently taken into account and this will be done in subsequent work. Also, the distortions of the toroidal field will be limited by magnetic reconnection.
4.2. Configurations with larger η0
We have already mentioned in Sect. 2 that there are big uncertainties about how to model the turbulent magnetic diffusivity within the disc and the surrounding corona. This quantity is often discussed in terms of the turbulent magnetic Prandtl number, Pm ≡ ν/η, which links it with the turbulent viscosity.
Within the kinematic approximation, one does not solve self-consistently for the velocity field and so it is necessary assume some profile for it. As outlined in Sect. 3.1, in the present calculations we are using the velocity prescription given by the Shakura & Sunyaev thin disc model, which also embodies a particular connection between the viscosity and other disc quantities. This gives (following e.g. Szuszkiewicz & Miller 2001) ν = α h cs, with 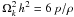 (assuming vertical hydrostatic equilibrium), where cs is the sound speed, p is the pressure and ρ is the density. Using the isothermal sound speed, the Keplerian angular velocity profile and the parameters given in Sect. 3.1, one gets ν ~ 1013 cm2 s-1 which, in turn, gives Pm ~ 103 in the disc and ~10 in the corona of our reference model. These values may seem rather high, but one should be cautious about using them because there are several further factors which need to be taken into account.
(assuming vertical hydrostatic equilibrium), where cs is the sound speed, p is the pressure and ρ is the density. Using the isothermal sound speed, the Keplerian angular velocity profile and the parameters given in Sect. 3.1, one gets ν ~ 1013 cm2 s-1 which, in turn, gives Pm ~ 103 in the disc and ~10 in the corona of our reference model. These values may seem rather high, but one should be cautious about using them because there are several further factors which need to be taken into account.
Note, first, that calculating the viscosity with the α disc model certainly gives an over-estimate for Pm, because one is neglecting the contribution of the magnetic field in the equation of motion. Also, there is a degeneracy in the profile of the velocity field, in the sense that one can obtain the same velocity profile, and hence the same results for our numerical calculations, using different combinations of α and ṁ: an increase/decrease by a factor of λ in the accretion rate, together with a decrease/increase by a factor of 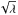 in α (and hence ν), causes no change in the velocity profile. These considerations can easily bring down the true values of Pm for our calculations well below the approximations quoted above. In any case, there is currently no general consensus about the correct value for Pm: we note that rather high values have recently been found in some numerical MRI simulations (e.g. see Takahashi & Masada 2010; Romanova et al. 2011).
in α (and hence ν), causes no change in the velocity profile. These considerations can easily bring down the true values of Pm for our calculations well below the approximations quoted above. In any case, there is currently no general consensus about the correct value for Pm: we note that rather high values have recently been found in some numerical MRI simulations (e.g. see Takahashi & Masada 2010; Romanova et al. 2011).
We chose our values for η bearing in mind which values would give significant field distortions in the disc and therefore be most interesting. However, it is clearly important to investigate the effects of varying these numbers, and so we also made some calculations using larger values of η (smaller Pm). We show here results for η0 = 4 × 1010 cm2 s-1 and η0 = 1011 cm2 s-1 with ηc being, as usual, two orders of magnitude larger (in the reference configuration we used η0 = 1010 cm2 s-1).
Results for both configurations are presented in Figs. 7–9, where we show the poloidal field lines, the contour plot of the toroidal field component and the radial profile of its shell average, respectively3.
 |
Fig. 7 Poloidal magnetic field lines. Comparison between two configurations having values of η0 larger than that of the reference configuration. |
 |
Fig. 8 Contour plots of Bφ. Comparison between two configurations having values of η0 larger than that of the reference configuration. |
Increasing η0 (i.e. decreasing the magnetic distortion function Dm, our generalisation of the magnetic Reynolds number introduced in Paper I) makes the field diffuse more efficiently and therefore the solution gets progressively nearer to being a dipole field (see Fig. 7). Reducing the poloidal field distortions in turn changes the toroidal component, and the modifications are quite substantial. The structure with four extrema gradually turns into one with only two (see Fig. 8), where the sign of Bφ is positive for radii smaller than the corotation radius and negative for larger ones. This transition is clearly seen when plotting the shell average of the toroidal field (see Fig. 9). The behaviour of the sign of the shell average of Bφ is then the same as that for Bφ in the early analytic models, although the details of the profiles have significant differences (see Fig. 13 below).
 |
Fig. 9 Shell average of the toroidal component. Comparison between two configurations having turbulent magnetic diffusivity, η0, larger than that of the reference configuration. The values of η0 are 4 × 1010 cm2 s-1 for the solid curve and 1011 cm2 s-1 for the dashed curve. |
Finally we note that the magnitude of the toroidal component decreases with increasing η0, the maximum of the shell average being ~14 × 10-3 B0 for the configuration with η0 = 4 × 1010 cm2 s-1 and ~6 × 10-3 B0 for the one with η0 = 1011 cm2 s-1 (compare the shell averages in Fig. 9 with each other and with the one in Fig. 6), while the maximum for the poloidal component has remained at ~3.5 × 10-3 B0 (this is because the maximum for the poloidal componant occurs at the inner edge, where the field depends more on the boundary conditions than on the value of η).
4.3. Configurations with constant η
Although the η profile that we have used so far is the one that we consider to be the most appropriate when studying accretion within the kinematic approximation (for the reasons given in Sect. 2), we have considered also configurations where the diffusivity is constant through all of the disc and the corona, in order to have a clear understanding of how sensitive the results are to this quantity. Cases with η = 1010 cm2 s-1 and 4 × 1010 cm2 s-1 proved unsatisfactory because of having very abrupt changes away from the dipole field at the top of the corona (this is exactly the behaviour that we have tried to avoid by using a larger value of η in the corona in our reference configuration). Results for η = 1011 cm2 s-1 and η = 1012 cm2 s-1 are shown in Figs. 10–12.
 |
Fig. 10 Poloidal magnetic field lines. Comparison between two configurations with constant η. |
 |
Fig. 11 Shell average of the toroidal component for η = 1011 cm2 s-1. For η = 1012 cm2 s-1, the curve has exactly the same shape, but the values are about 100 times smaller (in absolute value). |
 |
Fig. 12 Contour plots of Bφ. Comparison between two configurations with constant η. |
For configurations with constant η, the analysis is made simpler since there are no regions with diffusivity gradients. As stated in the previous subsection, using a larger value of η reduces the deviations away from the dipolar field. However, in contrast with the previous case, the distortions are now more uniform throughout the disc (compare Figs. 7 and 10), because η is constant and the magnetic distortion function is monotonically decreasing with r (while previously ∂rDm had a peak). We note that deviations away from a pure dipole are very small when using η = 1012 cm2 s-1, and for η comparable to or larger than this, the poloidal component of the field can be well approximated by a dipole. As regards the toroidal component, it has only two extrema which are both located just beneath the surface of the disc (see Figs. 11 and 12). These two extrema have been observed in all of the configurations which we have studied; they are also present in the models of Wang (1987) and Campbell (1987, 1992) and therefore seem to be robust features.
5. Discussion
5.1. Comparison with analytic models
In the analytic models of Wang (1987) and Campbell (1987), who we will refer to now as W&C, the toroidal component of the magnetic field is written as being proportional to the relative angular velocity between the disc and the star multiplied by the vertical field, which is taken to be a pure dipole (see Eq. (1)). For models where Ωdisc is Keplerian and the inner edge of the disc is inward of the corotation point, Bφ has a positive global maximum at the inner edge of the disc, is zero at the corotation point, reaches a global negative minimum somewhere outward of this and then tends towards zero at very large r. If Ω deviates from Keplerian in the inner part of the disc (reaching a maximum and then decreasing again as one moves inwards), then the location of the maximum of Bφ is not in general at the inner edge, but depends on the precise profile of Ω in this inner region.
The above description is only partially in agreement with the results of our present two dimensional calculations. They share the feature of having a zero of Bφ at the corotation point (or extremely close to it, see Fig. 6). As regards the predicted global maximum of Bφ in the inner part of the disc, all of our calculations show a positive maximum close to where Ω has a maximum (compare Figs. 5, 8 and 12 with Fig. 2). However, when η is not constant, magnetic field lines accumulate and a second maximum can appear outward of the corotation point, and this can also become a (positive) global maximum depending on the value of η0. Finally, regarding the minimum: as in the W&C models, we always find a global negative minimum before the outer edge of the disc; however, when η is not constant a second minimum can appear, thus producing a structure with four extrema: two maxima and two minima (see Fig. 4). We note here that even in the configurations with only two extrema, as in W&C, the profile of the toroidal component is still different from that predicted by those models. In particular, the location of the minimum and the magnitude of the field at both extrema can be very different.
The main features of the toroidal field component, as given by our present numerical calculations and by the analytic models, can be seen in Fig. 13, where we show three profiles for Bφ: the dotted curve is the W&C profile for our model, as resulting from Eq. (1) but where we have used our profile for the angular velocity near to the equatorial plane (i.e. Eq. (23) at θ = 88°), the solid curve shows the shell average for our reference configuration, and the dashed curve is for the configuration with constant η (1011 cm2 s-1).
 |
Fig. 13 Comparison of three different profiles of the toroidal field: (1) the solid curve is the shell average for the reference configuration, (2) the dashed curve is the equivalent one for the configuration with constant η (1011 cm2 s-1), (3) the dotted curve is given by the W&C formula with our Ω profile at θ = 88°. All of the curves have been normalised so as to have their peak at 1. |
The properties of having additional extrema of Bφ and of varying the location and magnitude of the two standard extrema, are not seen in the W&C models.
5.2. Role of Bp and Dm
In Fig. 14, we show the quantity ΔΩ Bθ, where ΔΩ = Ωdisc − Ωstar and Bθ is the θ-component of the poloidal field as obtained from our numerical calculations for the reference configuration. This quantity has one global maximum and one global minimum. The maximum is located very close to where Bφ and Ω have their first maxima, and the minimum is at a radial location close to that of the first minimum of Bφ (only a few rg smaller – see Fig. 5 and Table 1). This shows that the quantity ΔΩ Bθ is still relevant for grasping the fundamental properties of the toroidal component of the field, although care must be taken in choosing the profile of Bθ. Some differences between the predictions of the W&C models and our numerical results can, in fact, be explained in terms of the distortion of the θ component of the magnetic field. However, in Fig. 14 there is no evidence for the additional maximum and minimum, and so this is not the whole story. We need to consider the distortions of the field in more detail, and not focus only on the quantity ΔΩ Bθ.
 |
Fig. 14 Contour plot of ΔΩ Bθ for the reference configuration. |
In Paper I we have shown that the distortions of the poloidal component due to the plasma motion can be well described by a generalisation of the magnetic Reynolds number (which we have called the magnetic distortion function), defined as4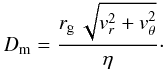 (30)We studied Dm in detail in Paper I (see Sect. 4 of that paper); here we just recall that the magnitude of the peak in its radial derivative is a measure of the degree of accumulation of poloidal field lines in its vicinity. For the cases with constant η, the field amplification caused by this distortion is negligible (the distortion is more homogeneous and the field lines do not accumulate) and Dm is just proportional to vr in all of the disc (so that there is no peak at all in the radial derivative). For the reference case, instead, ∂rDm does have a peak and its radial location (r ~ 28.5 rg) is near to that of the additional maximum (r ~ 30 rg). Increasing η0 reduces the magnitude of the peak and also the additional maximum of Bφ becomes less pronounced, eventually disappearing for ∂rDm ≤ 0.037 (see Fig. 15). We can therefore draw the conclusion that it is the radial derivative of the magnetic distortion function which is responsible for the additional maximum in the toroidal field profile.
(30)We studied Dm in detail in Paper I (see Sect. 4 of that paper); here we just recall that the magnitude of the peak in its radial derivative is a measure of the degree of accumulation of poloidal field lines in its vicinity. For the cases with constant η, the field amplification caused by this distortion is negligible (the distortion is more homogeneous and the field lines do not accumulate) and Dm is just proportional to vr in all of the disc (so that there is no peak at all in the radial derivative). For the reference case, instead, ∂rDm does have a peak and its radial location (r ~ 28.5 rg) is near to that of the additional maximum (r ~ 30 rg). Increasing η0 reduces the magnitude of the peak and also the additional maximum of Bφ becomes less pronounced, eventually disappearing for ∂rDm ≤ 0.037 (see Fig. 15). We can therefore draw the conclusion that it is the radial derivative of the magnetic distortion function which is responsible for the additional maximum in the toroidal field profile.
 |
Fig. 15 Radial derivative of the magnetic distortion function Dm near the equatorial plane (at θ = 89°) for three configurations: (1) the solid line is for the reference configuration with η0 = 1010 cm2 s-1, (2) the dotted line is for the configuration with η0 = 4 × 1010 cm2 s-1, (3) the dashed line is for η0 = 1011 cm2 s-1. |
5.3. Our picture for Bφ
In this subsection, we develop our alternative picture for the structure of the toroidal component of the magnetic field, following the same general approach as W&C, but with a more detailed representation of the poloidal magnetic field and the velocity field, and a two-dimensional model. This is still a very simplified picture but we believe that it can represent a useful step forward, giving some additional insights. Our starting point is the φ component of the induction equation: ![\begin{equation} \partial_t B_\phi = [\nabla \times ( \vec{v} \times \vec{B})]_\phi - [\nabla \times (\eta \nabla \times \vec{B} )]_\phi . \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq223.png) (31)The advective term is the one responsible for generating the field, while the diffusive term causes field losses. We then define the following scalar quantities:
(31)The advective term is the one responsible for generating the field, while the diffusive term causes field losses. We then define the following scalar quantities: ![\begin{eqnarray} G \equiv \partial_t B_\phi|_+ &=& \left[ \nabla \times (\vec{v} \times \vec{B}) \right]_\phi\\ L \equiv \partial_t B_\phi|_- &=& \left[ \nabla \times (\eta \nabla \times \vec{B}) \right]_\phi . \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq224.png) In a steady state ∂tBφ| + = ∂tBφ| − so that G = L and ∂tBφ = 0.
In a steady state ∂tBφ| + = ∂tBφ| − so that G = L and ∂tBφ = 0.
We focus first on the generation term and split it into two parts: one involving the poloidal motion (Gp) and the other involving the toroidal motion (Gφ): 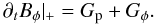 (34)In spherical coordinates, these two terms are written as
(34)In spherical coordinates, these two terms are written as ![\begin{eqnarray} G_{\rm p} \equiv [\nabla \times (\vec{v}_{\rm pol} \times \vec{B})]_\phi &=& -\frac{1}{r}\left[ \partial_r(r\,v_r\,B_\phi) + \partial_\theta(v_\theta\,B_\phi) \right]\\ G_\phi \equiv \left[\nabla \times (\vec{v_\phi} \times \vec{B})\right]_\phi &=& \frac{1}{r} [ \partial_r ( r\,v_\phi\,B_r) + \partial_\theta (v_\phi \, B_\theta) ]. \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq231.png) From these expressions we can see that, in general, the generation rate depends on several quantities and not only on the vertical gradient of the angular velocity (as in the W&C models). In fact, all of the components of the velocity field and magnetic field are present. However, usually in discs vφ ≫ vr,vθ5 and one can expect the second term to dominate. An important difference between Gp and Gφ is that the former cannot generate any toroidal field from zero, but can only modify Bφ once it has already been produced by some other means, e.g. coming from advection by the azimuthal motion (i.e. from Gφ).
From these expressions we can see that, in general, the generation rate depends on several quantities and not only on the vertical gradient of the angular velocity (as in the W&C models). In fact, all of the components of the velocity field and magnetic field are present. However, usually in discs vφ ≫ vr,vθ5 and one can expect the second term to dominate. An important difference between Gp and Gφ is that the former cannot generate any toroidal field from zero, but can only modify Bφ once it has already been produced by some other means, e.g. coming from advection by the azimuthal motion (i.e. from Gφ).
We have calculated the ratio Gφ/Gp for our configurations and have found that the toroidal term always dominates, even if the ratio is not as large as would have been expected just by comparing the velocities (because one should consider also the magnetic field). However even neglecting the contribution from the poloidal advection, the generation rate for Bφ is still considerably different from the one considered in the W&C models. In fact, it contains also the radial derivative of the term r vr Br and the vertical derivative of Bθ.
So far, we have focused only on the generation term. In order to obtain the profile of the toroidal field we have to equate it to the loss term, for which we have ![\begin{eqnarray} L &\equiv& \left[ \nabla \times ( \eta \nabla \times \vec{B} ) \right]_\phi \\ &=& -\frac{1}{r} \left\{ \partial_r \left[ \eta \, \partial_r \left( r\,B_\phi \right) \right] + \partial_\theta \left[ \frac{\eta}{r\,\sin\theta} \partial_\theta \left( B_\phi\,\sin\theta \right) \right] \right\} . \end{eqnarray}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq235.png) If we consider only typical values (
If we consider only typical values (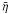 and
and 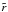 ), then we can write
), then we can write 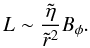 (39)In a steady state, when L = G ≃ Gφ, one has
(39)In a steady state, when L = G ≃ Gφ, one has 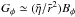 , and one gets
, and one gets 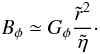 (40)In our configuration, η has two main characteristic values: η0 in the main disc region and ηc = 102 η0 in the corona and in the inner part of the disc. If in Eq. (40) we replace
(40)In our configuration, η has two main characteristic values: η0 in the main disc region and ηc = 102 η0 in the corona and in the inner part of the disc. If in Eq. (40) we replace 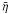 with the actual profile of the magnetic diffusivity, and choose
with the actual profile of the magnetic diffusivity, and choose 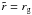 , then we find that the variation of Bφ can be well approximated by that of the coefficient a0 in Eq. (8):
, then we find that the variation of Bφ can be well approximated by that of the coefficient a0 in Eq. (8): ![\begin{equation} \label{eq:my_bp} B_\phi \simeq \frac{r_{\rm g}^2}{r\eta} \Big[ \partial_r ( r\,v_\phi\,B_r) + \partial_\theta (v_\phi \, B_\theta) \Big] = B_0 \, a_0 \end{equation}](/articles/aa/full_html/2011/07/aa16314-10/aa16314-10-eq244.png) (41)where B0 is the reference unit of the magnetic field and we recall that in Eq. (8) the fields are dimensionless (while here they are dimensional).
(41)where B0 is the reference unit of the magnetic field and we recall that in Eq. (8) the fields are dimensionless (while here they are dimensional).
This formula for Bφ is rather well confirmed by our numerical calculations. In Fig. 16 we show the contour plot for a0: this is very similar to that for the toroidal field (compare with Fig. 4), the differences being due to the approximations made in evaluating the loss term L, and to neglecting Gp in the generation term.
 |
Fig. 16 Contour plot of a0 in Cartesian coordinates, in the region r = [10−115] rg. This should be compared with Fig. 4. |
5.4. Consistency check with the W&C models
From Eq. (41) we can see that the profile of the toroidal field is basically determined by four factors: (1) the radial derivative of Br, (2) the radial derivative of r vφ, (3) the vertical derivative of Bθ and (4) the vertical derivative of vφ.
In the W&C models, the first three of these are neglected because Br is taken to be zero everywhere and Bθ is supposed not to vary with θ. If one adds also the other assumptions used in their models (about the velocity profile and the disc thickness), one then finds that Eq. (41) reduces to 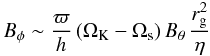 (42)which is the same as Eq. (1) with γa = (ϖ/h) and
(42)which is the same as Eq. (1) with γa = (ϖ/h) and 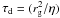 . We can therefore recover the expression appearing in the earlier analytic models from our result.
. We can therefore recover the expression appearing in the earlier analytic models from our result.
We now want to check a posteriori whether or not the simplifications made in the W&C models are still valid in our more general 2D model and, if so, in which parts of the disc. One can do this by calculating the ratio (Q) between the two terms on the right-hand-side of Eq. (41): 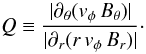 (43)Clearly, a necessary condition required for matching with the W&C models is that Q ≫ 1. In Fig. 17 we show a contour plot of this quantity for the reference configuration. We show in red all of the regions where Q > 1, while regions having the condition clearly being violated are colour-coded to show by how much Q is smaller than 1.
(43)Clearly, a necessary condition required for matching with the W&C models is that Q ≫ 1. In Fig. 17 we show a contour plot of this quantity for the reference configuration. We show in red all of the regions where Q > 1, while regions having the condition clearly being violated are colour-coded to show by how much Q is smaller than 1.
 |
Fig. 17 Contour plot of Q for the reference configuration. All locations with Q > 1 are marked in red so as to highlight the regions where Q < 1. |
There are large parts of the disc where this necessary condition is not met, with Q even reaching values as small as 10-3. Moreover, even in regions where Q ≫ 1, the further necessary condition ∂θBθ ≪ ∂θΩ may not be met. In the main disc region the angular velocity is almost constant with θ (the transition from Keplerian rotation to corotation happens in the corona), and here we are exactly in an opposite regime, i.e. ∂θBθ ≫ ∂θΩ ~ 0. Only in the corona and in the upper part of the disc are the vertical gradients of Ω not negligible.
For a pure dipolar field, Eq. (43) becomes 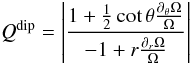 (44)which, for Keplerian motion, gives exactly 2/5. Therefore the necessary condition is never met for a pure dipole and Keplerian rotation, which is a good description for the parts of our discs near to the mid plane. This should not surprise us, since two key assumptions made in the W&C models hold only in different parts of our discs and not together: the field was supposed to have both Br and ∂θBθ vanishing and decaying as for a dipole (which we have only very close to the equatorial plane or for large η) and the transition to corotation in the angular velocity was supposed to be very sharp (which we have just beneath the disc surface, where Ω has to become equal to Ωs, far from the equatorial plane). We have calculated Q for a configuration with constant η (1012 cm2 s-1): in this case the diffusivity is so strong that deviations away from the dipole are quite small and so changes in Q come almost entirely from the angular velocity (according to Eq. (44)). As expected, in the lower part of the disc we find Q ~ 0.4.
(44)which, for Keplerian motion, gives exactly 2/5. Therefore the necessary condition is never met for a pure dipole and Keplerian rotation, which is a good description for the parts of our discs near to the mid plane. This should not surprise us, since two key assumptions made in the W&C models hold only in different parts of our discs and not together: the field was supposed to have both Br and ∂θBθ vanishing and decaying as for a dipole (which we have only very close to the equatorial plane or for large η) and the transition to corotation in the angular velocity was supposed to be very sharp (which we have just beneath the disc surface, where Ω has to become equal to Ωs, far from the equatorial plane). We have calculated Q for a configuration with constant η (1012 cm2 s-1): in this case the diffusivity is so strong that deviations away from the dipole are quite small and so changes in Q come almost entirely from the angular velocity (according to Eq. (44)). As expected, in the lower part of the disc we find Q ~ 0.4.
Therefore having a larger value of η does not necessarily imply that the necessary conditions hold in a larger region of the disc, it just implies that the field is closer to a dipole (which is what we are imposing at the boundaries). In order to get Q to go to infinity (which is what was assumed in the W&C models) not only does one need Br = 0 and ∂θBθ = 0 6 but also that the vertical gradient of the angular velocity, at the same location, has to be non-zero, or much larger than the vertical derivative of Bθ.
6. Conclusions
In this paper we have considered a system consisting of a rotating neutron star, having a dipole magnetic field aligned with the rotation axis and surrounded by an accretion disc. The disc is truncated at the Alfven radius and has a coronal layer above and below it. The region outside the corona is taken to be vacuum and we impose dipolar boundary conditions on all of the boundaries.
Our aim was to improve on the analytic models developed by Wang (1987) and Campbell (1987) (W&C). As in those models, we have made the kinematic approximation and have looked for an axisymmetric stationary solution of the induction equation, but we have gone beyond those models in solving for all of the components of the magnetic field and not assuming the poloidal component to be dipolar within the disc. We have also retained all of the components of the velocity field rather than putting vr and vθ to zero everywhere. We have performed a fully two-dimensional calculation, without making any vertical average or Taylor expansion in h (the semi-height of the disc). Finally we have neglected dynamo action but have included a turbulent magnetic diffusivity.
The analysis of the poloidal component of the magnetic field has been presented in a previous paper (Naso & Miller 2010, Paper I); in the present paper we have focused on the toroidal component. We have solved the φ component of the induction equation numerically and have shown that the profile obtained for Bφ can be very different from that in the earlier analytic models.
In the W&C models, the toroidal field strength was taken to be proportional to the relative angular velocity between the disc and the central object multiplied by the vertical field, which was taken to be dipolar. However in Paper I we found that, when calculated consistently, the poloidal field component was often far from being dipolar. Therefore a first improvement with respect to the earlier models was to use the poloidal field as obtained in our calculations, i.e. a field dragged inwards by the plasma motion. This behaviour explains why we then find different intensities for the toroidal field, and also a different location for its global minimum.
When the turbulent magnetic diffusivity η increases or the radial velocity decreases one expects the field to be progressively less distorted by the plasma motion. This is indeed what we have found both here and in Paper I. Our results show that when the diffusivity η0 is larger than about 1012 cm2 s-1, with the characteristic velocity v0 being of the order of 105 cm s-1, then the field is barely modified. Therefore whenever we expect the magnetic field to deviate from the stellar dipole, η should not be larger than 107 |vcgs| cm2 s-1, where |vcgs| is the characteristic magnitude of the radial velocity expressed in cm s-1.
When the turbulent magnetic diffusivity is not constant throughout the disc and corona, two additional extremal points may well appear: if the radial derivative of the magnetic distortion function Dm is larger than a critical value (about 0.04 in the equatorial plane), there is an additional maximum and minimum, and in some cases Bφ can even become positive again outward of the corotation point, so that there are additional locations where Bφ = 0. It is clear that under these circumstances the picture of which regions of the disc tend to spin the star up or down has to be radically redrawn (this will be the subject of a future investigation). However we should emphasise here that there are still many uncertainties among experts about which profile of η should be used and we have therefore made very simple choices here in line with our step-by-step approach.
We have presented a new suggestion for the Bφ profile, which reduces to that of W&C if one imposes Br = ∂θBθ = 0 and Ω = ΩK. In general there are large parts of the disc where the additional terms included in our new picture for Bφ dominate over the one retained by W&C (see Fig. 17). Our simplified expression (Eq. (41)) reproduces the numerical results quite well (compare Figs. 4 and 16), the differences being due to approximations made in calculating the generation and loss terms for Bφ.
Summarising, in our calculations we have found that Bφ can have two maxima and two minima (see Fig. 4). The first maximum (positive and inward of the corotation point) and the first minimum (negative and outward of the corotation point) can be explained referring to the quantity ΔΩ Bθ, which has two extrema at the same locations as for Bφ (see Fig. 14). These extrema appear also in the W&C models, where the toroidal field is, in fact, taken to be proportional to ΔΩ Bz. There is a fundamental difference however: in W&C Bz is a pure dipole, whereas the Bθ which we consider here is that of a field being dragged inward by the motion of the accreting material. When η is not constant, there is an additional maximum whose magnitude and sign depend on the diffusivity in the disc, and whose radial location is always outward of the first minimum, coinciding with that of the maximum in the radial derivative of the magnetic distortion function Dm. Outward of this maximum, the field tends to come back to the profile that it would have had if η were constant, and this produces the last minimum (compare Figs. 9 and 11).
The main conclusion of this analysis is that, when the poloidal component of the magnetic field is treated self-consistently in the calculations, the profile for Bφ can be significantly different from that obtained by W&C, and the magnetic torque generated by it would then be different as well. Moreover, when the turbulent magnetic diffusivity η is not constant throughout the disc and corona, some additional unexpected features can appear (such as a region of positive Bφ outward of the corotation point). In the present work, we have retained the very simple Keplerian rotation law in the main part of the disc. Even within a purely hydrodynamical treatment, more complicated velocity fields than this are expected (see Kluzniak & Kita 2000; Jiao & Wu 2011) and further changes are expected when back-reaction from the magnetic field on the velocity field is included. The effects of this will be another topic for investigation in subsequent stages of our step-by-step approach.
Note that the error-function widths in the radial and angular directions are larger than those used in Paper I (there dr = 2 rg and dθ = 10-3 radians = 0.057°). The reasons for this are explained in Appendix A.2.
Acknowledgments
This work has been partially supported by CompStar, a Research Networking Programme of the European Science Foundation, and by the National Natural Science Foundation of China (40890161, 2011CB811403, 11025315, 10873020 and 10921303). L.N. is currently supported by a Chinese Academy of Sciences fellowship for young international scientists (grant No. 2010Y2JB12) and would also like to thank the Department of Physics (Astrophysics) of the University of Oxford for support granted during the development of this work, CAMK (Centrum Astronomiczne im. M. Kopernika) in Warsaw, which provided partial support through Polish Ministry of Science grant N N203 381436, and SISSA (Trieste) whose high performance computing facilities have been used for running the numerical calculations.
References
- Campbell, C. G. 1987, MNRAS, 229, 405 [NASA ADS] [Google Scholar]
- Campbell, C. G. 1992, GApFD, 63, 179 [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Jiao, C.-L., & Wu, X.-B. 2011, ApJ, 733, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Kluzniak, W., & Kita, D. 2000, unpublished [arXiv:astro-ph/0006266] [Google Scholar]
- Naso, L., & Miller, J. C. 2010, A&A, 521, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rekowski, M. V., Ruediger, G., & Elstner, D. 2000, A&A, 353, 813 [NASA ADS] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. K., & Lovelace, R. V. E. 2011, MNRAS, submitted [arXiv:1102.1089v1] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Szuszkiewicz, E., & Miller, J. C. 2001, MNRAS, 328, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, H. R., & Masada, Y. 2011, ApJ, 727, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Tessema, S. B., & Torkelsson, U. 2010, A&A, 509, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tessema, S. B., & Torkelsson, U. 2011, MNRAS, 412, 1650 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1987, A&A, 183, 257 [NASA ADS] [Google Scholar]
- Wang, Y.-M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
Appendix A: Testing of the code
In this Appendix we discuss some of the tests that we have performed on the numerical code used to solve Eq. (8). For a description of the Gauss-Seidel relaxation procedure and of the discretization scheme see Appendix A.1 of Paper I.
Before describing the tests, we should underline a difference in the boundary conditions with respect to the code used for the poloidal analysis. In Paper I we were not imposing the dipolar boundary conditions on the magnetic field directly but rather on the magnetic stream function 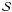 . The poloidal magnetic field was then calculated by differentiating
. The poloidal magnetic field was then calculated by differentiating 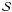 . Because of this, Br and Bθ were not precisely dipolar on the boundaries. For the calculations in the present paper, we have introduced a row of ghost points, where we set the field to be exactly dipolar, i.e. the poloidal component is a pure dipole and the toroidal component is zero.
. Because of this, Br and Bθ were not precisely dipolar on the boundaries. For the calculations in the present paper, we have introduced a row of ghost points, where we set the field to be exactly dipolar, i.e. the poloidal component is a pure dipole and the toroidal component is zero.
We divide the tests into two groups. In the first group we chose the coefficients of Eq. (8) in such a way that it was possible to find an analytic solution, while in the second group we used the values given by Eqs. (9)–(13). Here is a schematic description of these tests:
-
Tests with analytic solutions. In addition tofixing the coefficients, one also has to choose the boundaryconditions. We considered three sub-cases:
- 1.1
all coefficients constant and set to 1.0. There is then the following analytic solution:
 (A.1)
(A.1) - 1.2
all coefficients set to 0.0 except for
 The general solution is then:
The general solution is then: 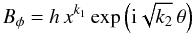 (A.4)where k1 is a function of b and k2. We chose h = 10, k2 = 362 and b = 2 − k2, so as to include a complete period of the angular part of the solution within our angular domain. The solution is then:
(A.4)where k1 is a function of b and k2. We chose h = 10, k2 = 362 and b = 2 − k2, so as to include a complete period of the angular part of the solution within our angular domain. The solution is then: 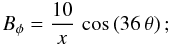 (A.5)
(A.5) - 1.3
the same choice of coefficients as in test 1.2 but with different boundary conditions: h = 10, k2 = 0 and b = 70. The analytic solution is then:
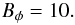 (A.6)
(A.6)
- 1.1
-
Testing the model setup. In this group of tests we used a setup which was very similar to that used for our actual physical analysis but varied some numerical parameters so as to test the code. We performed four tests aimed at:
- 2.1
checking convergence by changing the number ofgrid-points;
studying the dependence of the solution on the location of the radial outer boundary;
studying dependence on the initial estimate for the solution;
optimising the iteration step size by simple benchmarking.
- 2.1
A.1. Tests with analytic solutions
For all of the tests in this category, we considered the code stability and convergence. We used grids with different numbers of points in both directions and compared the analytic errors and the solutions.
In all cases, the stability of the code was related to the size of the iteration step, the code being stable for values smaller than a certain threshold.
To check convergence, we considered how the maximum of the analytic errors changed with varying the total number of iterations. We considered both absolute and relative errors and analysed them in the region of interest (i.e. for r < rlc) by calculating their maximum and looking at their 2D profile. As the iteration procedure continues, the errors decrease and at a certain point they saturate, so that making more iterations no longer leads to smaller errors. In addition to the errors, we have also considered the evolution of the root mean square (rms) of the solution.
The size of the errors at saturation depends on the grid resolution, being smaller for grids with more points (the size of the domain is fixed, so that increasing the number of points means increasing the resolution). Moreover the improvement obtained when increasing the number of grid-points becomes progressively smaller, as it should do in a convergent regime. We calculated an effective order of convergence peff by considering the maximum value of the relative error at the final iteration, and how it changed with the grid size. Doing this we obtained peff ~ 1.5.
All of the tests gave satisfactory results, confirming stability and giving convergence within ~104 iterations for tests 1.1 and 1.2, and within ~107 iterations for test 1.3. The maximum saturation error was ~10-9% for test 1.3 and ~10-3% for test 1.1. As regards test 1.2, since the solution has some zeros in the considered domain, we could not estimate the error by considering the relative error (since it diverges at the zeros). We instead considered the maximum of the absolute error and compared it with the rms of the solution, finding that it was less than 1%.
A.2. Tests with the model setup
For these tests we had no analytic solutions, and so could not calculate analytic errors but only residuals. When considering stability, we looked at the residuals, while for testing convergence we considered the change in the θ-average of the solution (or in its rms) when changing the number of grid-points.
We recall that we cannot change the number of grid-points freely. In fact, one of the coefficients (a0) is not calculated from an analytic function but comes instead from the numerical results of Paper I for the poloidal field. This coefficient is therefore directly defined only on the grid used in that calculation, which had 1001 × 21 points. We consider this grid as our reference one. When using a grid with fewer points, we have to choose them as a subset of our reference grid, while when using a larger number of points, we have to interpolate. Similarly when changing the size of the domain (by reducing rout), we must also decrease the number of grid points Ni accordingly, as explained at the end of Sect. 3.4 (see also Eq. (29)).
A very important result of test 2.1 is that if the transition in η between the disc and the corona is not well-enough resolved, then we find convergence to a different solution. More precisely, using an angular width for the transition of 5 × 10-2 radians we need to have at least 20 grid points overall in the θ direction in order to converge to the correct solution, i.e. to the same solution as for grids with larger values of Nj (we tested with Nj = 39 and Nj = 77). This gives a minimum number of angular zones required for convergence of about 5 within the transition region.
Test 2.2 tells us that the solution is not very dependent on the location of the radial outer boundary, contrary to the situation in Paper I for the poloidal field. The θ-averaged solution obtained using rout = 290 differs from that obtained with rout = 750 by less than 0.02% in all of the region of interest. If we consider the solution rms, the difference is even smaller, being less than 5 × 10-4%.
For test 2.3, we ran calculations with quite different, and even unphysical, initial estimates for Bφ, in order to see whether the solution still converged correctly. We used (1) a constant value Bφ = 1; two decaying profiles: (2) Bφ = (10/x)3 and (3) Bφ = (10/x); (4) a growing profile  and (5) a Gaussian profile in both directions (centred at x = 100 rg, θ = 85° with widths 15 rg and 2°). We obtained the same final solution for all of the cases; profiles (3) and (5) converged after ~2 × 106 iterations, while all of the others converged after ~4 × 106 iterations.
and (5) a Gaussian profile in both directions (centred at x = 100 rg, θ = 85° with widths 15 rg and 2°). We obtained the same final solution for all of the cases; profiles (3) and (5) converged after ~2 × 106 iterations, while all of the others converged after ~4 × 106 iterations.
Finally in test 2.4 we changed the iteration step size Δt, looking for the largest possible value still giving stability. As in Paper I, we found that the maximum value depends more sensitively on Nj than on Ni. For Nj = 81 we found Δtmax = 4.7476 × 10-4.
All Tables
All Figures
 |
Fig. 1 Schematic representation of our model (not to scale). We use rin = 10 rg, rtr ~ 22 rg and rlc ~ 115 rg. The opening angles are 8° for the disc alone and 10° for the disc plus corona. The outer disc extends much further out than the main region shown here: the grid continues until rout = 380 rg. |
| In the text | |
 |
Fig. 2 Contour plot of Ω(r,θ). This is the same for all of the configurations. The straight white line indicates the boundary between the disc and the corona. The corotation point is at r = 18.8 rg. |
| In the text | |
 |
Fig. 3 Poloidal field lines from the numerical solution (solid) and those for a dipole (dotted). In this configuration, v0 = 105 cm s-1 while the diffusivity η0 = 1010 cm2 s-1 with a transition width in θ direction of 2° (3.5 × 10-2 radians). Straight lines indicate the top surface of the corona (solid) and the boundary between disc and corona (dashed). |
| In the text | |
 |
Fig. 4 Contour plot of the toroidal field in Cartesian coordinates, in the region r = [10−115] rg and θ = 80°−90°. The black solid lines are lines of positive Bφ, while black dashed lines are used for negative Bφ. Bφ = 0 is shown with triple dotted-dashed white lines. The straight white line indicates the boundary between disc and corona. |
| In the text | |
 |
Fig. 5 The same as in Fig. 4 but showing an expanded view of the region r = [10−35] rg. The corotation point is at r = 18.8 rg. |
| In the text | |
 |
Fig. 6 Toroidal field strength plotted against r at different values of θ, in the region r = [10−50] rg (it is equal to zero on the equatorial plane). Negative values mean that Bφ is pointing backwards with respect to the disc rotation. The thick solid line is the shell average of Bφ. |
| In the text | |
 |
Fig. 7 Poloidal magnetic field lines. Comparison between two configurations having values of η0 larger than that of the reference configuration. |
| In the text | |
 |
Fig. 8 Contour plots of Bφ. Comparison between two configurations having values of η0 larger than that of the reference configuration. |
| In the text | |
 |
Fig. 9 Shell average of the toroidal component. Comparison between two configurations having turbulent magnetic diffusivity, η0, larger than that of the reference configuration. The values of η0 are 4 × 1010 cm2 s-1 for the solid curve and 1011 cm2 s-1 for the dashed curve. |
| In the text | |
 |
Fig. 10 Poloidal magnetic field lines. Comparison between two configurations with constant η. |
| In the text | |
 |
Fig. 11 Shell average of the toroidal component for η = 1011 cm2 s-1. For η = 1012 cm2 s-1, the curve has exactly the same shape, but the values are about 100 times smaller (in absolute value). |
| In the text | |
 |
Fig. 12 Contour plots of Bφ. Comparison between two configurations with constant η. |
| In the text | |
 |
Fig. 13 Comparison of three different profiles of the toroidal field: (1) the solid curve is the shell average for the reference configuration, (2) the dashed curve is the equivalent one for the configuration with constant η (1011 cm2 s-1), (3) the dotted curve is given by the W&C formula with our Ω profile at θ = 88°. All of the curves have been normalised so as to have their peak at 1. |
| In the text | |
 |
Fig. 14 Contour plot of ΔΩ Bθ for the reference configuration. |
| In the text | |
 |
Fig. 15 Radial derivative of the magnetic distortion function Dm near the equatorial plane (at θ = 89°) for three configurations: (1) the solid line is for the reference configuration with η0 = 1010 cm2 s-1, (2) the dotted line is for the configuration with η0 = 4 × 1010 cm2 s-1, (3) the dashed line is for η0 = 1011 cm2 s-1. |
| In the text | |
 |
Fig. 16 Contour plot of a0 in Cartesian coordinates, in the region r = [10−115] rg. This should be compared with Fig. 4. |
| In the text | |
 |
Fig. 17 Contour plot of Q for the reference configuration. All locations with Q > 1 are marked in red so as to highlight the regions where Q < 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


