EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 531 (July 2011) A&A, 531 (2011) A60 Full HTML
Free Access
Issue
A&A
Volume 531, July 2011
Article Number A60
Number of page(s) 6
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201016208
Published online 13 June 2011

© ESO, 2011

1. Introduction

To date, 107 transiting extrasolar planets have been discovered1, the majority of which are gas giants in short orbits. The radii of a subset of these exoplanets are larger than predicted by standard models of irradiated gas giants (e.g., Burrows et al. 2007; Fortney et al. 2007), including TrES-4b (Mandushev et al. 2007; Sozzetti et al. 2009), WASP-12b (Hebb et al. 2009), and WASP-17b (Anderson et al. 2010, 2011b). A number of mechanisms have been proposed as potential solutions to the radius anomaly (see Fortney et al. 2010, for a review), each of which involves either injecting heat into the planet from an external source or slowing heat loss from the planet.

One such mechanism is the dissipation of energy within a planet as heat during the tidal circularisation of an eccentric orbit (Bodenheimer et al. 2001; Gu et al. 2003; Jackson et al. 2008; Ibgui & Burrows 2009). Such studies suggest that tidal heating may be sufficient to explain the large radii of even the most bloated exoplanets, though we would have to be observing some systems at very special times. A high heating rate, as suggested by Leconte et al. (2010), would mean most tidal energy is radiated away by the age typical of the very most bloated planets (a few Gyr) and so could not have played a significant role in their observed bloating. However, the current uncertainty in tidal theory allows for a wide range of heating rates (e.g. Ibgui et al. 2011). Though most studies have considered a transient phase of tidal heating, ongoing tidal heating (e.g. Ibgui et al. 2010) would occur if an additional companion continues to excite the orbital eccentricity of the bloated planet (e.g. Mardling 2007).

Burrows et al. (2007) proposed that enhanced opacities would retard the loss of internal heat and thus slow contraction of bloated planets. They suggested that enhanced opacities may arise due to the strong optical and UV irradiation of short-orbit, gas giants that could alter their atmospheres, producing thick hazes, absorbing clouds and non-equilibrium chemical species (e.g. tholins or polyacetylenes).

The bloated planets are all very strongly irradiated by their host stars, and a small fraction of stellar insolation energy would be sufficient to account for the observed degrees of bloating. Guillot & Showman (2002) suggested that the kinetic energy of strong winds, induced in the atmosphere by the large day-night temperature contrasts that result from tidal locking, may be transported downward and deposited as thermal energy in the deep interior. However, a mechanism to convert the kinetic energy into thermal energy would still be required. Li & Goodman (2010) and Youdin & Mitchell (2010) found that turbulence is efficient at dissipating kinetic energy. Magnetic drag on weakly ionized winds (Perna et al. 2010) and Ohmic heating (Batygin & Stevenson 2010) are alternative mechanisms. The non-bloated planets are also highly irradiated. Hence, such a mechanism would either have to act more efficiently on the bloated planets, or some other property must counteract its effect. One such possibility is the presence of a massive core. Indeed, Guillot et al. (2006) and Burrows et al. (2007) found a correlation between the core masses required to reproduce the observed radii of known exoplanets and the metallicities of their host stars.

In this paper, we present the discovery of the bloated, transiting, giant planet WASP-31b. Compared to the ensemble of known short-period planets, WASP-31b is moderately irradiated by its low-metallicity host star.

2. Observations

WASP-31 is a V = 11.7, F7–8 dwarf star located in the constellation Crater. WASP-31 has been observed by WASP-South (Pollacco et al. 2006) during the first five months of each year since the start of full-scale operations (2006 May 4). A transit search (Collier Cameron et al. 2006) of the resulting 24 614 usable photometric measurements (Fig. 1) found a strong, 3.4-d periodicity.

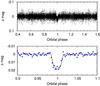thumbnail Fig. 1

WASP-South discovery light curve. Upper panel: photometry folded on the orbital period of P = 3.4 d. Points with error above three times the median error (0.012 mag) were clipped for display purposes. Lower panel: photometry folded on the orbital period and binned in phase (Δφ = 0.025), with the transit model generated from the parameters of Table 4 superimposed.

WASP-31 is a visual double with a V ~ 15.8 star (2MASS 11174477-1903521) approximately 35″ away. The 2MASS colours of the companion suggest that it is a mid-to-late K-type star. The proper motions for the two stars listed in the PPMXL (Roeser et al. 2010) and UCAC3 (Zacharias et al. 2010) catalogues suggest that this is a common proper motion pair (Table 1). The companion is blended with WASP-31 in the WASP images, so we corrected the WASP photometry for this contamination to prevent dilution of the transit.

Table 1

Proper motions of WASP-31 and its visual companion.

Using the CORALIE spectrograph mounted on the 1.2-m Euler-Swiss telescope (Baranne et al. 1996; Queloz et al. 2000b), we obtained 34 spectra of WASP-31 during 2009 and a further 13 spectra during 2010. As pressure variations can cause CORALIE to drift on short timescales, we calibrated the stellar spectra by obtaining simultaneous spectra of a thorium-argon lamp. In April 2010, we obtained an additional 10 spectra with the HARPS spectrograph mounted on the 3.6-m ESO telescope. As HARPS is stable at the 1 m s-1 night-1 level, we obtained a calibration at the start of each night of observations. This avoids contamination of the stellar spectra by the thorium-argon lamp. The CORALIE measurement taken at BJD = 2 454 971.548671 and the HARPS measurement taken at BJD = 2 455 299.716991 were both affected by cloud cover.

The typical signal-to-noise ratio (S/N) per pixel at 550 nm is 18 for the CORALIE spectra, with exposure times of 30 min, and 26 for the HARPS spectra, with exposure times of 15 min. Radial-velocity (RV) measurements were computed by weighted cross-correlation (Baranne et al. 1996; Pepe et al. 2005) with a numerical G2-spectral template. RV variations were detected with the same period found from the WASP photometry and with a semi-amplitude of 58 m s-1, consistent with a planetary-mass companion. The RV measurements are plotted in the upper panel of Fig. 2.

thumbnail Fig. 2

Upper panel: spectroscopic orbit of WASP-31, as illustrated by radial velocities from CORALIE (blue circles) and HARPS (red squares). The best-fitting Keplerian model, generated from the parameters of Table 4, is overplotted as a solid line. An RV taken at BJD = 2 455 168.8468, depicted in the plot by an open circle, fell during transit. As we did not treat the Rossiter-McLaughlin effect (e.g., Queloz et al. 2000a), we excluded this measurement from our combined analysis. Lower panel: a lack of correlation between bisector spans and radial velocities rules out a blended eclipsing binary or starspots as the cause of the photometric and spectroscopic variaitions. We adopted uncertainties on the bisector spans twice the size of those on the radial velocities. For both plots, the centre-of-mass velocity, γ = −124.92 m s-1, was subtracted from the radial velocities and the Keplerian model.

To test the hypothesis that the RV variations are due to spectral line distortions caused by the presence of cool stellar spots or a blended eclipsing binary, a line-bisector analysis (Queloz et al. 2001; Santos et al. 2002) of the CORALIE and HARPS cross-correlation functions was performed. The lack of correlation between bisector span and RV (Fig. 2, lower panel), especially for the high-precision HARPS measurements, supports the identification of the transiting body as a planet. As an additional test for spots or a blend, we also computed CORALIE RVs by weighted cross-correleation with a numerical K5-spectral template. The amplitude and phase of the RV variations are the same within errors, irrespective of the choice of cross-correlation mask, as would be expected if the variations were caused by the presence of a planet (e.g. Huélamo et al. 2008).

To refine the system paramters, we obtained high-S/N transit photometry. Photometric follow-up observations of WASP-31 were obtained with the LCOGT2 2.0-m Faulkes Telescope North (FTN) on Mt. Haleakala, Maui on the night of 2010 Feb. 26. The fs03 Spectral Instruments camera was used with a 2  ×  2 binning mode, giving a field of view of 10′  ×  10′ and a pixel scale of 0.303″ pixel-1. The data were taken through a Pan-STARRS z filter, with the telescope defocussed to minimise flat-fielding errors and to allow 60-s exposure times to be used without saturating.

The data were pre-processed using the WASP Pipeline (Pollacco et al. 2006) to perform masterbias and flat construction, debiassing and flatfielding. Due to the very low dark current of the fs03 Fairchild CCD (<0.0001 e− pix-1 s-1), dark subtraction was not performed. Aperture photometry was performed using DAOPHOT within the IRAF environment using an aperture with a radius of 11 pixels. Differential photometry was then performed relative to 20 comparison stars that were within the FTN field of view (Fig. 3). The rms of the residuals about the best-fitting model (Sect. 4) was 1.4 mmag.

On 2010 April 15 we obtained 4.1 h of photometry in the Gunn r filter with the CCD camera on the Euler-Swiss telescope, covering from 40 min before the start of transit until 55 min after it ended. The conditions were variable, with seeing of 0.6−1.7″ and an airmass range of 1.15−1.34. Euler now employs absolute tracking to keep the stars on the same pixels during a whole transit. By identifying point sources in each image and matching them with a catalogue, the image centre is calculated. Drifts from the nominal position are then corrected by adjusting the telescope pointing between exposures.

After bias-subtracting and flat-fielding the images, we performed aperture photometry. The flux was extracted for all stars in the field and the final light curve (Fig. 3) was obtained by differential photometry of the target and a reference source obtained by combining the 4 brightest reference stars. The rms of the residuals about the best-fitting model (Sect. 4) was 2.6 mmag, which was limited by the number of available reference stars.

thumbnail Fig. 3

High-S/N transit light curves. The upper observations (blue circles) were obtained by FTN, using a Pan-STARRS z filter, on 2010 Feb. 26. The lower observations (red diamonds), offset in relative flux by 0.026 for display, were obtained by Euler, using a Gunn r filter, on 2010 Apr. 15. The best-fitting transit models generated from the parameters of Table 4 are overplotted.

3. Stellar parameters

The individual HARPS spectra of WASP-31 were co-added to produce a single spectrum with an average S/N of around 100:1. The analysis was performed using the methods given in Gillon et al. (2009). The Hα line was used to determine the effective temperature (Teff), while the Na i D and Mg i b lines were used as surface gravity (log g∗) diagnostics. The parameters obtained from the analysis are listed in Table 2. The elemental abundances were determined from equivalent width measurements of several clean and unblended lines. A value for microturbulence (ξt) was determined from Fe i using the method of Magain (1984). The quoted error estimates include that given by the uncertainties in Teff, log g∗ and ξt, as well as the scatter due to measurement and atomic data uncertainties.

The sky-projected stellar rotation velocity (vsinI) was determined by fitting the profiles of several unblended Fe i lines. We assumed a value for macroturbulence (vmac) of 5.2  ±  0.3  km s-1, based on the tabulation by Gray (2008), and we used an instrumental FWHM of 0.06  ±  0.01 Å, determined from the telluric lines around 6300 Å. A best-fitting value of vsinI = 7.6  ±  0.4  km s-1 was obtained. However, recent work by Bruntt et al. (2010) suggests a lower value for macroturbulence of vmac = 4.2  ±  0.3  km s-1 which yields a slightly higher vsinI = 8.1  ±  0.4  km s-1. We therefore adopt the average of these two determinations, vsinI = 7.9  ±  0.6  km s-1, with the uncertainty being the quadrature addition of the individual uncertainties. If vmac = 0  km s-1, then a value of vsinI = 8.7  ±  0.4  km s-1 is found, which is the upper-limit of the sky-projected rotation velocity.

Table 2

Stellar parameters from the spectroscopic analysis.

4. Combined analysis

The WASP, FTN and Euler photometry were combined with the CORALIE and HARPS radial velocities in a simultaneous Markov-chain Monte Carlo (MCMC) analysis (Collier Cameron et al. 2007; Pollacco et al. 2008). The transit light curve was modeled using the formulation of Mandel & Agol (2002) with the assumption that Rpl  ≪  R∗. Limb-darkening was accounted for using a four-coefficient nonlinear limb-darkening model, using fixed coefficients (Table 3) appropriate to the passbands and interpolated in effective temperature, surface gravity and metallicity from the tabulations of Claret (2000).

The transit light curve is parameterized by the epoch of midtransit T0, the orbital period P, the planet-to-star area ratio (Rpl/R∗)2, the approximate duration of the transit from initial to final contact T14, and the impact parameter b = acosi/R∗ (the distance, in fractional stellar radii, of the transit chord from the star’s centre). 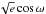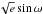The radial-velocity orbit is parameterized by the stellar reflex velocity semi-amplitude K∗, the systemic velocity γ, and ecosω\hbox{$\sqrt{e} \cos \omega$} and esinω\hbox{$\sqrt{e} \sin \omega$} (Anderson et al. 2011a), where e is orbital eccentricity and ω is the argument of periastron.

The linear scale of the system depends on the orbital separation a which, through Kepler’s third law, depends on the stellar mass M∗. At each step in the Markov chain, the latest values of stellar density ρ∗, effective temperature Teff and metallicity [Fe/H] are input in to the empirical mass calibration of Enoch et al. (2010) to obtain M∗. The shapes of the transit light curves (Seager & Mallén-Ornelas 2003) and the radial-velocity curve constrain ρ∗, which combines with M∗ to give R∗. Teff and [Fe/H] are proposal parameters constrained by Gaussian priors with mean values and variances derived directly from the stellar spectra (Table 2).

As the planet-star area ratio is constrained by the measured transit depth, Rpl follows from R∗. The planet mass Mpl is calculated from the measured value of K1 and M∗; the planetary density ρpl and surface gravity log gpl then follow. We also calculate the blackbody equilibrium temperature Teql (assuming zero albedo and efficient redistribution of heat from the planet’s presumed permanent day side to its night side), the transit ingress and egress durations, T12 and T34, and the orbital semi-major axis a.

Table 3

Limb-darkening coefficients.

At each step in the MCMC procedure, model transit light curves and radial-velocity curves are computed from the proposal parameter values, which are perturbed from the previous values by a small, random amount. The χ2 statistic is used to judge the goodness of fit of these models to the data and a step is accepted if χ2 is lower than for the previous step. A step with higher χ2 is accepted with a probability exp(−Δχ2/2). In this way, the parameter space around the optimum solution is thoroughly explored. To give proper weighting to each transit and RV data set, the uncertainties are scaled at the start of the MCMC so as to obtain a reduced χ2 of unity. We allow for a systematic instrumental offset, ΔγHARPS, between the CORALIE and HARPS spectrographs.

From an initial MCMC fit for an eccentric orbit, we found 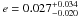e=0.027-0.020+0.034\hbox{$e = 0.027^{+0.034}_{-0.020}$}, with a 3-σ upper limit of 0.13. The F-test approach of Lucy & Sweeney (1971) indicates that there is a 66% probability that an eccentricity of or above the fitted value could have arisen by chance if the the underlying orbit is in fact circular. As such, we impose a circular orbit, but we note that doing so has no signicant effect as the fitted eccentricity was so small.

The median values and 1σ uncertainties of the system parameters derived from the MCMC model fit are presented in Table 4. The corresponding best-fitting transit light curves are shown in Figs. 1 and 3, and the best-fitting RV curve is shown in Fig. 2.

Though the visual companion is 40 times fainter than WASP-31 and is resolved in the Euler and FTN images, we did correct the WASP photometry for the contamination prior to producing the MCMC solution presented. We checked the effect of the contamination by producing another MCMC solution using the non-corrected WASP photometry. The best-fitting parameter values were the same to within a tenth of an error bar.

Without exquisite photometry, our implentation of MCMC tends to bias the impact parameter, and thus R∗ and Rpl, to higher values. This is because, with low-S/N photometry, the transit ingress and egress durations are uncertain, and symmetric uncertainties in those translate into asymmetric uncertainties in b and thus in R∗. The effect on the stellar and planetary radii is larger for high-impact-parameter planets such as WASP-31b. Therefore we explored an MCMC with a main-sequence (MS) prior imposed (Collier Cameron et al. 2007). This employs a Bayesian penalty to ensure that, in accepted steps, the values of stellar radius are consistent with the values of stellar mass for a main-sequence star. The differences between the solutions with and without MS priors are small and within errors, indicating that the transit light curves are of a quality such that the ingress and egress durations are measured sufficiently well. As such, we adopt the solution without the MS prior, which has slightly more conservative error bars.

Table 4

System parameters from the combined analysis.

5. System age

Using 2MASS photometry we constructed a colour − magnitude diagram (Fig. 4) for WASP-31 and its common proper motion, K-type companion. A distance modulus of 7.8  ±  0.2 (360  ±  30 pc) is required to place the companion on the main-sequence, which puts WASP-31 between the zero-age main sequence and 1-Gyr age lines. Thus, if the two stars are of common origin, they are most probably around 1-Gyr old, with an approximate upper age limit of 4 Gyr. Combining the absolute Vmag of an F7–8 star (Gray 2008) with the measured J − K and H − K colours of WASP-31 from 2MASS and the intrinsic colours from Koornneef (1983), we derive an interstellar extinction AV = 0 and a distance of 360  ±  20 pc. This agreement with the distance determined from the colour − magnitude diagram supports the inference that the companion is associated with WASP-31 rather than being a mere line-of-sight neighbour. At a distance of 360 pc, the sky-projected separation of the two stars suggests that they would be separated by at least 12 600 AU (0.2 light-year).

thumbnail Fig. 4

Colour–magnitude diagram for WASP-31 and its companion. Various isochrones from Marigo et al. (2008) are given, with ages indicated in the figure. No de-reddening has been applied as AV = 0.

Assuming aligned stellar-spin and planetary-orbit axes, the measured vsinI of WASP-31 and its derived stellar radius indicate a rotational period of Prot = 7.9  ±  0.7 d. Combining this with the B − V colour of an an F8 star from Gray (2008), we used the relationship of Barnes (2007) to estimate a gyrochronological age of 950  ±  250 Myr. This is an upper limit as the star would be rotating faster, and so be younger, than suggested by spectroscopic vsinI if the stellar spin axis were inclined with respect to the sky plane. We used the method of Maxted et al. (2011) to search for rotational modulation of the WASP light curves, as can be caused by the combination of magnetic activity and stellar rotation. No evidence of modulation was found.

The lithium abundance (ALi = 2.75  ±  0.10) found in WASP-31 implies an age (Sestito & Randich 2005) between that of open clusters such as M34 (250 Myr; ALi = 2.92  ±  0.13) and NGC 752 (2 Gyr; ALi = 2.65  ±  0.13). However, lithium is a poor indicator of age for a star as hot as WASP-31, and the measured abundance is consistent at the 1-σ level with that of the upper envelope of the 5-Gyr M67 (ALi = 2.55  ±  0.18).

We interpolated the stellar evolution tracks of Marigo et al. (2008) using ρ∗ from the MCMC analysis and using Teff and [Fe/H] from the spectral analysis (Fig. 5). This suggests an age of 4  ±  1 Gyr and a mass of 1.0  ±  0.1 M⊙ for WASP-31.

thumbnail Fig. 5

Modified H-R diagram. The isochrones (Z = 0.012  ≈  [Fe/H] = −0.20) for the ages 0.5, 1, 2, 3, 4, 5 and 10 Gyr and the evolutionary mass tracks (Z = 0.012  ≈  [Fe/H] = −0.20; Y = 0.30) are from Marigo et al. (2008). To obtain the mass tracks, we performed a simple linear interpolation of their Z = 0.0008 and Z = 0.017 tracks.

Taking account of each age indicator, we suggest a likely age of 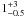1-0.5+3\hbox{$1^{+3}_{-0.5}$} Gyr.

6. Discussion

With a mass of 0.48 MJup and a radius of 1.55 RJup, WASP-31b has a density 13 per cent that of Jupiter and is  ~0.3 RJup larger than predicted by standard models of irradiated gas giants (Fortney et al. 2007). Only WASP-17b (Anderson et al. 2010), which has a similar mass (0.49 MJup), is known to have a lower density (0.06 ρJup, Anderson et al. 2011b).

With an increasingly large sample of well-characterised planets, we can begin to make statistical inferences as to the physical reasons behind their diverse natures. Enoch et al. (2011) showed the radii of 16 of the 18 known low-mass (0.1−0.6 MJup) planets strongly correlate with equilibrium temperature and host-star metallicity. The calibration of Enoch et al. (2011) predicts a radius of 1.39 RJup for WASP-31b. In a similar study, but using a different metallicity dependence and treating the 74 known Jupiter-mass (0.2−2.5 MJup) planets, Anderson & Iro (in prep.) also found a strong correlation between planetary radius and equilibrium temperature and host-star metallicity. The calibration of Anderson & Iro (in prep.) predicts a radius of 1.23 RJup for WASP-31b. In each case, the predicted radius of WASP-31b is smaller than the measured radius (1.55  ±  0.05 RJup).

WASP-31 has a similarly low metallicity to WASP-17 ([Fe/H] = −0.19  ±  0.09; Triaud et al. 2010), thus both WASP-31b and WASP-17b could reasonably be expected to have small cores (Guillot et al. 2006; Burrows et al. 2007). However, this would only somewhat explain why the two planets are so large. Both planets are highly irradiated, with WASP-17b being more irradiated than WASP-31b as, despite being in a slightly wider orbit (a = 0.052 AU), its host star is larger (R∗ = 1.58 R⊙) and hotter (Teff = 6650 K; Anderson et al. 2011b). This results in an equilibrium temperature for WASP-17b hotter by 200 K than for WASP-31b and, from this, we could expect WASP-17b to be larger than WASP-31b. Both planets, though, are larger than predicted by standard models of irradiated giant planets (e.g. Fortney et al. 2007), and by the empirical relations of Enoch et al. (2011) and Anderson & Iro (in prep.). Hence, it seems likely that some additional physics, such as Ohmic heating (Batygin & Stevenson 2010), is at play.

The RV data place a stringent upper limit on WASP-31b’s orbital eccentricity (e < 0.13; 3σ). It is therefore unlikely that tidal heating resulting from the circularisation of an eccentric orbit (e.g. Bodenheimer et al. 2001) was responsible for significantly inflating the planet. However, we could happen to be viewing the system soon after circularisation occurred and prior to the planet significantly contracting. This would have made finding the planet easier due to the greater transit depth.

The metallicity of WASP-31 is at the lower end of what may be expected for a star of its age in the Solar neighbourhood (at a Galactocentric radius of 8.5 kpc; Magrini et al. 2009).

1

2010 Nov. 25, http://exoplanet.eu

Acknowledgments

WASP-South is hosted by the South African Astronomical Observatory and we are grateful for their ongoing support and assistance. Funding for WASP comes from consortium universities and from the UK’s Science and Technology Facilities Council. M. Gillon acknowledges support from the Belgian Science Policy Office in the form of a Return Grant.

References

  1. Anderson, D. R., Hellier, C., Gillon, M., et al. 2010, ApJ, 709, 159 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anderson, D. R., Collier Cameron, A., Hellier, C., et al. 2011a, ApJ, 726, L19 [NASA ADS] [CrossRef] [Google Scholar]
  3. Anderson, D. R., Smith, A. M. S., Lanotte, A. A., et al. 2011b, MNRAS, accepted [arXiv:1101.5620] [Google Scholar]
  4. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
  6. Batygin, K., & Stevenson, D. J. 2010, ApJ, 714, L238 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bodenheimer, P., Lin, D. N. C., & Mardling, R. A. 2001, ApJ, 548, 466 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bruntt, H., Bedding, T. R., Quirion, P., et al. 2010, MNRAS, 405, 1907 [NASA ADS] [Google Scholar]
  9. Burrows, A., Hubeny, I., Budaj, J., & Hubbard, W. B. 2007, ApJ, 661, 502 [NASA ADS] [CrossRef] [Google Scholar]
  10. Carlsson, M., Rutten, R. J., Bruls, J. H. M. J., & Shchukina, N. G. 1994, A&A, 288, 860 [NASA ADS] [Google Scholar]
  11. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  12. Collier Cameron, A., Pollacco, D., Street, R. A., et al. 2006, MNRAS, 373, 799 [NASA ADS] [CrossRef] [Google Scholar]
  13. Collier Cameron, A., Wilson, D. M., West, R. G., et al. 2007, MNRAS, 380, 1230 [NASA ADS] [CrossRef] [Google Scholar]
  14. Enoch, B., Collier Cameron, A., Parley, N. R., & Hebb, L. 2010, A&A, 516, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Enoch, B., Cameron, A. C., Anderson, D. R., et al. 2011, MNRAS, 410, 1631 [NASA ADS] [Google Scholar]
  16. Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fortney, J. J., Baraffe, I., & Militzer, B. 2010, Giant Planet Interior Structure and Thermal Evolution, ed. S. Seager, 397 [Google Scholar]
  18. Gillon, M., Smalley, B., Hebb, L., et al. 2009, A&A, 496, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gray, D. F. (ed.) 2008, The Observation and Analysis of Stellar Photospheres [Google Scholar]
  20. Gu, P., Lin, D. N. C., & Bodenheimer, P. H. 2003, ApJ, 588, 509 [NASA ADS] [CrossRef] [Google Scholar]
  21. Guillot, T., & Showman, A. P. 2002, A&A, 385, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Hebb, L., Collier-Cameron, A., Loeillet, B., et al. 2009, ApJ, 693, 1920 [NASA ADS] [CrossRef] [Google Scholar]
  24. Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Ibgui, L., & Burrows, A. 2009, ApJ, 700, 1921 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ibgui, L., Burrows, A., & Spiegel, D. S. 2010, ApJ, 713, 751 [NASA ADS] [CrossRef] [Google Scholar]
  27. Ibgui, L., Spiegel, D. S., & Burrows, A. 2011, ApJ, 727, 75 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jackson, B., Greenberg, R., & Barnes, R. 2008, ApJ, 681, 1631 [NASA ADS] [CrossRef] [Google Scholar]
  29. Koornneef, J. 1983, A&A, 128, 84 [NASA ADS] [Google Scholar]
  30. Leconte, J., Chabrier, G., Baraffe, I., & Levrard, B. 2010, A&A, 516, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Li, J., & Goodman, J. 2010, ApJ, 725, 1146 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lucy, L. B., & Sweeney, M. A. 1971, AJ, 76, 544 [NASA ADS] [CrossRef] [Google Scholar]
  33. Magain, P. 1984, A&A, 134, 189 [NASA ADS] [Google Scholar]
  34. Magrini, L., Sestito, P., Randich, S., & Galli, D. 2009, A&A, 494, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mandushev, G., O’Donovan, F. T., Charbonneau, D., et al. 2007, ApJ, 667, L195 [NASA ADS] [CrossRef] [Google Scholar]
  37. Mardling, R. A. 2007, MNRAS, 382, 1768 [NASA ADS] [Google Scholar]
  38. Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Maxted, P. F. L., Anderson, D. R., Collier Cameron, A., et al. 2011, PASP, 123, 547 [NASA ADS] [CrossRef] [Google Scholar]
  40. Pepe, F., Mayor, M., Queloz, D., et al. 2005, The Messenger, 120, 22 [NASA ADS] [Google Scholar]
  41. Perna, R., Menou, K., & Rauscher, E. 2010, ApJ, 719, 1421 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pollacco, D. L., Skillen, I., Cameron, A. C., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
  43. Pollacco, D., Skillen, I., Collier Cameron, A., et al. 2008, MNRAS, 385, 1576 [NASA ADS] [CrossRef] [Google Scholar]
  44. Queloz, D., Eggenberger, A., Mayor, M., et al. 2000a, A&A, 359, L13 [NASA ADS] [Google Scholar]
  45. Queloz, D., Mayor, M., Weber, L., et al. 2000b, A&A, 354, 99 [NASA ADS] [Google Scholar]
  46. Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
  48. Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Sozzetti, A., Torres, G., Charbonneau, D., et al. 2009, ApJ, 691, 1145 [NASA ADS] [CrossRef] [Google Scholar]
  52. Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
  53. Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Youdin, A. N., & Mitchell, J. L. 2010, ApJ, 721, 1113 [NASA ADS] [CrossRef] [Google Scholar]
  55. Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Proper motions of WASP-31 and its visual companion.

In the text
Table 2

Stellar parameters from the spectroscopic analysis.

In the text
Table 3

Limb-darkening coefficients.

In the text
Table 4

System parameters from the combined analysis.

In the text

All Figures

thumbnail Fig. 1

WASP-South discovery light curve. Upper panel: photometry folded on the orbital period of P = 3.4 d. Points with error above three times the median error (0.012 mag) were clipped for display purposes. Lower panel: photometry folded on the orbital period and binned in phase (Δφ = 0.025), with the transit model generated from the parameters of Table 4 superimposed.
In the text
thumbnail Fig. 2

Upper panel: spectroscopic orbit of WASP-31, as illustrated by radial velocities from CORALIE (blue circles) and HARPS (red squares). The best-fitting Keplerian model, generated from the parameters of Table 4, is overplotted as a solid line. An RV taken at BJD = 2 455 168.8468, depicted in the plot by an open circle, fell during transit. As we did not treat the Rossiter-McLaughlin effect (e.g., Queloz et al. 2000a), we excluded this measurement from our combined analysis. Lower panel: a lack of correlation between bisector spans and radial velocities rules out a blended eclipsing binary or starspots as the cause of the photometric and spectroscopic variaitions. We adopted uncertainties on the bisector spans twice the size of those on the radial velocities. For both plots, the centre-of-mass velocity, γ = −124.92 m s-1, was subtracted from the radial velocities and the Keplerian model.
In the text
thumbnail Fig. 3

High-S/N transit light curves. The upper observations (blue circles) were obtained by FTN, using a Pan-STARRS z filter, on 2010 Feb. 26. The lower observations (red diamonds), offset in relative flux by 0.026 for display, were obtained by Euler, using a Gunn r filter, on 2010 Apr. 15. The best-fitting transit models generated from the parameters of Table 4 are overplotted.
In the text
thumbnail Fig. 4

Colour–magnitude diagram for WASP-31 and its companion. Various isochrones from Marigo et al. (2008) are given, with ages indicated in the figure. No de-reddening has been applied as AV = 0.
In the text
thumbnail Fig. 5

Modified H-R diagram. The isochrones (Z = 0.012  ≈  [Fe/H] = −0.20) for the ages 0.5, 1, 2, 3, 4, 5 and 10 Gyr and the evolutionary mass tracks (Z = 0.012  ≈  [Fe/H] = −0.20; Y = 0.30) are from Marigo et al. (2008). To obtain the mass tracks, we performed a simple linear interpolation of their Z = 0.0008 and Z = 0.017 tracks.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.