EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 531 (July 2011) A&A, 531 (2011) A125 Full HTML
Free Access
Issue
A&A
Volume 531, July 2011
Article Number A125
Number of page(s) 4
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201016098
Published online 28 June 2011

© ESO, 2011

1. Introduction

The study of millisecond pulsars (MSPs) enables several types of research in astrophysics, ranging from binary evolution (e.g. Edwards & Bailes 2001), to the potential detection of background gravitational radiation using a large set of pulsars with stable timing properties (Jaffe & Backer 2003). Furthermore, high-precision timing provides opportunities for fundamental physics research: by measuring and modeling pulse arrival times from binary systems, one can constrain neutron star masses and equations of state (Demorest et al. 2010), or study strong-field general relativity (Taylor & Weisberg 1989).

Finding such millisecond pulsars is done through wide-area surveys or through targeted surveys, each with specific advantages: with limited telescope time, a directed search can afford to dwell on a specifically interesting part of the sky for longer than an undirected search. A directed search is therefore more sensitive to faint pulsars in specific locations than an undirected search would be that only incidentally scans over such a location. An undirected search however covers a larger area. Directed searches have targeted sources associated with MSPs, such as globular clusters (Ransom et al. 2005), steep spectrum sources (Backer et al. 1982), unidentified Fermi sources (Ransom et al. 2011) and low mass-white dwarfs (van Leeuwen et al. 2007; Agüeros et al. 2009). Here we report the results of a directed search for radio pulsations from four short-orbit sub-luminous B dwarf (sdB) binaries identified through spectroscopy as possibly containing neutron stars (Geier et al. 2008).

Sub-luminous B dwarfs are some of the most abundant faint blue objects (Green et al. 1986). They are thought to be light (about 0.5   M⊙) core helium burning stars with very thin hydrogen envelopes. After the helium burning in the core stops, sdB stars evolve directly to the white dwarf cooling sequence (cf. a recent review by Heber 2009). In their survey of subdwarf B stars Maxted et al. (2001) find that 2/3 of field sdB stars are in short-orbit (P <  ~  10 days) binaries. Taking into account the insensitivity of their survey to longer-period binaries, Maxted et al. (2001) conclude that binary star evolution is fundamental to the formation of sdB stars.

Table 1

Pulsar search targets based on sdB-NS candidate binaries identified by Geier et al. (2008).

Several such binary formation channels have been hypothesized. For an sdB to form, a light star must lose most of its hydrogen envelope and ignite helium in its core. In these binary systems, sdB stars can be formed through phases of Common Envelope evolution where the envelope is ejected, or through stable Roche Lobe overflow stripping the donor star of its hydrogen envelope. Binary population synthesis models for the above scenarios in the case of white-dwarf companions were recently compared by Han et al. (2003) and Hu et al. (2007).

Specifically interesting for finding new millisecond pulsars, is the channel that leads to short-period binary systems containing an sdB star and a neutron star or a black hole (Podsiadlowski et al. 2002; Geier et al. 2010). Here, the binary system contains a star that is massive enough to evolve into a neutron star or a black hole and a secondary, lighter star that is the progenitor of the sdB star. The secondary is in a wide orbit with a period of about 20 years. The system undergoes two phases of common envelope evolution, a supernova and a short X-ray binary phase. A first common envelope phase starts soon after the primary becomes a red supergiant and starts overflowing its Roche Lobe. During this first common envelope phase the orbit of the binary shrinks. After the subsequent supernova, the primary leaves a neutron star or black hole. This neutron star remains visible as a normal radio pulsar for on average 107 − 8 years, and turns off. Once the secondary evolves off the main sequence the second phase of mass transfer starts when the secondary begins to overflow its Roche Lobe. The system undergoes a short X-ray binary phase, in which the neutron star is recycled (Bhattacharya & van den Heuvel 1991). The second common-envelope phase starts shortly thereafter, further shrinking the orbit of the binary and dissipating the envelope of the secondary. The secondary, which is now mostly stripped of its hydrogen envelope, ignites helium in its core and continues its evolution as a sdB star (Podsiadlowski et al. 2002; Geier et al. 2010). From population modeling, Pfahl et al. (2003) find that about 1% of sdB stars evolve as outlined above and orbit a neutron star or black hole. In such systems the secondary is an sdB star for  ~108 years (Heber 2009), before evolving to a white dwarf.

While low-mass companions (white dwarfs, main sequence stars) to sdB stars have been optically confirmed (e.g. Geier et al. 2010), the unambiguous identification of a high-mass companion in the form of a radio pulsar would provide further constraints on the relative likelihood of different binary evolution models (as was similarly done for companions of low-mass white dwarfs in van Leeuwen et al. 2007). Furthermore, timing of a possible MSP companion will likely provide an sdB mass measurement, either through the modeling of the orbital parameters, or more directly and precisely through a Shapiro delay measurement (e.g. Ferdman et al. 2010). As millisecond pulsars can turn on shortly after the cessation of accretion (Archibald et al. 2009) and can shine for more than the  ~108 year sdB star lifetime, MSPs will be active throughout the sdB star phase. Thus, non-detections of radio pulsations from these systems could mean the absence of any neutron star, the presence of only a very weak radio pulsar, or of a brighter one that is beamed away from Earth. Non-detections in a large enough sample of sdB stars eventually provide statistics on sdB formation channels.

In Sect. 2 we describe how sources were selected; in Sect. 3 our observing and data reduction setup is outlined. Section 4 contains our results. In Sect. 5 we discuss these results and compare to recent optical results on some of our sources.

2. Source selection

Our source selection was based on the report by Geier et al. (2008) of the detection of the first four sdB systems that possibly contain a neutron star or black hole companion: HE 0532-4503, HE 0929-0424, TON S 183 and PG 1232-136.

These candidate sdB-neutron star (sdB-NS) systems were identified through spectroscopic observations of sdB binaries (Geier et al. 2008). In sdB-NS systems, the optical spectrum is single lined and the compact companion cannot be detected directly optically. Assuming tidal synchronization between the orbital period and the sdB rotational period, it is possible to constrain the binary inclination from measurements of the sdB surface gravity, projected rotational velocity and sdB mass. In their 2010 follow-up paper Geier et al. give a detailed description of this method. In binaries with periods shorter than 1.2 days the orbit and stellar rotation are found to be synchronized. Thus, for such systems the companion mass can be derived from the sdB mass, which is known either from independent mass measurements (e.g. Fontaine et al. 2008) or inferred from binary population synthesis (Han et al. 2002, 2003). Our sources all have orbital periods shorter than these 1.2 days. In Table 1 we describe further target parameters such as galactic coordinates, local background sky temperature, distance and estimated dispersion measure.

3. Observations and data reduction

On 2008 Oct 15, 18 and 20 we observed these four sdB binaries with the Robert C. Byrd Green Bank Telescope (GBT). We used the lowest-frequency receiver PF1, which provided a bandwidth Δf = 50   MHz centered around 350   MHz. Every 81.92 μs the Spigot backend (Kaplan et al. 2005) recorded 2048 spectral channels in 16-bit total intensity. Over the three sessions, three test pulsars (Table 2) and four sdB-star binaries (Table 3) were observed. Due to scheduling and weather constraints, integration times of the binaries varied, ranging from 12 to 68 min (Table 3).

Table 2

List of the previously known pulsars that were used as a check of the telescope, back-end and pulsar-search systems.

For each system in our sample, we derived the expected dispersion measures (DM) from their measured distance, using the NE 2001 free electron model (Cordes & Lazio 2002). These expected DMs, listed in Table  1, are all well below 100   pccm-3. Up to 200   pccm-3 the trial DMs were spaced such that our search remains sensitive to pulsars with rotational periods down to 1 ms; faster pulsars are not generally expected (Chakrabarty et al. 2003). Beyond 200   pccm-3 the intra-channel smearing begins to dominate, so trial DMs up to 1000   pccm-3 where created at a lower time resolution. We next searched these trial DMs for pulsar signals, in both the time and frequency domain, using the PRESTO data reduction package (Ransom 2001). In the time domain we searched for single dispersed pulses of radio emission. In the frequency-domain search we have to take into account the acceleration present in these binary systems. One could potentially derive the neutron-star orbital phase from the optical modulation of the sdB star, and thus estimate the acceleration at the time of the observations. This however relies on the assumption that there is no lag between the optical light curve and the orbital motion. We have taken the conservative approach to search over the full range of possible accelerations throughout the orbit. As each integration time tint was shorter than 10% of the binary period, our search in period and period-derivative space sufficed (Johnston & Kulkarni 1991). Using standard PRESTO routines, for each observation the radio-frequency interference was flagged, candidate period signals were sifted to remove harmonics, and the top 30 candidates we folded and further refined by searching nearby dispersion measures, periods and period derivatives to maximize signal-to-noise ratio. All candidate plots were subsequently visually inspected.

At the start of each observing session a known pulsar was observed; as listed in Table 2, these were all blindly re-detected by the above sdB-NS search pipeline, thus confirming the effectiveness of the search method.

Table 3

Integration time tint, flux upper limit Smin derived from radiometer equation, pseudo luminosity limit L calculated from the flux upper limit, and completeness C compared to the known MSPs in the ATNF database.

4. Results

No new pulsars were detected toward any of the four sdB stars in our sample.

We next investigate how strongly these non-detections rule out the presence of an MSP. We derive the minimum detectable mean flux density Smin for each observation from the pulsar radiometer equation (Dewey et al. 1985; Bhattacharya 1998):

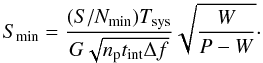In this equation S/Nmin is the minimum signal-to-noise ratio at which a pulse profile can clearly be recognized as a pulsar profile. The system temperature Tsys is defined as Tsys = Tsys,GBT + Tsky where Tsys,GBT = 46   K1. For each source, Tsky was extracted from Haslam et al. (1982) and scaled from 408 to 350 MHz using the Tsky ∝ ν-2.6 scaling law from Lawson et al. (1987). The gain G for the GBT is 2   K   Jy-12, the number of polarizations np, added for these total intensity observations, is 2. Integration time tint and bandwidth Δf for each observation are described in Sect. 3. Finally, W is the pulse width and P is the rotational period. As these are unknown for non-detections, we use the average pulse duty cycle W/P = 0.12    ±    0.10 determined by averaging over the MSP W50/P duty cycles in the ATNF pulsar database (Manchester et al. 2005). Here and below, we define MSPs in the ATNF database as those sources with periods shorter than 50   ms (thus, moderately to fully recycled) and magnetic fields lower than 1011   Gauss. For each source, we list the resulting Smin value in Table 3.

The errors on our values of Smin have contributions from the error on the average pulse duty cycle and from the systematic error on the minimum signal-to-noise ratio S/Nmin. The S/Nmin at which a pulsar can be detected depends on the shape of its profile: a strongly peaked profile at high DM is more easily identified as a pulsar than a same-S/N sinusoidal profile at low DM, as the latter can also be terrestrial interference. We estimate this systematic error as follows. To set a lower limit to the possible (S/Nmin) range we inspected the pulse profiles of the test pulsars for increasing fractions of the total integration time. We concluded that starting from a peak (S/Nmin) of 7 the pulsar re-detections become unambiguous. As an upper limit to the range of (S/Nmin) values we adopt a value of 10.

To estimate the completeness of our search we derived pseudo luminosity L = Sd2 limits for each of the binaries in our sample and compared them with the pseudo luminosities of known MSPs. We define the completeness of our pulsar search as the percentage of known millisecond pulsars that have pseudo luminosities higher than our derived pseudo luminosity upper limits, i.e., as the percentage of known MSPs that would be detected if placed at the distance of the candidate. We searched the literature for distances d to the binaries in our sample and used the most recent values. For HE 0532-4503 and HE 0929-0424 these are from Lisker et al. (2005), while the distances to TON S 183 and PG 1232-136 are from Altmann et al. (2004), where TON S 183 is known as SB 410. The former article claims an error on the distance of 10%. In the latter article distance errors are not estimated, so for those sources we also propagate a 10% error. All distances were derived from models of sdB atmospheres combined with the magnitude measurement.

In Fig. 1 we compare our limits to the pseudo luminosities of the millisecond pulsar population. For this statistical comparison, we have selected all 50 MSPs with known 400   MHz fluxes in the ATNF database (Manchester et al. 2005). We scale these 400   MHz fluxes to our central observing frequency of 350   MHz, using the  − 1.6 average spectral index that Kramer et al. (1998) find for MSPs. We find that our limits exclude with high confidence the presence of pulsar emission: in Table 3 we list the exact values for this completeness C.

thumbnail Fig. 1

Cumulative histogram of pseudo luminosities for the known MSP population in the ATNF database. The left axis is labelled with the cumulative fraction of MSPs; the right axis is labelled with survey completeness for each candidate. The errors on the pseudo luminosity upper limits contain errors on the distance, pulse duty cycle and our estimate of the relevant range of (S/Nmin) values used with the pulsar radiometer equation (see Sect. 4).
Open with DEXTER

5. Discussion

As no radio pulsations were found in any of our observations, we place upper limits on the pulsed radio emission from the putative neutron stars in these systems. Assuming the known MSP luminosity distribution, we can exclude the presence of such pulsed radio emission with 100% certainty for 2 systems: PG 1232-136 and TON S 183 (Fig. 1). For 2 other systems, HE 0532-4503 and HE 0929-0424, we were not able to put as strict upper limits on the pseudo luminosity due to their larger distance and the shorter integration time for these pointings. For HE 0929-0424, our survey would have detected 96% of MSPs at the HE 0929-0424 distance. For HE 0532-4503, this completeness C is 88% (Table 3, Fig. 1).

In relation to these non-detections we now discuss two selection effects: the fraction of the sdB lifetime during which an MSP is on; and the beaming fraction, which is the fraction of sky over which an MSP beam sweeps, and thus from which the MSP is in principle detectable. As outlined in Sect. 1, the MSP and sdB star are formed simultaneously; as MSPs have ages up of to 109−10 years and sdBs have ages up to 108 years, an MSP formed in a binary with an sdB star will shine for the entire age of the sdB, and longer. We thus conclude there is no age bias against detecting MSPs around sdB stars. There is however a non-zero chance that for some of our non-detections a bright MSP emission beam is present, but missing the Earth. The beaming fraction of MSPs is 0.7    ±    0.2 (Kramer et al. 1998); high compared to normal pulsars, but not unity and thus an important factor.

So far we have discussed MSPs, as any regular (non-recycled) pulsar originally present in these systems will have long shut off before the formation of the sdB began (cf. Sect. 1). For any non-recycled pulsars that are in the beam by chance, the Smin in Table 3 list the minimum detectable flux for that pointing. The pseudo-luminosity distributions of non-recycled and millisecond pulsars are similar (Manchester et al. 2005), but as the distance to any chance-coincident non-recycled pulsar is unknown, their pseudo luminosity is unknown too.

We now compare the results of our search, triggered by the sample from Geier et al. (2008), with the follow-up results of further spectroscopic investigation recently published in Geier et al. (2010). For PG 1232-136, where we put a very strict (100% complete) limit on the pseudo luminosity, Geier et al. (2010) now report the mass of the unseen companion Mcomp to be higher than 6M⊙. This indicates the compact companion is a black hole; therefore no pulsed radio emission is expected from that system, in agreement with our non-detection. For TON S 183  the new spectroscopic results point to a Mcomp of 0.9M⊙ but the error bars allow for a low mass white dwarf (WD). Our non-detection of pulsed radio emission is compatible with a WD companion, and since the constraint we put on pulsed radio emission from TON S 183 is strict (100% complete) we rule out an MSP beamed towards Earth. For HE 0929-0424 a Mcomp slightly above the Chandrasekhar limit is reported, but with error bars that also allow for a high mass WD. Our 96%-complete non-detection in this case cannot exclude either possibility but an MSP is unlikely. The system with the least strict pseudo luminosity upper limit, HE 0532-4503, is reported to contain a companion to the sdB star of 3M⊙. Even if one allows for an sdB star as light as 0.3M⊙ the companion remains more massive than the Chandrasekhar limit. Given our non-detection corresponding to the 12th percentile of the known MSP population (88% complete), an MSP is not likely, but this system remains an interesting candidate for deeper radio follow-up. Further observations of this source and of new candidate sdB-NS systems from Geier et al. (2010) are currently ongoing.

6. Conclusions

We have searched for pulsed emission from potential pulsar companions of four subdwarf B stars. No pulsed emission was found down to luminosities corresponding to, on average over the 4 sources, the 4th percentile of the known millisecond pulsar population.

2

Prestage, R., et al. (2006), ftp://ftp.gb.nrao.edu/NRAO-staff/rprestag/prestage.ppt

Acknowledgments

We thank Jason Hessels for help with the search pipeline. This work was supported by The Netherlands Research School for Astronomy (Grant NOVA3-NW3-2.3.1) and by the European Commission (Grant FP7-PEOPLE-2007-4-3-IRG #224838). Computing resources were provided by ASTRON. Pulsar research at UBC is supported by an NSERC Discovery Grant. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.

References

  1. Agüeros, M. A., Camilo, F., Silvestri, N. M., et al. 2009, ApJ, 697, 283 [NASA ADS] [CrossRef] [Google Scholar]
  2. Altmann, M., Edelmann, H., & de Boer, K. S. 2004, A&A, 414, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Archibald, A. M., Stairs, I. H., Ransom, S. M., et al. 2009, Science, 324, 1411 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Backer, D. C., Kulkarni, S. R., Heiles, C., Davis, M. M., & Goss, W. M. 1982, Nature, 300, 615 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bailes, M., Harrison, P. A., Lorimer, D. R., et al. 1994, ApJ, 425, L41 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bhattacharya, D. 1998, in NATO ASIC Proc. 515: The Many Faces of Neutron Stars., ed. R. Buccheri, J. van Paradijs, & A. Alpar, 103 [Google Scholar]
  7. Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chakrabarty, D., Morgan, E. H., Muno, M. P., et al. 2003, Nature, 424, 42 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  9. Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
  10. Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  11. Dewey, R. J., Taylor, J. H., Weisberg, J. M., & Stokes, G. H. 1985, ApJ, 294, L25 [NASA ADS] [CrossRef] [Google Scholar]
  12. Edwards, R. T., & Bailes, M. 2001, ApJ, 547, L37 [NASA ADS] [CrossRef] [Google Scholar]
  13. Ferdman, R. D., Stairs, I. H., Kramer, M., et al. 2010, ApJ, 711, 764 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fontaine, G., Brassard, P., Charpinet, S., et al. 2008, in Hot Subdwarf Stars and Related Objects, ed. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 231 [Google Scholar]
  15. Geier, S., Karl, C., Edelmann, H., Heber, U., & Napiwotzki, R. 2008, Mem. Soc. Astron. Ital., 79, 608 [NASA ADS] [Google Scholar]
  16. Geier, S., Heber, U., Podsiadlowski, P., et al. 2010, A&A, 519, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Green, R. F., Schmidt, M., & Liebert, J. 1986, ApJS, 61, 305 [NASA ADS] [CrossRef] [Google Scholar]
  18. Han, Z., Podsiadlowski, P., Maxted, P. F. L., Marsh, T. R., & Ivanova, N. 2002, MNRAS, 336, 449 [NASA ADS] [CrossRef] [Google Scholar]
  19. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  20. Haslam, C. G. T., Salter, C. J., Stoffel, H., & Wilson, W. E. 1982, A&AS, 47, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
  21. Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hu, H., Nelemans, G., Østensen, R., et al. 2007, A&A, 473, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Jaffe, A. H., & Backer, D. C. 2003, ApJ, 583, 616 [NASA ADS] [CrossRef] [Google Scholar]
  24. Johnston, H. M., & Kulkarni, S. R. 1991, ApJ, 368, 504 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kaplan, D. L., Escoffier, R. P., Lacasse, R. J., et al. 2005, PASP, 117, 643 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kramer, M., Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lawson, K. D., Mayer, C. J., Osborne, J. L., & Parkinson, M. L. 1987, MNRAS, 225, 307 [NASA ADS] [CrossRef] [Google Scholar]
  28. Lisker, T., Heber, U., Napiwotzki, R., et al. 2005, A&A, 430, 223 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  30. Maxted, P. F. L., Heber, U., Marsh, T. R., & North, R. C. 2001, MNRAS, 326, 1391 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pfahl, E., Rappaport, S., & Podsiadlowski, P. 2003, ApJ, 597, 1036 [NASA ADS] [CrossRef] [Google Scholar]
  32. Podsiadlowski, P., Rappaport, S., & Pfahl, E. D. 2002, ApJ, 565, 1107 [NASA ADS] [CrossRef] [Google Scholar]
  33. Ransom, S. M. 2001, Ph.D. Thesis, Harvard University [Google Scholar]
  34. Ransom, S. M., Hessels, J. W. T., Stairs, I. H., et al. 2005, Science, 307, 892 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  35. Ransom, S. M., Ray, P. S., Camilo, F., et al. 2011, ApJ, 727, L16 [NASA ADS] [CrossRef] [Google Scholar]
  36. Taylor, J. H., & Weisberg, J. M. 1989, ApJ, 345, 434 [NASA ADS] [CrossRef] [Google Scholar]
  37. van Leeuwen, J., Ferdman, R. D., Meyer, S., & Stairs, I. 2007, MNRAS, 374, 1437 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Pulsar search targets based on sdB-NS candidate binaries identified by Geier et al. (2008).

In the text
Table 2

List of the previously known pulsars that were used as a check of the telescope, back-end and pulsar-search systems.

In the text
Table 3

Integration time tint, flux upper limit Smin derived from radiometer equation, pseudo luminosity limit L calculated from the flux upper limit, and completeness C compared to the known MSPs in the ATNF database.

In the text

All Figures

thumbnail Fig. 1

Cumulative histogram of pseudo luminosities for the known MSP population in the ATNF database. The left axis is labelled with the cumulative fraction of MSPs; the right axis is labelled with survey completeness for each candidate. The errors on the pseudo luminosity upper limits contain errors on the distance, pulse duty cycle and our estimate of the relevant range of (S/Nmin) values used with the pulsar radiometer equation (see Sect. 4).
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.