| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016378 | |
| Published online | 06 May 2011 | |
Reducing star leakage with a nuller coronagraph
An analytic approach for a Sonine apodized circular aperture
1
Université de Nice Sophia-Antipolis, Centre National de la Recherche
Scientifique, Laboratoire Fizeau, Observatoire de la Côte d’Azur,
Parc Valrose,
06108
Nice,
France
e-mail: claude.aime;gilbert.ricort@unice.fr; yves.rabbia@obs-azur.fr;
acarlott@princeton.edu
2
Princeton University, Mechanical & Aerospace Engineering, Olden
street, Princeton,
08544
NJ,
USA
Received:
21
December
2010
Accepted:
29
March
2011
Aims. Our objective is to test the improvement of the detection capabilities of a nuller coronagraph when it is coupled to an apodizer. We call this instrument an apodized nuller coronagraph (ANC).
Methods. With the usual Fourier optics formalism we first derive the analytical expression of the intensity distribution for an off-axis point-like source in the aperture and the focal plane of an ANC. Then the star leakage is obtained by integration of this response over the angular extension of the star. In this process are included the star’s angular diameter, the apodization strength and the diameter of the telescope. Eventually we consider an application to the specific case of Sonine apodization.
Results. From this analytical approach we obtain expressions of the contrast and signal-to-noise ratio for the direct detection of an exoplanet. These expressions involving instrumental parameters allow one to optimize the required minimum telescope’s diameter and apodization strength with respect to the detection of a given target in spite of star leakage. We show that the direct detection of an exoplanet in a solar-like system can be obtained with a nuller coronagraph as soon as the aperture is sufficiently apodized, although the energy throughput of the system is reduced. For a system at 10 pc, an 8-m class telescope appears necessary to detect an exo-Earth, while no larger than a 2-m class telescope is required for an exo-Jupiter.
Key words: instrumentation: high angular resolution / instrumentation: interferometers / techniques: high angular resolution / techniques: interferometric / methods: analytical
© ESO, 2011
1. Introduction
By the end of 2010 the community knew about more than five hundred exoplanets. An interactive catalog of the discoveries of exoplanets, categorized by detection type, can be found in The Extrasolar Planets Encyclopaedia at exoplanet.eu, an URL remarkably held up to date since 1995. Another catalog can be found at exoplanets.org (Wright et al. 2011). A large majority of these planets has been detected with the radial velocity method. The transit technique (Seager & Sasselov 2000) was used for example with the Corot and Kepler satellites, which provide semi-direct detections, but the ultimate goal is to collect photons from Earth-like exoplanets for a direct spectral analysis.
So far images of 12 planetary systems have been obtained with coronagraphic instruments, adaptive optics, and data processing techniques. The targeted stars are young and they have mostly been observed in the infrared, allowing the discovery of young, therefore warm and bright, companions. Ideally, an imaging instrument should be able to detect older, therefore colder and fainter, planets, such as those of our own 4.6 billion years old solar system, which are expected to be dramatically fainter than their parent star, typically at the level of 10-6 in the thermal infrared and down to 10-10 in the visible.
The last fifteen years have seen considerable efforts to devise concepts and instruments able to perform these observations. There are several ways to classify them (Perryman 2000; Aime 2007; Guyon 2009; Oppenheimer & Hinkley 2009).
These concepts include external occulters (Cash 2006; Vanderbei et al. 2007; Arenberg et al. 2007), nuller interferometers (Bracewell 1978), various pupil apodization techniques (Nisenson & Papaliolios 2001; Kasdin et al. 2003; Guyon 2003; Aime 2005), and coronagraphs (Gay & Rabbia 1996; Roddier & Roddier 1997; Rouan et al. 2000; Mawet et al. 2005; Guyon et al. 2006).
These instrumental techniques work each in a different way, but they share a common objective, which is to gather as many planet photons as possible in the broadest bandwidth and in the shortest exposure time. Thus they have to suppress the diffracted starlight as much as possible over a broad enough spectral bandwidth and with the highest possible throughput, which is beneficial for the detection performance. Moreover, they should have a small inner working angle (IWA) for angular resolution capabilities, though this feature makes them sensitive to star leakage for a star with a finite diameter. Removing this kind of drawback is the role of the coupling to an apodizer.
In this paper we focus on nuller coronagraphs, a type of coronagraphs whose first model was the achromatic interfero-coronagraph (AIC, Gay & Rabbia 1996). The AIC is a system that is at the same time a coronagraph and a nulling interferometer. The technique has been described in several papers (Rabbia et al. 1998; Baudoz et al. 2000a,b) and is recalled in Sect. 2. Although AIC is based on a Michelson interferometer, some other nuller coronagraphs are based on different interferometers: the Sagnac interferometer (Tavrov et al. 2005) and the Mach-Zehnder interferometer (Allouche et al. 2009).
Nuller coronagraphs have the ability to fully reject the light of an on-axis point-like source. They possess a very narrow inner working angle (IWA) with the drawback that their efficiency degrades when the coherence of the wavefront is reduced because of the angular diameter of the source. To rule out this problem, Tavrov et al. (2008) proposed to use a double pass, and we have recently proposed a variant of the AIC called the achromatic rotation-shearing coronagraph (ARC) in Aime et al. (2010), cited as Paper I here.
In the present paper we develop the idea suggested in Paper I to couple an apodizer and a nuller coronagraph to reduce the star leakage. In this regard our approach is similar to the numerical study described in Nishikawa et al. (2005) for a somewhat different device. As already noted by these authors, apodization and nulling coronagraphy have complementary effects. The nuller coronagraph provides a strong rejection for an on-axis point source, while apodization makes the background (diffraction wings) at the location of the planet image faint enough to render it detectable, with the drawbacks of an increased IWA and a decrease of throughput. Though we consider the coupling of an apodizer with AIC, this coupling is immediately applicable to another nuller coronagraph.
The apodization we consider here consists in giving a smooth transmission with a circular geometry to the exit pupil. We use Sonine functions as transmission profile, and the main interest of these functions is that they allow us to derive analytically the theoretical performance of the system. We can thus stress the dramatic influence of star leakage on the detectability of the planet, and then show how apodization can greatly improve this capability. Optimizing the transmission, contrast, and IWA associated with the apodization profile is a different problem, and it will be but briefly considered at the end of the paper.
The paper is organized as follows. Section 2 gives the general expressions for an apodized nuller coronagraph. Section 3 consider the case when a Sonine apodization is used. Section 4 provides simple analytical expressions for the contrast and for the signal-to-noise ratio (SNR). Section 5 presents a discussion and gives a conclusion.
2. General expressions for an apodized nuller coronagraph (ANC)
In this section we focus on the AIC, which is the concept behind the whole class of nuller coronagraphs (NC). Because it has been described extensively (see the papers mentioned above, starting with Gay & Rabbia 1996) only short reminders are given here for the reader’s convenience.
The AIC is basically a Michelson Fourier interferometer (and as such it has two output beams), modified by inserting a subsystem (cat’s eye) along one arm providing both an achromatic π phase shift and a 180 degrees pupil rotation (around the propagation axis). A focusing component is used to form the images in the focal plane. For an on-axis point source, the recombination of the waves results in a fully destructive interference at the destructive port, the light being rejected through the constructive port. Alternatively one may consider that in the focal planes two point spread functions (PSF) obtained through the two arms of the instrument are added destructively, thanks to the π phase shift. For an off-axis source the system yields two separated images because of the tilted incident wavefront, displayed symmetrically with respect to the axis. No strongly destructive interference occurs if the star-planet separation is larger than a fraction of an Airy radius, and a planet is seen as twin images. In between these two cases, for a source just slightly off-axis, for example owing to guiding errors, the AIC produces a more complex illumination of the focal plane that is the result of the interference of two complex amplitudes of opposite signs.
If we consider a star perfectly on-axis, but with a finite diameter, the light from the central point of the star will be fully cancelled by the AIC, but not the light coming from the rest of the star. This will result in an unwanted illumination of the focal plane that is called star leakage. The object of this paper is to quantify the star leakage reduction when the Airy images are replaced by aperture responses with lower diffraction wings, which is the effect produced by aperture apodization.
We shall consider below how apodization modifies the overall transmission of the nuller
coronagraph for an off-axis point source, and then derive the expression of the star
leakage. We restrict ourselves to a circular unobstructed aperture of diameter
D, whose transmission is modified in amplitude by a function
t(r), and the effective pupil transmission is
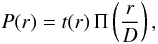 (1)where
r is the distance to the center, and
Π(r/D) equals 1 if
r < D/2, and 0 otherwise. This will reduce the
effective collecting area to the quantity:
(1)where
r is the distance to the center, and
Π(r/D) equals 1 if
r < D/2, and 0 otherwise. This will reduce the
effective collecting area to the quantity: 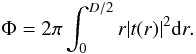 (2)The calculations
below draw heavily on Paper I. Let us consider the propagation of a tilted plane wavefront
through the telescope and the AIC. On the telescope aperture, the phase term associated with
a wavefront coming from a point source in the direction
α0 = ρ0cos(ϕ0)
and
β0 = ρ0sin(ϕ0)
on the sky can be written in cartesian and polar coordinates as
(2)The calculations
below draw heavily on Paper I. Let us consider the propagation of a tilted plane wavefront
through the telescope and the AIC. On the telescope aperture, the phase term associated with
a wavefront coming from a point source in the direction
α0 = ρ0cos(ϕ0)
and
β0 = ρ0sin(ϕ0)
on the sky can be written in cartesian and polar coordinates as 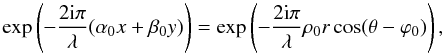 (3)where we use
(r,θ) for the polar coordinates in the aperture, with
x = rcos(θ) and
y = rsin(θ). The phasors in the above
equation are the expressions of the incoming amplitude for a tilted wavefront in the two
systems of coordinates.
(3)where we use
(r,θ) for the polar coordinates in the aperture, with
x = rcos(θ) and
y = rsin(θ). The phasors in the above
equation are the expressions of the incoming amplitude for a tilted wavefront in the two
systems of coordinates.
As already indicated, a nuller coronagraph such as the AIC works by making the subtraction
of two wavefronts rotated one relative to the other by an angle of π. It is
convenient to write this rotation symmetrically as ± π/2. Changing
cos(θ − ϕ0) in Eq. (3) for
cos(θ − ϕ0 ± π/2) = ± sin(θ − ϕ0),
the complex amplitude in the subtractive output of the AIC for an incident wave of unit
amplitude can be written as ![\begin{eqnarray} \label{Eq3} &&A(r, \theta, \rho_0, \varphi_0)=\nonumber\\ &&\quad \frac{1}{2} P(r)\left[\exp\left(\frac{2 {\rm i} \pi}{\lambda} \rho_0 r \sin\left(\theta-\varphi_0\right) \right)-\exp\!\left(- \frac{2 {\rm i} \pi}{\lambda} \rho_0 r \sin(\theta-\varphi_0) \right)\right]\nonumber\\ &&\quad ={\rm i} P(r)\sin\left(\frac{2 \pi}{\lambda} \rho_0 r \sin\left(\theta-\varphi_0\right)\right). \end{eqnarray}](/articles/aa/full_html/2011/06/aa16378-10/aa16378-10-eq20.png) (4)The
corresponding intensity is written
(4)The
corresponding intensity is written ![\begin{equation} \label{Eq3bis} I(r, \theta, \rho_0, \varphi_0)= \frac{1}{2} |P(r)|^2 \left[1- \cos\left(\frac{4 \pi}{\lambda}\rho_0 r \sin(\theta-\phi_0)\right)\right]. \end{equation}](/articles/aa/full_html/2011/06/aa16378-10/aa16378-10-eq21.png) (5)The integrated intensity
transmitted by the apodized nuller coronagraph for a point source at the angular distance
ρ0, normalized by the flux collected through the apodized
aperture, can be written as
(5)The integrated intensity
transmitted by the apodized nuller coronagraph for a point source at the angular distance
ρ0, normalized by the flux collected through the apodized
aperture, can be written as 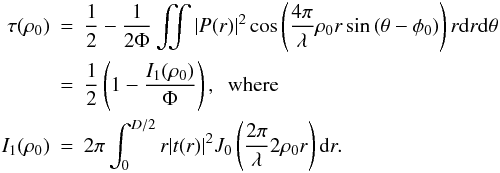 (6)This
latter integral is the Hankel transform of the transmission in intensity (and not in
amplitude) of the aperture for the variable
2ρ0/λ (and not simply for
ρ0/λ). This expression shows that the light
transmission at the output of the apodized nuller coronagraph goes from 0 for an on-axis
point source (ρ0 = 0, and the starlight is perfectly cancelled)
up to transmission values that oscillate around 0.5 when ρ0
becomes larger than the width of
I1(ρ0).
(6)This
latter integral is the Hankel transform of the transmission in intensity (and not in
amplitude) of the aperture for the variable
2ρ0/λ (and not simply for
ρ0/λ). This expression shows that the light
transmission at the output of the apodized nuller coronagraph goes from 0 for an on-axis
point source (ρ0 = 0, and the starlight is perfectly cancelled)
up to transmission values that oscillate around 0.5 when ρ0
becomes larger than the width of
I1(ρ0).
It is interesting to note that because of the factor 2 in the variable 2ρ0/λ, the IWA of nuller coronagraphs are twice as small as the telescope nominal resolution. The use of apodization will therefore increase this IWA by a factor governed by the shape of the Hankel transform of the transmission in intensity |t(r)|2, as already indicated.
Because the leakage depends on the behavior of
I1(ρ0) for low values of
ρ0, if the goal is to reduce the effect of an offset caused by
a poor centering of the star, one would like to use an apodization function with a flat
response near the origin. Unfortunately, because the relevant function is
|t(r)|2, the on-sky transmission near the
origin must follow a 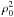 behavior, no
matter what apodization profile is used, and switching between different apodization
profiles will only change the coefficient of this quadratic behavior. Examples are given
below.
behavior, no
matter what apodization profile is used, and switching between different apodization
profiles will only change the coefficient of this quadratic behavior. Examples are given
below.
A function that is more relevant than the integrated leakage is the level of the leakage at
the planet position. For that we need to express the residual intensity in the focal plane
for an off-axis point source. Returning to Eq. (4), we have 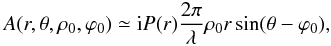 (7)where we made the
approximation sin(u) ≃ u. This approximation is legitimate
because ρ0 is very small, its maximal value being the apparent
angular radius of the star.
(7)where we made the
approximation sin(u) ≃ u. This approximation is legitimate
because ρ0 is very small, its maximal value being the apparent
angular radius of the star.
The scaled Fourier transform in polar coordinates of
A(r,θ) yields the amplitude in the image plane (see
Eq. (11) of Paper I) as the function Â(ρ,ϕ). The
derivation is similar to the one given in Appendix A of Paper I, but for the insertion of
the variable transmission factor t(r) in the circular
aperture of diameter D. We have 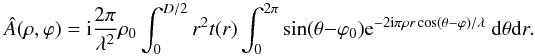 (8)Here as in Paper I
we make θ − ϕ = θ′, and develop
sin(θ′ + ϕ − ϕ0) = sin(θ′)cos(ϕ − ϕ0) + cos(θ′)sin(ϕ − ϕ0).
The integral on sin(θ′) is canceled because of the parity properties of
this function. We have
(8)Here as in Paper I
we make θ − ϕ = θ′, and develop
sin(θ′ + ϕ − ϕ0) = sin(θ′)cos(ϕ − ϕ0) + cos(θ′)sin(ϕ − ϕ0).
The integral on sin(θ′) is canceled because of the parity properties of
this function. We have 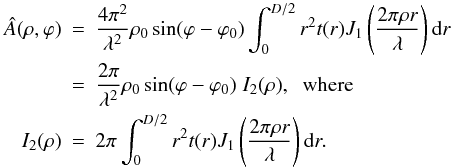 (9)This
latter integral is the first order Hankel transform of the function
r t(r) for the variable
ρ/λ, including in our definitions of Hankel transforms
the factor 2π. The intensity becomes
(9)This
latter integral is the first order Hankel transform of the function
r t(r) for the variable
ρ/λ, including in our definitions of Hankel transforms
the factor 2π. The intensity becomes 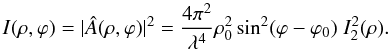 (10)Because of the term
sin2(ϕ − ϕ0), the residual
intensity I(ρ,φ) is not a radial function. Still,
considering the approximation where ρ0 is small,
I(ρ,φ) increases as
(10)Because of the term
sin2(ϕ − ϕ0), the residual
intensity I(ρ,φ) is not a radial function. Still,
considering the approximation where ρ0 is small,
I(ρ,φ) increases as
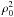 .
.
The leakage energy distribution is obtained through the integration over the angular
brightness distribution of the star (of angular diameter Θ): 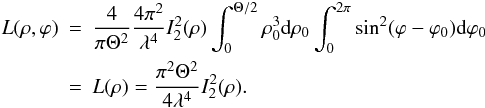 (11)The
resulting function is now a radial function, and we normalized the expression on the angular
surface of the star πΘ2/4, to handle the star brightness and
star diameter separately. To obtain an analytical expression for the star leakage, we have
to use an aperture transmission t(r) whose integral in the
above relation can be written as known functions. This is the case if we use for
t(r) the so-called Sonine functions. We briefly recall
the properties of these functions in the next section before using them for the ANC.
(11)The
resulting function is now a radial function, and we normalized the expression on the angular
surface of the star πΘ2/4, to handle the star brightness and
star diameter separately. To obtain an analytical expression for the star leakage, we have
to use an aperture transmission t(r) whose integral in the
above relation can be written as known functions. This is the case if we use for
t(r) the so-called Sonine functions. We briefly recall
the properties of these functions in the next section before using them for the ANC.
3. Expressions for a circular Sonine ANC
3.1. Sonine-apodized circular aperture and corresponding PSF
The transmission in amplitude of a radial Sonine apodization of a circular aperture of
diameter D can be written 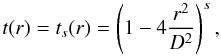 (12)where
s is the so-called Sonine parameter that defines the apodization’s
strength. The value s = 0 corresponds to the unapodized case.
Illustrations of the apodized transmission
ts(r) for a few values of
the Sonine parameter s are shown in Fig. 1. The curves are drawn for an aperture of diameter unity.
(12)where
s is the so-called Sonine parameter that defines the apodization’s
strength. The value s = 0 corresponds to the unapodized case.
Illustrations of the apodized transmission
ts(r) for a few values of
the Sonine parameter s are shown in Fig. 1. The curves are drawn for an aperture of diameter unity.
The point-spread function (PSF)
Rs(ρ) in the focal plane
of this apodized aperture can be written as (Osterberg
& Wilkins 1949; Jacquinot &
Roizen-Dossier 1964) 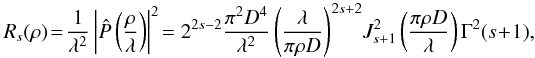 (13)where λ
is the light wavelength and ρ is the angular radial distance. We assume a
unit amplitude for the incoming wave on the aperture. For integer values of
s, Γ(s + 1) = s ! , but
s may take any positive real value.
(13)where λ
is the light wavelength and ρ is the angular radial distance. We assume a
unit amplitude for the incoming wave on the aperture. For integer values of
s, Γ(s + 1) = s ! , but
s may take any positive real value.
From there we can derive three relevant quantities for further use in this work: the
effective collection area Φs of the apodized aperture
(governing the energy throughput), the value of the PSF at the origin
(Rs(0)), and the equivalent angular area
△ s of the PSF. Following the approach given in Aime (2005), we have 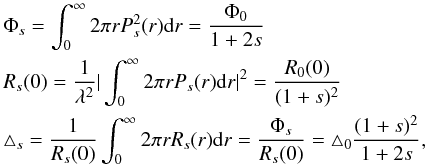 (14)where
the quantities Φ0, R0(0) and △ 0 refer
to a NC used with a clear aperture:
(14)where
the quantities Φ0, R0(0) and △ 0 refer
to a NC used with a clear aperture: 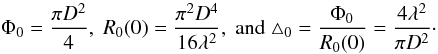 (15)It is interesting to note
that the effect of apodization simply is a multiplicative factor.
(15)It is interesting to note
that the effect of apodization simply is a multiplicative factor.
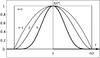 |
Fig. 1 Radial cuts of the aperture transmission (in amplitude) modified by the Sonine functions ts(r) given in Eq. (12), for s = 0 (clear aperture), 1, 2, and 6. |
For high enough values of its argument, the Bessel function can be approximated and
majored by 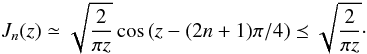 (16)This approximation is
fair enough even for low values (as soon as z is farther than the second
lobe), and the last term of the equation gives the envelope of the function. By
substituting this expression for the Bessel function into
Rs(ρ), we have
(16)This approximation is
fair enough even for low values (as soon as z is farther than the second
lobe), and the last term of the equation gives the envelope of the function. By
substituting this expression for the Bessel function into
Rs(ρ), we have
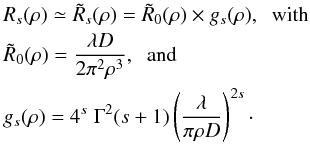 (17)This
approximation shows that the diffraction wings of the Sonine-apodized PSF decrease as
ρ to the power 3 + 2s, against just to the power 3 for
the Airy pattern. This interesting behavior is obtained, however, at the expense of a
reduced transmission and a larger size of the central part of the PSF.
(17)This
approximation shows that the diffraction wings of the Sonine-apodized PSF decrease as
ρ to the power 3 + 2s, against just to the power 3 for
the Airy pattern. This interesting behavior is obtained, however, at the expense of a
reduced transmission and a larger size of the central part of the PSF.
An illustration of Rs(ρ)
for s equal to 0 (the Airy pattern), 2, and 6 respectively is shown in
Fig. 2 together with the approximate expression
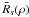 . This figure clearly shows
that
. This figure clearly shows
that 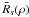 is a very fair estimate of
the envelope of Rs(ρ), as
soon as ρ is larger than the central part of the PSF.
is a very fair estimate of
the envelope of Rs(ρ), as
soon as ρ is larger than the central part of the PSF.
3.2. Star leakage for a Sonine ANC
When using Sonine apodizations, the integrals
I1(ρ0) and
I2(ρ) introduced in Eqs. (6) and (9) become 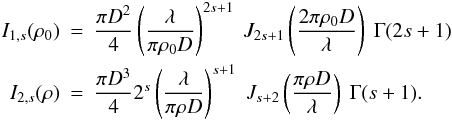 (18)We
can rewrite the integrated and normalized intensity transmitted by the ANC for a point
source off-axis by ρ0 as given in Eq. (6)
(18)We
can rewrite the integrated and normalized intensity transmitted by the ANC for a point
source off-axis by ρ0 as given in Eq. (6) ![\begin{equation} \label{EqOnSky} \tau_{s}(\rho_{0})= \frac{1}{2}\left[1- \left( \frac{\lambda}{\pi \rho_{0} D} \right)^{2s+1} \; J_{2s+1}\left(\frac{2 \pi \rho_{0} D}{\lambda}\right) \; \Gamma(2s+2) \right]. \end{equation}](/articles/aa/full_html/2011/06/aa16378-10/aa16378-10-eq81.png) (19)In Fig. 3 we display the on-sky transmission profiles
τs(ρ0) of the
ANC for various values of s. These profiles are normalized to 0.5 for
each value of s. Evidently increasing the apodization strength results in
a decrease of the transmission for slightly off-axis point-like sources. They either come
from small pointing errors or from the finite diameter of the star. Besides, the
apodization globally decreases the overall transmission and it widens the IWA.
(19)In Fig. 3 we display the on-sky transmission profiles
τs(ρ0) of the
ANC for various values of s. These profiles are normalized to 0.5 for
each value of s. Evidently increasing the apodization strength results in
a decrease of the transmission for slightly off-axis point-like sources. They either come
from small pointing errors or from the finite diameter of the star. Besides, the
apodization globally decreases the overall transmission and it widens the IWA.
 |
Fig. 2 PSF Rs(ρ) and their envelopes in a logarithmic scale, given in Eq. (12), for s = 0 (dashed line), 2 and 6 (full lines). The angular distance ρ is in units of λ/D. The envelopes starts at 1, 2.5 and 4λ/D respectively. |
 |
Fig. 3 On-sky normalized transmission τs(ρ0) of an ANC for s = 0 (no apodization), 2, 6. Angular distance is in units of λ/D. |
 |
Fig. 4 Illustration of I(ρ,ϕ) for s = 0 (left) and s = 2 (right). The intensity (logarithmic scale) was normalized and white corresponds to 1, while black corresponds to 10-3. Angular distances are in units of λ/D. |
Using for t(r) the Sonine transmission
ts(r), we have a new
expression for the intensity of the residual light from an off-axis point-like source (as
given in Eq. (10)): 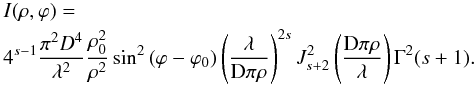 (20)An
illustration of I(ρ,ϕ) for s = 0 and
s = 2 is given in Fig. 4. In this
specific example the off-axis point source’s coordinates are
φ0 = π/3 and
ρ0 = 0.08λ/D.
(20)An
illustration of I(ρ,ϕ) for s = 0 and
s = 2 is given in Fig. 4. In this
specific example the off-axis point source’s coordinates are
φ0 = π/3 and
ρ0 = 0.08λ/D.
The Sonine transmission of Eq. (12) can
also replace t(r) in the expression of the star leakage
given in Eq. (11). We then have
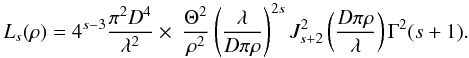 (21)This circular
distribution is the background against which the twin-images of the planet are to be
extracted.
(21)This circular
distribution is the background against which the twin-images of the planet are to be
extracted.
Here it is also possible to obtain an approximate expression of the star leakage outside
the central region. Replacing again the Bessel function by its approximation,
Ls(ρ) can be written as
the function 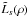 , envelope of
Ls(ρ), as follows:
, envelope of
Ls(ρ), as follows:
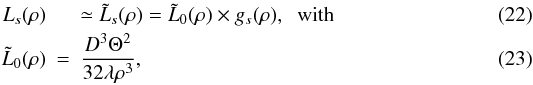 (22)where
(22)where
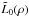 is the leakage for the
non-apodized AIC as given in Eq. (18) of Paper I, and
gs(ρ) is the attenuation
factor caused by the apodization, the same already given for the direct PSF response in
Eq. (17). This simple result is not
surprising since the leakage originates in the finite difference of the two diffraction
responses, as already noted in Sect. 2.
is the leakage for the
non-apodized AIC as given in Eq. (18) of Paper I, and
gs(ρ) is the attenuation
factor caused by the apodization, the same already given for the direct PSF response in
Eq. (17). This simple result is not
surprising since the leakage originates in the finite difference of the two diffraction
responses, as already noted in Sect. 2.
It is interesting to estimate the rejection gain obtained using an ANC against a simple
apodized aperture. This gain is evaluated by the ratio
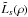 to
to
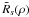 . Making use of the previous
expressions, we have
. Making use of the previous
expressions, we have 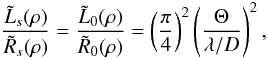 (23)which means that
the effect of a nuller coronagraph is decoupled from the effect of apodization. This
expression also shows that the addition of a nuller coronagraph to an apodized coronagraph
is relevant when the apparent star diameter Θ is small enough with respect to the
resolution unit λ/D.
(23)which means that
the effect of a nuller coronagraph is decoupled from the effect of apodization. This
expression also shows that the addition of a nuller coronagraph to an apodized coronagraph
is relevant when the apparent star diameter Θ is small enough with respect to the
resolution unit λ/D.
A few illustrative examples of the star leakage are given in Figs. 5 to 8. To draw these curves, it is necessary to take fixed values for the parameters ε (the flux ratio planet to star) and Θ. In the following figures, the underlying astronomical target is a solar-like system at 10 pcs, the stellar diameter is then 1 mas (milli arc second). In Fig. 5 we compared the leakage for a s value of 6 to what could be obtained with a clear aperture. These curves are also compared to the PSF for an experiment operated without a NC. The x-axis is in units of resolution, the star diameter is of 0.08λ/D. In Fig. 6 we make a comparison of star leakages for s values equal to 0, 2, and 6 together with the corresponding envelopes in the diffraction wings.
 |
Fig. 5 Continuous curves: star leakage Ls(ρ) (logarithmic scale) with Θ = 0.08λ/D for two Sonine apodizations. Top: s = 0 (clear aperture), bottom: s = 6. Dashed curves: apodized PSFs Rs(ρ) for the same apodizations. |
 |
Fig. 6 Star leakage Ls(ρ) and the corresponding envelope (logarithmic scale) with Θ = 0.08λ/D for three Sonine apodizations. From top to bottom: s = 0 (clear aperture, dashed line), 2, 6 (continuous lines). The angular distance ρ is in units of λ/D. The envelopes start at 1, 1.5, and 2.5λ/D. |
 |
Fig. 7 Intensity in logarithmic scale of a 10 pc distant star and a planet located at 1 AU from it (0.1′′) with a flux ratio of 1010 for a 10 m aperture. Left: without a nuller coronagraph. Right: with a nuller coronagraph. Top: with a clear aperture. Bottom: with a Sonine-apodized aperture s = 6. The intensity scale is the same as in Fig. 8 and goes from −15 (black) to 0 (white). The crosses in the two bottom images indicate the position of the planet. |
 |
Fig. 8 Intensity in logarithmic scale of a 10 pc distant star and a planet located at 1 AU from it (0.1′′) with a flux ratio of 1010. The diameter of the telescope is 10 m and the observation wavelength 600 nm. Top: without a nuller coronagraph, bottom: with a nuller coronagraph. The cases of a clear aperture (blue curve) and apodized aperture (red curve) are compared. The dashed curves correspond to the image of the star alone. The gray areas highlight the contributions of the planet. |
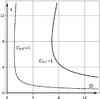 |
Fig. 9 Set of points in the D × s plane such that Cs(ρP) = 1 for a planet at 0.1′′ (continuous curve) and at 0.5′′ (dashed curve) from the star (apodization parameter s and telescope diameter D). The intensity ratio star/planet is 1010. The curves show that there is a minimal diameter size required for exoplanet detection. |
Although so far we have given the expressions of the functions as radial functions, the
image formed at the telescope focus must be described in two dimensions. If we denote as
ρ the angular vector position in the focal plane, with
|ρ| = ρ, and
ρP the angular vector position of the planet,
neglecting the possible interferences between the twin images of the planet, the observed
intensity in the focal plane is written as 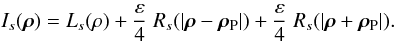 (24)The intensity is
reduced by a factor of 4 because of the partition of the planet light into four images
(two-twin images at each of the two outputs of the system). Figure 7 shows what could be obtained for an Earth-like planet (at 100 mas of
the star), with ε = 10-10. The observation is made with a 10-m
telescope at 600 nm. A comparison is made in the figure of what could be obtained with an
AIC alone (unapodized), with apodization alone and when coupling apodization with an AIC.
For the representation of the apodization alone image, the background used is the mere
PSF, e.g. ignoring the smoothing effect of the star (the convolution between the PSF and
the star image). In fact, numerical simulations that are not reported here for the sake of
conciseness show that the effect is insubstantial as long as the star diameter remains
smaller than λ/D.
(24)The intensity is
reduced by a factor of 4 because of the partition of the planet light into four images
(two-twin images at each of the two outputs of the system). Figure 7 shows what could be obtained for an Earth-like planet (at 100 mas of
the star), with ε = 10-10. The observation is made with a 10-m
telescope at 600 nm. A comparison is made in the figure of what could be obtained with an
AIC alone (unapodized), with apodization alone and when coupling apodization with an AIC.
For the representation of the apodization alone image, the background used is the mere
PSF, e.g. ignoring the smoothing effect of the star (the convolution between the PSF and
the star image). In fact, numerical simulations that are not reported here for the sake of
conciseness show that the effect is insubstantial as long as the star diameter remains
smaller than λ/D.
The figure shows that the visibility of the Earth-like planet is significantly improved by coupling an apodizer with a NC, and reciprocally a system based on apodization alone will highly benefit from the introduction of a NC. Of course the gain will strongly depend on the value of Θ, as shown by Eq. (23). Cuts of these images are shown in Fig. 8 for a Sonine-apodized aperture of s = 6 with and without a NC. While the planet is located at 100 mas from the star, its diffraction spot may appear to be centered at a different location. This observational bias is caused by the logarithmic scale used to represent the data, and also because the star leakage is not constant over the area of the planet’s image.
4. Contrast and signal-to-noise ratio considerations
We consider in this section two quantities, the local contrast and the signal-to-noise ratio (SNR), which might appear similar but are essentially different because the contrast is an estimator that assumes a classical detection of the light while the SNR takes into account the photodetection process leading to the so-called photon noise. Both quantities are useful but the SNR is the ultimate quantity that can define whether a detection can be achieved for a given wavelength, bandwidth, etc. The contrast remains an interesting quantity however because it will be difficult in practice if the contrast is not high enough to distinguish between the planet and unwanted perturbative effects such as the residual speckles not considered in this analysis.
We define the local contrast as the ratio between the height
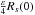 of the twin images of the planet
to the level Ls(ρp)
of the star leakage at the central location
ρ = ρp of the planet. Using the simplified
expression for the envelope of the leakage, we have
of the twin images of the planet
to the level Ls(ρp)
of the star leakage at the central location
ρ = ρp of the planet. Using the simplified
expression for the envelope of the leakage, we have 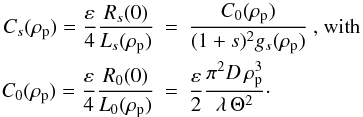 (25)An
illustration of the use of these relations is given in Fig. 9, to derive the optimal diameters and Sonine apodizations for the extra solar
system at 10 pc already considered. The curves give the solution of the equation that equals
the local contrast to 1 for an exo-Earth and an exo-Jupiter. The value of ε
is fixed to 10-10 for both exoplanets though, as expected, the exo-Earth is a
more difficult target than the exo-Jupiter. We just consider in our illustration the
difference of angular separation. In both cases there is an optimal value of
s that minimizes the necessary aperture diameter. This value is not
extremely critical, but if the choice of s is not optimal, the minimum
telescope diameter increases substantially. For example, when observing a planet at 0.1
arcsec from its star, the minimum telescope diameter is 7 m for the optimal value of
s = 8. For s = 4, the minimum diameter becomes 8.5 m,
and 11 m for s = 3 . For Jupiter-like planets the minimum diameters
correspond to telescopes down to the 2 m class.
(25)An
illustration of the use of these relations is given in Fig. 9, to derive the optimal diameters and Sonine apodizations for the extra solar
system at 10 pc already considered. The curves give the solution of the equation that equals
the local contrast to 1 for an exo-Earth and an exo-Jupiter. The value of ε
is fixed to 10-10 for both exoplanets though, as expected, the exo-Earth is a
more difficult target than the exo-Jupiter. We just consider in our illustration the
difference of angular separation. In both cases there is an optimal value of
s that minimizes the necessary aperture diameter. This value is not
extremely critical, but if the choice of s is not optimal, the minimum
telescope diameter increases substantially. For example, when observing a planet at 0.1
arcsec from its star, the minimum telescope diameter is 7 m for the optimal value of
s = 8. For s = 4, the minimum diameter becomes 8.5 m,
and 11 m for s = 3 . For Jupiter-like planets the minimum diameters
correspond to telescopes down to the 2 m class.
We define the SNR as the ratio between the number of photons
NP gathered from the planet’s twin images and the statistical
fluctuations produced by the star leakage. Denoting with NL the
number of photons of the star leakage underneath the planet images, the total number of
photons at the planet position is
NL + NP. Assuming a Poisson
process for the photodetection, the root mean square of the statistical fluctuations is
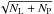 ,
which reduces to
,
which reduces to 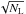 for a low contrast. The expression of the SNR is then
for a low contrast. The expression of the SNR is then 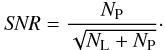 (26)The numbers
NP and NL can be written as
(26)The numbers
NP and NL can be written as
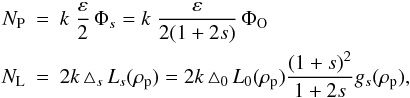 (27)where
k is the factor that converts the energy collected by the experiment into
a number of photons per unit of surface.
(27)where
k is the factor that converts the energy collected by the experiment into
a number of photons per unit of surface.
It can be evaluated through the standard expression: 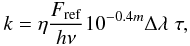 (28)where
η stands for the efficiency of the optical system including the quantum
efficiency of the detector, Fref is the reference flux,
m is the apparent magnitude of the star, Δλ is the
bandwidth, and τ is the exposure time.
(28)where
η stands for the efficiency of the optical system including the quantum
efficiency of the detector, Fref is the reference flux,
m is the apparent magnitude of the star, Δλ is the
bandwidth, and τ is the exposure time.
We chose to consider a bandwidth of 88nm centered at λ = 555 nm, which makes it very similar to the V band. The value of η was chosen to be 0.5. The solar-like star being at 10 pc, its apparent magnitude is therefore the same as its absolute magnitude (m = 4.83). In these conditions the value of k is 4.91 × 107 photons per surface unit for an exposure time of 1 s.
 |
Fig. 10 Set of points in the D × s plane such that SNRs(ρP) = 1, 5, and 10, for angular distances ρP = 0.5′′ (dashed curves) and 0.1′′ (continuous curves). The intensity ratio star/planet is 1010, the other observing parameters are given in the body of the paper. There is a minimal diameter size required to reach a given SNR value. |
Figure 10 is a representation similar to Fig. 9, but considering the SNR instead of contrast. It displays the evolution of the telescope’s diameter as a function of s for three different values of the SNR (1, 5, and 10) obtained with an exposure time of 1 h. For low values of the SNR the curves are similar to those of the contrast but higher values of the SNR lead to higher curvatures. For SNRs of 5 and 10 and for both planets these functions have the same asymptotes. As for the contrast, minimum values of D are found for specific s.
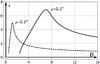 |
Fig. 11 Optimal Sonine parameter s as a function of the telescope diameter D for the Earth-like planet (continuous curve) and the Jupiter-like planet (dashed curve). |
Figure 11 represents the optimal s as a function of D for the Earth-like and the Jupiter-like planets. A maximum smax is reached for a particular value of D. The closer to the star, the higher smax, because the star leakage, which is also higher, has to be compensated for. That we associated an optimal apodization to a given diameter D does not mean that this pairing will be efficient for any astronomical target. One may wonder if an apodizer based on the same optimal s can be used to observe two planets at different angular separations ρ1 and ρ2 from their star. It is true that a unique, common pair (D,s) can be found at the intersection of the two curves Dρ1(s) and Dρ2(s). However, if we consider the case highlighted in Fig. 11, we have D ≈ 3 m and s ≈ 2. If the SNR associated with the detection of the Jupiter-like planet can reach 10 for an exposure time of almost 9 h, the same SNR cannot be reached when looking for the Earth-like planet unless the exposure time exceeds 8.7 years.
A telescope of diameter 8 m observing for one hour offers the possibility of detecting planets at 0.1 arcsec and 0.5 arcsec for SNRs of respectively 5 and 10 (but for different values of s). Table 1 gives an extensive list of the exposure times needed to detect planets at these two angular distances for telescope diameters of 2, 10, and 30 m. Although a 2 m telescope cannot detect a planet at 0.1 arcsec in a reasonable amount of time (the limit was set to 105 s, which is a little more than one day), a 10 m telescope can achieve this detection with an SNR of 10 for an exposure time of 1.6 h. Even if the star-leakage effect is higher for bigger telescope, this time decreases to less than 6 min for a 30 m telescope. The apodization parameters associated with these detections are smaller than those found by looking at Fig. 9.
Required exposure times and optimal apodization parameters to detect the Earth-like and Jupiter-like planets for three different telescopes’ diameters with three different SNRs.
5. Discussion and conclusion
We showed that using an apodized aperture with a nuller coronagraph leads to a decisive improvement of the detection performance. The apodization has two major consequences: the first is that it allows the coronagraph to greatly reduce the on-sky transmission of slightly off-axis sources of light. The star-leakage is thus reduced, as are small pointing errors. The second is that, as can be observed in other apodized coronagraphs, the apodization also helps concentrating the diffracted energy in the central lobe, which improves the detectability of the companion.
Given an angular separation between the star and the planet, there is a minimum telescope diameter (associated with a specific apodization parameter s of the Sonine function) that allows a detection with a sufficient local contrast ratio, or a sufficient SNR for a typical exposure time. In the specific case of the Sonine functions, detecting an exo-earth around a solar-type star at 10 pc with an SNR of 10 can be done in 1.6 h with a 10 m telescope and an apodization parameter s of 4.4, or in less than 6 min if the telescope has a diameter of 30 m (and the apodization strength is in this case 2). The study proposed here has been solely limited to Sonine apodizers because they make it possible to obtain algebraic expressions for the star leakage. Other apodization profiles might be more efficient than Sonine apodizers however, and may be used in practice, even if it will not be possible to express their effect using analytic expressions. Some candidates among the possible apodization profiles are the spheroidal prolate functions (Slepian 1965) that, as was well described in Frieden (1971), maximally concentrate in the mean square sense the light in the diffraction central spot. The properties of the spheroidal prolate functions make them very interesting for the Lyot coronagraph, as was pointed out in several papers (Aime et al. 2002; Soummer et al. 2003; Soummer 2005).
The coupling of a nuller coronagraph and an apodizer has an additional advantage: it relaxes their respective specifications, in particular for apodizers with a continuously variable transmission. Nevertheless, the difficulty of manufacturing these apodizers may lead the observer to use microdot apodizers, as studied in Martinez et al. (2010) in the context of the prolate-apodized Lyot coronagraph (PALC) of the ESO-Sphere project (and possibly for the coronagraphic instrument of the E-ELT). Micron-size dots with a transmission of zero are deposited on a substrate. This type of apodizer is therefore a binary apodizer. The density of the dots is such that it approximates the apodization profile. This type of apodizer has also been selected and tested for the PALC of the Gemini Planet Imager project (Sivaramakrishnan et al. 2010). As noted by the authors, the design of microdot apodizers has to be carefully chosen because the diffraction from the size of the microdots can create unwanted effects on the PSF.
There are several other types of binary masks. Some early examples have been described in Boivin (1952) and Jacquinot & Roizen-Dossier (1964). They were more recently studied in detail for direct detection of exoplanets. Besides, numeric optimizations of coronagraphic problems can lead to various designs of pupil masks: shaped pupils, barcode masks, checkerboard masks, and other types of binary apodizers are described in Spergel & Kasdin (2001), Vanderbei et al. (2003), and Kasdin et al. (2003). These apodizers can provide very high contrasts and possess the advantage of having achromatic transmissions. The Space Infrared telescope for Cosmology and Astrophysics (SPICA, Spica Working Group et al. 2010) for example has selected checkerboard masks (among other types of pupil masks) for its coronagraph.
Finally, apodization can also be obtained using a phase induced amplitude apodizer (PIAA, see Guyon 2003; Vanderbei 2006). The specific properties of PIAA are complex however and cannot be introduced in passing in the present analysis. Whatever the apodizing technique is, combining it with a nuller coronagraph can greatly improve the detection capabilities of the instrument.
References
- Aime, C. 2005, A&A, 434, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aime, C. 2007, C. R. Phys., 8, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Aime, C., Soummer, R., & Ferrari, A. 2002, A&A, 389, 334 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aime, C., Ricort, G., Carlotti, A., Rabbia, Y., & Gay, J. 2010, A&A, 517, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allouche, F., Glindemann, A., Aristidi, E., & Vakili, F. 2009, A&A, 500, 1277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenberg, J. W., Lo, A. S., Glassman, T. M., & Cash, W. 2007, C. R. Phys., 8, 438 [Google Scholar]
- Baudoz, P., Rabbia, Y., & Gay, J. 2000a, A&AS, 141, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baudoz, P., Rabbia, Y., Gay, J., et al. 2000b, A&AS, 145, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boivin, A. 1952, J. Opt. Soc. Am. (1917–1983), 42, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Bracewell, R. N. 1978, Nature, 274, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 2006, Nature, 442, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Frieden, B. R. 1971, Progress in Optics, ed. E. Wolf (North-Holland Publishing, Co.) [Google Scholar]
- Gay, J., & Rabbia, Y. 1996, Academie des Science Paris Comptes Rendus Ser. B Sci. Phys., 322, 265 [Google Scholar]
- Guyon, O. 2003, A&A, 404, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guyon, O. 2009, in Am. Inst. Phys. Conf. Ser., ed. T. Usuda, M. Tamura, & M. Ishii, 1158, 285 [Google Scholar]
- Guyon, O., Pluzhnik, E. A., Kuchner, M. J., Collins, B., & Ridgway, S. T. 2006, ApJS, 167, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jacquinot, P., & Roizen-Dossier, B. 1964, Progress in Optics, ed. E. Wolf (North-Holland Publishing, Co.), 31 [Google Scholar]
- Kasdin, N. J., Vanderbei, R. J., Spergel, D. N., & Littman, M. G. 2003, ApJ, 582, 1147 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez, P., Dorrer, C., Kasper, M., Boccaletti, A., & Dohlen, K. 2010, A&A, 520, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mawet, D., Riaud, P., Absil, O., Baudrand, J., & Surdej, J. 2005, in SPIE Conf., ed. D. R. Coulter, 5905, 502 [Google Scholar]
- Nisenson, P., & Papaliolios, C. 2001, ApJ, 548, L201 [NASA ADS] [CrossRef] [Google Scholar]
- Nishikawa, J., Kotani, T., Murakami, N., et al. 2005, A&A, 435, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppenheimer, B. R., & Hinkley, S. 2009, ARA&A, 47, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Osterberg, H., & Wilkins, Jr., J. E.,1949, J. Opt. Soc. Am. (1917–1983), 39, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C. 2000, Reports Progr. Phys., 63, 1209 [Google Scholar]
- Rabbia, Y., Baudoz, P., & Gay, J. 1998, in The Next Generation Space Telescope: Science Drivers and Technological Challenges, ed. B. Kaldeich, ESA Special Publication, 429, LIA Colloq., 34, 279 [Google Scholar]
- Roddier, F., & Roddier, C. 1997, PASP, 109, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rouan, D., Riaud, P., Boccaletti, A., Clénet, Y., & Labeyrie, A. 2000, PASP, 112, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Seager, S., & Sasselov, D. D. 2000, ApJ, 537, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Sivaramakrishnan, A., Soummer, R., Oppenheimer, B. R., et al. 2010, in SPIE Conf., 7735 [Google Scholar]
- Slepian, D. 1965, J. Opt. Soc. Am. (1917–1983), 55, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R. 2005, ApJ, 618, L161 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Aime, C., & Falloon, P. E. 2003, A&A, 397, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spergel, D., & Kasdin, J. 2001, in American Astronomical Society Meeting Abstracts, BAAS, 33, 1431 [Google Scholar]
- Spica Working Group, Enya, K., & SPICA Working Group. 2010, Adv. Space Res., 45, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Tavrov, A. V., Otani, Y., Kurokawa, T., & Takeda, M. 2005, in SPIE Conf. Ser., 5905, ed. D. R. Coulter, 398 [Google Scholar]
- Tavrov, A. V., Nishikawa, J., Tamura, M., et al. 2008, Appl. Opt., 47, 4915 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Vanderbei, R. J. 2006, ApJ, 636, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderbei, R. J., Spergel, D. N., & Kasdin, N. J. 2003, ApJ, 599, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderbei, R. J., Cady, E., & Kasdin, N. J. 2007, ApJ, 665, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Fakhouri, O., Marcy, G. W., et al. 2011, PASP, accepted [arXiv:1012.5676] [Google Scholar]
All Tables
Required exposure times and optimal apodization parameters to detect the Earth-like and Jupiter-like planets for three different telescopes’ diameters with three different SNRs.
All Figures
 |
Fig. 1 Radial cuts of the aperture transmission (in amplitude) modified by the Sonine functions ts(r) given in Eq. (12), for s = 0 (clear aperture), 1, 2, and 6. |
| In the text | |
 |
Fig. 2 PSF Rs(ρ) and their envelopes in a logarithmic scale, given in Eq. (12), for s = 0 (dashed line), 2 and 6 (full lines). The angular distance ρ is in units of λ/D. The envelopes starts at 1, 2.5 and 4λ/D respectively. |
| In the text | |
 |
Fig. 3 On-sky normalized transmission τs(ρ0) of an ANC for s = 0 (no apodization), 2, 6. Angular distance is in units of λ/D. |
| In the text | |
 |
Fig. 4 Illustration of I(ρ,ϕ) for s = 0 (left) and s = 2 (right). The intensity (logarithmic scale) was normalized and white corresponds to 1, while black corresponds to 10-3. Angular distances are in units of λ/D. |
| In the text | |
 |
Fig. 5 Continuous curves: star leakage Ls(ρ) (logarithmic scale) with Θ = 0.08λ/D for two Sonine apodizations. Top: s = 0 (clear aperture), bottom: s = 6. Dashed curves: apodized PSFs Rs(ρ) for the same apodizations. |
| In the text | |
 |
Fig. 6 Star leakage Ls(ρ) and the corresponding envelope (logarithmic scale) with Θ = 0.08λ/D for three Sonine apodizations. From top to bottom: s = 0 (clear aperture, dashed line), 2, 6 (continuous lines). The angular distance ρ is in units of λ/D. The envelopes start at 1, 1.5, and 2.5λ/D. |
| In the text | |
 |
Fig. 7 Intensity in logarithmic scale of a 10 pc distant star and a planet located at 1 AU from it (0.1′′) with a flux ratio of 1010 for a 10 m aperture. Left: without a nuller coronagraph. Right: with a nuller coronagraph. Top: with a clear aperture. Bottom: with a Sonine-apodized aperture s = 6. The intensity scale is the same as in Fig. 8 and goes from −15 (black) to 0 (white). The crosses in the two bottom images indicate the position of the planet. |
| In the text | |
 |
Fig. 8 Intensity in logarithmic scale of a 10 pc distant star and a planet located at 1 AU from it (0.1′′) with a flux ratio of 1010. The diameter of the telescope is 10 m and the observation wavelength 600 nm. Top: without a nuller coronagraph, bottom: with a nuller coronagraph. The cases of a clear aperture (blue curve) and apodized aperture (red curve) are compared. The dashed curves correspond to the image of the star alone. The gray areas highlight the contributions of the planet. |
| In the text | |
 |
Fig. 9 Set of points in the D × s plane such that Cs(ρP) = 1 for a planet at 0.1′′ (continuous curve) and at 0.5′′ (dashed curve) from the star (apodization parameter s and telescope diameter D). The intensity ratio star/planet is 1010. The curves show that there is a minimal diameter size required for exoplanet detection. |
| In the text | |
 |
Fig. 10 Set of points in the D × s plane such that SNRs(ρP) = 1, 5, and 10, for angular distances ρP = 0.5′′ (dashed curves) and 0.1′′ (continuous curves). The intensity ratio star/planet is 1010, the other observing parameters are given in the body of the paper. There is a minimal diameter size required to reach a given SNR value. |
| In the text | |
 |
Fig. 11 Optimal Sonine parameter s as a function of the telescope diameter D for the Earth-like planet (continuous curve) and the Jupiter-like planet (dashed curve). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


