| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 6 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201016328 | |
| Published online | 11 May 2011 | |
Oxygen depletion in dense molecular clouds: a clue to a low O2 abundance?
1
Université de Bordeaux, Observatoire Aquitain des Sciences de l’Univers, 2 rue de l’Observatoire, BP 89, 33271 Floirac Cedex, France
e-mail: Ugo.Hincelin@obs.u-bordeaux1.fr
2
CNRS, UMR 5804, Laboratoire d’Astrophysique de Bordeaux, 2 rue de l’Observatoire, BP 89, 33271 Floirac Cedex, France
3
Université de Bordeaux, Institut des Sciences Moléculaires, 351 Cours de la Libération, 33405 Talence Cedex, France
4
CNRS UMR 5255, Institut des Sciences Moléculaires, 351 Cours de la Libération, 33405 Talence Cedex, France
5
Université de Franche-Comté, Institut UTINAM, UMR CNRS 6213, 25030 Besançon Cedex, France
6
Laboratoire Interdisciplinaire Carnot de Bourgogne, UMR CNRS 5209, Université de Bourgogne, 9 Av. A. Savary, 21078 Dijon Cedex, France
7
Georg-August-Universität Göttingen, Institut für Physikalische Chemie, Tammannstrasse 6, 37077 Göttingen, Germany
8
Max-Planck-Institut für Biophysikalische Chemie, Am Fassberg 11, 37077 Göttingen, Germany
Received: 15 December 2010
Accepted: 21 March 2011
Context. Dark cloud chemical models usually predict large amounts of O2, often above observational limits.
Aims. We investigate the reason for this discrepancy from a theoretical point of view, inspired by the studies of Jenkins and Whittet on oxygen depletion.
Methods. We use the gas-grain code Nautilus with an up-to-date gas-phase network to study the sensitivity of the molecular oxygen abundance to the oxygen elemental abundance. We use the rate coefficient for the reaction O + OH at 10 K recommended by the KIDA (KInetic Database for Astrochemistry) experts.
Results. The updates of rate coefficients and branching ratios of the reactions of our gas-phase chemical network, especially N + CN and H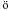 + O, have changed the model sensitivity to the oxygen elemental abundance. In addition, the gas-phase abundances calculated with our gas-grain model are less sensitive to the elemental C/O ratio than those computed with a pure gas-phase model. The grain surface chemistry plays the role of a buffer absorbing most of the extra carbon. Finally, to reproduce the low abundance of molecular oxygen observed in dark clouds at all times, we need an oxygen elemental abundance smaller than 1.6 × 10-4.
+ O, have changed the model sensitivity to the oxygen elemental abundance. In addition, the gas-phase abundances calculated with our gas-grain model are less sensitive to the elemental C/O ratio than those computed with a pure gas-phase model. The grain surface chemistry plays the role of a buffer absorbing most of the extra carbon. Finally, to reproduce the low abundance of molecular oxygen observed in dark clouds at all times, we need an oxygen elemental abundance smaller than 1.6 × 10-4.
Conclusions. The chemistry of molecular oxygen in dense clouds is quite sensitive to model parameters that are not necessarily well constrained. That O2 abundance may be sensitive to nitrogen chemistry is an indication of the complexity of interstellar chemistry.
Key words: astrochemistry / ISM: abundances / ISM: molecules / ISM: individual objects: L134N / ISM: individual objects: TMC-1
© ESO, 2011
1. Introduction
Chemical models predict that gas-phase oxygen should be mainly in the form of O2 and CO in the cold interstellar medium (see for instance Wakelam et al. 2006a; Quan et al. 2008). Since the 1980’s, there have been searches for O2 in the interstellar medium using ground-based and space telescopes (see Pagani et al. 2003, and references therein). First, analyses of data from the SWAS satellite gave an upper limit of about 10-6 in dense clouds (Goldsmith et al. 2000). The ODIN satellite also initially gave negative results (Pagani et al. 2003) with improved upper limits of ≈ (1−2) × 10-7 for nine sources. However, a reanalysis by Larsson et al. (2007), using more precise knowledge of the telescope behavior, resulted in a detection of O2 in ρ Ophiuchi cloud, with a beam-averaged abundance of 5 × 10-8 relative to H2. Using ground-based observations of 16O18O and C18O lines, Liseau et al. (2010) argue that the emitting region may be much smaller than the beam of ODIN thus the O2 abundance could be larger by one or two orders of magnitude. Regardless of the exact numbers, the sparsity of O2 detections in the various target molecular clouds is an indication that this molecule may not be a reservoir of oxygen.
Many explanations have been proposed to reconcile observations and models. From a chemical modeling point of view, pure gas-phase chemical models can explain the observed upper limits for clouds younger than 105 yr (Wakelam et al. 2006a). Viti et al. (2001) explored the possibility that chemical models can display bistabilities (Le Bourlot et al. 1993). In the parameter space where bistability exists, one of the solutions is characterized by a very low abundance of O2. In this solution however, all molecular specie abundances are very small, including the CO abundance (Wakelam et al. 2006b), which is not what is observed. As another possibility, the effect of uncertainties in the rate coefficient of the main reaction of production of O2 (O + OH − → O2 + H) was explored by Quan et al. (2008). One needs however to decrease this rate coefficient by a considerable amount to modify the predicted abundance of O2.
In the presence of dust, molecular oxygen in the gas phase can be adsorbed onto grain surfaces. Adsorption of O2 onto dust grains is insufficient in itself to lower the O2 abundance after 106 yr, because of the balance with thermal evaporation and cosmic-ray-induced desorption. However, the adsorbed O2 molecule can be successively hydrogenated to form HO2 and H2O2. Then H2O2 reacts with H to form water (see also Roberts & Herbst 2002), which is more difficult to release from the grains. This surface chemistry allows one to decrease the abundance of O2 after 106 years, but a peak in the abundance larger than observational limits remains between 105 and 106 years. Unfortunately, this time range encompasses the “age” of cold cores determined by the comparison between large network chemical models and observations of more than 30 species in TMC-1CP and L134N (N) (see Wakelam et al. 2006a; Garrod et al. 2007; Smith et al. 2004). Bergin et al. (2000) found a small abundance of O2 in the gas at all times, in agreement with observations, using a simplified version of grain surface chemistry assuming conversion of O to H2O and C to CH4, and choosing the branching ratio of the reaction H3O+ + e− − → H + H2O that equals 0.33 to reproduce the H2O abundance. Experimental measurements from Jensen et al. (2000) showed that this branching ratio is 0.25. Finally, Hollenbach et al. (2009) studied the chemistry of O2 as a function of the depth in molecular clouds using a one-dimensional steady-state PDR model. The authors studied the influence of many parameters and found that the O2 abundance peaks at Av between 4 and 6 and that molecules would be strongly depleted at larger Av.
In this paper, we revisit the question of the O2 abundance in dark clouds using the gas-grain model Nautilus with the most recent gas-phase network from the KIDA database and new insight into the oxygen elemental abundances provided by Jenkins (2009). In the next two sections, we introduce the problem of the choice of oxygen elemental abundance for dense cloud chemical modeling and describe our chemical model. The results of our simulations and comparisons with observations in the two dark clouds L134N and TMC-1CP are shown in Sect. 4. We present our conclusions about our work in the last section.
2. Carbon and oxygen depletion
The depletion of oxygen related to cosmic reference values has been investigated for many years. For instance, Meyer et al. (1998) concluded that there was no evidence for density-dependent oxygen depletion from the gas phase based on the analysis of their observations of 13 stars using the Goddard High Resolution Spectrograph (GHRS) onboard the Hubble Space Telescope (HST). They thus proposed a mean interstellar gas-phase oxygen abundance (O/H) of 3.19 × 10-4. A few years later, Cartledge et al. (2004) found a weak correlation between the oxygen gas-phase abundance and the density of the clouds, analyzing a larger sample of sources observed with the Space Telescope Imaging Spectrograph (STIS) of HST and Far Ultraviolet Spectroscopic Explorer (FUSE ). At densities below 1 cm-3, they found an O/H abundance of 3.9 × 10-4 and an abundance of 2.8 × 10-4 at densities above 1 cm-3.
A comprehensive study of the depletion problem by Jenkins (2009) brought additional findings to light. Jenkins re-analyzed archival data of atomic lines in more than two hundred lines of sight. The main result of his analysis is that all elements (except nitrogen), and even sulphur, seem to deplete with density. The depletion factor for carbon is much smaller than for oxygen (but mostly less certain) so that one expects an increase in the C/O gas-phase elemental ratio with the density of the cloud. The main mechanism capable of explaining this depletion is accretion onto grains. The depletion of oxygen, however, cannot be accounted for by the formation of silicates and oxides since the oxygen depletion appears to be larger than that of Mg + Si + Fe. In the diffuse medium, densities are so low that the collision probability between grains and gas-phase species cannot explain the depletion. It is usually assumed that depletion occurs in denser regions and that the mass exchange between the dense and diffuse medium explains these observations (Draine 1990). In a sense, the observation of the elemental depletion as a function of the cloud density traces the survival of refractory compounds to the UV radiation in the ISM. This may indicate that depletion of the elements is stronger in denser regions. There is indirect evidence of this high depletion, such as the small abundance of SiO in dense clouds (Ziurys et al. 1989) compared to that of cosmic silicon. To reproduce observations of gas-phase molecules in dense clouds, Graedel et al. (1982) proposed to use a “depletion factor” of ten on observed atomic abundances in diffuse clouds for all elements except He, C, N, and O. These elemental abundances constitute the largely used “low metal” elemental abundances. The value of the “depletion factor” is however poorly constrained and remains a free parameter in chemical models. A sensitivity analysis by Wakelam et al. (2010a) show that this is one of the most important parameters.
Carbon and oxygen are usually assumed not to display additional depletion compared to diffuse clouds but this view is now changing. Additional depletion of oxygen in an organic refractory component of interstellar dust seems to be the most probable way of accounting for all oxygen in dense environments as shown by Whittet (2010). Following fresh insight from Jenkins about oxygen depletion, Whittet compiled an inventory of the different forms of O-bearing species as a function of cloud density from an observational point of view (see his Fig. 3). In diffuse clouds, oxygen is partly depleted in silicates and oxides (this is the fraction of cosmic oxygen already depleted in the diffuse gas), in atomic form (which is observed), and in an unidentified form (i.e. “unidentified depleted oxygen” called UDO, possibly organic refractory compounds). As the density increases, the fraction of UDO increases whereas that of atomic oxygen decreases. At densities high enough for chemistry to be efficient (atomic oxygen then cannot be observed anymore), oxygen goes into gas-phase CO and ice compounds (mainly CO, CO2 and H2O). At hydrogen densities of around 1000 cm-3, 28% of oxygen would be in gas-phase CO and icy species, 19% would be in refractory silicate and oxide forms, and presumably 49% would in UDO. The net result of this is that only 32% of the oxygen would be available for the chemistry. We note that the missing oxygen in the dust phase has been debated in Voshchinnikov & Henning (2010).
3. The model
3.1. Nautilus
We used the Nautilus chemical model described in Hersant et al. (2009). The model solves the kinetic equations for gas-phase and grain surface chemistries. Details of the physical and chemical processes included in the model are given in a benchmark paper by Semenov et al. (2010). We use typical dense cloud conditions: a gas and dust temperature of 10 K, an H density of 2 × 104 cm-3, a visual extinction of 10, and a cosmic-ray ionization rate of 1.3 × 10-17 s-1. A single grain size of 0.1 μm is used to compute adsorption rates following Hasegawa et al. (1992). The cross-section per H nucleus used is 5.72 × 10-22 cm2 and we assumed thermal velocities. The adsorption energy used for O2 is 1000 K (Herma Cuppen private communication). As cosmic rays can penetrate deep into grains, we do not restrict the evaporation of species by cosmic rays to the surface layer of molecules. The species are assumed to be initially in an atomic form as in diffuse clouds except for hydrogen, which is converted entirely into H2. Elements with an ionization potential below the maximum energy of ambient UV photons (13.6 eV, the ionization energy of H atoms) are initially in a singly ionized state, i.e., C, S, Si, Fe, Na, Mg, Cl, and P.
3.2. Chemical network
The chemical network, adapted from Garrod et al. (2007), includes 6142 reactions, of which 4394 are pure gas-phase reactions and 1748 are grain-surface and gas-grain interaction reactions. The model follows the chemistry of 458 gas-phase species and 196 species on grains. The gas-phase network has been updated according to the recommendations from the experts of the KIDA database1. KIDA, for KInetic Database for Astrochemistry, is a recently opened online database of gas-phase reactions of interest for astrochemical (interstellar medium and planetary atmospheres) studies (see Wakelam 2010; Wakelam et al. 2010b). Recommendations on rate coefficients by experts in physico-chemistry are given for key reactions.
The rate coefficient of the reaction O + OH − → O2 + H is a subject of debate (see Quan et al. 2008). The KIDA experts suggest that the rate coefficient at 10 K is between 2 × 10-11 and 8 × 10-11 cm3 molecule-1 s-1 (see Sect. 3.2.1). In the rest of the paper, we use the lower limit for this rate coefficient. Results using the upper limit are discussed in Sect. 4.2.
3.2.1. Experimental and theoretical determination of the rate coefficient of the reaction O + OH − → O2 + H
The study of this reaction has attracted considerable experimental attention (Howard & Smith 1980, 1981; Lewis & Watson 1980; Brune et al. 1983; Smith & Stewart 1994; Robertson & Smith 2002, 2006; Carty et al. 2006), and there have also been a large number of theoretical studies using a variety of methods (Harding et al. 2000; Troe & Ushakov 2001; Xu et al. 2007; Lin et al. 2008; Lique et al. 2009; Quéméner et al. 2009; Maergoiz et al. 2004; Jorfi et al. 2009; Li et al. 2010). The experimental rate constant is well determined between 140 and 300 K decreasing from 7 × 10-11 cm3 molecule-1 s-1 at 140 K to 3 × 10-11 cm3 molecule-1 s-1 at 300 K. Between 40 and 140 K, the reaction has been studied in a CRESU (Cinétique de Réaction en Ecoulement Supersonique Uniforme) apparatus (Carty et al. 2006) leading to a value of around 3.5(± 1.0) × 10-11 cm3 molecule-1 s-1 which however has large uncertainties. Quasi-classical trajectory calculations give good agreement with experiment between 300 K and 3000 K (Troe & Ushakov 2001) and between 40 K and 140 K (Jorfi et al. 2008) but the relatively good agreement at low temperature may be fortuitous. The reaction, which proceeds through a relatively long-lived HO2 complex, should be amenable to a statistical treatment and the statistical adiabatic channel model should be appropriate (Harding et al. 2000; Troe & Ushakov 2001) but has to deal with dynamical barriers. Surface hopping forward and backward between adiabatic channel potentials on several electronic states allows the system to avoid the dynamical bottleneck to some extent leading to a marked increase in the rate constant around 50 K. The rate constant calculated by this method (Harding et al. 2000) may be considered as an upper value. Time-dependent wave packet methods are unsuitable for the low temperature regime leading to an unreliably low rate that is constant at low temperature (Xu et al. 2007; Lin et al. 2008). Time-independent quantum mechanical calculations, supposed to be the more accurate at low temperature, have been applied to this system leading to value around 4 × 10-11 cm3 molecule-1 s-1 at 10 K (Lique et al. 2009; Quéméner et al. 2009). However, they neglect spin orbit coupling and electronic fine structure of O and OH, as well as surface hopping dynamics between the ground and excited potentials at large O-OH distances. Among these effects, surface hopping dynamics is suspected to be important at low temperature (Maergoiz et al. 2004; Li et al. 2010) and the rate constant may be as high as 8 × 10-11 cm3 molecule-1 s-1 at 10 K. Taking into account the various calculations and measurements, the KIDA experts recommend that the rate coefficient at 10 K is between 2 × 10-11 and 8 × 10-11 cm3 molecule-1 s-1.
3.3. Elemental abundances
Elemental abundances (/H).
For each element, we define the elemental abundance as the ratio of the number of nuclei both in the gas and on the dust grains to the total number of H nuclei. This excludes the nuclei locked in the refractory part of the grains. With this definition, the elemental abundance would be the “gas phase elemental abundance” at high temperature, when all ices are sublimated. Since the amount of the oxygen depletion is only based on indirect measurements, we consider four values for the oxygen elemental abundance: 1) 3.3 × 10-4: a “low depletion” case, using the gas-phase abundance observed in the diffuse cloud ζ Oph, frequently used as a reference derived by Jenkins (2009) (this is also the mean abundance observed by Meyer et al. 1998); 2) 2.4 × 10-4: an “intermediate depletion”; 3) 1.8 × 10-4, following Whittet (2010): this value is very close to the “low metal” case; 4) 1.4 × 10-4: a “high depletion” case determined from Fig. 16 of Jenkins (2009) with an extrapolation to a density of 2 × 104 cm-3.
For simplicity, we use the “low metal” elemental abundances for the other elements except for He, C, and N. Carbon is in a similar situation as oxygen in the sense that no additional depletion is usually assumed, although Jenkins (2009) showed that it does exist the trend being much weaker and less robust. From the observations, Jenkins (2009) determined an atomic carbon abundance of 1.7 × 10-4 in ζ Oph. We use this value, as the extrapolation to a density of 2 × 104 cm-3 using Jenkins’ relations would only reduce the carbon abundance to 1.2 × 10-4. The C/O elemental ratio corresponding to our four models are 0.5, 0.7, 0.9, and 1.2. Nitrogen is the only element that was not found by Jenkins (2009) to deplete with density. Although it may be an observational bias as argued by Jenkins, we use the gas-phase abundance observed in ζ Oph of 6.2 × 10-5. The helium abundance is assumed to be 0.09 (see Wakelam & Herbst 2008, for discussion). All elemental abundances are listed in Table 1.
4. Results of the chemical simulations
4.1. Computed abundances
Figure 1 shows the computed abundances of O2 in the gas phase as a function of time for the four elemental abundances of oxygen described in Sect. 3.3 (left panel) and as a function of the oxygen elemental abundance for different times (right panel). A decrease in the oxygen elemental abundance produces a general decrease in the O2 abundances at any time, although the effect is stronger between 3 × 105 and 2 × 106 yr. Assuming that O2 has been searched for in a variety of clouds with ages across this range, the non-detection of O2 with abundances above 10-7 compared to total hydrogen would require the elemental abundance of oxygen to be smaller than 1.6 × 10-4.
 |
Fig. 1 O2 abundance (/H) as a function of time for four values of oxygen depletion (top) and as a function of oxygen elemental abundance for four ages (bottom). |
 |
Fig. 2 Gas-phase abundances relative to total hydrogen of a selection of species as a function of time computed for two different oxygen elemental abundances: 3.3 × 10-4 (grey line) and 1.4 × 10-4 (black line). |
Figure 2 shows the computed abundances of a selection of gas phase species as a function of time, for the extreme “low” and “high depletion” cases. As expected, the abundances of carbon-rich species (such as cyanopolyynes) are higher in the “high oxygen depletion” case (higher C/O ratio), whereas the abundance of O-bearing species is lower. The various O-bearing species are however not influenced to the same extent. CO, OH, and H2O are changed only slightly. O2 and SO2 are lower by two orders of magnitude and more than one order of magnitude, respectively, at the peak abundance (~4 × 105 yr).
In our four cases, the elemental C/O ratio varies over a large range. Pure gas-phase chemical models would be very sensitive to these variations: for example, Wakelam et al. (2010a) show that the HC7N abundance can be modified by four orders of magnitude at 107 yr when C/O goes from 0.7 to 1. In our present study and at 107 yr, the HC7N abundance does not depend much on the different values of C/O that we adopted, as can be seen in Fig. 2. When the C/O ratio increases, this occurs because the available C is mainly used to form C-rich molecules, e.g. CnHm, on the grains (see also Garrod et al. 2007). However, the modeled abundances are not only sensitive to the elemental C/O ratio but also to the elemental abundances themselves. Increasing both elemental abundances by a factor of two would for instance increase the CO gas-phase abundance by two orders of magnitude at 5 × 106 yr in all the models, but the O2 abundance at the peak (~4 × 105 yr) remains unchanged. In this dense cloud modeling, the CO abundance in the gas phase decreases after a few 105 because CO sticks onto grains and is then hydrogenated to form H2CO and CH3OH. When the C and O elemental abundances are increased, the gas phase CO abundance, and as a consequence the solid CO abundance, increases and takes longer to decrease its abundance. If we allow the system to evolve up to 108 yr, the CO gas phase abundance is only two times larger than the one obtained with our previous elemental abundances. Decreasing C and O elemental abundance by a factor of two would slightly decrease the O2 abundance.
We started our chemistry assuming that all species were initially atomic, except for hydrogen. If we instead assume that all carbon is initially in carbon monoxide, the results change drastically before 105 years. Carbon chains are obviously the most affected species. Using these initial abundances increases the time taken to form the carbon-bearing molecules observed in dense clouds by a factor of between 102 and 106 depending on the molecule.
4.2. Effects of the new rate coefficients
Among the updates of the network, the new values for the rate coefficients and branching ratios of the reactions O + CnH (n = 2, 3), O + C2, C+ + H2 and particularly O + H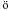 (see also Wakelam et al. 2010b) and N + CN have changed the model sensitivity to the oxygen elemental abundance. In the “high depletion” case, the new rates result in smaller O2 abundances (4 × 10-8 instead of 3.3 × 10-7 at the abundance peak near ~4 × 105 yr), while this abundance is not affected in the “low depletion” case. The O2 abundance is also unexpectedly sensitive to the reaction N + CN. Decreasing the N + CN rate coefficient by a factor 3 increases the CN abundance at 3 × 105 yr by a factor of 2.3, and the reaction CN + O2 becomes an efficient destruction channel reducing the O2 abundance (see also discussion about CN + O2 reaction in Sect. 4.3). This shows that the chemistry of a relatively simple molecule can be difficult to predict, and that unexpected reactions can be important. These results underline the importance of using accurate rate coefficients in all circumstances. Note that using the upper limit instead of the lower one for O + OH rate coefficient increases the abundance peak of O2 by a factor two in the high depletion case, and the maximum elemental abundance of oxygen required to reproduce O2 abundance in dark cloud is changed to 1.5 × 10-4.
(see also Wakelam et al. 2010b) and N + CN have changed the model sensitivity to the oxygen elemental abundance. In the “high depletion” case, the new rates result in smaller O2 abundances (4 × 10-8 instead of 3.3 × 10-7 at the abundance peak near ~4 × 105 yr), while this abundance is not affected in the “low depletion” case. The O2 abundance is also unexpectedly sensitive to the reaction N + CN. Decreasing the N + CN rate coefficient by a factor 3 increases the CN abundance at 3 × 105 yr by a factor of 2.3, and the reaction CN + O2 becomes an efficient destruction channel reducing the O2 abundance (see also discussion about CN + O2 reaction in Sect. 4.3). This shows that the chemistry of a relatively simple molecule can be difficult to predict, and that unexpected reactions can be important. These results underline the importance of using accurate rate coefficients in all circumstances. Note that using the upper limit instead of the lower one for O + OH rate coefficient increases the abundance peak of O2 by a factor two in the high depletion case, and the maximum elemental abundance of oxygen required to reproduce O2 abundance in dark cloud is changed to 1.5 × 10-4.
4.3. Agreement with observations in dark clouds
 |
Fig. 3 Parameter D as a function of time for TMC-1CP (black lines) and L134N (grey lines) and three different oxygen elemental abundances: 3.3 × 10-4 (dotted line), 2.4 × 10-4 (dashed line), and 1.4 × 10-4 (solid line). |
We compared the abundances predicted by our model for different depletion cases (“high”, “intermediate” and “low”) with observations of gas-phase molecules in two cold clouds TMC-1CP (the so-called cyanopolyyne peak) and L134N (N) (north peak) to check for the effects of oxygen depletion. The observed abundances of some relevant species are listed in Table 2. A more complete list can be found in Garrod et al. (2007). The observational limits on the O2 abundance relative to total hydrogen in TMC-1CP and L134N are 3.85 × 10-8 and 8.5 × 10-8 (see Pagani et al. 2003), respectively, and they are reproduced by our models. SO2 is less efficiently produced in the gas-phase, which is in closer agreement with the observations, whereas CN is now overproduced (CN abundance relative to total hydrogen in TMC-1CP and L134N (N) are, respectively, 2.5 × 10-9, see Smith et al. 2004; and 4.1 × 10-10, see Ohishi et al. 1992). Because of the importance of CN to the destruction of O2 underlined in Sect. 4.2, this excess of CN may artificially destroy O2. However, reducing the rate coefficient of CN + O2 by a factor of 10 (to simulate a lower abundance of CN) does not affect the O2 abundance, because other destruction channels take over, in particular C + O2 − → CO + O. Raising the rate coefficient of CN + O2 would however continue to lower O2 abundance.
For a more global view, we define a pseudo-distance D between the models and the observations 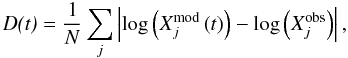 (1)where
(1)where 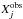 is the observed abundance of species j and
is the observed abundance of species j and 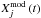 the abundance of species j computed by the model at the time t, and N is the number of observed species, i.e., 53 in TMC-1CP and 42 in L134N. The smaller the value of D, the closer the agreement. D is displayed for our three main models in Fig. 3. The O2 abundance predicted by our model for the “low”, “intermediate” and “high” depletion cases at the time of maximum agreement are, respectively, 4 × 10-9, 3 × 10-9, and 8 × 10-9 for TMC-1CP and 3 × 10-8, 7 × 10-8, and 10-9 for L134N. The elemental O abundance does not significantly affect the agreement in the case of L134N. However, as expected, the agreement in TMC-1CP is closer in the “high” oxygen depletion case between 2 × 105 and 2 × 106 years. This closer agreement comes from the higher abundance of cyanopolyynes during this range of time.
the abundance of species j computed by the model at the time t, and N is the number of observed species, i.e., 53 in TMC-1CP and 42 in L134N. The smaller the value of D, the closer the agreement. D is displayed for our three main models in Fig. 3. The O2 abundance predicted by our model for the “low”, “intermediate” and “high” depletion cases at the time of maximum agreement are, respectively, 4 × 10-9, 3 × 10-9, and 8 × 10-9 for TMC-1CP and 3 × 10-8, 7 × 10-8, and 10-9 for L134N. The elemental O abundance does not significantly affect the agreement in the case of L134N. However, as expected, the agreement in TMC-1CP is closer in the “high” oxygen depletion case between 2 × 105 and 2 × 106 years. This closer agreement comes from the higher abundance of cyanopolyynes during this range of time.
We must keep in mind that the data obtained by observations indicate that the average abundance along the line of sight, and the abundances of species varies very considerably from the cloud surface to the cloud interior where the photodesorption is less important, as pointed out by Hollenbach et al. (2009).
5. Conclusions
Our study has demonstrated that the low abundance of O2 in dark clouds can be explained by gas-grain chemical models based on the fresh insight into elemental oxygen depletion obtained by Jenkins (2009) and Whittet (2010). High oxygen depletion also improves the overall agreement between models and observations for other molecules. We have found that gas-grain models are less critically sensitive to the C/O ratio than pure gas chemistry. This is fortunate because the elemental C depletion remains poorly constrained by current observational studies. This limited sensitivity makes our conclusion more robust.
Besides this important result about the impact of the O depletion on the O2 abundance, our study has also revealed that unexpected reactions may become very significant when the elemental abundances are modified. The example of the N + CN reaction is notable in this respect. This may have consequences for models using limited reaction networks: while they may be valid over a limited range of input parameters (and for a limited number of predicted species), they should not be utilized in other conditions without re-assessing their performance.
Acknowledgments
This research was partially funded by the program PCMI from CNRS/INSU. U.H. is funded by a grant from the french “Région Aquitaine”. The authors thank Anne Dutrey for helpful discussions. We are grateful to Marcelino Agúndez for helpful comments on the manuscript. The authors also thank the referee for making this paper clearer and more useful to the reader.
References
- Bergin, E. A., Melnick, G. J., Stauffer, J. R., et al. 2000, ApJ, 539, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Brune, W. H., Schwab, J. J., & Anderson, J. G. 1983, J. Phys. Chem., 87, 4503 [CrossRef] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2004, ApJ, 613, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Carty, D., Goddard, A., Kahler, S. P. K., Sims, I. R., & Smith, I. W. M. 2006, J. Phys. Chem. A, 110, 3101 [CrossRef] [PubMed] [Google Scholar]
- Dickens, J. E., Irvine, W. M., Snell, R. L., et al. 2000, ApJ, 542, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1990, in The Evolution of the Interstellar Medium, ed. L. Blitz, ASP Conf. Ser., 12, 193 [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Melnick, G. J., Bergin, E. A., et al. 2000, ApJ, 539, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Graedel, T. E., Langer, W. D., & Frerking, M. A. 1982, ApJS, 48, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, L. B., Maergoiz, A. I., Troe, J., & Ushakov, V. G. 2000, J. Chem. Phys., 113, 11019 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Hersant, F., Wakelam, V., Dutrey, A., Guilloteau, S., & Herbst, E. 2009, A&A, 493, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollenbach, D., Kaufman, M. J., Bergin, E. A., & Melnick, G. J. 2009, ApJ, 690, 1497 [CrossRef] [Google Scholar]
- Howard, M. J., & Smith, I. W. M. 1980, Chem. Phys. Lett., 69, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, M. J., & Smith, I. W. M. 1981, in J. Chem. Soc., Faraday Transactions 2, 77, 997 [CrossRef] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, M. J., Bilodeau, R. C., Safvan, C. P., et al. 2000, ApJ, 543, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Jorfi, M., Honvault, P., Halvick, P., Lin, S. Y., & Guo, H. 2008, Chem. Phys. Lett., 462, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Jorfi, M., Honvault, P., Bargueño, P., et al. 2009, J. Chem. Phys., 130, 184301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Larsson, B., Liseau, R., Pagani, L., et al. 2007, A&A, 466, 999 [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., Roueff, E., & Schilke, P. 1993, ApJ, 416, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, R. S., & Watson, R. T. 1980, J. Phys. Chem., 84, 3495 [CrossRef] [Google Scholar]
- Li, A., Xie, D., Dawes, R., et al. 2010, J. Chem. Phys., 133, 144306 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lin, S. Y., Guo, H., Honvault, P., Xu, C., & Xie, D. 2008, J. Chem. Phys., 128, 014303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lique, F., Jorfi, M., Honvault, P., et al. 2009, J. Chem. Phys., 131, 221104 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Liseau, R., Larsson, B., Bergman, P., et al. 2010, A&A, 510, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maergoiz, A. I., Nikitin, E. E., Troe, J., & Ushakov, V. 2004, in NATO ASI Series, ed. G. Lendvay, 21 [Google Scholar]
- Meyer, D. M., Jura, M., & Cardelli, J. A. 1998, ApJ, 493, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ohishi, M., & Kaifu, N. 1998, in Chemistry and Physics of Molecules and Grains in Space, Faraday Discussions, 109, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Ohishi, M., Irvine, W. M., & Kaifu, N. 1992, in Astrochemistry of Cosmic Phenomena, IAU Symp., 150, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Olofsson, A. O. H., Bergman, P., et al. 2003, A&A, 402, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quan, D., Herbst, E., Millar, T. J., et al. 2008, ApJ, 681, 1318 [NASA ADS] [CrossRef] [Google Scholar]
- Quéméner, G., Balakrishnan, N., & Kendrick, B. K. 2009, Phys. Rev. A, 79, 022703 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, H., & Herbst, E. 2002, A&A, 395, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, R., & Smith, G. P. 2002, Chem. Phys. Lett., 358, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, R., & Smith, G. P. 2006, J. Phys. Chem. A, 110, 6673 [CrossRef] [PubMed] [Google Scholar]
- Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, I. W. M., & Stewart, D. W. A. 1994, in J. Chem. Soc., Faraday Transactions, 90, 3221 [Google Scholar]
- Smith, I. W. M., Herbst, E., & Chang, Q. 2004, MNRAS, 350, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Snell, R. L., Howe, J. E., Ashby, M. L. N., et al. 2000, ApJ, 539, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Troe, J., & Ushakov, V. G. 2001, J. Chem. Phys., 115, 3621 [NASA ADS] [CrossRef] [Google Scholar]
- Viti, S., Roueff, E., Hartquist, T. W., Pineau des Forêts, G., & Williams, D. A. 2001, A&A, 370, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V., & Henning, T. 2010, A&A, 517, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V. 2010, in SF2A-2010: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, ed. S. Boissier, M. Heydari-Malayeri, R. Samadi, & D. Valls-Gabaud , 239 [Google Scholar]
- Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Herbst, E., & Selsis, F. 2006a, A&A, 451, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., Selsis, F., & Massacrier, G. 2006b, A&A, 459, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., Le Bourlot, J., et al. 2010a, A&A, 517, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010b, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B. 2010, ApJ, 710, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C., Xie, D., Honvault, P., Lin, S. Y., & Guo, H. 2007, J. Chem. Phys., 127, 024304 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ziurys, L. M., Friberg, P., & Irvine, W. M. 1989, ApJ, 343, 201 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 O2 abundance (/H) as a function of time for four values of oxygen depletion (top) and as a function of oxygen elemental abundance for four ages (bottom). |
| In the text | |
 |
Fig. 2 Gas-phase abundances relative to total hydrogen of a selection of species as a function of time computed for two different oxygen elemental abundances: 3.3 × 10-4 (grey line) and 1.4 × 10-4 (black line). |
| In the text | |
 |
Fig. 3 Parameter D as a function of time for TMC-1CP (black lines) and L134N (grey lines) and three different oxygen elemental abundances: 3.3 × 10-4 (dotted line), 2.4 × 10-4 (dashed line), and 1.4 × 10-4 (solid line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


