| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 5 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201016281 | |
| Published online | 17 May 2011 | |
Research Note
The possibility of determining open-cluster parameters from BVRI photometry
UNIFEI, DFQ – Instituto de Ciências Exatas, Universidade Federal de Itajubá, Itajubá MG, Brazil
e-mail: hektor.monteiro@gmail.com
Received: 7 December 2010
Accepted: 7 March 2011
In the last decades we witnessed an increase in studies of open clusters of the Galaxy, especially because of the good determination for a wide range of values of parameters such as age, distance, reddening, and proper motion. The reliable determination of the parameters strongly depends on the photometry available and especially on the U filter, which is used to obtain the color excess E(B − V) through the color–color diagram (U − B) by (B − V) by fitting a zero age main-sequence. Owing to the difficulty of performing photometry in the U band, many authors have tried to obtain E(B − V) without the filter. But because of the near linearity of the color–color diagrams that use the other bands, combined with the fact that most fitting procedures are highly subjective (many done “by eye”), the reliability of those results has always been questioned. Our group has recently developed, a tool that performs isochrone fitting in open-cluster photometric data with a global optimization algorithm, which removes the need to visually perform the fits and thus removes most of the related subjectivity. Here we apply our method to a set of synthetic clusters and two observed open clusters (Trumpler 1 and Melotte 105) using only photometry for the BVRI bands. Our results show that, considering the cluster structural variance caused only by photometric and Poisson sampling errors, our method is able to recover the synthetic cluster parameters with errors of less than 10% for a wide range of ages, distances, and reddening, which clearly demonstrates its potential. The results obtained for Trumpler 1 and Melotte 105 also agree well with previous literature values.
Key words: open clusters and associations: general / methods: statistical / methods: observational / techniques: photometric
© ESO, 2011
1. Introduction
Our research group has a particular interest in using open clusters in our studies of the spiral structure of our Galaxy. Some interesting results were obtained with data of these objects that are compiled in our catalog (Dias et al. 2002): the rotation speed of the spiral pattern as 25 ± 1 km-1 s-1 kpc-1 and the co-rotation radius at 1.06 ± 0.08 × the solar Galactocentric distance (Dias & Lépine 2005) and 4 determined the epicyclic frequency to be 43 ± 5 km-1 s-1 kpc-1 at the solar radius.
In this kind of study and in many others that involve open clusters it is crucial to accurately determine the fundamental parameters (distance, reddening, and age) of the objects. Traditionally this is done using the color-magnitude diagrams via the should read main sequence fitting (MSF) technique, which in the majority of cases is fit to the data by visual inspection. The work of 7 (hereafter PN06) indicates that the usual method applied up to now can determine distances of open clusters with absolute errors of less than 20% (see all details in the cited paper).
From the observational point of view, the determination of fundamental parameters of open clusters requires accurate photometry (errors lower than 0.03 in magnitude and lower than 0.05 in color index), deep photometry (mainly for objects not previously studied) and also seems to require data in the U-filter. The U-filter in principle allows a better determination of the color excess and therefore leads to an accurate determination of the distance modulus via MSF. The determination of the color excess toward the cluster is performed based on the observed photometric data, typically by visual MSF of the (B − V) vs. (U − B) diagram. Results on determining the color excess without the use of the U-filter are unreliable if done in the usual manner by visual fits because of the near linearity of the color–color diagrams and the subjectivity of the analysis.
We have addressed the subjectivity of the isochrone fits in 6 (hereafter MDC10), where we developed a global optimization tool using the cross-entropy optimization algorithm (CE) to automatically fit open cluster UBV photometric data with well defined criteria (see paper for details). We showed that the method was robust and the results obtained for 10 open clusters agreed well with previous studies found in the literature. Although the work used only UBV photometry and the usual sequence to fit isochrones (determine E(B − V) and then distance and age), the results obtained with the global optimization indicated that it might be possible to address the color excess determination without the use of the U-filter. The advantages of such a procedure are clear, given that the U-filter is possibly one of the most problematic ones to get good data for, which typically requires longer exposure times.
In this work we investigate the possibility of determining open cluster fundamental parameters from BVRI photometry alone. In Sect. 2 we briefly describe the global optimization method developed in MDC10 and the adaptations made for the present problem. In Sect. 3 we describe benchmark tests using a set of synthetic open clusters generated with known parameters. In Sect. 4 we apply the method to the well studied open clusters Trumpler 1 and and Melotte 105 and discuss the results. In Sect. 5 we present our conclusions.
2. The cross-entropy optimization method
The CE procedure provides a simple adaptive way of estimating the optimal model parameters. Basically, the CE method involves an iterative procedure where each iteration consists of:
-
1.
Random generation of the initial parameter sample, respectingpre-defined criteria;
-
2.
Selection of the best candidates based on some mathematical criteria;
-
3.
Random generation of updated parameter samples from the previous best candidates to be evaluated in the next iteration;
-
4.
Optimization process repeats steps (ii) and (iii) until a pre-specified stopping criterion is fulfilled.
In MDC10 we fully describe the algorithm and the fitting method applied to open clusters and we refer the reader to that work and references therein for more details. In short, the algorithm generates a set of possible isochrone solutions (simulated open clusters) given a pre-defined initial mass function, binary fraction, and metallicity. Each generated solution is then compared to the observed data through an objective function. The best solutions are selected, a new set of solutions is generated from them and the process iterated until convergence. In the present work we maintain the complete structure of the previous algorithm discussed in detail in MDC10, changing only the objective function to use the BVRI data instead of only UBV.
In the case of isochrone fitting, the objective function used is the likelihood of the data (in the present case BVRI photometry) for a given model isochrone, which is obtained from the product of probabilities of the m stars observed and is given by: 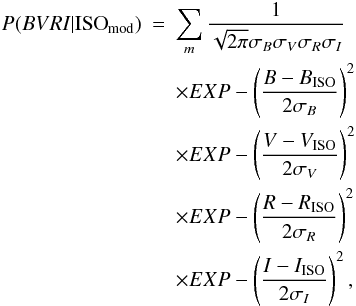 (1)\\where B, V, R, and I are the observed magnitudes and σB, σV, σR, and σI are the photometric uncertainties in each filter. Here ISOmod designates the model isochrone for a set of parameters (E(B − V), distance and age) and BISO, VISO, RISO, and IISO are the model magnitudes for each point generated from the model.
(1)\\where B, V, R, and I are the observed magnitudes and σB, σV, σR, and σI are the photometric uncertainties in each filter. Here ISOmod designates the model isochrone for a set of parameters (E(B − V), distance and age) and BISO, VISO, RISO, and IISO are the model magnitudes for each point generated from the model. 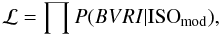 (2)\\where ℒ is the likelihood obtained in the usual manner.
(2)\\where ℒ is the likelihood obtained in the usual manner.
As in MDC10, the tabulated isochrones are taken from 3 and 5 and are specified by four parameters, namely, age, distance, extinction constant and metallicity. In the isochrone fitting we defined the parameter space as follows:
-
1.
Age: from log (age) = 6.60 to log (age) = 10.15;
-
2.
distance: from 1 to 10 000 parsecs;
-
3.
E(B − V): from 0.0 to 3.0.
To simplify the analysis we kept the metallicity constant at the solar value. This should have no major impact on the evaluation of the capability of the method to determine the fundamental parameters because the changes due to metallicity are relatively small when compared to the other parameters.
3. Synthetic clusters
To test the capability of recovering fundamental parameters using the CE method we constructed a series of synthetic open clusters. The generated clusters were chosen to be representative of clusters present in the catalog (2) and were generated from the isochrone tables of 3 and 5, which are the same as those used in the fitting algorithm.
We also generated clusters with distinct numbers of stars from low to high density to evaluate the capacity of the method to retrieve the parameters in unfavorable conditions.
All clusters were generated adopting solar metallicities, sampled from a Salpeter IMF and with a 50% binary population at a distance of 1000 pc, E(B − V) = 0.40, 3σphot = 0.8% and limiting mV magnitude of 18. All fits were executed 20 times to perform an error analisis via bootstrap re-sampling.
We did not include simulated contamination from field stars, but this evaluation is already under way. But as we show in MDC10, the filtering method we developed removed a good part of the contamination and we expect that the main effect would likely be an increase in the estimated uncertainty for the parameters.
The results obtained for the synthetic clusters fitted with our method and BVRI photometry only are summarized in Figs. 1 and 2 where the relative errors for fits as a function of synthetic cluster age and relative errors for fits as a function of number of generated stars are shown. The distance and E(B − V) were not varied in the results presented in Figs. 1 and 2 because the major changes were caused by the variation in age and number of stars. Varying the distance only affects the photometric errors, which we assumed here to be some percentage of the observed magnitudes, and so would only increase the final uncertainty. In Fig. 2 the age was also fixed at log (age) = 8.0.
To check the reliability of the method under distinct reddening values, we performed a set of tests with synthetic clusters generated with E(B − V) varying from 0.3 to 3.0, covering the observed parameter range, and with log (age) = 8.70 yr at a distance of 2100 pc. We note that an increase in the magnitude limit to mV = 22 was necessary for the synthetic clusters with E(B − V) > 2 so that the main sequence could be minimally sampled. The results presented in Fig. 3 indicate that the uncertainty of the distance determination tends to increase with increasing E(B − V), which is to be expected. Interestingly, the uncertainties obtained for the various reddening values studied were essentially constant around 0.03, which shows up as declining relative errors in Fig. 2.
 |
Fig. 1 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only as a function of synthetic cluster age. The synthetic clusters have fixed E(B − V) = 0.4, 3σphot = 0.8% and are at a distance of 1000 pc. |
 |
Fig. 2 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only as a function of number of generated stars. The synthetic clusters have fixed E(B − V) = 0.4, 3σphot = 0.8%, log (age) = 8.0 and are at a distance of 1000 pc. |
 |
Fig. 3 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only, as a function of number of generated E(B − V) values. The synthetic clusters have fixed log (age) = 8.70 yr at a distance of 2100 pc. |
We also tested the fitting method on a synthetic cluster generated with the same parameters as the one presented in Sect. 5.1 of MDC10, i.e., 400 stars with photometric error 3σphot = 1% sampled from an isochrone with log (age) = 8.70 yr, at a distance of 2100 pc, E(B − V) = 0.40 and Z = 0.019. The results obtained from the fitting algorithm were
-
log (age) = (8.73 ± 0.05) yr
-
distance = (2100 ± 70) pc
-
E(B − V) = (0.39 ± 0.03).
The results indicate that the method using only BVRI is capable of recovering the cluster parameters with about the same accuracy as the UBV method presented in MDC10. The precision is also about the same exept for the reddening, where the BVRI-fitted value shows larger uncertainty.
 |
Fig. 4 Final-fit results for Trumpler 1 overplotted on color-magnitude diagrams where the symbol sizes are proportional to the weight determined for each star as described in MDC10. |
4. Application to observed clusters
We applied this new approach of fitting isochrones to a couple of well-studied open clusters. The selected clusters were Trumpler 1 and Melotte 105, which have observational data in the BVRI filters obtained by 9 (hereafter YS02) and Sagar et al. (2001) (hereafter SMB01) respectively. The main reason for choosing these particular clusters is that they are the only ones that have BVRI data and were also studied in our previous work (MDC10), where we applied the CE method using UBV photometry only, following the traditional route of first determining the reddening through the (U − B) versus (B − V) diagram and then fitting the theoretical isochrones.
The results obtained for Trumpler 1 and Melotte 105 using our fitting method and the BVRI photometry agrees very well with the results obtained by YS02 and SMB01 and the results from our previous work using only UBV photometry. The values also agree with those of PN06. In Fig. 4 we show the final-fit results (isochrones) for Trumpler 1 and in Fig. 5 for Melotte 105, overplotted on color-magnitude diagrams where the symbol sizes are proportional to the weight determined for each star based on the filtering scheme described in MDC10.
For Trumpler 1 the results obtained from our BVRI fit agrees well with the values obtained by YS02 (see Table 1). Some small but significant differences are found when we consider the results of PN06 and MDC10, but these are likely due to weights given to the bright stars as discussed in MDC10. The weight of the bright stars are likely the main cause for the age differences. Notice, however, that using the BVRI only we obtain almost the same E(B − V) as in the fit made with the (U − B) versus (B − V) diagram.
For Melotte 105 we find a similar situation where we found small significant differences in E(B − V) and distance when comparing our results with those of SMB01. The differences are again likely due to distinct weights given to particular stars. The weight might be particularly relevant when comparing the results of MDC10, where the red giants received a lower weight compared to this work, which could be the reason for the lower distance encountered in that work.
5. Conclusions
We investigated the possibility of fitting theoretical tabulated isochrones to open cluster BVRI photometry with a global optimization method developed in MDC10. In the context of upcoming ground-based telescopes and space missions that will produce massive amounts of data, this tool, wich additionally has the possibility of full automation, is of great value.
CE fit and literature results for Trumpler 1.
CE fit and literature results for Melotte 105.
The results obtained with synthetic open clusters that are generated with parameters that cover typical values found in the literature show that even without the use of the U-filter, fundamental parameters can be determined with a relative precision of about 10% or better in most cases in the studied parameter space, also with an accuracy similar to the method described in MDC10 using UBV photometry only. In particular we showed that the reddening can be determined for a wide range of cluster ages, despite the lack of visual structure in the color–color diagrams of the clusters. Even when considering objetcs with few stars the method was able to recover the original parameters within the uncertainties, showing some systematic behavior for clusters with a low number of stars as shown in Fig. 2.
It is important to point out that the relative uncertainties discussed previously are to be taken as lower limits to the real expected uncertainties that are attainable with real data. The errors reported are only due to the adopted error in the photometry and Poisson statistics that arise from drawing a finite number of stars from model isochrones. Real clusters will have structural variations because of binary fraction or chemical composition among many other factors, will affect the final uncertainty of the method. Because it is difficult to quantify the nature of these
factors and their effect on the final uncertainty, a definitive error analysis should be carried out in a case-by-case basis.
Applying the method to two observed clusters also studied with our optimization method and UBV photometry (see MDC10 for details) showed that the use of BVRI filters only also produced consistent results. The results agree well with those obtained by previous works, in particular when considering the results of PN06, where the authors included a large number of independent literature determinations. Assuming that the results of PN06 are the best estimates of the real cluster parameters, we can estimate a better value of the final uncertainty of the method for these objetcs. For Trumpler 1 the highest relative uncertainty comes from the distance and is about 15%. For Mellote 105 the largest relative error is due to the reddening being approximately 13%. These values are likely more realistic estimates of the real uncertainty of the method for these two clusters.
Our results show that it is indeed possible to reliably determine open-cluster fundamental parameters from BVRI photometry only despite the lack of visual features in the color–color diagrams.
Acknowledgments
H. Monteiro would like to thank CNPq (grant number 470135/2010-7). W. S. Dias thanks CNPq (grant number 302762/2007-8) and FAPEMIG (process number APQ-00090-08). We also thank the referee Dr. Bailer-Jones for extremely useful comments that greatly improved the paper.
References
- Dias, W. S., & Lépine, J. R. D. 2005, ApJ, 629, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Dias, W. S., Alessi, B. S., Moitinho, A., & Lépine, J. R. D. 2002, A&A 389, 871 [Google Scholar]
- Girardi, L., Bressan, A., Bertelli, C., & Chiosi, C. 2000, A&AS, 141, 371 [Google Scholar]
- Lépine, J. R. D., Dias, W. S., & Mishurov, Y. 2008, MNRAS, 386, 2081 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monteiro, H., Dias, W. S., & Caetano, T. C. 2010, A&A, 516, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Sagar, R., Munari, U., & de Boer, K. S. 2001, MNRAS, 327, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K. S., & Sagar, R. 2002, MNRAS, 337, 133 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only as a function of synthetic cluster age. The synthetic clusters have fixed E(B − V) = 0.4, 3σphot = 0.8% and are at a distance of 1000 pc. |
| In the text | |
 |
Fig. 2 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only as a function of number of generated stars. The synthetic clusters have fixed E(B − V) = 0.4, 3σphot = 0.8%, log (age) = 8.0 and are at a distance of 1000 pc. |
| In the text | |
 |
Fig. 3 Relative errors for fits of the synthetic clusters fitted with our method and BVRI photometry only, as a function of number of generated E(B − V) values. The synthetic clusters have fixed log (age) = 8.70 yr at a distance of 2100 pc. |
| In the text | |
 |
Fig. 4 Final-fit results for Trumpler 1 overplotted on color-magnitude diagrams where the symbol sizes are proportional to the weight determined for each star as described in MDC10. |
| In the text | |
 |
Fig. 5 Same as Fig. 3 for Melotte 105. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


