| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201016093 | |
| Published online | 18 May 2011 | |
X-ray spectroscopy of MXB 1728–34 with XMM-Newton
1
Dipartimento di Fisica, Università degli Studi di Cagliari, SP Monserrato-Sestu, KM 0.7, 09042 Monserrato, Italy
e-mail: elise.egron@dsf.unica.it
2
Dipartimento di Scienze Fisiche ed Astronomiche, Università di Palermo, via Archirafi 36, 90123 Palermo, Italy
3
Dr. Karl Remeis-Sternwarte and Erlangen Centre for Astroparticle Physics, Friedrich-Alexander-Universität Erlangen-Nürnberg, Sternwartstraße 7, 96049 Bamberg, Germany
4 INAF – Osservatorio Astronomico di Cagliari, Poggio dei Pini, Strada 54, 09012 Capoterra (CA), Italy
Received: 6 November 2010
Accepted: 29 March 2011
We analyzed an XMM-Newton observation of the low-mass X-ray binary and atoll source MXB 1728–34. The source was in a low-luminosity state during the XMM-Newton observation, corresponding to a bolometric X-ray luminosity of 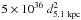 erg s-1. The 1–11 keV X-ray spectrum of the source, obtained combining data from all the five instruments on-board XMM-Newton, is well fitted by a Comptonized continuum. Evident residuals are present at 6−7 keV, which are ascribed to the presence of a broad iron emission line. This feature can be equally well fitted by a relativistically smeared line or by a self-consistent, relativistically smeared reflection model. Under the hypothesis that the iron line is produced by reflection from the inner accretion disk, we can infer important information on the physical parameters of the system, such as the inner disk radius, Rin = 25−100 km, and the inclination of the system, 44° < i < 60°.
erg s-1. The 1–11 keV X-ray spectrum of the source, obtained combining data from all the five instruments on-board XMM-Newton, is well fitted by a Comptonized continuum. Evident residuals are present at 6−7 keV, which are ascribed to the presence of a broad iron emission line. This feature can be equally well fitted by a relativistically smeared line or by a self-consistent, relativistically smeared reflection model. Under the hypothesis that the iron line is produced by reflection from the inner accretion disk, we can infer important information on the physical parameters of the system, such as the inner disk radius, Rin = 25−100 km, and the inclination of the system, 44° < i < 60°.
Key words: line: formation / line: identification / stars: neutron / stars: individual: MXB 1728 / 34 / X-rays: binaries / X-rays: general
© ESO, 2011
1. Introduction
Broad iron emission lines in the energy range 6.4−6.97 keV have been detected in high-energy resolution spectra of many X-ray sources containing a compact object, such as active galactic nuclei (e.g., Tanaka et al. 1995; Fabian et al. 2000) and X-ray binary systems containing a stellar-mass black hole (e.g., Miller et al. 2002; Miller 2007, for a review), or a weakly-magnetized neutron star (e.g., Bhattacharyya & Strohmayer 2007; Cackett et al. 2008; Di Salvo et al. 2009; Papitto et al. 2009; Iaria et al. 2009; D’Aì et al. 2009, and references therein). Identified with fluorescent Kα transition of iron at different ionization states, these lines are generally interpreted in terms of reflection of the central hard X-ray emission on the accretion disk (Fabian et al. 1989). Under this hypothesis, these lines are made broad and asymmetric by Doppler and relativistic effects induced by the Keplerian motion in the accretion disk near the compact object. The shape of the line is therefore an almost unique proxy of the innermost accretion disk close to the compact object (see Reynolds & Nowak 2003, for a review), and, in particular, on the inner disk radius. It also indicates the inclination angle of the system and the ionization state of the reflecting matter. Other reflection components like absorption edges and the Compton hump, which are usually observed between 20 − 40 keV, are also expected to result from photoelectric absorption and Compton scattering of the main Comptonization continuum on the accretion disk matter.
MXB 1728–34 (4U 1728 − 34, GX 354 − 0) is a low-mass X-ray binary containing a weakly magnetized accreting neutron star. The optical counterpart of this “galactic bulge” source has not been identified yet, owing to the high optical extinction toward the Galactic center. Discovered in 1976 with the Small Astronomy Satellite SAS-3 (Lewin et al. 1976; Hoffman et al. 1976), this source belongs to the so-called atoll class (Hasinger & van der Klis 1989) and shows frequent type-I X-ray bursts (e.g., Basinska et al. 1984) that are caused by thermonuclear flashes on the neutron star surface. Furthermore, double-peaked burst profiles have been observed (Hoffman et al. 1976), which are explained as caused by photospheric radius expansion during the burst (Taam 1982). These bursts have been used to constrain the distance to the source, between 4.1 and 5.1 kpc (Di Salvo et al. 2000; Galloway et al. 2003). The power spectrum of MXB 1728–34 displays kilohertz quasi-periodic oscillations (QPOs) in the persistent emission, and a nearly coherent oscillation at ~363 Hz during some bursts that has been interpreted as the spin frequency of the neutron star (Strohmayer et al. 1996).
Spectral analysis of MXB 1728–34 has been performed in the past using data from different satellites, such as Einstein (Grindlay & Hertz 1981), SAS-3 (Basinska et al. 1984), EXOSAT (White et al. 1986), SIGMA (Claret et al. 1994), ROSAT (Schulz 1999), and more recently using BeppoSAX (Piraino et al. 2000; Di Salvo et al. 2000), ASCA (Narita et al. 2001), RXTE, Chandra (D’Aì et al. 2006), INTEGRAL (Falanga et al. 2006), and XMM-Newton (Ng et al. 2010). The X-ray spectrum is generally composed of a soft and a hard component. The first one can be described by a blackbody or a multicolor disk blackbody, and may originate from the accretion disk. The second one can be fitted either by a Comptonized spectrum or a thermal bremsstrahlung. The Comptonized model seems to be more realistic, because it is efficiently produced by soft photons coming from the neutron star surface and/or boundary layer between the accretion disk and the neutron star and/or the accretion disk, which are up-scattered by electrons in a hot corona.
A broad emission line at 6.7 keV has been often detected in the X-ray spectra of this source and has been interpreted as emission from highly ionized iron (e.g., Di Salvo et al. 2000). The large width of the line suggests that it could come from an ionized inner accretion disk (Piraino et al. 2000), or alternatively it could be emitted from a strongly ionized corona. D’Aì et al. (2006) have proposed an alternative model to describe the iron line region using two absorption edges associated with ionized iron instead of a Gaussian line.
In this paper, we present a spectral analysis of high-energy resolution data taken by XMM-Newton on 2002 October 3 using all five X-ray instruments on-board this satellite. The EPIC-pn data have already been published by Ng et al. (2010), in a “catalog” paper dedicated to the study of the iron line in 16 neutron star LMXBs observed by XMM-Newton. Here we present a different approach to the analysis of these data, because we fitted for the first time the XMM-Newton data of MXB 1728-34 with a self-consistent modeling of the continuum emission and of the reflection component. We also tried several models to fit the iron line profile, such as diskline or relline, which are different from the models proposed by Ng et al. (2010) (Gaussian or Laor). All our results favor the relativistic nature of the line profile. We simultaneously fitted the spectra from all five X-ray instruments on-board XMM-Newton, while the pn data alone are analyzed by Ng et al. (2010).
2. Observation and data reduction
MXB 1728–34 was observed by XMM-Newton on 2002 October 3 for a total on-source observing time of 28 ks. The observation details for the instruments on-board XMM-Newton including the European Photon Imaging Camera (EPIC-pn, Struder et al. 2001), the MOS1 and MOS2 cameras (Turner et al. 2001), and the Reflection Grating Spectrometer (RGS1 and RGS2, den Herder et al. 2001) are presented in Table 1. The Optical Monitor (OM, Mason et al. 2001) was not active during this observation.
Instrument modes, filters and exposure times.
The 1.5−12 keV lightcurve of the All Sky Monitor (ASM) on-board RXTE extracted within ~450 days the XMM-Newton observation indicates that the source was not in a high activity state, because it shows an average count rate of about 3 counts/s.
 |
Fig. 1 RXTE/ASM lightcurve covering the 1.5−12 keV energy range. The vertical line indicates the time of the XMM-Newton observation performed on 2002 October 3rd. |
The XMM-Newton data were processed using the Science Analysis Software v. 9. The EPIC-pn camera was operated in timing mode to prevent photon pile-up. We created a calibrated photon event file using the pn processing tool epproc. Before extracting the spectra, we checked for contamination from background solar flares by producing a lightcurve in the energy range 10−12 keV. There were no high background periods during this observation. We used the task epfast to correct rate-dependent CTI effects in the event list. The source spectrum was extracted from a rectangular area, covering all pixels in the Y direction, and centered on the brightest RAWX column (RAWX = 38), with a width of 13 pixels around the source position (because 90% of the source counts up to 9 keV is encircled by 53 arcsec, and 1 pn pixel is equivalent to 4.1 arcsec). We selected only events with PATTERN ≤ 4 (single and double pixel events) and FLAG = 0 as a standard procedure to eliminate spurious events. We extracted the background away from the source (in the RAWX = 6−18). We also checked that pile-up did not affect the pn spectrum using the task epatplot. The total count rate registered by EPIC-pn CCDs was around 110 count/s, and was 64 count/s in the 2.4−11 keV range, slightly increasing (by 5%) during the observation.
The MOS data were also taken in timing mode and processed with the routine emproc to produce calibrated event list files. The source spectra were extracted from a rectangular box centered on RAWX = 320 (MOS1), and on RAWX = 308 (MOS2), selecting an area 30 pixels wide around the source position, and covering 722 pixels on the Y (PHA) direction. Only events corresponding to PATTERN ≤ 12 and FLAG = 0 were selected, corresponding to standard filters. The background spectra were extracted far from the source, centered on the column RAWX = 240. We checked that the MOS spectra were not affected by pile-up. The count rates were estimated to be around 30 counts/s for each MOS unit (20 counts/s considering 2.4−11 keV energy range).
Spectral channels of EPIC-pn and MOS spectra were rebinned to have three channels per energy resolution element and at least 25 counts per energy channel.
The two RGS were operated in the standard spectroscopy mode. The RGS data were processed using the rgsproc pipeline to produce calibrated event list files, spectra and response matrices. The count rates measured by RGS1 and RGS2 were around 2.5 and 3.5 counts/s, respectively. The RGS data were rebinned to provide a minimum of 25 counts per energy channel.
Best-fitting parameters of the continuum emission for the XMM-Newton pn, MOS1, MOS2, RGS1 and RGS2 spectra of MXB 1728–34.
3. Spectral analysis
Data were fitted by using Xspec (Arnaud 1996) v.12.5.1. All uncertainties are given at the 90% confidence level (Δχ2 = 2.706). We simultaneously fitted the broad band energy spectra of the source obtained from all five instruments. Considering the best calibration ranges of the different detectors, the data analysis from EPIC-pn, MOS1 and MOS2 cameras was restricted to the energy range 2.4−11 keV. This excluded the region around the detector Si K-edge (1.8 keV) and the mirror Au M-edge (2.3 keV) that could affect our analysis. This problem was already noticed for the EPIC-pn observations performed in timing mode, e.g., Boirin et al. (2005), Iaria et al. (2009), D’Aì et al. (2009), Papitto et al. (2009), D’Aì et al. (2010), Papitto et al. (2010). We only used the RGS1 and RGS2 data between 1−2 keV to constrain the softest band.
The different cross calibrations of the five instruments were taken into account by including normalizing factors in the model. These factors were fixed to 1 for pn and kept free for the other instruments.
We first fitted the continuum with a thermal Comptonized model using comptt (Titarchuk 1994), modified at low energy by the interstellar photoelectric absorption modeled by phabs using photoelectric cross-sections of Balucinska-Church & McCammon (1992) with a new He cross-section based on Yan et al. (1998) and standard abundances of Anders & Grevesse (1989). The χ2/degrees of freedom (d.o.f.) of the fit was large, 1732/903. We then tried to add a blackbody component (bbody model) to improve the fit. The addition of this component turned out to be statistically insignificant, thus we decided not to include the blackbody in our model. The values of the parameters of the continuum emission are reported in Table 2.
With respect to this continuum model, an excess was present in the residuals between 5.5 and 8 keV, probably indicating the presence of iron discrete features. The fit was improved by adding a broad iron emission line, modeled by a simple Gaussian line (Model 1 in Table 3), centered at 6.6 keV with the σ parameter frozen at 0.6 keV. Indeed, the width of the line was poorly constrained, but when we fitted the MOS data independently from the pn data, a significantly broadened line was detected, with a lower limit on σ of 0.55 keV. With the addition of the Gaussian, the fit gave a χ2/d.o.f. = 1489/901 (resulting in a significant improvement of the fit, with a Δχ2 = 243 for the addition of two parameters). We also tried to fit the line with a combination of two emission lines instead of a broad line, but the χ2 was worse (χ2/d.o.f. = 1531/901). So this broad line does not result from a blending of iron line at different ionization state.
Results of the fitting of MXB 1728–34 XMM-Newton data with different models.
We then tried to substitute the Gaussian at 6.6 keV with a diskline profile and obtained a slightly better result with a χ2/d.o.f. = 1463/899 . The data and the residuals obtained using this model are shown in Fig. 2. Owing to the large uncertainties on the outer radius of the disk and on the inclination of the system if they were let free, we froze the first one at 1000 Rg and the inclination at 60° (the source does not show any dip in its lightcurve, implying i < 60°). The improvement of the fit corresponds to Δχ2 = 26 for the addition of two parameters (the F-test gives a probability of chance improvement of about 10-4).
The F-test gives a reliable result in this case. In fact, according to Protassov et al. (2002), the conditions that have to be satisfied to use the F-test properly are: i) the two models that are being compared must be nested; ii) the null values of the additional parameters should not be on the boundary of the set of possible parameter values. A comparison between a Gaussian and a diskline satisfies these conditions, because a Gaussian profile can be obtained by a diskline (which is indeed given by a narrow, σ = 0, Gaussian multiplied by the kernel rdblur) and a good approximation of a Gaussian profile is obtained by a diskline for values of the parameters not at their boundary. However, to assess the significance of the relativistic line smearing on a statistical basis, we used another statistical method based on the posterior predictive p values described by Hurkett et al. (2008). For simplicity, we restricted our data to two instruments (pn and MOS2). These data were fitted with Model 1 and Model 2, respectively. We obtained an improvement of the fit corresponding to a Δχ2 of 18 for the addition of two parameters when we substituted Model 1 with Model 2. Then, we simulated 200 pn and MOS2 spectra according to Model 1, which were fitted in a second step using Model 2. The Δχ2 was registered for each simulation. Among the 200 simulations, we twice found a Δχ2 higher than 18. So the probability of chance improvement we gain from these simulations is 1%, which agrees with the 0.75% calculated by the F-test performed on the real data restricted to two instruments. Therefore, we can conclude that the diskline model is to be preferred because it gives a probability of chance improvement of the fit of about 10-4 using all instruments.
This model (Model 2 in Table 3) gives an estimate of the inner radius of the disk Rin ~ 18 Rg (Rg = GM/c2 is the gravitational radius). Fixing the inclination to lower values (i.e. i < 60°), worse χ2 were obtained with the other diskline parameters drifting toward lower Rin, higher rest-frame energies, and higher emissivity indices in absolute value. We searched for an absorption edge in the energy range 7 − 10 keV, but none was significantly detected.
To fit the iron line, we also used a new model for a relativistically distorted diskline, called relline1 (Dauser et al. 2010), which calculates line profiles taking into account all relativistic distortions in a disk around the compact object. We also fixed the outer radius of the disk and the inclination of the system to the same values used in the diskline model. The χ2/d.o.f. obtained in these conditions is 1464/899. The best-fit line parameters obtained in this way are perfectly consistent with those obtained using the diskline model. In particular this model (Model 3 in Table 3) estimates the inner radius of the disk to be Rin ~ 19 Rg.
We tried an alternative model for the iron features (see D’Aì et al. 2006) using two absorption edges (instead of an emission line), which are found at 7.50 keV (τ ~ 0.06) and 8.49 keV (τ ~ 0.06), associated to mildly and highly ionized iron, respectively. The χ2/d.o.f. for this fit is 1519/899 (which has to be compared to 1489/901 that we obtained fitting the iron line with a Gaussian (Model 1) or to 1463/899 that we obtained fitting the iron line with a diskline (Model 2)). Therefore this model (called Model 4 in Table 3) gives a worse fit of the iron features than the previous ones.
In order to test the consistency of the broad iron line with a reflection component, we fitted the data using reflion, a self-consistent reflection model including both the reflection continuum and the corresponding discrete features (Ross & Fabian 2005), in addition to a thermally Comptonized continuum modeled with nthcomp, by Zdziarski et al. (1996), and extended by Zycki et al. (1999), instead of comptt. The χ2/d.o.f. was 1555/901, without the inclusion of relativistic smearing. Because the iron line was found to be significantly broad in the previous models (Model 1, 2, and 3), we added the relativistic smearing using the rdblur component. The addition of this component to the model constitutes Model 5 in Table 3 and led to a χ2/d.o.f. = 1466/899. The decrease of the χ2 for the addition of the relativistic smearing was Δχ2 = 89 for the addition of two parameters (corresponding to an F-test probability of chance improvement of ~ 10-12). Assuming that iron has a solar abundance and freezing the emissivity betor index to − 2.8 (value obtained with the diskline model) and the ionization parameter ξ = LX / (nr2) to 660 (this parameter tends to take high values but is unstable during the fit, which is why we preferred to freeze it), where LX is the ionizing X-ray luminosity, n is the electron density in the reflector, and r the distance of the reflector to the emitting central source, the inner radius was estimated again to be 20 Rg and a lower limit to the inclination angle was found to be 44°. In Fig. 3 we plot the residuals obtained with this self-consistent reflection model in comparison with the continuum and the relline model using the EPIC-pn data.
The residuals found with respect to the different models described above do not show any evident systematic trend; the large χ2 could be due to mismatches in the cross-calibration between the different instruments (for more details, see the cross-calibration document available on the XMM-Newton webpage2) or to unresolved and unfitted features.
 |
Fig. 2 Top panel: EPIC-pn (black), MOS1 (red), MOS2 (green), RGS1 (cyan), RGS2 (blue) data points of MXB 1728–34 in the range 1 − 11 keV. Bottom panel: residuals (data-model) in unit of sigmas for the diskline model (Model 2 in Table 3). |
 |
Fig. 3 Top panel: EPIC-pn data points of MXB 1728–34 in the range 2.4−11 keV. Bottom panels: residuals (data-model) in unit of sigmas for the continuum model reported in Table 2, for Model 3 including a relativistic line (relline), and for Model 5 using a relativistic reflection component (reflion), respectively. Data were rebinned for graphical purposes. |
4. Discussion
We performed a spectral analysis of MXB 1728–34 observed by XMM-Newton on 2002 October 3 in the 1−11 keV energy range. The best-fit continuum model consists of an absorbed Comptonized component; the addition of a soft blackbody component does not improve the fit significantly. With respect to this continuum model, evident residuals are present at 6−8 keV, which can be fitted either by a relativistic line (such as diskline or relline) or by a self-consistent relativistic reflection model.
4.1. The continuum emission
The X-ray spectra of black-hole and neutron star in X-ray binaries are generally described by models that include a soft/thermal and a hard/Comptonized component; the electron temperature of the Comptonized component significantly decreases when the source transits from the hard to the soft state while its optical depth increases. For hard spectra, Comptonization is unsaturated and the spectrum may be approximated by a cutoff power-law. In soft states, Comptonization is saturated and the spectral shape can be approximated with a blackbody emission at the electron temperature. During the observation with XMM-Newton, MXB 1728–34 was in a low-luminosity state, and presumably an unsaturated Comptonization is the expected spectral shape. We chose a continuum that consists of an absorbed Comptonization model (comptt or nthComp) because these models gave the best fit to the broad-band (0.1 − 200 keV) BeppoSAX spectrum of MXB 1728–34 (Piraino et al. 2000; Di Salvo et al. 2000).
A different continuum was used by Ng et al. (2010) to fit the sample of neutron star LMXBs. Most of the observations, including MXB 1728–34, were well fitted by a blackbody plus a disk blackbody component, absorbed by neutral interstellar matter. The temperature of the blackbody and of the disk blackbody component had values between 1.5 and 2.8 keV and between 0.6 and 1.3 keV, respectively, except for MXB 1728–34, for which temperatures were found between 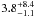 keV and 1.9 ± 0.3 keV, respectively. An alternative model consisting of a blackbody and a power-law was also used to fit the continuum. However, in this case Ng et al. warn the reader that different continuum parameters were found when fitting the residuals at the Fe band with different models, meaning that this line fit may not be realistic. Moreover, it is noted that MXB 1728–34 was in a low-luminosity state during the XMM-Newton observation and that for such dim sources Compton scattering is expected to play an important role but was not included in their models. In our case, fitting the X-ray continuum with a Comptonization component, the parameters of the continuum do not change significantly when we add a Gaussian or a relativistic line (such as diskline or relline) to the continuum. Our choice of the continuum modeling allows us to better constrain the profile of the broad iron line. In this context, the choice of a particular fitting to the line does not result in sensible changes of the parameters determining the continuum emission. Moreover, when we tried a self-consistent reflection model, we again found similar values of the spectral parameters, which again indicates that the fit is stable and does not depend on the particular choice of the model used to fit the continuum or the iron line.
keV and 1.9 ± 0.3 keV, respectively. An alternative model consisting of a blackbody and a power-law was also used to fit the continuum. However, in this case Ng et al. warn the reader that different continuum parameters were found when fitting the residuals at the Fe band with different models, meaning that this line fit may not be realistic. Moreover, it is noted that MXB 1728–34 was in a low-luminosity state during the XMM-Newton observation and that for such dim sources Compton scattering is expected to play an important role but was not included in their models. In our case, fitting the X-ray continuum with a Comptonization component, the parameters of the continuum do not change significantly when we add a Gaussian or a relativistic line (such as diskline or relline) to the continuum. Our choice of the continuum modeling allows us to better constrain the profile of the broad iron line. In this context, the choice of a particular fitting to the line does not result in sensible changes of the parameters determining the continuum emission. Moreover, when we tried a self-consistent reflection model, we again found similar values of the spectral parameters, which again indicates that the fit is stable and does not depend on the particular choice of the model used to fit the continuum or the iron line.
The equivalent hydrogen column inferred from the Galactic photoelectric absorption component, NH ~ 2.8 × 1022 cm-2, agrees with typical values for this source (NH ~ 2.6−2.7 × 1022 cm-2, Di Salvo et al. 2000; Piraino et al. 2000; D’Aì et al. 2006). The Comptonized component can be produced by inverse Compton scattering from relatively hot electrons (kTe ~ 3.3 keV using the comptt model or kTe ~ 4.8 keV using the nthcomp model) off soft photons (kTseed ~ 0.7 keV using the comptt model or the nthcomp model). The seed photons for Comptonization are compatible with coming from the neutron star surface. Indeed, we can estimate the size of the emitting region of the soft photons using the formula given by in’t Zand et al. (1999). For this, one assumes that the bolometric luminosity of the soft photons is equal to the corresponding blackbody luminosity at the Wien temperature. The relative gain y = 5.01 (for a spherical geometry) takes into account the energy gained by the photons scattered off relativistic electrons through the inverse Comptonization process. This leads to a value Rseed = 4.9d5.1 km, where d5.1 is the distance in units of 5.1 kpc, considering the unabsorbed flux that we extrapolated in the energy range 0.1–150 keV, Fbol ~ 1.5(2) × 10-9 ergs cm-2 s-1.
Usually a soft blackbody component is required to fit the broad band X-ray spectra of LMXBs, most frequently interpreted as emitted by an accretion disk. This component is not significantly detected in the XMM-Newton spectrum. This may be ascribed to the relatively low X-ray luminosity of the source during the XMM-Newton observation, specially in the soft band. The bolometric X-ray flux in the range 0.1 − 150 keV also implies a bolometric X-ray luminosity of 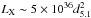 erg s-1, corresponding to 2% of the Eddington luminosity, that is LEdd = 2.5 × 1038 erg s-1 for a 1.4 M⊙ neutron star (e.g., van Paradijs & McClintock 1994). Indeed, during the high/soft state the disk is expected to be very close to the compact object, while in the low/hard state the disk should be truncated far from the compact object, and therefore its contribution is expected to be less important. We therefore conclude that the blackbody component is just too weak to be detected. This agrees with the results obtained from the fit of the iron feature with a reflection model. This indicates that the inner accretion disk is probably truncated far from the neutron star (Rin > 25 km), and with a relatively high value for the system inclination with respect to the line of sight estimated at 44° < i < 60°, which would further reduce the disk luminosity with respect to the Comptonized component in the hypothesis that the last one has a spherical geometry around the compact object.
erg s-1, corresponding to 2% of the Eddington luminosity, that is LEdd = 2.5 × 1038 erg s-1 for a 1.4 M⊙ neutron star (e.g., van Paradijs & McClintock 1994). Indeed, during the high/soft state the disk is expected to be very close to the compact object, while in the low/hard state the disk should be truncated far from the compact object, and therefore its contribution is expected to be less important. We therefore conclude that the blackbody component is just too weak to be detected. This agrees with the results obtained from the fit of the iron feature with a reflection model. This indicates that the inner accretion disk is probably truncated far from the neutron star (Rin > 25 km), and with a relatively high value for the system inclination with respect to the line of sight estimated at 44° < i < 60°, which would further reduce the disk luminosity with respect to the Comptonized component in the hypothesis that the last one has a spherical geometry around the compact object.
4.2. The iron line emission
Recently Ng et al. (2010) and Cackett et al. (2010) presented a spectral analysis of a sample of neutron star LMXBs observed by XMM-Newton and Suzaku, respectively, with particular interest in the iron discrete features in these sources. While Cackett et al. (2010) conclude that Fe K line profiles are well fitted by a relativistic line model for a Schwarzschild metric in most cases and imply a narrow range of inner disk radii (6 − 15 GM / c2), Ng et al. (2010) conclude there is no evidence for asymmetric (relativistic) line profiles in the XMM-Newton data, although the line profiles (fitted with a simple Gaussian or a laor model) again appear to be quite broad, with Gaussian sigmas ranging between 0.17 up to 1.15 keV. Another aspect relevant in this context is the impact of photon pile-up on relativistic disk lines and continuum spectra. However, as shown in Miller et al. (2010), while severe photon pile-up may distort relativistic disk lines and continuum shape, a modest pile-up fraction does not sensibly affect the line shape. This is certainly the case of MXB 1728–34.
We tried different models to fit the iron line profile. Although a Gaussian line provides an acceptable fit of the line profile, we tried to physically interpret its large width using models for a relativistically smeared line in an accretion disk.
Using the diskline profile (Model 2), we find the line centroid energy at 6.45 keV, compatible with a fluorescent Kα transition from mildly ionized iron (Fe i − xx). The inner radius is in the range 12 − 21 Rg. The line profile appears therefore to be significantly broad and compatible with a diskline profile. The results obtained by using a relativistic line profile corresponding to Model 3, which uses the more recent relline instead of diskline, are perfectly consistent with the diskline model. The inner radius is estimated to be in the range 15 − 22 Rg.
The line profile can be equally well fitted using a self-consistent relativistic reflection model (Model 5). The addition of the rdblur component significantly improves the χ2. This indicates that the line is indeed broad, and that the width of the line agrees with a relativistic smearing in the disk. The value of the inner radius is again consistent with that found using a diskline or a relline profile, even if the uncertainty is larger (Rin = 13–43 Rg). For a neutron star mass of 1.4 M⊙, the inner disk radius is in the range 25 − 100 km from the neutron star center, and so the disk would be truncated quite far from the neutron star surface. The inclination angle of the system with respect to the line of sight is found to be > 44°, which is still compatible with the absence of dips in its lightcurve (which implies i < 60°).
We also attempted to fit the iron feature using an alternative model (Model 4), consisting of two absorption edges instead of a broad emission line (see D’Aì et al. 2006). Their energies correspond to moderately ionized iron, Fe from IX to XVI, and highly ionized iron, Fe XXIII, respectively. The fit was not as good as with the previous models, because the corresponding χ2 was larger by 56 with the same number of degrees of freedom. We can compare these results with those obtained by (D’Aì et al. 2006), using simultaneous Chandra and RXTE observations. The edges were found at slightly different energies of 7.1 and 9.0 keV, corresponding to weakly (Fe i − v) and highly ionized iron (Fe xxv − xxvi), respectively. Although the fitting with two iron edges cannot be completely excluded yet, we think that the most probable explanation is that a couple of edges may mimic the shape of a broad iron line, given the relatively low statistics. We therefore favor the interpretation of the iron feature as a broad and relativistic emission line produced in the accretion disk, because this gives a better fit of the XMM-Newton spectrum and very reasonable values of the reflection parameters.
Acknowledgments
This work was supported by the Initial Training Network ITN 215212: Black Hole Universe funded by the European Community. We thank the referee for useful comments which helped in improving the manuscript.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Balucinska-Church, M., & McCammon, D. 1992, ApJ, 400, L699 [NASA ADS] [CrossRef] [Google Scholar]
- Basinska, E. M., Lewin, W. H. G., Sztajno, M., Cominsky, L. R., & Marshall, F. J. 1984, ApJ, 281, L337 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharyya, S., & Strohmayer, T. E. 2007, ApJ, 664, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Boirin, L., Mendez, M., Diaz Trigo, M., Parmar, A. N., & Kaastra, J. S. 2005, A&A, 436, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cackett, E. M., Miller, J. M., Bhattacharyya, S., et al. 2008, ApJ, 674, L415 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Miller, J. M., Ballantyne, D. R., et al. 2010, ApJ, 720, L205 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., Goldwurm, A., Cordier, B., et al. 1994, ApJ, 423, L436 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., Di Salvo, T., Iaria, R., et al. 2006, A&A, 448, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Aì, A., Iaria, R., Di Salvo, T., Matt, G., & Robba, N. R. 2009, ApJ, 693, L1 [NASA ADS] [CrossRef] [Google Scholar]
- D’Aì, A., Di Salvo, T., Ballantyne, D., et al. 2010, A&A, 516, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dauser, T., Wilms, J., Reynolds, C. S., & Brenneman, L. W. 2010, MNRAS, 409, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Salvo, T., Iaria, R., Burderi, L., & Robba, N. R. 2000, ApJ, 542, L1034 [NASA ADS] [CrossRef] [Google Scholar]
- Di Salvo, T., D’Aì, A., Iaria, R., et al. 2009, MNRAS, 398, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Iwasawa, K., Reynolds, C. S., & Young, A. J. 2000, PASP, 112, 1145 [NASA ADS] [CrossRef] [Google Scholar]
- Falanga, M., Gotz, D., Goldoni, P., et al. 2006, A&A, 458, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galloway, D. K., Psaltis, D., Chakrabarty, D., & Muno, M. P. 2003, ApJ, 590, L999 [NASA ADS] [CrossRef] [Google Scholar]
- Grindlay, J. E., & Hertz, P. 1981, ApJ, 247, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Hasinger, G., & van der Klis, M. 1989, A&A, 225, 79 [NASA ADS] [Google Scholar]
- Hoffman, J. A., Lewin, W. H. G., Doty, J., et al. 1976, ApJ, 210, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Hurkett, C. P., Vaughan, S., Osborne, J. P., et al. 2008, ApJ, 679, L587 [NASA ADS] [CrossRef] [Google Scholar]
- Iaria, R., D’Aì, A., di Salvo, T., et al. 2009, A&A, 505, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in’t Zand, J. J. M., Verbunt, F., Strohmayer, T. E., et al. 1999, A&A, 345, 100 [NASA ADS] [Google Scholar]
- Lewin, W. H. G., Clark, G., & Doty, J. 1976, 2922, 1 [Google Scholar]
- Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, 36 [Google Scholar]
- Miller, J. M. 2007, ARA&A, 45, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Fabian, A. C., Wijnands, R., et al. 2002, ApJ, 570, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., D’Aì, A., Bautz, M. W., et al. 2010, ApJ, 724, 1441 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, T., Grindlay, J. E., & Barret, D. 2001, ApJ, 547, L420 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C., Daz Trigo, M., Cadolle Bel, M., & Migliari, S. 2010, A&A, 522, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papitto, A., Di Salvo, T., D’Aì, A., et al. 2009, A&A, 493, 39 [Google Scholar]
- Papitto, A., Riggio, A., Di Salvo, T., et al. 2010, MNRAS, 407, 2575 [NASA ADS] [CrossRef] [Google Scholar]
- Piraino, S., Santangelo, A., & Kaaret, P. 2000, A&A, 360, 35 [Google Scholar]
- Protassov, R., van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2002, ApJ, 571, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S., & Nowak, M. A. 2003, Phys. Rep., 377, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, R. R., & Fabian, A. C. 2005, MNRAS, 358, 211 [Google Scholar]
- Schulz, N. S. 1999, ApJ, 511, L304 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T. E., Zhang, W., Swank, J. H., et al. 1996, ApJ, 469, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Struder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, 18 [Google Scholar]
- Taam, R. E. 1982, ApJ, 258, L761 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, L570 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, 27 [Google Scholar]
- van Paradijs, J., & McClintock, J. E. 1994, A&A, 290, 133 [NASA ADS] [Google Scholar]
- White, N. E., Peacock, A., Hasinger, G., et al. 1986, MNRAS, 218, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, M., Sadeghpour, H. R., & Dalgarno, A. 1998, ApJ, 496, L1044 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zycki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fitting parameters of the continuum emission for the XMM-Newton pn, MOS1, MOS2, RGS1 and RGS2 spectra of MXB 1728–34.
All Figures
 |
Fig. 1 RXTE/ASM lightcurve covering the 1.5−12 keV energy range. The vertical line indicates the time of the XMM-Newton observation performed on 2002 October 3rd. |
| In the text | |
 |
Fig. 2 Top panel: EPIC-pn (black), MOS1 (red), MOS2 (green), RGS1 (cyan), RGS2 (blue) data points of MXB 1728–34 in the range 1 − 11 keV. Bottom panel: residuals (data-model) in unit of sigmas for the diskline model (Model 2 in Table 3). |
| In the text | |
 |
Fig. 3 Top panel: EPIC-pn data points of MXB 1728–34 in the range 2.4−11 keV. Bottom panels: residuals (data-model) in unit of sigmas for the continuum model reported in Table 2, for Model 3 including a relativistic line (relline), and for Model 5 using a relativistic reflection component (reflion), respectively. Data were rebinned for graphical purposes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


