| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015954 | |
| Published online | 26 May 2011 | |
Formation scenarios and mass-radius relation for neutron stars
N. Copernicus Astronomical Center PAS, Bartycka 18, 00-716 Warszawa, Poland
e-mail: jlz@camk.edu.pl; haensel@camk.edu.pl
Received: 20 October 2010
Accepted: 28 March 2011
Aims. A neutron star crust, which is formed by accretion of matter from a companion in a low-mass X-ray binary (LMXB), has a stiffer equation of state (EOS) than that of catalyzed matter. At a given neutron star mass, M, the radius of a star with an accreted crust is therefore larger by ΔR(M) than for the usually considered star built of catalyzed matter.
Methods. Using a compressible liquid drop model of nuclei, we calculated, within the one-component plasma approximation, the EOSs corresponding to different nuclear compositions of the ashes of X-ray bursts in LMXB. These EOSs are then applied to study the effect of different formation scenarios on the neutron-star mass-radius relation.
Results. Assuming the SLy EOS for neutron star’s liquid core, we find that at M = 1.4 M⊙ the star with accreted crust has a radius more than 100 m larger than for the crust of catalyzed matter. Using smallness of the crust mass compared to M, we derive a formula that relates ΔR(M) to the difference in the crust EOS. This very precise formula also gives analytic dependence of ΔR on M and R of the reference star built of catalyzed matter. The formula is valid for any EOS of the liquid core. Rotation of neutron star makes the ΔR(M) larger. We derive an approximate but very precise formula that gives the difference in equatorial radii, ΔReq(M), as a function of stellar rotation frequency.
Key words: dense matter / equation of state / stars: neutron
© ESO, 2011
1. Introduction
Establishing the mass versus radius relation for neutron stars by observations is crucial for determining the equation of state (EOS) of dense matter. It is expected that finding even a few points of the M(R) curve could severely limit the range of considered theoretical models of matter in a liquid neutron star core. The general method of determining the EOS at supranuclear densities (i.e. higher densities than the normal nuclear density ρ0 = 2.7 × 1014 g cm-3) from the M(R) curve was developed by Lindblom (1992). A simplified method of determining a supranuclear segment of the EOS from three measured points of the M(R) has recently been described in (Özel et al. 2010). In these studies, the EOS of neutron star crust is considered as well established and fixed. This assumption is valid, within relatively small uncertainties, provided the crust matter is in full thermodynamical equilibrium (catalyzed matter, corresponding at T = 0 to the ground state of the matter). Such a condition is not fulfilled for the crust formed by accretion of matter onto a neutron star surface, from a companion in a low-mass X-ray binary (accreted crust, Haensel & Zdunik 1990a,b). The EOS of accreted crust is stiffer than for the ground-state one (Haensel & Zdunik 1990b). Therefore, at the same stellar mass, M, the radius of the neutron star with an accreted crust is larger by ΔR(M) than that of the star with crust built of catalyzed matter (catalyzed crust). We expect that the millisecond pulsars, spun-up by accretion in LMXBs (Bhattacharya & van den Heuvel 1991) have accreted crusts, different from the catalyzed crusts of pulsars born in supernova explosions.
We study the effect of the formation scenario on the radius-mass relation for neutron stars. Formation scenarios and corresponding equations of state of the crust are presented in Sect. 2. In Sect. 3 we calculate ΔR(M) for nonrotating stars, assuming different crust formation scenarios. Numerical results for ΔR(M), at fixed EOS of the liquid core, are presented in Sect. 3.1. In Sect. 3.2 we derive an approximate, but very precise, general formula that relates the difference in radii to the difference in the EOSs of the crust. The dependence of ΔR(M) on the EOS of the core enters via a dependence on the mass and radius of the reference star with catalyzed crust. Rotation of neutron star increases ΔR(M), and in Sect. 4 we study ΔR(M) (defined as the difference between the equatorial radii) for rotating neutron stars. Section5 contains a summary of our results, discussion, and conclusion.
Calculations that led to the present note were inspired by questions from the audience during a talk by one of the authors (P.H.) at the CompStar Workshop “Neutron star physics and nuclear physics”, held at GANIL, Caen, France, February 14–16, 2010.
2. Scenarios and equations of state
2.1. Catalyzed crust
We assume that a neutron star was born in a core-collapse supernova. Initially, the outer layers of the star are hot and fluid. Their composition corresponds to nuclear equilibrium, because all reactions are sufficiently rapid at T ≳ 1010K. The crust solidifies in the process of cooling in a newly born neutron star. One assumes that, while cooling and solidifying, the outer layers keep the nuclear equilibrium, and after reaching the strong degeneracy limit, the state of the EOS of the crust is approximated well by the EOS of the cold catalyzed matter, corresponding (in the T = 0 limit) to the ground of the matter (for a detailed discussion, see, e.g., Haensel et al. 2007). This EOS of the crust will be denoted as EOS [cat ] .
2.2. Accreted crusts
We assume that this neutron star has remained ~108 − 109 yr in an LMXB. Its crust was formed via accretion of matter onto the neutron-star surface from a companion in the binary. Typical accretion rates in LMXBs are ~10-10 − 10-9 M⊙ yr-1. Therefore, as a result of the accretion stage, the original, catalyzed crust formed in scenario described in Sect. 2.1 (typical mass of ~10-2 M⊙) has been fully replaced by the accreted one.
Accretion and X-ray bursts. Many LMXBs are sites of type I X-ray bursts (hereafter: X-ray bursts), which are thermonuclear flashes in the surface layers of an accreting neutron star (Woosley & Taam 1976; Maraschi & Cavaliere 1977; Joss 1977). In the simplest model of the X-ray bursts, accreted matter, composed mostly of 1H, accumulates on the star surface and undergoes compression from the weight of the continuously accreting matter. The accreted layer is also heated by the plasma hitting the star surface and transforming its kinetic energy into heat. The compressed and heated hydrogen layer burns steadily in its bottom shell with ρ ~ 105 g cm-3 into 4He. The helium produced in the burning of hydrogen accumulates in a growing He layer beneath the H-burning shell. After some recurrence time (typically ~ hours), the helium is ignited at the bottom of the He layer, typically at ρ ~ 106 g cm-3. The helium burning starts in a strongly degenerate plasma (temperature ~108 K and ρ ~ 106 g cm-3). Therefore, helium burning is thermally unstable and proceeds initially in an explosive detonation mode, with local temperature exceeding 109 K, and burns the overlaying helium and hydrogen layers into elements with mass number A ~50−100 (see next paragraph). Finally, the thermonuclear explosion develops into a thermonuclear flash of the surface layer, observable as an X-ray burst. After a few minutes, the H-He envelope has been transformed into a layer of nuclear ashes. The energy released in thermonuclear burning has been radiated in an X-ray burst. Continuing accretion again leads to the accumulation of the H-He fuel for the next X-ray burst, and the cycle accretion-burst repeats in a quasi-periodic way every few hours.
Ashes of the X-ray burst. The composition of ashes from thermonuclear burning of an accreted H-He layer deserves a more detailed discussion (see, e.g., Beard & Wiescher 2003). Early calculations have indicated that thermonuclear explosive burning produces mostly 56Ni, which then converts into 56Fe by the electron captures (Taam 1982; Ayasli & Joss 1982). This picture had to be revised in the light of more recent simulations of nuclear evolution during cooling following the temperature peak of ~2 × 109 K. These simulations have shown that a few minutes after the initial temperature peak, nuclear ashes contain a mixture of nuclei with A ~ 50−100 (Schatz et al. 2001).
Reactions in accreting crust. During accretion, the crust is a site of exothermic reactions in a plasma that is far from the catalyzed state. A layer of ashes from X-ray bursts is compressed under the weight of cumulating overlaying accreted layers. The ashes of density over 105 g cm-3 are a plasma composed of nuclei immersed in an electron gas. The temperature in the deeper layer of thermonuclear ashes (a few 108 K at the depth of a few meters) is too low for the thermonuclear fusion to proceed: the nuclei have Z ~ 30−50 and the fusion reactions are blocked by the Coulomb barriers. Therefore, the only nuclear processes are those induced by compression of matter. These processes are electron captures and neutron emissions and absorptions. Compression of ashes results in increasing the density of their layer (and its increasing depth below the stellar surface), and leads to the electron captures on nuclei and the neutronization of the matter. To be specific, let us consider a neutron star with M = 1.4M⊙ (Fig. 39 in Chamel & Haensel 2008). For densities exceeding ~5 × 1011 g cm-3 (neutron drip point in accreted crust, at the depth ~300m) electron captures are followed by the neutron emission from nuclei. Therefore, apart from being immersed in electron gas, nuclei become immersed in a neutron gas. At density over 1012 g cm-3 (depth greater than ~350 m), the value of Z becomes so low and the energy of the quantum zero-point motion of nuclei around the lattice sites so high that the pycnonuclear fusion (see, e.g., Shapiro & Teukolsky 1983) of neighboring nuclei might be possible. This would lead to a further neutronization of the considered layer of accreted matter. With increasing depth and density, the element of matter under consideration becomes more and more neutronized, and the fraction of free neutrons outside nuclei in the total number of nucleons increases. At the density 1014 g cm-3 (depth ~1 km) the crust matter element dissolves into a homogeneous n − p − e plasma, containing only a few percent of protons.
Nuclear composition of accreted crusts. The composition of a fully accreted crust is calculated, assuming a simple model of one-component plasma, as in Haensel & Zdunik (2003). All the crust, including its bottom layer, is obtained by compression of an initial shell with ρ = 108 g cm-3. Two initial values of the mass number of nuclei in the X-ray bursts ashes are assumed, Ai = 56,106. Thermal effects are neglected. Extensive numerical simulations of the nuclear evolution of multicomponent ashes, assuming a large reaction network, and taking temperature effects into account, were carried out by (Gupta et al. 2007). However, these calculations were restricted to densities less than 1011 g cm-3, where the EOS is not significantly different from EOS [cat ] , albeit the nuclear composition is very different from the one for catalyzed matter.
A model of the EOS of a fully accreted crust will be denoted as ![\hbox{${\rm EOS}[{\rm acc}.{\cal A}]$}](/articles/aa/full_html/2011/06/aa15954-10/aa15954-10-eq38.png) , where
, where 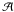 refers to the assumptions underlying the model: composition of X-ray bursts ashes, types of reactions included in the model, etc.
refers to the assumptions underlying the model: composition of X-ray bursts ashes, types of reactions included in the model, etc.
2.3. Equations of state
 |
Fig. 1 EOS for the crusts calculated using the Mackie-Baym model of nuclei and neutron matter. Explanation of the labels: cat – cold catalyzed matter; acc.56.P – initial X-ray burst ashes Ai = 56, pycnonuclear fusion switched on; acc.56.NP – initial X-ray burst ashes Ai = 56, pycnonuclear fusion switched off till 1013 g cm-3. For further details see Sect. 2.3. (Color online.) |
To disentangle the effect of formation scenario from the EOS of the crust, one has to compare the EOSs calculated not only for the same nuclear Hamiltonian, but also for the same model of nuclei and of nuclear matter in nuclei and neutron matter outside nuclei. In this respect, the analysis of Haensel & Zdunik (1990b) was not correct, because the EOSs of accreted and catalyzed crusts were based on different nuclear models. In the present paper we consistently use the compressible liquid drop model of nuclei of Mackie & Baym (1977): this model was used in all previous calculations of accreted crusts. We calculated several EOSs of accreted crust corresponding to different Ai of X-ray bursts ashes and for different models of pycnonuclear reaction rates. These EOSs are plotted in Fig. 1, where we also show EOS [cat ] for the same model of the nucleon component (nuclei and neutron gas) of dense matter. For ρ < 1011 g cm-3 all EOSs are very similar, so we only display EOS plots for ρ > 1011 g cm-3.
Stiffness of the EOS. Significant differences in this property of the EOS exist in the inner crust, from the neutron drip point on and up to 1013 g cm-3. In this density range EOS [acc ] are significantly stiffer than EOS [cat ] . The difference already starts at the neutron drip point, which in the accreted crust is found at a higher density. The softening that follows after the neutron drip is much stronger in EOS [cat ] than in EOS [acc ] . Then, for ρ > 1013 g cm-3, EOS [acc ] converge (from above) to EOS [cat ] , because at such high density the nuclei play a lesser rôle in the EOS, and the crust pressure is mostly determined by the neutron gas outside nuclei.
Jumps and smoothness. EOS [acc ] shows numerous pronounced density jumps at constant pressure, to be contrasted with the smooth curve of EOS[cat]. Actually, both features are artifacts of the models used. For example, EOS [cat ] is completely smooth because we used a compressible liquid drop model without any shell correction for neutrons and protons, and treated neutron and proton numbers within the Wigner-Seitz cells as continuous variables, in which we minimized the enthalpy per nucleon at a given pressure. For EOS [acc ] we used one-component plasma approximation, with integer neutron and proton numbers in the Wigner-Seitz cells. Since we neglected thermal effects, we got a density jump at each threshold for electron capture. Had we used a multicomponent plasma model and included thermal effects and a large reaction network, the jumps in the EOS [acc ] would be smoothed (see Gupta et al. 2007).
Pycnonuclear fusion. The process of pycnonuclear fusion (see, e.g., Shapiro & Teukolsky 1983) may proceed after electron captures followed by neutron emission – a reaction chain that results in decreasing Z and A. In our simulations based on the one-component plasma model, pycnonuclear fusion proceeds as soon as the time τpyc (inverse of the pycnonuclear fusion rate) is less than the timescale τacc needed for a matter element to pass, owing to accretion, across the (quasistationary) crust shell with specific (A,Z). This time can be estimated as τacc = Mshell(A,Z)/Ṁ. Typical values of the mass of shells in the inner accreted crust are Mshell ~ 10-5M⊙. At accretion rates Ṁ ~ 10-10 − 10-9M⊙ yr-1, formulae used to calculate the fusion rates in (Haensel & Zdunik 1990a, 2003) lead to pycnonuclear fusions proceeding at ρ ≳ 1012 g cm-3. However, theoretical evaluation of τpyc is plagued by huge uncertainties (see Yakovlev et al. 2006). It is not certain whether pycnonuclear fusions do indeed occur below 1013 g cm-3. If they do not, then EOS [acc ] is represented quite well by models with pycnonuclear fusion switched off. The two extremes – pycnonuclear fusions starting at 1012 g cm-3 and pycnonuclear fusion shifted to densities above 1013 g cm-3 – correspond to curves EOS [acc.Ai.P ] and EOS [acc.Ai.NP ] in Fig. 1.
Bottom crust layer with ρ > 1014 g cm-3. Our plots of EOS in Fig. 1 are restricted to ρ < 1014 g cm-3. For the densities above 1014 g cm-3 and up to the crust bottom density ρb, the precision of our models lowers significantly compared to the precision of our EOS at lower densities. Fortunately, the contribution of the bottom layer of the crust (1014 g cm-3 < ρ < ρb) to the difference Racc − Rcat is negligible, and therefore the uncertainties in the crust EOS at the highest densities do not affect our main results. This favorable situation will be justified in Sect. 3.2.
3. Effect of the change of the crust EOS on the star radius
3.1. Accreted vs. catalyzed crust: numerical results for nonrotating models
We matched EOSs of the crust described in the preceding section to several EOSs of the liquid core. We checked that the difference ΔR(M) = Racc(M) − Rcat(M) does not depend on the details of matching in the crust-core interface. On the other hand, ΔR(M) can be shown to depend on the EOS of the core via the factor (Rcat/rg − 1)Rcat, where rg = 2GM/c2 = 2.96 M/M⊙ km is the gravitational (Schwarzschild) radius. These two properties are derived using the equations of hydrostatic equilibrium in Sect. 3.2.
In Fig. 2 we show the M(R) relation for neutron stars with catalyzed and accreted crust (EOS[acc.56.P]). For the liquid core we use the SLy EOS of (Douchin & Haensel 2001). For M = 1.4M⊙, we get ΔR ≈ 100m. The value of ΔR grows to 200 m if M decreases to 1M⊙. It decreases to 40m for 1.8M⊙.
 |
Fig. 2 Solid lines give gravitational mass M versus radius R for nonrotating neutron stars with accreted [acc.56.P] and catalyzed crust. Dashed red lines correspond to the approximation of the crust thickness by Eq. (5). Zoomed region illustrates the very high accuracy of this approximation. For the explanation of the procedure of getting dashed lines, see the last part of Sect. 3.2. (Color online.) |
3.2. An analytic approximation for ΔR
We consider hydrostatic equilibrium of a nonrotating neutron star. The (circumferential) radius of the star is R and its (gravitational) mass – M. The pressure at the bottom of the crust is Pb, and the mass of the crust is Mcr. We assume that Mcr/M ≪ 1, but we account for the radial extension of the crust and the radial dependence of the pressure and of the density within the crust, following the method formulated in (Zdunik et al. 2008). We use the fact that P/c2 ≪ ρ and 4πr3P/Mc2 ≪ 1 within the crust. We define a dimensionless function of pressure within the crust (0 ≤ P ≤ Pb) 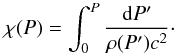 (1)The function χ(P) is determined solely by the EOS of the crust.
(1)The function χ(P) is determined solely by the EOS of the crust.
 |
Fig. 3 Upper panel: functions χ(P) for EOS[acc.56.P] (dashed, red), EOS[acc.106.NP] (dotted, blue), and EOS[cat] (solid, black). Lower panel: function Δχ(P) (Eq. (4)) for EOS[acc.56.P] (dashed, red) and EOS[acc.106.NP] (dotted, blue). (Color online.) |
Using the Tolman-Oppenheimer-Volkoff equation of hydrostatic equilibrium (Shapiro & Teukolsky 1983), and neglecting within the crust P/c2 compared to ρ and to M/(4πr3), we can go over in Eq. (1) to the radial coordinate r, getting ![\begin{equation} \chi[P(r)]=\frac{1}{2}\ln \left[ \frac{1-r_{\rm g}/R}{1-r_{\rm g}/r} \right], \label{eq:chi-r} \end{equation}](/articles/aa/full_html/2011/06/aa15954-10/aa15954-10-eq82.png) (2)where rg ≡ 2GM/c2.
(2)where rg ≡ 2GM/c2.
The dimensionless function χ ≪ 1 can be treated as a small parameter in systematic expansions of the crust thickness. This function increases monotonously with P, from zero to ~10-2 (upper panel of Fig. 3). Therefore, an expression for the crust layer thickness, from the surface to the pressure at the layer bottom P, t(P) ≡ R − r(P), obtained from Eq. (2) in the linear approximation in χ, is expected to be very precise, 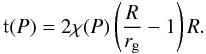 (3)Our aim is to evaluate the change in the radius of neutron star of mass M and radius R, when EOS [cat ] is replaced by EOS [acc ] . These EOSs differ for pressures below P1 = 1032 erg cm-3 (Sect. 2.3 ). To calculate Racc − Rcat it is therefore sufficient to know the difference in values of χ at P1. We introduce a function Δχ(P), measuring the difference between two EOSs of the crust for pressures from zero to P,
(3)Our aim is to evaluate the change in the radius of neutron star of mass M and radius R, when EOS [cat ] is replaced by EOS [acc ] . These EOSs differ for pressures below P1 = 1032 erg cm-3 (Sect. 2.3 ). To calculate Racc − Rcat it is therefore sufficient to know the difference in values of χ at P1. We introduce a function Δχ(P), measuring the difference between two EOSs of the crust for pressures from zero to P, 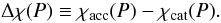 (4)In Fig. 3 we show functions χ(P) and Δχ(P) for several EOSs of accreted crust. In spite of the jumps in density at constant pressure, characteristic of the EOSs of accreted crusts (Fig. 1), both χ and Δχ are smooth functions of P. This is due to the integration over P′ < P in the definition of χ(P). As seen in Fig. 3, dependence of χ and Δχ on the particular scenario underlying EOS [acc ] is very weak. Additionally, Δχ is nearly constant for P > 2 × 1031 erg cm-3, because EOS[cat] and EOS[acc] converge at high pressures (see Fig. 1). Therefore, Δχ(P1) is a very good approximation for Δχ(Pb).
(4)In Fig. 3 we show functions χ(P) and Δχ(P) for several EOSs of accreted crust. In spite of the jumps in density at constant pressure, characteristic of the EOSs of accreted crusts (Fig. 1), both χ and Δχ are smooth functions of P. This is due to the integration over P′ < P in the definition of χ(P). As seen in Fig. 3, dependence of χ and Δχ on the particular scenario underlying EOS [acc ] is very weak. Additionally, Δχ is nearly constant for P > 2 × 1031 erg cm-3, because EOS[cat] and EOS[acc] converge at high pressures (see Fig. 1). Therefore, Δχ(P1) is a very good approximation for Δχ(Pb).
Our final formula, obtained using Eqs. (3) and (4), combined with approximations explained above, is ![\begin{equation} R_{\rm acc}-R_{\rm cat}\simeq 2\Delta[\chi]\cdot \left({R/r_{\rm g}}-1\right){R}, \label{eq:R.acc.cat} \end{equation}](/articles/aa/full_html/2011/06/aa15954-10/aa15954-10-eq99.png) (5)where Δ [χ ] = Δχ(P1) and R = Rcat.
(5)where Δ [χ ] = Δχ(P1) and R = Rcat.
The precision of the approximation (5) is illustrated in Fig. 2. The dashed line for the accreted crust was obtained from exact Rcat(M) using Eq. (5) with R = Rcat. On the other hand, the dashed line for catalyzed crust was obtained from exact Racc(M) using Eq. (5) with R = Racc.
Up to this point, we have neglected the contribution of elastic strain to the stress tensor within the crust, and used the perfect liquid approximation in the equations of hydrostatic equilibrium. Recent numerical simulations indicate that, on the timescales of years and longer (which are of astrophysical interest), the breaking stress of the ion crystal of the crust is ~10-3 of the crust pressure (Chugunov & Horowitz 2010). This is much less than the difference between EOS[acc] and EOS[cat]. Therefore, as long as we restrict ourselves to a timescale longer than a few years, the contribution of elastic strain to ΔR(M) can be neglected.
4. Combined effects of accretion and rotation on ΔR(M)
Millisecond pulsars are thought to be recycled old (“dead”) pulsars, spun-up by accretion of matter from their companion in LMXBs (Alpar et al. 1982; Bhattacharya & van den Heuvel 1991). This scenario is corroborated by the discovery of rapid X-ray pulsations with frequencies up to 619 Hz in more than a dozen LMXBs. The most rapid millisecond pulsar (isolated one) rotates at 716 Hz. To reach such high rotation frequencies, neutron star had to accrete some five times the mass of the crust of a 1.4M⊙ neutron star. Therefore, one has to conclude that millisecond pulsars have fully accreted crusts.
In the case of rotating stars, we define Racc − Rcat as the difference in circumferential equatorial radii. Rotation increases the difference Racc − Rcat compared to the static case. A rough Newtonian argument relies on the proportionality of the centrifugal force to the distance from the rotation axis. Therefore, centrifugal force that acts against gravity is strongest at the equator. In order to get the precise value of the effect of rotation on Racc − Rcat, we performed 2-D simulations of stationary configurations of rigidly rotating neutron stars with catalyzed and accreted crusts. The calculations were performed using the rotstar code from the LORENE library (http://www.lorene.obspm.fr). Our results, obtained for f = 716Hz (maximum frequency measured for a pulsar) and for a half of this frequency, are shown in Fig. 4.
 |
Fig. 4 Dependence of ΔR(M) = Racc(M) − Rcat(M) on the frequency of rotation of neutron star, f. Equations of state as in Fig. 2. Upper curve – f = 716Hz. Middle curve – f = 358Hz. Bottom curve – nonrotating. |
Consider hydrostatic equilibrium of the crust of rotating star in the equatorial plane. In the Newtonian approximation, the ratio of centrifugal force to the gravitational pull at the equator is, neglecting rotational deformation, Ω2R3/GM, where Ω is angular frequency of rigid rotation. This expression is exact in the quadratic approximation in Ω, because an increase of R due to rotation introduces higher powers of Ω. We propose modeling the centrifugal-force effect within crust by modifying the Tolman-Oppenheimer-Volkoff equation in the equatorial plane in following way: 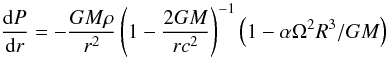 (6)where M is the total mass of the star and α a numerical coefficient to be determined by fitting the exact results of 2-D calculations. The validity of Eq. (6) relies on the smallness of the rotational flattening of the liquid core compared to that of crust. We included terms quadratic in Ω and used a standard approximation valid for a low-mass crust, applied in the preceding section. Equation (6) could be solved explicitly by assuming constant M and taking the changes in r throughout the crust into account, as in the case of nonrotating star in (Zdunik 2002). However, to be consistent with the approach leading to formula (3), we prefer to use a solution method based on the smallness of χ. The rotation effect enters via a constant factor (1 − αΩ2R3/GM). This results in a simple relation between Ω = 0 and Ω > 0 difference in radii:
(6)where M is the total mass of the star and α a numerical coefficient to be determined by fitting the exact results of 2-D calculations. The validity of Eq. (6) relies on the smallness of the rotational flattening of the liquid core compared to that of crust. We included terms quadratic in Ω and used a standard approximation valid for a low-mass crust, applied in the preceding section. Equation (6) could be solved explicitly by assuming constant M and taking the changes in r throughout the crust into account, as in the case of nonrotating star in (Zdunik 2002). However, to be consistent with the approach leading to formula (3), we prefer to use a solution method based on the smallness of χ. The rotation effect enters via a constant factor (1 − αΩ2R3/GM). This results in a simple relation between Ω = 0 and Ω > 0 difference in radii: ![\begin{eqnarray} \Delta R_{\rm eq} (\Omega)&=&R_{\rm eq, acc}(\Omega)-R_{\rm eq,cat}(\Omega)\nonumber\\ &=&\frac{2\Delta[\chi]\cdot \left({R/r_{\rm g}}-1\right){R}}{1-\alpha\Omega^2R^3/GM}=\frac{\Delta R (\Omega=0)}{1-\alpha\Omega^2R^3/GM}\cdot \label{eq:dromega} \end{eqnarray}](/articles/aa/full_html/2011/06/aa15954-10/aa15954-10-eq120.png) (7)The dimensionless parameter α has been determined numerically by fitting formula (7) to the exact 2-D results obtained in General Relativity using LORENE numerical library. We find that α ≈ 4/3. As one sees in Fig. 4, our approximate formula for ΔReq(Ω) works extremely well. The actual Ω-dependence of ΔReq is stronger than quadratic because Ω2 appears in the denominator in Eq. (7).
(7)The dimensionless parameter α has been determined numerically by fitting formula (7) to the exact 2-D results obtained in General Relativity using LORENE numerical library. We find that α ≈ 4/3. As one sees in Fig. 4, our approximate formula for ΔReq(Ω) works extremely well. The actual Ω-dependence of ΔReq is stronger than quadratic because Ω2 appears in the denominator in Eq. (7).
5. Summary and conclusion
We have studied the effect of the formation scenario on the mass-radius relation for neutron stars. For a given M, a star with an accreted crust has a larger radius by ΔR(M), than a star built of catalyzed matter formed in stellar core collapse. We derived an approximate but very precise formula for ΔR(M), valid for slowly rotating neutron stars. ΔR(M) factorizes into a prefactor depending solely on the EOS of neutron star crusts formed in different scenarios and a simple function of M for a given EOS of the core. We studied the dependence of the difference between the equatorial radii on the angular rotation frequency, ΔReq(Ω). We derived an approximate formula for ΔReq(Ω), which reproduces ΔReq with high precision even for neutron stars rotating at 716 Hz, the highest rotation frequency measured for a radio pulsar.
We found that an accreted crust makes the radius of a 2 M⊙ − 1 M⊙ star some 50 − 200 m larger than in the standard catalyzed matter case. The highest hopes of a simultaneous measurement of a neutron star M and R are, in this decade, associated with high-resolution X-ray spectroscopy (Arzoumanian et al. 2009; Paerels et al. 2009). Unfortunately, expected uncertainty in determining R(M) is ± 5%. It significantly exceeds the effects of formation scenarios, as calculated here.
Acknowledgments
This work was partially supported by the Polish MNiSW grant No. N N203 512838. This work was also supported in part by CompStar, a Research Networking Program of the European Science Foundation and the LEA Astro-PF.
References
- Alpar, M. A., Cheng, A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 728 [Google Scholar]
- Arzoumanian, Z., et al. 2009, in Astro2010: The Astronomy and Astrophysics Decadal Survey, White paper no. 6 [arXiv:0902.3264] [Google Scholar]
- Ayasli, S., & Joss, P. C. 1982, ApJ, 256, 267 [Google Scholar]
- Beard, M., & Wiescher, M. 2003, Rev. Mex. Fisica, 49, 139 [Google Scholar]
- Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Haensel, P. 2008, Liv. Rev. Rel., 11, 10 [Google Scholar]
- Chugunov, A. I., & Horowitz, C. J. 2010, MNRAS, 407, L54 [NASA ADS] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, S., Brown, E. F., Schatz, H., Möller, P., & Kratz, K.-L. 2007, ApJ, 662, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., Özel, F., Cabrera-Lavers, A., & Wroblewski, P. 2010, ApJ, 712, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990a, A&A, 227, 431 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990b, A&A, 229, 117 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1, Equation of State and Structure (New York: Springer) [Google Scholar]
- Joss, P. C. 1977, Nature 270, 310 [Google Scholar]
- Lindblom, L. 1992, ApJ, 398, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Mackie, F. D., & Baym, G. 1977, Nucl. Phys. A, 285, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Cavaliere, A. 1977, in Highlights of Astronomy, ed. E. A. Mueller (Dordrecht: Reidel), Part I, 4, 127 [Google Scholar]
- Özel, F. 2006, Nature, 441, 1115 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Özel, F., Güver, T., & Psaltis, D. 2009, ApJ, 693, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., Baym, G., & Güver, T. 2010, Phys. Rev. D, 82, 101301 [Google Scholar]
- Paerels, F., M. Mendez., M., Agueros, et al. 2009, in Astro2010: The Astronomy and Astrophysics Decadal Survey, White paper no. 230 [arXiv:0904.0435] [Google Scholar]
- Schatz, H., Aprahamian, A., Barnard, V., et al. 2001, Phys. Rev. Lett., 86, 3471 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects (New York: Wiley) [Google Scholar]
- Taam, R. E. 1982, ApJ, 258, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Taam, R. E. 1976, Nature, 263, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gasques, L., & Wiescher M. 2006, MNRAS, 371, 1322 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L. 2002, A&A, 394, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdunik, J. L., Bejger, M., & Haensel, P. 2008, A&A, 491, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 EOS for the crusts calculated using the Mackie-Baym model of nuclei and neutron matter. Explanation of the labels: cat – cold catalyzed matter; acc.56.P – initial X-ray burst ashes Ai = 56, pycnonuclear fusion switched on; acc.56.NP – initial X-ray burst ashes Ai = 56, pycnonuclear fusion switched off till 1013 g cm-3. For further details see Sect. 2.3. (Color online.) |
| In the text | |
 |
Fig. 2 Solid lines give gravitational mass M versus radius R for nonrotating neutron stars with accreted [acc.56.P] and catalyzed crust. Dashed red lines correspond to the approximation of the crust thickness by Eq. (5). Zoomed region illustrates the very high accuracy of this approximation. For the explanation of the procedure of getting dashed lines, see the last part of Sect. 3.2. (Color online.) |
| In the text | |
 |
Fig. 3 Upper panel: functions χ(P) for EOS[acc.56.P] (dashed, red), EOS[acc.106.NP] (dotted, blue), and EOS[cat] (solid, black). Lower panel: function Δχ(P) (Eq. (4)) for EOS[acc.56.P] (dashed, red) and EOS[acc.106.NP] (dotted, blue). (Color online.) |
| In the text | |
 |
Fig. 4 Dependence of ΔR(M) = Racc(M) − Rcat(M) on the frequency of rotation of neutron star, f. Equations of state as in Fig. 2. Upper curve – f = 716Hz. Middle curve – f = 358Hz. Bottom curve – nonrotating. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


