| Issue |
A&A
Volume 530, June 2011
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015224 | |
| Published online | 27 April 2011 | |
Characteristics of thick disks formed through minor mergers: stellar excesses and scale lengths
GEPI, Observatoire de Paris, CNRS, Université Paris Diderot,
5 place Jules Janssen,
92190
Meudon,
France
e-mail: yan.qu@obspm.fr
Received: 16 June 2010
Accepted: 3 February 2011
By means of a series of N-body/SPH simulations we investigate the morphological properties of thick stellar disks formed through minor mergers with, e.g. a range of gas-to-stellar mass ratios. We show that the vertical surface density profile of the post-merger thick disk follows a sech function and has an excess in the regions furthest away from the disk mid-plane (z ≳ 2 kpc). This stellar excess also follows a sech function with a larger scale height than the main thick disk component (except at large radii). It is usually dominated by stars from the primary galaxy, but this depends on the orbital configuration. Stars in the excess have a rotational velocity lower than that of stars in the thick disk, and they may thus be confused with stars in the inner galactic halo, which can have a similar lag. Confirming previous results, the thick disk scale height increases with radius and the rate of its increase is smaller for more gas rich primary galaxies. On the contrary, the scale height of the stellar excess is independent of both radius and gas fraction. We also find that the post-merger thick disk has a radial scale length which is 10−50% larger than that of the thin disk. Two consecutive mergers have basically the same effect on heating the stellar disk as a single merger of the same total mass, i.e., the disk heating effect of a few consecutive mergers does not saturate but is cumulative. To investigate how thick disks produced through secular processes may differ from those produced by minor mergers, we also simulated gravitationally unstable gas-rich disks (“clumpy disks”). These clumpy disks do not produce either a stellar excess or a ratio of thick to thin disk scale lengths greater than one. Comparing our simulation results with observations of the Milky Way and nearby galaxies shows that our results for minor mergers are consistent with observations of the ratio of thick to thin disk scale lengths and with the “Toomre diagram” (the sum in quadrature of the vertical and radial versus the rotational kinetic energies) of the Milky Way. The simulations of clumpy disks do not show such agreement. We conclude that minor mergers are a viable mechanism for the creation of galactic thick disks and investigating stars at several kpc above the mid-plane of the Milky Way and other galaxies may provide a quantitative method for studying the (minor) merger history of galaxies.
Key words: galaxies: interactions / galaxies: formation / galaxies: evolution / galaxies: structure / galaxies: kinematics and dynamics
© ESO, 2011
1. Introduction
Ever since the existence of a thick disk component was shown by star counts in the Milky Way (Gilmore & Reid 1983) and by stellar luminosity distribution studies of external early- and late-type galaxies (Burstein 1979; Tsikoudi 1979; van der Kruit & Searle 1981a; Shaw & Gilmore 1989; Dalcanton & Bernstein 2002; Pohlen et al. 2004; Tikhonov et al. 2005), its origin and properties have been the subject of a continuing vigorous debate. The distinctive properties of their stars, e.g. their metallicity distribution and kinematics, suggest that the thick disk is a distinct and perhaps intermediate component between the thin disk and the halo (Norris 1986; Wyse & Gilmore 1986; Sandage & Fouts 1987; Carney et al. 1989; Ratnatunga & Freeman 1989).
A large variety of models has been proposed to explain the formation of thick disks – involving either secular heating of the disk through scattering by spiral waves (Barbanis & Woltjer 1967; Carlberg & Sellwood 1985), molecular clouds (Spitzer & Schwarzschild 1951; Lacey 1984), bars, self-gravitating clumps (Bournaud et al. 2009), or heating disk stars through external processes such as galaxy mergers, infalling clumpy gas coalescing into a thin disk, and proto-galactic fragments coalescing before thin disk formation. On the other hand, a thick disk component can also be formed by violent heating and relaxation due to satellite accretion(s) or from directly accreting dynamically hot stars through mergers and interactions (Statler 1988; Hernquist & Quinn 1989; Quinn et al. 1993; Walker et al. 1996; Aguerri et al. 2001; Abadi et al. 2003; Yoachim & Dalcanton 2005; Brook et al. 2007; Villalobos & Helmi 2008, 2009). As recently discussed by Sales et al. (2009) and Di Matteo et al. (2010), these different formation mechanisms should produce different signatures in the eccentricities of the stellar orbits, thus providing a potential diagnostic to disentangle the dominant formation scenarios (see Di Matteo et al. 2010; Dierickx et al. 2010; Wilson et al. 2011, and Casetti-Dinescu et al. 2011, for a comparison of model predictions and observations). Nevertheless, the main astrophysical processes which drive thick disk formation remain unclear.
The structure, kinematics and enrichment of the thick disk provide important clues for solving the mystery of its origin. Many photometric and spectroscopic observations show that thick disk stars are generally old, and have lower metallicity and larger velocity dispersion than thin disk stars (Nissen 1995; Chiba & Beers 2000; Gilmore et al. 2002; Soubiran et al. 2003; Parker et al. 2004). The vertical surface density profile of thick disk stars follows a sechn profile with a scale height several times larger than the thin disk, whereas their radial profile has a scale length that is generally 1 to 2 times larger than that of the thin disk (Morrison et al. 1997; Abe et al. 1999; Dalcanton & Bernstein 2002; Neeser et al. 2002; Pohlen et al. 2004; Yoachim & Dalcanton 2005). In models, the thick disk scale height is usually assumed to be independent of radius (Pohlen et al. 2004; Yoachim & Dalcanton 2005), in accordance with earlier observational studies on thin and thick disk scale heights (van der Kruit & Searle 1981a,b; Shaw & Gilmore 1990; Näslund & Jörsäter 1997; Rauscher et al. 1998). However, for a sample of 48 early- and late-type galaxies de Grijs & Peletier (1997) found an increase in disk scale height with radius, where early-type galaxies show the largest increase. Also Narayan & Jog (2002) pointed out that an increasing scale height was consistent with two of the galaxies studied by van der Kruit & Searle (1981a,b), and that their vertical velocity dispersion distribution does not scale as twice the disk scale length with radius, thus supporting the possibility of a moderate flaring in these disks. Recently, Bournaud et al. (2009) modeled the formation of a thick disk through gravitational instabilities and pointed out that thick disks produced in this way have constant scale heights, while this is not likely to be the case if they were formed through minor mergers.
Therefore, the properties of vertical disk profiles can help in understanding their formation processes. It appears that thick disk scale height is related to both galaxy mass (Yoachim & Dalcanton 2006) and Hubble type (de Grijs & Peletier 1997). Moreover, some disk-dominated galaxies do not show an obvious thick disk, e.g. NGC 4244 (Fry et al. 1999; but see Comerón et al. 2011, for evidence of a subtle thick disk), and some even have thick disks that counter-rotate relative to their thin disks (Morrison et al. 1994; Yoachim & Dalcanton 2005). These observations, taken all together, favor a merger-induced thick disk formation mechanism (see, e.g., Yoachim & Dalcanton 2005, 2006, and references therein).
Interestingly, it has recently been shown by Purcell et al. (2010) and Zolotov et al. (2010) that minor and major mergers cannot only efficiently heat a pre-existing stellar disk, but also contribute to the building of galaxy halos. A trace of this heated population may be found in the inner Milky Way halo, as recently discussed by Nissen & Schuster (2010).
Despite considerable effort, we are still far from having a detailed understanding of the origin and properties of galactic thick disks. In this paper, we investigate if N-body/SPH numerical simulations of minor mergers, with a mass ratio of 10:1 and 20:1, can produce realistic thick disks. We concentrate on certain aspects of post-merger thick disks – i.e., vertical surface density profiles and disk scale heights – that are well suited for comparison with the observed properties of thick disks in the Milky Way and nearby galaxies. In particular, we investigate the “excess” of stars at great heights (z > 2 kpc) from the galaxy mid-plane that is naturally formed through minor mergers. This stellar excess, as already discussed by Purcell et al. (2010) and Zolotov et al. (2010), may have contributed to the stellar population currently found in inner galactic halos. For the first time, we describe its main properties and the impact on them of initial orbital configurations, primary galaxy gas fraction and consecutive minor mergers. In addition, we compare the scale length ratios of the thick and the thin disk to observations, and the Toomre diagrams of minor mergers with that of the Milky Way. Furthermore, we will compare the vertical structure of thick disks formed through minor mergers and through scattering by clumps in the distribution of mass within the thin disk, and discuss the expected differences in their observable properties.
The paper is organized as follows. In Sect. 2 we describe the numerical code, the initial galaxy models and orbital conditions adopted for simulation runs. Section 3 presents the vertical structure and kinematics of merger-induced thick disks and their dependence on initial configuration parameters in our simulations. Finally, we discuss the results in Sect. 4 and draw our conclusions in Sect. 5.
2. Models and initial conditions
We study the interaction and coalescence of a satellite galaxy with a much more massive disk galaxy. These minor merger simulations are part of an on-going program to model and understand the role minor mergers play in the evolution of angular momentum and morphological and kinematic properties of galaxies (see also Qu et al. 2010). The massive disk galaxy (primary galaxy) consists of a dark matter halo which is initially not rotating, a central bulge, and a stellar disk – hereafter we refer to this model with the nomenclature gS0 (=giant S0 galaxy). We also consider initial models containing a gaseous disk, whose mass, Mgas, is 10% or 20% of that of the stellar disk, and to which we refer as “gSa” and “gSb”, respectively. The spherical dark matter halo and the stellar bulge are represented by Plummer spheres (Binney & Tremaine 1987) and neither has any rotation at the beginning of the simulation. The stellar and gaseous disks are represented by Miyamoto-Nagai density profiles (Binney & Tremaine 1987). Table 1 lists the total masses of the halo, bulge and disk components (MH, MB, M∗ and Mgas) and the core radii of the halo and the bulge (rH and rB), as well as the vertical and radial exponential scale lengths of the stellar and gaseous disks (h∗, a∗ and hgas, agas). The elliptical satellite galaxy has a total mass equal to 10% or 5% of that of the primary galaxy – we refer to these models as dE0 and sE0, respectively. It consists of a spherical stellar and a dark matter component, both modeled with initially non-rotating Plummer profiles, whose parameters are also given in Table 1. As we have done in Qu et al. (2010), all galaxy models are evolved in isolation for 1 Gyr before the interaction starts. The orbital parameters for these minor interactions have been described in Chilingarian et al. (2010, Table 9) and Qu et al. (2010, Table 2) and we refer the reader to these papers for a detailed description.
Parameters of the initial models of halo, bulge, stellar and gaseous disks.
In this paper, we follow the nomenclature adopted in Qu et al. (2010), i.e., using a six-character string to indicate the morphology of the interacting galaxies: the first three describe the type of the primary galaxy, “gS0”, “gSa” or “gSb”, depending on its gas fraction, and the following three describe the satellite galaxy, dE0 or sE0. This is followed by the suffix “dir” or “ret”, for prograde or retrograde orbits, respectively. The subsequent two numbers, either “33” or “60”, indicate the initial inclination of the satellite orbit with respect to the disk plane of the primary galaxy. Thus, for example, the nomenclature “gS0dE001dir33” refers to a prograde encounter between a gS0 galaxy and a dwarf elliptical satellite galaxy, with an initial inclination i = 33°, whose initial orbital parameters are those corresponding to the id = “01dir” case listed in Table 9 of Chilingarian et al. (2010).
To study the effect of multiple mergers on the properties of post-merger stellar disk, we ran some simulations in which the primary galaxy accretes consecutively two satellites over a period of 3–5 Gyr. We have considered both the case in which both satellites coming from a fixed direction inclined 33° with respect to the primary disk, as well as the case in which the second satellite comes from a different direction – hereafter we will refer to these models as “multi-A” and “multi-B” respectively. For example, the nomenclature “multi-A, 2 × 10:1” refers to the successive mergers of two satellite galaxies whose mass is one-tenth of that of the primary galaxy and whose orbits are inclined 33° with respect to the primary disk.
All simulations (50 in total) were run using the Tree-SPH code described in Semelin & Combes (2002). A total of NTOT = 528 000 particles have been distributed between the primary and satellite galaxies (see Table 2) for all simulations. We also test the dependence of results on the particle number used in the simulation by running some additional simulations with a total of NTOT = 1 056 000 particles. A Plummer potential is used to soften gravity on small scales, with constant softening lengths of ϵ = 200 pc (ϵ = 170 pc for the high resolution simulations), for all particles. The equations of motion are integrated using a leapfrog algorithm with a fixed time step of 0.5 Myr. With these choices, the relative error in the conservation of the total energy is about 10-6 per time step.
In this study we also compare the vertical structure of minor merger-induced thick disks with those generated by an internal process, through scattering by massive clumps formed in an initially unstable disk, as recently proposed by Bournaud et al. (2009). For this, we analyzed two simulations of gas-rich, unstable disk galaxies from Di Matteo et al. (2008). These use a total number of 120 000 particles, equally distributed among the gas, stars, and dark matter components, whose parameters are the same as those of the gSb model (see Table 1), except for the gas mass, which is initially 50% that of the stellar disk. These gas-rich galaxies are characterized by a very small initial Toomre disk stability parameter for the gaseous component (Qgas = 0.3 and Qgas = 0.1, hereafter called “gSb+u1” and “gSb+u2”, respectively). Reducing the local disk stability causes the gaseous disk to fragment into many clumps, particularly in the “gSb+u2” case. Once formed, these clumps migrate towards the galaxy center; some dissolve under the influence of the tidal field of the disk, while others survive and merge in the galaxy center, contributing to the formation of the central bulge. As recently proposed by Bournaud et al. (2009), these clumps can scatter stars in the pre-existing thin disk, contributing to the formation of a thick disk component.
Particle numbers for primary galaxies and satellites.
3. Results
During the merging process, tidal interactions between merging galaxies deposit part of their energy into stellar motions in the disk of the primary galaxy, thus causing the disk to become kinematically hotter and to spread out both radially and vertically, changing its morphology as well as its kinematics. In this section we will analyze both dissipationless and dissipative minor mergers and their possible role in the formation of the thick disk.
 |
Fig. 1 Stellar distribution in a gSb galaxy model in its initial configuration (left panel) and at 3 Gyr after the start of the simulation (middle and right panels). All panels show the galaxy from an edge-on perspective. Of the post-merger galaxy, both the original stellar population and the new thin disk formed during the merger are shown in the middle panel, while in the right panel we show only stars from the original stellar population of both galaxies. The thickening of the disk is entirely due to stars from the original thin disk and the satellite. The same color and contour scales are used in all panels. Surface density contours are spaced logarithmically and each panel is 40 kpc × 40 kpc in size. |
3.1. Characteristics of the post-merger stellar disk
Here we investigate the vertical stellar distribution of remnant disks in minor mergers, for which we assume a generalized sech profile, 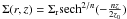 , where Σr is the radial exponential surface density profile and z0 is the disk scale height. This profile can fit, for example, an isothermal sheet if n = 1, and an exponential if n = ∞ – the two limiting cases of this generalized profile. Based on the study of the three-dimensional distribution of disk stars, van der Kruit (1988) found that an intermediate disk model with n = 2 is the most appropriate (see also Schwarzkopf & Dettmar 2000), which is also supported by the theoretical study of Banerjee & Jog (2007). We analyze, as far as possible, the properties of remnant disks as they typically would be observed. First, we project the post-merger stellar disk to edge-on, then average the vertical surface density profiles on both sides of the stellar disk mid-plane and fit them using a sech profile with n = 2, i.e., sech
, where Σr is the radial exponential surface density profile and z0 is the disk scale height. This profile can fit, for example, an isothermal sheet if n = 1, and an exponential if n = ∞ – the two limiting cases of this generalized profile. Based on the study of the three-dimensional distribution of disk stars, van der Kruit (1988) found that an intermediate disk model with n = 2 is the most appropriate (see also Schwarzkopf & Dettmar 2000), which is also supported by the theoretical study of Banerjee & Jog (2007). We analyze, as far as possible, the properties of remnant disks as they typically would be observed. First, we project the post-merger stellar disk to edge-on, then average the vertical surface density profiles on both sides of the stellar disk mid-plane and fit them using a sech profile with n = 2, i.e., sech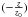 , allowing the scale height parameter z0 to be unconstrained. We also fit the disk scale height for the two limiting cases of the generalized sech profile, n = ∞ and n = 1: the exponential fit gives an on average 1.4 times larger disk scale height than the sech profile, whereas the sech2 fit gives a value which is 0.8–0.9 times smaller.
, allowing the scale height parameter z0 to be unconstrained. We also fit the disk scale height for the two limiting cases of the generalized sech profile, n = ∞ and n = 1: the exponential fit gives an on average 1.4 times larger disk scale height than the sech profile, whereas the sech2 fit gives a value which is 0.8–0.9 times smaller.
The vertical stellar surface density profiles are analyzed between 0.5 and 1 Gyr after the merger is complete, at a time when the post-merger stellar disk has settled roughly into a new equilibrium configuration. At later post-merger times, i.e., t > 1 Gyr, the difference in disk scale height with respect to the value at t = 0.5−1 Gyr is no more than 15% inside r < 6rd. The stellar disk scale length, rd, has been evaluated by projecting the galaxy to face-on. The difference between the final and initial disk scale length is always small, Δrd < 10%, except for dissipative minor mergers with a gas-to-stellar mass fraction fgas = 0.2, where the disk scale length shrinks by ~15−20%. Thus the exact time at which the merger simulations are analyzed beyond 0.5–1 Gyr after the completion of the merger makes little difference in the final results. In this study we also mask the contribution of the bulge component by excluding stars that were initially in the bulge of the primary galaxy and we consider only stars which were initially in the disk of the primary galaxy or in the satellite.
We note that in the case of dissipative minor merger simulations, a new stellar disk forms during the merging process due to star formation in the gaseous disk. This “new” stellar disk component is thin, with scale heights of 300−400 pc only (see Fig. 1 as an example). We will not discuss in detail this newly formed thin disk component, but concentrate on the old stellar disk, i.e., the one that was already in place before the interaction, in order to make a direct comparison with that found in dissipationless mergers. We do not find any young stars at scale heights larger than that of the thin disk formed during the merger.
In the rest of this section, we will examine the vertical structure of the remnant disk after a single dissipationless minor merger, to illustrate the process of thick disk formation during a gas-free minor merger. We will present the vertical stellar distribution and the fitting results, and will later compare these properties with those of remnant thick disks found in dissipative or two consecutive minor merger simulations, as well as with thick disks formed through massive clumps in a gravitationally unstable disk.
3.1.1. Vertical structure of the post-merger thick stellar disk: evidence for a stellar excess
The vertical surface density profile of a thick disk formed through a dissipationless minor merger is shown in Fig. 2. This profile has been evaluated 0.5 Gyr after the completion of the merger. The main features of the profile fits are:
-
a single sech function cannot fit the entire vertical profile. Whilethe lower regions, at z ≤ 2 kpc, can be described by a sechfunction, after removing this sech function there remains a largeexcess of stars at greater heights above the mid-plane(z > 2 kpc);
-
this excess is especially prominent in the inner regions of the disk, at r ≲ 3rd, and it virtually disappears at larger radii;
-
the excess has a scale height several times larger than that of the main thick disk component (i.e., the one at z ≤ 2 kpc): at r = 0, for example, the scale height of the stellar excess is z0 ≈ 2.3 kpc, about 5 times that of the main thick disk component, which has z0 ≈ 0.42 kpc;
-
the excess has a scale height that is approximately constant with distance from the galaxy center, while the thick disk scale height increases with radius, as already shown by Bournaud et al. (2009) and Kazantzidis et al. (2008) – this will be discussed further in Sect. 3.2;
-
due to this excess, two sech functions of different scale heights are needed to fit the entire vertical stellar profile.
 |
Fig. 2 Vertical stellar surface density profiles of a post-merger thick stellar disk at 0.5 Gyr after the completion of a dissipationless minor merger (black). We show profiles at a variety of distances from the galaxy center along the galactic mid-plane, in units of the disk scale length rd. Also shown are the double sech functions fitted to the profiles and their corresponding scale heights z0 in kpc (labeled in red). |
3.1.2. Thick disk and stellar excess: formation, growth and composition
How do the thick disk and the stellar excess develop in the simulations? We show an example of the formation and growth of a thick disk in Fig. 3. After the first pericenter passage of the satellite galaxy (at t = 0.5 Gyr) the thin stellar disk component has already thickened and grown vertically, and after the second pericenter passage, at t = 1.5 Gyr, the stellar disk has acquired the double sech profile. Since the stellar excess is already in place well before the satellite merges with the primary it is not associated generally with stars from the satellite galaxy, but rather composed of stars which were initially in the primary disk and subsequently heated, reaching greater heights during the merging process. In all dissipative mergers and in most of dissipationless ones, stars initially in the disk dominate at all disk heights, in agreement with the results of Purcell et al. (2010). Only in few dissipationless mergers do we find that the outer vertical profile is dominated by stars from the satellite galaxy.
The formation of a double sech profile in the vertical density distribution is not due to the presence of the bulge. Although we excluded bulge stars from the analysis of the vertical profile of the thick disk, we did run simulations of dissipationless minor mergers with bulgeless galaxies. In these simulations we also found a stellar excess with characteristics very similar to simulations including a bulge component.
In summary, stars in the stellar excess have their origin in different regions of the thin disk, which means that they are not only heated vertically, but also redistributed radially. As discussed in Sect. 4, this has consequences for the expected metallicity gradient in the merger remnant.
 |
Fig. 3 Upper panel: vertical stellar surface density profiles as function of radius and time (indicated by color; see lower panel) for a dissipationless minor merger. The radius is indicated by the 4 black labels. Lower panel: the distance between the centers of the satellite and the primary galaxy as function of time. Arrows mark the merger phases which correspond to profiles with the same color and line styles shown in the upper panel. |
3.2. Varying orbital and morphological parameters
3.2.1. Dependence on initial orbital configurations
Regardless of the initial orbital parameters (orbital energy and angular momentum, direct and retrograde orbits, initial orbital inclination of the satellite orbit) we always find a thickened stellar disk in the merger remnant, whose scale height increases with the radial distance along the major axis of the disk-plane (Fig. 4). For the dissipationless mergers over the range rd < r < 3rd the scale height is z0 = 1.4−2.5 kpc, or about 3-6 times larger than the z0 value near the disk center, where z0 = 0.4 kpc. The six sets of different orbital configurations produce a scatter around the mean value of |Δz0|/z0, mean ≲ 15%. The increase in the disk scale height with radius implies that the disk heating is the most significant in the outer regions of the disk. We do not find such a strong thickening of the stellar disk if the galaxy is evolved in isolation for 3 Gyr (see Fig. 4): the disk scale height increases only marginally, less than 25% at r ~ rd, and the thickening is independent of radius.
Early research in self-gravitating stellar disks suggested that the thick disk scale height is independent of radius, assuming that the vertical velocity dispersion decreases exponentially with radius and relates to the disk scale length as hvel = 2rd (van der Kruit & Searle 1981a). Narayan & Jog (2002) generalized this picture by taking into account the gravitational contributions from the gas and the dark matter halo and allowing the ratio hvel/rd to vary. Contrary to previous results, they found that scale heights increased with disk radius within 4 or 5 disk scale lengths, and that the hvel/rd ratio ranged from about 2 to 4.
As pointed out by Quinn et al. (1993), in mergers of primary galaxies with their satellites, the stellar disk is heated in three dimensions and although the velocity dispersion profiles of the remnant disk are similar to those of the initial disk, they show more extended exponential profiles. Fitting both the initial and post-merger vertical velocity dispersion profiles with exponential functions, we found that while the initial profiles usually have hvel/rd ~ 2, in agreement with an initial stellar disk of constant scale height, as assumed in our model, the hvel/rd ratio of the post-merger vertical velocity profile was increased to the range of ~2.5−4, which is in agreement with what Narayan & Jog (2002) found.
From the definition of z0 deduced from Poisson’s and Jeans’ equations, this link between the hvel/rd ratio and the thick disk scale height is not difficult to understand. Assuming the velocity dispersion follows an exponential profile, the definition of z0 (see Eq. (3) in van der Kruit & Searle 1981b) can be rewritten as
![\begin{eqnarray} z_{0}=C_{0}\exp\left[-\left(\frac{2r_{\rm d}}{h_{\rm vel}}-1\right)\frac{r}{2r_{\rm d}}\right] \end{eqnarray}](/articles/aa/full_html/2011/06/aa15224-10/aa15224-10-eq79.png) (1)where
(1)where 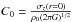 and G is the gravitation constant. σz(r = 0) and ρ0 are the vertical velocity dispersion and the volume density at the galactic center, respectively. It is quite clear from Eq. (1) that z0 is independent of radius if hvel/rd = 2, whereas z0 increases with radius when hvel/rd > 2.
and G is the gravitation constant. σz(r = 0) and ρ0 are the vertical velocity dispersion and the volume density at the galactic center, respectively. It is quite clear from Eq. (1) that z0 is independent of radius if hvel/rd = 2, whereas z0 increases with radius when hvel/rd > 2.
Figure 4 also shows the scale height of the stellar excess present in the vertical surface density profiles seen at z ≳ 4−5 kpc and r ≲ 3rd (see also Fig. 2). The final scale height of the stellar excesses in the simulations are independent of radius and are sensitive to the characteristics of the satellite orbit. Variations in the orbital parameters lead to a large scatter in the vertical scale height of the stellar excesses, of up to 30% (| Δz0|/z0, mean ≲ 30%).
3.2.2. Dependence on satellite central density
Do the flaring of the thick disk and the scale height of the stellar excess found in Fig. 4 depend on the central density of the satellite galaxy? To investigate this point, we ran some simulations changing the central density of the baryonic component of the dE0 satellite, using satellites having a central volume density 50% higher (dE0h) or lower (dE0l) than the reference dE0 galaxy. A denser satellite heats the thick disk more effectively, especially in the inner regions of the primary galaxy (inside ~2rd), thus resulting in a thick disk scale height about 20% higher than that found after the merger of less dense satellites. However, no clear dependence on the satellite central density is found for the characteristics of the stellar excess (see Fig. 5).
 |
Fig. 4 The scale heights z0 of the merger-induced thick disk and stellar excess as function of radius in units of disk scale length, r/rd, for dissipationless minor mergers with six sets of different initial orbital parameters (see also Fig. 2). The shaded regions indicate the scatter in the scale heights. Most of this scatter results from the differences in initial orbital configurations. Also shown are the scale heights of the original stellar disk (dotted line) and after its evolution in isolation for 3 Gyr (dashed line). |
 |
Fig. 5 The scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, for dissipationless minor mergers with three different baryonic central mass concentrations of the merging satellite. The mass of the satellite is the same, but the central volume density is 50% higher (dE0m, dashed lines) or 50% lower (dE0l, dotted lines) than in the reference satellite dE0 (solid lines). |
3.2.3. Dependence on gas fraction
How does including gas in the primary galaxy’s disk affect the outcome of these simulations? In Fig. 6 we compare the disk scale heights of dissipative minor mergers (with gas-to-stellar mass fractions fgas = 0.1 and 0.2) with those of dissipationless mergers. A thick stellar disk is present in all merger remnants, independent of the gas fraction in the primary, and its scale height always increases with radius. Dissipative mergers with fgas = 0.1 have similar scale heights as the dissipationless (gas-free) ones. However, in mergers with fgas = 0.2 a significantly thinner remnant stellar thick disk is formed, of which the scale height at r > 2rd is on average ~20%–30% smaller than in dissipationless mergers. Interestingly, this reduction is comparable to the 25% found for 10:1 dissipative mergers with 20% gas fraction by Moster et al. (2010), which indicates that their conclusions are robust to the use of different initial galaxy models, orbital conditions and numerical codes.
On the other hand, the stellar excess in dissipative minor mergers still has scale heights that are independent of radius, and very similar to those found in dissipationless mergers (see left panel in Fig. 6). This implies that the dissipative gas component and further induced star formation mainly affects the higher density regions close to the remnant disk mid-plane and that it has almost no effect in regions at greater heights above the disk mid-plane. This is consistent with the excess being predominately due to tidal effects early in the merger event.
3.3. Dissipative minor mergers versus clump instabilities
It is of great interest to investigate the differences in the properties of merger-induced thick disks to those formed by secular processes such as scattering due to clumps formed in a gravitationally unstable disk, as recently suggested by Bournaud et al. (2009). To this end, we compare the vertical surface density profiles of thick disks induced by minor mergers with those formed in gas-rich galaxies which are initially unstable to clump formation and were evolved in isolation for 3 Gyr (see Sect. 2 for details of these galaxy models). We found that the resulting scale height in the clumpy isolated galaxies is about 2 times larger, z0 ≈ 0.85, than the initial value and nearly constant with radius, thus confirming the results of Bournaud et al. (2009). Scattering by gas clumps do not only produce thick disks with constant scale heights, but also vertical surface density profiles which do not show any stellar excess (Fig. 7). In principle, this may indicate an observational way to distinguish a secular from a merger origin for thick disks. We will elaborate on this further in the Sect. 4.
 |
Fig. 6 Scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, for minor mergers with three different gas-to-stellar mass fractions, fgas = 0, 0.1 and 0.2. The shaded regions indicate the scatter in the scale heights due to the variety of initial orbital configurations. |
 |
Fig. 7 Vertical density profiles of the post-merger stellar disk in a dissipative minor merger with fgas = 0.2 (upper panel) and of an isolated “clumpy disk” galaxy with fgas = 0.5 (lower panel). Profiles are shown at four different exponential disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. The best fitting sech(z) functions to these profiles and corresponding scale heights are also shown (in red). |
3.4. Consecutive minor mergers and their impact on the thick disk and stellar excess scale heights
In hierarchical structure formation scenarios, galaxies grow through both minor and major mergers and periods of gas accretion from either cooling gas in their halos or from cosmic filaments. Satellite accretion is expected to be quite common in a ΛCDM universe and important for galaxy growth (Guo & White 2008). The dynamical timescale for a satellite in the dark matter halo of a significantly more massive primary galaxy can be, and often is, long compared to the merging time scale. In such a situation we may expect multiple minor mergers to be common since this allows the primary galaxy to have several satellite galaxies that have yet to merge.
What is the effect of consecutive mergers on the vertical stellar distribution of disks and their impact on the thick disk and stellar excess? Do the effects “saturate” – in other words, does the additional heating caused by each subsequent merger have an increasingly smaller effect on heating of the disk? In order to gain insight in this, we compared the impact on the heating of the disk of a single minor merger to that of two sequential minor mergers. We adopted four merger histories and two mass-ratios – a single 20:1 merger and two sequential 20:1 mergers, a single 10:1 and two sequential 10:1 mergers, which we will label as 20:1, 2 × 20:1, 10:1, and 2 × 10:1, respectively. All of these mergers are dissipationless and intended only as an initial exploration of the effects of multiple minor mergers on galaxy disks.
 |
Fig. 8 Vertical stellar surface density profiles of a post-merger thick stellar disk 0.5 Gyr after the completion of a single dissipationless minor merger with a mass ratio of 20:1 (upper panel), and two consecutive dissipationless minor mergers with a mass ratio of 10:1 (lower panel). We show profiles at four different exponential disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. Superposed on these distributions are the fitted double sech functions and their corresponding scale heights (in red). |
 |
Fig. 9 Scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, after a single or two consecutive minor mergers. We show single mergers with a mass ratio of 10:1 and 20:1, and 2 × 10:1 and 2 × 20:1 consecutive merger events. In the consecutive merger cases the satellites are either accreted from the same direction (multi-A) or from different directions (multi-B). |
The vertical surface density profiles of the remnant of a 20:1 and a 2 × 10:1 merger are shown in Fig. 8. Comparing these profiles with those of a single 10:1 merger (Fig. 2), we find, as expected, that the thickness of the final disk increases with the total mass acquired by a galaxy through mergers. In other words, the more mass accreted, the more internal energy accrued, and the more efficient the heating of the stellar disk. But changing the mass of the satellite has an impact also on the formation and resultant scale height of the stellar excess. A 20:1 minor merger bring less energy to the system, which means not only a smaller thick disk scale height, but also a obscure stellar excess: stars originally in the thin disk are not heated enough to reach high vertical distances from the galaxy mid-plane. On the other hand, a 2 × 10:1 heats the thick disk considerably, especially in the outer parts. This depends on our original definition of thick disk and stellar excess. The behavior of thick disk and stellar excess scale heights as a function of radius, for six representative single and two consecutive mergers, is shown in Fig. 9.
In the outer regions, beyond 2rd, the scale height of the remnant disk in the single 10:1 minor merger case is ~1.5 times larger than in the 20:1 merger, whereas the 2 × 20:1 merger has a similar disk scale height as a single 10:1 minor merger. Varying the orbital inclination of the second satellite (“multi-A” and “multi-B” cases) only causes a rather trivial change in the disk scale height. The effect on disk scale height of two 20:1 mergers appears to be cumulative, and almost the same as for a single 10:1 merger (Fig. 9). Thus comparing a 2 × 10:1 merger is like comparing with a 4 × 20:1 merger, provided the effect of multiple mergers does not saturate. From the very simple arguments of Liouville’s theorem and the conservation of energy, this is expected to be the case for dissipationless systems (Binney & Tremaine 1987).
In our simulations of a 2 × 10:1 minor merger, after the first 10:1 merger the resultant thick disk still responds dynamically to the heating induced by the subsequent 10:1 merger (Fig. 9). After the second merger the final disk scale height is 1.5−2 times larger than in a single 10:1 merger. Similarly, the stellar excesses found at greater heights in the vertical stellar distribution have also increased in the subsequent merger events (Fig. 9) – their disk scale heights after a single 10:1 merger are 1.5 times larger than that after a single 20:1 merger. In the 2 × 10:1 mergers, their scale heights are not only ~1.4−2 times larger than in single 10:1 mergers but they also increase with radius. Thus, we find that the effect of two consecutive minor mergers in dissipationless systems does not saturate but is cumulative. However, we note that after the second 1:10 merger the stellar excess begins to develop a scale height that depends (weakly) on radius, and is more pronounced at larger radii where its scale height becomes very similar to that of the thick disk itself (Fig. 9). Thus, at least for the highest mass ratios and in the outer disk, the stellar excess becomes almost indistinguishable from the thick disk. For most of our two consecutive interaction models we confirm what we found for the single mergers, that is stars from the primary disk galaxy dominate the vertical stellar distribution everywhere in the thick disk.
 |
Fig. 10 Tangential velocity profiles of the post-merger stellar disk as function of height from the galaxy mid-plane in dissipationless (upper panels) and dissipational (lower panels) minor mergers with a gas mass fraction of 0.2. Profiles are shown at different disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. |
3.5. Kinematics of thick disk and stellar excess
Do the thick disk and stellar excess have similar kinematic properties? A detailed study of various kinematic properties of minor merger remnants will be made separately (Qu et al. 2011), and here we will discuss only one of the kinematical characteristics of the stellar excess: its rotational lag with respect to thick disk stars. This rotational lag is clear in Fig. 10, where the tangential velocity of stars is shown as a function of the vertical distance from the galaxy mid-plane, for a dissipationless and a dissipative merger. In both cases the tangential velocity decreases with distance from the mid-plane, thus indicating that stars far from the mid-plane plane, which populate the stellar excess, have lower specific angular momentum than stars in the thick disk (which are closer to the mid-plane). This is consistent with the trend found by Di Matteo et al. (2010) for the eccentricities of stellar orbits after minor mergers: stars tend to move on more eccentric orbits as their vertical distance increases and thus tend to rotate more slowly than they did originally.
This increase in the rotational lag is qualitatively in agreement with observations (Ivezić et al. 2008), and based on our models we would expect to find high metallicity, small lag stars at low height, and stars with lower metallicity and larger lag at greater height – this is due to the way the thick disk is formed in our model, through the heating of a thin disk that continuously forms stars.
4. Discussion
 |
Fig. 11 Toomre diagrams of stars at 2–3rd after a prograde minor merger (left), a retrograde minor merger (middle) and in a clumpy disk evolved in isolation for 3 Gyr. Plotted are the quadrature sum of vertical and radial velocities (u and w) as function of the rotational velocity, v, relative to the Local Standard of Rest. The primary galaxy in the merger models has a gas-to-stellar mass ratio of fgas = 0.2. The dashed line marks a total velocity of 180 km s-1, which serves as a potential criteria to separate thick disk stars and halo stars (Venn et al. 2004), and the dotted line is the Local Standard of Rest in these models. Also shown are the observed thick disk stars (triangles), halo stars with high α/Fe abundance (squares) and low α/Fe value (crosses) in the solar neighborhood, see Nissen & Schuster (2010) for further details. The halo stars in retrograde motion are shown in green whereas those in prograde motion are in blue. |
To what extent do the properties of our modeled thick disks formed through minor mergers agree with observations? As previously discussed by Purcell et al. (2010) and Zolotov et al. (2010), minor mergers are able to considerably heat a pre-existing thin disk. We have shown (Sect. 3.1) that the resulting stellar vertical profile is characterized by a thick disk component and a stellar excess, both of which can be fitted by sech profiles with different scale heights. The excess is a natural characteristic of minor merger models, which cannot be reproduced by secular mechanisms, not even through scattering by clumps in unstable gas-rich disks. Identifying these excess stars and determining their properties may thus provide a way to constrain thick disk formation scenarios, but they may be confused with stars in the inner halo and be difficult to find and study in practice (Stanway et al. 2008; Carollo et al. 2010).
Interestingly, some of the excess stars may already have been observed. Nissen & Schuster (2010) reported the presence in the solar neighborhood of stars with halo kinematics, but α/Fe abundances similar to those of thick disk stars. These stars may well be part of the stellar excess component, as we have shown (Sect. 3.5) that excess stars lag rotationally with respect to thick disk stars. If the Milky Way thick disk formed through the heating of a pre-existing thin component by minor mergers at early epochs, we should expect to find an inner halo population (the excess), with abundances similar to those of stars in the thick disk, but lagging with respect to them. Compared to stars originally in the thin disk, stars accreted from satellite galaxies may have abundances which are lower (though probably higher than those of dwarf galaxies currently orbiting in the Milky Way halo) and probably also a lower angular momentum content (see Villalobos et al. 2010). In summary, in the merger scenario the inner halo stars would probably have a population with abundances similar to those of the thick disk, lagging with respect to thick disk stars, but rotating more rapidly than accreted satellites.
The Toomre diagram shows the relationship between the total radial and vertical kinetic energy of stars and the rotational energy relative to the Local Standard of Rest (Sandage & Fouts 1987). As it is based on kinematic energy, it provides us with an appropriate tool to evaluate the results of our models, which are kinematic in nature, and a way to compare with the kinematic properties of various components in the Milky Way.
In minor merger models the stellar excess stars lie exactly in the area of the Toomre diagram where α enhanced stars are found (Nissen & Schuster 2010), thus strengthening the hypothesis that they may originally have been in the thin disk. Of course, the dynamical and chemical properties of thick disks and halos will depend on the properties of the satellite galaxy. We expect the scatter in the dynamics and metallicity to increase with vertical distance, as the fraction of satellite stars increases with height. On the other hand, the clumpy disk model does not reproduce the Toomre diagram of the Milky Way (see the right panel of Fig. 11), since it cannot heat disk stars as efficiently in the vertical direction as minor mergers do. It should be pointed out that our models agree with the Toomre diagram of the Milky Way, although they are neither tuned to reproduce the Milky Way galaxy, nor meant to capture the complex accretion history that it may have had.
Adding a dissipative component (gas) decreases both the vertical scale height and the radial scale length of the thick disk created during a minor merger (see Sect. 3.3). For a gas-to-stellar mass fraction fgas = 0.2, the decrease in thick disk scale height is about ~20% with respect to the dissipationless case, and the decrease in scale length is up to 15%–20%. The ratio of thick disk scale length and particle-number-averaged scale height (rd/z0, aver) is shown in Fig. 12 as function of the circular velocity of the disk, vcir, for simulations with a variety of mass ratio, gas fraction and merger histories. Here vcir is estimated at 4 times the disk scale length, rd, where the disk rotation curve becomes flat, and z0, aver is the number-of-particles-weighted average thick disk scale height within r < 4rd. Since all our primary galaxies have the same mass, as we are basically concerned with primary:satellite mass ratios in our merger simulations, we only sample a single circular velocity. However, we note that more or less massive primaries would produce similar results. We compare our results with observations of late-type galaxies and the MW (Larsen & Humphreys 2003; Yoachim & Dalcanton 2005). For all our minor merger models, whether gas-free or with gas, or single or double merger events, the ratios are consistent with those of extragalactic thick disks and the Milky Way old thick disk. Without a gas component, two consecutive mergers effectively halve the ratio by doubling the disk scale height and keeping the radial scale length almost unchanged. The impact of accreting additional gas on the scale height of the thick disk (which is likely to lead to its contraction) would likely lower the rd/z0, aver ratio, irrespective of whether this additional gas is accreted by merging of gas rich satellites or through accreting gas from the halo or intergalactic medium.
Also shown in Fig. 12 are the ratios for two thick disks formed through internal clumps scattering, which are radially more extended but less thick. Their ratios are on average about 2 times larger than those of the observed thick disks. In this case, additional gas accretion from the galaxy halo or surroundings would only increase the discrepancy between observations and the models.
The loss of angular momentum in the gas during the merger causes both the deepening of the gravitational potential and enhanced star-formation in the densest regions of the disk, which is expected to lead to a larger scale length of the thick disk than of the thin disk newly formed during the merger. This is also supported by observations (Pohlen et al. 2007). In order to estimate the scale length of the thin disk, we consider only stars at disk height |z| < 1 kpc, whereas stars at greater heights (1 < |z| < 5 kpc) are considered to constitute the thick disk – as was done in the analysis of observations of external galaxies (e.g., Neeser et al. 2002). A comparison between our results and observations (Fig. 13) shows a very good overall agreement in the ratio of thick to thin disk scale lengths. This is a natural outcome of minor mergers with a primary disk containing gas and does not require any fine tuning.
Stewart et al. (2008), in a study of the merger history of dark matter halos, found that virtually every MW-sized halo has experienced at least one minor merger with mass ratio ≲10:1 in the last 10 Gyr (see also Guo & White 2008). One minor merger of mass ratio ≲10:1, as we have shown, is not going to destroy the disk and leads to something that looks like a thin+thick disk. However, the effect of dissipationless minor mergers on thickening the stellar disk is cumulative. If the merger frequency is higher, then the merger-induced disk thickening will efficiently destroy the original thin disk, leading to a spheroid dominated early type galaxy. This predicament implies that the evolution history of most disk galaxies must be relatively quiet and suggests that there is a limit to how much mass can be accreted solely through minor mergers. However, we have yet to investigate dissipative multiple mergers and expect that the addition of gas will allow some additional dissipation of the energy and angular momentum of the merger. This would also have the effect of erasing the perhaps unique signatures of the timing of the previous event and result in a more complex evolution (see also Brook et al. 2005).
 |
Fig. 12 Ratio of the thick disk scale length and scale height as function of circular velocity, vcir, for five of our dissipative/dissipationless and single/double minor merger models, as well as for two unstable gas-rich clump disk models (gSb+u1 and gSb+u2, see Fig. 6 for the notations). Also shown are observations of a sample of late-type galaxies from Yoachim & Dalcanton (2005) (open and filled circles) and of the thin and old thick disk of the Milky Way (Larsen & Humphreys 2003). |
 |
Fig. 13 Comparison between observations and our model results of thick-to-thin disk scale length ratios, rd, thick/rd, thin, as function of circular velocity, vcir, from our minor merger models with two gas fractions, fgas = 0.1 and 0.2, and two clumpy gas-rich disk models (gSb+u1 and gSb+u2, see Sect. 2 for the notations). Observations are shown for samples of late-type spirals (Yoachim & Dalcanton 2006, solid black and open circles), (Wu et al. 2002; Abe et al. 1999; Neeser et al. 2002, diamond and triangles), a sample of early type galaxies (Pohlen et al. 2004, diamond with a cross) and the Milky Way (Larsen & Humphreys 2003, square). In addition, a cosmological simulation is shown (from Brook et al. 2004, asterisk). |
The question arises if metallicity or metallicity gradients can be used to distinguish between various thick disk formation models. Within a cosmological context, Brook et al. (2005) discussed that merger-induced star-formation and on-going gas accretion could result in a thick disk stellar population with a homogeneous age and metallicity distribution. In local edge-on galaxies (Mould 2005; Seth et al. 2005; Rejkuba et al. 2009), no-significant vertical color gradients are observed, which suggests the absence of metallicity or age gradients. Although some disk galaxies in the local universe show strong radial metallicity gradients (e.g., Shields 1990), they do not constitute a stringent test of the merger hypothesis, given the dependence on the pre-existing disk and the strong mixing expected.
Our models would not necessarily predict a strong radial or vertical gradient in metallicity or age, for two main reasons: the first is that a vast majority of the stars in the thick disk at heights ≲4–5 kpc are dominated by stars originally in the thin disk, which implies that any radial or vertical gradients in either age or metallicity depend on the properties of the pre-existing disk and not on the properties of the merging satellite galaxy. The second is that mergers are effective in radial mixing, as the induced changes in the orbital families of the disk and in the velocity dispersion would diminish any intrinsic gradients that the original disk may have had (Haywood 2008; Schönrich & Binney 2009).
Furthermore, accreting gas from either the surrounding dark matter halo or cosmic filaments will lower the disk scale height over time. This would have the impact of increasing the ratio of the scale lengths of the thin and thick disks. We have found good agreement for this ratio between our simulations and observations of nearby galaxies (Fig. 12). The agreement would still be reasonable if the scale height of the thick disk were to decrease by almost a factor of 2 (through an accretion-induced increase in the mass surface density of a factor of 2) in our minor merger simulations. For the unstable disk models, which already produce a ratio that is too large, a decrease in the scale height would make the discrepancy even worse.
However, we have yet to investigate multiple mergers which are separated by episodes of significant gas accretion from the halo or filaments. We would expect that such gas will allow for additional dissipation of energy and angular momentum of any subsequent mergers and make the disk more robust against destruction. Thus if gas accretion is important for galaxy growth, the limit on the number of minor mergers before the effective destruction of the disk may be larger than indicated by the results presented here.
The caveat is of course that the variance in the metallicity of the thick disk stars will have increased if the stellar population of the disk has evolved significantly in between merger events. Of course, if gas is accreted and depending on its metallicity and how much star-formation occurs, the metallicity of the disk may have increased or perhaps even decreased. Therefore, for an inherently stochastic process like the minor merger-induced thick disk formation scenario, the key factor for determining the characteristics of the mergers is not the mean value of the stellar metallicity, but its variance in abundances (Richard et al. 2010).
As observations indicate that thick disks are clearly distinct from the thin disk component (e.g., Prochaska et al. 2000; Feltzing et al. 2003; Bensby et al. 2004a,b; Bensby & Feltzing 2006; Fuhrmann 2008) and that they must have formed early and relatively fast, this implies that the only viable formation scenarios are those that form thick disks early, with the thin and the thick disk aligned – with either a parallel or a perpendicular angular momentum vector – and with a generally relatively larger scale length for the thick disks (Pohlen et al. 2007). The minor merger-induced thick disk formation scenario merely requires a pre-existing disk in order to work. In all other scenarios the thick disk either relies critically on the pre-existing disk itself, with the thick and the thin disk at least partially co-evolving – as in the secular evolution models, which must also explain lagging and counter-rotating thick disks – or the thick disk predates the thin disk formation. The difference in scale lengths of the thick and thin disks and the weak chemical and dynamical relationship between the two suggest that any viable mechanism should preserve their rough alignment and have much of the mass of the thin disk form later. Clearly, an early phase of multiple minor mergers would be consistent with the data if such a phase were to last sufficiently long to allow for some enrichment due to type Ia supernovae. Issues of timing and total accreted mass are also important, so as not to destroy the disk completely, which would then provide a natural way for the angular momentum vectors to remain parallel over a Hubble time.
Because mergers can cause strong gas inflows (e.g., Montuori et al. 2010), we would also expect that the properties of the merger-induced thick disk relate somehow to the bulge growth. Although not discussed in detail in this study, we indeed find that the bulge component does grow during minor mergers, thus slowly shifting the galaxies towards earlier Hubble types, and that the effects of minor mergers are cumulative in thickening the disk. A natural outcome of minor mergers is therefore that both the significance and scale height of the thick disk should be related to whether a galaxy is a late- or early-type disk type. Moreover, since mergers can have a wide range of initial orbital parameters, we would expect to find counter-rotating thick disk stars if the interaction are violent enough or that the some satellites haves sufficiently high density to begin to contribute significantly to the kinematics of the thick disk (Qu et al. 2011). Observations have suggested that the thick disk scale height is related to Hubble type (de Grijs & Peletier 1997), that some disk dominated late-type galaxies do not have significant thick disks, and that some thick disks counter-rotate (Morrison et al. 1994; Gilmore et al. 2002; Yoachim & Dalcanton 2005).
Finally, our galaxy models show properties typical of local disk galaxies. Although the details are controversial, if the MW formed both its halo and thick disk at around the same time, over 10 Gyr ago (Prochaska et al. 2000; Feltzing et al. 2003; Bensby et al. 2004a,b; Fuhrmann 2004), then the initial conditions of the MW disk would have been probably different from what we assumed. However, due to the lack of knowledge of the properties of disks in the early universe, the initial conditions adopted for our galaxy models represent a reasonable starting point for an exploration of the impact of gas fraction, orbital parameters and merging history on thick disk formation.
5. Conclusions
We used N-body numerical simulations to investigate if minor mergers are a plausible mechanism to form thick disks that have morphological and kinematic properties consistent with the observations, in particular the vertical surface density profile and the disk scale height. We explored in particular the stellar excess formed through minor mergers. The possibility that minor mergers can scatter stars originally in the thin disk (or in the bulge) to large heights from the galaxy mid-plane has recently been pointed out by Purcell et al. (2010) and Zolotov et al. (2010), but we have for the first time systematically studied the properties of this excess: its vertical distribution, its dependence on gas fraction, orbital parameters and consecutive mergers. Our minor merger simulations cover a variety of initial configuration parameters, e.g. gas-to-stellar mass fractions (fgas = 0, 0.1, and 0.2), initial orbital energies and orientations, two different mass ratio (20:1 and 10:1), as well as the cumulative effect of two consecutive dissipationless minor mergers.
The main results of our study can be summarized as follows:
-
minor interactions efficiently and gradually start heating pre-existing thin stellar disks from the first pericenter passage of the satellite galaxy, well before merging is complete. The resulting vertical surface density profile of the stellar thick disk is characterized by a sech function. Furthermore, a stellar excess is visible in the profile at greater heights z ≳ 4−5 kpc in the inner regions (r ≲ 3Rd), which can also be fitted by an additional sech function with a relatively larger scale height. Due to this excess, a double-sech profile is necessary to fit the entire vertical surface density profile;
-
usually the vertical stellar profile is dominated at all disk heights by stars that were initially in the disk of the primary galaxy. Only in a few dissipationless merger models we find that the stellar excess at greater heights is dominated by the contribution of satellite stars;
-
the excess has morphological and kinematical properties which are distinct generally, but see the 2 × 10:1 case in Fig. 8 from those of thick disk stars (however, see our most massive accretion simulation in Fig. 8, the 2 × 10:1 case);
-
the scale height of the stellar excess is constant in radius, while the thick disk scale height increases with radius – this disk flaring is a characteristic of thick disks formed by minor mergers, as shown previously by Bournaud et al. (2009);
-
the scale height of the thick disk decreases with an increase in the gas-to-stellar mass fraction of the primary disk, while that of the stellar excess does not: no significant dependence on the gas fraction in the primary disk is found, at least for fgas ≤ 0.2;
-
the effect of two consecutive mergers is cumulative, both on thick disk and stellar excess scale height. However, obviously, after some number of consecutive mergers, their impact will saturate, but the exact number necessary for this will depend on a variety of factors such as mass ratio, orbital parameters, etc., which has yet to be explored;
-
stars in the stellar excess rotate slower than stars in the thick disk, and their kinematics are compatible with those of high-α abundant stars found recently by Nissen & Schuster (2010) in the solar neighborhood;
-
in minor mergers the scale length of the thick disk is larger than that of the thin disk, consistent with observations of the Milky Way and other nearby galaxies. In simulations with higher (or lower) gas fractions the ratio of thick to thin disk scale lengths is lower (or higher). Whereas ratios larger than one are a natural outcome of minor mergers, the evolution of a “clumpy disk” (simulating, at least to some extent, the influence of secular processes on the evolution of the disk) produces small ratios that are generally inconsistent with observations. Subsequent gas accretion from the halo, or along filaments in the inter-galactic medium, will likely decrease the thick disk scale height. While this does not represent a major problem for the minor merger scenario, for the unstable disk model it makes its discrepancy with observations worse.
We also compared the properties of thick disks formed by minor mergers and through strong scattering by self-gravitating clumps in unstable gas rich disks (a secular “clumpy disk” scenario). We find that the clumpy disks have smaller disk scale heights, z0 ≈ 0.85 kpc, which are independent of radius (in agreement with the results of Bournaud et al. 2009) and unlike the merger-driven thick disks. The thick disks formed through scattering do not show any stellar excess at large disk scale heights, unlike the merger simulations. Thus a possible way to distinguish between this secular thick disk formation scenario and minor merger models is to investigate the radial distribution of scale heights, as well as the presence and properties of the excess component in the vertical stellar profile at large disk heights.
Our results also put limits on the amount of accretion that thin disks can undergo in their lifetimes. This is not a simple function of accreted mass, as merger-induced star formation within the pre-existing disk will act to both stabilize the disk against destruction and to limit the mass fraction of thick disk stars by dissipating part of the energy of the interaction. Another component which may play an important role in thick disk formation is the bulge component, as observations have implied that thick disk properties relate to the Hubble type. The existence of a pre-merger bulge component, or its growth during the merger process, could prevent the stellar disk from being tidally distorted, or weaken the disk heating, and thus result in a relatively less thick stellar disk in the post-merger phase. Detailed study of the interplay between galactic bulge growth and thick disk formation could further our knowledge of the thick disk component as well as galaxy evolution in general.
Acknowledgments
YQ and PDM are supported by a grant from the French Agence Nationale de la Recherche (ANR). We are grateful to Benoît Semelin and Françoise Combes for developing the code used in this paper and for their permission to use it. We thank the anonymous referee for his/her useful and insightful comments which improved the paper substantially. We also wish to thank Chanda Jog and Gary Mamon for their useful comments. These simulations are available as part of the GalMer simulation data base (http://galmer.obspm.fr).
References
- Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003, ApJ, 597, 21 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Abe, F., Bond, I. A., Carter, B. S., et al. 1999, AJ, 118, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Balcells, M., & Peletier, R. F. 2001, A&A, 367, 428 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, A., & Jog, C. J. 2007, ApJ, 662, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Barbanis, B., & Woltjer, L. 1967, ApJ, 150, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., & Feltzing, S. 2006, MNRAS, 367, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004a, A&A, 415, 155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2004b, A&A, 421, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galacitc Dynamics (Princeton: princeton Univ. Press) [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Kawata, D., Gibson, B. K., & Freeman, K. C. 2004, ApJ, 612, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Gibson, B. K., Martel, H., & Kawata, D. 2005, ApJ, 630, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C., Richard, S., Kawata, D., Martel, H., & Gibson, B. K. 2007, ApJ, 658, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Burstein, D. 1979, ApJ, 234, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., & Sellwood, J. A. 1985, ApJ, 292, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Carney, B. W., Latham, D. W., & Laird, J. B. 1989, AJ, 97, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Carollo, D., Beers, T. C., Chiba, M., et al. 2010, ApJ, 712, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Casetti-Dinescu, D. I., Girard, T. M., Korchagin, V. I., & van Altena, W. F. 2011, ApJ, 728, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Chiba, M., & Beers, T. C. 2000, AJ, 119, 2843 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I., Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2010, A&A, 518, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S., Knapen, J. H., Sheth, K., et al. 2011, ApJ, 729, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., & Bernstein, R. A. 2002, AJ, 124, 1328 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., & Peletier, R. F. 1997, A&A, 320, 21 [Google Scholar]
- Di Matteo, P., Bournaud, F., Martig, M., et al. 2008, A&A, 492, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Lehnert, M. D., Qu, Y., & van Driel, W. 2010, A&A, 525, L3 [Google Scholar]
- Dierickx, M., Klement, R., Rix, H.-W., & Liu, C. 2010, ApJ, 725, 186 [Google Scholar]
- Feltzing, S., Bensby, T., & Lundström, I. 2003, A&A, 397, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fry, A. M., Morrison, H. L., Harding, P., & Boroson, T. A. 1999, AJ, 118, 1209 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, K. 2004, AN, 325, 3 [Google Scholar]
- Fuhrmann, K. 2008, MNRAS, 384, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Wyse, R. F. G., & Norris, J. E. 2002, ApJ, 574, 39 [Google Scholar]
- Guo, Q., & White, S. D. M. 2008, MNRAS, 384, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L., & Quinn, P. J. 1989, in The Epoch of Galaxy Formation, ed. C.S. Frenk, NATO ASI Ser. C, 264, 435 [Google Scholar]
- Ivezić, Z., Sesar, B., Jurić, M., et al. 2008, ApJ, 684, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantzidis, S., Bullock, J. S., Zentner, A. R., Kravtsov, A. V., & Moustakas, L. A. 2008, ApJ, 688, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C. G. 1984, MNRAS, 208, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, J. A., & Humphreys, R. M. 2003, AJ, 125, 1958 [NASA ADS] [CrossRef] [Google Scholar]
- Montuori, M., Di Matteo, P., Lehnert, M. D., Combes, F., & Semelin, B. 2010, A&A, 518, 56 [Google Scholar]
- Morrison, H. L., Boroson, T. A., & Harding, P. 1994, AJ, 108, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, H. L., Miller, E. D., Harding, P., Stinebring, D. R., & Boroson, T. A. 1997, AJ, 113, 2061 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Macció, A. V., Somerville, R. S., Johansson, P. H., & Naab, T. 2010, MNRAS, 403, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Mould, J. 2005, AJ, 129, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, C. A., & Jog, C. J. 2002, A&A, 390, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Näslund, M., & Jörsäter, S. 1997, A&A, 325, 915 [Google Scholar]
- Neeser, M. J., Sackett, P. D., De Marchi, G., & Paresce, F. 2002, A&A, 383, 472 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E. 1995, IAUS, 164, 109 [NASA ADS] [Google Scholar]
- Nissen, P. E., & Schuster, W. J. 2010, A&A, 511, A10 [Google Scholar]
- Norris, J. 1986, ApJS, 61, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, J. E., Humphreys, R. M., & Beers, T. C. 2004, AJ, 127, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., Balcells, M., Lütticke, R., & Dettmar, R. 2004, A&A, 422, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M., Zaroubi, S., Peletier, R. F., & Dettmar, R. 2007, MNRAS, 378, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Prochaska, J. X., Naumov, S. O., Carney, B. W., McWilliam, A., & Wolfe, A. M. 2000, AJ, 120, 2513 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. W., Bullock, J. S., & Kazantzidis, S. 2010, MNRAS, 404, 1711 [NASA ADS] [Google Scholar]
- Qu, Y., Di Matteo, P., Lehnert, M., van Driel, M., & Jog, C. J. 2010, A&A, 515, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qu, Y., Di Matteo, P., Lehnert, M., van Driel, M., & Jog, C. J. 2011, A&A, submitted [Google Scholar]
- Quinn, P. J., Hernquist, L., & fullager, D. P. 1993, ApJ, 403, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ratnatunga, K. U., & Freeman, K. C. 1989, ApJ, 339, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, B. J., Lloyd, J. P., Barnaby, D., et al. 1998, ApJ, 506, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Rejkuba, M., Mouhcine, M., & Ibata, R. 2009, MNRAS, 396, 1231 [Google Scholar]
- Richard, S., Brook, C. B., Martel, H., et al. 2010, MNRAS, 402, 1489 [Google Scholar]
- Sales, L. V., Helmi, A., Abadi, M. G., et al. 2009, MNRAS, 400, 61 [Google Scholar]
- Sandage, A., & Fouts, G. 1987, AJ, 93, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzkopf, U., & Dettmar, R.-J. 2000, A&A, 361, 451 [NASA ADS] [Google Scholar]
- Semelin, B., & Combes, F. 2002, A&A, 388, 826 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seth, A. C., Dalcanton, J. J., & de Jong, R. S. 2005, AJ, 130, 1574 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, M. A., & Gilmore, G. 1989, MNRAS, 237, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, M. A., & Gilmore, G. 1990, MNRAS, 242, 59 [NASA ADS] [Google Scholar]
- Shields, G. A. 1990, ARA&A, 28, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., & Siebert, A. 2003, A&A, 398, 141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. J., & Schwarzschild, M. 1951, ApJ, 114, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Stanway, E. R., Bremer, M. N., Lehnert, M. D., & Eldridge, J. J. 2008, MNRAS, 384, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Statler, T. S. 1988, ApJ, 331, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, K. R., Bullock, J. S., Wechsler, R. H., Maller, A. H., & Zentner, A. R. 2008, ApJ, 683, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Tikhonov, N. A., Galazutdinova, O. A., & Drozdovsky, I. O. 2005, A&A, 431, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsikoudi, V. 1979, ApJ, 234, 842 [NASA ADS] [CrossRef] [Google Scholar]
- van der Kruit, P. C. 1988, A&A, 192, 117 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1981a, A&A, 95, 105 [NASA ADS] [Google Scholar]
- van der Kruit, P. C., & Searle, L. 1981b, A&A, 95, 116 [NASA ADS] [Google Scholar]
- Venn, K. A., Irwin, M., Shetrone, M. D., et al. 2004, AJ, 128, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, A., & Helmi, A. 2008, MNRAS, 391, 1806 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, A., & Helmi, A. 2009, MNRAS, 399, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, Á., Kazantzidis, S., & Helmi, A. 2010, ApJ, 718, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, I. R., Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, M., Helmi, A., Morrison, H. L., et al. 2011, MNRAS, in press [arXiv:1009.2052] [Google Scholar]
- Wu, H., Burstein, D., Deng, Z., et al. 2002, AJ, 123, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, R. F. G., & Gilmore, G. 1986, AJ, 91, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. 2005, ApJ, 624, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Zolotov, A., Willman, B., Brooks, A. M., et al. 2010, ApJ, 721, 738 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Stellar distribution in a gSb galaxy model in its initial configuration (left panel) and at 3 Gyr after the start of the simulation (middle and right panels). All panels show the galaxy from an edge-on perspective. Of the post-merger galaxy, both the original stellar population and the new thin disk formed during the merger are shown in the middle panel, while in the right panel we show only stars from the original stellar population of both galaxies. The thickening of the disk is entirely due to stars from the original thin disk and the satellite. The same color and contour scales are used in all panels. Surface density contours are spaced logarithmically and each panel is 40 kpc × 40 kpc in size. |
| In the text | |
 |
Fig. 2 Vertical stellar surface density profiles of a post-merger thick stellar disk at 0.5 Gyr after the completion of a dissipationless minor merger (black). We show profiles at a variety of distances from the galaxy center along the galactic mid-plane, in units of the disk scale length rd. Also shown are the double sech functions fitted to the profiles and their corresponding scale heights z0 in kpc (labeled in red). |
| In the text | |
 |
Fig. 3 Upper panel: vertical stellar surface density profiles as function of radius and time (indicated by color; see lower panel) for a dissipationless minor merger. The radius is indicated by the 4 black labels. Lower panel: the distance between the centers of the satellite and the primary galaxy as function of time. Arrows mark the merger phases which correspond to profiles with the same color and line styles shown in the upper panel. |
| In the text | |
 |
Fig. 4 The scale heights z0 of the merger-induced thick disk and stellar excess as function of radius in units of disk scale length, r/rd, for dissipationless minor mergers with six sets of different initial orbital parameters (see also Fig. 2). The shaded regions indicate the scatter in the scale heights. Most of this scatter results from the differences in initial orbital configurations. Also shown are the scale heights of the original stellar disk (dotted line) and after its evolution in isolation for 3 Gyr (dashed line). |
| In the text | |
 |
Fig. 5 The scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, for dissipationless minor mergers with three different baryonic central mass concentrations of the merging satellite. The mass of the satellite is the same, but the central volume density is 50% higher (dE0m, dashed lines) or 50% lower (dE0l, dotted lines) than in the reference satellite dE0 (solid lines). |
| In the text | |
 |
Fig. 6 Scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, for minor mergers with three different gas-to-stellar mass fractions, fgas = 0, 0.1 and 0.2. The shaded regions indicate the scatter in the scale heights due to the variety of initial orbital configurations. |
| In the text | |
 |
Fig. 7 Vertical density profiles of the post-merger stellar disk in a dissipative minor merger with fgas = 0.2 (upper panel) and of an isolated “clumpy disk” galaxy with fgas = 0.5 (lower panel). Profiles are shown at four different exponential disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. The best fitting sech(z) functions to these profiles and corresponding scale heights are also shown (in red). |
| In the text | |
 |
Fig. 8 Vertical stellar surface density profiles of a post-merger thick stellar disk 0.5 Gyr after the completion of a single dissipationless minor merger with a mass ratio of 20:1 (upper panel), and two consecutive dissipationless minor mergers with a mass ratio of 10:1 (lower panel). We show profiles at four different exponential disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. Superposed on these distributions are the fitted double sech functions and their corresponding scale heights (in red). |
| In the text | |
 |
Fig. 9 Scale heights of the merger-induced thick disk and stellar excess as function of radial distance in units of disk scale length, r/rd, after a single or two consecutive minor mergers. We show single mergers with a mass ratio of 10:1 and 20:1, and 2 × 10:1 and 2 × 20:1 consecutive merger events. In the consecutive merger cases the satellites are either accreted from the same direction (multi-A) or from different directions (multi-B). |
| In the text | |
 |
Fig. 10 Tangential velocity profiles of the post-merger stellar disk as function of height from the galaxy mid-plane in dissipationless (upper panels) and dissipational (lower panels) minor mergers with a gas mass fraction of 0.2. Profiles are shown at different disk scale lengths, rd, from the galaxy center along the major axis of the galactic mid-plane. |
| In the text | |
 |
Fig. 11 Toomre diagrams of stars at 2–3rd after a prograde minor merger (left), a retrograde minor merger (middle) and in a clumpy disk evolved in isolation for 3 Gyr. Plotted are the quadrature sum of vertical and radial velocities (u and w) as function of the rotational velocity, v, relative to the Local Standard of Rest. The primary galaxy in the merger models has a gas-to-stellar mass ratio of fgas = 0.2. The dashed line marks a total velocity of 180 km s-1, which serves as a potential criteria to separate thick disk stars and halo stars (Venn et al. 2004), and the dotted line is the Local Standard of Rest in these models. Also shown are the observed thick disk stars (triangles), halo stars with high α/Fe abundance (squares) and low α/Fe value (crosses) in the solar neighborhood, see Nissen & Schuster (2010) for further details. The halo stars in retrograde motion are shown in green whereas those in prograde motion are in blue. |
| In the text | |
 |
Fig. 12 Ratio of the thick disk scale length and scale height as function of circular velocity, vcir, for five of our dissipative/dissipationless and single/double minor merger models, as well as for two unstable gas-rich clump disk models (gSb+u1 and gSb+u2, see Fig. 6 for the notations). Also shown are observations of a sample of late-type galaxies from Yoachim & Dalcanton (2005) (open and filled circles) and of the thin and old thick disk of the Milky Way (Larsen & Humphreys 2003). |
| In the text | |
 |
Fig. 13 Comparison between observations and our model results of thick-to-thin disk scale length ratios, rd, thick/rd, thin, as function of circular velocity, vcir, from our minor merger models with two gas fractions, fgas = 0.1 and 0.2, and two clumpy gas-rich disk models (gSb+u1 and gSb+u2, see Sect. 2 for the notations). Observations are shown for samples of late-type spirals (Yoachim & Dalcanton 2006, solid black and open circles), (Wu et al. 2002; Abe et al. 1999; Neeser et al. 2002, diamond and triangles), a sample of early type galaxies (Pohlen et al. 2004, diamond with a cross) and the Milky Way (Larsen & Humphreys 2003, square). In addition, a cosmological simulation is shown (from Brook et al. 2004, asterisk). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


