| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201116544 | |
| Published online | 06 April 2011 | |
Hot HCN around young massive stars at 0.1′′ resolution
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
e-mail: rrolffs@mpifr.de
2
I. Physikalisches Institut, Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
e-mail: schilke@ph1.uni-koeln.de
3
Institut für Theoretische Astrophysik, Universität Heidelberg, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
4
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
Received: 19 January 2011
Accepted: 3 March 2011
Massive stars form deeply embedded in dense molecular gas, which they stir and heat up and ionize. During an early phase, the ionization is confined to hypercompact Hii regions, and the stellar radiation is entirely absorbed by dust, giving rise to a hot molecular core. To investigate the innermost structure of such high-mass star-forming regions, we observed vibrationally excited HCN (via the direct ℓ-type transition of v2 = 1, ΔJ = 0, J = 13, which lies 1400 K above ground) toward the massive hot molecular cores G10.47+0.03, SgrB2-N, and SgrB2-M with the Very Large Array (VLA) at 7 mm, reaching a resolution of about 1000 AU (0.1′′). We detect the line both in emission and in absorption against Hii regions. The latter allows to derive lower limits on the column densities of hot HCN, which are several times 1019 cm-2. We see indication of expansion motions in G10.47+0.03 and detect velocity components in SgrB2-M at 50, 60, and 70 km s-1 relative to the Local Standard of Rest. The emission originates in regions of less than 0.1 pc diameter around the hypercompact Hii regions G10.47+0.03 B1 and SgrB2-N K2, and reaches brightness temperatures of more than 200 K. Using the three-dimensional radiative transfer code RADMC-3D, we model the sources as dense dust cores heated by stars in the Hii regions, and derive masses of hot (>300 K) molecular gas of more than 100 solar masses (for an HCN fractional abundance of 10-5), challenging current simulations of massive star formation. Heating only by the stars in the Hii regions is sufficient to produce such large quantities of hot molecular gas, provided that dust is optically thick to its own radiation, leading to high temperatures through diffusion of radiation.
Key words: ISM: molecules / ISM: structure / ISM: clouds / stars: formation
© ESO, 2011
1. Introduction
The formation of massive stars occurs deep inside dense molecular cloud cores. The high luminosity of massive (proto)stars stirs and heats up the surrounding gas, leading to the evaporation of ice mantles around dust grains and to high degrees of excitation of the molecules. This stage, just prior to ionization and destruction of the molecular gas, is characterized by strong line and dust emission from a compact region, and is called a hot molecular core (e.g. Cesaroni 2005). Since these sources are short-lived, they are rare and hence far away, which hampers the determination of their physical structure (density, temperature, velocity, molecular abundances). Nonetheless, such knowledge is a key information for understanding the process of massive star formation (Zinnecker & Yorke 2007) and for the interpretation of molecular line surveys (e.g. Schilke et al. 2006; Belloche et al. 2007; Bergin et al. 2010), and has been constrained by radiative transfer modeling of both single-dish (e.g. Hatchell & van der Tak 2003; Rolffs et al. 2011) and interferometry observations (e.g. Osorio et al. 2009).
Especially interesting is the hottest molecular gas, which is closest to the heating sources. A good tracer is vibrationally excited HCN (v2 = 1), whose rotationally excited levels lie ~1000 K higher in energy than the ground vibrational state, and which has transitions in the cm-wave regime, whose radiation is not obscured by dust. These so-called direct ℓ-type transitions are intrinsically weak, but have been detected in Galactic high-mass star-forming regions (Thorwirth 2001) as well as toward the proto-planetary nebula CRL618 (Thorwirth et al. 2003b) and the starburst galaxy Arp220 (Salter et al. 2008).
Obviously, this hot gas is very compact, and high spatial resolution is needed to investigate it. In this paper, we present VLA observations (with among the highest resolution ever obtained for thermal molecular line emission) of three massive hot cores which have strong HCN direct ℓ-type lines (as measured with the Effelsberg 100-m telescope, Sect. 3.4). The sources are G10.47+0.03 (e.g. Wyrowski et al. 1999), which lies at a distance of 10.6 kpc (Pandian et al. 2008) and has a luminosity of about 7 × 105 L⊙ (Cesaroni et al. 2010), and SgrB2-N and -M near the Galactic center at 7.8 kpc distance (Reid et al. 2009), which have total luminosities of about 8.4 × 105 and 6.3 × 106 L⊙, respectively (Goldsmith et al. 1992). All sources are sites of very active high-mass star formation and contain several Hii regions.
After describing observations and data reduction (Sect. 2), we present the results (Sect. 3) and the radiative transfer modeling (Sect. 4), discuss the implications (Sect. 5) and draw conclusions (Sect. 6).
Observational summary.
2. Observations and data reduction
2.1. VLA
With the National Radio Astronomy Observatory’s (NRAO’s)1 Very Large Array (VLA) in its BnA configuration we observed three massive star forming regions in the direct ℓ-type line of vibrationally excited HCN at 40.7669 GHz (project AR687). This transition connects the two levels of the v2 = 1, J = 13 doublet, whose energies lie 1411 and 1413 K above the ground state, respectively.
Each of the sources was observed during LST 15-21; G10.47+0.03 on 2009 January 30, SgrB2-M on January 31, and SgrB2-N on February 1. Bandpass calibration was done on 3C 279 and 3C 454.3, and primary flux calibration on 3C 286. The observations were performed in fast-switching mode with 150 s on the source and 30 s on a phase calibrator (1755-225 for G10.47+0.03 and SgrA* for SgrB2), yielding an on-source integration time of about 4.5 h per source. For amplitude calibration, 1733-130 (G10.47+0.03) or SgrA* (SgrB2) was observed every 20 min, and reference pointing was done every hour on these sources.
For G10.47+0.03, we centered one IF with 6.25 MHz bandwidth at 40.762 GHz (shifted from the rest frequency due to the apparent source motion) and one with 25 MHz bandwidth at 40.78 GHz to increase the continuum sensitivity. For the SgrB2 sources, the line is broader, so we used two overlapping IFs with 6.25 MHz bandwidth centered at 40.761 GHz and 40.765 GHz. The channel width is 0.72 km s-1.
Calibration and editing was done in AIPS: Bad data points were flagged; phase, amplitude, and flux were calibrated using the continuum data of the calibrator sources, and bandpass calibration was applied. In MIRIAD2 (Sault et al. 1995), Doppler correction was done and the channels were averaged to a width of 1 km s-1, covering LSR velocities of 48 − 87 km s-1 in G10.47+0.03 and 27 − 93 km s-1 in SgrB2. The continuum was fitted using line-free channels (excluding 58–77, 44 − 80, and 42 − 82 km s-1 in G10.47+0.03, SgrB2-N, and SgrB2-M, respectively) and subtracted from the line data. Imaging was done with almost uniform weighting for continuum maps (MIRIAD robust parameter –2, resulting in beams of 0.12′′ × 0.06′′ for G10.47 and 0.12′′ × 0.08′′ for SgrB2) and more natural weighting for line maps (robust 0.5, resulting in beams of 0.14′′ × 0.1′′ for G10.47 and 0.15′′ × 0.11′′ for SgrB2). For total fluxes and lower noise levels, the continuum was also imaged in natural weighting.
A pixel size of 0.02′′ and a cutoff for cleaning of twice the rms noise in the image was used. Table 1 summarizes beam sizes and noise levels.
For G10.47+0.03, the continuum clean components were used to self-calibrate the phases and apply the solutions to the line data. The absorption lines in this source were almost invisible before self-calibration. The procedure did not improve the SgrB2 data, presumably due to the good calibration with SgrA* only 0.7° away. All figures shown in this paper were created with the GILDAS software3.
2.2. Effelsberg
With the Effelsberg 100-m telescope of the Max-Planck-Institut für Radioastronomie, we observed several sources in HCN direct ℓ-type lines in 2000 (Thorwirth 2001), 2002, and 2007. The lines were the J = 9 transition at 20.18 GHz, J = 10 at 24.66 GHz, J = 11 at 29.58 GHz, and J = 12 at 34.95 GHz. Beam sizes are 37, 31, 26, and 22′′, respectively. Pointing was done on nearby quasars, and is accurate to about 10′′. The different polarizations and scans were averaged, and a baseline was subtracted by fitting a polynomial of order 0 to 5 to line-free channels. The noise tube units measured by the telescope were converted to fluxes by comparison with a source of known flux, mostly NGC 7027 (Ott et al. 1994), which was observed once per day. To correct the deformation of the telescope at low elevations, the resulting flux was multiplied by an additional factor of (1 − 0.01 × (30° − elv))-1 (Gallimore et al. 2001), which is 1.25 at an elevation of 10°, typical for SgrB2.
The observations were complemented by data from the millimeter-wave line survey of SgrB2 with the IRAM 30-m telescope (Belloche et al. 2008).
3. Results
For each source we show spectra (Fig. 1), continuum and integrated line maps, as well as position-velocity diagrams. Absorption lines are summarized in Table 2 and emission lines in Table 3.
From Gaussian fits to the absorption lines, lower limits on the optical depth τ and on the column density of hot HCN can be derived: the line-to-continuum ratio is e − τ if line emission can be neglected, i.e. if the beam-averaged (excitation) temperature of the absorbing gas is much lower than the beam-averaged background brightness temperature – else the line-to-continuum ratio is larger than e − τ. The background radiation is provided by free-free emission from ionized gas of around 104 K, which is at least an order of magnitude larger than the temperature of the absorbing gas. However, the observed continuum is lower than 104 K due to optically thin free-free radiation in parts of the beam (see e.g. Cesaroni et al. 2010, for spectral energy distributions of Hii regions with density gradient). Additionally, the hot molecular gas could emit over the whole beam. Therefore, the real optical depths can be much higher than derived from the line-to-continuum ratio, and the values given in Table 2 are only lower limits.
 |
Fig. 1 The v2 = 1, J = 13 direct ℓ-type line of HCN observed toward several positions in G10.47+0.03 (left column), SgrB2-N (central column), and SgrB2-M (right column). The emission lines are averaged over the areas shown in Figs. 2, 4, and 6, while the absorption lines are observed with the beams given in Table 1. Overlaid in green are Gaussian fits, whose parameters are given in Tables 2 and 3. The vertical dashed lines mark the assumed systemic velocities. |
From τ and the observed line width Δv (FWHM), the HCN column density can be derived, assuming Local Thermodynamic Equilibrium (LTE, see also Sect. 4.1) at a temperature T: using 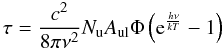 (1)with frequency ν = 40.7669 GHz, Einstein A coefficient Aul = 3.75 × 10-8 s-1 and profile function at Gaussian line center
(1)with frequency ν = 40.7669 GHz, Einstein A coefficient Aul = 3.75 × 10-8 s-1 and profile function at Gaussian line center 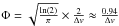 , the total column density N can be obtained from the column density in the upper state
, the total column density N can be obtained from the column density in the upper state 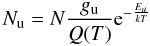 (2)inserting the statistical weight gu = 2J + 1 = 27, the energy of the upper level Eu = 1413 K, and the partition function Q(T) (Barber et al. 2002). The temperature has two competing effects on these equations: while a higher temperature raises Nu, it lowers the population difference between upper and lower level (last factor of Eq. (1)). For given τ and Δv, a minimum of N is reached around 500 K, while twice as many molecules are required at around 300 and 1000 K, and 10 times as many at 200 and 1800 K (100 times at 140 K). In Table 2, we give this minimum, which can be regarded as a lower limit on the column density of hot HCN. Only if the level population difference is higher than expected from LTE, the true HCN column density would be lower.
(2)inserting the statistical weight gu = 2J + 1 = 27, the energy of the upper level Eu = 1413 K, and the partition function Q(T) (Barber et al. 2002). The temperature has two competing effects on these equations: while a higher temperature raises Nu, it lowers the population difference between upper and lower level (last factor of Eq. (1)). For given τ and Δv, a minimum of N is reached around 500 K, while twice as many molecules are required at around 300 and 1000 K, and 10 times as many at 200 and 1800 K (100 times at 140 K). In Table 2, we give this minimum, which can be regarded as a lower limit on the column density of hot HCN. Only if the level population difference is higher than expected from LTE, the true HCN column density would be lower.
 |
Fig. 2 VLA maps of G10.47+0.03. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 3 was obtained. The map size is 2.5′′, about 0.13 pc. |
3.1. G10.47+0.03
The 7 mm continuum (Fig. 2 left) shows the two hypercompact Hii regions B1 and B2 as well as the cometary-shaped ultracompact Hii region A (see also Cesaroni et al. 2010). The total fluxes are 80 mJy for B1, 48 mJy for B2, and 79 mJy for A.
The integrated line map (Fig. 2 right) shows the absorption and the distribution of line emission, which is concentrated around B1 and especially strong between B1 and B2. The absorption lines toward B1 and B2 have a component at lower velocities than the systemic velocity of around 68 km s-1 (derived from emission lines), indicating expansion motions (Figs. 1 and 3).
3.2. SgrB2-N
 |
Fig. 3 Position-velocity diagram of G10.47+0.03, along the arrow shown in Fig. 2. The velocity of 68 km s-1 is marked as a dashed line, and the color scale is centered at 0 K. |
 |
Fig. 4 VLA maps of SgrB2-N. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 5 was obtained. The map size is 3.5′′, about 0.13 pc. |
The continuum map (Fig. 4 left) shows K2 and K3 (Gaume et al. 1995) with fluxes of 70 and 140 mJy, respectively. Outside of the range shown in Fig. 4, we also detect K4, K1 (as a north-south elongated, 0.5′′ long Hii region of around 100 mJy), and a 10 mJy point source at RA 17:47:19.905, Dec –28:22:13.46 (4′′ north of K3). This latter source is associated with C2H5CN emission at 75 km s-1 and 3mm continuum detected by Liu & Snyder (1999). We note that emission from complex molecules (such as amino acetonitrile, Belloche et al. 2008) peaks at K2.
The integrated line map (Fig. 4 right) shows wide-spread line emission around K2. Toward K2 itself, the line absorbs over 80% of the continuum, implying an enormous optical depth (Fig. 1 and Table 2). The southern part seems to have a bit lower velocities than the northern part (Figs. 1 and 5).
3.3. SgrB2-M
The continuum map (Fig. 6 left) resembles the one obtained by de Pree et al. (1998). This source consists of a whole cluster of hypercompact Hii regions, including F3 with 1.3 Jy and F1c/e/f with about 0.5 Jy.
Line absorption is concentrated toward the strongest sources F1 and F3 (Fig. 6 right). Toward F1, the line is at 60 km s-1 with a component at 50 km s-1 in F1f (Fig. 7 left). A northeast-southwest velocity gradient from 69 to 73 km s-1 over 0.3′′ (2300 AU ) is detected in F3 (Fig. 7 right). In addition to the lines from Fig. 1, there is a possible absorption line toward F2 at 57 km s-1 with a width of 7 km s-1 and a line-to-continuum ratio of 0.8. Although not visible in the integrated line map, there is also line emission present, as seen by averaging over a field outside the Hii regions.
 |
Fig. 5 Position-velocity diagram of SgrB2-N, along the arrow shown in Fig. 4. The velocity of 64 km s-1 is marked as a dashed line, and the color scale is centered at 0 K. |
3.4. Single-dish data
We investigated several sources with the Effelsberg 100-m telescope for HCN direct ℓ-type transitions, with no detections in G31.41+0.31, G34.26+0.15, W3(H2O), and W51d. Toward W51e, the J = 12 line was detected (with half the intensity of G10.47+0.03), but the lower-J transitions are questionable (J = 9 at least 10 times lower than in G10.47+0.03). Clear detections in Galactic star-forming regions were only made in Orion-KL, G10.47+0.03, SgrB2-N, and -M. These latter three sources are shown in Fig. 8, with additional IRAM 30-m data for SgrB2. J = 19 is contaminated by an Hγ recombination line whose frequency corresponds to a ~0 km s-1 higher velocity. J = 20 is blended with a transition of ethanol in SgrB2-N and possibly with Heγ in -M.
To compare our VLA data to the single-dish data, Fig. 9 shows the line integrated over the whole map of Figs. 2, 4, and 6. The VLA flux in G10.47+0.03 and SgrB2-N agrees well with the expectations from the Effelsberg data. In SgrB2-M, absorption dominates at low frequencies, but in the IRAM 30-m data weak emission can be seen. Emission also contributes to the VLA flux.
A bit puzzling is the different widths of J = 9 and 10 in the Effelsberg data of SgrB2-M: it is 20 km s-1 in J = 9 and only 6.6 km s-1 in J = 10 (Fig. 8). As we found no blending at the J = 9 frequency, this is probably due to different ratios of the 50, 60, and 70 km s-1 components: for J = 10, the 60 km s-1 component dominates.
 |
Fig. 6 VLA maps of SgrB2-M. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 7 was obtained. The map size is 4′′, about 0.15 pc. |
 |
Fig. 7 Position-velocity diagrams of SgrB2-M, along the arrows shown in Fig. 6. The cut through F1 is shown on the left, F3 on the right. The velocity of 60 km s-1 is marked as a dashed line, and the color scale is dominated by absorption. |
 |
Fig. 8 Single-dish spectra of G10.47+0.03 (left), SgrB2-N (central), and SgrB2-M (right). J = 9 (20 GHz) to 12 (35 GHz) were observed with the Effelsberg 100-m telescope, J = 19 (85 GHz) to 22 (113 GHz) with the IRAM 30-m telescope. Beam sizes vary between 20 and 37′′, so the whole flux is received by the telescope. |
 |
Fig. 9 VLA line flux of G10.47+0.03 (left), SgrB2-N (central), and SgrB2-M (right), integrated over the whole maps shown in Figs. 2, 4, and 6. |
 |
Fig. 10 Rotation diagram for SgrB2-N, based on the single-dish fluxes. The integrated line flux is source-averaged for a source size of 1′′. The first four data points are from Effelsberg, the last four from IRAM 30-m; the VLA flux fits very well to the expectation. |
In SgrB2-N, also the higher-J transitions with level energies up to 2100 K were clearly detected. This allows to construct a rotation diagram (Fig. 10), yielding a temperature of 485 ± 50 K and an HCN column density in a 1′′ source of (5.8 ± 2) × 1019 cm-2. Note that taking absorption and optical depth into account would lead to a higher column density and a lower temperature, since both effects weaken especially the lower-J lines.
4. Modeling
In an attempt to constrain the spatial structure of the hot molecular gas, we constructed radiative-transfer models that reproduce the observations. We employed a trial-and-error technique and compared the model to the data by eye. This method yields (at best) a model that is consistent with the data, but it cannot provide errors of the parameters, and different models could fit as well. The three-dimensional radiative-transfer code RADMC-3D4 was used to compute the radiation that a model emits. It allows adaptive mesh refinement, following user-defined criteria. Dust properties and the dust density distribution as well as location, surface temperature and radius of stars are given as input. The program then computes the dust temperature by tracing photon packets which are randomly emitted by the stars. Additional inputs are density and temperature of ionized gas, the velocity field, fundamental molecular data, and the molecular abundance.
4.1. Assumptions
We use the dust opacity from Ossenkopf & Henning (1994) without grain mantles or coagulation. This is reasonable assuming that ice mantles around dust grains have evaporated completely and recently, so that the grains have had no time to coagulate again. Since the VLA continuum is dominated by free-free emission, the data are not sensitive to the dust emission and so we cannot constrain the dust optical depth, which is a combination of dust opacity and density, through the dust emission. However, the heating is strongly affected by the dust optical depth.
The temperature of the ionized gas is assumed to be 104 K, which is the order of magnitude expected from cooling by trace species. A different temperature would require a different electron density to account for the observed fluxes.
The HCN molecular data are from Thorwirth et al. (2003a) and taken from the Cologne Database for Molecular Spectroscopy (Müller et al. 2001, 2005). We use an HCN abundance of 10-5 relative to H2 for our models. Since we mainly constrain the density of HCN, a different abundance would require different dust densities (with the gas/dust mass ratio of 100). Dust continuum data (from the SMA) indicate that the resulting dust densities are on the right order of magnitude, which justifies this abundance assumption.
The line radiative transfer assumes LTE (full non-LTE radiative transfer is also planned for RADMC-3D). LTE is a reasonable assumption for the observed line as HCN thermalizes to the ambient dust temperature: it is vibrationally excited by 14 μm radiation emitted by warm dust, which is very optically thick at this wavelength due to the high densities (an optical depth of 1 is reached after about 25 AU in a density of 108 cm-3). In this warm and dense environment, also the levels in the ground vibrational state are thermalized by infrared pumping as well as by collisions and radiative excitation. Deviations from LTE occur at low temperatures, where the vibrational levels are not populated anyway.
The models have no macroscopic velocity field. We assume a constant intrinsic line width (microturbulence) throughout the source, which reflects internal motions. The resulting spectra are shifted by the source velocity (68 km s-1 for G10.47+0.03, 64 km s-1 for SgrB2-N, 61 km s-1 for SgrB2-M F1e, and 71 km s-1 for SgrB2-M F3).
 |
Fig. 11 Column density maps of the models for the three sources. The lower panels show the column density (in H2 cm-2) in z-direction, the central panels in y-direction, and the upper panels in x-direction (the arrow points to the observer, who is at positive z). Two Hii regions are marked for each source. The model radiation is compared to the observations in Figs. 12 to 14. |
4.2. Modeling results
To compare the model to the observational data, the synthetic map produced by RADMC-3D, supplemented by distance and coordinate information, is Fourier-transformed, folded with the uv coverage of the observations, and imaged again. The first step of our fitting procedure is to reproduce the observed continuum by creating Hii regions whose sizes and densities are based on Cesaroni et al. (2010) for G10.47+0.03 and de Pree et al. (1998) for SgrB2-M. For SgrB2-N, we use similar models as for G10.47+0.03 since the 1.3 cm data of Gaume et al. (1995) are not sufficient in terms of angular resolution and wavelength. Sizes and densities of the Hii regions are slightly modified to fit the observed continuum. The hypercompact Hii regions B1 and B2 in G10.47+0.03 and K2 in SgrB2-N have thus density gradients (with r-1.5 and outer radii of 1590 AU in B1, 950 AU in B2 and 1000 AU in K2), while all other Hii regions have constant densities.
Cesaroni et al. (2010) and de Pree et al. (1998) also give spectral types of the exciting stars, which are converted to luminosity following Panagia (1973). These stars heat the dust and are, for simplicity, placed in the plane of the sky, except for two Hii regions in SgrB2-M. The dust density distribution is adapted to fit the line observations. Figure 11 shows the column densities in x, y, and z directions of the three models that are described in the following.
G10.47+0.03.
The model consists of a clump centered at B1 whose density follows a Gaussian with 7 × 107 H2 cm-3 at the half-power radius of 7000 AU. This dust is heated by B1 with 105 L⊙, B2 with 8.3 × 104 L⊙, and A with 4.6 × 104 L⊙. The intrinsic line width (FWHM) is 8.3 km s-1. The model output is compared to the observations in Fig. 12.
SgrB2-N.
In the model for SgrB2-N, the dust is heated by K2 with 105 L⊙ and K3 with 8.3 × 104 L⊙. The dust density follows a Gaussian centered at K2 with 7 × 107 H2 cm-3 at the half-power radius of 104 AU . An additional core (Gaussian with 5 × 108 H2 cm-3 at the half-power radius of 1000 AU ) 3000 AU in front of K2 provides the strong absorption. The intrinsic line width is 10 km s-1. Figure 13 shows the comparison to the observations.
SgrB2-M.
In this model, the dust density follows two radial power laws with index 1.5, centered at F1f and F3. The first one starts with 5.5 × 108 H2 cm-3 at a radius of 660 AU , the latter one with 5 × 108 H2 cm-3 at 750 AU. Inside this latter radius, there is an Hii region that contains a star of 8 × 104 L⊙. Additionally, a larger Hii region is located 5000 AU closer to us with a star of 2.5 × 105 L⊙ – F3 is thus split into these two different Hii regions. F1e with 2.5 × 104 L⊙ is located 2000 AU farther away from us than the other Hii regions to facilitate absorption (Fig. 11). Further heating is provided by F1c, F1f, F2, F4 (each 5.4 × 104 L⊙), F1a (3.8 × 104 L⊙), and F3a (2.5 × 104 L⊙). The intrinsic line width is 6.7 km s-1. A comparison to the observations is shown in Fig. 14.
These models are as simple as possible to approach a good fit to the observations, but are not unique. The model maps shown in Figs. 12 to 14 would appear more similar to the data if corresponding noise was added. This noise also makes it difficult to constrain more complicated models, since it is not clear how much of the clumpy substructure is real (which is on the order of only 2 or 3 times the rms noise).
 |
Fig. 12 Model for G10.47+0.03 (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
 |
Fig. 13 Model for SgrB2-N (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
5. Discussion
In this section, we discuss implications from the observational results and the modeling efforts.
5.1. Optical depth
As explained in Sect. 3, lower limits on optical depth and HCN column density can be derived from the absorption lines (Table 2). Outstanding is K2 in SgrB2-N, where the line is optically thick. The column densities of hot HCN toward the Hii regions where it is detected are at least a few times 1019 cm-2, which translates into H2 column densities of 1024 to 1025 cm-2 even for a high HCN fractional abundance of 10-5. This represents only the molecular gas at temperatures above roughly 300 K. In the models, the mass above 300 K is 350 M⊙ in G10.47+0.03, 500 M⊙ in SgrB2-N, and 200 M⊙ in SgrB2-M.
Such large quantities of hot molecular gas are necessary to explain the observations, and challenge theories of massive star formation. Current hydrodynamical simulations produce far too little hot molecular gas (e.g. Peters et al. 2010, with a total mass of 1000 M⊙), both absolute and relative to the total mass, since the highly inhomogeneous structure (filamentary disks) does not lead to diffusion of the heating radiation. This is probably due to the lower initial mass and hence lower column densities and dust optical depths of these models, and it is to be hoped that in the future simulations of cores as massive as the ones presented in the current paper will reproduce our results. Also a high abundance of HCN (on the order of 10-5) in the dense, warm gas is needed, since the dust densities of our models are consistent with dust continuum data from the SMA and a lower abundance would mean an even higher mass of the hot gas. We expect future chemical models to compute such a high HCN abundance, probably through high-temperature gas-phase reactions.
Although HCN thermalizes to the ambient dust temperature, the population difference between the two ℓ-type levels is very small, making them sensitive to the exact excitation conditions. The line optical depth is proportional to the population difference, 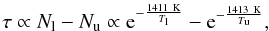 (3)where Tl and Tu are the excitation temperatures for the lower and upper state, respectively. A difference of 0.1% between Tl and Tu causes τ to change by more than 70%; inversion occurs if Tu is 0.14% larger than Tl. The two levels are independently coupled to the ground vibrational state through the 14 μm transitions, which determine the excitation temperatures. If these are different, the analysis would be far more difficult, as one would have to know the exact 14 μm radiation field, where lines could slightly affect the optical depths. However, there is no such mechanism known, and an extreme sub-thermal population difference, which would greatly reduce the required absorption column densities, is highly unlikely because of the agreement between absorption and emission, between J = 13 and other direct ℓ-type lines (Fig. 10), and between the derived column densities and dust emission data. Therefore, we consider LTE a good assumption for this transition.
(3)where Tl and Tu are the excitation temperatures for the lower and upper state, respectively. A difference of 0.1% between Tl and Tu causes τ to change by more than 70%; inversion occurs if Tu is 0.14% larger than Tl. The two levels are independently coupled to the ground vibrational state through the 14 μm transitions, which determine the excitation temperatures. If these are different, the analysis would be far more difficult, as one would have to know the exact 14 μm radiation field, where lines could slightly affect the optical depths. However, there is no such mechanism known, and an extreme sub-thermal population difference, which would greatly reduce the required absorption column densities, is highly unlikely because of the agreement between absorption and emission, between J = 13 and other direct ℓ-type lines (Fig. 10), and between the derived column densities and dust emission data. Therefore, we consider LTE a good assumption for this transition.
If we assume a similar optical depth for the emission lines, say 0.3, and a temperature of 400 K, then the line intensity should be 100 K, which is just the noise level in 1 km s-1 channels and 0.13′′ beams. Owing to the strength of the free-free radiation, we are thus more sensitive to absorption than emission lines. Averaging over a larger region (Fig. 1 and Table 3) lowers both noise and peak intensities. The latter reach up to 300 K in G10.47+0.03, suggesting that optical depth and temperature are higher than the above mentioned assumptions. Surprising is the detection of the line toward G10.47+0.03 A, since no NH3(4, 4) satellites were detected by Cesaroni et al. (2010).
In the model for SgrB2-M, we have placed the Hii regions F3 and F1e in front of and behind the bulk of the molecular gas, respectively. This prevents absorption toward most of F3 and leads to stronger absorption toward F1e. The exact offsets in z are not well constrained, however. To obtain the very strong absorption toward K2 in SgrB2-N, we put a very dense core just in front of the Hii region. This is of course not very satisfying as it is unlikely that such a core is exactly along the line-of-sight. It was however not possible to reproduce both emission and absorption with a more symmetric distribution.
 |
Fig. 14 Model for SgrB2-M (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
5.2. Heating
Heating up large masses of molecular gas requires deeply embedded massive (proto)stars with high luminosities. Their radiation is either originally in the infrared (Hosokawa & Omukai 2009), not producing Hii regions, or is quickly processed to the infrared by dust absorption of the UV radiation. Due to high column densities in all directions, the dust is optically thick even in the infrared and this radiation cannot escape, but diffuses outwards by multiple absorption/emission events until the dust is optically thin to its own radiation. This diffusion (or radiative trapping) leads to much higher temperatures in the inner part; e.g. at 2000 AU from the HCHii region B1, diffusion raises the temperature from 150 K in a low-density model, where diffusion is not effective, to 450 K in the high-density model for G10.47+0.03. This mechanism therefore seems indispensable to account for large masses of hot gas. Additionally, by absorbing stellar UV radiation the dust protects the molecules from dissociation. In general, heating is more efficient if the heating source is inside a density condensation (Kaufman et al. 1998) than if it is external, as could be the case for G34.26+0.15 (Watt & Mundy 1999; Mookerjea et al. 2007).
In our models, the diffusion mechanism is accomplished by dense spherical clumps around heating sources. It is however not clear how many heating sources there are: the stars in the Hii regions are sufficient to reproduce the observed line strength, as the presented models demonstrate. But a good fit can also be achieved when lower-luminosity stars are added to the models according to the Initial Luminosity Function, without changing the stars in the Hii regions. So on the basis of these data it seems not possible to distinguish between the scenarios of heating only by the stars ionizing the Hii regions and heating by Hii regions plus embedded sources which do not emit in the radio regime. We may speculate that there are much more stars present than detected from the free-free radiation, since the observed sources are clusters in formation. Also, there could be more extended (faint) line emission (and the absorption coming from a larger column) than in the models, which would point to additional heating sources. Furthermore, the simple models predict strong self-absorption in the (optically thick) submm rotational transitions within the v2 = 1 state of HCN and H13CN, which is however not observed with the SMA, presumably due to clumpiness (Rolffs et al. 2011, in prep.).
While not excluding the possibility of additional heating sources, we could show that heating by the stars in the hypercompact Hii regions is sufficient to reproduce the observations. Hence, our modeling results suggest that it is unlikely that the main heating is due to embedded objects without ionized gas. Given that the sources are dense condensations deeply embedded in giant molecular clouds and have high column densities, diffusion of radiation, which is necessary to increase the heating, is reasonable even for more inhomogeneous and asymmetric structures than modeled.
5.3. Velocity field
Many systematic motions are hidden in the line width of around 10 km s-1, which contains both turbulent and macroscopic motions. These components (e.g. the presence of rotation, infall, or outflows) can not be disentangled. For all emission lines, the signal-to-noise ratio is too poor to gain accurate information on the velocity structure.
G10.47+0.03.
The most striking feature in this source is an additional blue-shifted absorption component in both B1 and B2 at a velocity of around 60 km s-1, compared to the source velocity of 68 km s-1 (Fig. 1). The NH3(4, 4) absorption (Cesaroni et al. 1998, 2010) is at 53 km s-1 toward B1 and at 61 km s-1 toward B2, with much lower optical depth than the emission component. An explanation could be that the colder gas, probed by NH3(4, 4) with its level energy of 200 K, is mainly in an outflow cone, while the hot gas probed by HCN, v2 = 1, J = 13 is mainly at the systemic velocity close to the HCHii regions and only partly expanding. With the SMA, we see broad blue-shifted absorption in several lines toward the dust continuum peak between B1 and B2 (Rolffs et al., in prep.). This indicates expansion motions involving many different molecular excitation conditions, while at the same time large-scale infall is present (Rolffs et al. 2011). Given the high excitation and the different velocities, an unrelated foreground velocity component is unlikely. The region west of B1 appears to move at a velocity of 67 km s-1, while south of B1 the velocity is 69 km s-1.
SgrB2-N.
While the strong absorption line toward K2 has a line width of 10 km s-1 at the source velocity of 64 km s-1, the emission lines north of K2 have a higher line width and higher velocity, possibly indicating an additional component at ~70 km s-1.
SgrB2-M.
Three velocity components can be seen from the absorption lines (Fig. 7), one at around 50 km s-1 in F1f, one at 60 km s-1 in F1c, F1e, and F1f, and one at around 70 km s-1 in F3. Relative to the ambient velocity of 60 or 64 km s-1, which itself is not well determined due to different components, the F1f line shows blue-shifted absorption, indicating an expansion component, and the F3 line is red-shifted. This could mean infall or a motion of the whole F3 core. The F3 line shows a northeast-southwest velocity gradient from 69 to 73 km s-1 over 0.3′′ (2300 AU ). If that is interpreted as Keplerian rotation, and if it is assumed that the whole orbit is seen and is edge-on, the lower limit on the central mass would be 5 M⊙. The large-scale velocity field shows expansion in the inner parts and infall in the outer parts (Rolffs et al. 2010).
6. Conclusions
With the VLA, we have obtained maps of a high-excitation (1400 K) HCN line at high angular resolution (0.1′′) toward three massive star-forming regions. We see both absorption toward small and dense Hii regions and emission. The infered optical depths require on the order of 1024 H2 cm-2 and 100 solar masses of hot (>300 K) molecular gas within a region of less than 0.1 pc. We note that the column densities of hot HCN derived from the absorption lines are only lower limits, and can be substantially higher especially due to beam dilution. Heating is provided by the stars powering hypercompact Hii regions, possibly complemented by heating sources invisible in the radio domain. Diffusion of radiation in an optically thick dusty environment is likely to increase the temperatures. The line velocities reveal expansion motions in G10.47+0.03 and components at 50, 60, and 70 km s-1 in SgrB2-M, the latter with a velocity gradient. Our three-dimensional radiative transfer modeling with RADMC-3D demonstrate the great power and potential of our approach to constrain the source structure of high-mass star-forming regions. HCN direct ℓ-type lines are a unique tool, whose future observation will also be possible with ALMA and the SKA.
Acknowledgments
We thank the VLA staff for having carried out the observations. S.T. acknowlegdes support by the Deutsche Forschungsgemeinschaft through grant TH 1301/3-1.
References
- Barber, R. J., Harris, G. J., & Tennyson, J. 2002, J. Chem. Phys., 117, 24 [Google Scholar]
- Belloche, A., Comito, C., Hieret, C., et al. 2007, in Molecules in Space and Laboratory, 10 [Google Scholar]
- Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 482, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cesaroni, R. 2005, in Massive Star Birth: A Crossroads of Astrophysics, ed. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 59 [Google Scholar]
- Cesaroni, R., Hofner, P., Walmsley, C. M., & Churchwell, E. 1998, A&A, 331, 709 [NASA ADS] [Google Scholar]
- Cesaroni, R., Hofner, P., Araya, E., & Kurtz, S. 2010, A&A, 509, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Pree, C. G., Goss, W. M., & Gaume, R. A. 1998, ApJ, 500, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Gallimore, J. F., Henkel, C., Baum, S. A., et al. 2001, ApJ, 556, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Gaume, R. A., Claussen, M. J., de Pree, C. G., Goss, W. M., & Mehringer, D. M. 1995, ApJ, 449, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Lester, D. F., & Harvey, P. M. 1992, ApJ, 389, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchell, J., & van der Tak, F. F. S. 2003, A&A, 409, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hosokawa, T., & Omukai, K. 2009, ApJ, 691, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., Hollenbach, D. J., & Tielens, A. G. G. M. 1998, ApJ, 497, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, S.-Y., & Snyder, L. E. 1999, ApJ, 523, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Mookerjea, B., Casper, E., Mundy, L. G., & Looney, L. W. 2007, ApJ, 659, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Osorio, M., Anglada, G., Lizano, S., & D’Alessio, P. 2009, ApJ, 694, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ott, M., Witzel, A., Quirrenbach, A., et al. 1994, A&A, 284, 331 [NASA ADS] [Google Scholar]
- Panagia, N. 1973, AJ, 78, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Pandian, J. D., Momjian, E., & Goldsmith, P. F. 2008, A&A, 486, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peters, T., Banerjee, R., Klessen, R. S., et al. 2010, ApJ, 711, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Rolffs, R., Schilke, P., Comito, C., et al. 2010, A&A, 521, L46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rolffs, R., Schilke, P., Wyrowski, F., et al. 2011, A&A, 527, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salter, C. J., Ghosh, T., Catinella, B., et al. 2008, AJ, 136, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, ASP Conf. Ser., 77, 433 [Google Scholar]
- Schilke, P., Comito, C., Thorwirth, S., et al. 2006, A&A, 454, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorwirth, S. 2001, Ph.D. Thesis, Universität zu Köln [Google Scholar]
- Thorwirth, S., Müller, H. S. P., Lewen, F., et al. 2003a, ApJ, 585, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Wyrowski, F., Schilke, P., et al. 2003b, ApJ, 586, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Watt, S., & Mundy, L. G. 1999, ApJS, 125, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrowski, F., Schilke, P., & Walmsley, C. M. 1999, A&A, 341, 882 [NASA ADS] [Google Scholar]
- Zinnecker, H., & Yorke, H. W. 2007, ARA&A, 45, 481 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The v2 = 1, J = 13 direct ℓ-type line of HCN observed toward several positions in G10.47+0.03 (left column), SgrB2-N (central column), and SgrB2-M (right column). The emission lines are averaged over the areas shown in Figs. 2, 4, and 6, while the absorption lines are observed with the beams given in Table 1. Overlaid in green are Gaussian fits, whose parameters are given in Tables 2 and 3. The vertical dashed lines mark the assumed systemic velocities. |
| In the text | |
 |
Fig. 2 VLA maps of G10.47+0.03. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 3 was obtained. The map size is 2.5′′, about 0.13 pc. |
| In the text | |
 |
Fig. 3 Position-velocity diagram of G10.47+0.03, along the arrow shown in Fig. 2. The velocity of 68 km s-1 is marked as a dashed line, and the color scale is centered at 0 K. |
| In the text | |
 |
Fig. 4 VLA maps of SgrB2-N. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 5 was obtained. The map size is 3.5′′, about 0.13 pc. |
| In the text | |
 |
Fig. 5 Position-velocity diagram of SgrB2-N, along the arrow shown in Fig. 4. The velocity of 64 km s-1 is marked as a dashed line, and the color scale is centered at 0 K. |
| In the text | |
 |
Fig. 6 VLA maps of SgrB2-M. The 7 mm continuum emission is shown on the left, the integrated line map on the right (beams are depicted in the lower left). Contours denote 3 and 6σ levels of the naturally weighted continuum (white, left) and of the integrated line emission convolved to 0.25′′ resolution (black, right). The white crosses give the positions toward which the absorption spectra were obtained and the white boxes the area over which the emission spectra are integrated, shown in Fig. 1. The arrow denotes the direction along which the position-velocity plot of Fig. 7 was obtained. The map size is 4′′, about 0.15 pc. |
| In the text | |
 |
Fig. 7 Position-velocity diagrams of SgrB2-M, along the arrows shown in Fig. 6. The cut through F1 is shown on the left, F3 on the right. The velocity of 60 km s-1 is marked as a dashed line, and the color scale is dominated by absorption. |
| In the text | |
 |
Fig. 8 Single-dish spectra of G10.47+0.03 (left), SgrB2-N (central), and SgrB2-M (right). J = 9 (20 GHz) to 12 (35 GHz) were observed with the Effelsberg 100-m telescope, J = 19 (85 GHz) to 22 (113 GHz) with the IRAM 30-m telescope. Beam sizes vary between 20 and 37′′, so the whole flux is received by the telescope. |
| In the text | |
 |
Fig. 9 VLA line flux of G10.47+0.03 (left), SgrB2-N (central), and SgrB2-M (right), integrated over the whole maps shown in Figs. 2, 4, and 6. |
| In the text | |
 |
Fig. 10 Rotation diagram for SgrB2-N, based on the single-dish fluxes. The integrated line flux is source-averaged for a source size of 1′′. The first four data points are from Effelsberg, the last four from IRAM 30-m; the VLA flux fits very well to the expectation. |
| In the text | |
 |
Fig. 11 Column density maps of the models for the three sources. The lower panels show the column density (in H2 cm-2) in z-direction, the central panels in y-direction, and the upper panels in x-direction (the arrow points to the observer, who is at positive z). Two Hii regions are marked for each source. The model radiation is compared to the observations in Figs. 12 to 14. |
| In the text | |
 |
Fig. 12 Model for G10.47+0.03 (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
| In the text | |
 |
Fig. 13 Model for SgrB2-N (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
| In the text | |
 |
Fig. 14 Model for SgrB2-M (right) compared to the data (left). The model spectra are also overlaid in red. The white contours denote the continuum in steps of 1000 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


