EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 529 (May 2011) A&A, 529 (2011) A29 Full HTML
Free Access
Issue
A&A
Volume 529, May 2011
Article Number A29
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201016265
Published online 25 March 2011

© ESO, 2011

1. Introduction

Solar-like stellar magnetic activity relies on rotation and the presence of a convection zone. According to interior models based on mixing-length theory the transition from radiative to convective envelope takes place near Teff ~ 8300 K (e.g. Christensen-Dalsgaard 2000). This is in rough accordance with X-ray and UV observations, which place the onset of significant chromospheric and coronal emission somewhere between spectral type A7 and F4 (Schmitt et al. 1985; Simon et al. 1994; Schmitt 1997). However, as a consequence of the low spatial resolution of the early-day X-ray instruments, the contaminating X-ray emission from a possible (or known) low-mass binary companion has always been a problem in confirming intermediate-mass stars as intrinsic X-ray sources (e.g. Drake et al. 1994).

Up to 20% of A and B main-sequence (MS) stars are “chemically peculiar” (CP) stars. These stars show enhanced lines of some elements in their spectra which are ascribed to atmospheric abundance anomalies. A sub-group of the CP stars possess strong predominantly dipolar magnetic fields (Borra et al. 1982). It is unclear if these fields are fossil relics of the star formation process or if they have a dynamo origin.

The rapidly oscillating Ap stars (roAp stars; Kurtz 1982) hold special promise for elucidating the potential of dynamos and ensuing magnetic activity within the CP class: the roAp stars have a photometrically and spectroscopically estimated temperature range from 8400 K down to 6800 K corresponding to spectral types A5 to F2. A shallow convective layer is expected to be present. However, these stars have large-scale organized magnetic fields, and suppression of convection by the magnetic field has been invoked to explain the mechanism of the excitation of their pulsations (Balmforth et al. 2001). Consistent with the expected weakness of convection, no evidence for chromospheres have been found so far (Shore et al. 1987; Seggewiss 1990). On the other hand, the possible detection of Pm II lines with short half-life may be explained by flaring activity (Fivet et al. 2007). None of the roAp stars is a spectroscopic binary (Hubrig et al. 2000) facilitating the interpretation of eventually detected signs of activity.

X-ray emission is one of the most efficient indicators of magnetic activity. In this paper we present the results from a Chandra observation of the roAp star γ Equ, the slowest rotator of the CP class and, thus, the least likely to exhibit activity generated by a rotation-dependent dynamo. We introduce the target in Sect. 2. In Sects. 3 and 4 we provide the findings from our investigation of the nature of our target. The X-ray observations and their results are described in Sect. 5. A synthesis and our conclusions are given in Sect. 6.

2. The target, γ Equ

What made us suspicious of magnetic activity on γ Equ is the detection of a nearby X-ray source the ROSAT Faint Star Catalogue (FSC). The offset between the FSC X-ray position and the optical position of γ Equ is 28.1′′, i.e. at the limit of the ROSAT error box. γ Equ shows no signs for radial velocity variability due to orbital motion, and thus it has no spectroscopic companions (Hubrig et al. 2000). However, it is known to be a close visual binary (see Sect. 3) that can be resolved in X-rays only with Chandra.

Measurements of the longitudinal magnetic field of γ Equ over nearly six decades show a clear sinusoidal pattern for which Bychkov et al. (2006) derived a period of 91.3 ± 3.6 yrs. Rotational modulation of an inclined dipole is the most widely favored scenario for explaining this presumably cyclic variability, implying extremely slow rotation for γ Equ, and indeed making it the slowest rotator among all magnetic CP stars.

For our study we adopt the fundamental parameters of γ Equ from Hubrig et al. (2007): log Teff    [K]  = 3.882 ± 0.017 and log (L/L⊙) = 1.144 ± 0.049 with the Hipparcos parallax 28.38 ± 0.90 mas (Perryman et al. 1997). We note that the stellar parameters derived by Perraut et al. (2011) combining interferometric measurements of the star’s angular diameter with modeling of the spectral energy distribution are compatible within the error bars with those given by Hubrig et al. (2007). Hubrig et al. (2007) have estimated the mass and age of γ Equ interpolating the solar-abundance Schaller et al. (1992) tracks. In this paper we resort to the MS evolutionary calculations of Pietrinferni et al. (2004). These models have the advantage of covering a wide range of masses, 0.5...10 M⊙, such that they can be applied to both γ Equ and its fainter visual companion (see Sect. 3). Isochrones and tracks of these models can be downloaded from the BaSTI database1 for various sets of parameters. We use the standard solar model with initial He abundance of Y = 0.273 and metallicity Z = 0.0198. For stars with mass above 1.1 M⊙ overshooting from the convective core is taken into account in these calculations. Interpolating these models we find for γ Equ a mass of 1.81 ± 0.04 M⊙ and an age of 0.88 ± 0.17 Gyr. The uncertainties on the mass and age are derived considering the uncertainties of Teff and Lbol given by Hubrig et al. (2007). Our results are consistent with the mass and age obtained by Hubrig et al. (2007).

3. The nature of the companion

The Washington Double Star Catalogue (henceforth WDS; Mason et al. 2001) lists three companions for γ Equ. The closest companion was also detected in recent adaptive optics imaging with NACO at the VLT (Schöller et al., in prep.) at a separation of a = 0.826′′ ± 0.003′′ and position angle of θ = 256.8° ± 0.5°; see Fig. 1 (left). Schöller et al. estimate K = 4.09 ± 0.26 mag for the primary and K = 6.80 ± 0.29 mag for the secondary.

thumbnail Fig. 1

Left: NACO K-band image centered on γ Equ  B. Right: X-ray image in 0.3−8.0 keV with 0.25′′ pixel size. The position of the X-ray source is highlighted with a yellow (small) circle. Positions indicated by x-shaped symbols denote the proper motion corrected Hipparcos position of γ Equ A at the time of the Chandra observation (black) and the corresponding expected position of the companion according to the orbit solution (yellow and smaller). The expected position of the primary, γ Equ A, as inferred from the orbit solution for the assumption that the companion is located at the X-ray position, is shown as black (larger) circle.

To constrain the nature of the companion we searched for further information in the literature. We extracted optical photometry from the Tycho catalog (ESA 1997): BT = 9.85 ± 0.03 mag and VT = 8.69 ± 0.02. These values can be converted to the Johnson system using the transformations given in the Introduction to the Hipparcos and Tycho Catalogues. We assume coevality with γ Equ  A, i.e. an age of  ~0.88 Gyr, in order to derive the stellar parameters from the evolutionary models. Pietrinferni et al. (2004) provide B − V colors for each grid point in their calculations. For our measured (B − V)J = 0.99 ± 0.03 we obtain a mass of 0.8 M⊙, a luminosity of log (L/L⊙) = −0.6, and an effective temperature log Teff    [K]  = 3.68. According to Kenyon & Hartmann (1995) this temperature corresponds to a spectral type of K2.5 V.

4. A preliminary orbit solution

We combined our NACO measurement of γ Equ with data from the WDS catalog2 (WDS coordinates 21103 + 1008) and from Hipparcos to derive the preliminary orbit of γ Equ  AB shown in Fig. 2. The measurements listed in the WDS cover the years between 1867 and 1994. Uncertainties on the WDS astrometry were estimated based on the scatter of separation (0.160′′) and position angle (2.4°) relative to quadratic polynomial fits of these quantities versus time. The resulting reduced χ2 of the orbital fit is 1.8, and preliminary orbital elements with their formal uncertainties are given in Table 1. Using the Hipparcos parallax, we derive a total mass for the system γ Equ AB of 2.4 ± 0.4 M⊙. With the primary mass given from the HR diagram, the mass of component B is estimated to be 0.6 ± 0.4 M⊙ consistent with its photometry.

Given the large uncertainties of the astrometric data points, we do not put emphasis on the mass derived from the orbit. The orbit solution is, however, useful to predict the position of the secondary relative to the primary at the epoch of the X-ray observations, shown in Figs. 1 and 2 and in Table 2.

thumbnail Fig. 2

Apparent orbit of γ Equ  AB. The position of the primary is off to the left outside the displayed portion of the orbit. The NACO measurement uncertainty ellipse is enlarged by a factor of 2 for clarity. The Hipparcos measurement is labeled “Hp”. A diamond marks the expected position of the companion at the date of the Chandra observations.

Table 1

Preliminary orbit for γ Equ  AB (see Fig. 2).

Table 2

Separation between γ Equ A and B measured with different instruments at different epochs and corresponding predictions from orbit.

5. X-ray observations

γ Equ was observed under Obs-ID 9910 for 10 ks with Chandra using the Advanced CCD Imaging Spectrometer (ACIS-I). The data analysis was performed with the CIAO software package3 version 4.2. We have applied standard filtering to the event file and applied the good time interval file. We checked that there are no cosmic ray afterglows in the image around the position of γ Equ. Source detection was carried out with the wavdetect algorithm (Freeman et al. 2002) using an image with spatial resolution of 0.25′′/pixel and a congruent, monochromatic exposure map for 1.5 keV.

5.1. X-ray image

A zoom into the X-ray image for the 5′′ × 5′′ around γ Equ is shown in Fig. 1 (right). The proper motion corrected Hipparcos position of the roAp star is marked with a large black x-point. The only X-ray source detected in the vicinity of γ Equ A (marked with a small yellow circle in Fig. 1) is located 1.31′′ to the south-west (θ = 247.6°). The position angle is roughly coincident with the direction of the companion γ Equ B. Table 2 summarizes the separations between γ Equ A and the companion measured with Hipparcos, NACO and Chandra, and compares them to the separation expected from the orbit solution. The expected position of the companion at the time of the Chandra observation with respect to the proper motion corrected Hipparcos position of γ Equ A according to the orbit solution is marked with a small yellow x-point in Fig. 1. Given the difference in the separation between the expected position of γ Equ B and the X-ray source it is appropriate to consider the astrometry.

The positional accuracy of ACIS-I is  ~ 0.6′′ at 90% confidence. We have performed source detection on the full Chandra image (ACIS-0123) with the aim to better constrain the astrometry of the X-ray coordinates by cross-correlation with optical and infrared (IR) catalogs. However, only few of the 26 X-ray sources detected across the ACIS-I image have known counterparts at other wavelengths, and all of them are either very weak (<10 counts) or at large off-axis angle. No systematic offset between optical/IR and X-ray coordinates can be deduced. The adaptive optics image of the VLT does not allow for absolute astrometry and there are no other objects in the NACO field to which we could tie γ Equ.

In the following we assume that γ Equ  B coincides with the X-ray source position. This seems a reasonable hypothesis, given the fact that the accuracy of the absolute X-ray position may be uncertain by up to two pixels in Fig. 1, while the Hipparcos positional accuracy (~1 mas) and proper motion accuracy (1−2 mas/yr) are superb. Shifting the image accordingly, the position of the primary, γ Equ  A, would then correspond to the large black circle in Fig. 1, using the separation and position angle from the orbit solution (Sect. 4).

It seems that there is an excess of photons over the average background emission near the position of the primary, that we shall tentatively call “Source 2”. This suggests that γ Equ  A is a faint X-ray source. However, this emission seems to be separated by more than the expected  ~ 0.8′′ from the center of the brighter source associated with the secondary. The precise location of this emission can not be determined given its small separation from the secondary’s X-ray emission and the low photon statistics (4 counts; see below). As a test on the significance of “Source 2” we computed the expected contribution from the wing of the point-spread-function of the X-ray source to the observed counts at the proper motion corrected Hipparcos position of γ Equ  A. In a 0.5′′ radius around this position 1.41 counts are expected. The Poisson probability of finding the observed 4 photons in the same radius is 5%.

5.2. X-ray properties of the γ Equ binary

When examining the properties of the X-ray source associated with the companion we consider only photons within a 0.75′′ radius, to avoid the (small) contribution from “Source 2”. There are 89 counts in this photon extraction region. No evidence for flaring is present.

An individual response matrix and auxiliary response were extracted using standard CIAO tools. The background of ACIS is negligibly low. We fitted the spectrum, rebinned to a minimum of 5 counts per bin, in the XSPEC 12.6.0 environment with a one-temperature thermal model subject to absorption (wabs · apec) for a range of initial values for temperature and column density. The elemental abundances relative to hydrogen are adopted from Wilms et al. (2000) and are globally tied to Z = 0.3 Z⊙, such that the free parameters of this model are temperature (kT), emission measure (EM) and column density (NH).

The best fit parameters are given in Table 3 together with uncertainties for a 68% confidence level. As expected for a nearby star without circumstellar matter, the best fit has no absorption. The spectrum is formally also compatible with an absorbed plasma of nearly one dex higher emission measure (see Table 3). However, this solution goes along with quite low temperature and we consider it unlikely. The luminosity in the 0.3−8.0 keV band is log Lx    [erg/s]  = 28.06, where we have corrected for the flux in the PSF wings that were missed because of our limitation of the photon extraction radius.

For the ROSAT FSC source (0.020 ± 0.008 cts/s) we derive with PIMMS4 a similar X-ray luminosity of log Lx    [erg/s]  = 28.3. For this estimate that refers to the 0.12−2.48 keV band we have assumed a Raymond-Smith spectrum with the temperature derived from the Chandra data.

Table 3

XSPEC fit results for the X-ray source associated with γ Equ B.

The total of only four photons ascribed to “Source 2” prohibits any firm conclusions on its X-ray properties. The photon energies are 0.7,0.9,1.2 and 1.8 keV, suggesting spectral hardness similar to that of the emission associated with γ Equ  B. From the arrival time distribution of the photons we do not infer evidence for flaring. Assuming the same X-ray temperature as for γ Equ  B we obtain with PIMMS a luminosity of log Lx    [erg/s]  = 26.6.

6. Discussion and conclusions

The atmospheres of the roAp stars can be termed pathological. Cowley et al. (2004) and Fivet et al. (2007) called attention to the possible presence of unstable elements (Tc and Pm) in some roAp stars. The longest-lived Pm isotope has a half-life of only 17.7 years. Accelerated particles may lead to nucleosynthesis of short-lived elements on the surface of Ap stars (Goriely 2007). It is a well-known fact that charged particles are accelerated during stellar and solar flares (Hudson & Ryan 1995). These particles thermalize their energy, giving rise to high-energy X-ray and γ-ray emission. While the latter has remained undetectable on stars other than the Sun, part if not all of the X-ray emission from magnetically active stars is usually attributed to such flare events. Therefore, it is not implausible to attribute the presence of isotopes with short half-lifetime in roAp stars to flare activity. The detection or failure to find X-rays from these stars may, therefore, provide critical information on the state of the plasma in their atmospheres.

Our search of several X-ray catalogues for X-ray sources coinciding with a roAp star, brought forth only one object, γ Equ. We have now shown in a dedicated Chandra observation that the bulk of this X-ray emission must be ascribed to a late-type companion. The photometry of this object points to an early-K spectral type, assuming coevality with γ Equ  A. The physical pairing with the primary is corroborated by clear evidence for orbital motion. The X-ray luminosity (log Lx = 28.1), X-ray temperature (kT = 0.5 keV) and fractional X-ray luminosity  [log (Lx/Lbol) = −5]  are in accordance with the expectation for the age and spectral type of γ Equ  B; cf. Preibisch & Feigelson (2005); Schmitt et al. (1990).

More important is the possible identification of faint X-ray emission from the roAp star. The enhanced number of photons to the north-east of the secondary has low probability to be a statistical fluctuation but its association with γ Equ  A could not be established with certainty due to uncertain astrometry. If this faint emission is attributed to γ Equ  A, its fractional X-ray luminosity is extremely low, log (Lx/Lbol) = −7.9.

The mass and age of γ Equ  A are similar to the normal, i.e. non-peculiar, A-type star Altair shown by Robrade & Schmitt (2009) to be an X-ray emitter with log (Lx/Lbol) = −7.4. Contrary to γ Equ  A, Altair is a fast rotator and its X-ray properties are ascribed to compact structures at low latitudes, i.e. its X-ray emission can reasonably be explained by a weak solar-like corona. The extremely long period derived from the magnetic field variations for γ Equ  A makes such an interpretation difficult as it translates to extreme values for the Rossby number (R0 = τconv/Prot) that have never been investigated. Extrapolation of the empirical relation between X-ray emission and rotation rate for MS stars of masses  < 1.3 M⊙ (Pizzolato et al. 2003), if valid for stars of the mass of γ Equ  A, would predict several orders of magnitude fainter X-ray luminosity than inferred from the detection of 4 counts in our Chandra observation. Therefore, for γ Equ  A, either the magnetic period is not identical with the rotation period or the X-ray emission mechanism is not due to a solar-like dynamo on the roAp star.

While residual dynamo activity connected to a (shallow) convection zone is the only viable mechanism for intrinsic X-ray production in normal intermediate-mass stars, magnetically confined wind-shocks (MCWS) provide an alternative in the case of Ap stars. MCWS have been invoked as explanation for the X-ray emission from the Ap star IQ Aur (Babel & Montmerle 1997). The X-ray luminosity of IQ Aur (log Lx = 29.6) is about 1000 times higher than that of γ Equ  A (see Sect. 5.2). According to Babel & Montmerle (1997) for the MCWS model Lx scales with the magnetic field strength (B ∗ ), the mass loss rate (ṀW) and the terminal wind velocity (v∞) as 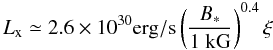(1)and 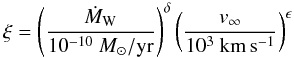(2)with δ = 1 and ϵ ≈ 1...1.3. In the case of γ Equ  A, the value measured for the maximum longitudinal field is Bl,max ≈ 1 kG (Bychkov et al. 2006). According to Aurière et al. (2007), the surface field of a dipole is Bs ≥ 3.3Bl,max. We further assume v∞ ≃ 600 km s-1, the value derived for IQ Aur by Babel & Montmerle (1997). With these numbers the mass loss rate required to sustain the X-ray luminosity estimated from our observation is 2 × 10-14 M⊙/yr. Michaud & Charland (1986) showed that the CP phenomenon appears only for ṀW < 10-12 M⊙/yr and that mass loss rates on magnetic Ap stars may, indeed, be as small as 10-15 M⊙/yr. If we further set for the velocity of the shock (vsh) forming from the collision of the winds from the two hemispheres in the equatorial plane vsh ≃ v∞, the strong shock condition implies a shock temperature of  ≈ 0.35 keV. As argued in Sect. 5.2 the energies of the four photons from “Source 2” hint at a similar spectral temperature as measured for γ Equ B, 0.52 keV, which is roughly consistent with the above estimate. Clearly, these order of magnitude estimates that rely on a reasonable guess and approximations for some parameters can serve as an argument for plausibility of the MCWS scenario on γ Equ  A but do not demonstrate its actual presence on this star.

An alternative explanation for the X-ray photons that we ascribed to γ Equ  A would be an additional unseen companion. Such an object would also solve the problem of the discrepancy between the separations of γ Equ  AB measured in the near-IR from the NACO image on the one hand and in the X-ray image (γ Equ B vs. “Source 2”) on the other hand; see Fig. 1. This close companion would have to have a separation of only  ~ 0.4′′ from γ Equ  A. At this separation 90% completeness is reached in the NACO image for companions with a flux of at least 1% of the primary (Fig. 4 of Schöller et al. 2010), i.e. any such hidden companion in our case would likely be fainter than K ~ 9 mag because it escaped detection with NACO.

Clearly, the possible detection of X-ray emission from the roAp star γ Equ  A based on 4 photons needs to be corroborated by future deeper observations. If confirmed, the X-ray emission may be a diagnostic for the energetic events that are believed to be at the origin of the production of unstable elements on some roAp stars. The fact that radioactive elements are not currently seen on γ Equ  A itself does not exclude this scenario. The exotic elements may be concentrated in localized regions on the stellar surface which, as a consequence of its very slow rotation, may remain hidden to the observer for decades. Spots of rare-earth elements are well-established in the Ap star HR 465 (e.g. Cowley & Rice 1981; Rice 1988), for which the presence of Pm II has been suggested. HR 465 shares with γ Equ  A the characteristic of a very long rotation period (~22−24 yrs) but it is not a roAp star.

1

The Bag of Stellar Tracks and Isochrones database is accessible at http://albione.oa-teramo.inaf.it/

3

CIAO is made available by the CXC and can be downloaded from http://cxc.harvard.edu/ciao/download/

4

The Portable Interactive Multi-Mission Simulator (PIMMS) is accessible at http://asc.harvard.edu/toolkit/pimms.jsp

Acknowledgments

B.S. wishes to thank Loredana Prisinzano and Ettore Flaccomio for stimulating discussions. We would like to thank Serge Correia

for contribution to the NACO data reduction. We appreciate the valuable feedback of the referee, M.Aurière. B.S. acknowledges financial support by ASI-INAF agreement I/009/10/0. We have used data and the software CIAO obtained from and provided by the Chandra X-ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of the National Aeronautics Space Administration under contract NAS8-03060. Observations were also made at the ESO Paranal Observatory with the VLT under programme ID 079.D-0537(A). Moreover this research has made use of the Bag of Stellar Tracks and Isochrones (BaSTI) database and of the Washington Double Star Catalog maintained at the US Naval Observatory.

References

  1. Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Babel, J., & Montmerle, T. 1997, A&A, 323, 121 [NASA ADS] [Google Scholar]
  3. Balmforth, N. J., Cunha, M. S., Dolez, N., Gough, D. O., & Vauclair, S. 2001, MNRAS, 323, 362 [NASA ADS] [CrossRef] [Google Scholar]
  4. Borra, E. F., Landstreet, J. D., & Mestel, L. 1982, ARA&A, 20, 191 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bychkov, V. D., Bychkova, L. V., & Madej, J. 2006, MNRAS, 365, 585 [NASA ADS] [CrossRef] [Google Scholar]
  6. Christensen-Dalsgaard, J. 2000, ASPC, 210, 187 [NASA ADS] [Google Scholar]
  7. Cowley, C. R., & Rice, J. B. 1981, Nature, 294, 636 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cowley, C. R., Bidelman, W. P., Hubrig, S., Mathys, G., & Bord, D. J. 2004, A&A, 419, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Drake, S. A., Linsky, J. L., Schmitt, J. H. M. M., & Rosso, C. 1994, ApJ, 420, 387 [NASA ADS] [CrossRef] [Google Scholar]
  10. ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
  11. Fivet, V., Quinet, P., Biémont, É., et al. 2007, MNRAS, 380, 771 [NASA ADS] [CrossRef] [Google Scholar]
  12. Freeman, P. E., Kashyap, V., Rosner, R., & Lamb, D. Q. 2002, ApJS, 138, 185 [NASA ADS] [CrossRef] [Google Scholar]
  13. Goriely, S. 2007, A&A, 466, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Hubrig, S., Kharchenko, N., Mathys, G., & North, P. 2000, A&A, 355, 1031 [NASA ADS] [Google Scholar]
  15. Hubrig, S., North, P., & Schöller, M. 2007, Astron. Nachr., 328, 475 [NASA ADS] [CrossRef] [Google Scholar]
  16. Hudson, H., & Ryan, J. 1995, ARA&A, 33, 239 [NASA ADS] [CrossRef] [Google Scholar]
  17. Kenyon, S. J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
  18. Kurtz, D. W. 1982, MNRAS, 200, 503 [NASA ADS] [Google Scholar]
  19. Mason, B. D., Wycoff, G. L., Hartkopf, W. I., Douglass, G. G., & Worley, C. E. 2001, AJ, 122, 3466 [NASA ADS] [CrossRef] [Google Scholar]
  20. Michaud, G., & Charland, Y. 1986, ApJ, 311, 326 [NASA ADS] [CrossRef] [Google Scholar]
  21. Perraut, K., Brandão, I., Mourard, D., et al. 2011, A&A, 526, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
  23. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
  24. Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Preibisch, T., & Feigelson, E. D. 2005, ApJS, 160, 390 [NASA ADS] [CrossRef] [Google Scholar]
  26. Rice, J. B. 1988, A&A, 199, 299 [NASA ADS] [Google Scholar]
  27. Robrade, J., & Schmitt, J. H. M. M. 2009, A&A, 497, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [NASA ADS] [Google Scholar]
  29. Schmitt, J. H. M. M. 1997, A&A, 318, 215 [NASA ADS] [Google Scholar]
  30. Schmitt, J. H. M. M., Golub, L., Harnden, Jr., F. R., et al. 1985, ApJ, 290, 307 [NASA ADS] [CrossRef] [Google Scholar]
  31. Schmitt, J. H. M. M., Collura, A., Sciortino, S., et al. 1990, ApJ, 365, 704 [NASA ADS] [CrossRef] [Google Scholar]
  32. Schöller, M., Correia, S., Hubrig, S., & Ageorges, N. 2010, A&A, 522, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Seggewiss, W. 1990, A&A, 229, 186 [NASA ADS] [Google Scholar]
  34. Shore, S. N., Brown, D. N., Sonneborn, G., & Gibson, D. M. 1987, A&A, 182, 285 [NASA ADS] [Google Scholar]
  35. Simon, T., Landsman, W. B., & Gilliland, R. L. 1994, ApJ, 428, 319 [NASA ADS] [CrossRef] [Google Scholar]
  36. Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Preliminary orbit for γ Equ  AB (see Fig. 2).

In the text
Table 2

Separation between γ Equ A and B measured with different instruments at different epochs and corresponding predictions from orbit.

In the text
Table 3

XSPEC fit results for the X-ray source associated with γ Equ B.

In the text

All Figures

thumbnail Fig. 1

Left: NACO K-band image centered on γ Equ  B. Right: X-ray image in 0.3−8.0 keV with 0.25′′ pixel size. The position of the X-ray source is highlighted with a yellow (small) circle. Positions indicated by x-shaped symbols denote the proper motion corrected Hipparcos position of γ Equ A at the time of the Chandra observation (black) and the corresponding expected position of the companion according to the orbit solution (yellow and smaller). The expected position of the primary, γ Equ A, as inferred from the orbit solution for the assumption that the companion is located at the X-ray position, is shown as black (larger) circle.
In the text
thumbnail Fig. 2

Apparent orbit of γ Equ  AB. The position of the primary is off to the left outside the displayed portion of the orbit. The NACO measurement uncertainty ellipse is enlarged by a factor of 2 for clarity. The Hipparcos measurement is labeled “Hp”. A diamond marks the expected position of the companion at the date of the Chandra observations.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.