| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A61 | |
| Number of page(s) | 5 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201016204 | |
| Published online | 01 April 2011 | |
Research Note
Observational constraints on interacting dark matter model without dark energy
Department of AstronomyBeijing Normal University, Beijing 100875, PR China
e-mail: zhuzh@bnu.edu.cn; liangn@bnu.edu.cn
Received: 25 November 2010
Accepted: 2 March 2011
Aims. The interacting dark matter (IDM) scenario allows for the acceleration of the Universe without dark energy.
Methods. We constrain the IDM model by using the newly revised observational data including H(z) data and Union2 SNe Ia via the Markov chain Monte Carlo method.
Results. When mimicking the ΛCDM model, we obtain a more stringent upper limit to the effective annihilation term at κC1 ≈ 10-3.4 Gyr-1, and a tighter lower limit to the relevant mass of dark matter particles at Mx ≈ 10-8.6 Gev. When mimicking the wCDM model, we find that the effective equation of state of IDM is consistent with the concordance ΛCDM model and appears to be most consistent with the effective phantom model with a constant EoS for which w < −1.
Key words: dark matter / cosmology: observations
© ESO, 2011
1. Introduction
Recent observations of type Ia sPerlmutterupernovae (SNe Ia, Riess et al. 1998; Perlmutter et al. 1999) have predicted that our present universe is passing through an accelerated phase of expansion proceeded by a period of deceleration. A new type of matter with negative pressure, which is popularly known as dark energy, has been proposed to explain the present phase of acceleration. The most simple dark energy candidate, the cosmological constant (ΛCDM model), though known to be consistent with various observations such as SNe Ia, the galaxy cluster gas mass fraction data (Wilson et al. 2006; Davis et al. 2007; Allen et al. 2008), and the CMB temperature and polarization anisotropies (Jassal et al. 2010), is always affected by the coincidence problem. Until now, many other dark energy models have been brought forward to explain this comic acceleration such as the scalar fields with a dynamical equation of state (e.g., quintessence, Peebles & Ratra 1988a,b; Caldwell et al. 1998; phantom, Caldwell 2002; k-essence, Armendariz-Picon et al. 2001; quintom, Feng et al. 2005; Guo et al. 2005; Liang et al. 2009), the Chaplygin gas (Kamenshchik et al. 2001; Bento et al. 2002), holographic dark energy (Cohen 1999; Li 2004), and so on. Many alternatives to dark energy in which gravity is modified have been proposed as a possible explanation of the acceleration (e.g., the braneworld models, Dvali et al. 2000; Zhu & Alcaniz 2005; the Cardassian expansion model, Freese & Lewis 2002; Zhu & Fujimoto 2002), as well as the f(R) theory (Capozziello & Fang 2002; Carroll et al. 2004) and the f(T) theory (Bengochea & Ferraro 2009; Wu & Yu 2010).
It has been shown that the dark matter self-interactions could provide the accelerated expansion of the Universe without any dark energy component (Zimdahl et al. 2001; Balakin et al. 2003). In the framework of the Boltzmann formalism, if there is a disequilibrium between the dark matter particle creation and annihilation processes, an effective source term with negative pressure could be created. Basilakos & Plionis (2009) investigated the circumstances under which the analytical solution space within the framework of the interacting dark matter (IDM) scenario allows for a late accelerated phase of the Universe, and find that the effective annihilation term of the simplest IDM model is quite small by using the nine observational H(z) data points of Simon et al. (2005). The gravitational matter creation model that is fully dominated by cold dark matter (Lima et al. 2008; Basilakos & Lima 2010) is mathematically equivalent to one case of the IDM models (Basilakos & Plionis 2009).
In this paper, we use the newly revised H(z) data (Stern et al. 2010; Gazta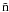 aga et al. 2009) and the Union2 set of 557 SNe Ia (Amanullah et al. 2010) to constrain the relevant IDM models (Basilakos & Plionis 2009) by using the Markov chain Monte Carlo (MCMC) method. This paper is organized as follows. In Sect. 2, we briefly indicate the basic equations of the IDM models. Observational data including H(z) and SNe Ia are given in Sect. 3. In Sect. 4, MCMC constraint results from different combined data sets are illustrated. Finally, we summarize our main conclusions in Sect. 5.
aga et al. 2009) and the Union2 set of 557 SNe Ia (Amanullah et al. 2010) to constrain the relevant IDM models (Basilakos & Plionis 2009) by using the Markov chain Monte Carlo (MCMC) method. This paper is organized as follows. In Sect. 2, we briefly indicate the basic equations of the IDM models. Observational data including H(z) and SNe Ia are given in Sect. 3. In Sect. 4, MCMC constraint results from different combined data sets are illustrated. Finally, we summarize our main conclusions in Sect. 5.
2. The basic equations of the IDM models
We assume that the IDM density obeys the collisional Boltzmann equation (Kolb & Turner 1990) 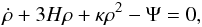 (1)where Ψ is the rate of creation of DM particle pairs and the annihilation parameter κ = ⟨ σu ⟩ /Mx (where Mx is the mass of the DM particle, σ is the cross-section for annihilation, and u is the mean particle velocity). Compared to the usual fluid equation, the effective pressure term is
(1)where Ψ is the rate of creation of DM particle pairs and the annihilation parameter κ = ⟨ σu ⟩ /Mx (where Mx is the mass of the DM particle, σ is the cross-section for annihilation, and u is the mean particle velocity). Compared to the usual fluid equation, the effective pressure term is 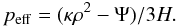 (2)When the IDM particle creation term is larger than the annihilation term (κρ2 − Ψ < 0), IDM may serve as a negative pressure source in the global dynamics of the Universe (Zimdahl et al. 2001; Balakin et al. 2003). Basilakos & Plionis (2009) phenomenologically identified two functional forms for which the previous Boltzmann equation can be solved analytically, only one of which is of interest since it indicates the dependence of the scale factor on a “ ∝ a-3”. We refer to Appendix B in Basilakos & Plionis (2009) for details. We assume that
(2)When the IDM particle creation term is larger than the annihilation term (κρ2 − Ψ < 0), IDM may serve as a negative pressure source in the global dynamics of the Universe (Zimdahl et al. 2001; Balakin et al. 2003). Basilakos & Plionis (2009) phenomenologically identified two functional forms for which the previous Boltzmann equation can be solved analytically, only one of which is of interest since it indicates the dependence of the scale factor on a “ ∝ a-3”. We refer to Appendix B in Basilakos & Plionis (2009) for details. We assume that 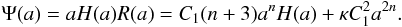 (3)And the total energy density is
(3)And the total energy density is ![\begin{equation} \rho(a)=C_{1}a^{n}+a^{-3}\frac{F(a)} {\left[C_2-\int_{1}^{a} x^{-3} f(x) F(x){\rm d}x\right]}, \label{8} \end{equation}](/articles/aa/full_html/2011/05/aa16204-10/aa16204-10-eq20.png) (4)where n, C1, and C2 are the corresponding constants of the problem (κC1 in the unit of Gyr-1), and the kernel function
(4)where n, C1, and C2 are the corresponding constants of the problem (κC1 in the unit of Gyr-1), and the kernel function ![\hbox{$ F(a)={\rm exp} [-2 \kappa C_{1}\int_{1}^{a} x^{n-1}/{H(x)}{\rm d}x] $}](/articles/aa/full_html/2011/05/aa16204-10/aa16204-10-eq26.png) . The first term on the right side of Eq. (4) obviously corresponds to the residual matter creation that results from the possible disequilibrium between the IDM particle creation and annihilation processes, while the second term can be viewed as the energy density of the self IDM particles that are dominated by the annihilation process.
. The first term on the right side of Eq. (4) obviously corresponds to the residual matter creation that results from the possible disequilibrium between the IDM particle creation and annihilation processes, while the second term can be viewed as the energy density of the self IDM particles that are dominated by the annihilation process.
2.1. Model 1: mimicking the ΛCDM model
If n = 0, the global density evolution can be transformed as ![\begin{equation} \rho(a)=C_{1}+a^{-3}\frac{{\rm e}^{-2 \kappa C_{1} (t-t_0)}} {\left[C_{2}- \kappa Z(t) \right]}, \label{13} \end{equation}](/articles/aa/full_html/2011/05/aa16204-10/aa16204-10-eq29.png) (5)where
(5)where 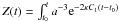 (Basilakos & Plionis 2009). At the present epoch, the density evolves according to ρ(a) ≃ C1 + a-3/C2, which is approximately equivalent to the corresponding evolution in the ΛCDM model, in which the C1 term resembles the cosmological constant term (ρΛ) and the 1/C2 term resembles the density of matter (ρm). The Hubble parameter can be written as (Basilakos & Plionis 2009)
(Basilakos & Plionis 2009). At the present epoch, the density evolves according to ρ(a) ≃ C1 + a-3/C2, which is approximately equivalent to the corresponding evolution in the ΛCDM model, in which the C1 term resembles the cosmological constant term (ρΛ) and the 1/C2 term resembles the density of matter (ρm). The Hubble parameter can be written as (Basilakos & Plionis 2009) 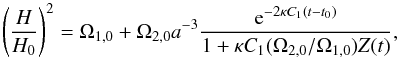 (6)where
(6)where 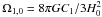 and
and 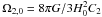 , which relate to ΩΛ and Ωm0 in the ΛCDM model, respectively. The mass of the DM particle can also be related to the range of κC1 (Basilakos & Plionis 2009)
, which relate to ΩΛ and Ωm0 in the ΛCDM model, respectively. The mass of the DM particle can also be related to the range of κC1 (Basilakos & Plionis 2009) 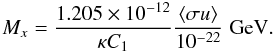 (7)
(7)
2.2. Model 2: mimicking the wCDM model
When the annihilation term is negligible (κ = 0) and the particle creation term dominates, it is straightforward to obtain the evolution of the total energy density (Basilakos & Plionis 2009) 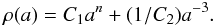 (8)The conditions n > −2 implies that the IDM fluid has an inflection point, and the current model acts as the wCDM model with a constant EoS with wIDM = −1 − n/3, but with a totally different intrinsic nature. This situation is mathematically equivalent to the gravitational DM particle creation process within the context of non-equilibrium thermodynamics (Lima et al. 2008). The Hubble parameter is now given by
(8)The conditions n > −2 implies that the IDM fluid has an inflection point, and the current model acts as the wCDM model with a constant EoS with wIDM = −1 − n/3, but with a totally different intrinsic nature. This situation is mathematically equivalent to the gravitational DM particle creation process within the context of non-equilibrium thermodynamics (Lima et al. 2008). The Hubble parameter is now given by 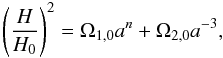 (9)where
(9)where 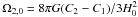 and
and 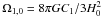 , respectively (Basilakos & Plionis 2009).
, respectively (Basilakos & Plionis 2009).
3. Observational data
To constrain the relevant IDM models (Basilakos & Plionis 2009), we use the newly revised H(z) data (Stern et al. 2010; Gazta aga et al. 2009) and the Union2 set of 557 SNe Ia (Amanullah et al. 2010).
aga et al. 2009) and the Union2 set of 557 SNe Ia (Amanullah et al. 2010).
3.1. The observational H(z) data
It is known that the Hubble parameter H(z) depends on the differential age as a function of redshift z in the form 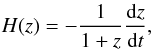 (10)which provides a direct measurement on H(z) based on dz/dt. Jimenez et al. (2003) demonstrated the feasibility of this method by applying it to a z ~ 0 sample. Moreover, compared with other observational data, it is more rewarding to investigate the observational H(z) data directly, because it can take the fine structure of H(z) into consideration and then use the important information that this structure provides.
(10)which provides a direct measurement on H(z) based on dz/dt. Jimenez et al. (2003) demonstrated the feasibility of this method by applying it to a z ~ 0 sample. Moreover, compared with other observational data, it is more rewarding to investigate the observational H(z) data directly, because it can take the fine structure of H(z) into consideration and then use the important information that this structure provides.
By using the differential ages of passively evolving galaxies determined from the Gemini Deep Deep Survey (GDDS) (Abraham et al. 2004) and archival data (Treu et al. 2001, 2002; Nolan et al. 2003a,b), Simon et al. (2005) determined nine values of the Hubble parameter H(z) in the range 0 ≤ z ≤ 1.8, which have been used to constrain the parameters of various dark energy models (Samushia & Ratra 2006; Wei & Zhang 2007; Wu & Yu 2007a,b; Zhang & Zhu 2007; Kurek & Szydlowski 2007; Lazkoz & Majerotto 2007; Sen & Scherrer 2008; Yi & Zhang 2007; Wan et al. 2007; Xu et al. 2008; Zhai et al. 2010). The H(z) data at 11 different redshifts were determined from the differential ages of red-envelope galaxies (Stern et al. 2010), and two more Hubble parameter data points H(z = 0.24) = 79.69 ± 4.61 and H(z = 0.43) = 86.45 ± 5.96 were obtained by Gaztañaga et al. (2009) from observations of BAO peaks (for a review of the observational H(z) data, see Zhang et al. 2010). Studies using these newly H(z) data for cosmological constraint include Gong et al. (2010), Liang et al. (2010a), Liang & Zhu (2010), Cao & Liang (2010), Ma & Zhang (2011), and Xu & Wang (2010c). We emphasize the use of the Hubble constant H0 in our analysis. Many previous have determined its present value. Freedman et al. (2001) presented the final results of the Hubble Space Telescope (HST) key project that measured the Hubble constant H0 = 72 ± 8 km s-1 Mpc-1, Gott et al. (2001) and Chen et al. (2003) proposed that H0 = 68 km s-1 Mpc-1 was a more likely value, and Tammann et al. (2008) obtained H0 = 62.3 ± 1.3 km s-1 Mpc-1 from 28 independently calibrated Cepheids and the distant, Cepheid-calibrated SNe Ia. More recently, Riess et al. (2009) determined H0 = 74.2 ± 3.6 km s-1 Mpc-1 by combining the observations of 240 Galactic Cepheid variables using HST. In this work, we follow Basilakos & Plionis (2009) and adopt H0 = 72 ± 8 km s-1 Mpc-1. The observational H(z) data are given in Table 1. In this case, χ2 can be defined as 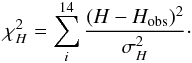 (11)
(11)
3.2. The observational SNe Ia data
SNe Ia have long been used as “standard candles”. It is commonly believed that measuring both their redshifts and apparent peak fluxes gives a direct measurement of their luminosity distances, thus SNe Ia provide the strongest constraints on the cosmological parameters (Riess et al. 2004, 2007; Astier et al. 2006; Davis et al. 2007; Wood-Vasey et al. 2007; Kowalski et al. 2008; Hicken et al. 2009; Chen et al. 2010). The present analysis uses the Union2 (557 sample) data set of the Supernova Cosmology project covering a redshift range 0.015 ≤ z ≤ 1.4 (Amanullah et al. 2010), which was used to constrain cosmological models in Wei (2010), Liang et al. (2010a,b), Liang et al. (2011), Xu & Wang (2010a,b), and Wang et al. (2010).
In the calculation of the likelihood from SNe Ia, we marginalize the nuisance parameter by minimizing (Di Pietro & Claeskens 2003), 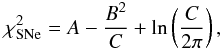 (12)where A =
(12)where A = 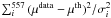 , B =
, B = 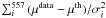 , C =
, C = 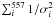 , and the distance modulus is μ = 5log (dL/Mpc) + 25, with the 1σ uncertainty σi from the observations of SNe Ia and the luminosity distance dL as a function of redshift z,
, and the distance modulus is μ = 5log (dL/Mpc) + 25, with the 1σ uncertainty σi from the observations of SNe Ia and the luminosity distance dL as a function of redshift z, 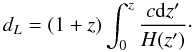 (13)
(13)
4. Constraint results
We define the total likelihood to be the product of the separate likelihoods of the two cosmological probes, in other words, 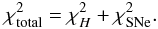 (14)To determine the best-fit cosmological parameters, we use a χ2 minimization and the 68.3% and 95.4% confidence levels are defined by the conventional two-parameters χ2 levels 2.30 and 6.17, respectively. We perform a global fitting to determine the cosmological parameters using the Markov chain Monte Carlo (MCMC) method and our MCMC code is based on the publicly available package COSMOMC (Lewis & Bridle 2002).
(14)To determine the best-fit cosmological parameters, we use a χ2 minimization and the 68.3% and 95.4% confidence levels are defined by the conventional two-parameters χ2 levels 2.30 and 6.17, respectively. We perform a global fitting to determine the cosmological parameters using the Markov chain Monte Carlo (MCMC) method and our MCMC code is based on the publicly available package COSMOMC (Lewis & Bridle 2002).
4.1. Model 1: mimicking the ΛCDM model
In this model, there are two free parameters: Ω2,0 and κC1 (or Mx) for a flat background (Ω1,0 + Ω2,0 = 1). In this paper, we follow Basilakos & Plionis (2009) and adopt t0 = 1/H0 = 13.6 Gyr (roughly the age of the universe in the corresponding ΛCDM cosmology). The constraint results from different data combinations are shown in Figs. 1 − 3 and summarized in Table 2.
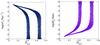 |
Fig. 1 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the H(z) data. |
 |
Fig. 2 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the SNe Ia data. |
 |
Fig. 3 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the H(z)+SNe data. |
In Fig. 1, we show the results from the H(z) data. The best-fit solution corresponds to fit 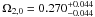 and log (κC1·Gyr) ≈ − 6.85 with an upper limit log (κC1·Gyr) ≈ − 3. This effective annihilation term is obviously still unconstrained towards lower values. Correspondingly, the best-fit value of Mx is log Mx/Gev ≈ − 5.15 with a relatively stringent lower limit of log Mx/Gev ≈ − 9. These results are consistent with previous work that uses fewer observational H(z) data
and log (κC1·Gyr) ≈ − 6.85 with an upper limit log (κC1·Gyr) ≈ − 3. This effective annihilation term is obviously still unconstrained towards lower values. Correspondingly, the best-fit value of Mx is log Mx/Gev ≈ − 5.15 with a relatively stringent lower limit of log Mx/Gev ≈ − 9. These results are consistent with previous work that uses fewer observational H(z) data 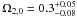 and log (κC1·Gyr) ≈ − 9.3 (Basilakos & Plionis 2009). In Fig. 2, we show the constraint results from SNe Ia with the best-fit model parameters
and log (κC1·Gyr) ≈ − 9.3 (Basilakos & Plionis 2009). In Fig. 2, we show the constraint results from SNe Ia with the best-fit model parameters 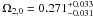 and log (κC1·Gyr) ≈ − 4.42. A more stringent upper limit is obtained at around log (κC1·Gyr) ≈ − 3.5. The best-fit DM particle mass is log Mx/Gev ≈ − 7.58 with a relatively stringent lower limit log Mx/Gev ≈ − 8.5. To obtain a tighter constraint on the model parameters, we combine the H(z) and SNe Ia data, and the results are shown in Fig. 3. The best-fit model parameters are
and log (κC1·Gyr) ≈ − 4.42. A more stringent upper limit is obtained at around log (κC1·Gyr) ≈ − 3.5. The best-fit DM particle mass is log Mx/Gev ≈ − 7.58 with a relatively stringent lower limit log Mx/Gev ≈ − 8.5. To obtain a tighter constraint on the model parameters, we combine the H(z) and SNe Ia data, and the results are shown in Fig. 3. The best-fit model parameters are 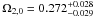 and log (κC1·Gyr) ≈ − 5.35 with a much more stringent upper limit log (κC1·Gyr) ≈ − 3.4. Moreover, the best-fit value of Mx is log Mx/Gev ≈ − 6.65 with a relatively stringent lower limit of log Mx/Gev ≈ − 8.6 at 2σ. Since Mx is unbound at small values, it is consistent with currently accepted lower bounds of Mx (10 GeV) (see Cirelli et al. 2009, and references therein).
and log (κC1·Gyr) ≈ − 5.35 with a much more stringent upper limit log (κC1·Gyr) ≈ − 3.4. Moreover, the best-fit value of Mx is log Mx/Gev ≈ − 6.65 with a relatively stringent lower limit of log Mx/Gev ≈ − 8.6 at 2σ. Since Mx is unbound at small values, it is consistent with currently accepted lower bounds of Mx (10 GeV) (see Cirelli et al. 2009, and references therein).
Summarizing the results of parameter constraints from model 1 considered in this work.
4.2. Model 2: mimicking the wCDM model
In this case, there are two free parameters: Ω2,0 and n (or wIDM). The constraint results from different data combinations are shown in Figs. 4 − 6 and summarized in Table 3.
 |
Fig. 4 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the H(z) data. |
 |
Fig. 5 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the SNe Ia data. |
 |
Fig. 6 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the H(z)+SNe data. |
For the H(z) data and the results shown in Fig. 4, the best-fit parameter values are 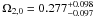 and
and 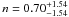 . For the EoS of IDM, the best-fit value is
. For the EoS of IDM, the best-fit value is 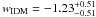 . These results are consistent with the previous results of Basilakos & Plionis (2009) by using fewer observational H(z) data (n ≃ − 0.30 and wIDM ≃ − 0.90, which favors the effective quintessence model with a constant EoS for which w > − 1). In Fig. 5, we show the constraint results from SNe Ia. By minimizing the corresponding χ2, we find that the best-fit model values are
. These results are consistent with the previous results of Basilakos & Plionis (2009) by using fewer observational H(z) data (n ≃ − 0.30 and wIDM ≃ − 0.90, which favors the effective quintessence model with a constant EoS for which w > − 1). In Fig. 5, we show the constraint results from SNe Ia. By minimizing the corresponding χ2, we find that the best-fit model values are 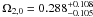 and
and 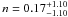 (
(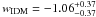 ). For the combined data H(z)+ SNe shown in Fig. 6, we find the best-fit values are
). For the combined data H(z)+ SNe shown in Fig. 6, we find the best-fit values are 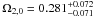 and
and 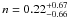 (
(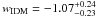 ). Obviously, all of the above constraints are consistent with the concordance ΛCDM model and appear to be most consistent with the effective phantom model and a constant EoS for which w < − 1.
). Obviously, all of the above constraints are consistent with the concordance ΛCDM model and appear to be most consistent with the effective phantom model and a constant EoS for which w < − 1.
Summarizing the results of constraint on parameters from model 2.
5. Conclusions
We have investigated the interacting dark matter (IDM) scenario mimicking either the ΛCDM model or the wCDM model, which can create the cosmic acceleration without dark energy (Basilakos & Plionis 2009). In our work, the scale of the effective annihilation term κC1 and therefore the mass of DE particles Mx are constrained with different newly revised observational data including H(z) and Union2 SNe Ia data. When mimicking a Λ cosmology and using three different data combinations of H(z), SNe Ia, and SNe Ia+H(z), we have found that κC1 is quite small, which is consistent with the previous results in Basilakos & Plionis (2009), which used fewer observational H(z) data. Meanwhile, for the combined data sets, we obtain a more stringent upper limit to the effective annihilation term with log (κC1·Gyr) ≈ − 3.4. By relating the range of values of κC1 to the mass of the DM particle, we have inferred an apparent lower limit of Mx ≈ 10-8.6 Gev. Furthermore, when mimicking wCDM model and assuming that the particle creation term dominates (κ = 0), we obtained the effective equation of state of IDM is consistent with the concordance ΛCDM model and appears to be consistent with the effective phantom model with a constant EoS for which w < − 1.
To sum up, we conclude that the interacting dark matter (IDM) model may provide a practical alternative to dark energy in explaining the present cosmic acceleration. The hope of proving this conclusion should be pinned on analyses of future observational data such as high redshift SNe Ia data from SNAP (Albrecht et al. 2006), more precise CMB data from the ESA Planck satellite (Balbi 2007), and complementary data, such as the X-ray gas mass fraction in clusters (Allen et al. 2004, 2008; Ettori et al. 2009), gravitational lensing data (Zhu 1998; Sereno 2002), as well as gamma-ray bursts (GRBs) at high redshift (Schaefer 2007; Liang et al. 2008; Basilakos & Perivolaropoulos 2008; Liang & Zhang 2008; Wang & Liang 2010; Gao et al. 2010; Liang et al. 2011).
Acknowledgments
We thank Yun Chen, Hao Wang, Yan Dai, Chunhua Mao, Fang Huang, Yu Pan, Jing Ming, Kai Liao and Dr. Yi Zhang for discussions. This work was supported by the National Science Foundation of China under the Distinguished Young Scholar Grant 10825313, the Key Project Grants 10533010, and by the Ministry of Science and Technology national basic science Program (Project 973) under grant No. 2007CB815401.
References
- Abraham, R. G., Glazebrook, K., McCarthy, P. J., et al. 2004, ApJ, 127, 2455 [Google Scholar]
- Albrecht, A., et al. 2006, Report of the Dark Energy Task Force [arXiv:0609591] [Google Scholar]
- Allen, S. W., Schmidt, R. W., Ebeling, H., Fabian, A. C., & van Speybroeck, L. 2004, MNRAS, 353, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Rapetti, D. A., Schmidt, R. W., et al. 2008, MNRAS, 383, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Amanullah, R., Lidman, C., Rubin, D., et al. (Supernova Cosmology Project Collaboration) 2010, ApJ, 716, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balakin, A. B., Pavon, D., Schwarz, D. J., & Zimdahl, W. 2003, N. J. Phys, 5, 85 [Google Scholar]
- Balbi, A. 2007, New A. R., 51, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Lima, J. A. S. 2010, Phys. Rev. D, 82, 023504 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Perivolaropoulos, L. 2008, MNRAS, 391, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Basilakos, S., & Plionis, M. 2009, A&A, 507, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bengochea, G. R., & Ferraro, R. 2009, Phys. Rev. D, 79, 124019 [NASA ADS] [CrossRef] [Google Scholar]
- Bento, M. C., Bertolami, O., & Sen, A. A. 2002, Phys. Rev. D, 66, 043507 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cao, S., & Liang, N. 2010 [arXiv:1012.4879] [Google Scholar]
- Caldwell, R. 2002, PLB, 545, 23 [Google Scholar]
- Caldwell, R., Dave, R., & Steinhardt, P. J. 1998, PRL, 80, 1582 [Google Scholar]
- Capozziello, S., & Fang, L. Z. 2002, Internat. J. Mod. Phys. D, 11, 483 [Google Scholar]
- Carroll, S. M., Duvvuri, V., Trodden, M., & Turner, M. S. 2004, Phys. Rev. D, 70, 043528 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G., Gott, J. R., III, & Ratra, B. 2003, Publ. Astron. Soc. Pac., 115, 1269 [Google Scholar]
- Chen, Y., Zhu, Z.-H., Alcaniz, J. S., & Gong, Y. G. 2010, ApJ, 711, 439 [Google Scholar]
- Cirelli, M., Iocco, F., & Panci, P. 2009, JCAP, 10, 9 [Google Scholar]
- Cohen, A., Kaplan, D., & Nelson, A. 1999, PRL, 82, 4971 [Google Scholar]
- Davis, T. M., Mörtsell, E., Sollerman, J., et al. 2007, ApJ, 666, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Dvali, G., Gabadadze, G., & Porrati, M. 2000, PLB, 485, 208 [CrossRef] [Google Scholar]
- Di Pietro, E., & Claeskens, J. F. 2003, MNRAS, 341, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Morandi, A., Tozzi, P., et al. 2009, A&A, 501, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farrar, G. R., & Peebles, P. J. E. 2004, ApJ, 604, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, B., Wang, X., & Zhang, X. 2005, PLB, 607, 35 [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Freese, K., & Lewis, M. 2002, PLB, 540, 1 [Google Scholar]
- Gao, H., Liang, N., & Zhu, Z.-H. 2010 [arXiv:1003.5755] [Google Scholar]
- Gaztañaga, E., Cabré, A., & Hui, L. 2009, MNRAS, 399, 1663 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, Y. G., Cai, R. G., Chen, Y., & Zhu, Z.-H. 2010, JCAP, 01, 019 [NASA ADS] [Google Scholar]
- Gott, J. R., III, Vogeley, M. S., Podariu, S., & Ratra, B. 2001, ApJ, 549, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gubser, S. S., & Peebles, P. J. E. 2004, Phys. Rev. D, 70, 123510 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, Z.-K., Piao, Y.-S., Zhang, X., & Zhang, Y. Z. 2005, PLB, 608, 177 [Google Scholar]
- Hicken, M., Wood-Vasey, W. M., Blondin, S., et al. 2009, ApJ, 700, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Jassal, H. K., Bagla, J. S., & Padmanabhan, T. 2010, MNRAS, 405, 2639 [NASA ADS] [Google Scholar]
- Jimenez, R., Verde, L., Treu, T., & Stern, D. 2003, ApJ, 593, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Kamenshchik, A., Moschella, U., & Pasquier, V. 2001, PLB, 511, 265 [Google Scholar]
- Kolb, E. W., & Turner, M. S. 1990, The Early Universe (Addison-Wesley Publishing) [Google Scholar]
- Kowalski, M., Rubin, D., Aldering, G., et al. 2008, ApJ, 686, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Kurek, A., & Szydlowski, M. 2008, ApJ, 675, 1 [Google Scholar]
- Lazkoz, R., & Majerotto, E. 2007, JCAP, 0707, 015 [NASA ADS] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Li, M. 2004, PLB, 603, 1 [Google Scholar]
- Liang, N., & Zhang, S. N. 2008, AIP Conf. Proc., 1065, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, N., & Zhu, Z.-H. 2010, Res. Astron. Astrophys., in press [arXiv:1010.2681] [Google Scholar]
- Liang, N., Xiao, W. K., Liu, Y., & Zhang, S. N. 2008, ApJ, 685, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, N., Gao, C. J., & Zhang, S. N. 2009, Chin. Phys. Lett., 26, 069501 [NASA ADS] [CrossRef] [Google Scholar]
- Liang, N., Wu, P., & Zhang, S. N. 2010a, Phys. Rev. D, 81, 083518 [Google Scholar]
- Liang, N., Wu, P., & Zhu, Z.-H. 2010b [arXiv:1006.1105] [Google Scholar]
- Liang, N., Xu, L., & Zhu, Z.-H. 2011, A&A, 527, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lima, J. A. S., Silva, F. E., & Santos, R. C. 2008, Class and Quantum Gravity, 25, 205006 [Google Scholar]
- Ma, C., & Zhang, T. J. 2011, ApJ, 730, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, L. A., Dunlop, J. S., Jimenez, R., & Heavens, A. F. 2003a, MNRAS, 341, 464 [Google Scholar]
- Nolan, P. L., Tompkins, W. F., Grenier, I. A., & Michelson, P. F. 2003b, ApJ, 597, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 1988a, ApJ, 325, L17 [Google Scholar]
- Peebles, P. J. E., & Ratra, B. 1988b, Phys. Rev. D, 37, 3406 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Ratra, B., & Peebles, P. J. E. 1988, Phys. Rev. D, 37, 3406 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Tonry, J., et al. (Supernova Search Team Collaboration) 2004, ApJ, 607, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Strolger, L.-G., Casertano, S., et al. 2007, ApJ, 659, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Li, W., et al. 2009, ApJS, 183, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Sahani, T. D., Raychaudhury, S., Sahni, V., & Starobinsky, A. A. 2000, PRL, 85, 1162 [Google Scholar]
- Samushia, L., & Ratra, B. 2006, ApJ, 650, L5 [Google Scholar]
- Schaefer, B. E. 2007, ApJ, 660, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, A. A., & Scherrer, R. J. 2008, PLB, 659, 457 [Google Scholar]
- Sereno, M. 2002, A&A, 393, 757 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, J., Verde, L., & Jimenez, R. 2005, Phys. Rev. D, 71, 123001 [Google Scholar]
- Stern, D., Jimenez, R., Verde, L., Kamionkowski, M., & Stanford, S. A. 2010, JCAP, 02, 008 [CrossRef] [Google Scholar]
- Tammann, G. A., Sandage, A., & Reindl, B. 2008, A&ARv, 15, 289 [NASA ADS] [Google Scholar]
- Treu, T., Stiavelli, M., Møller, P., Casertano, S., & Bertin, G. 2001, MNRAS, 326, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Stiavelli, M., Casertano, S., Møller, P., & Bertin, G. 2002, ApJ, 564, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Wan, H. Y., Yi, Z. L., Zhang, T. J., & Zhou, J. 2007, PLB, 651, 352 [Google Scholar]
- Wang, T. S., & Liang, N. 2010, ScChG, 53, 1720 [NASA ADS] [Google Scholar]
- Wang, S., Li, X. D., & Li, M. 2011, Phys. Rev. D, 83, 023010 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, H. 2010, JCAP, 08, 020 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, H., & Zhang, S. N. 2007, PLB, 644, 7 [Google Scholar]
- Wilson, K. M., Chen, G., & Ratra, B. 2006, Modern Phys. Lett. A, 21, 2197 [Google Scholar]
- Wood-Vasey, W. M., Miknaitis, G., Stubbs, C. W., et al. 2007, ApJ, 666, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P. X., & Yu, H. W. 2007a, PLB, 644, 16 [Google Scholar]
- Wu, P. X., & Yu, H. W. 2007b, JCAP, 0703, 015 [NASA ADS] [Google Scholar]
- Wu, P. X., & Yu, H. W. 2010, PLB, 693, 415 [Google Scholar]
- Xu, L. X., & Wang, Y. T. 2010a, Phys. Rev. D, 82, 043503 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L. X., & Wang, Y. T. 2010b, JCAP, 11, 014 [NASA ADS] [Google Scholar]
- Xu, L. X., & Wang, Y. T. 2010c [arXiv:1009.0963] [Google Scholar]
- Xu, L. X., Zhang, C. W., Chang, B. R., & Liu, H. Y. 2008, Modern Phys. Lett. A, 23, 1939 [Google Scholar]
- Yi, Z. L., & Zhang, T. J. 2007, Modern Phys. Lett. A, 22, 41 [Google Scholar]
- Zhai, Z. X., Wan, H. Y., & Zhang, T. J. 2010, PLB, 689, 8 [Google Scholar]
- Zhang, H. S., & Zhu, Z.-H. 2008, JCAP, 0803, 007 [NASA ADS] [Google Scholar]
- Zhang, T. J., Ma, C., & Lan, T. 2010, Adv. Astron., 184284 [Google Scholar]
- Zimdahl, W., Schwarz, D. J., Balakin, A. B., & Pavon, D. 2001, Phys. Rev. D, 64, 3501 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Zhu, Z.-H. 1998, A&A, 338, 777 [NASA ADS] [Google Scholar]
- Zhu, Z.-H., & Alcaniz, J. S. 2005, ApJ, 620, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z.-H., & Fujimoto, M.-K. 2002, ApJ, 581, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summarizing the results of parameter constraints from model 1 considered in this work.
All Figures
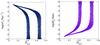 |
Fig. 1 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the H(z) data. |
| In the text | |
 |
Fig. 2 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the SNe Ia data. |
| In the text | |
 |
Fig. 3 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − κC1 and Ω2,0 − Mx planes provided by fitting model 1 to the H(z)+SNe data. |
| In the text | |
 |
Fig. 4 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the H(z) data. |
| In the text | |
 |
Fig. 5 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the SNe Ia data. |
| In the text | |
 |
Fig. 6 The likelihood contours at the 68.3% and 95.4% confidence levels in the Ω2,0 − n and Ω2,0 − wIDM planes provided by fitting model 2 to the H(z)+SNe data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


