| Issue |
A&A
Volume 529, May 2011
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015002 | |
| Published online | 04 April 2011 | |
Study of stellar populations in the bulges of barred galaxies⋆,⋆⋆
1
Dep. Física Teórica y del Cosmos, Campus de Fuentenueva, Universidad de Granada, 18071 Granada, Spain
e-mail: isa@ugr.es
2 Instituto Carlos I de Física Teórica y Computación, Spain
3
Dep. Física Teórica, Universidad Autonoma de Madrid, Cantoblanco, 28049 Madrid, Spain
4
Instituto de Astrofísica de Canarias, c/vía Láctea s/n, 38200 La Laguna, Tenerife, Spain
5
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
6
Jeremiah Horrocks Institute, UCLan, Preston, PR1 2HE, UK
e-mail: p.sanchezblazquez@uam.es
Received: 17 May 2010
Accepted: 10 January 2011
Aims. We wish to determine the influence of bars on the building of galaxy bulges through analysis of ages and metallicities derived from stellar absorption line-strength indices.
Methods. Long-slit spectroscopy was obtained for a sample of 20 early-type barred galaxies. Line-strength indices were measured and used to derive age and metallicity gradients in the bulge region by comparing them with stellar population models. The same analysis was carried out with similar data for unbarred galaxies taken from the literature.
Results. The bulges of barred galaxies seem to be more metal rich, at a given velocity dispersion (σ), than the bulges of unbarred galaxies, as measured by a few metallicity sensitive indices. There are indications that the ratio of relative abundance of alpha elements with respect to iron, [E/Fe], derived for the bulges of barred galaxies tend to lie above the values of the unbarred galaxies at a given σ. The metallicity gradients for the majority of the bulges are negative so less metal-rich towards the end of the bulge. The gradient values show a large scatter for galaxies with σ below 150 km s-1. The age distribution is related to the presence of a bulge substructure, such as a nuclear ring or an inner disk. The metallicity of both the bulge and the bar are very well correlated, indicating a close link between the enrichment histories of both components.
Conclusions. Bulges of barred early type galaxies might have experienced a different chemical enrichment than do the bulges of unbarred galaxies of the same morphological type, the same central velocity dispersion, and low inclination angles. The hinted stellar populations differences separating the bulges of barred and unbarred galaxies and the strong link between the metallicity of the bulge and the presence of a bar points to scenarios where they both form simultaneously in processes that lead to rapid and massive episodes of star formation, possibly linked to the bar formation. To confirm and generalise the results found here, it would be useful to extend the data set to a larger number of unbarred galaxies and a wider range of morphological types
Key words: Galaxy: abundances / galaxies: bulges / galaxies: structure / galaxies: stellar content / galaxies: evolution
Based on observations obtained at Siding Spring Observatory (RSAA, ANU, Australia) and the INT telescope at the ING, La Palma, Spain.
Appendix A is only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
If we consider that galaxy bulges of disk galaxies are the excess of light from the exponential disk, excluding the bar (e.g. Freeman 1970; Fisher 2006; Peletier 2008), we can find two types of bulges. In the standard picture, the two types of bulges are separated between those formed through violent processes (“classical bulges”) and those formed slowly through internal processes (i.e., through secular evolution) (e.g. Simkin et al. 1980; Pfenniger & Friedli 1991; Hopkins et al. 2010). They are expected to have very different structural properties, because the bulges formed via secular evolutionary processes are expected to have more disk-like properties, while the so-called “classical” bulges are expected to have properties that are more related to elliptical galaxies (e.g. Athanassoula 2005; Fisher & Drory 2008; Gadotti 2009; Fisher & Drory 2010, for a detail discussion on the properties on both types of bulges, see the review by Kormendy & Kennicutt 2004, and referencies therein). However, both bulges can coexist and the observed properties sometimes depend on the geometry chosen to derive the bulge properties.
Much work has been done to characterise the influence of the disk in the bulge evolution by comparing the stellar populations of bulges and those of elliptical galaxies and to date there has been no consensus. Some authors (e.g. Thomas & Davies 2006; Goudfrooij et al. 1999) have concluded that galaxies with morphological types from E to as late as Sbc have stellar population properties that are correlated to the central velocity dispersion (σ) and that, at a given σ, bulges and elliptical galaxies cannot be distinguished by their stellar populations, indicating very little influence of the disk on the evolution of the bulge. Recent work by MacArthur et al. (2009) have derived the whole star formation histories for the bulges of a sample of eight galaxies, finding that the mass-weighted stellar ages of the bulges are old and that secular evolution effects therefore only contribute minimally to the total bulge mass.
However, other authors (e.g. Falcón-Barroso et al. 2002; Peletier et al. 2007; Ganda et al. 2007) find that the Mg–σ relation for the bulges lies below that found for elliptical galaxies. Proctor & Sansom (2002) go further by concluding that the stellar population trends differ strongly between early and late type galaxies.
Part of the discrepancy between different studies can come from the selection of the sample. For example, inclination effects can make the contribution to the integrated spectra of the different galaxy components appear larger or smaller depending on the inclination (see Peletier et al. 2007). Furthermore, the morphological selection and the range in chosen luminosities might bias the conclusions, as kinematical studies indicate that secularly formed bulges are more important in late type spirals and especially in low-luminosity ones.
An alternative way to determine the influence of secular evolution on the growth of bulges is to compare similar spiral galaxies (in terms of luminosity, morphology, and inclination) with and without bars. Bars are expected to play an important role in the secular evolution of disk galaxies, and they are obvious candidates for secular evolution by creating a bulge secularly in disk galaxies. The bar gravity torques make the gas lose angular momentum, which in turn provokes an inflow of gas towards the central parts (e.g. Pfenniger & Norman 1990; Combes et al. 1990; Friedli & Benz 1995). Star formation might be triggered and possibly also the formation of a stellar bulge. One obvious way to study the efficiency of this process is to compare the star formation history of bulges in galaxies with and without bars. These types of studies have to be done for face-on galaxies where it is easy to morphologically identify the bar. There have only been a handful of studies characterising the bulges from samples of face-on galaxies. Thirty nine of them have been analysed by Moorthy & Holtzman (2006). From these, 19 have low inclination, and eleven are barred. They find that bars have smaller Hβ (indicating older luminosity-weighted ages) than unbarred galaxies at a fixed central velocity dispersion and maximum rotational velocity. They also analysed the distribution of the stellar populations with radius, finding that, when positive age gradients exists, they are always found in barred galaxies. In contrast, studies focused only on edge-on galaxies attempting to classify bars such as Jablonka et al. (2007) do not find any difference between the indices in barred and unbarred galaxies, wether in the central values or in the gradients.
We have started a project to characterise the stellar properties of barred galaxies so as to understand the influence of bars on the evolution of the different galaxy components and to study their formation. In Pérez et al. (2007) and Pérez et al. (2009, hereafter, Paper I), we presented a detailed analysis of the stellar population parameters along the bar of a sample of 20 galaxies. From the results (kinematics and SSP-derived stellar population parameters along the bar), we determined that the bulge kinematics is closely linked to the presence of a bar. Some studies, however, have not found any correlation between the presence of a bar and the bulge properties, probably due to an inclination bias, because studies of more inclined objects will avoid the contribution of the inner disk-like components. To conclude whether bars have a strong influence on the properties of bulges, a systematic comparison of bulges of barred and unbarred galaxies needs to be done, using galaxies with similar inclination, morphological type, and central velocity dispersion. We present, in this paper, the study of the stellar population properties of the central regions of the 20 barred galaxies analysed in Paper I. For an analysis of the differences between the bulges of barred and unbarred galaxies, our sample would need to be complemented by a similar sample of galaxies without bars. In addition to the bulges of barred galaxies, we therefore present a comparison with the Moorthy et al. (2006) data from a sample of both barred and unbarred galaxies, because it is the only sample available in the literature with similar characteristics to our data; namely, spectral coverage and resolution, morphological type, and inclination values. The data has been re-analysed in the same way as for our sample. This is the first time that such a study has been done for a large sample of barred galaxies, with a total of 31 barred galaxies combining both samples. Due to the low number of unbarred galaxies compared to the barred galaxies in the total sample, we will extend the sample in the future to include a larger number of unbarred galaxies and to cover a wider range of morphological types.
In Sects. 2–4 we give a brief introduction to the sample selection, observations, and data reduction and line-strength measurements. A more detailed explanation of these sections is given in Paper I. An analysis of the central line-strength indices and a comparison between barred and unbarred galaxies is given in Sect. 5.1. The line-strength index distributions in the bulge region are presented in Sect. 5.3. The single stellar population equivalent parameters are discussed in Sect. 6. The age and metallicity gradients are presented in Sect. 6.1, while a comparison between the stellar parameters in the bulge and bar region is given in Sect. 6.2. The conclusions and discussion are presented in Sect. 7.
2. Sample characterisation
We selected barred galaxies from the Third Reference Catalogue of bright galaxies (RC3) (de Vaucouleurs 1948) with the following criteria: to be classified as barred, to have inclinations between 10° and 70°, and to be nearby (cz ≤ 4000 km s-1). The sample is biased towards early-type barred galaxies, which have higher surface brightness. This morphological criteria was set to ensure that we could obtain data with enough signal-to-noise in the bar region (see Paper I). In the future, we plan to enlarge the sample towards later types to analyse the trends with morphological type. Half of our galaxies have nuclear activity to analyse possible trends between the nuclear activity, the bar characteristic of the bar, and the bulge. Furthermore, eight of the galaxies present nuclear bars. Our final sample comprises 20 galaxies. For ease of use, we reproduce here the table (Table 1), already shown in Paper I, with the main characteristics of the sample as taken from the Hyperleda catalogue (Paturel et al. 2003)1. The bar strength shown in Table 12 has been taken from the literature, where strength is defined as the torque of a bar embedded in its disk (Combes & Sanders 1981); see Table 1 for the references for the individual galaxies. The nuclear types were obtained from Verón-Cetty & Véron (2006). The sample shows a wide distribution of maximum rotational velocities (80 − 260 km s-1).
General properties of the sample.
As a working definition, we used a bulge size based on the kinematic and the line profile information. We considered the end of the bulge region the radius at which the σ starts decreasing after a plateau or dip. In Paper I, we noticed that it also coincides with a change in the slope of the line-strength profiles for all the indices. After analysing broad band images, as in Paper I, and also the HST images published in the literature (e.g. Comerón et al. 2010), we have also seen that this region coincides with changes in the morphology. Therefore, the bulge end defined using the kinematics is almost always coincident with the end of the nuclear structure: nuclear ring, double bar, inner spiral, etc., found in the broad-band images. Table 2 shows the approximate bulge and bar sizes, the latter given by the minimum ellipticity in the bar region (see Paper I for further explanation). In Table 2 we give the central structure and bar semi-major axis size values only for those galaxies for which we have good broad-band imaging; see Paper I for a more detailed explanation. In the same paper, we present the line-of-sight position diagrams and velocity dispersion for the galaxies (Fig. 8). From a close examination of the stellar kinematics in the bulge region we showed that all the galaxies in the sample have disk-like structures in their centres.
Bar and bulge sizes.
The presence of these disk-like structures in our galaxies led us to use in this work, a maximum velocity dispersion instead of a central velocity dispersion. This velocity dispersion is defined as the maximum velocity dispersion in the bulge region. We chose this dispersion value to avoid being dominated in some galaxies by the low central velocity dispersion that could indicate nuclear star formation (e.g. nuclear disk); therefore, the maximum velocity dispersion should be closer to the velocity dispersion of the bulge.
3. Observations and reduction
We obtained long-slit spectra along the bar major axis for our sample of 20 barred galaxies. The bar position angles were derived using the Digital Sky Survey (DSS) images. The observations were performed in two different runs, with the double beam spectrograph at Siding Spring Observatory (Australia) and with the IDS spectrograph at the Isaac Newton Telescope (La Palma, Spain). The observations were described in detail in Paper I. To summarise, spectra for six galaxies were obtained in the first run, covering a wavelength range from 3892 − 5815 Å and a spectral resolution of FHWM ~ 2.2 Å. In the second run, spectra for 14 galaxies were obtained, covering a wavelength range of 3020 − 6665 Å and a spectral resolution of ~3 Å (FWHM).
The reduction of the two runs was carried out with the package REDUCEME (Cardiel 1999). Standard data reduction procedures (flat-fielding, cosmic ray removal, wavelength calibration, sky subtraction, and fluxing) were performed. Error images were created at the beginning of the reduction and were processed in parallel with the science images. For details about the reduction steps see Paper I.
To derive the index spatial distribution for the fully reduced galaxy frames, a final frame was created by extracting spectra along the slit and binning in the spatial direction to guarantee a minimum signal-to-noise ratio of 20 per Å in the spectral region of Mgb. This minimum signal-to-noise ratio ensures errors lower than 15% in most of the Lick/IDS indices (Cardiel et al. 1998). A careful emission-line removal was performed with GANDALF (Sarzi et al. 2006). The details of the procedure can be found in Paper I. This procedure simultaneously fits the stellar and the emission line spectra by treating the emission lines as additional Gaussian templates and iteratively searching for the best radial velocity and velocity dispersion. When the nebular emission-line profiles are clearly asymmetric (i.e. in the nuclei of active galaxies) and cannot be fitted by a single Gaussian, double Gaussians are used to fit the emission lines.
4. Line-strength indices
Lick/IDS line-strength indices using the definition in Trager et al. (1998) were measured in all the binned spectra, cleaned of emission, along the radius. The errors were calculated from the uncertainties caused by photon noise, wavelength calibration, and flux calibration.
Line-strength indices depend on the broadening of the lines caused by instrumental resolution and by the internal motion of the stars. Before measuring the indices, we broadened our spectra to the Lick/IDS wavelength-dependent resolution following the prescriptions of Worthey & Ottaviani (1997). Afterwards, we applied a correction for the velocity dispersion of the galaxies using the template obtained in the derivation of the velocity dispersion for each spectrum, as described in Paper I. Offsets to transform into the Lick/IDS spectrophotometric system using stars in common with this library were derived (see Paper I). However, we only applied the offset to the indices when comparing with the Thomas et al. (2003) models based on the Lick/IDS fitting functions. To study the central and global properties of the bulges, we also extracted the spectra in three different apertures by averaging line-strength indices inside 1.2, 3.6, and 10 arcsec and a fourth one averaging the indices inside the whole bulge, using the sizes given in Table 2. The process is different from adding the spectra inside those apertures and measuring the indices afterwards. We decided to proceed in this way, first, to be able to compare with other authors when only line-strength indices were available but not the whole image and, secondly, to magnify the differences in the external parts of the bulges, which normally do not have much weight when a normal extraction, necessarily weighted with the light, is performed. The error is calculated as the standard error of the mean that is the standard deviation of the sampling distribution of the mean.
5. Results
To analyse the influence of bars in building bulges, we compare the line-strength indices in the bulge of barred and unbarred galaxies in this section. We also analyse the spatial distribution of the indices, as differences may be expected owing to the differences in the gas dissipation processes and star formation events in bulges built via mergers and via secular evolution. We also compare our line-strength indices to stellar population models to derive SSP-equivalent ages and metallicities both in central apertures and along the radius.
5.1. Comparison of the central line strengths of bulges of barred and unbarred galaxies
We mainly compared our results with those obtained by Moorthy et al. (2006), since the galaxy morphologies are similar in both samples. We selected those galaxies with b/a between 0.70 and 1.00, and early type galaxies with inclinations from the literature between 10° and 70°, for which no b/a was given in Morthy et al. (2006). NGC 2787 and NGC 3945 inclinations from Erwin and Sparke (2003) and the inclination of NGC 3384 from Busarello et al. (1996). This selection matches our inclination criteria. Their low-inclination sample contains 19 galaxies, eleven of which are barred. Using these data we can also not only test the consistency of the results, but also search for differences between the barred and the unbarred sample. Moorthy kindly provided all the index values along the radius for their sample. This made it possible to extract the indices measured in exactly the same way, with the same resolution (they broadened their spectra to the Lick/IDS resolution as we did) and the same apertures as in our own data. We subtracted the offsets they applied to transform their indices to Lick/IDS system. Because their study, like ours, measured the indices in flux-calibrated spectra at the Lick/IDS resolution, there should not be any additional offsets between their line-strength values and ours.
Figure 1 shows the variation in three representative indices inside an aperture of 1.2, 3.6, and 10.0 arcsec vs. σ. As can be seen, all bulges with σ > 150 km s-1 have almost the same index values (except for Mgb and CN2, not shown in the figure), while there is a large scatter in the index-values for bulges with σ < 150 km s-1 This behaviour has already been noticed by several authors in elliptical galaxies (e.g., Caldwell et al. 2003; Nelan et al. 2005; Sánchez-Blázquez et al. 2006; Ogando et al. 2006). There is a tendency in the metallicity-sensitive indices for the barred galaxies to be larger than those derived for unbarred galaxies, while the opposite is observed for the Balmer indices. We performed a significance test (3σ) on the index distributions with σ. For some of the indices, namely, the Balmer indices, Fe4383, and Mgb there is a statistically significant difference between the bulges of barred and unbarred galaxies at all apertures, while the difference is not statistically significant for the other indices.
 |
Fig. 1 Distribution of three representative central averaged indices vs. σ for our galaxies and the Moorthy et al. galaxies: 1.2 arcsec average (top panel), averaged 3.6 arcsec (middle panel), and averaged 10.0 arcsec (bottom panel). Empty symbols represent unbarred galaxies, while filled symbols represent barred galaxies with the crosses being our galaxies and the diamonds Moorthy’s sample. |
In Sect. 6 we compare the line-strength with stellar population models to transform the differences in differences in stellar population parameters (name it, age, metallicity ( [Z/H ] ) and relative abundance of α-elements ( [E/Fe ] ). We do not see that the AGN presence affects the calculated line-strength values after comparing the values for galaxies with and without an AGN nucleus.
5.2. Comparison of the central line strengths of bulges and elliptical galaxies
Because of the proposed continuation of properties between bulges and elliptical galaxies (e.g. Kuntschner et al. 2006), we would like to compare our results with those obtained for elliptical galaxies. Figure 2 shows the central Mgb, Hβ, Fe5015, and Mgb/F5015 values against the σ, together with the values presented in Kuntschner et al. (2006) for a sample of ellipticals and S0’s. For reference, we also plotted the values for the late-type galaxies in Ganda et al. (2007), which covers the same indices and spectral resolution as the Kuntschner et al. (2006) data. We have also plotted the sample by Moorthy et al. (2006) studied here. There is a tight correlation between σ and Mgb. The trend of Hβ, Fe5015 indices with σ for all the galaxies is almost flat, showing a large dispersion for galaxies with maximum velocity dispersion below 150 km s-1. The spread is also larger for the galaxies classified as barred. The central Fe5015 index of the unbarred galaxies seems to follow more closely the values of ellipticals while the Mgb follows the opposite trend, with barred galaxies showing values more similar to those of elliptical galaxies. This results in a Mgb/Fe5015 ratio where the central values of unbarred galaxies follow more closely those of ellipticals while the barred galaxies tend to lie above those values for the larger central velocity dispersion galaxies. Those galaxies showing the lower Mgb values are also the ones with lower Balmer indices.
 |
Fig. 2 Central 1.2 arcsec indices for a reference sample of late spirals, Ganda et al. (2007). Open circles: a sample of ellipticals from Kuntschner et al. (2006); stars, unbarred galaxies used in this work from Moorthy et al. (2006); open diamonds: barred galaxies used in this work from Moorthy et al. (2006). Filled diamonds and the filled circles represent the values from our sample of barred galaxies. |
 |
Fig. 3 Central index vs. central Mgb. From top to bottom and from left to right; CN1, CN2, Ca4227, G4300, Fe4383, Ca4455, Fe4531, C4668, Hβ, Fe5015, Hδ, Hγ, Mg1, Mg2, Fe5270, Fe5335. Overplotted are the models by Vazdekis et al. (2010) for a range of ages (0.5 to 18 Gyr) and metallicities (−1.68 to 0.0). |
It is interesting to notice that, although Thomas & Davies (2006) found that ellipticals and the bulges of early-type galaxies cannot be indistinguished at fixed σ, their sample did not contain any barred galaxies. However, Moorthy et al. (2006) find that for a given σ the bulges of barred and unbarred galaxies show differences similar to those found by us with a larger sample. The implications of these results will be discussed in Sect. 7.
5.3. Line-strength distribution gradients
The variation in the indices with radius in the bulge region was presented in Paper I. The distribution of the indices in the bulge regions is, in some of the cases, far from a linear one. The distribution of the Balmer index is generally characterised by a maximum in the bulge region, close to the bulge end. These profiles are due to the presence of central structures such as nuclear rings. Despite this non-linear distribution and in order to quantitatively characterise the gradients, we performed a linear fit to the data in the bulge region. Tables in Appendix A.1 show the gradients resulting from the fit to the indices for each of the galaxies. Most galaxies show negative or no gradients in their metallicity sensitive indices and positive or zero gradients in their Balmer indices. NGC 2273 and NGC 2665 show a small positive gradient in their metallicity-sensitive indices. NGC 1832 and NGC 2217 also show this trend in their metallicity-sensitive indices, but it is likely due to the presence of a nuclear ring in the outer part of the bulge. For a long-lasting ring, we would expect an enrichment of the ring area due to continuous star formation activity. Recent work (Ellison et al. 2011) shows that bars are efficient mechanisms in triggering central star formation.
Previous studies of line-strength gradients in bulges (Moorthy et al. 2006; Jablonka et al. 2007; Morelli et al. 2008) also find that most galaxies show negative gradients in the metallicity sensitive indices. With respect to the age sensitive gradients (i.e. Balmer indices), Moorthy et al. find that, when a positive age gradient is present, it is always in a barred galaxy. In our case, where only barred galaxies are analysed, we find galaxies with a variety of index distributions with negative, positive or zero Balmer indices gradients. The galaxies that show a negative gradient seem to be associated with the presence of a nuclear ring.
 |
Fig. 4 SSP-equivalent age and metallicity along the radius. Dashed lines indicate the end of the bulge and of the bar region. A linear fit to the bulge region is also plotted. |
6. Ages and metallicities
To transform our measured indices into single stellar population equivalent parameters, we used two different set of models. The first one, from Vazdekis et al. (2010)3, is built using the MILES library (Cenarro et al. 2007; Sánchez-Blázquez et al. 2006). The second set of models we used is that of Thomas, Maraston & Bender (2003), which are based on the Lick/IDS fitting functions (Gorgas et al. 1993; Worthey 1994). These two sets of models use different isochrones and stellar libraries, and the comparison between the results obtained with them can be used to estimate the errors affecting the predictions. The details about the uncertainties are carefully discussed in Paper I. It is clear that the true star formation history in these objects will be more complicated than a simple SSP. However, very useful information can still be retrieved from the SSP analysis if they are properly interpreted. Roughly, the SSP-equivalent age of a composite stellar population (CSP) is dominated primarily by the age of the youngest component and the mass fraction of the different populations. The SSP-equivalent metallicity is very similar to a V - band luminosity-weighted chemical composition (Serra & Trager 2007). Figure 3 shows the central line indices vs. the central Mgb with the Vazdekis et al. (2010) models overplotted. The plot shows a tight correlation among the different indices for the central region and very good agreement with the models, except for some well-known exceptions. In particular, some galaxies show values of CN, Mgb, G4300, and C4668 that are higher than the models, while this is not true for the Fe-sensitive indices. This can be reflecting an overabundance of Mg/Fe and probably C/Fe and N/Fe with respect to the solar neighbourhood, as suggested by many authors (e.g. Worthey 1998; Tantalo et al. 1998; Trager et al. 2000; Sánchez-Blázquez et al. 2003; Graves & Schiavon 2008). Similar to Paper I, to obtain stellar population parameters we use 4 indices, namely HδA, HγA, Fe4383, and Mgb, and follow a multi-index approach as described in Proctor & Samson (2002). A detailed explanation of the error calculation is given in Paper I.
 |
Fig. 4 continued. |
 |
Fig. 4 continued. |
 |
Fig. 4 continued. |
The SSP-equivalent age and metallicity distributions along the radius are shown in Fig. 4. As for our data, we also derived the ages and metallicities in the way explained in Paper I for the data published by Moorthy et al. (2006). From Fig. 5 it can be seen that the metallicity and ages in both barred and unbarred galaxies seem to cover the same range of values, but barred galaxies tend to have higher metallicities than unbarred galaxies at a given σ. No clear difference is found for the central ages. The [E/Fe] values for unbarred galaxies tend to lie below the values of barred galaxies at a given σ. When we open the aperture to include the whole bulge, the trends become clearer, with the metallicities of the unbarred galaxies lying below those of the barred galaxies at a given σ. Also the [E/Fe] still remains lower for the unbarred galaxies when the aperture is as large as the whole bulge region. Similar results are found when comparing them with elliptical galaxies (see Fig. 2 and Sect. 5.1), although in that case, we have just compared the Mgb/Fe5015 ratio. However, these trends are weak, and a significance test applied to the stellar parameters does not reveal any statistically significant difference, although the low number of unbarred galaxies might be driving the significance test. At this point, due to the large dispersion of the values and the lack of statistical significance, this apparent trend in the [E/Fe] values should be confirmed in the future with a larger set of data. The results for the bulge metallicity confirm the bulge’s spectral indices trends (see Sect. 5.1), where we found that the metallicity-sensitive indices of barred galaxies are larger than those of unbarred galaxies.
Linear fit age and metallicity gradients to the bulge region.
 |
Fig. 5 Age, [Z/H] and [E/Fe] for the average central 10 and 3.6 arcsec apertures. Symbols as in Fig. 1. |
6.1. Age and metallicity gradients
Linear fits were performed on the derived ages, metallicities, and [E/Fe] values vs. radius (see Table 3). Figure 4 shows the radial distribution of ages and metallicities for all the galaxies. Figure 6 shows that, on average, galaxies with lower σ tend to have negative age gradients, while larger central velocity dispersion galaxies show positive age gradients. The relation between [Z/H] gradient and the central velocity dispersion is shown in Fig. 6. Most galaxies show a negative [Z/H] gradient. The mean metallicity gradient is −0.19 ± 0.07 dex for the barred galaxies and −0.3 ± 0.1 for the non-barred ones. These gradients are calculated using a log scale for the radius to be able to compare with the literature, while the gradients given in Table 3 and Fig. 6 have been derived using a linear scale. Both values are within the values obtained by other authors for the bulge of galaxies. For example, Morelli et al. find a mean value of (−0.15 dex) and Jablonka et al. (2007), d[Z/H]/dr = −0.2 dex for a sample containing both barred and non-barred galaxies. The differences between the metallicity gradient of barred and non-barred galaxies are not statistically significant. We also do not find any correlation between the metallicity gradient of barred galaxies and the central velocity dispersion. In early-type galaxies, a possible correlation between the metallicity gradient and the mass for elliptical galaxies with central sigma ≤ 150−175 km s-1 has been claimed (Sánchez-Blázquez et al. 2007; Spolaor et al. 2009; Kuntschner et al. 2010). Other studies of both early-type galaxies (Ogando et al. 2005) and bulges (Jablonka et al. 2007) find a lower boundary instead of a correlation in the sense that massive galaxies do not show strong gradients, but less massive galaxies show a larger scatter. In our sample we observe neither a correlation nor a lower boundary and, after comparison with the data from Jablonka et al. (2007), our gradients are distributed similarly to their gradients, so there is no systematic effect affecting our results. Very high signal-to-noise ratio data might help answer whether there is a real correlation between metallicity gradients and velocity dispersion. The [E/Fe] gradients are shown in Fig. 6. The [E/Fe] gradients are very small, almost compatible with zero, although they take both positive and negative values. Bulges with low velocity dispersion (σ < 100 km s-1) tend to have systematically positive values, while the same is not true for more massive bulges. In either case, the values of the gradients are, as said above, very small. This is compatible with what is found in elliptical galaxies, where the [E/Fe] is also found to be compatible with zero in most cases (e.g. Mehlert et al. 2003; Sanchez-Blazquez et al. 2006, 2007) and in other studies of bulges (e.g. Jablonka et al. 2007; MacArthur et al. 2009). For comparison, we have also derived age, metallicity, and [E/Fe] gradients for Moorthy’s sample in a similar way. The values of the barred galaxies in this sample coincide with those of our galaxies and we do not find any difference between the values of barred and unbarred galaxies. Interpreting the gradients is complicated as their value may change owing to many different physical processes and also because substructures inside the galaxy, such as rings or disks which are common in our sample, change the value of the slope that is intrinsic to the spheroid.
 |
Fig. 6 Age, [Z/H], and [E/Fe] gradient in the bulge region vs. maximum central dispersion. Symbols as in previous figures; i.e., empty symbols represent unbarred galaxies, while filled symbols represent barred galaxies with the crosses our galaxies and the diamonds Moorthy’s galaxies for which a reliable gradient could be obtained. |
6.2. Comparison between the SSP stellar parameters in the bulge and the bar region
It is interesting to relate the bulge mean age and metallicity gradients to the gradients and mean values in the bar region, because in Paper I we found seven galaxies with metallicity gradients in the bar region significantly (more than 3-σ significance) different from zero: NGC 1169, NGC 2217, NGC 4394, and NGC 5101 (positive) and NGC 2665, NGC 2681, NGC 4245 (negative). We excluded NGC 1530, NGC 3081, NGC 4314, and NGC 2935 from this analysis due to the large fitting errors in the bar region. In Fig. 7 we can see the relation between the mean metallicities in the bulge and the bar region. The good correlation is striking between the metallicities in both the bar and the bulge. This result points to a bulge enrichment linked to that of the bar.
Although the mean values of both bars and bulges are correlated, the bulge gradients do not show any correlation with the bar gradients, because the bulge gradients are more indicative of the presence of morphological substructures in the bulge.
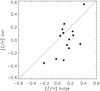 |
Fig. 7 Average metallicity values of the bulge and the bar region (from Paper I) for the sample galaxies. |
7. Summary and discussion
Following the results from Pérez et al. (2009) for the stellar line-strength indices and the age and metallicity distribution along the bars of a sample of 20 galaxies, we carried out a detailed study of the populations of the central regions of those galaxies. We compared the results with the bulge properties of a similar sample of unbarred galaxies (Moorthy et al. 2006), deriving the SSP equivalent stellar parameters in the same way as for our sample. We found differences in the bulge stellar population properties between barred and unbarred galaxies. We find that some of the metallicity sensitive indices of the bulges of barred galaxies lie above those of unbarred galaxies, and the Balmer indices tend to follow the opposite trend, as already hinted at by Moorthy et al. (2006). It is interesting to note that, although one could say that there is a good correlation between line-strength indices and σ, it would be a better description of the index distribution with σ to say that there is an almost constant value of the indices with σ, plus a tail in the distribution for the smaller σ galaxies (below ≈ 150 km s-1). Most galaxies show negative gradients for metal-sensitive indices while the opposite is true for Balmer line indices, although NGC 1832 and NGC 2665 clearly show the opposite trend. The index distributions are closely linked to morphological substructures in the bulge region such as nuclear rings.
We derived the ages, metallicities, and [E/Fe] values using two different sets of models. The central parts of barred galaxies tend to be more metal rich than the unbarred counterparts. Interestingly, [E/Fe] seems to be enhanced for the barred galaxies over the unbarred central regions. These trends are not statistically significant perhaps because of the low number of unbarred galaxies in the sample and would need to be followed up with a larger sample of unbarred galaxies. The age gradients follow the index trend with σ, most galaxies show no gradient or slightly positive gradient; however, the distribution of gradients for galaxies with σ below ≈150 km s-1 shows a larger dispersion. The same behaviour is found for the metallicity trends, with most values negative with grad[Fe/H] around −0.05. The only outliers are found in galaxies with σ below 150 km s-1. Galaxies with σ above 150 km s-1 show a zero [E/Fe] gradient, while galaxies with central velocity dispersion below this value show a positive [E/Fe] gradient. We also calculated the gradients in Moorthy’s data. There is very good agreement in the values of both samples, and we do not find any difference between barred and unbarred galaxies. Interpretation of the gradients is difficult since there are too many processes that can modify their shape. Furthermore, the presence of substructures, such as disks or rings, which are very common in our sample, makes it very difficult to measure the real gradient of the spheroid.
That barred galaxies show a similar age and a lower [E/Fe] is, in principle, a puzzling result. In a classical scenario of secular building of the bulge, the star formation extends for much longer timescales than in a merger-built scenario, where star formation happens very efficiently and in short periods of time. In contrast, we find (in agreement with Moorthy et al. 2006), the opposite result. One possible bias to this study is that our sample mostly contains early-type spirals. We showed in Paper I that the bars in these galaxies are old and have high values of E/Fe (see also Gadotti & de Souza 2006). The epoch of formation of these bars is probably associated with the epoch of formation of the bulge, which would be compatible with the strong correlation we find in the stellar parameters of both components. Some proposed mechanisms for forming bars are, e.g., mergers and interactions. These processes can create both the bar and the bulge, in particular in those galaxies with early type morphologies (see, e.g., Walker et al. 1996; Berentzen et al. 2004; Peirani et al. 2009). During the formation of the bulge, the star formation could have been enhanced by the presence of this bar, increasing the metallicity and the [E/Fe] values of the bulge with respect to those bulges lacking this structure (e.g. Pérez & Freeman 2006). Later accretion of gas can then be funneled towards the centre forming nuclear disks and rings (Emsellem et al. 2001; Wozniak et al. 2003; Wozniak & Champavert 2006), producing substructures with a low level of star formation, i.e. slightly younger (showing a lower SSP-equivalent age in our data), but that would not contain enough stars to produce a change in the SSP-equivalent metallicities and [E/Fe], because the metallicity and [E/Fe] values reflect more the values of the dominant (in mass) stellar population (see Serra & Trager 2007), while the SSP-equivalent age is very biased towards the youngest components. To test this hypothesis, further work and analysis would be needed to derive star formation histories. If this hypothesis is confirmed, it would imply that bars are old and long-lasting features and that bar formation is, at least for this early type barred galaxies, closely linked to the formation of the bulge. The large dispersion in the values for some of the trends found in this study means that to confirm them, we will need to extend the unbarred galaxy sample and the morphological range covered by it.
Online material
Appendix A: Linear fits to the line-strength distribution in the bulge region
Linear fit parameters (Y = a + bx) in the bulge region of NGC 1169.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 1358.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 1433.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 1530.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 1832.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2217.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2273.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2523.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2665.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2681.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2859.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2935.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2950.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 2962.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 3081.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 4245.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 4314.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 4394.
Linear fit parameters (Y = a + bx) in the bulge region of NGC 5101.
Bar strength is shown here as bar class; for assignment of bar class to a certain bar strength, see Buta & Block (2001), it is on a scale from 0 to 6, 6 as the strongest bar.
The models are publicly available at http://miles.iac.es
Acknowledgments
We really thank B. Moorthy for kindly providing us with the radial values of all the indices of their sample. We want to thank the anonymous referee for the very useful comments and discussion. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. I. Pérez acknowledges the support of a postdoctoral fellowship from the Netherlands Organisation for Scientific Research (NWO, Veni-Grant 639.041.511), and she is currently supported by the Spanish Plan Nacional del Espacio del Ministerio de Educación y Ciencia(via grant C-CONSOLIDER AYA 2007-67625-C02-02). She also thanks the Junta de Andalucía for support through the FQM-108 project. PSB is supported by the Ministerio de Ciencia e Innovación (MICINN) of Spain through the Ramon y Cajal programme. She also acknowledges the support of the European for a ERC under their 6th programme. This work has been supported by the Programa Nacional de Astronomía y Astrofísica of th e Spanish Ministry of Science and Innovation under the grant AYA2007-67752-C03-01.
References
- Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Berentzen, I., Athanassoula, E., Heller, C. H., & Fricke, K. J. 2004, MNRAS, 347, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Block, D., Puerari, I., Knapen, J., et al. 2001, A&A, 375, 761 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Block, D., Buta, R., Knapen, J., Elmegreen, D., & Puerari, I. 2004, AJ, 128, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Busarello, G., Capaccioli, M., D’Onofrio, M., et al. 1996, A&A, 314, 32 [NASA ADS] [Google Scholar]
- Buta, R. 1986, ApJS, 61, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., & Block, D. L. 2001, ApJ, 550, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., Laurikainen, E., Salo, H., Block, D., & Knapen, J. 2006, AJ, 132, 1859 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N., Rose, J. A., & Concannon, K. D. 2003, AJ, 125, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Cardiel, N. 1999, PhD Thesis [Google Scholar]
- Cardiel, N., Gorgas, J., Cenarro, J., & González, J. 1998, A&AS, 127, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cenarro, A. J., Peletier, R. F., Sánchez-Blázquez, P., et al. 2007, MNRAS, 374, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., & Sanders, R. 1981, A&A, 96, 164 [NASA ADS] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Comerón, S., Knapen, J. H., Beckman, J. E., et al. 2010, MNRAS, 402, 2462 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Ann. Astrophys., 11, 24 [Google Scholar]
- Ellison, S. L., Patton, D. R., Nair, P., et al. 2011 [arXiv:1101.3566] [Google Scholar]
- Emsellem, E., Greusard, D., Combes, F., et al. 2001, A&A, 368, 52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erwin, P. 2004, A&A, 415, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erwin, P., & Sparke, L. S. 2003, ApJS, 146, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Peletier, R. F., & Balcells, M. 2002, MNRAS, 335, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B. 2006, ApJ, 642, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2008, AJ, 136, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2010, ApJ, 716, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Friedli, D., & Benz, W. 1995, A&A, 301, 649 [NASA ADS] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D., & de Souza, R. 2006, ApJS, 163, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Ganda, K., Peletier, R. F., McDermid, R. M., et al. 2007, MNRAS, 380, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Gorgas, J., Faber, S., Burstein, D., et al. 1993, ApJS, 86, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Goudfrooij, P., Gorgas, J., & Jablonka, P. 1999, Ap&SS, 269, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Graves, G. J., & Schiavon, R. P. 2008, ApJS, 177, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Bundy, K., Hernquist, L., Wuyts, S., & Cox, T. J. 2010, MNRAS, 401, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Jablonka, P., Gorgas, J., & Goudfrooij, P. 2007, A&A, 474, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jungwiert, B., Combes, F., & Axon, D. J. 1997, A&AS, 125, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntschner, H., Emsellem, E., Bacon, R., et al. 2006, MNRAS, 369, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., Buta, R., & Vasylyev, S. 2004, MNRAS, 355, L1251 [NASA ADS] [CrossRef] [Google Scholar]
- MacArthur, L. A., González, J. J., & Courteau, S. 2009, MNRAS, 395, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Mehlert, D., Thomas, D., Saglia, R. P., Bender, R., & Wegner, G. 2003, A&A, 407, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moorthy, B., & Holtzman, J. 2006, MNRAS, 371, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Nelan, J. E., Smith, R. J., Hudson, M. J., et al. 2005, ApJ, 632, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ogando, R. L. C., Maia, M. A. G., Chiappini, C., et al. 2005, ApJ, 632, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ogando, R. L. C., Maia, M. A. G., Chiappini, C., et al. 2006, in Rev. Mex. Astron. Astrofis. Conf. Ser., 26, 119 [Google Scholar]
- Paturel, G., Petit, C., Prugniel, P., et al. 2003, A&A, 412, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peirani, S., Hammer, F., Flores, H., Yang, Y., & Athanassoula, E. 2009, A&A, 496, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peletier, R. F. 2008, in Pathways Through an Eclectic Universe, ed. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, ASP Conf. Ser., 390, 232 [Google Scholar]
- Peletier, R., Falcón-Barroso, J., Bacon, R., et al. 2007, MNRAS, 379, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, I., & Freeman, K. 2006, A&A, 454, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, I., Sánchez-Blázquez, P., & Zurita, A. 2007, A&A, 465, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez, I., Sánchez-Blázquez, P., & Zurita, A. 2009, A&A, 495, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfenniger, D., & Friedli, D. 1991, A&A, 252, 75 [NASA ADS] [Google Scholar]
- Pfenniger, D., & Norman, C. 1990, ApJ, 363, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Proctor, R. N., & Sansom, A. E. 2002, MNRAS, 333, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Gorgas, J., Cardiel, N., Cenarro, J., & González, J. J. 2003, ApJ, 590, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Forbes, D. A., Strader, J., Brodie, J., & Proctor, R. 2007, MNRAS, 377, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Falcón-Barroso, J., Davies, R. L., et al. 2006, MNRAS, 366, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., & Trager, S. 2007, MNRAS, 374, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Simkin, S. M., Su, H. J., & Schwarz, M. P. 1980, ApJ, 237, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Spolaor, M., Proctor, R. N., Forbes, D. A., & Couch, W. J. 2009, ApJ, 691, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Tantalo, R., Chiosi, C., & Bressan, A. 1998, A&A, 333, 419 [NASA ADS] [Google Scholar]
- Thomas, D., & Davies, R. L. 2006, MNRAS, 366, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., & Bender, R. 2003, MNRAS, 339, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., Worthey, G., Faber, S. M., Burstein, D., & Gonzalez, J. J. 1998, ApJS, 116, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Trager, S. C., Faber, S. M., Worthey, G., & González, J. J. 2000, AJ, 119, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Verón-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, I. R., Mihos, J. C., Hernquist, L., Bolte, M., & Mendes de Oliveira, C. 1996, in Barred Galaxies, ed. R. Buta, D. A. Crocker, & B. G. Elmegreen, IAU Colloq., ASP Conf. Ser., 91, 157, 486 [Google Scholar]
- Worthey, G. 1994, ApJS, 95, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G. 1998, PASP, 110, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Worthey, G., & Ottaviani, D. L. 1997, ApJS, 111, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, H., & Champavert, N. 2006, MNRAS, 369, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, H., Friedli, D., Martinent, L., Martin, P., & Bratschi, P. 1995, A&A, 111, 115 [Google Scholar]
- Wozniak, H., Combes, F., Emsellem, E., & Friedli, D. 2003, A&A, 409, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution of three representative central averaged indices vs. σ for our galaxies and the Moorthy et al. galaxies: 1.2 arcsec average (top panel), averaged 3.6 arcsec (middle panel), and averaged 10.0 arcsec (bottom panel). Empty symbols represent unbarred galaxies, while filled symbols represent barred galaxies with the crosses being our galaxies and the diamonds Moorthy’s sample. |
| In the text | |
 |
Fig. 2 Central 1.2 arcsec indices for a reference sample of late spirals, Ganda et al. (2007). Open circles: a sample of ellipticals from Kuntschner et al. (2006); stars, unbarred galaxies used in this work from Moorthy et al. (2006); open diamonds: barred galaxies used in this work from Moorthy et al. (2006). Filled diamonds and the filled circles represent the values from our sample of barred galaxies. |
| In the text | |
 |
Fig. 3 Central index vs. central Mgb. From top to bottom and from left to right; CN1, CN2, Ca4227, G4300, Fe4383, Ca4455, Fe4531, C4668, Hβ, Fe5015, Hδ, Hγ, Mg1, Mg2, Fe5270, Fe5335. Overplotted are the models by Vazdekis et al. (2010) for a range of ages (0.5 to 18 Gyr) and metallicities (−1.68 to 0.0). |
| In the text | |
 |
Fig. 4 SSP-equivalent age and metallicity along the radius. Dashed lines indicate the end of the bulge and of the bar region. A linear fit to the bulge region is also plotted. |
| In the text | |
 |
Fig. 4 continued. |
| In the text | |
 |
Fig. 4 continued. |
| In the text | |
 |
Fig. 4 continued. |
| In the text | |
 |
Fig. 5 Age, [Z/H] and [E/Fe] for the average central 10 and 3.6 arcsec apertures. Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 6 Age, [Z/H], and [E/Fe] gradient in the bulge region vs. maximum central dispersion. Symbols as in previous figures; i.e., empty symbols represent unbarred galaxies, while filled symbols represent barred galaxies with the crosses our galaxies and the diamonds Moorthy’s galaxies for which a reliable gradient could be obtained. |
| In the text | |
 |
Fig. 7 Average metallicity values of the bulge and the bar region (from Paper I) for the sample galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


