| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 7 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201016404 | |
| Published online | 25 February 2011 | |
Research Note
A study of NIR atmospheric properties at Paranal Observatory
1
European Southern Observatory,
Casilla 19001,
Santiago 19,
Chile
e-mail: glombard@eso.org
2 ESA-STScI, 3700 San Martin Drive, MD 21218, Baltimore, USA
3
Australian Astronomical Observatory, PO Box 296, Epping
NSW
1710,
Australia
4
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029
Blindern, 0315
Oslo,
Norway
Received: 23 December 2010
Accepted: 29 January 2011
Aims. In order to maximize the scientific return of the telescopes located at the Paranal Observatory, we analyse the properties of the atmosphere above Paranal in the near-infrared (NIR).
Methods. We estimate atmospheric extinction in the spectral range 1.10–2.30 μm (J, Js, H, and Ks) using standard stars that were observed during photometric and clear nights with ISAAC on the Very Large Telescope UT1 between 2000 and 2004. We have built a database consisting of hundreds of observations, which allows us to examine how extinction varies with airmass and the column density of water vapour. In addition, we use theoretical models of the atmosphere to estimate Rayleigh scattering and molecular absorption in order to quantify their fractional contribution to the total extinction in each filter. Finally, we have observed 8 bright red standard stars to evaluate filter color terms.
Results. We find that extinction coefficients are < 0.1 mag airmass-1 in all the considered bands. The extinction coefficient in the J-band strongly depends on the column density of water vapour. Molecular absorption dominates the extinction in J, H and Ks, while Rayleigh scattering contributes most to the extinction in Js. We have found negligible color terms for J, H and Ks and a non-negligible color term for Js.
Key words: atmospheric effects / Site testing
© ESO, 2011
1. Introduction
The ESO Paranal Observatory is located on the edge of the Atacama Coast in Northern Chile, 120 km south of the city of Antofagasta, at an altitude of 2635 meters above sea level. The conditions at the observatory are characterised by a high fraction of clear nights and low levels of humidity (Lombardi et al. 2009), which are important for near-infrared (NIR) observations. However, there has been little direct measurement of the properties of the atmosphere above Paranal in the NIR. In order to fill this gap, we have calculated the extinction coefficients using photometric standard stars observed with the Infrared Spectrometer And Array Camera (ISAAC) at the Very Large Telescope (VLT) Unit Telescope 1 (UT1) as part of the ISAAC calibration plan. In addition, we have estimated the fractional contribution of Rayleigh scattering, molecular absorption and aerosol scattering to the extinction. This estimation required the application of a theoretical approach retrieved from the literature. Finally, to complete the analysis, we also calculated the instrumental color terms using 8 red stars observed under photometric conditions.
Properties of ISAAC SW imaging filters used in this study.
 |
Fig. 1 Evolution in time of the zeropoints for J, Js, H and Ks. The solid vertical lines indicate M1 recoating events, while dotted vertical lines indicate ISAAC interventions. |
2. Database and data reduction
Our dataset consists of standard star observations covering a period of 5 years (from March 2000 through to December 2004). The observations were made during clear nights with the ISAAC short-wavelength (SW) arm in J, Js, H, and Ks. All data, including the relevant calibration frames, were retrieved from the ESO archive. Clear nights were identified by inspecting the nightly observatory weather reports. All stars have magnitudes on the LCO system (Persson et al. 1998).
Table 1 lists the characteristics of ISAAC filters (ISAAC User Manual 2009), while in Table 9, at the end of this Research Note, we note all the standard stars used in the analysis. The data reduction has been performed using the ISAAC Pipeline. Each frame has been corrected for electronic artifacts, dark subtracted and flat fielded. Each standard star is imaged over a grid of five positions, one just above the center of the array and one in each quadrant. The pipeline computes a set of instrumental magnitudes which are averaged to deliver the zeropoint (ZP) uncorrected for extinction.
ZP uncertainties are computed as 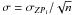 , where n is the number of times, usually five, a single standard is observed, and σZPi is the scatter about the mean ZP reported by the pipeline. In our analysis, we have rejected points having σ > 0.050 mag. Our final sample contains 575 data points in J, 603 data points in Js, 604 data points in H and 667 data points in Ks.
, where n is the number of times, usually five, a single standard is observed, and σZPi is the scatter about the mean ZP reported by the pipeline. In our analysis, we have rejected points having σ > 0.050 mag. Our final sample contains 575 data points in J, 603 data points in Js, 604 data points in H and 667 data points in Ks.
3. Data analysis
3.1. Time evolution of the zeropoint
In Fig. 1, the zeropoints of the four bands are shown as four time series. Different colors represent different bands. We clearly see that, for each band, the zeropoints are characterized by trends within well defined time intervals. A further inspection demonstrated that the intervals are delimited by technical or maintenance interventions, either on the instrument or the telescope (e.g. M1 recoating). This means that, in the mentioned intervals (or periods, P), the computed zeropoints are affected by deterioration of the telescope optics after a recoating of UT1 primary mirror (M1) or instruments troubles (ISAAC technical interventions). A list of the events that occurred between 2000 and 2005 is reported in Table 2.
Technical events occurred between 2000 and 2005.
 |
Fig. 2 ZP0 for each period. |
The deterioration in the aluminum coating of the telescope mirrors is mainly due to dust and oxidation. It results in a progressive reduction in the mirror reflectivity, an increase in the thermal background emission (Frogel 1998) and a consequent decrease in the zeropoints. A change (increase or decrease) in the zeropoint can also be due to interventions on ISAAC, as they affect the instrument configuration. Our idea was to consider each period separately and to remove, from each one of them, the time dependency by subtracting a linear fit of the zeropoint with time. In practice we adjust all zeropoints to the value of the intercept of the fit at the beginning of the considered period. During the analysis we have confirmed that a linear fit was accurate enough, therefore higher polynomials have not been used. The fits for periods P3 and P6 are not well constrained, because the small number of points within these two periods. Therefore, they are not been considered further in this analysis.
The evolution in the zeropoint within each period is fitted with 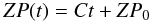 (1)where t is the time, ZP0 corresponds to the zeropoint at the beginning (t = 0) of the considered period, and C the slope of the fit. The differences ZP(t = 0) − ZPi have been computed and added to each observed ZPi.
(1)where t is the time, ZP0 corresponds to the zeropoint at the beginning (t = 0) of the considered period, and C the slope of the fit. The differences ZP(t = 0) − ZPi have been computed and added to each observed ZPi.
Finally, in each period, we subtracted the intercept of the fit at t = 0 from the corrected ZPi. In this way we have eliminated both the offset between periods and the evolution with time within a period. This represents a clear advantage. We can now work with a single dataset, rather than 9.
It is interesting to check the variation in ZP0 after each event. If the event did not affect the instrument performance, ZP0 values should be all identical. As shown in Fig. 2, we observe significant offsets between events.
 |
Fig. 3 Monthly trend of the PWV on Paranal in photometric and clear nights. |
3.2. Effects of the precipitable water vapour
The transmission of the atmosphere in the NIR is greatly affected by the presence of water. Considering the classical Johnson filters, an increase in the column density of water vapour causes (J − K) and (H − K) to be bluer, because the effect of water vapour is stronger in K (Δλ = 0.41 μm) than in J and H (Frogel 1998; see also Fig. 1 in Manduca & Bell 1979). On the other hand, the ISAAC Ks filter has a narrower bandwidth (Δλ = 0.27 μm, see Table 1) and avoids the strongest water lines. Therefore we expect that, in our case, J and H will suffer more from large amounts of water in the atmosphere.
The amount of water above Paranal has been continuously monitored since July 2000 using the images from the Geostationary Operational Environmental Satellite (GOES). The sampling is every 3 h starting at 00h UT.
To retrieve the Precipitable Water Vapour (PWV) from GOES images a model exists developed by A. Erasmus under contract with ESO (Erasmus & Peterson 1997; Erasmus & Sarazin 2000; Erasmus & Sarazin 2002). The method is based on combining satellite current image in the 6.7 μm and 10.7 μm channel with wind and temperature profiles forecasted by a prediction center.
Typical satellite observations at about 6.5 μm are sensitive to emissions from water vapour resident in the layer between about 600 mbar (~4400 m) and 300 mbar (~9000 m). For what concerns GOES vertical resolution, the 6.7 μm channel is located near the center of a strong water vapor absorption band and under clear sky conditions it is primarily sensitive to the relative humidity averaged over a depth of atmosphere extending from 200 to 500 mbar (Soden & Bretherton 1993). The horizontal resolution is sufficient since the atmosphere surrounding Paranal is not expected to vary significantly over an area that extends several 10’s of km.
Figure 3 shows the yearly trend in the amount of PWV sampled at Paranal during photometric and clear nights. We do see a yearly periodic modulation with high values (up to 13 mm in 2002) in the trimester January-March corresponding to the so called Bolivian winter. As shown in the figure, the median PWV at Paranal during photometric and clear nights is 2.3 mm.
Figure 4 shows the relationship between zeropoints and the PWV in the considered bands. For each band we have calculated a weighted linear fit. The fits are repeated twice more after rejecting 3-σ outliers. In Table 3 we report the slopes and the RMS of the fits. For Js, H, and Ks the trend with the column density of PWV is quite slight, while for J it is very significant. The scatter about the best fit for J is between 2 and 4 times larger that the scattered measured for the other filters.
 |
Fig. 4 Weighted linear fit of the zeropoints as a function of the PWV in the four bands. |
Zeropoints-versus-PWV slope and dispersion (RMS).
Calculated κ in [mag airmass-1] for J, Js, H and Ks at Paranal.
4. Determination of the atmospheric extinction coefficients
The relationship between ZP and airmass (X) defines the extinction curve (Bouguer curve). The extinction coefficient (κ) is the slope of a linear fit to this curve. The fit is done three times. Between each fit, 3-σ outliers are rejected.
The extinction coefficients have been calculated in two different ways:
-
a)
correcting the zeropoints for the amount of PWV before computing κ;
-
b)
considering separately the zeropoints in different PWV ranges in order to evaluate κ as a function of the PWV.
In case a we offset the zeropoints using the fits calculated in Sect. 3.2 and reported in Fig. 4 and Table 3. The offset to each zeropoint is 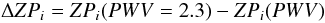 (2)where the index i refers to one of the four filters. The zeropoint is corrected to the median amount of PWV. The PWV-corrected zeropoint, rZPi, is then
(2)where the index i refers to one of the four filters. The zeropoint is corrected to the median amount of PWV. The PWV-corrected zeropoint, rZPi, is then 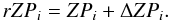 (3)In Fig. 5 we have plotted the weighted linear fits to the curves for the rZP in the four bands. The extinction coefficients are reported in Col. 2 of Table 4. The dispersion (RMS) of the points around the best fits are also reported.
(3)In Fig. 5 we have plotted the weighted linear fits to the curves for the rZP in the four bands. The extinction coefficients are reported in Col. 2 of Table 4. The dispersion (RMS) of the points around the best fits are also reported.
 |
Fig. 5 Bouguer curves computed for the PWV rescaled zeropoints in J, Js, H and Ks. |
In case b we have calculated the extinction coefficients for three different PWV ranges: PWV = 0–2 mm, PWV = 2–4 mm, and PWV = 4–7 mm. The results are reported in Cols. 3–5 of Table 4 and plotted in Figure 6. As expected, the J-band extinction coefficient has the greatest sensitivity to the amount of PWV. It increases by ~ 0.05 mag airmass-1 over the range of PWVs considered here. The increase in the extinction coefficients for Js and H are less (~0.03 and ~ 0.02 mag airmass-1, respectively), while there is a negligible effect in Ks.
The dependence of the extinction coefficients on the amount of PWV underlines the importance of observing IR standards (more important for J and less important for Ks) at roughly the same airmass and at roughly the same time as the science target.
 |
Fig. 6 Extinction coefficients in J, Js, H and Ks calculated for PWV = 0–2 mm, PWV = 2–4 mm, PWV = 4–7 mm. The dotted line represents the κ calculated with the PWV rescaled ZP, while the gray zone is the dispersion (see Col. 2 of Table 4). |
5. The fractional contribution to the extinction
According to Hayes & Latham (1975) the largest contributors to atmospheric extinction are Rayleigh scattering (κRay), molecular absorption (κmol) and aerosol scattering (κaer). The efficiency of aerosol scattering from particles that are smaller than a few microns at λ > 1.0 μm is negligible (Lombardi et al. 2008), therefore for the ISAAC filters (Table 1) we have computed the vertical atmospheric extinction coefficients as the sum of κRay and κmol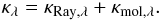 (4)Variations in κRay and κmol with time are linked to occasional and periodic climatic changes in the atmosphere above the site (Lombardi et al. 2009). For this reason, theoretical models are valid only to calculate average contributions to the extinction coefficients.
(4)Variations in κRay and κmol with time are linked to occasional and periodic climatic changes in the atmosphere above the site (Lombardi et al. 2009). For this reason, theoretical models are valid only to calculate average contributions to the extinction coefficients.
5.1. Rayleigh scattering
Rayleigh scattering of unpolarised light is due to particles with dimensions that are ≪ λ. It has been extensively discussed by Penndorf (1957). According to Hayes & Latham (1975), Rufener (1986) and Burki et al. (1995) the vertical Rayleigh extinction can be expressed as 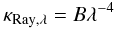 (5)where the Rayleigh scattering coefficient B is a complex function of the refractive index, n(T,P,λ), and the number of particles, N(T,P). T and P are the site’s mean temperature and pressure. B can be written as B(T,P,λ) and expressions for n, N and B are given by Penndorf (1957).
(5)where the Rayleigh scattering coefficient B is a complex function of the refractive index, n(T,P,λ), and the number of particles, N(T,P). T and P are the site’s mean temperature and pressure. B can be written as B(T,P,λ) and expressions for n, N and B are given by Penndorf (1957).
In the years between 2000 and 2004 a mean temperature of (12.8 ± 0.5) °C and a mean pressure of (743.5 ± 0.2) hPa have been measured at Paranal (Lombardi et al. 2009). We have used the expressions in Penndorf (1957) and Hayes & Latham (1975) to compute B(T,P,λ) and κRay,λ for the four ISAAC filters. The values are reported in Table 5.
As expected, Rayleigh scattering is more efficient in J and Js. It is an order of magnitude less efficient in H and Ks.
Rayleigh scattering coefficients and vertical Rayleigh extinction in [mag airmass-1] calculated for Paranal.
5.2. Molecular absorption
The contribution to the extinction originating from molecular absorption was modeled using an IDL driver to the Reference Forward Model (RFM). RFM is a GENLN2-based line-by-line radiative transfer code developed by Anu Dudhia at the Atmospheric, Oceanic and Planetary Physics Institute at Oxford University (UK) to analyse data from MIPAS on-board ENVISAT1. The code was run using the 2008 version of the HITRAN database (Rothman et al. 2009).
For the current work, only lines caused by H2O, CO2, N2O, CH4 and O2 were considered. We slightly modified the tropical atmospheric profile available with the RFM code to carry-out simulations corresponding to a temperature of 12.8 °C and an atmospheric pressure of 743.5 hPa (Lombardi et al. 2009). The amount of water vapour was scaled to match the median PWV for Paranal (2.3 mm). The code also allows one to vary the airmass of the line-of-sight or to select a specific molecule. The extinction in each filter was estimated by multiplying the atmospheric transmission produced by the model with the filter transmission curve (see ISAAC User Manual 2009). Results are reported in Table 6.
Calculated vertical molecular extinction in [mag airmass-1] for Paranal.
Vertical atmospheric extinction coefficients [in mag airmass-1] and fractional contributions of Rayleigh scattering and molecular absorption.
Observed Persson’s red standard stars for the determination of the color terms (the computed Cm is also reported).
Observed Persson’s standard stars from the ISAAC Calibration Plan.
 |
Fig. 7 Plots of (mcat − mIS)i versus (J − Ks)i. The slope of the linear fit is Cm and is tabulated in Table 8. |
5.3. Fractional contributions
In Col. 1 of Table 7, we list κλ for J, Js, H and Ks. The values have been derived using equation (4) and the computed values for κRay,λ and κmol,λ. The uncertainties derive from the propagation of the uncertainties of T and P in Lombardi et al. (2009) and as to be assumed has an upper limit to the variation of the theoretical κλ.
For Js, H and Ks, there is good agreement between the theoretical κλ and the empirical κ calculated from the PWV rescaled zeropoints (Col. 2 of Table 4). For the J-band, there is a significant discrepancy, which is due to the high opacity of the atmosphere at the red end of the J filter. The red end of the J filter is effectively defined by the atmosphere. Changes in the amount of PWV in the atmosphere shifts this edge, which leads to larger photometric uncertainties, as demonstrated by the large scatter about the best fits in Figs. 4 and 5. As noted in Sect. 4, this result demonstrates the importance of observing IR standards at roughly the same airmass and at roughly the same time as the science target when aiming for precise photometry in the J-band.
Columns 2 and 3 of Table 7 show the fractional contributions of κRay,λ and κmol,λ to the total vertical atmospheric extinction. Molecular absorption dominates the absorption in J (82%), H (88%) and Ks (98%). Molecular absorption and Rayleigh scattering contribute almost equally to the absorption observed in Js. This is due to the design of the ISAAC Js filter which is narrower than J and avoids the strong atmospheric absorption lines at the end of J-band.
6. Determination of the color terms
According to Amico et al. (2002), the J, H and Ks filters of ISAAC closely match the filters tabulated in Persson et al. (1998). We therefore expect negligible color terms for these filters. The Js filter of ISAAC, on the other hand, is significantly different to J, so we expect a significant color term for Js.
We observed 8 bright red stars from Persson et al. (1998) with ISAAC in J, Js, H and Ks under photometric conditions (see Table 8). Each star has been observed over a grid of four positions (one for each quadrant of the detector) with a windowed detector and short integrations (<1 s) to avoid saturation. The integrations were shorter than the minimum integration time required for full readout of the array, so only a subarray of the detector was read out.
We integrated the flux in apertures of fixed size to derive instrumental magnitudes for each star. The final instrumental magnitude associated to the star (mIS) is the weighted average of the four instrumental magnitudes corrected using the atmospheric extinction coefficients determined in Sect. 4 (see Col. 2 in Table 4).
In Fig. 7 we plot (Mcat − mIS)i against (J − Ks)i and fit for the slope Cm. An arbitrary constant vertical offset has been applied to the points in each of the graphs.
Table 8 lists (mcat − mIS)i for J, Js, H and Ks and the color (J − Ks)i. The slopes, Cm, are also reported.
As expected, Cm does not differ from 0 for J, H or Ks, while Cm = 0.020 ± 0.009 for Js.
7. Conclusions
In this Research Note, we have characterized the extinction properties in the NIR at the Paranal Observatory (Chile). We have used standard stars observed with ISAAC in J, Js, H, and Ks during photometric and clear nights at the Very Large Telescope UT1 between 2000 and 2004.
For each star we calculated the zeropoint uncorrected for extinction using the ISAAC Pipeline. A correction is then performed on the whole dataset in order to eliminate the affects on the zeropoints due to technical events (such as recoatings of the primary mirror and ISAAC interventions).
We used two different methods to derive extinction co-efficients. In the first method, we account for the varition in the ZPs with the PWV by rescaling the zeropoints to the median PWV (2.3 mm) measured at Paranal between 2001 and 2005. We then fit a linear relation to Bouguer curves to determine the extiction coefficients. We have obtained κJ = 0.072 ± 0.040, κJs = 0.048 ± 0.019, κH = 0.034 ± 0.015 and κKs = 0.043 ± 0.013 mag airmass-1. In the second method, we have calculated κ considering the zeropoints in three different PWV ranges: PWV = 0–2 mm, PWV = 2–4 mm, and PWV = 4–7 mm. As expected, the extinction coefficient in J is more sensitive to the amount PWV than the extinction coefficients of other filters, increasing by ~0.05 mag airmass-1 between lower and upper ranges for the PWV. For comparison the coefficients for Js and H increase by ~0.03 mag airmass-1 and ~0.02 mag airmass-1, respectively, while there is negligible change for Ks.
Using a theoretical approach, we have found that molecular absorption contributes most to the total absorption in J (82%), H (88%) and Ks (98%), while Rayleigh scattering contributes most to the total absorption in the Js-band.
We have calculated the color terms using 8 bright stars observed in photometric conditions. We have found negligible color terms in J, H and Ks and a non-negligible color term in Js (0.020 ± 0.009).
Acknowledgments
The authors acknowledge the reviewer for the useful comments. The authors also acknowledge Poshak Gandhi of Institute of Astronomy (University of Cambridge) for the useful codes used in the preliminary part of the study and Marc Sarazin of ESO for the useful comments on the GOES satellite data.
References
- Allen, C. W. 2000, Allen’s Astrophysical Quantities, 4th edn., ed. A. N. Cox [Google Scholar]
- Amico, P., Cuby, J. G., Devillard, N., Jung, Y., & Lidman, C. 2002, ISAAC Data Reduction Guide 1.5, ESO Very Large Telescope [Google Scholar]
- Burki, G., Rufener, F., Burnet, M., et al. 1995, A&AS, 112, 383 [NASA ADS] [Google Scholar]
- Erasmus, A., & Peterson, R. 1997, PASP, 109, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Erasmus, A., & Sarazin, M. 2000, SPIE Proc., 4168, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Erasmus, A., & Sarazin, M. 2002, in Astronomical Site Evaluation in the Visible and Radio Range, ed. J. Vernin, Z. Benkhaldoun, & C. Muñoz-Tuñón, ASP Conf. Proc., 266, 310 [Google Scholar]
- Frogel, J. A. 1998, PASP, 110, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, D. S., & Latham, D. W. 1975, ApJ, 197, 593 [NASA ADS] [CrossRef] [Google Scholar]
- ISAAC User Manual 2009, Issue 2, ESO Very Large Telescope, http://www.eso.org/sci/facilities//paranal/instruments/isaac/doc/ [Google Scholar]
- Johnson, H. L. 1965, Comm. Lunar Planet. Lab. 3, 67 [Google Scholar]
- Lombardi, G., Zitelli, V., Ortolani, S., Pedani, M., & Ghedina, A. 2008, A&A, 483, 651 [Google Scholar]
- Lombardi, G., Zitelli, V., & Ortolani, S. 2009, MNRAS, 399, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Manduca, A., & Bell R. A. 1979, PASP, 91, 848 [NASA ADS] [CrossRef] [Google Scholar]
- Penndorf, R. 1957, J. Opt. Soc. Amer., 47, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, S. E., Murphy, D. C., Krezeminsky W., Roth M., & Rieke, M. J. 1998, ApJ, 116, 2475 [Google Scholar]
- Rothman, L. S., Gordon I. E., A. Barbe, A., et al. 2009, J. Quant. Spectr. Radiat. Transf., 110, 533 [Google Scholar]
- Rufener, F. 1986, A&A, 165, 275 [NASA ADS] [Google Scholar]
- Soden, B. J., & Bretherton, F. P. 1993, J. Geophys. Res., 98(D9), 16669 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Rayleigh scattering coefficients and vertical Rayleigh extinction in [mag airmass-1] calculated for Paranal.
Vertical atmospheric extinction coefficients [in mag airmass-1] and fractional contributions of Rayleigh scattering and molecular absorption.
Observed Persson’s red standard stars for the determination of the color terms (the computed Cm is also reported).
All Figures
 |
Fig. 1 Evolution in time of the zeropoints for J, Js, H and Ks. The solid vertical lines indicate M1 recoating events, while dotted vertical lines indicate ISAAC interventions. |
| In the text | |
 |
Fig. 2 ZP0 for each period. |
| In the text | |
 |
Fig. 3 Monthly trend of the PWV on Paranal in photometric and clear nights. |
| In the text | |
 |
Fig. 4 Weighted linear fit of the zeropoints as a function of the PWV in the four bands. |
| In the text | |
 |
Fig. 5 Bouguer curves computed for the PWV rescaled zeropoints in J, Js, H and Ks. |
| In the text | |
 |
Fig. 6 Extinction coefficients in J, Js, H and Ks calculated for PWV = 0–2 mm, PWV = 2–4 mm, PWV = 4–7 mm. The dotted line represents the κ calculated with the PWV rescaled ZP, while the gray zone is the dispersion (see Col. 2 of Table 4). |
| In the text | |
 |
Fig. 7 Plots of (mcat − mIS)i versus (J − Ks)i. The slope of the linear fit is Cm and is tabulated in Table 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


