| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201016200 | |
| Published online | 18 March 2011 | |
XMM-Newton observations of the low-mass X-ray binary EXO 0748−676 in quiescence
1
ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
e-mail: mdiaztri@eso.org
2
Observatoire Astronomique de Strasbourg, 11 rue de l’Université, 67000 Strasbourg, France
3
SRON, Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
4
Kapteyn Astronomical Institute, University of Groningen, Postbus 800, 9700 AV Groningen, The Netherlands
5
European Space Astronomy Centre (ESAC), Science Operations Department, Villanueva de la Cañada (Madrid), Spain
Received: 25 November 2010
Accepted: 5 February 2011
The neutron star low-mass X-ray binary EXO 0748−676 started a transition from outburst to quiescence in August 2008, after more than 24 years of continuous accretion. The return of the source to quiescence has been monitored extensively by several X-ray observatories. Here, we report on four XMM-Newton observations elapsing a period of more than 19 months that started in November 2008. The X-ray spectra contain a soft thermal component that we fit with a neutron-star atmosphere model. In only the first observation do we find a significant second component above ~3 keV accounting for ~7% of the total flux, which might be indicative of residual accretion. The thermal bolometric flux and the temperature of the neutron star crust decrease steadily by 40% and 10%, respectively, between the first and the fourth observations. At the time of the last observation in June 2010, we obtain a thermal bolometric luminosity of 5.6 × 1033 (d/7.1 kpc)2 erg s-1 and a temperature of the neutron star crust of 109 eV. The cooling curve is consistent with a relatively hot medium-mass neutron star cooling by standard mechanisms. From the spectral fits to a neutron-star atmosphere model, we infer limits to the mass and the radius of the neutron star. We find that to achieve self-consistency between the neutron-star masses derived using the different methods, the value of the distance is constrained to be ≲6 kpc. For this value of the distance, the derived mass and radius contours are consistent with a number of EoSs with nucleons and hyperons.
Key words: X-rays: binaries / accretion, accretion disks / X-rays: individuals: EXO 0748 − 676 / stars: neutron
© ESO, 2011
1. Introduction
EXO 0748−676 is one of the most interesting transient low mass X-ray binaries (LMXBs) observed to date. It was discovered with EXOSAT (Parmar et al. 1986). It exhibits 8.3 min X-ray eclipses every 3.82 h, irregular dipping activity, and type I X-ray bursts (Parmar et al. 1986; Gottwald et al. 1986).
Assuming Roche lobe overflow, a main-sequence companion, and a 1.4 M⊙ neutron star (NS), Parmar et al. (1986) first constrained the inclination and companion mass to be 75° < i < 83° and 0.45 M⊙, respectively. From measurements of the radial velocity of the companion and applying the technique of Doppler tomography to optical spectra, Muñoz-Darias et al. (2009) derived a mass for the neutron star of between 1 and 2.4 M⊙ and a mass ratio 0.11 < q < 0.28. Bassa et al. (2009) used the same technique to analyse observations performed after detecting in 2008 a significant cessation of accretion activity in EXO 0748−676, which placed a lower limit on the NS mass of 1.27 M⊙ and constrained the mass ratio to be 0.075 < q < 0.105. For a 1.4 M⊙ NS, this translates into a mass for the companion star of 0.11 < M2 < 0.15 M⊙.
Quasi-periodic oscillations (QPOs) were discovered during persistent emission at Hz and kHz frequencies (Homan et al. 1999; Homan & van der Klis 2000). Burst oscillations were first detected at 45 Hz in an average of 38 type-I X-ray bursts by Villarreal & Strohmayer (2004), which were interpreted as the spin frequency of the neutron star. However, Galloway et al. (2010) reported oscillations in the rising phase of two type-I X-ray bursts at a frequency of 552 Hz and concluded that the latter is the spin frequency of the NS, while the 45 Hz oscillation may arise in the boundary layer between the disc and the NS (Balman 2009) or be a statistical fluctuation (Galloway et al. 2010).
From the analysis of a photospheric radius expansion (PRE) X-ray burst, Wolff et al. (2005) estimated the distance of EXO 0748−676 to be 5.9–7.7 kpc. Extending the analysis to several type-I X-ray bursts, Galloway et al. (2008a) and Galloway et al. (2008b) estimated a distance of 7.4 ± 0.9 kpc and 7.1 ± 1.2 kpc, respectively, the latter value taking into account the touch-down flux and the high inclination of EXO 0748−676.
EXO 0748−676 is the only source for which gravitationally redshifted absorption lines during X-ray bursts have been reported (Cottam et al. 2002). A gravitational redshift of z = 0.35 at the star surface was inferred from these measurements, which translates to a mass-to-radius ratio of M/R = 0.152 M⊙/km (Cottam et al. 2002). This provides an empirical constraint on the equation of state (EoS) of dense, cold nuclear matter. Özel (2006) used the value of the gravitational redshift, combined with an estimate of the stellar radius, to infer a mass for the NS of 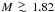 M⊙ for a stellar radius of
M⊙ for a stellar radius of 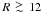 km in the coordinate frame of the NS. Rauch et al. (2008) regarded the line identifications of Cottam et al. (2002) as highly uncertain from computations of LTE and non-LTE NS model atmospheres and derived instead a redshift of z = 0.24 with an alternative line identification and a NS radius of R = 12–15 km for the mass range M = 1.4–1.8 M⊙. The spectral features seen in the burst spectra from the initial data (Cottam et al. 2002) could not be reproduced in the 68 burst spectra from a longer observation in 2003 (Cottam et al. 2008). This might be due to changes in the ionisation conditions in the NS photosphere (Cottam et al. 2008). However, it remains difficult to reconcile the narrowness of the absorption lines detected in the initial data if they originate in the surface of the NS after the rapid spin reported by Galloway et al. (2010) (e.g. Lin et al. 2010).
km in the coordinate frame of the NS. Rauch et al. (2008) regarded the line identifications of Cottam et al. (2002) as highly uncertain from computations of LTE and non-LTE NS model atmospheres and derived instead a redshift of z = 0.24 with an alternative line identification and a NS radius of R = 12–15 km for the mass range M = 1.4–1.8 M⊙. The spectral features seen in the burst spectra from the initial data (Cottam et al. 2002) could not be reproduced in the 68 burst spectra from a longer observation in 2003 (Cottam et al. 2008). This might be due to changes in the ionisation conditions in the NS photosphere (Cottam et al. 2008). However, it remains difficult to reconcile the narrowness of the absorption lines detected in the initial data if they originate in the surface of the NS after the rapid spin reported by Galloway et al. (2010) (e.g. Lin et al. 2010).
An alternative method for placing constraints on the EoS of NSs consists of deriving their mass and radius from X-ray spectral fitting to the thermal emission component after accretion ceases. The theory behind this method is the so-called deep crustal heating of accreting NSs, according to which the nuclear ashes sink in the NS crust under the weight of newly accreting matter and with increasing pressure, undergo a sequence of nuclear transformations (pycnonuclear reactions) accompanied by heat deposition (e.g. Haensel & Zdunik 1990). The heat gained via this process is lost during quiescent episodes, resulting in thermal emission from the NS surface. The equilibrium temperature is set by the temperature of the NS core, which in turn depends on the long-term time-averaged mass accretion rate of the NS and the extent to which the core is able to cool via neutrino emission (Rutledge et al. 2002). Thus, fitting the thermal component with NS atmosphere models allows us to gain insight into the structure and composition of the NS crust and core, if a reliable distance estimate is available. The significant cessation of accretion in EXO 0748−676 in 2008 (see below) opened the possibility of constraining its mass and radius using this method.
Wolff et al. (2008a) reported on RXTE observations of EXO 0748−676 during August 2008, which indicated the lowest flux level, 6.8 × 10-11 erg cm-2 s-1 between 3 and 12 keV, since the beginning of the RXTE mission in 1996. The flux level appeared near the detection threshold of the RXTE All Sky Monitor (ASM) during September 2008. Subsequent Swift and RXTE observations of the source in October 2008 confirmed that accretion had largely ceased and EXO 0748−676 was returning to quiescence (Wolff et al. 2008b).
Following the significant cessation of accretion, we successfully applied to perform four long (30–100 ks) observations of EXO 0748−676 with XMM-Newton, three equally spaced during the first year and a fourth one in the second year. With the sensitivity provided by these observations, we aimed to obtain new constraints on the EoS of dense matter via three complementary methods: analysis of the heating and cooling curves and spectral fitting with NS atmosphere models. The cessation of accretion in EXO 0748−676 has also been monitored with Chandra and Swift (Degenaar et al. 2009, 2011). However, the shorter observations and the lower sensitivities of these observatories relative to XMM-Newton, limit their capability to obtain significant constraints on the mass and radius of EXO 0748−676. In this paper, we report on our monitoring program with XMM-Newton (the first of these observations was also analysed by Zhang et al. 2011). The set of four observations analysed here constitute the most sensitive dataset of EXO 0748−676 after its return to a quiescent state.
XMM-Newton observations of EXO 0748−676 since November 2008.
 |
Fig. 1 0.3–10 keV EPIC pn background-subtracted lightcurves with a binning of 50 s. The narrow eclipses are clearly evident. The thick horizontal lines mark the good time intervals used for spectral extraction. |
2. Observations
The XMM-Newton Observatory (Jansen et al. 2001) includes three 1500 cm2 X-ray telescopes each with an EPIC detector (0.1–15 keV) at their focus. Two of the EPIC imaging spectrometers use MOS CCDs (Turner et al. 2001) and one uses pn CCDs (Strüder et al. 2001). The RGSs (0.35–2.5 keV, Den Herder et al. 2001) are located behind two of the telescopes. In addition, there is a co-aligned 30 cm diameter Optical/UV Monitor telescope (OM, Mason et al. 2001), providing simultaneous coverage with the X-ray instruments. Data products were reduced using the Science Analysis Software (SAS) version 10.0. We present the analysis of EPIC data, RGS data from both gratings and OM data.
Table 1 is a summary of the XMM-Newton observations reported in this paper. All the observations were performed using the EPIC full frame mode. In this mode, all the CCDs are read out and the full field of view of the pn (MOS) is covered every 73 ms (2.6 s). The source count rate is well below the threshold of 6 (0.7) s-1, where pile-up effects become important for the pn (MOS) cameras. We extracted source events from a circle of radius between 37 and 47′′ centered on the PSF core and background events from a circle with the same radius centered well away from the source. Ancillary response files were generated using the SAS task arfgen. Response matrices were generated using the SAS task rmfgen. Background-subtracted light curves were generated with the SAS task epiclccorr, which corrects for a number of effects such as vignetting, bad pixels, PSF variation, and quantum efficiency and accounts for time- dependent corrections within a exposure, such as dead time and GTIs.
The SAS task rgsproc with the option spectrumbinning=lambda was used to produce calibrated RGS event lists, spectra, and response matrices in a uniform wavelength grid space. We also chose the option keepcool=no to discard single columns that give signals a few percent below the values expected from their immediate neighbours. These signals could be mis-interpreted as weak absorption features in spectra with high statistics. We generated RGS light curves with the SAS task rgslccorr. We used the SAS task rgscombine to add spectra from the same RGS and order of different observations and to add spectra from RGS1 and RGS2 for one single observation in order to reduce the statistical errors.
The OM was operated in image mode with UVW1, UVM2, and UVW2 filters in observation (obs) 1 and in image+fast mode with U filter in obs 2–4. In the image mode, the instrument produces images of the entire 17′ × 17′ FOV with a time resolution between 800 and 5000 s. In the fast mode, event lists with a time resolution of 0.5 s from a selected 11′′ × 11′′ region are also stored. The SAS tasks omichain and omfchain were used to extract images and light curves of EXO 0748−676.
3. Results
3.1. X-ray lightcurves
Figure 1 shows 0.3–10 keV EPIC pn EXO 0748−676 background-subtracted lightcurves with a binning of 50 s for each of the observations listed in Table 1. Despite the low count rate of the source in these observations, the narrow eclipses are clearly evident. Intervals used for spectral analysis (not affected by high background flares) are marked at the top of each panel. We inspected the light curves together with the hardness ratio (counts in the 2–10 keV energy range divided by those between 0.3–2 keV) to search for variations in the out-of-eclipse emission, which could reveal residual accretion. For instance, detection of dipping activity would indicate that there is absorption in an ionised atmosphere, hence an accretion disc. Detailed plots of the light curves are shown in Fig. 2. The eclipses ingresses and egresses are sharp.
Outside the eclipses the light curves do not show large deviations from the average count rate and the hardness ratio is consistent with being constant. As an example, the distribution of count rate between the first two eclipses in obs 2 is consistent with a Poisson distribution of mean 0.54 s-1 (χ2 of 21 for 13 degrees of freedom).
 |
Fig. 2 Detail of 0.3–10 keV EPIC pn lightcurves with a binning of 50 s. |
3.2. X-ray spectra
For each observation, we first extracted EPIC and RGS spectra excluding the times of eclipses. We rebinned all the EPIC spectra to oversample the FWHM of the energy resolution by a factor of three, and to have a minimum of 25 counts per bin, to allow the use of the χ2 statistic. We used the RGS spectra with two different binnings: in Sects. 3.2.2–3.2.3 we rebinned the RGS spectra to oversample the FWHM of the energy resolution by a factor of three and to have a minimum of 25 counts per bin, to be able to consistently use the χ2 statistic for both EPIC and RGS spectra. In Sect. 3.2.1, we rebinned the RGS spectra with different methods to be sensitive to narrow features (see below). For the EPIC (RGS) spectra, we used the 0.3–10 keV (0.5–1.8 keV) energy band. Constant factors, fixed to one for the EPIC pn spectrum but allowed to vary for the EPIC MOS and RGS spectra, were included multiplicatively to account for cross-calibration uncertainties.
We performed spectral analysis using XSPEC (Arnaud 1996) version 12.6.0. We used the photoelectric cross-sections and abundances of Wilms et al. (2000) to account for absorption by neutral gas (the tbabs XSPEC model). Spectral uncertainties are given at 90% confidence (Δχ2 = 2.71 for one interesting parameter) and upper limits at 95% confidence.
3.2.1. RGS spectral analysis
We examined the 0.5–1.8 keV (7–25 Å) first- and second-order RGS spectra to constrain the NH in the direction of the source and search for the signature of narrow absorption and emission features.
We first rebinned the RGS spectra for each observation to oversample the FWHM of the energy resolution by a factor of three and to ensure a minimum of ten counts per bin.
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for each observation individually with the tbabs*(nsatmos+po) model.
We could fit the RGS spectra of all the observations with a continuum consisting of a neutron-star atmosphere model component, suitable for cooling NSs (see Sect. 3.2.2), modified by photoelectric absorption from neutral material. We obtained a C-statistic (Cash 1979) of 283, 377, 612, and 561 for 242, 357, 591, and 530 degrees of freedom (d.o.f.) for obs 1 to 4, respectively. The values of NH in units of 1021 cm-2 were 1.6 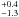 , < 0.7, < 0.5, and < 1.5 for obs 1–4, respectively. None of the observations showed narrow features.
, < 0.7, < 0.5, and < 1.5 for obs 1–4, respectively. None of the observations showed narrow features.
To increase the sensitivity to narrow lines and edges, we combined the RGS spectra of all the observations and rebinned the combined spectra to oversample the FWHM of the energy resolution by a factor of three and used the C-statistic. We could fit the spectra with the same model as the individual observations and obtained a C-statistic (d.o.f.) of 1651(1673) and NH < 0.5 × 1021 cm-2.
To evaluate the effect of the absorption component in our fit, we substituted the tbabs component with the more recent tbnew component and refitted the combined spectra. We obtained a C-statistic of 1651(1673) and NH < 0.4 × 1021 cm-2.
Finally, we rebinned the merged spectra by imposing a minimum signal-to-noise ratio (SNR) of 5 per channel to minimise the background effects, and refitted the first-order spectra (the second-order spectra do not have enough SNR to be fitted). We obtained a C-statistic of 115 (70) and NH < 0.3 × 1021 cm-2.
In summary, we obtained consistent values of NH for different models of interstellar absorption and rebinning methods. However, we obtained significantly different values of NH when using different continuum components. This is expected because of a combination of the limited energy band of the RGS and the low quality statistics of these observations. As an example, substituting the neutron star atmosphere component by a power-law component in the fits to the merged spectra we obtained values of NH of 2.4 ± 0.8 and < 1.6 × 1021 cm-2 and a C-statistic of 1647(1674) and 103(71) for a rebinning with oversampling by a factor of three and a minimum SNR of 5, respectively. Therefore, we conclude that the RGS spectra alone cannot constrain the value of NH for these observations due to the poor statistics and the limited bandwidth, which are both necessary to determine the continuum.
We did not detect any significant narrow feature in the RGS merged spectra.
3.2.2. EPIC and RGS spectral analysis
We then fitted the EPIC and RGS spectra simultaneously for each observation with a continuum consisting of a neutron-star atmosphere component to account for the thermal emission below ~3 keV, and a power-law component to account for emission above ~3 keV modified by photoelectric absorption from neutral material (model tbabs*(nsatmos+po) in XSPEC). The nsatmos model (Heinke et al. 2006) includes a range of surface gravities and effective temperatures and incorporates thermal electron conduction and self-irradiation by photons from the compact object. It also assumes negligible (< 109 G) magnetic fields and a pure hydrogen atmosphere. The parameters of the nsatmos component are the NS mass and radius, the effective temperature in the NS frame, the source distance, and a normalisation factor, which parameterizes the fraction of the surface that is radiating. Throughout our analysis, we imposed a lower limit to the mass of the NS of 1.27 M⊙, as derived by Bassa et al. (2009). Furthermore, since NSs in LMXBs do not display evidence, such as spin-powered pulsations or cyclotron spectral features, of a strong magnetic field, we fixed the normalisation of the neutron-star atmosphere model to 1, which corresponds to the entire NS surface emitting.
 |
Fig. 3 Left: EPIC pn spectra fitted with the model tbabs*(nsatmos+po). Obs 1–4 are shown in black, red, blue and green, respectively. Right: Unfolded EPIC pn spectra. The colours are the same as in the left panel. |
 |
Fig. 4 Contour plots for the mass and radius of the NS for the fits shown in Table 3 for a distance of 5.9 (left), 7.1 (centre), and 8.3 (right) kpc. The solid, dotted, and dashed lines represent the 68, 90, and 99% probability contours. Examples of mass and radius predictions for representative equations of state with neutron and protons (blue lines) including quarks, hyperons, or kaons (red lines) are shown for comparison (see Lattimer & Prakash 2001, 2007). |
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for all the observations simultaneously with the tbabs*(nsatmos+po) model.
We performed three fits per observation: we first left the mass of the NS as a free parameter during the fit and then fixed its value to the canonical mass of 1.4 M⊙ and 1.8 M⊙ for comparison. We extrapolated the flux of the thermal component to the energy range of 0.01–100 keV to estimate the thermal bolometric flux. The fits were acceptable, with reduced χ2, 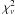 , ~1 for 250–450 d.o.f., for all the observations. The inclusion of a power-law component improved the goodness of the fit only for obs 1. The best-fit results are shown in Table 2 for a distance of 7.1 kpc. The errors in the temperature and radius of the NS are significantly smaller when the mass of the NS is fixed. The value of NH shows significant differences among observations. This clearly affects the accuracy with which we can measure the value of the NS radius and its effective temperature, and shows that a single observation is insufficient to impose constraints on the mass and radius of the NS.
, ~1 for 250–450 d.o.f., for all the observations. The inclusion of a power-law component improved the goodness of the fit only for obs 1. The best-fit results are shown in Table 2 for a distance of 7.1 kpc. The errors in the temperature and radius of the NS are significantly smaller when the mass of the NS is fixed. The value of NH shows significant differences among observations. This clearly affects the accuracy with which we can measure the value of the NS radius and its effective temperature, and shows that a single observation is insufficient to impose constraints on the mass and radius of the NS.
3.2.3. Simultaneous fits for all the datasets
To obtain the tightest possible constraints on the mass and radius of the NS with the XMM-Newton set of observations, we next fitted the EPIC and RGS spectra of all the observations simultaneously. We first assumed that the value of the absorption does not change among observations and tied the values of NH, and the mass and radius of the NS for all the observations. Since the contribution of the power-law component was only significant in the first observation (see Sect. 3.2.2), we also tied the index of the power-law component for the simultaneous fit and allowed the normalisation of this component to vary from one observation to another. Similarly, we allowed the temperature of the NS atmosphere component to vary between observations to account for the expected cooling of the NS crust. Table 3 shows the results of the best-fit model for 3 values of the distance: 5.9, 7.1, and 8.3 kpc. The fits are acceptable with a 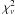 of 1.03 for 1419 d.o.f. Fig. 3 shows the results of the fits for a distance of 7.1 kpc (note that we only show the EPIC pn spectra for clarity, but the fit included data for the EPIC MOS1 and MOS2 as well as the RGSs spectra). Fits of the thermal component to a blackbody model yielded similar
of 1.03 for 1419 d.o.f. Fig. 3 shows the results of the fits for a distance of 7.1 kpc (note that we only show the EPIC pn spectra for clarity, but the fit included data for the EPIC MOS1 and MOS2 as well as the RGSs spectra). Fits of the thermal component to a blackbody model yielded similar 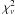 , but implied an emitting area much smaller than a neutron star surface, in agreement with the expectations (since the emergent spectra at Teff ≲ 5 × 106 K is very different from a blackbody, Brown et al. 1998). Therefore, we do not discuss the blackbody fits in greater detail. Substituting the power-law component by a thermal Comptonisation component (model comptt in XSPEC) yielded a similar
, but implied an emitting area much smaller than a neutron star surface, in agreement with the expectations (since the emergent spectra at Teff ≲ 5 × 106 K is very different from a blackbody, Brown et al. 1998). Therefore, we do not discuss the blackbody fits in greater detail. Substituting the power-law component by a thermal Comptonisation component (model comptt in XSPEC) yielded a similar 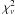 and the parameters of the NS atmosphere were unaffected, i.e. the values obtained for the mass, radius, and temperature of the NS are insensitive to changes in the model for the emission component above ~ 3 keV.
and the parameters of the NS atmosphere were unaffected, i.e. the values obtained for the mass, radius, and temperature of the NS are insensitive to changes in the model for the emission component above ~ 3 keV.
Figure 4 shows the contour plots obtained for the mass and radius of the NS for the three distances considered in Table 3. As we increase the distance of the source in the model, both the best-fit values of the mass and the radius and the allowed region for these parameters increase.
We next investigated how the errors in the fit vary when some parameters are fixed or allowed to vary during the fitting. First, since we have indications from the individual fits performed in Sect. 3.2.2 that the value of NH may differ between observations, we allowed this parameter to vary (case 1 in Table 4). Second, since the index of the power law component is not tightly constrained, we fitted the spectra by fixing the index to either the best-fit value (Γ = 0.24) or 1 (cases 2 and 3 in Table 4). Finally, we fixed the mass to the best-fit value of 1.78 M⊙ and then to a more canonical value of 1.40 M⊙, but allowed the index of the power law to vary (cases 4 and 5 in Table 4).
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for all the observations simultaneously with the tbabs*(nsatmos+po) model.
 |
Fig. 5 Decay of effective temperature (left panel) and thermal bolometric flux (right panel) with time for the XMM-Newton observations of EXO 0748−676. The dashed and dotted lines show the fit to a exponential function and a power law, respectively. The XMM-Newton, Chandra, and Swift points are represented by black circles, dark grey squares, and light grey diamonds, respectively. The XMM-Newton points are the values obtained for case 4 in Table 4. The Chandra and Swift points have been taken from Degenaar et al. (2011). |
The NH has slightly different values when allowed to vary among observations. However, this small change of NH does not influence the values of the other parameters significantly. In contrast, Table 4 shows that the large uncertainty in the mass of the NS drives the uncertainties in the other parameters of the fit to unrealistically large values. For example, we detect variations in the effective temperature of the NS atmosphere between observations as small as 1 eV, but the calculated uncertainty is more than an order of magnitude larger. The large uncertainty in the mass arises from the fact that there are three parameters required to specify a NS model fully: its mass, radius and effective temperature (Heinke et al. 2006). Therefore, for a given effective temperature, there are several acceptable pairs MNS-RNS (see Appendix B of Heinke et al. 2006, for details). The uncertainty in the index of the power-law component does not have a significant effect on the uncertainties in the other parameters. Therefore, when studying the variations in the temperature of the NS atmosphere among observations that follow we took into account the errors listed in Table 4 for case 4. We also found that changing the index of the power-law component from the best-fit value 0.24 to 1 has the effect of significantly increasing the normalisation of this component, although the contribution to the total flux remains unchanged.
We investigated the decay shape of the thermal flux and the temperature of the NS atmosphere as inferred from the nsatmos parameters. We fitted the temperature curve with two models: an exponential decay function of the form y(t) = ae − (t − t0)/τ + b, where a is a normalisation constant, t0 the start time of the cooling curve, and τ the e-folding time (timescale for the temperature to decay by a factor of e-1), and a power-law component of the form y(t) = A(t − t0)B. Following Degenaar et al. (2011), we fixed t0 to 2008 September 5, which is between the first non-detection by RXTE/PCA and the first Swift observation of the source. Taking into account only the XMM-Newton observations presented here, we found an e-folding time of 133.5 ± 87.8 d, a normalisation of 17.2 ± 5.8 eV, and a constant level of 109.1 ± 2.2 for the exponential fit (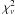 of 0.06 for 1 d.o.f.). When fitting the decay curve with a power law, we found parameter values of A = 141.0 ± 8.4 eV and B = − 0.04 ± 0.01 (
of 0.06 for 1 d.o.f.). When fitting the decay curve with a power law, we found parameter values of A = 141.0 ± 8.4 eV and B = − 0.04 ± 0.01 (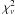 of 0.4 for 2 d.o.f.). The results of these fits are shown in Fig. 5. We note that with only four points we cannot favour one of the above fits. However, the very small changes in temperature and flux between observations 3 and 4 (less than 2 and 6%, respectively) could point to a flattening of the cooling curve. If this were confirmed by future observations, the current power-law fit could be discarded in favour of a broken power-law fit with a tentative break between days 200 and 300.
of 0.4 for 2 d.o.f.). The results of these fits are shown in Fig. 5. We note that with only four points we cannot favour one of the above fits. However, the very small changes in temperature and flux between observations 3 and 4 (less than 2 and 6%, respectively) could point to a flattening of the cooling curve. If this were confirmed by future observations, the current power-law fit could be discarded in favour of a broken power-law fit with a tentative break between days 200 and 300.
We then fitted the temperature curve taking into account the XMM-Newton, Chandra, and Swift values simultaneously. We found an e-folding time of 220 ± 65 d, a normalisation of 14.0 ± 1.4 eV, and a constant level of 107.6 ± 1.5 eV for the exponential fit (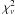 of 0.39 for 19 d.o.f.). When fitting the decay curve with a power law, we found parameter values of A = 135.8 ± 2.5 eV and B = − 0.035 ± 0.003 (
of 0.39 for 19 d.o.f.). When fitting the decay curve with a power law, we found parameter values of A = 135.8 ± 2.5 eV and B = − 0.035 ± 0.003 (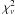 of 0.51 for 20 d.o.f.). In summary, the best-fit values obtained when Chandra and Swift values are taken into account are consistent within the errors with the values obtained only with the XMM-Newton values. We note that we took the Chandra and Swift values from Degenaar et al. (2011), who fixed the mass of the NS to 1.4 M⊙ and the distance to EXO 0748−676 to 7.4 kpc in their fits. Although we fixed the mass of the NS to its best-fit value of 1.78 M⊙ and the distance to 7.1 kpc to obtain the XMM-Newton points, Table 4 shows that the temperature values are consistent within the errors for a mass of 1.78 M⊙ (case 4) and 1.4 M⊙ (case 5). In addition, Table 3 shows that increasing the distance from 7.1 to 8.3 kpc causes significant changes in the values of the mass and radius of the NS but not in the effective temperature. This explains that we obtain consistent decay curves when the Chandra and Swift values are included in the fit. We attribute the small errors of the Chandra points compared to the XMM-Newton points (despite the poorer quality of the Chandra spectra) to the fact that Degenaar et al. (2011) fixed all the parameters of the fit except the effective temperature and the normalisation of the power-law component. Therefore, the added value of the Chandra and Swift points should be taken with caution.
of 0.51 for 20 d.o.f.). In summary, the best-fit values obtained when Chandra and Swift values are taken into account are consistent within the errors with the values obtained only with the XMM-Newton values. We note that we took the Chandra and Swift values from Degenaar et al. (2011), who fixed the mass of the NS to 1.4 M⊙ and the distance to EXO 0748−676 to 7.4 kpc in their fits. Although we fixed the mass of the NS to its best-fit value of 1.78 M⊙ and the distance to 7.1 kpc to obtain the XMM-Newton points, Table 4 shows that the temperature values are consistent within the errors for a mass of 1.78 M⊙ (case 4) and 1.4 M⊙ (case 5). In addition, Table 3 shows that increasing the distance from 7.1 to 8.3 kpc causes significant changes in the values of the mass and radius of the NS but not in the effective temperature. This explains that we obtain consistent decay curves when the Chandra and Swift values are included in the fit. We attribute the small errors of the Chandra points compared to the XMM-Newton points (despite the poorer quality of the Chandra spectra) to the fact that Degenaar et al. (2011) fixed all the parameters of the fit except the effective temperature and the normalisation of the power-law component. Therefore, the added value of the Chandra and Swift points should be taken with caution.
3.3. OM data
We extracted images from the UVW1, UVM2, and UVW2 filter OM exposures for obs 1. On the basis of the expected decreasing optical magnitude of the source, we chose to perform obs 2–4 with the U filter to maximise the sensitivity. OM data were unavailable for obs 3 because of a technical error. For obs 2 and 4, we extracted images and light curves for all OM exposures.
The images show a source consistent with the position of EXO 0748−676, which fades from obs 1 to 4. In obs 1, we obtained an average magnitude of 18.4 ± 0.1 in the UVW1 filter. The source was not detected in the UVM2 or UVW2 filters. For obs 2 and 4, we obtained average U optical magnitudes of 21.7 ± 1.8 and 22.3 ± 3.2, respectively. We note that EXO 0748−676 is not detected in four out of ten exposures in obs 2 and in 14 out of 19 exposures in obs 4.
Figure 6 shows the detections in all observations as a function of phase. The optical magnitude was clearly still decreasing in obs 4 relative to obs 2. Unfortunately, the errors are too large because the source is falling below the detectability limit of OM. Therefore, we cannot determine the presence of a modulation with orbital phase.
 |
Fig. 6 Detections of EXO 0748−676 with the OM monitor as a function of phase. |
4. Discussion
We have analysed four XMM-Newton observations of EXO 0748−676 spanning 19 months and starting in November 2008, when a significant halt of accretion into the NS was detected.
The light curves show a persistent level of emission without significant variations in intensity, except for the eclipse periods, which are clearly visible in all the observations. The persistent count rate decreased steadily by 40% from the first to the fourth observation.
All the observations show a soft spectral component between 0.3 and ~3 keV, which we fitted with a NS atmosphere model. The bolometric flux of the thermal component decreased by 30% between the first and the last observation. In parallel, we observe a 10% decrease in the effective surface temperature of the NS from 120 to 109 eV, which we interpret as the cooling of the NS crust towards thermal equilibrium with the core, after having been heated by accretion during the 24 year outburst. We detected only a 5% decrease in flux and a 1.2% decrease in temperature between the last two observations, indicating that the NS crust may be close to reaching thermal equilibrium with the core. Fitting the inferred temperatures with an exponential decay plus a constant offset yields an e-folding time of 133 ± 88 days.
In addition to the thermal component, the first observation shows a component above ~2–3 keV that we fitted with a power-law component, which represents ~7% of the total 0.3–10 keV flux. The index of the power law is poorly constrained, with a value of 0.24 ± 0.7. This value is much lower than the one found by Degenaar et al. (2011) in a previous analysis of this observation, 1.7 ± 0.5, but the flux contribution to the total flux is similar. The index found in obs 1 is consistent within the errors with values found for power-law components in other cooling NSs (e.g. Cackett et al. 2010b). Although the origin of this component is still unknown, it has been suggested that residual low-level accretion onto the magnetosphere or a shock from a pulsar wind could account for the flux levels observed (Campana et al. 1998). That we do not detect dips in the light curves indicates that residual accretion onto the NS via an accretion disc is unlikely.
We do not observe any significant contribution of the power-law component after 6 November 2008. We determined upper limits to the contribution of this component to the total flux of 1.1, 0.8 and 1.7% in the XMM-Newton observations on 17 March and 1 July 2009 and 17 June 2010, respectively. In contrast, Degenaar et al. (2011) report a significant changing contribution between 5% and 15% of the power-law component to the total flux based on Chandra observations of the source in 10 February and 5 June 2009 and in 15 April 2010 (note the proximity in time of the Chandra observations to the ones analysed in this work). The ability to detect and accurately model the power-law component is crucial to constrain the behaviour of the thermal component. In this sense, the larger effective area of XMM-Newton compared to Chandra and the longer exposures make the observations presented in this work more suitable to determining the contribution of the power law to the total flux. However, the different power-law fluxes could be explained if the source varied between the Chandra and XMM-Newton observations.
We observe a significant decrease in the optical magnitude of the system. The most significant drop of intensity occurs after obs 1 and is very small between obs 2 and 4. This supports the results from X-ray spectral fitting in the sense that any residual accretion present in obs 1 has disappeared in subsequent observations. Hynes & Jones (2009) observed EXO 0748−676 between November 2008 and January 2009 using Andicam and the SMARTS 1.3 m telescope. They found an average magnitude of R = 22.4 and J = 21.3 for the optical counterpart and a periodicity consistent with the orbital period of the system, indicating that at the time of the observations emission from the accretion disc and/or X-ray heated inner face of the companion star dominate the optical emission. We do not observe any significant modulation in obs 2 and 4, indicating that the emission from the accretion disc has most likely disappeared and the inner face of the companion star has subsequently cooled down. However, given the large errors in the measurements in obs 2 and 4, the existence of a small modulation due to a remaining temperature gradient between the illuminated and dark face of the companion cannot be ruled out.
We attempted to constrain the value of the interstellar absorption with the high-resolution RGS spectra. This is important especially when spectral variability in the power-law component is detected. Coupled variations between the power-law index and the value of NH were found for Aql X-1 and Cen X-4 (Campana & Stella 2003; Campana et al. 2004), which could be explained if the power-law arises as shocked emission from the pulsar wind and the infalling material (Campana et al. 1998). Unfortunately, the absorption edges are not strong for these observations because of the low interstellar absorption in the direction of the source, < 1021 cm-2, hence the value of NH determined from the RGS spectra alone depends on the continuum used. However, since we only detect the contribution of a power-law component in the first of the four observations, the variations in the value of NH obtained are non-critical to our analysis.
We do not find absorption lines in the high-resolution RGS spectra, in agreement with expectations. The detection of lines from the NS surface in the spectra of quiescent NSs would allow the determination of the gravitational redshift (Brown et al. 1998; Rutledge et al. 2002) and are therefore of great interest. However, given the high spin and inclination of EXO 0748−676, the probability of detecting these features is very low (Chang et al. 2006; Lin et al. 2010).
4.1. Constraints from the cooling and heating curves
The gradual decrease in thermal flux and neutron star temperature can be interpreted as the NS crust cooling down in quiescence after it has been heated during its long accretion outburst. We found an e-folding time for this cooling of 133 ± 88 d, a normalisation of 17 ± 6 eV, and a constant level of 109 ± 2 eV when fitting the temperature decay curve with an exponential law. The normalisation and the constant level are consistent with those inferred from a similar fit to Chandra (13.4 ± 0.2 eV and 107.9 ± 0.2) and Swift (17.2 ± 1.8 eV, 106.2 ± 2.5 eV) observations. In contrast, the e-folding time, although consistent within the errors, is smaller than the one inferred from Chandra (192 ± 10 d) and Swift (257 ± 100 d) observations (Degenaar et al. 2011). When fitting the decay curve with a power law, we find parameter values of A = 141.0 ± 8.4 eV and B = − 0.04 ± 0.01, consistent with the values inferred from a similar fit to Chandra (A = 134.4 ± 1 eV, B = −0.03 ± 0.01) and Swift (A = 144.7 ± 3.8 eV, B = −0.05 ± 0.01) observations (Degenaar et al. 2011).
The cooling curve of EXO 0748−676 is much flatter than the currently cooling NSs KS 1731 − 260 and MXB 1658 − 298. KS 1731 − 260 shows cooling consistent with a power-law decay with index − 0.125 ± 0.007 that persists eight years after the end of outburst (Cackett et al. 2010a). MXB 1658 − 298 has instead cooled following an exponential decay with an e-folding time of 465 ± 25 d reaching a temperature of 54 ± 2 eV, which has remained constant for ~1000 days (Cackett et al. 2008). In contrast, the cooling curve of the NS XTE J1701 − 462 can be fitted with an exponential law and shows an e-folding time of 120 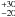 d (Fridriksson et al. 2010), very similar to the value found for EXO 0748−676 in this work.
d (Fridriksson et al. 2010), very similar to the value found for EXO 0748−676 in this work.
The decay time provides a measure of the thermal relaxation time of the NS crust (e.g. Rutledge et al. 2002; Brown & Cumming 2009). In particular, observing the decline in luminosity permits us to measure the thermal timescale of the crust and the relative magnitude of the drop tells us about the presence or absence of enhanced neutrino emission from the core. Rutledge et al. (2002) simulated the thermal relaxation of the NS crust in the transient KS 1731 − 260 by considering different impurity fractions and thus conductivities of the crust and the possible presence of “enhanced” core neutrino mechanisms such as direct Urca or pion condensation. Comparing the shapes of the curves in their Fig. 3 with Fig. 5, we conclude that EXO 0748−676 is consistent with having a NS crust with a high thermal conductivity and low-impurity material, in agreement with Degenaar et al. (2011) and consistent with the other three cooling NSs (Wijnands et al. 2002, 2004; Brown & Cumming 2009; Fridriksson et al. 2010).
From the cooling curve, we infer that the NS crust is close to reaching thermal equilibrium with the core. Therefore, we can compare our results with theoretical predictions of the quiescent thermal luminosities of accreting NS transients. Yakovlev et al. (2004) computed the quiescent bolometric thermal luminosity as a function of long-term time-averaged mass accretion rate for several models of accreting NSs warmed by deep crustal heating. We calculated the average accretion rate during the past 11.5 years of the outburst monitored with the RXTE/ASM. Considering only daily detections above 3σ, we obtained an average count rate of 1.20 s-1. We found an average ASM count rate of 0.68 s-1 during the XMM-Newton monitoring of EXO 0748−676 in 2003, for which a bolometric (0.1–100 keV) unabsorbed flux of 8.44 × 10-10 erg cm-2 s-1 was obtained (Díaz Trigo et al. 2006; Boirin et al. 2007). Using this flux as a conversion factor, we obtained an average bolometric flux of 1.49 × 10-9 erg cm-2 s-1 during the second half of the outburst. Comparing the thermal bolometric luminosity of 5.6 × 1033 (d/7.1 kpc)2 erg s-1 in June 2010 and the average accretion rate during outburst with the heating curves calculated by Yakovlev et al. (2004) (see their Fig. 3), we conclude that if the crust of EXO 0748−676 has reached or is almost reaching thermal equilibrium with the core, a low to medium-mass NS with a near-standard cooling scenario is more likely than that of a high-mass star with significantly enhanced cooling.
We note that the values of the thermal bolometric flux from which we calculate the thermal bolometric luminosity are similar to the values inferred from Swift data but higher than values from Chandra data, as previously noted by Degenaar et al. (2011). This probably indicates that there is an offset in the flux calibration among these observatories.
4.2. Constraints from spectral fitting to the thermal emission
We attempted to constrain the mass and radius of the NS from spectral fits to the observed thermal emission from the NS surface. Zhang et al. (2011) performed a similar analysis but only with the first of the observations presented here. They found that fitting the thermal emission with two different NS atmosphere models, nsgrav and nsatmos, yielded similar results. Therefore we only used the nsatmos model in our analysis. By fitting the four observations simultaneously, we were able to reduce significantly the contours that define the mass and radius of the NS with respect to the analysis by Zhang et al. (2011).
Steiner et al. (2010) determined an empirical dense matter EoS from a heterogeneous dataset of six NSs. They found significant constraints on the mass-radius relation for NSs, hence on the pressure-density relation of dense matter. For example, for NSs where the photospheric radius equals the NS radius, they found radii of 11.0 and 10.6 km for NS masses of 1.5 and 1.8 M⊙, respectively. For NSs where they allowed a photospheric radius larger than the NS radius, they found radii of 11.8 and 11.6 km for a NS mass of 1.5 and 1.8 M⊙, respectively. We obtained a mass of 1.78 M⊙ and a radius of 13.7 km for a distance of 7.1 kpc and of 1.53 M⊙, and 11.8 km for the lower limit of the distance of 5.9 kpc. Interestingly, our solution for a distance of 5.9 kpc agrees very well with the EoS found by Steiner et al. (2010) and would imply a medium-mass NS, in agreement with the mass derived by comparison with the heating curves obtained by Yakovlev et al. (2004, see Sect. 4.1. In contrast, comparing the contours in Fig. 4 with predictions for the mass to radius relation for representative EoSs (e.g. Lattimer & Prakash 2001), the solution for a distance of 7.1 kpc rules out most of the EoSs derived for an interior of nucleons and hyperons.
There are several factors that can include uncertainties in the calculation of the distance for EXO 0748−676. Firstly, EXO 0748−676 is a high-inclination, dipping source, and as such there may be a changing partial obscuration of the NS and its expanding photosphere by the disc during the radius expansion of the type I bursts (Galloway et al. 2008b). The ratio of the peak burst flux to the flux at touch-down (at the moment when the photosphere “touches down” on to the NS) is expected to increase with increasing radius of the photosphere, with respect to low-inclination sources, thus the distance could be overestimated. Taking this into account, Galloway et al. (2008b) estimated a value for the distance to EXO 0748−676 of 7.1 ± 1.2 kpc. However, the value of the distance could be smaller if the obscuration at the touch-down flux were still underestimated. We note that in an analysis of all the dipping sources observed by XMM-Newton (Díaz Trigo et al. 2006), EXO 0748−676 showed the least ionised atmosphere and a relatively cool plasma was present at all phases, indicating that obscuration in this source was larger than in other dippers. This result was confirmed by an analysis of 600 ks of high-resolution RGS spectra of EXO 0748−676 (van Peet et al. 2009). Secondly, the distance calculations from type I X-ray bursts assume that at touch-down, the photosphere radius is equal to the NS radius. However, Steiner et al. (2010) argue that a photosphere with a radius larger than the NS provides internal consistency in their analysis, thus the assumption that the photospheric radius is equal to the NS radius may be unreliable. Furthermore uncertainties arise from variations in the composition of the photosphere, the NS mass or variations in the typical maximum radius reached during the type I burst episodes, which affects the gravitational redshift, and hence the observed Eddington luminosity (Galloway et al. 2008b).
Therefore, we conclude that major uncertainty in the current limits on the mass and radius of EXO 0748−676 are driven by the uncertainty in the distance estimate. Moreover, to obtain consistency between the mass obtained from the heating curves and the spectral fits to the thermal component, the distance to EXO 0748−676 should be ≲ 6 kpc. Alternatively, a low/medium mass NS, albeit with a radius of 14–15 km, is possible at ~ 7 kpc for harder EoS (e.g. Lattimer & Prakash 2007).
4.3. A revision of the distance estimate to EXO 0748−676
All current distance estimates to EXO 0748−676 are based on the analysis of thermonuclear (type-I) X-ray bursts (Jonker & Nelemans 2004; Wolff et al. 2005; Özel 2006; Galloway et al. 2008a,b). This method assumes that the peak flux for very bright bursts reaches the Eddington luminosity at the surface of the NS, at which point the outward radiation pressure equals or exceeds the gravitational force binding the outer layers of accreted material to the star. Once the Eddington flux is reached, the spectral evolution during the first few seconds indicates that a maximum in blackbody radius has been reached simultaneously with a minimum in colour temperature, while the flux remains constant, indicating that the photosphere expands and the effective temperature decreases to maintain the luminosity at the Eddington limit. A large uncertainty in the theoretical Eddington luminosity arises from variations in the photospheric composition. A second large uncertainty arises because different bursts exhibit different peak fluxes. These differences may be caused by variable obscuration (e.g. Galloway et al. 2003). If this is true, the uncertainty will be significantly larger for high-inclination sources, such as EXO 0748−676, for which strong absorption along the line of sight is common. Indeed, Asai & Dotani (2006) found that the burst profiles of EXO 0748−676 in the soft energy band are highly affected by the presence of a photo-ionised plasma, whose ionisation degree changes largely by the strong X-ray irradiation of the burst. Since absorption along the line of sight reduces the observed flux, bursts with higher flux will be more reliable as distance estimators since they are less affected by obscuration. Additional uncertainties include the mass of the NS and the gravitational redshift.
Until now three photospheric-radius expansion bursts have been detected by RXTE in May 2004 and June and August 2005 (Wolff et al. 2005; Galloway et al. 2008a). The burst in May 2004 corresponds to the highest yet detected peak flux. Based on a spectral analysis of this burst, Wolff et al. (2005) estimated a distance of 7.7 kpc (5.9 kpc) for a helium(hydrogen)-dominated burst photosphere. Galloway et al. (2008a) used the three bursts to infer a distance of 8.3/(1 + X) kpc, where X is 0 for solar abundances and 0.7 for hydrogen-rich material. Furthermore, they constrained the distance to be 7.4 kpc arguing that the burst short rise-times and short duration suggest ignition in a He-rich environment. We note that Galloway et al. (2008a) derive a peak flux for the brightest burst of 4.7 × 10-8 erg cm-2 s-1, which is 9% lower than the flux obtained by Wolff et al. (2005) because of the smaller effective area of LHEASOFT v5.3, used in the latter paper (Galloway et al. 2008a).
We estimate that Compton scattering in a highly ionised plasma (log ξ ~ 4) for a high-inclination source such as EXO 0748−676 can reduce the flux by 1 to 10% for a column density of between 1022 and 1023 cm-2. If the plasma has a lower degree of ionisation, the flux is reduced by a larger factor. Therefore, if the flux of the burst on May 2004 is underestimated by 1–10%, this translates into a distance of 6.8–6.5 kpc for a helium-dominated burst photosphere and of 5.2–5.0 kpc for a hydrogen-dominated burst photosphere. These values are consistent with an upper limit to the distance of ≲ 7 kpc, required by physical EoSs (see Fig. 4).
5. Conclusions
We have analysed four observations of EXO 0748−676 spanning 19 months after a significant decrease in the mass accretion rate onto the NS was detected. We conclude that:
-
The emission above 3 keV decreased significantly within six months of the end of the accretion phase.
-
The NS crust has a high thermal conductivity and low impurity material.
-
The NS crust is very likely close to reaching thermal equilibrium with the core.
-
The NS has a low-medium mass and is cooling by standard mechanisms.
-
A consistent solution between spectral fitting to the thermal spectra and the heating curves requires a distance of ≲ 6 kpc to EXO 0748−676.
Acknowledgments
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). M. Díaz Trigo thanks useful discussions with J. Trümper, R. Rutledge and F. Haberl.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Asai, K., & Dotani, T. 2006, PASJ, 58, 587 [NASA ADS] [Google Scholar]
- Balman, S. 2009, The Astronomer’s Telegram, #2097 [Google Scholar]
- Bassa, C. G., Jonker, P. G., Steeghs, D., & Torres, M. A. P. 2009, MNRAS, 339, 2055 [NASA ADS] [CrossRef] [Google Scholar]
- Boirin, L., Keek, L., Méndez, M., et al. 2007, A&A, 465, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, E. F., & Cumming, A. 2009, ApJ, 698, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., Bildsten, L., & Rutledge, R. E. 1998, ApJ, 504, L95 [Google Scholar]
- Cackett, E. M., Wijnands, R., Miller, J. M., Brown, E. F., & Degenaar, N. 2008, ApJ, 687, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Brown, E. F., Cumming, A., et al. 2010a, ApJ, 722, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Brown, E. F., Miller, J. M., & Wijnands, R. 2010b, ApJ, 720, 1325 [Google Scholar]
- Campana, S., & Stella, L. 2003, ApJ, 597, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Colpi, M., Mereghetti, S., Stella, L., & Tavani, M. 1998, A&ARv, 8, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Israel, G. L., Stella, L., Gastaldello, F., & Mereghetti, S. 2004, ApJ, 601, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., Morsink, S., Bildsten, L., & Wasserman, I. 2006, ApJ, 636, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Cottam, J., Paerels, F., & Méndez, M. 2002, Nature, 420, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cottam, J., Paerels, F., Méndez, M., et al. 2008, ApJ, 672, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Wijnands, R., Wolff, M. T., et al. 2009, MNRAS, 396, L26 [NASA ADS] [Google Scholar]
- Degenaar, N., Wolff, M. T., Ray, P. S., et al. 2011, MNRAS, in press [arXiv:1007.0247] [Google Scholar]
- Den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz Trigo, M., Parmar, A. N., Boirin, L., Méndez, M., & Kaastra, J. 2006, A&A, 445, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fridriksson, J. K., Homan, J., Wijnands, R., et al. 2010, ApJ, 714, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Psaltis, D., Chakrabarty, D., & Muno, M. P. 2003, ApJ, 590, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Muno, M., Hartman, J. S., Psaltis, D., & Chakrabarty, D. 2008a, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Özel, F., & Psaltis, D. 2008b, MNRAS, 387, 268 [Google Scholar]
- Galloway, D. K., Lin, J., Chakrabarty, D., & Hartman, J. M. 2010, ApJ, 711, L148 [NASA ADS] [CrossRef] [Google Scholar]
- Gottwald, M., Haberl, F., Parmar, A. N., & White, N. E. 1986, ApJ, 308, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990, A&A, 227, 431 [NASA ADS] [Google Scholar]
- Heinke, C. O., Rybicki, G. B., Narayan, R., & Grindlay, J. E. 2006, ApJ, 644, 1090 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., & van der Klis, M. 2000, ApJ, 539, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Jonker, P. G., Wijnands, R., van der Klis, M., & van Paradijs, J. 1999, ApJ, 516, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Hynes, R. I., & Jones, E. I. 2009, ApJ, 697, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonker, P. G., & Nelemans, G. 2004, MNRAS, 354, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2001, ApJ, 550, 426 [Google Scholar]
- Lattimer, J. M., & Prakash, M. 2007, Phys. Rep., 442, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, J., Özel, F., Chakrabarty, D., & Psaltis, D. 2010, ApJ, 723, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muñoz-Darias, T., Casares, J., O’Brien, K., et al. 2009, MNRAS, 394, L136 [NASA ADS] [Google Scholar]
- Özel, F. 2006, Nature, 441, 1115 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Parmar, A. N., White, N. E., Giommi, P., & Gottwald, M. 1986, ApJ, 308, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, T., Sulemainov, V., & Werner, K. 2008, A&A, 490, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutledge, R. E., Bildsten, L., Brown, E. F., et al. 2002, ApJ, 580, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Peet, J. C. A., Costantini, E., Méndez, M., Paerels, F. B. S., & Cottam, J. 2009, A&A, 497, 805 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villarreal, A. R., & Strohmayer, T. E. 2004, ApJ, 614, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Guainazzi, M., van der Klis, M., & Méndez, M. 2002, ApJ, 573, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Homan, J., Miller, J. M., & Lewin, W. H. G. 2004, ApJ, 606, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, M. T., Becker, P. A., Ray, P. S., & Wood, K. S. 2005, ApJ, 632, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, M. T., Ray, P. S., & Wood, K. S. 2008a, The Astronomer’s Telegram, #1736 [Google Scholar]
- Wolff, M. T., Ray, P. S., Wood, K. S., & Wijnands, R. 2008b, The Astronomer’s Telegram, #1812 [Google Scholar]
- Yakovlev, D. G., Levenfish, K. P., Potekhin, A. Y., Gnedin, O. Y., & Chabrier, G. 2004, A&A, 417, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, C. G., Méndez, M., Jonker, P. G., & Hiemstra, B. 2011, MNRAS, in press [arXiv:1007.0647] [Google Scholar]
All Tables
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for each observation individually with the tbabs*(nsatmos+po) model.
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for all the observations simultaneously with the tbabs*(nsatmos+po) model.
Best-fits to the 0.3–10 keV EPIC and 0.5–1.8 keV RGS spectra for all the observations simultaneously with the tbabs*(nsatmos+po) model.
All Figures
 |
Fig. 1 0.3–10 keV EPIC pn background-subtracted lightcurves with a binning of 50 s. The narrow eclipses are clearly evident. The thick horizontal lines mark the good time intervals used for spectral extraction. |
| In the text | |
 |
Fig. 2 Detail of 0.3–10 keV EPIC pn lightcurves with a binning of 50 s. |
| In the text | |
 |
Fig. 3 Left: EPIC pn spectra fitted with the model tbabs*(nsatmos+po). Obs 1–4 are shown in black, red, blue and green, respectively. Right: Unfolded EPIC pn spectra. The colours are the same as in the left panel. |
| In the text | |
 |
Fig. 4 Contour plots for the mass and radius of the NS for the fits shown in Table 3 for a distance of 5.9 (left), 7.1 (centre), and 8.3 (right) kpc. The solid, dotted, and dashed lines represent the 68, 90, and 99% probability contours. Examples of mass and radius predictions for representative equations of state with neutron and protons (blue lines) including quarks, hyperons, or kaons (red lines) are shown for comparison (see Lattimer & Prakash 2001, 2007). |
| In the text | |
 |
Fig. 5 Decay of effective temperature (left panel) and thermal bolometric flux (right panel) with time for the XMM-Newton observations of EXO 0748−676. The dashed and dotted lines show the fit to a exponential function and a power law, respectively. The XMM-Newton, Chandra, and Swift points are represented by black circles, dark grey squares, and light grey diamonds, respectively. The XMM-Newton points are the values obtained for case 4 in Table 4. The Chandra and Swift points have been taken from Degenaar et al. (2011). |
| In the text | |
 |
Fig. 6 Detections of EXO 0748−676 with the OM monitor as a function of phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


