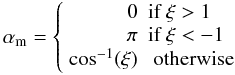| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015688 | |
| Published online | 10 March 2011 | |
Distortion of the ultrahigh energy cosmic ray flux from rare transient sources in inhomogeneous extragalactic magnetic fields
1
Institut d’Astrophysique de Paris, CNRS – Université Pierre &
Marie Curie, 98bis boulevard
Arago, 75014
Paris,
France
e-mail: kalli@iap.fr
2 Université Mohamed
Boudiaf, Msila,
Algérie
3 Laboratoire de Physique Mathématique
et Physique Subatomique (LPMPS), Université Mentouri, Constantine,
Algérie
4
Department of Astronomy & Astrophysics, Enrico Fermi
Institute, and Kavli Institute for Cosmological Physics, The University of
Chicago, Chicago,
Illinois
60637,
USA
Received:
3
September
2010
Accepted:
29
December
2010
Detecting and characterizing the anisotropy pattern of the arrival directions of the highest energy cosmic rays are crucial steps towards the identification of their sources. We discuss a possible distortion of the cosmic ray flux induced by the anisotropic and inhomogeneous distribution of extragalactic magnetic fields in cases where sources of ultrahigh energy cosmic rays are rare transient phenomena, such as gamma-ray bursts and/or newly born magnetars. This distortion does not involve an angular deflection but the modulation of the flux related to the probability of seeing the source on an experiment lifetime. To quantify this distortion, we construct sky maps of the arrival directions of these highest energy cosmic rays for various magnetic field configurations and appeal to statistical tests proposed in the literature. We conclude that this distortion cannot affect present experiments but should be considered when performing anisotropy studies with future large-scale experiments that record as many as hundreds of events above 6 × 1019 eV.
Key words: astroparticle physics / magnetic fields
© ESO, 2011
1. Introduction
The origin of ultrahigh energy cosmic rays (UHECR) – particles with energy E ≳ 1019 eV – remains one of the longest running outstanding problems of astrophysics. The extremely low flux that prevails at the highest energies, ~1/km2/century, makes it difficult to accumulate more than a handful of events per year at ~1020 eV (=100 EeV). The construction of large-scale detectors has nevertheless brought a wealth of significant results in the past few years. In particular, the Fly’s Eye experiment (Abbasi et al. 2008, 2010) and the Pierre Auger Observatory (Abraham et al. 2008a; Pierre Auger Collaboration et al. 2010) have detected a high energy cut-off at ~6 × 1019 eV, in excellent agreement with the predicted Greisen-Zatsepin-Kuzmin (GZK) cut-off (Greisen 1966; Zatsepin & Kuzmin 1966), which results from the pion production interaction of protons above that energy with cosmic microwave background photons. Strictly speaking, one cannot exclude at this stage that this cut-off represents the maximal energy during acceleration, yet if one accepts the GZK interpretation, this result would confirm that the sources of ultrahigh energy cosmic rays are extragalactic and located within the GZK sphere of radius ~100 Mpc. Similar arguments and conclusions can be drawn for ultrahigh energy nuclei, although the energy loss differs, being caused by the photodissociation of the nuclei.
The Pierre Auger Observatory has also announced the detection of anisotropy at the 99% c.l. in the arrival direction map of UHECR with E ≳ 6 × 1019 eV (Abraham et al. 2007, 2008b). This anisotropy is expected if the (unknown) sources of ultrahigh energy cosmic rays reside in large-scale structure – which itself appears anisotropic up to depths of several hundreds of Mpc – provided that the magnetic deflection accumulated by the UHECR is not too large. A detailed analysis of the anisotropy pattern indicates that it is consistent with a distribution of UHECR sources across the local large-scale structure (Kashti & Waxman 2008; Koers & Tinyakov 2009; Pierre Auger Collaboration et al. 2009).
If confirmed by future data – this anisotropy is at present rejected by the HiRes experiment in the northern hemisphere (Abbasi et al. 2010) – this result would be of prime importance, notably because it would open the way to charged particle astronomy. In particular, one could envisage probing the distribution of the population of ultrahigh energy cosmic ray sources with future large-scale cosmic ray detectors, a crucial step towards the identification of the sources of these particles. This, of course, would require a large effort on the experimental side, to build detectors with an aperture significantly larger than already achieved. On the theoretical side, it also requires the understanding of the various biases that can distort our reconstruction of source properties from sky maps of arrival directions.
Magnetic fields on large scales, Galactic and intergalactic, are prime suspects in this regard, and many studies have been devoted to characterizing their influence on the arrival directions (see the discussion in Kotera & Lemoine 2008 and references therein). As our understanding of cosmic magnetic fields has improved over the years, the models have evolved. In particular, it is now understood that the typical amount of deflection must vary according to the direction in the sky, not only because the Galactic magnetic field exerts a different influence in different directions (e.g. Alvarez-Muniz et al. 2001; Takami & Sato 2008), but also because the projected extragalactic magnetic field appears to be anisotropic, as does the large-scale structure on the GZK sphere length scale.
In the present paper, we discuss a possible distortion of the maps of arrival directions that is associated with the inhomogeneous distribution of large-scale magnetic fields which has so far not been discussed. If sources of ultrahigh energy cosmic rays are rare and powerful events, such as gamma-ray bursts (Milgrom & Usov 1995; Vietri 1995; Waxman 1995) or newly born extragalactic magnetars (Arons 2003), the probability of detection of cosmic rays from a given source is extremely small in an experiment lifetime unless the arrival times of these cosmic rays have been substantially dispersed by intervening intergalactic magnetic fields. As we discuss in Sect. 2.1, this implies that the flux in those directions of the sky with small integrated column densities of magnetized gas should be low relative to the mean background flux. To assess the magnitude of this effect, we perform numerical Monte Carlo simulations of the event detection, assuming that the source distribution of ultrahigh cosmic rays follows the large-scale structure (traced using the PSCz catalogue, Saunders et al. 2000) and accounting for the inhomogeneous distribution of intervening magnetic fields.
Our study indicates that the above-mentioned effect could only marginally affect the results of current experiments such as the Pierre Auger Observatory, but that it should be taken into account by future experiments that might record as many as 102 − 103 events above 60 EeV. The magnitude of this effect is directly controlled by the average depth to scattering against magnetized structures in the intergalactic medium. The layout of the present paper is as follows. In Sect. 2, we discuss the general conditions relating to the source characteristics, the degree of magnetization of the Universe for which the above effect applies and we specify how the bias is modeled. In Sect. 3, we construct maps of arrival directions of ultrahigh energy cosmic rays for various magnetic configurations and we present quantitative estimates of the magnitude of the effect for simulated sets of events. We draw our conclusions in Sect. 4.
2. Model
2.1. Magnetic field topology
As discussed in detail in Kotera & Lemoine (2008), the distribution of magnetic fields in the Universe, as experienced by a ultrahigh energy cosmic ray, is quite likely to be highly inhomogeneous, being comprised of magnetized structures such as filaments, halos of starburst galaxies, lobes of radio-galaxies, and halos of clusters, separated by giant unmagnetized voids. As long as the magnetic field B ≲ 10-12 G in some region, this region can be considered as unmagnetized from the point of view of the cosmic rays that traverse it. We note that even extreme models that predict magnetogenesis at high redshift with a strong magnetic field lead to the above picture, of a Universe in which filaments are much more strongly magnetized than the voids, as a result of the amplification of the magnetic field during structure formation and the dilution of the magnetic field in expanding voids.
In this situation, one may describe the propagation of the ultrahigh energy cosmic rays as a sequence of stochastic interactions with magnetized structures, which play the role of scattering agents. Notwithstanding deflection by the Galactic magnetic field, the overall effect is characterized in particular by the typical optical depth for magnetic deflection, τ. The optical depth is dominated by the structures with the largest nσ, where n represents the space density and σ the cross-section of the magnetized halo. Scanning through the possible scattering agents in the Universe, Kotera & Lemoine (2008) pointed out that the major protagonists in this stochastic UHECR propagation model are: (1) halos of old radio-galaxies with number density, typical radius and magnetic field in the range of nrg ~ 3 × 10-3 − 3 × 10-2 Mpc-3, rrg ~ 1−3 Mpc, and Brg ~ 1−10 × 10-8 G respectively (Medina-Tanco & Enßlin 2001; Furlanetto & Loeb 2001); (2) magnetized galactic winds with ngw = 2−5 × 10-5 Mpc-3, rgw = 0.5−1 Mpc, and Brg ~ 1−10 × 10-8 G (Bertone et al. 2006); and/or (3) the filaments/walls themselves if they have been magnetized by some process or the filling factor of the above radio relics and superwinds in the filaments reaches unity. This can be summarized by saying that magnetized scattering centers are distributed in filaments/walls of large-scale structure – with typical interaction lengths of df ~ 30 Mpc – and that these magnetized structures account for a covering fraction η < 1 of the filament/wall projected area. The typical optical depth for magnetic scattering on a GZK distance scale then reads 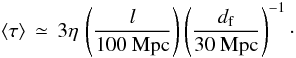 (1)It is important to recall that one might well find η to be significantly smaller than unity if the filling factor of magnetized regions is small, as suggested for instance by the latest numerical simulations of enrichment of the intergalactic medium reported in Donnert et al. (2009). Nevertheless, one can bound the average optical depth below by the contribution of clusters of galaxies to the scattering depth: with a density nc ~ 10-5 Mpc-3, and a radius out to which magnetization can be considered sufficient for UHECR deflection, rc ~ a few Mpc, one finds that ⟨ τ ⟩ c ~ 0.08(r/5 Mpc)2(l/100 Mpc). We use a lower bound of 0.1 for ⟨ τ ⟩ to a depth of 100 Mpc in what follows.
(1)It is important to recall that one might well find η to be significantly smaller than unity if the filling factor of magnetized regions is small, as suggested for instance by the latest numerical simulations of enrichment of the intergalactic medium reported in Donnert et al. (2009). Nevertheless, one can bound the average optical depth below by the contribution of clusters of galaxies to the scattering depth: with a density nc ~ 10-5 Mpc-3, and a radius out to which magnetization can be considered sufficient for UHECR deflection, rc ~ a few Mpc, one finds that ⟨ τ ⟩ c ~ 0.08(r/5 Mpc)2(l/100 Mpc). We use a lower bound of 0.1 for ⟨ τ ⟩ to a depth of 100 Mpc in what follows.
Since the source distance of protons of energy ≥ 60 EeV cannot exceed 200 Mpc – comparable or smaller horizons are found for heavy nuclei – one expects the optical depth τ to that distance to depend on direction angle, just as the projected large-scale structure.
2.2. UHECR bursting sources and inhomogeneous cosmic magnetic fields
Henceforth, we assume that the sources of ultrahigh energy cosmic rays are of the bursting type, with a rate per unit volume of ṅs. If the sources were steady emitters, then the effect described in this paper would not take place. The time delay imparted by the magnetic field cannot modify the flux predictions of steady emitters; the only effect of intervening magnetic fields is in this case limited to deflection. Nevertheless, we note that there are phenomenological arguments against the existence of steady sources of ultrahigh energy cosmic rays (see Lemoine & Waxman 2009, for instance).
We consider a volume element δV located at a distance r from us, with an optical depth τ against magnetic scattering. Cosmic rays emitted by sources in δV have a probability pτ = 1 − exp(−τ) of suffering at least one interaction with a magnetized system, hence of suffering a dispersion Σt in their arrival times, which can be calculated as follows. One interaction with a structure of magnetic field strength B, coherence length λB, and typical transverse size r, implies a time delay of δt ≃ 103 yr (r/2 Mpc)2(B/10 nG)2(λB/100 kpc)(E/100 EeV)-2 (Kotera & Lemoine 2008); the total time delay then scales as the number of interactions Nint (which is Poisson distributed with a mean of τ). As pion production occurs in a stochastic way, the dispersion in the arrivaltimes at energies above 60 EeV is comparable to the total time delay (Waxman & Miralda-Escude 1996; Lemoine et al. 1997; Kotera & Lemoine 2008), hence Σt ~ Nintδt. The average dispersion for those particles that experience at least one interaction can be straightforwardly evaluated as Σt = τ[1 − exp(−τ)]-1δt. Consequently, a detector of area Aexp and exposure time Texp (with Texp ≪ σt expected) will record a mean number of Nev/s,Σt = NUHECRAexpTexp/(4πr2Σt) from each source, assuming each produces NUHECR cosmic rays above some threshold energy Ethr. The mean number of sources contributing is Ns,Σt = ṅsδVΣt, so that the mean total number of events received is Nobs,σt = NUHECRAexpTexpṅsδV/(4πr2). As expected, the dispersion in arrival times does not influence the flux. As is well-known, the cosmic-ray energy output EUHECR per source and the source density rate ṅs are related to each other, in this case, through the normalization of the experimentally determined cosmic ray flux: EUHECRṅs ≃ 0.5 × 10-44 erg/Mpc3/yr (Katz et al. 2009, for a recent estimate).
In principle, cosmic rays emitted by these sources also have a probability 1 − pτ = exp(−τ) of traveling to Earth without suffering an interaction with a magnetized system in the intergalactic medium. However, from the point of view of an experiment, with lifetime T, the detection of these particles is extremely unlikely if the sources are rare and bursting, such as gamma-ray bursts. For instance, the occurrence rate of sources within a finite solid angle ΔΩ, out to some distance r, is given by: 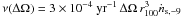 , where ṅs, − 9 = ṅs/10-9 Mpc-3 yr-1, r100 = r/100 Mpc, and ΔΩ is expressed in steradians. For reference, the most recent estimate of the local long gamma-ray burst rate is 1.3 + 0.6 − 0.7 × 10-9 Mpc-3 yr-1 (Wanderman & Piran 2010). The probability of detecting cosmic rays in that area of the sky is then Tν(ΔΩ) ≪ 1.
, where ṅs, − 9 = ṅs/10-9 Mpc-3 yr-1, r100 = r/100 Mpc, and ΔΩ is expressed in steradians. For reference, the most recent estimate of the local long gamma-ray burst rate is 1.3 + 0.6 − 0.7 × 10-9 Mpc-3 yr-1 (Wanderman & Piran 2010). The probability of detecting cosmic rays in that area of the sky is then Tν(ΔΩ) ≪ 1.
If such cosmic rays were detected, they would produce a giant flare in the detector, i.e., a localized anomalously large number of cosmic ray events detected during a short period in time, if ṅs is as low as that considered above. In the absence of intergalactic deflection, the total dispersion in arrival times indeed reduces to the contribution of the turbulent component of the Galactic magnetic field; with a scale height of rB ~ 2 kpc (Han et al. 2006), strength δBMW ~ 3 μG and coherence length λB ~ 100 pc, one finds a time delay 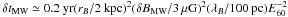 and σt,MW ≲ δtMW, assuming that these cosmic rays are protons (see further below for heavier nuclei). Cosmic rays can be expected to have a similar dispersion in arrival times upon exiting the host galaxy of their source. Assuming that the total time dispersion for these particles is δtMW ≪ T, the mean number of events per source is Nev/s,0 = NUHECRAexp/(4πr2), much larger than expected according to the previous limit by a factor of Σt/Texp. As to the mean number of sources contributing to the flux, one finds Ns,0 = ṅsδVTexp. To provide quantitative estimates, we write EUHECR = 1053 E53 erg (E53 ~ 1 provides the correct normalization of the flux for ṅs ~ 10-9 Mpc-3 yr-1) and estimate that
and σt,MW ≲ δtMW, assuming that these cosmic rays are protons (see further below for heavier nuclei). Cosmic rays can be expected to have a similar dispersion in arrival times upon exiting the host galaxy of their source. Assuming that the total time dispersion for these particles is δtMW ≪ T, the mean number of events per source is Nev/s,0 = NUHECRAexp/(4πr2), much larger than expected according to the previous limit by a factor of Σt/Texp. As to the mean number of sources contributing to the flux, one finds Ns,0 = ṅsδVTexp. To provide quantitative estimates, we write EUHECR = 1053 E53 erg (E53 ~ 1 provides the correct normalization of the flux for ṅs ~ 10-9 Mpc-3 yr-1) and estimate that 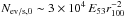 (for Aexp = 3000 km2 corresponding to the Pierre Auger Observatory). No such flare has been observed by the Pierre Auger Observatory, for which the typical number of events per source above 60 EeV is on the order of unity or less (Abraham et al. 2008a).
(for Aexp = 3000 km2 corresponding to the Pierre Auger Observatory). No such flare has been observed by the Pierre Auger Observatory, for which the typical number of events per source above 60 EeV is on the order of unity or less (Abraham et al. 2008a).
When such flares are not detected, and one assumes that the sources are rare and bursting, then the arrival direction flux must be modulated by the probability of suffering at least one interaction with a magnetized system, which is pτ = 1 − exp(−τ) as discussed above. We note that this modulation might be even more extreme if the particle had to encounter more than one scattering event in order to disperse its arrival time sufficiently for it to be detectable; we adopt the above (slightly conservative) modulation in the following.
The above modulation formally corresponds to the conditional probability of detection given that no flare has been detected (under our model assumption that the source is bursting, of rare occurrence). It can also be seen as the consequence of a hierarchy of timescales. At a continuous rate, the detector registers particles that have experienced at least one interaction with magnetized systems in the intergalactic medium, provided that the occurrence rate ν of bursting sources in the GZK sphere and the average dispersion across that distance scale satisfy Σtν ≫ 1. However, the arrival direction map of these particles is modulated by pτ. To detect flares of particles that have traveled without interacting with magnetized structures, one would need to integrate over a timescale ν-1, but ν-1 ≫ Texp for rare bursting sources.
Obviously, if the energy output of each source is small enough (see below), i.e. if the source occurence rate is sufficiently high, the flares detected without intergalactic deflection could produce fewer than one event in the detector, in which case one could not tell whether intergalactic deflection has taken place, and the modulation 1 − exp(−τ) should not be applied. The latter statement depends of course directly on the exposure of the instrument. For the Pierre Auger Observatory, for instance, if no significant clustering is found (Abraham et al. 2008a) then no such flare (i.e. without intergalactic time dispersion) has been detected from bursting sources with energy output EUHECR ≳ 1049 erg. This implies that for sources with an occurrence rate ṅs ≪ 10-5 Mpc-3 yr-1, the above modulation 1 − exp(−τ) should be taken into account when comparing the arrival directions of ultrahigh energy cosmic rays with possible source distributions. For future instruments with an aperture ten times that of the Pierre Auger Observatory, this upper bound on the density rate should be increased tenfold.
To summarize, the distortion of arrival directions maps that we examine in the following section takes place for bursting sources that rarely occur in the GZK sphere, as measured comparatively to an experiment lifetime. Gamma-ray bursts sources of ultrahigh energy cosmic rays and magnetars fall into this category. Regarding the latter, the typical energy output is ~1051 erg at 1020 eV for a typical rate of 10-5/yr per galaxy, i.e. ~10-7 Mpc-3 yr-1 (Arons 2003). The acceleration of ultrahigh energy cosmic rays in blazar flares has also been discussed (Dermer et al. 2009); however, in this scenario the particles experience a substantial time delay ~105 yr upon exiting the lobes of the associated radio-galaxy, hence the source appears as a steady emitter of ultrahigh cosmic ray sources for all phenomenological purposes. The effect that we discuss therefore does not apply to these models.
One cannot exclude that ongoing or future detectors could detect a giant flare associated with the observation of events that have not suffered dispersion in their arrival times, all the more so at source occurrence rates of ṅs ~ 10-6 Mpc-3 yr-1 and small depth to magnetic scattering of τ < 1. The typical rise and decay timescale then corresponds to ≲ δtMW, a fraction of a year. In this case, one would be able to asses directly the cosmic ray energy output of the source, along with the possible detection of a counterpart, which would provide unvaluable information.
Finally, we should mention that we have assumed that ultrahigh energy cosmic rays are protons. There is currently no clear determination of the chemical composition of ultrahigh energy cosmic rays. While the HiRes experiment has reported a composition with a proton fraction that increases beyond the ankle (Abbasi et al. 2010), the measurements of the Pierre Auger Observatory point instead toward a composition that becomes increasingly heavier beyond the ankle (Pierre Auger Collaboration et al. 2010). By themselves, these results of the Pierre Auger Observatory are somewhat puzzling because they may be in apparent contradiction with the anisotropy results (see e.g. Lemoine & Waxman 2009) and no hadronic model of shower reconstruction has so far been able to reproduce all of the composition data of the Pierre Auger Observatory (Pierre Auger Collaboration et al. 2010). Nevertheless, if the composition were predominantly heavy with charge Z ≫ 1, then the above discussion would remain valid, but the sky maps discussed below would not be realistic owing to the large deflection imparted by the Galactic magnetic field. In practice, our imperfect knowledge of the Galactic magnetic field would limit the impact of the distortion discussed below.
2.3. Flux calculation
To model the flux and simulate the events, we adapt the method introduced by Waxman et al. (1997): in a given volume element δV, the mean number of cosmic ray sources is written 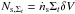 , where Σt = τδt/[1 − exp(−τ)] on average, following Sect. 2.2; in our simulations, we neglect the random nature of Σt, which can be regarded as a higher order effect as its magnitude does not modify the average flux, only the random fluctuations around this average. The mean number of cosmic ray events emitted by each source is then, following the earlier discussion, Nev/s,Σt = NUHECRAexpTexp/(4πr2Σt) and the mean contribution to the flux from this region is therefore Nev/s,ΣtNs,Σt. To account for multiple events per source, one considers the probability that Si sources produce i events; these Si variables are indeed independent of each other and Poisson distributed with mean Ns,ΣtPi, where
, where Σt = τδt/[1 − exp(−τ)] on average, following Sect. 2.2; in our simulations, we neglect the random nature of Σt, which can be regarded as a higher order effect as its magnitude does not modify the average flux, only the random fluctuations around this average. The mean number of cosmic ray events emitted by each source is then, following the earlier discussion, Nev/s,Σt = NUHECRAexpTexp/(4πr2Σt) and the mean contribution to the flux from this region is therefore Nev/s,ΣtNs,Σt. To account for multiple events per source, one considers the probability that Si sources produce i events; these Si variables are indeed independent of each other and Poisson distributed with mean Ns,ΣtPi, where 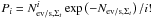 is the Poisson probability that a given source produces i events (Waxman et al. 1997).
is the Poisson probability that a given source produces i events (Waxman et al. 1997).
One can use the above direct averages multiplied by 1 − exp(−τ) to compute an average flux distribution, as we do in Sect. 2.3.1. Direction-dependent effects are incorporated as follows. We use the following law to express the optical depth at distance r in direction n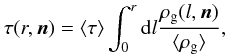 (2)which amounts to scaling the density of magnetized structures according to the galaxy density ρg(l,n) (at distance l, in the direction n). The average optical depth against scattering with magnetized structures ⟨ τ ⟩ , is calculated by averaging over all sky, and bears the typical values calculated in Eq. (1). In what follows, we use the definition ⟨ τ ⟩ 100 to express this quantity calculated to a depth of 100 Mpc. The galaxy density is traced through the PSCz survey of galaxies (Saunders et al. 2000). We also assume that the density of sources follow the galaxy density as traced by the PSCz survey. These choices are motivated by the PSCz being a good tracer of star-forming galaxies, which should host bursting sources of ultrahigh energy cosmic rays such as gamma-ray bursts and magnetars, and contribute to the magnetic enrichment of the intergalactic medium. We then integrate the contributions of each volume element along r in each direction of the sky, modulated by the appropriate 1 − exp(−τ) probability of intersection with magnetized structures, to compute the map of arrival directions.
(2)which amounts to scaling the density of magnetized structures according to the galaxy density ρg(l,n) (at distance l, in the direction n). The average optical depth against scattering with magnetized structures ⟨ τ ⟩ , is calculated by averaging over all sky, and bears the typical values calculated in Eq. (1). In what follows, we use the definition ⟨ τ ⟩ 100 to express this quantity calculated to a depth of 100 Mpc. The galaxy density is traced through the PSCz survey of galaxies (Saunders et al. 2000). We also assume that the density of sources follow the galaxy density as traced by the PSCz survey. These choices are motivated by the PSCz being a good tracer of star-forming galaxies, which should host bursting sources of ultrahigh energy cosmic rays such as gamma-ray bursts and magnetars, and contribute to the magnetic enrichment of the intergalactic medium. We then integrate the contributions of each volume element along r in each direction of the sky, modulated by the appropriate 1 − exp(−τ) probability of intersection with magnetized structures, to compute the map of arrival directions.
We note that, for a given average source density ṅs, the final average number of events detected depends on the average optical depth as a consequence of the flux modulation by 1 − exp(−τ) in each direction. To produce comparable sets of events, we thus rescale the density ṅs as a function of τ in order to keep the average number of events fixed as τ varies. It is straightforward to see that the all-sky average flux out to a distance d scales with average magnetic depth τ as [1−1/ ⟨ τ ⟩ + exp(− ⟨ τ ⟩ )/ ⟨ τ ⟩] (with ⟨ τ ⟩ calculated up to depth d) if one assumes a homogeneous and isotropic distribution of sources and magnetized structures; if ⟨ τ ⟩ ≪ 1, the flux is thus suppressed by ⟨ τ ⟩ /2, but the suppression factor converges to unity as 1−1/⟨ τ ⟩ for ⟨ τ ⟩ > 1. Therefore, for an average optical depth of order unity on the horizon distance scale for particles above the threshold energy Ethr, the source density must be renormalized by a factor of order unity. This renormalization lies well within the margins of the uncertainties in the absolute rate of possible sources.
To simulate a finite sets of events, we resort to Monte Carlo simulations, in which we rely on the above probability laws for Si: in each volume element of the sky, we draw the random variable Si, which characterizes the number of sources contributing i events. The total number of events detected from that volume element is then 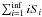 . In order to account for the modulation effect by pτ, we assume that the mean number of sources contributing to the flux in that volume element is pτNs,Σt.
. In order to account for the modulation effect by pτ, we assume that the mean number of sources contributing to the flux in that volume element is pτNs,Σt.
2.3.1. Mean flux
The cosmic ray (CR) differential flux produced by sources at distances smaller than rmax in direction n is given by 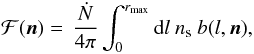 (3)where Ṅ is the injection rate of particles by each source, b denotes the bias of the source distribution, which we relate – as explained above – to the galaxy density, i.e. b(l,n) = ρg(l,n)/ ⟨ ρ ⟩ , ⟨ ρ ⟩ is the mean density of the PSCz catalog, ns = Σtṅs is the average apparent source density, and Σt is the typical dispersion in arrival times (which we keep its average value fixed to, as discussed above). We consider two values of the apparent source density: ns = 10-3 Mpc-3 and ns = 10-5 Mpc-5. The former corresponds to the number density of bright galaxies and the second is a lower bound inferred from experimental data, as follows. First of all, the distance traveled by the highest energy event (E > 1020 eV) detected by the Fly’s Eye experiment (Bird et al. 1994) cannot exceed 50 Mpc; its detection thus indicates that at least one CR source exists in the field of view of Fly’s Eye out to 50 Mpc, implying a source density ns ≳ 10-5 Mpc-3. Furthermore, the non-detection of significant clustering by the Pierre Auger Observatory (Abraham et al. 2008b) also implies that ns ≳ 10-5 Mpc-3 (see the discussion in Kashti & Waxman 2008).
(3)where Ṅ is the injection rate of particles by each source, b denotes the bias of the source distribution, which we relate – as explained above – to the galaxy density, i.e. b(l,n) = ρg(l,n)/ ⟨ ρ ⟩ , ⟨ ρ ⟩ is the mean density of the PSCz catalog, ns = Σtṅs is the average apparent source density, and Σt is the typical dispersion in arrival times (which we keep its average value fixed to, as discussed above). We consider two values of the apparent source density: ns = 10-3 Mpc-3 and ns = 10-5 Mpc-5. The former corresponds to the number density of bright galaxies and the second is a lower bound inferred from experimental data, as follows. First of all, the distance traveled by the highest energy event (E > 1020 eV) detected by the Fly’s Eye experiment (Bird et al. 1994) cannot exceed 50 Mpc; its detection thus indicates that at least one CR source exists in the field of view of Fly’s Eye out to 50 Mpc, implying a source density ns ≳ 10-5 Mpc-3. Furthermore, the non-detection of significant clustering by the Pierre Auger Observatory (Abraham et al. 2008b) also implies that ns ≳ 10-5 Mpc-3 (see the discussion in Kashti & Waxman 2008).
These two different apparent source densities lead to different predictions of the detection of multiplets of events. For ns = 10-5 Mpc-3 for instance, there are fewer sources in the GZK sphere, hence for a projected sample of Nev = 100 particles of energy above 80 EeV from sources located within a distance below rmax = 100 Mpc, the number of apparent sources is ~ 40 leading to the appearance of multiplets, which can be used to constrain the apparent source density. If ns = 10-3 Mpc-3 however, the number of sources is ~4 × 103, hence the average number of event per source is smaller than unity. For an energy threshold of 60 EeV, the horizon increases to 200 Mpc, hence for a sample of 1000 particles as considered further below, the conclusions are similar.
We expect to detect more data from future experiments, such as Auger North and JEM-EUSO. The development of Auger North is due to start in 2011 in Colorado (USA); this experiment should reach an area of more than 20 000 km2, which represents an increase of about nearly an order of magnitude when compared to Auger South (Blümer & the Pierre Auger Collaboration 2010). The Extreme Universe Space Observatory onboard the Japanese Experiment Module (JEM-EUSO) is to be developed on the International Space Station in 2014 (Ebisuzaki et al. 2010). With a field of view of 60° from a 430 km orbiting altitude, the integrated exposure time should exceed 106 km2 sr yr. One should thus expect to detect more than 103 particles above 7 × 1019 eV during its five year operation. For this experiment, the non-observation of multiplets of events of energy above 80 EeV would indicate that ns ≳ 10-3 Mpc-3.
In our simulations, the flux is normalized to the expected total flux above a threshold energy E, i.e. 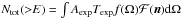 , where as before, Aexp denotes the effective detector area, Texp the observation time, and f(Ω) the aperture of our fiducial experiment.
, where as before, Aexp denotes the effective detector area, Texp the observation time, and f(Ω) the aperture of our fiducial experiment.
3. Simulations
3.1. Sky maps
Using Eq. (3), we construct sky maps of the average UHECR flux for two energy thresholds: 60 EeV and 80 EeV, corresponding to integration depths of 200 Mpc and 100 Mpc, respectively. These sky maps, that do not include any experiment exposure factor for completeness, are shown in Figs. 1 and 2 respectively. In each figure, the top panel shows the mean flux expected, if the sources follow the large-scale structure distribution and the modulation pτ discussed above is ignored. In the bottom panel, a modulation of ⟨ τ ⟩ 100 = 1 has been adopted. Plotting this mean flux corresponds formally to what would be observed for a continuous distribution of sources (i.e. infinite apparent source density). The top panel, with no modulation, indicates what would be seen if the probability of scattering on the magnetized regions were everywhere unity, i.e. ⟨ τ ⟩ 100 → +∞, or if the sources were steady emitters. The bottom panel shows the same map, but for bursting sources and including the modulation by the patchy distribution of magnetic field in the local Universe. For the sake of clarity, we have constructed these plots with a relatively narrow Gaussian filter in HEALPix (Górski et al. 2005) in order to smooth the galaxy distribution to a relatively high resolution ~1°. This resolution is higher than that of the PSCz catalog (about 7°) and smaller than the typical deflection expected for the interaction with magnetic fields. In the actual simulations discussed below, we used a degraded filter with 4° × 4° pixels.
To take into account the effect of the magnetic configuration on the received flux, we multiply the mean flux from each individual cell (in three-dimensional Galactic coordinates r,l,b) by the probability pτ. We use several values of ⟨ τ ⟩ 100: 0.1,1,3, and ∞. We then obtain different models of CR distribution depending on the optical depth value. In the case ⟨ τ ⟩ → ∞, the probability pτ is equal to 1 and we are able to observe all p particles roduced from powerful bursting sources that follow the large-scale structure (LSS). Hereafter, we refer to this configuration as “the LSS model”. The two other magnetic configurations will be named according to the value of the optical depth, e.g. ⟨ τ ⟩ = 3 model and ⟨ τ ⟩ = 1 model.
 |
Fig. 1 Sky maps in Galactic coordinates of the UHECR differential flux indicated in Eq. (3) for an energy threshold E = 60 EeV corresponding to a depth of 200 Mpc. Top panel: LSS model, in which sources follow the matter distribution according to the PSCz survey and in which ⟨ τ ⟩ 100 → + ∞, corresponding to the assumption that the probability of scattering on a magnetized system is unity; bottom panel: same, but with ⟨ τ ⟩ 100 = 1. The grey zone represents the mask of the PSCz catalog in which there is no information. |
Figures 1 and 2 present the sky maps of the UHECR differential flux normalized over the total expected flux for UHECR energy thresholds E = 60 EeV and E = 80 EeV. Generally speaking, the distribution of the flux reflects the galaxy distribution following the LSS, but in the bottom map (corresponding to ⟨ τ ⟩ = 1) the flux seems to be lower than in the top panel (corresponding to the LSS model, ⟨ τ ⟩ 100 → ∞); in the bottom panel, the smaller number of scattering centers in the voids concentrate the flux around regions of overdensity such as the Virgo cluster (b ~ 74°,l ~ −80°), the Shapley cluster (b ~ 29°,l ~ −54°), the Centaurus cluster (b ~ 21°,l ~ −58°), the Hydra cluster (b ~ 26°,l ~ −101°), the Pavo-Indus cluster (b ~ −23°,l ~ −28°), the Fornax cluster (b ~ −53°,l ~ −124°), and the Perseus Pices cluster (b ~ −17°,l ~ 124°), with a concomittant reduction in the underdense areas of the sky. The general effect of the distortion that we discuss here is thus to cluster the arrival directions more strongly in the densest areas of the sky.
3.2. Statistical tests
To quantify the observed effect on the sky maps, we use various statistical tests that have been discussed in the literature and are related to the anisotropy of ultrahigh energy cosmic ray arrival directions: the χ2 test (Cuoco 2007), the one-dimensional Kolmogorov-Smirnov test (Koers & Tinyakov 2009), the two-dimensional Kolmogorov-Smirnov test (Harari et al. 2009), the Y test (Koers & Tinyakov 2009), the correlation test XC (Kashti & Waxman 2008), and the Kuiper test. Although we tested them all, we present in what follows the results of those tests that have proven to be the most sensitive: the XC test, the two-dimensional Kolmogorov-Smirnov test, and the Kuiper test. The XC test was found in Kashti & Waxman (2008) to be more sensitive to the anisotropy signature than the power spectrum and the two-point correlation function. The two-dimensional Kolmogorov-Smirnov test was used in Harari et al. (2009) to exclude isotropy when studying the UHECR distribution. And finally the Kuiper test, which is similar to the Y test defined in Koers & Tinyakov (2009), was found to have the highest statistical power of all considered statistical tests when considering a small number of high energy events. We tried to span different types of tests: the XC test relies on binning the sky, and the Kuiper and two-dimensional Kolmogorov-Smirnov tests depend on cumulative functions of the flux, the first being one dimensional, the second involving the Galactic coordinatesl andb. Using these tests, we compare the distributions of simulated events from different models to the average distributions of events in the LSS model. (i.e. ⟨ τ ⟩ 100 → ∞).
As explained in Sect. 2.3, we generate two sets of simulated events for each model, corresponding to two possible threshold energies E = 60 EeV and E = 80 EeV, i.e. a set of Nev = 100 particles sampled neglecting the contribution from sources beyond 100 Mpc (corresponding to the horizon for particles above 80 EeV) and a set of Nev = 1000 particles from possible sources within 200 Mpc (corresponding to the horizon for particles above 60 EeV).
For the XC test, we divide the sky into angular bins of size 4° × 4° to avoid the local magnetic field effect as mentioned above and use two reference models: the isotropic model in which the arrival directions are purely isotropic (in the absence of experimental aperture sensitivity) and the LSS model with ⟨ τ ⟩ 100 → ∞. We then compare the number of simulated events per bin in the tested model to average numbers of events from the two reference models following the formula 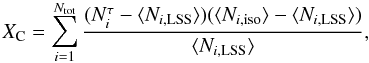 (4)where
(4)where 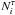 denotes the number of simulated events in angular bin i from the model to be tested with magnetic optical depth τ, ⟨ Ni,LSS ⟩ denotes the average number of events expected in angular bin i in the reference LSS model and ⟨ Ni,iso ⟩ corresponds similarly to the average number of events expected in angular bin i in the isotropic model.
denotes the number of simulated events in angular bin i from the model to be tested with magnetic optical depth τ, ⟨ Ni,LSS ⟩ denotes the average number of events expected in angular bin i in the reference LSS model and ⟨ Ni,iso ⟩ corresponds similarly to the average number of events expected in angular bin i in the isotropic model.
For the other two tests, we take as a reference model the LSS model and use cumulative distributions of the flux. The Kuiper test measures the quantity V, which is defined as the maximum deviation above and below the two considered cumulative distributions. Following Koers & Tinyakov (2009), we name 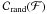 the cumulative distribution of the simulated integrated flux from the model to be tested and
the cumulative distribution of the simulated integrated flux from the model to be tested and 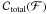 the cumulative distribution of the expected integrated flux from the reference model. We then have
the cumulative distribution of the expected integrated flux from the reference model. We then have ![\begin{eqnarray} \label{eq:kuiper} V = \max[\mathcal{C}_{\rm rand}(\mathcal{F}) - \mathcal{C}_{\rm total}(\mathcal{F})] +\max[\mathcal{C}_{\rm total}(\mathcal{F}) - \mathcal{C}_{\rm rand}(\mathcal{F})] . \end{eqnarray}](/articles/aa/full_html/2011/04/aa15688-10/aa15688-10-eq187.png) (5)For the two-dimensional Kolmogorov-Smirnov test, each simulated event n is characterized by its galactic coordinates (ln, bn); the sky plane is then divided into four quadrants close to this direction
(5)For the two-dimensional Kolmogorov-Smirnov test, each simulated event n is characterized by its galactic coordinates (ln, bn); the sky plane is then divided into four quadrants close to this direction 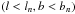 ,
, 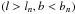 ,
, 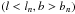 , and
, and 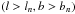 and the test computes the differences between the cumulative distributions of the tested and reference models in each of the four quadrants. This procedure is repeated 4 × Nev times and Dks is defined as the maximum of these differences (between the cumulative distributions of the tested and reference models). In other words,
and the test computes the differences between the cumulative distributions of the tested and reference models in each of the four quadrants. This procedure is repeated 4 × Nev times and Dks is defined as the maximum of these differences (between the cumulative distributions of the tested and reference models). In other words, ![\begin{equation} \label{eq:ks2d} D_{\rm KS} = \max_{Q=1..4}\left[\left|\mathcal{C}_{\rm rand}^{Q}(l,b) - \mathcal{C}_{\rm total}^{Q}(l,b)\right|\right], \end{equation}](/articles/aa/full_html/2011/04/aa15688-10/aa15688-10-eq196.png) (6)where (l,b) are the Galactic coordinates of the cosmic ray positions and Q is one of the four quadrants with respect to a simulated event position in which data can be accumulated.
(6)where (l,b) are the Galactic coordinates of the cosmic ray positions and Q is one of the four quadrants with respect to a simulated event position in which data can be accumulated.
 |
Fig. 3 Distribution of XC from 1000 Monte Carlo realisations of 100 simulated events with energy above 80 EeV (top) and 1000 simulated events with energy above 60 EeV (bottom). Mean source density ns = 10-3 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
 |
Fig. 4 Distribution of V (top) and DKS (bottom) from 1000 Monte Carlo realisation 1000 simulated events with energy above 60 EeV. Mean source density ns = 10-3 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from right to left we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
 |
Fig. 5 Distribution of XC from 1000 Monte Carlo realisations of of 1000 simulated events with energy above 60 EeV. The adopted mean source density is ns = 10-5 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
With that being defined, we plot the histograms of the XC, V, and DKS distributions from 1000 Monte Carlo realizations. In detail, Fig. 3 presents the distributions of XC from 1000 Monte Carlo realisations of 100 simulated events of energy above 80 EeV (top panel) and 1000 simulated events with energy above 60 EeV (bottom panel). In the top panel, we note some overlap between the LSS and the other models with finite ⟨ τ ⟩ 100, the magnitude of which depends on the value of ⟨ τ ⟩ 100. However, the effect of the finite magnetic optical depth becomes pronounced in the lower panel, representing the case of Nev = 1000 above 60 EeV. We note that these statistics are for instance well within the capabilities of the JEM-EUSO mission. In Fig. 4, we plot the distributions of V (top) and DKS (bottom) for 1000 Monte Carlo realisations of 1000 simulated events with energy above 60 EeV; we have chosen this set of events for illustration because it appears more sensitive, as indicated by the previous figure. Qualitatively speaking, the XC distribution appears to be a more efficient discriminator of the effect discussed here. One might resort to definite statistical tests to quantify the sensitivity of these tests to the effect of finite optical depth but, given the exploratory nature of this discussion, the general trend indicated by the above figures suffices.
The comparison of the top and bottom panels of Fig. 3 indicates that a larger number of events is more important in probing this effect, than a stronger anisotropy of the arrival directions.
Figure 5 allows us to probe the sensitivity of the above results to the mean source density. In this figure, we show the distribution of XC from 1000 Monte Carlo realisations of 1000 simulated events of energy above 60 EeV for ns = 10-5 Mpc-3, which corresponds to the existing lower bound on ns. When comparing with the bottom panel of Fig. 3 where ns = 10-3 Mpc-3, we note that a lower source density implies a relatively weaker sensitivity to the effect of finite magnetic optical depth. This results directly from the stronger clustering of events in given locations of the sky, which limits the number of directions with which one can sample the sky maps shown in Fig. 1. Several remarks are in order in this respect. First of all, one may hope that future large-scale experiments will be able to determine the mean source number density from the statistics of multiplets. If not, at the very least, one would infer that ns ≳ 10-3 Mpc-3, hence for the present purpose the exact value of the present parameter is unimportant. Assuming that the mean source density is known, it would be interesting to explore the information contained in the statistics of multiplets in different regions of the sky, as these would obviously provide additional tools that are sensitive to the above effect; this a study requires us to handle a larger dimensionality of parameter space, thus is left to future work.
3.3. Application to the Pierre Auger Observatory data
To date, the only catalog of events above 60 EeV publicly available is that released by the Pierre Auger Collaboration (Abraham et al. 2008b). We thus now use this catalog as a testbed for the previous tests. Since the catalog contains 27 events above 57 EeV, which is reduced further to 18 by applying the PSCz mask, the statistics is obviously limited and the present exercise should be taken as an example.
We use the Auger aperture given by
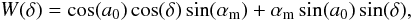 where a0 = −35° is the Auger southern site latitude and αm is given by
where a0 = −35° is the Auger southern site latitude and αm is given by
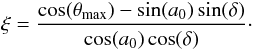 Figure 6 shows the statistical distributions of XC reconstructed for the different models using Monte Carlo simulations, while the vertical line indicates the value obtained for the Auger events. In accordance with the choice of threshold energy, we have limited the horizon to 200 Mpc. There is an almost complete overlap between the histograms of the LSS and the other models. Our study confirms that the statistics of these published Pierre Auger events appear inconsistent with the isotropic model and consistent with the LSS model (see Kashti & Waxman 2008; Koers & Tinyakov 2009; Pierre Auger Collaboration et al. 2009). We also recover a (marginal) tendency, as noted in Kashti & Waxman (2008), for the arrival directions to favor a scenario in which the apparent arrival directions cluster more strongly than the LSS traced through the PSCz; in our case, this is represented by the XC test for the Auger events tending to measure smaller ⟨ τ ⟩ 100 values, although we note that this tendency remains at most marginal.
Figure 6 shows the statistical distributions of XC reconstructed for the different models using Monte Carlo simulations, while the vertical line indicates the value obtained for the Auger events. In accordance with the choice of threshold energy, we have limited the horizon to 200 Mpc. There is an almost complete overlap between the histograms of the LSS and the other models. Our study confirms that the statistics of these published Pierre Auger events appear inconsistent with the isotropic model and consistent with the LSS model (see Kashti & Waxman 2008; Koers & Tinyakov 2009; Pierre Auger Collaboration et al. 2009). We also recover a (marginal) tendency, as noted in Kashti & Waxman (2008), for the arrival directions to favor a scenario in which the apparent arrival directions cluster more strongly than the LSS traced through the PSCz; in our case, this is represented by the XC test for the Auger events tending to measure smaller ⟨ τ ⟩ 100 values, although we note that this tendency remains at most marginal.
 |
Fig. 6 Distribution of XC from 1000 Monte Carlo realizations of 18 simulated events of energy above 60 EeV. The mean source density is ns = 10-5 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model, and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. The vertical line corresponds to the value obtained for the Pierre Auger data. |
We noted in Figs. 3 and 4 that the studied effect becomes noticeable when the number of simulated events with energy above 60 EeV is of the order of 102 − 103; as expected, the effect is too weak to affect the Pierre Auger results and allow any clear distinction between the different models.
4. Conclusions
We have discussed the possible distortion of the sky maps of UHECR arrival directions associated with the inhomogeneous distribution of large-scale magnetic fields. As the effect of the extragalactic magnetic field on the UHECR trajectories may be described by a set of stochastic interactions with magnetized structures, its influence can be conveniently characterized by the optical depth to magnetic deflection τ. Assuming that the UHECR sources are of the bursting type, such as gamma-ray bursts or newly born magnetars, and that their occurrence rate in the GZK sphere is low, we have argued that the relative lack of magnetized structures in those areas of the sky that have τ < 1 should lead to a depleted cosmic-ray flux from these directions compared to those detected from these directions if one assumed that the sources were steady emitters. This is mainly related to the particles in those areas of the sky, having a probability τ of interacting with a magnetized structure, which in the above scenario represents a necessary condition for the source to be observable in an experiment lifetime. It is important to emphasize that the effect that we have discussed here is different from the standard angular deflection associated with extragalactic magnetic fields. While angular deflection modifies the arrival direction without altering the flux, the effect that we discuss directly affects the flux from some regions of the sky.
To quantify this distortion, we have constructed sky maps of UHECR arrival directions from bursting sources residing in the large scale structure for two energy thresholds of 60 EeV and 80 EeV (see Figs. 1 and 2). We have considered different configurations of the large-scale magnetic field and taken into account the modulation associated with the probability of experiencing at least one interaction with a magnetized system pτ = 1 − exp(−τ). Each model is then characterized by the value of ⟨ τ ⟩ 100, which expresses the average optical depth of magnetic deflection calculated to a depth of 100 Mpc. We have then used various statistical tests previously described in the literature, particularly the XC test (see Eq. (4)), which measures the correlation between the simulated events from the model to be tested and the average expected number of events from two reference models, one model with isotropic arrival directions and one model in which the sources are distributed according to the large-scale structure such that the effect of finite magnetic optical depth is neglected. Inspired by the statistics expected for future large-scale experiments, we have applied these tests to two sets of events: Nev = 100 events with E > 80 EeV and Nev = 1000 events with E > 60 EeV, respectively. The histograms from the second set of events show more distinguishable models because of the high number of expected events (see Figs. 3 and 4). We have also considered the catalog of events (27 events above 57 EeV) released by the Pierre Auger Observatory as an example.
In conclusion, we have found that the distortion examined here cannot affect present scale experiments but should be considered when performing anisotropy studies with future large-scale experiments. We have noted a slight sensitivity of the distortion strength to the mean ultrahigh energy cosmic ray source density, which would however disappear if this latter were determined using the statistics of multiplets.
References
- Abbasi, R. U., Abu-Zayyad, T., Allen, M., et al. 2008, Phys. Rev. Lett., 100, 101101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Abbasi, R. U., Abu-Zayyad, T., Allen, M., et al. 2010, ApJ, 713, L64 [Google Scholar]
- Abraham, J., Aglietta, M., Aguirre, C., et al. 2007, Astropart. Phys., 27, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Abraham, J., Abreu, P., Aglietta, M., et al. 2008a, Phys. Rev. Lett., 101, 061101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abraham, J., Abreu, P., Aglietta, M., et al. 2008b, Astropart. Phys., 29, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Alvarez-Muniz, J., Engel, R., & Stanev, T. 2001, in International Cosmic Ray Conf., 5, 1972 [Google Scholar]
- Arons, J. 2003, ApJ, 589, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, S., Vogt, C., & Enßlin, T. 2006, MNRAS, 370, 319 [NASA ADS] [Google Scholar]
- Bird, D. J., Corbato, S. C., Dai, H. Y., et al. 1994, ApJ, 424, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Blümer, J., & the Pierre Auger Collaboration. 2010, New J. Phys., 12, 035001 [Google Scholar]
- Cuoco, A. 2007, Nucl. Phys. B Proc. Suppl., 165, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., Razzaque, S., Finke, J. D., & Atoyan, A. 2009, New J. Phys., 11, 065016 [Google Scholar]
- Donnert, J., Dolag, K., Lesch, H., & Müller, E. 2009, MNRAS, 392, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisuzaki, T., Takahashi, Y., Kajino, F., et al. 2010, in AIP Conf. Ser. 1238, ed. H. Susa, M. Arnould, S. Gales, T. Motobayashi, C. Scheidenberger, & H. Utsunomiya, 369 [Google Scholar]
- Furlanetto, S. R., & Loeb, A. 2001, ApJ, 556, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Greisen, K. 1966, Phys. Rev. Lett., 16, 748 [Google Scholar]
- Han, J. L., Manchester, R. N., Lyne, A. G., Qiao, G. J., & van Straten, W. 2006, ApJ, 642, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Harari, D., Mollerach, S., & Roulet, E. 2009, MNRAS, 394, 916 [NASA ADS] [CrossRef] [Google Scholar]
- Kashti, T., & Waxman, E. 2008, J. Cosmol. Astro-Part. Phys., 5, 6 [Google Scholar]
- Katz, B., Budnik, R., & Waxman, E. 2009, J. Cosmol. Astro-Part. Phys., 3, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Koers, H. B. J., & Tinyakov, P. 2009, J. Cosmol. Astro-Part. Phys., 4, 3 [Google Scholar]
- Kotera, K., & Lemoine, M. 2008, Phys. Rev. D, 77, 123003 [NASA ADS] [CrossRef] [Google Scholar]
- Lemoine, M., & Waxman, E. 2009, J. Cosmol. Astro-Part. Phys., 11, 9 [Google Scholar]
- Lemoine, M., Sigl, G., Olinto, A. V., & Schramm, D. N. 1997, ApJ, 486, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Medina-Tanco, G., & Enßlin, T. A. 2001, Astropart. Phys., 16, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M., & Usov, V. 1995, ApJ, 449, L37 [Google Scholar]
- Pierre Auger Collaboration, Abraham, J., Abreu, P., et al. 2010, Phys. Lett. B, 685, 239 [Google Scholar]
- Pierre Auger Collaboration, Abraham, J., Abreu, P., et al. 2009, [arXiv:0906.2347] [Google Scholar]
- Saunders, W., Sutherland, W. J., Maddox, S. J., et al. 2000, MNRAS, 317, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, H., & Sato, K. 2008, ApJ, 681, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Vietri, M. 1995, ApJ, 453, 883 [Google Scholar]
- Wanderman, D., & Piran, T. 2010, MNRAS, 406, 1944 [NASA ADS] [Google Scholar]
- Waxman, E. 1995, Phys. Rev. Lett., 75, 386 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Waxman, E., & Miralda-Escude, J. 1996, ApJ, 472, L89 [Google Scholar]
- Waxman, E., Fisher, K. B., & Piran, T. 1997, ApJ, 483, 1 [Google Scholar]
- Zatsepin, G., & Kuzmin, V. 1966, J. Exp. Theor. Phys. Lett., 4, 78 [Google Scholar]
All Figures
 |
Fig. 1 Sky maps in Galactic coordinates of the UHECR differential flux indicated in Eq. (3) for an energy threshold E = 60 EeV corresponding to a depth of 200 Mpc. Top panel: LSS model, in which sources follow the matter distribution according to the PSCz survey and in which ⟨ τ ⟩ 100 → + ∞, corresponding to the assumption that the probability of scattering on a magnetized system is unity; bottom panel: same, but with ⟨ τ ⟩ 100 = 1. The grey zone represents the mask of the PSCz catalog in which there is no information. |
| In the text | |
 |
Fig. 2 Same as Fig. 1, for an energy threshold E = 80 EeV, corresponding to a depth of 100 Mpc. |
| In the text | |
 |
Fig. 3 Distribution of XC from 1000 Monte Carlo realisations of 100 simulated events with energy above 80 EeV (top) and 1000 simulated events with energy above 60 EeV (bottom). Mean source density ns = 10-3 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
| In the text | |
 |
Fig. 4 Distribution of V (top) and DKS (bottom) from 1000 Monte Carlo realisation 1000 simulated events with energy above 60 EeV. Mean source density ns = 10-3 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from right to left we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
| In the text | |
 |
Fig. 5 Distribution of XC from 1000 Monte Carlo realisations of of 1000 simulated events with energy above 60 EeV. The adopted mean source density is ns = 10-5 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. |
| In the text | |
 |
Fig. 6 Distribution of XC from 1000 Monte Carlo realizations of 18 simulated events of energy above 60 EeV. The mean source density is ns = 10-5 Mpc-3. The dotted curves represent the isotropic model, the hatched curves denote the LSS model, and from left to right we have ⟨ τ ⟩ 100 = 0.1, ⟨ τ ⟩ 100 = 1, and ⟨ τ ⟩ 100 = 3. The vertical line corresponds to the value obtained for the Pierre Auger data. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.