| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 10 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015596 | |
| Published online | 18 February 2011 | |
Mass loss out of close binaries
The formation of Algol-type systems, completed with case B RLOF
Astrophysical Institute, Vrije Universiteit Brussel,
Pleinlaan 2,
1050
Brussels,
Belgium
e-mail: wvanrens@vub.ac.be
Received:
16
August
2010
Accepted:
27
December
2010
Context. Several authors have previously introduced liberal evolution of interacting binaries, with the purpose of meeting various observed binary characteristics better than with conservative evolution. Since Algols are eclipsing binaries, the distribution of their orbital periods is known precisely. The distribution of their mass ratios contains, however, more uncertainties. We try to reproduce these two distributions theoretically using a liberal scenario in which the gainer star can lose mass into interstellar space as a consequence of its rapid rotation and the energy of a hot spot.
Aims. In a recent paper we calculated the liberal evolution of binaries with a B-type primary at birth where mass transfer starts during core hydrogen burning of the donor. In this paper we include the cases where mass transfer starts during shell hydrogen burning, and it is our aim to reproduce the observed distributions of the system parameters of Algol-type semidetached systems.
Methods. Our calculations reveal the amount of time that an Algol binary lives with a well-defined value of mass ratio and orbital period. We used these data to simulate the distribution of mass ratios and orbital periods of Algols.
Results. Binaries with a late B-type initial primary hardly lose any mass, whereas those with an early B primary evolve in a nonconservative way. Conservative binary evolution predicts only ~12% of Algols with a mass ratio q above 0.4. This value is raised up to ~17% using our scenario of liberal evolution, which is still far below the ~45% that is observed.
Conclusions. Observed orbital periods of Algol binaries longer than one day are faithfully reproduced by our liberal scenario. Mass ratios are reproduced better than with conservative evolution, but the resemblance is still poor.
Key words: binaries: eclipsing / stars: evolution / stars: mass-loss / stars: statistics
© ESO, 2011
1. Introduction
Warner (1978) introduced the denomination liberal to distinguish binary evolution with a mass loss and subsequent angular momentum loss from the conservative case where no mass leaves the system. Van Rensbergen et al. (2008) developed a liberal scenario in which mass can be lost from a binary during a short era of rapid mass transfer soon after the onset of Roche lobe overflow (RLOF). The joint catalog with evolutionary tracks was extended with the evolutionary tracks for binaries starting from sufficiently small orbital periods so that RLOF starts during core hydrogen burning of the donor (case A) as presented by Van Rensbergen et al. (2010). In this contribution these calculations have been extended towards longer initial orbital periods so that RLOF starts after exhaustion of hydrogen in the core of the donor (case B). Our catalog (Van Rensbergen et al. 2008) now contains 561 conservative and liberal evolutionary tracks and is available at the Centre de Données Stellaires (CDS). The grid of calculations covers binaries with a B-type primary at birth.
A binary is considered to be an Algol when the semidetached system shows the typical characteristics as mentioned by Peters (2001), where the less massive donor fills its Roche lobe, the more massive gainer does not fill its Roche lobe and is still on the main sequence and the donor is the cooler, fainter and larger star. The distribution of orbital periods of Algols is precisely known since the time between two subsequent eclipses for every system has been measured accurately. The catalog of Budding et al. (2004) extended with the semidetached Algols from Brancewicz et al. (1980) supplies us with 303 Algols that can be issued from binary evolution with a B-type primary at birth. Van Rensbergen et al. (2006) showed that the distribution of mass ratios strongly depends on the method used to interpret the observations. Substantial differences are found between mass ratios derived so as to make the parameters of the most massive star fit main sequence characteristics (qMS), those obtained with the light curve solution (qLC), and those using the characteristics shown by an Algol as a semidetached system (qSD). In this paper we used the observed mass ratio distribution of Van Rensbergen et al. (2008), who applied the mix of qMS and qLC that represents the numbers in the Pourbaix et al. catalog (2004) best.
Mass loss during liberal evolution is defined by a quantity
β ∈ [0, 1] giving the fraction of mass lost by the donor
(subscript d) that is accreted by the gainer (subscript g): 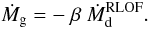 (1)Conservative
evolution is characterized by β = 1. Liberal theoretical calculations (i.e.
those in which, at least for some time, β < 1) depend not only on
the amount of mass lost from the system (related to the parameter β) but
also on the amount of angular momentum taken away by this matter (related to the parameter
α), formulated by the α, β-mechanism of
Podsiadlowski et al. (1992). The quantity
α is then defined by Rappaport et al. (1983) so that, for the angular momentum loss rate from the system
(1)Conservative
evolution is characterized by β = 1. Liberal theoretical calculations (i.e.
those in which, at least for some time, β < 1) depend not only on
the amount of mass lost from the system (related to the parameter β) but
also on the amount of angular momentum taken away by this matter (related to the parameter
α), formulated by the α, β-mechanism of
Podsiadlowski et al. (1992). The quantity
α is then defined by Rappaport et al. (1983) so that, for the angular momentum loss rate from the system
 in the case of mass loss rate of the donor
in the case of mass loss rate of the donor 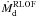 , one
has
, one
has  (2)with
a the semi-major axis and P the orbital period of the
binary system. The value of α thus depends on how much angular momentum is
carried away from the system by a given amount of mass loss, i.e. how matter leaves the
binary.
(2)with
a the semi-major axis and P the orbital period of the
binary system. The value of α thus depends on how much angular momentum is
carried away from the system by a given amount of mass loss, i.e. how matter leaves the
binary.
Values of β < 1 were proposed by Meurs & Van den Heuvel (1989) in order to theoretically reproduce the observed numbers of persistent strong massive binary X-ray sources and the number of observed Wolf-Rayet binaries. Binary evolutionary calculations with constant values of β (e.g. β = 0.5) were then reproduced by various authors, e.g. De Loore & De Greve (1992) and more recently by De Mink et al. (2007) (β = 0.25, 0.5, and 0.75).
Although mass loss from binaries is needed in evolutionary theory, it would be astonishing that β does not depend on the mass transfer rate. It is more plausible that the evolution of semidetached binaries remains conservative (β = 1) during the long-lasting quiet eras of slow RLOF and that mass can only be lost from the system (β < 1) during short-lived violent eras of rapid mass transfer.
The stellar radiation and the spin-up of the gainer as given by Packet (1981) is used by Langer (1998) to compute the mass loss rate for massive binaries. This scenario yields a time-dependent behavior of β as published by Wellstein et al. (2001) and Petrovic et al. (2005).
The stellar radiation of a rapidly rotating intermediate mass gainer is, however, insufficient for driving mass out of the system. Therefore, we introduced in the Brussels binary evolution code the possibility of mass loss from a binary as a consequence of spin-up and hot spots created on the gainer by mass transferred from the donor. The physics of this hot spot model, as well as the resulting mass loss from a binary with a B-type primary at birth, were discussed by Van Rensbergen et al. (2008; 2010) using this scenario.
2. Method
2.1. Brussels evolutionary code
Our results were obtained using the Brussels binary evolutionary code. A detailed description of this code can be found in De Loore & Doom (1992). It is, in fact, a solution to the stellar structure equations, which was introduced by Henyey et al. (1959; 1964) and adapted by Kippenhahn & Weigert (1967) and Kippenhahn et al. (1967) for binary evolution. The calculations were performed with the OPAL-opacities (Rogers & Iglesias 1992; Iglesias et al. 1992; Iglesias & Rogers 1996).
For the input physics, convective mixing, radius corrections, and nuclear physics, we refer to Prantzos et al. (1986). Moderate convective core overshooting is applied, as described in De Loore & De Greve (1992). Mass loss by stellar wind is included using the semi-empirical formalism of De Jager et al. (1988), and the period changes due to subsequent angular momentum loss are also taken into account. However, these small losses are of little importance to the evolution outcome. For the spin-up of the gainer star and the evolution of the orbital separation, an angular momentum balance is considered, which includes the orbital angular momentum of the system and the spin angular momentum of the gainer. The latter is calculated assuming solid-body rotation. When the gainer is spun up, its increase in spin angular momentum is extracted from the orbit. The spin angular momentum of the donor, which is small compared to the others, is currently not taken into account, but will be in future research.
2.2. Initial conditions for binaries with a B-type primary
Van Rensbergen et al. (2006) used unevolved systems in the 9th catalog of Spectroscopic Binaries by Pourbaix et al. (2004) to establish the initial conditions for the evolution of binaries with a B-type primary at birth. We distinguished between late B-type primaries in the mass-range [2.5,7] M⊙ and early B-type primaries in the range [7,16.7] M⊙. The following initial conditions were adopted.
-
Future donors follow a normalized IMF: ξ(Md) = C
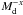 with x = 2.35 as given by Salpeter (1955).
with x = 2.35 as given by Salpeter (1955). -
Binaries with a B-type primary at birth have a normalized bimodal period distribution
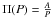 (with A such that the distribution is normalized over the entire
period range) for their initial orbital periods (Van Rensbergen et al. 2006): 79.3% of the systems with a late B primary
follow a distribution as proposed by Popova et al. (1982) from Pmin = 0.93 d to
Pmax = 33.37 d, whereas the remaining 20.7% follow a
similar distribution between Pmin = 33.37 d and
Pmax = 9000 d. Out of the systems with an early B
primary at birth, 79.1% follow a Popova distribution from
Pmin = 1.02 d to
Pmax = 12.91 d, whereas the remaining 20.9% follow a
similar distribution between Pmin = 12.91 d and
Pmax = 4000 d. Such a bimodal distribution has also
been found by Sana et al. (2009) for the
initial distribution of orbital periods of massive binaries in NGC 6611, where they
find 60% between Pmin = 2 d and
Pmax = 10 d, whereas the remaining 40% have initial
orbital periods between Pmin = 10 d and
Pmax = 3200 d.
(with A such that the distribution is normalized over the entire
period range) for their initial orbital periods (Van Rensbergen et al. 2006): 79.3% of the systems with a late B primary
follow a distribution as proposed by Popova et al. (1982) from Pmin = 0.93 d to
Pmax = 33.37 d, whereas the remaining 20.7% follow a
similar distribution between Pmin = 33.37 d and
Pmax = 9000 d. Out of the systems with an early B
primary at birth, 79.1% follow a Popova distribution from
Pmin = 1.02 d to
Pmax = 12.91 d, whereas the remaining 20.9% follow a
similar distribution between Pmin = 12.91 d and
Pmax = 4000 d. Such a bimodal distribution has also
been found by Sana et al. (2009) for the
initial distribution of orbital periods of massive binaries in NGC 6611, where they
find 60% between Pmin = 2 d and
Pmax = 10 d, whereas the remaining 40% have initial
orbital periods between Pmin = 10 d and
Pmax = 3200 d. -
Initial mass ratios (
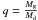 )
follow a normalized distribution:
Ψ(q) = C (1 + q) − δ;
δ = 0.65 for unevolved binaries with a late B primary and
δ = 1.65 for unevolved binaries with an early B primary, as given
by Van Rensbergen et al. (2006).
)
follow a normalized distribution:
Ψ(q) = C (1 + q) − δ;
δ = 0.65 for unevolved binaries with a late B primary and
δ = 1.65 for unevolved binaries with an early B primary, as given
by Van Rensbergen et al. (2006).
Data used to determine 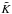 for 13 semidetached binaries.
for 13 semidetached binaries.
2.3. Liberal evolution of binaries
We completely followed the scenario as outlined in Van Rensbergen et al. (2010). The details of the scenario can be found in that paper. During mass transfer the gainer is spun up and a hot spot is created in the accretion region that is located at the surface of the gainer in the case of direct impact or at the edge of the accretion disk if the criterion of Lubow & Shu (1975) tells us that such a disk is created around the gainer.
2.3.1. Spin-up of the gainer
Disregarding tidal interactions, Packet (1981) showed that the spin-up of the gainer goes very fast during the short era of rapid mass transfer soon after the onset of RLOF. Figure 1 shows the spin-up for the gainer of a (6+3.6) M⊙ binary with an initial orbital period of three days. The spin-up was calculated with both strong and weak tidal interaction. The formalism was taken from Zahn (1977). Strong tidal interaction is calculated with fsync = 0.1, whereas fsync = 1 implies weak tides, as adopted by Langer et al. (2003) and discussed in detail by Wellstein (2001). One sees in Fig. 1 that the gainer is spun up to critical velocity very quickly during the rapid era of mass transfer during core hydrogen burning of the donor. This is the case for both weak tidal interaction and a binary undergoing strong tides. During the slow phase of mass transfer, the rotation of the gainer synchronizes rapidly in the case of strong tidal interaction. For weak tidal interaction, synchronization is never achieved before the onset of RLOF B. The rotation of the gainer spins up again towards critical velocity when a second era of fast mass transfer occurs during shell hydrogen burning of the donor. It is clear that with rapid rotation a favorable situation is created for the gainer to lose mass into interstellar space. The example shown in Fig. 1 will turn out to evolve marginally as liberal; that is, no mass will be lost from the system during core hydrogen burning of the donor, whereas only ΔM = 0.006 M⊙ will be lost during shell hydrogen burning of the donor owing to the combined action of rapid rotation and the creation of a hot spot on the gainer’s surface.
 |
Fig. 1 Equatorial velocity of the gainer of a (6+3.6) M⊙ binary with an initial orbital period of 3 days. Strong tidal interaction is represented by a dashed line, weak tides by a long-dashed one. The critical velocity is indicated by a solid line. |
2.3.2. The hot spot
The expression 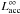 =
=
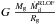 is often used to calculate the accretion luminosity. This expression is only valid in
the case of matter coming from infinity impacting on the gainer’s surface. In the case
of interacting binaries, the transferred matter is however issued from the first
Lagrangian point L1 and not from infinity, so
is often used to calculate the accretion luminosity. This expression is only valid in
the case of matter coming from infinity impacting on the gainer’s surface. In the case
of interacting binaries, the transferred matter is however issued from the first
Lagrangian point L1 and not from infinity, so
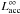 has to be
multiplied by a weakening factor D ∈ [0,1] in order to obtain the
real accretion luminosity:
has to be
multiplied by a weakening factor D ∈ [0,1] in order to obtain the
real accretion luminosity: 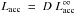 . The geometrical
factor D will be large when L1 is far away
from the point of impact P but can also be very small for binaries that
are almost in contact. Factor D is the geometrical factor included in
the last column of Table 1. Factor
S is the fractional surface area of the hot spot. This factor has
been observed in some cases, and Pringle (1985)
derived a theoretical expression1 starting from the
characteristics (surface and opening angle) of the opening in the first Lagrangian point
L1 and the fact that the stream keeps its shape until it
arrives at the point of impact P:
. The geometrical
factor D will be large when L1 is far away
from the point of impact P but can also be very small for binaries that
are almost in contact. Factor D is the geometrical factor included in
the last column of Table 1. Factor
S is the fractional surface area of the hot spot. This factor has
been observed in some cases, and Pringle (1985)
derived a theoretical expression1 starting from the
characteristics (surface and opening angle) of the opening in the first Lagrangian point
L1 and the fact that the stream keeps its shape until it
arrives at the point of impact P: 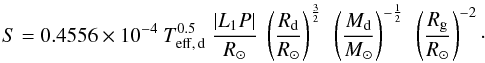 (3)The efficiency of the
liberal scenario is defined further by the value of the factor of radiative efficiency
(3)The efficiency of the
liberal scenario is defined further by the value of the factor of radiative efficiency
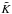 ,
which defines the fraction of Lacc that is used by the hot
spot as radiation pressure. This accretion luminosity is weakened, on the one hand, by
the fact that only a fraction can be converted into radiation (represented by a
weakening factor A > 1:
,
which defines the fraction of Lacc that is used by the hot
spot as radiation pressure. This accretion luminosity is weakened, on the one hand, by
the fact that only a fraction can be converted into radiation (represented by a
weakening factor A > 1: 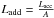 ) and,
on the other, strengthened because the energy of the impacting material is concentrated
in a hot spot that is significantly smaller than the entire gainer’s surface
(represented by the fractional surface area (
) and,
on the other, strengthened because the energy of the impacting material is concentrated
in a hot spot that is significantly smaller than the entire gainer’s surface
(represented by the fractional surface area (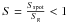 ). The radiation pressure of
the hot spot is thus supplied by
). The radiation pressure of
the hot spot is thus supplied by 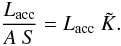 (4)Van Rensbergen et al.
(2010) showed that in the case of direct impact
on the gainer’s equator, the quantity
(4)Van Rensbergen et al.
(2010) showed that in the case of direct impact
on the gainer’s equator, the quantity 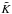 can be calculated as
can be calculated as 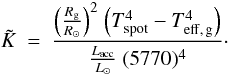 (5)There are only 13
reliable hot spot temperatures available in the literature. According to the criterion
of Lubow & Shu (1975) and as shown in
Fig. 2, ten systems are direct impact systems,
while the three others have a transient accretion disk. This figure also shows that a
permanent accretion disk, emitting continuously in Hα, can only be
formed when the size of the gainer is much smaller than the size of the orbit.
(5)There are only 13
reliable hot spot temperatures available in the literature. According to the criterion
of Lubow & Shu (1975) and as shown in
Fig. 2, ten systems are direct impact systems,
while the three others have a transient accretion disk. This figure also shows that a
permanent accretion disk, emitting continuously in Hα, can only be
formed when the size of the gainer is much smaller than the size of the orbit.
In the case of the formation of a hot spot on the edge of an accretion disk, we had to
replace Rg by Rdisk in Eq.
(5). We further replaced
Teff, g by Tdisk for
β Lyr, which has an opaque and optically thick accretion disk. The
adopted value of Tdisk ≈ 8900 K will be discussed in Sect.
A.2. Two other systems have a transparent and
optically thin accretion disk so that their hot spot is seen upon the effective
temperature of the gainer star. Table 1 contains
all the data to find a value for 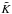 for 13 interacting binaries, with a (rather poor) best fit as a function of the total
mass of the system, which is luckily only slightly different from the expression found
by Van Rensbergen et al. (2010) at the time when
data were available on only 11 interacting binaries:
for 13 interacting binaries, with a (rather poor) best fit as a function of the total
mass of the system, which is luckily only slightly different from the expression found
by Van Rensbergen et al. (2010) at the time when
data were available on only 11 interacting binaries: 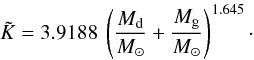 (6)This result
allows us to calculate the radiative efficiency η of accretion onto a
spinning main sequence gainer with a hot spot. Using
(6)This result
allows us to calculate the radiative efficiency η of accretion onto a
spinning main sequence gainer with a hot spot. Using
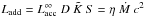 with the
mass-radius relation determined from the stellar evolutionary models of Schaller et al.
(1992) for gainers in the mass range considered
in this paper and in the middle of their main sequence life, one obtains
with the
mass-radius relation determined from the stellar evolutionary models of Schaller et al.
(1992) for gainers in the mass range considered
in this paper and in the middle of their main sequence life, one obtains 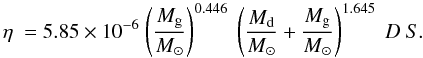 (7)As expected, we find
that this radiative efficiency is much lower than the values found for accretion onto
white dwarfs (η ~ 10-4), neutron stars
(η ≈ 0.2), and black holes (η up to 0.423 for the
most rapidly rotating black hole).
(7)As expected, we find
that this radiative efficiency is much lower than the values found for accretion onto
white dwarfs (η ~ 10-4), neutron stars
(η ≈ 0.2), and black holes (η up to 0.423 for the
most rapidly rotating black hole).
 |
Fig. 2 (q − r) diagram for the 13 interacting binaries that were used in our analysis. Algols (q < 1) are at the left of the vertical line q = 1.0. The ten direct impact systems are located above the curve ωd (filled squares). The three systems with a transient accretion disk around the gainer are located between the curves ωmin and ωd (filled circles). Permanent accretion disks would be located below ωmin. Systems with q > 1 have not reached Algol characteristics yet. |
2.3.3. Loss of mass
The effects of spin-up and accretion luminosity induced photon pressure increase with
higher mass accretion rates. The critical mass transfer rate
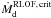 is the one at which both effects will just compensate the local gravity, so that the
local Eddington luminosity is reached. When the mass loss rate of the donor exceeds this
critical value, the gainer will nevertheless accept only a rate
is the one at which both effects will just compensate the local gravity, so that the
local Eddington luminosity is reached. When the mass loss rate of the donor exceeds this
critical value, the gainer will nevertheless accept only a rate
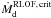 ,
and the surplus will be lost from the system, thus resulting in
β < 1. The exact formulation of
,
and the surplus will be lost from the system, thus resulting in
β < 1. The exact formulation of
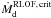 as a function of evolutionary parameters, as included in the code and thus used to
calculate the value of β at each moment of the evolution, is derived as
Eqs. (21) (for direct impact) and (22) (for systems with an accretion disk) in Van
Rensbergen et al. (2008). These equations imply
that each amount of energy extracted from the accretion stream can only be used once,
i.e. either for spinning up the gainer or for developing or maintaining its hot spot. It
also shows that when β < 1, this does not necessarily mean that
critical rotation is achieved or that the accretion luminosity alone exceeds the
Eddington luminosity, but that both effects combined exceed the local gravitation.
as a function of evolutionary parameters, as included in the code and thus used to
calculate the value of β at each moment of the evolution, is derived as
Eqs. (21) (for direct impact) and (22) (for systems with an accretion disk) in Van
Rensbergen et al. (2008). These equations imply
that each amount of energy extracted from the accretion stream can only be used once,
i.e. either for spinning up the gainer or for developing or maintaining its hot spot. It
also shows that when β < 1, this does not necessarily mean that
critical rotation is achieved or that the accretion luminosity alone exceeds the
Eddington luminosity, but that both effects combined exceed the local gravitation.
2.3.4. Loss of angular momentum
Our liberal code thus calculates a time-dependent β(t)
self-consistently within the model as described in the previous section, and assumes
that matter is lost from the hot spot on the gainer (or accretion disk around the
gainer) so that the escaping matter removes only the angular momentum of the gainer’s
orbit. However, the near-critical rotational velocity of the gainer considerably
enhances its spin angular momentum. The influence of the latter in the angular momentum
loss process has not been considered in this study, but will be included in future
research. One thus obtains a time dependent value of α, describing the
angular momentum loss from the system: 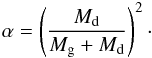 (8)A typical value
of α during the fast and liberal era of RLOF A is then
α ≈ 0.25 (q ≈ 1). When this liberal era is
succeeded by a fast and liberal era of RLOF B the value of α turns out
to be much smaller and can easily be calculated from relation (8).
(8)A typical value
of α during the fast and liberal era of RLOF A is then
α ≈ 0.25 (q ≈ 1). When this liberal era is
succeeded by a fast and liberal era of RLOF B the value of α turns out
to be much smaller and can easily be calculated from relation (8).
2.3.5. Values and uncertainties for Table 1
Table 1 does not contain the values of the present-day orbital periods of the systems since these values are very well known for the eclipsing binaries used in our analysis. The other values used to construct Table 1 are discussed in Appendix A.
Relation (6) was used in our code to
gauge the radiative efficiency of accretion by a main sequence gainer. Figure 3 shows the large uncertainty that remains in the
determination of 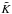 caused by the errors and uncertainties on the values quoted in Table 1. The curves above and below respectively add and
subtract one standard deviation from the values of
caused by the errors and uncertainties on the values quoted in Table 1. The curves above and below respectively add and
subtract one standard deviation from the values of
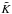 as obtained from relation (6). It is
clear that binary evolution would be more conservative than argued in this paper if the
lower curve were valid and less conservative for the higher curve.
as obtained from relation (6). It is
clear that binary evolution would be more conservative than argued in this paper if the
lower curve were valid and less conservative for the higher curve.
Figure 3 shows error bars obtained from the data
quoted in Appendix A. The calculation of 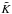 first requires the knowledge of the orbital period and of the masses, radii, and
effective temperatures of both binary components. The error on the sum of the masses of
a binary (horizontal axis of Fig. 3) is not
frequently mentioned by the authors. In some other cases an error on the masses could be
evaluated from various values found in the literature for a particular system.
first requires the knowledge of the orbital period and of the masses, radii, and
effective temperatures of both binary components. The error on the sum of the masses of
a binary (horizontal axis of Fig. 3) is not
frequently mentioned by the authors. In some other cases an error on the masses could be
evaluated from various values found in the literature for a particular system.
Moreover, the calculation of 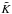 uses the knowledge of the mass transfer rate (
uses the knowledge of the mass transfer rate (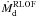 ),
the luminosity added to the gainer by the impinging mass
(Ladd), the surface area of the hot spot
(Sspot), and the hot spot temperature
(Tspot). These observed quantities are theoretically
interdependent. The quantity
),
the luminosity added to the gainer by the impinging mass
(Ladd), the surface area of the hot spot
(Sspot), and the hot spot temperature
(Tspot). These observed quantities are theoretically
interdependent. The quantity 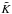 can, e.g., be calculated from Eq. (5)
and/or from the relation
can, e.g., be calculated from Eq. (5)
and/or from the relation 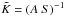 .
The quantity A can be determined from observation
.
The quantity A can be determined from observation
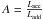 and/or calculated from S and Tspot. The
quantity S can be directly observed and/or calculated from Eq. (3). Erroneous evaluations of the observations
can therefore be rejected when they violate the required internal consistency, as
illustrated in Sect. A.3. This is the main reason
that only 13 binaries could be used in this analysis. Errors on
and/or calculated from S and Tspot. The
quantity S can be directly observed and/or calculated from Eq. (3). Erroneous evaluations of the observations
can therefore be rejected when they violate the required internal consistency, as
illustrated in Sect. A.3. This is the main reason
that only 13 binaries could be used in this analysis. Errors on
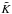 (vertical axis of Fig. 3) are obtained when the
quantities mentioned above can be combined into models that respect every observed
quantity within a reasonable range. The length of the vertical error bar then shows the
highest and the lowest values that can be calculated for
(vertical axis of Fig. 3) are obtained when the
quantities mentioned above can be combined into models that respect every observed
quantity within a reasonable range. The length of the vertical error bar then shows the
highest and the lowest values that can be calculated for
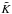 within this framework. No error is shown in Fig. 3
when the error is too small or when not every quantity has been measured so that the
internal consistency could not be completely explored.
within this framework. No error is shown in Fig. 3
when the error is too small or when not every quantity has been measured so that the
internal consistency could not be completely explored.
 |
Fig. 3 Radiative efficiency of accretion |
2.4. The distribution of mass ratios and orbital periods of Algols
2.4.1. The observed distributions
The distribution of orbital periods of Algols is well established. The distribution of
mass ratios is however biased. Van Rensbergen et al. (2008) used the mass ratio and orbital period distribution of Algols out of a
sample of 303 observed systems. These systems were taken from the catalog of Budding
et al. (2004) extended with semidetached Algols
from the catalog of Brancewicz et al. (1980). All
these systems are issued from a binary with a B-type primary at birth. A majority of
268 systems have a late B-type primary progenitor, leaving only 35 systems with an early
B-type primary at birth. When discussing initial conditions (e.g. in Sects. 2.2 and 3.1), we
use 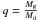 as definition of the mass ratio. However, since in Algols the gainer has become the most
massive component, we use
as definition of the mass ratio. However, since in Algols the gainer has become the most
massive component, we use 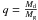 as the definition of the mass ratio of an Algol system.
as the definition of the mass ratio of an Algol system.
 |
Fig. 4 Calculated amounts of mass lost by a binary with a 7 M⊙ primary at birth undergoing strong tidal interaction during its evolution. The total amount of lost mass ΔM is on the vertical axis, and the initial orbital period is on the horizontal axis. Calculated cases are indicated by filled circles. Binaries starting with an initial mass ratio q = 0.4 are connected by a long-dashed line, those with q = 0.6 by a dashed line, and those with q = 0.9 by a solid line. |
2.4.2. The calculated distributions
Using the initial conditions of Sect. 2.2 and the data of our library with liberal binary evolutionary calculations yielding the durations that an Algol lives with well-defined values of the orbital period and mass ratio, Van Rensbergen et al. (2010) used a Monte Carlo simulation to calculate distributions of mass ratios and orbital periods of Algols that started RLOF during core hydrogen burning of the donor (case A). This paper extends these calculations with Algols issuing from binaries that started RLOF during shell hydrogen burning of the donor (case B). We compared the results obtained under the assumption of strong tidal interaction with those obtained with weak tides. Although significant differences frequently occur between both assumptions, they yield a very similar overall distribution of mass ratios and orbital periods of Algols.
Systems that become too faint with increasing distance to be included in the catalogs are removed by our Monte Carlo simulation. Therefore we added the spatial distribution of binaries into the simulation so that they either have a spherically uniform distribution around the Sun or are uniformly distributed in a flat structure such as Gould’s belt. These two different assumptions also yield however no significant or systematic differences.
3. Results
3.1. Calculated mass driven out of a close binary
Using the stellar evolution code to calculate the evolution of binaries including those performing case B RLOF, we find that the amount of mass driven out of a close binary (ΔM) increases with increasing initial mass of the donor and with increasing initial orbital period. Binaries having an initial mass of the donor star below 6 M⊙ lose no, or almost no, matter during their evolution. This is because the mass transfer rate in these systems never exceeds the critical value that is required for the combination of spin-up and accretion luminosity to overcome the gravitational potential of the system. Binaries with donors having initial masses between 6 M⊙ and 9 M⊙ undergo a moderate amount of mass loss starting at longer initial orbital periods. Binaries with an initial mass of the donor star above 9 M⊙ suffer from severe mass loss during their evolution within this scenario. Although large individual differences may occur between binaries evolving with strong, respectively weak, tidal interaction, there are no significant differences between the two groups. Figure 4 shows an example of the amount of mass lost by a binary with a 7 M⊙ primary at birth and evolving with strong tidal interaction. The grid of calculated cases covers initial mass ratios q = 0.4, 0.6, and 0.9. At short initial orbital periods no mass is lost because RLOF is ignited before the donor has become large enough to transfer mass to the gainer at a higher rate than the critical one. At higher initial orbital periods, most mass is lost in the q = 0.6 case, large enough to ensure a large enough separation (according to Kepler’s third law) so that the mass transfer rate is higher than with q = 0.4. The mass lost in the case of q = 0.9 is, however, lower because such systems grow into near contact more easily, leading to a small geometrical factor D and thus to a fading accretion luminosity. The largest amounts of mass are lost in those cases where RLOF starts after exhaustion of hydrogen in the core of the donor star. This will be achieved in this case with initial orbital periods above ~4 days. The liberal calculations in our catalog (Van Rensbergen et al. 2008) give also the amount of mass that is lost by many binaries with initial mass of the primary between 3 M⊙ and 15 M⊙.
3.2. The period distribution of Algols with a B-type primary at birth
Figure 5 compares the observed orbital period distribution of Algols with a B-type primary at birth with theoretical simulations as obtained with the liberal assumptions. This distribution is not affected by the different assumptions that were made about the tidal interaction. Algols observed with orbital periods of more than 15 days, which were not reproduced sufficiently by considering the case A RLOF alone (Van Rensbergen et al. 2010) are represented very well now that case B is included in the calculations. The maximum deviation in a one-sample Kolmogorov-Smirnov test decreases, moreover, from 0.115 obtained with the conservative simulation to the significantly better value of 0.067 when the liberal simulation is used. The observed period distribution of Algols is, however, only very closely reproduced by the liberal simulation for periods above one day. The number of ~9% of Algols observed with orbital periods below one day is largely underestimated by our simulation because these binaries tend to merge in our calculations. That their number is indeed observed could mean that binaries can survive overcontact better than tolerated by our code (see discussion in Sect. 4).
 |
Fig. 5 Observed distribution (white) of orbital periods of 303 Algols as compared to liberal (black) simulation. |
3.3. The mass ratio distribution of Algols with a B-type primary at birth
We used an observed distribution of Algols with a B-type primary at birth, having ~45% in the high mass ratios (q ∈ [0.4,1] ). More specifically we find ~24% with q ∈ [0.4, 0.55] and ~21% with q ∈ [0.55,1] . The fact that the conservative binary evolutionary code did not reproduce this observed mass ratio distribution for a sample of 303 Algols was the initial reason for us to start thinking about a liberal scenario.
Van Rensbergen et al. (2006) used β as a parameter taken equal to 0.5 during the entire binary evolution. They found that this a priori liberal assumption fits the observed mass ratio distribution better than the conservative assumption does. In our subsequent papers we upgraded the quantity from a free constant parameter to a time-dependent quantity β(t) which is determined by the physical characteristics of the system.
Conservative codes produce only ~12% of Algols with a mass ratio q above 0.4. Including case B binary evolution to our statistics, this fraction rises to ~17%. Both results are shown in Fig. 6. It is clear that this limited enhancement is entirely due to those binaries with an initial primary mass above ~7 M⊙, because in our scenario the less massive systems hardly lose any mass during their evolution. Moreover, only ~2% of the Algols are reproduced with a mass ratio above 0.55, a number that is largely inferior to the ~21% required by the observations.
 |
Fig. 6 Observed distribution of mass ratios of 303 Algols (white) as compared to conservative (gray) and liberal (black) simulation. |
In Sect. 3.1 we showed that binaries with an early B-type primary at birth lose a large fraction of the transferred mass during their evolution. The short liberal era during which mass is lost (β < 1) occurs when the mass transfer rate is high, i.e., soon after the onset of RLOF when the binary is in its pre- or early-Algol stage. The mass ratio distribution as obtained with the liberal assumptions for binaries with an early B-type primary at birth will differ very much from the one obtained using the conservative binary evolutionary code. We obtain ~33% of Algols with q ∈ [0.4,0.55] when we consider the liberal evolution of binaries with a mass of the initial primary above 7 M⊙. Above 8 M⊙, this fraction even rises to ~45%. The fraction with q ∈ [0.55,1] always remains, however, in the vicinity of 2%, a number that is far below what is required by our set of observations.
4. Discussion
Since more Algols are observed with orbital periods below one day than are produced by either evolutionary code, we propose that theoretical evolutionary calculations for binaries should allow for the survival of the system even after deep contact. This is similar to stating that such systems seem to survive a specific kind of common envelope evolution involving two main sequence stars. The nature of such evolution requires further exploration, as the physics are probably different from and more complex than the physics in the classical common envelope scheme as described by e.g. Webbink (1984) and Nelemans & Tout (2005).
Although the theoretically calculated liberal mass ratio distribution of Algols with an initial early B-type primary fits the observations better, the overall observed mass ratio distribution of Algols still shows too many systems with high mass ratios. This could partly be due to theoretical mass transfer rates that are too large and too short-living during the rapid era of mass transfer. We have compared mass transfer rates as obtained by our binary evolutionary code in the conservative mode with mass transfer rates for conservative evolution as produced by previous authors and published by Kippenhahn Weigert (1967), Kippenhahn et al. (1967), and Paczyński (1967a,b). The durations of our calculated phases of rapid mass transfer are very similar to those mentioned above, whereas our peak values are somewhat lower because our stellar models are calculated with OPAL opacities (Rogers & Iglesias 1992; Iglesias et al. 1992; Iglesias & Rogers 1996), which were not available previously. Our calculated durations and peak values of mass transfer rates agree very well with those published by Nelson & Eggleton (2001) for a representative set of interacting binaries. The occurrence of many observed Algols with high mass ratios thus remains unexplained.
Our scenario predicts only ~2% of Algols with a mass ratio above 0.55. It is not certain that the discrepancy with ~21% of observed Algols with these high mass ratios is entirely due to fundamental failures of the theory. We would suggest that the determination of mass ratios from observations is open for revision. Algols with a high mass ratio are present mainly when determined using main sequence characteristics for the gainer (qMS). Other methods generate an observed mass ratio distribution with much fewer high values (see Sect. 3 of Van Rensbergen et al. 2006). The validity of one method over another should be clearly decided before any conclusions can be attached to the difference between observed and predicted numbers of binaries in these high-q-bins.
Much work has to be done in the future on the calibration of the efficiency by which mechanical energy is transformed into radiation as represented by relation (6). This can only be done with refined and extended data for Table 1. Therefore, we make a call for observations.
The crucial quantity 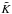 is
determined, on one hand, by relation (4) and,
on the other, by relation (5). Relation
(4) uses the product of
A > 1 with S ≪ 1. The quantity A
is determined from the knowledge of Lacc and
Ladd. Assuming that the geometry of the binary is perfectly
known, the value of Lacc is determined with the (O–C) method
(Sterken 2005), yielding the mass transfer rate only
when the ephemeris of the eclipse changes linearly with time. The luminosity added to the
gainer Ladd has been determined in only a few cases. The
fractional surface area has only been measured a few times, since small spot radii
( < 10°) are hard to observe (Van Hamme et al. 2001). Fortunately, we have the theoretical relation at our disposal as derived by
Pringle (Eq. (3)), which has no observational
limitations and which is reliable within a factor of two for each case that could be checked
in this paper. Relation (5) uses quantities
that are relatively well known, such as the radius of the gainer and its effective
temperature. The uncertainty on the quantity Lacc is discussed
above. Measurements of the spot temperature Tspot are crucial
and are given in Sects. A.1 and A.2. Binaries for which the value of
is
determined, on one hand, by relation (4) and,
on the other, by relation (5). Relation
(4) uses the product of
A > 1 with S ≪ 1. The quantity A
is determined from the knowledge of Lacc and
Ladd. Assuming that the geometry of the binary is perfectly
known, the value of Lacc is determined with the (O–C) method
(Sterken 2005), yielding the mass transfer rate only
when the ephemeris of the eclipse changes linearly with time. The luminosity added to the
gainer Ladd has been determined in only a few cases. The
fractional surface area has only been measured a few times, since small spot radii
( < 10°) are hard to observe (Van Hamme et al. 2001). Fortunately, we have the theoretical relation at our disposal as derived by
Pringle (Eq. (3)), which has no observational
limitations and which is reliable within a factor of two for each case that could be checked
in this paper. Relation (5) uses quantities
that are relatively well known, such as the radius of the gainer and its effective
temperature. The uncertainty on the quantity Lacc is discussed
above. Measurements of the spot temperature Tspot are crucial
and are given in Sects. A.1 and A.2. Binaries for which the value of
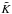 as
determined from relation (4) is not
compatible (within reasonable limits on the uncertainties on S,
Ladd, Lacc, and
Tspot) with the value as determined from relation (5) were removed from our sample. Although masses,
radii, and effective temperature of donor and gainer are usually well known, there is an
explicit need for more, and more reliable, determinations of characteristics of the gainer
star in semidetached binaries. Observable quantities such as S,
Ladd, Lacc, and
Tspot are needed to construct a better model that allows some
binaries to lose mass into interstellar space.
as
determined from relation (4) is not
compatible (within reasonable limits on the uncertainties on S,
Ladd, Lacc, and
Tspot) with the value as determined from relation (5) were removed from our sample. Although masses,
radii, and effective temperature of donor and gainer are usually well known, there is an
explicit need for more, and more reliable, determinations of characteristics of the gainer
star in semidetached binaries. Observable quantities such as S,
Ladd, Lacc, and
Tspot are needed to construct a better model that allows some
binaries to lose mass into interstellar space.
5. Conclusions
A catalog (Van Rensbergen et al. 2008) with 561 conservative and liberal evolutionary tracks is available at the Centre de Données Stellaires (CDS). Binaries with an initial primary mass ∈ [3, 5] M⊙ were calculated only in one mode since they evolve conservatively. Binaries with an initial primary mass ∈ [6, 15] M⊙ were calculated in the liberal mode. Results for evolution with weak and strong tidal interaction are given separately. Conservative tracks are always added so that the reader is able to compare the results of liberal evolution (in two different tidal modes) with those of conservative evolution.
Mass impinging from the donor spins up the gainer and creates a hot spot in its equatorial zone or at the edge of its accretion disk. The combined energy of the enhanced rotation and increased radiation from the hot spot may exceed the binding energy of the system. We presented the results of liberal evolutionary calculations for binaries with a B-type primary at birth. A significant fraction of the transferred mass is lost by the system in the case of binaries with an early B-type primary at birth. Systems with a late B-type primary at birth hardly lose any matter.
The observed distribution of orbital periods of Algols is reproduced well by our liberal theoretical calculations. Algols with an orbital period shorter than one day are present, however, for ~9% in the observations, whereas they are almost not created by our simulation. Our liberal theoretical calculations reproduce the adopted observed distribution of mass ratios of Algol binaries less satisfactorily. Algols with mass ratios over 0.55 are underrepresented. Section 4 proposes possible additions to the present scenario to meet these discrepancies.
Acknowledgments
We thank Ed van den Heuvel for his permanent interest in our work and his fruitful comments, Walter van Hamme for his clarifying comments on the measurement of hot spot sizes and Chris Sterken to make us acquainted with the (O–C) method which enabled us to calculate and confirm many mass transfer rates.
References
- Ak, H., Chadima, P., Harmanec, P., et al. 2007, A&A, 463, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albright, G., & Richards, M. 1996, ApJ, 489, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Banks, T., Sullivan, D., & Budding, E. 1990, ApSS, 173, 92 [Google Scholar]
- Bath, G., & Pringle, J. 1981, MNRAS, 194, 967 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J., Richards, M., & Malinowski, M. 1995, ApJ, 445, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Brancewicz, H., & Dworak, T. 1980, A&A, 30, 501 [Google Scholar]
- Brandi, E., Garcia, L, Kondo, Y., & Sahade, J. 1989, A&A, 215, 331 [NASA ADS] [Google Scholar]
- Budding, E., Marsden, S., & Slee, O. 2001, PASA, 18, 140 [NASA ADS] [Google Scholar]
- Budding, E., Erdem, A., Cicek, C., et al. 2004, A&A, 417, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clausen, J., & Gronbech, B. 1977, A&AS, 28, 389 [NASA ADS] [Google Scholar]
- Cugier, H., & Molaro, P. 1984, A&A, 140, 105 [NASA ADS] [Google Scholar]
- De Jager, C., Nieuwenhuijzen, H., & Van der Hucht, K. 1988, A&A, 72, 259 [Google Scholar]
- De Loore, C., & De Greve, J.-P. 1992, A&AS, 94, 453 [NASA ADS] [Google Scholar]
- De Loore, C., & Doom, C. 1992, in Structure and Evolution of Single and Binary Stars (Dordrecht: Kluwer) [Google Scholar]
- De Mink, S., Pols, O., & Hilditch, R. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dervisoglu, A., Tout, C., & Ibanoglu, C. 2010, MNRAS, 406, 1071 [NASA ADS] [Google Scholar]
- Devita, M., Bradstreet, D., Guinan, E., & Glownia, Z. 1997, in Stellar Evolution in Real Time, 23rd meeting of the IAU (Kyoto) [Google Scholar]
- Drechsel, H., Rahe, J., Wargau, W., & Wolf, B. 1982, A&A, 110, 246 [NASA ADS] [Google Scholar]
- Duerbeck, H., & Karimie, M. 1979, IBVS, 1617 [Google Scholar]
- Hall, D., Henry, G., & Murray, W. 1981, AcA, 31, 383 [NASA ADS] [Google Scholar]
- Harmanec, P. 2002, AN, 323, 87 [Google Scholar]
- Henyey, L., Wilets, L., Böhm, L., Lelevier, R., & Levee, R. 1959, ApJ, 129, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L., Forbes, J., & Gould, N. 1964, ApJ, 139, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, T., & Drechsel, H. 1985, ApSS, 114, 1 [Google Scholar]
- Hilditch, R., 2001, in An Introduction to Close Binary Stars (Cambridge University Press) [Google Scholar]
- Horne, K., 1985, MNRAS, 213, 129 [NASA ADS] [Google Scholar]
- Iglesias, C., & Rogers, F. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C., Rogers, F., & Wilson, B. 1992, ApJ, 397, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Kempner, J., & Richards, M. 1999, ApJ, 512, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1967, ZA, 65, 58 [Google Scholar]
- Kippenhahn, R., Kohl, L., & Weigert, A. 1967, ZA, 66, 58 [Google Scholar]
- Langer, N. 1998, A&A, 329, 551 [NASA ADS] [Google Scholar]
- Langer, N., Wellstein, S., & Petrovic, J. 2003, IAUS, 212, 275 [Google Scholar]
- Lee, J., Youn, J., Lee, C. L., Kim, S., & Koch, R. 2009, AJ, 138, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J., Kim, C., Kim, D., et al. 2010, AJ, 139, 2669 [NASA ADS] [CrossRef] [Google Scholar]
- Linnell, A. 2002, MNRAS, 334, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S., & Shu, F. 1975, ApJ, 198, 2669 [Google Scholar]
- Manzoori, D., & Gozaliazl, G. 2007, AJ, 133, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 2009, in Physics, Formation and Evolution of Rotating Stars (Springer) [Google Scholar]
- Meurs, E., & Van den Heuvel, E. 1989, A&A, 226, 88 [NASA ADS] [Google Scholar]
- Miller, B., Budaj, J., Richards, M., Koubsky, P., & Peters, G. 2007, ApJ, 656, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., & Tout, C. 2005 MNRAS, 356, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C., & Eggleton, P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Paczyński, B. 1967a, AcA, 17, 193 [Google Scholar]
- Paczyński, B. 1967b, AcA, 17, 355 [Google Scholar]
- Peters, G. 2001, ApSS, 264, 79 [Google Scholar]
- Peters, G. 2007, in Binary Stars as Critical Tools in Contemporary Astrophysics, IAU Symp., 240, 119 [Google Scholar]
- Peters, G., & Polidan, R. 1998, ApJ, 500, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, G., & Polidan, R. 2004, AN, 325, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Langer, N., & Van der Hucht, K. 2005, A&A, 435, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Podsiadlowski, P., Joss, P., & Hsu, J. 1992, ApJ, 391, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Polidan, R. 1989, SSRv, 50, 85 [NASA ADS] [Google Scholar]
- Popova, E., Tutukov, A., & Yungelson, L. 1982, ApSS, 88, 55 [Google Scholar]
- Pourbaix, D., Tokovinin, A., Batten, A., et al. 2004, A&A, 424, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., Doom, C., Arnould, M., & De Loore, C. 1986, ApJ, 304, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T., Chochol, D., Tremko, J., et al. 2000, CoSka, 30, 117 [NASA ADS] [Google Scholar]
- Pringle, J. 1985, in Interacting Binary Stars, ed. J. Pringle, & R. Wade (Cambridge University Press) [Google Scholar]
- Pustylnik, I. 1995, BaltA, 4, 64 [NASA ADS] [Google Scholar]
- Pustylnik, I., & Niarchos, P. 2000, A&A, 361, 982 [NASA ADS] [Google Scholar]
- Qian, S. 2002, MNRAS, 336, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S., Zhu, L., & Boonrucksar, S. 2002, A&A, 396, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafert, J., & Wilson, R. 1984, ApSS, 100, 117 [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, M. 2004, AN, 325, 229 [Google Scholar]
- Richards, M., & Albright, G. 1999, ApJS, 123, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F., & Iglesias, C. 1992, ApJS, 79, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Rucinski, S., Baade, D., Lu, W., & Udalski, A. 1992, AJ, 103, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R., Van Paradijs, J., & Tinbergen, J. 1992, A&A, 260, 213 [NASA ADS] [Google Scholar]
- Salpeter, E. 1955, ApJ, 121, 161 [Google Scholar]
- Samec, R., Laird, H., Mutzke, M., & Faulkner, D. 1998, IBVS, 4186 [Google Scholar]
- Sana, H., Gosset, E., & Evans, C. 2009, MNRAS, 400, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Schaller, G., Schaerer, D., Meynet, G., & Maeder, A. 1992, A&AS, 96, 269 [Google Scholar]
- Schmidtt, H., Pauls, T., Tycner, C., et al. 2009, ApJ, 691, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, V. 1999, A&AS, 134, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterken, C. 2005, ASP Conf. Ser., 335, 3 [Google Scholar]
- Van Hamme, W., Samec, R., Gothard, N., et al. 2001, ApJ, 122, 3436 [NASA ADS] [CrossRef] [Google Scholar]
- Van Rensbergen, W., De Loore, C., & Jansen, K. 2006, A&A, 446, 1071 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Rensbergen, W., De Greve, J. P., De Loore, C., & Mennekens, N. 2008, A&A, 487, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Rensbergen, W., De Greve, J. P., Mennekens, N., Jansen, K., & De Loore, C. 2010, A&A, 510, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vesper, D., Honeycutt, K., & Hunt, T. 2001, AJ, 121, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1978, A&A, 28, 303 [Google Scholar]
- Webbink, R. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Wellstein, S. 2001, PhD Thesis, Potsdam University [Google Scholar]
- Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R., & Starr, T. 1976, MNRAS, 176, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Yakut, K., & Eggleton, P. 2005, ApJ, 629, 1055 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J.-P. 1977, A&A, 57, 383 [NASA ADS] [Google Scholar]
- Zhao, M., Gies, D., Monnier, D., et al. 2008, ApJ, 684, 295 [NASA ADS] [Google Scholar]
Appendix A: Data for 13 semidetached binaries
A.1. Ten systems with direct impact
Data on the present masses and radii of the stars, mass transfer rate, temperature of the hot spot (Tspot), fractional size of the hot spot (S), and luminosity added by the hot spot (Ladd) were taken for the ten systems with direct impact on the gainer’s surface from the following references:
-
VW Cep: masses, radii, and effective temperatures of donor and gainer are from Pustylnik Niarchos (2000). Ladd, Tspot, Rspot (and thus the quantity S) on the gainer are from the same authors. Values for Ṗ and thus of the mass transfer rate Ṁ are from Pribulla et al. (2000) and Devita et al. (1997).
-
AR Boo: masses, radii, effective temperatures of donor and gainer, and also values for Tspot and Ṁ are from Lee et al. (2009).
-
CN And: masses, radii, effective temperatures of donor and gainer, and also values for Tspot, Sspot and Ṁ are from Van Hamme et al. (2001) and references therein. A mean value of Ṁ was taken by also considering a somewhat different value of Ṁ determined by Samec et al. (1998) and used by Qian (2002) in his analysis of near-contact binary systems.
-
KZ Pav: masses, radii, effective temperatures of donor and gainer, and also values for Ladd and Ṗ are from Budding et al. (2001). We used their value of Ṗ to calculate Ṁ.
-
V361 Lyr: masses, radii, and effective temperatures of donor and gainer are given by Hilditch (2001) and Yakut Eggleton (2005). Hilditch (2001) also gives values for Tspot, Ladd, and Ṁ. This binary is thus very completely described.
-
RT Scl: masses, radii, and effective temperatures of donor and gainer are given by Banks et al. (1990) and Pourbaix et al. (2004). Banks et al. (1990) also give a value for Tspot. Values for Ṁ are given by Clausen Gronbech (1977) and Duerbeck Karimie (1979). From this we calculated a mean value for Ṁ which is a factor of ~2 less than the value given by Rafert Wilson (1984).
-
CL Aur: all the data for this Algol binary, including a value for Tspot on the gainer, are given by Lee et al. (2010).
-
U Cep: masses, radii, and effective temperatures of donor and gainer are given by Budding et al. (2004). A value for Ṗ = + 9.796 × 10-7 d y-1 was derived by ourselves from the “Eclipsing Binaries Minima Base” of Kundera, completed with the epochs of the most recent eclipses that can easily be found on the CDS website. From this we derived a value of Ṁ that is a factor of ~2 less than the evaluation by Pustylnik (1995). The value of Tspot ∈ [20 000,40 000] K was determined by Peters (2007) from the observations with the FUSE satellite. A refined value of Tspot ≈ 30 000 K was then assigned to the hot spot by the same author who assumes that this HTAR (high temperature accretion region) radiates as a black body. It is also interesting to notice that the gainer in this binary rotates 7.8 times faster than the synodic value (Dervisoglu et al. 2010).
-
U Sge: masses, radii, and effective temperatures of donor and gainer are given by Kempner Richards (1999) and Vesper et al. (2001). Manzoori Gozaliazl (2007) have determined a value for Ṗ (thus Ṁ) and have seen a hot spot on the gainer’s surface for which a range of temperatures is given by Richards Albright (1999). A value for Ladd has been determined by Albright Richards (1996), which makes this binary a well-described system.
-
SV Cen: masses and radii of donor and gainer are given by Rucinski et al. (1992) because this author considers SV Cen not as a contact binary but as a semidetached binary. The effective temperatures of both components are taken from the calibration for a B6.5III-donor and a B2V-gainer. Although Wilson Starr (1976), Drechsel et al. (1982) and Herczeg Drechsel (1985) consider SV Cen as an over-contact binary, many of their observations have been interpreted with SV Cen as a very active interacting binary. Herczeg Drechsel (1985) report a high but variable value of Ṗ. High mass transfer rates of ~4 × 10-4 M⊙ yr-1 and “a few times” 10-4 M⊙ yr-1 have been calculated by Wilson Starr (1976) and Rucinski et al. (1992), respectively. Moreover a very high value for the hot spot temperature (Tspot ≈ 105 K) and a very low value for the relative size of the hot spot (S < 0.01) have been reported by Drechsel et al. (1982). To keep the values of Lacc (determined by Ṁ), A, S, and
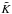 internally consistent and physically acceptable, we used the value of
Ṁ = 1.608 × 10-4 M⊙ yr-1
(Hilditch 2001) in Table 1. This leads to a spot temperature of
~37 500 K, well below the extremely high value of
~105 K cited above.
internally consistent and physically acceptable, we used the value of
Ṁ = 1.608 × 10-4 M⊙ yr-1
(Hilditch 2001) in Table 1. This leads to a spot temperature of
~37 500 K, well below the extremely high value of
~105 K cited above.
A.2. Three gainers with an accretion disk
We have three disk systems in our sample. A hot spot temperature is only available for
β Lyr. The quantity Ladd needed to
calculate the hot spot temperature is calculated with 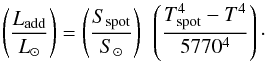 (A.1)The hot spot is now on
the edge of the disk, and its surface area has never been measured. Expression (3) was derived for calculating the size of a
hot spot on the surface of the gainer and can thus hardly be used in this case. Using
this expression nevertheless in the case of β Lyr we find an amount
Lacc that exceeds the calculated accretion luminosity by a
factor of three. In order to obtain the added luminosity we have therefore divided the
surface area of the impact zone as given by Pringle (1985) by the same factor of three for the three cases in this section. In Eq.
(A.1) we used the effective temperature
of the gainer for the two systems where the hot spot is located near the surface of the
gainer (SW Cyg and V356 Sgr), and we used the temperature in the middle of the accretion
disk where the spot is visible as a source of bipolar jets for β Lyr
(Linnell 2002). To calculate
(A.1)The hot spot is now on
the edge of the disk, and its surface area has never been measured. Expression (3) was derived for calculating the size of a
hot spot on the surface of the gainer and can thus hardly be used in this case. Using
this expression nevertheless in the case of β Lyr we find an amount
Lacc that exceeds the calculated accretion luminosity by a
factor of three. In order to obtain the added luminosity we have therefore divided the
surface area of the impact zone as given by Pringle (1985) by the same factor of three for the three cases in this section. In Eq.
(A.1) we used the effective temperature
of the gainer for the two systems where the hot spot is located near the surface of the
gainer (SW Cyg and V356 Sgr), and we used the temperature in the middle of the accretion
disk where the spot is visible as a source of bipolar jets for β Lyr
(Linnell 2002). To calculate
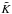 we replaced in relation (5)
Rg by Rdisk and
Teff, g by Tedge, disk,
using relations (A.2) and (A.3).
we replaced in relation (5)
Rg by Rdisk and
Teff, g by Tedge, disk,
using relations (A.2) and (A.3).
The characteristic disk temperature and the temperature distribution from the stellar
surface to the edge of the disk were calculated from the model of Bath & Pringle
(1981). Horne (1985) developed a method of eclipse mapping of accretion disks with this
model, and Rutten et al. (1992) applied the
latter method to construct models of accretion disks for six cataclysmic variables. The
values of Tdisk and
Tdisk, edge mentioned in Table 1 were thus calculated with 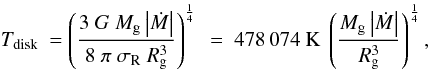 (A.2)with
σR = 5.67 × 10-5 erg cm-2 K-4 s-1
the Stefan-Boltzmann constant and
(A.2)with
σR = 5.67 × 10-5 erg cm-2 K-4 s-1
the Stefan-Boltzmann constant and 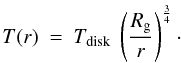 (A.3)For the three
systems with an accretion disk around the gainer, data on present masses and radii of
the stars, mass transfer rates, temperatures of the hot spot
(Tspot) and added luminosities through the hot spot
(Ladd) were taken from the following references:
(A.3)For the three
systems with an accretion disk around the gainer, data on present masses and radii of
the stars, mass transfer rates, temperatures of the hot spot
(Tspot) and added luminosities through the hot spot
(Ladd) were taken from the following references:
-
SW Cyg: masses, radii, and effective temperatures can be found in the catalog of Budding (2004) and Richards Albright (1999). Values for Ṗ (and thus Ṁ) are from Qian et al. (2002). Albright Richards (1996) argue that the luminosity added to the similar system TT Hya by accretion is five times higher as in the case of SW Cyg. Since Peters Polidan (2004) establish a hot spot temperature of 17 000 K in TT Hya (more than 60% hotter than the underlying effective temperature of the gainer), we conclude that the obtained hot spot temperature of ~13 000 K for SW Cyg is reasonable.
-
V356 Sgr: masses and radii of donor and gainer were found by Peters Polidan (1998). These authors also mention the existence of very hot circumstellar material around this binary and of a hot spot concentrated near the photosphere of the B-type gainer. Effective temperatures of donor and gainer are from Polidan (1989). We derived a value of Ṁ from the quadratic term in the ephemeris of eclipses as given by Hall et al. (1981). This value is in good agreement with the mass transfer rate given in Polidan (1989). It is pointed out by Simon (1999) and Dervisoglu et al. (2010) that the gainer rotates at the high equatorial velocity of ~212 km s-1. This is, however, far below the critical velocity of ~612 km s-1 so that in view of the Roche model (e.g. Maeder 2009) the gainer remains practically spherical, and the observed UV-excess cannot come from the oblateness of the gainer with polar regions much brighter than the equatorial ones, as suggested by Polidan (1989).
-
β Lyr: masses and radii of donor and gainer are from Simon (1999). Effective temperatures are from Harmanec (2002). We derived a mass transfer rate from the values of Ṗ given by Simon (1999) and Ak et al. (2007). Harmanec (2002) reveals a minimum temperature for a hot spot of 20 000 K. Linnell (2002) proposes that the kinetic energy of the mass transfer stream is converted into heat and radiation at a radius equal to half of the radius of the accretion disk. Schmidtt et al. (2009) observed strong Hα originating in the disk, possibly at the point of impact of the gas on the disk. The disk temperature of 8500 K as mentioned by Harmanec (2002) is very similar to the temperature we find at the edge of the opaque accretion disk of β Lyr (~8920 K). The masses of the components as derived by Zhao et al. (2008) are somewhat lower than those mentioned by Simon (1999). They yield somewhat lower values of the disk temperatures and somewhat higher values for
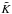 .
They are included in the error bars in Fig. 3.
.
They are included in the error bars in Fig. 3.
A.3. Systems removed from the sample
We had to exclude many binaries from our statistical analysis. Some systems are indeed extensively studied with one crucial quantity that was, however, never determined from the observations. For other systems we found observational values of physical quantities that were contradictory. We mention a few examples of systems that are excluded from our statistics for the time being.
-
TT Hya: many data are known for this Algol system with an accretion disk, including the value of 17000 K for the hot spot temperature by Peters Polidan (2004). The mass transfer rate of ≥2 × 10-10 M⊙ yr-1 as found by Miller et al. (2007) is, however, five orders of magnitude too low to obtain such a high hot spot temperature. The quoted value of the mass transfer rate would yield a hot spot with a temperature of 1000 K at most: only a little bit higher than the temperature at the edge of the accretion disk.
-
β Per: the same can be said about the one and only real Algol, β Per. Images of accretion structures containing a stable emission source on the gainer were obtained with Doppler tomography by Richards (2004). A high-temperature region (T ≈ 104–105 K) surrounding the gainer has been derived from the observation of high temperature resonance emission lines by Cugier & Molaro (1984) and Brandi et al. (1989). Blondin et al. (1995) found that the gas stream towards the gainer is heated up to a temperature of 2 to 4 × 106 K for this direct impact system. Such high temperatures cannot be produced by a mass transfer rate as low as 0.4 to 2 × 10-11 M⊙ yr-1 as proposed by Pustylnik (1995). A hot spot with a temperature of ~105 K can only be created through a mass transfer rate that is seven orders of magnitude higher. A mass transfer rate as low as ~10-11 M⊙ yr-1 would raise the photospheric temperature of the gainer with less than 1 K according to the scenario used to construct Table 1.
All Tables
All Figures
 |
Fig. 1 Equatorial velocity of the gainer of a (6+3.6) M⊙ binary with an initial orbital period of 3 days. Strong tidal interaction is represented by a dashed line, weak tides by a long-dashed one. The critical velocity is indicated by a solid line. |
| In the text | |
 |
Fig. 2 (q − r) diagram for the 13 interacting binaries that were used in our analysis. Algols (q < 1) are at the left of the vertical line q = 1.0. The ten direct impact systems are located above the curve ωd (filled squares). The three systems with a transient accretion disk around the gainer are located between the curves ωmin and ωd (filled circles). Permanent accretion disks would be located below ωmin. Systems with q > 1 have not reached Algol characteristics yet. |
| In the text | |
 |
Fig. 3 Radiative efficiency of accretion |
| In the text | |
 |
Fig. 4 Calculated amounts of mass lost by a binary with a 7 M⊙ primary at birth undergoing strong tidal interaction during its evolution. The total amount of lost mass ΔM is on the vertical axis, and the initial orbital period is on the horizontal axis. Calculated cases are indicated by filled circles. Binaries starting with an initial mass ratio q = 0.4 are connected by a long-dashed line, those with q = 0.6 by a dashed line, and those with q = 0.9 by a solid line. |
| In the text | |
 |
Fig. 5 Observed distribution (white) of orbital periods of 303 Algols as compared to liberal (black) simulation. |
| In the text | |
 |
Fig. 6 Observed distribution of mass ratios of 303 Algols (white) as compared to conservative (gray) and liberal (black) simulation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


