EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 528 (April 2011) A&A, 528 (2011) A8 Full HTML
Free Access
Issue
A&A
Volume 528, April 2011
Article Number A8
Number of page(s) 7
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201015433
Published online 17 February 2011

© ESO, 2011

1. Introduction

Among current exoplanet-hunting techniques, radial velocity (RV) measurements are nowadays the most successful method for detecting exoplanetary systems (Udry & Santos 2007; Cumming et al. 2008). Although the minimum mass is derived, a small correction including the distribution of inclination is expected to access the true mass distribution of the current candidate planets (Watson et al. 2010; Jorrissen et al. 2001). Originally focused on quiet solar-type stars that show numerous thin absorption lines, RV surveys have recently diversified their samples to consider a broader class of primary stars. Telluric planets are now primarily searched for around M dwarfs, since the habitable zone can be explored (Mayor et al. 2009; Charbonneau et al. 2009).

Giant planets have probably been discovered around intermediate-mass objects (Lagrange et al. 2009), giant stars (Dollinger et al. 2009; Lovis et al. 2007) and have actively been for searched around young active stars (Setiawan et al. 2008). Finally, planets are now scrutinized in multiple stellar systems where RV surveys used to exclude them. This was mainly related to the difficulty of processing the multiple stellar RV signals at the precision required for detecting planets (Konacki 2005; Eggenberger & Udry 2007a,b; Toyota et al. 2009; Desidera et al. 2010). Binaries and triple are particularly interesting for testing the predictions of the planetary formation and evolution processes. They enable us to understand how a perturber will affect the planetary system formation and dynamical evolution. Originally, planets were rapidly found in close spectroscopic binaries (Gliese 86, Queloz et al. 2000; γ Cep Hatzes et al. 2003), confirming that circumstellar planetary systems could form and survive in such a hostile environment (binary separation  ≲ 20 AU). Circumbinary planets, undiscovered up until now, remain more difficult to detect owing the limited size of the sample and only the recent start-up of dedicated programs.

A few years ago, studies and surveys were successful in tackling the problem of duplicity in planetary systems. Zucker & Mazeh (2002) initially showed that the planet properties in binaries were different to planets around single stars. Eggenberger et al. (2004) confirmed that the most massive short-period planets were found in binary systems and that planets with short (P ≤ 40 days) periods in binaries were likely to have low eccentricities. Tamuz et al. (2008) finally found that extremely high eccentric planets were all in binaries. In parallel to Doppler surveys, imaging surveys studied the effect of duplicity on the planet occurrence around longer period ( ≥ 100 AU) binaries. Catalogs compiled by Raghavan et al. (2006), Desidera & Barbieri (2007), and Bonavita & Desidera (2007) have not found any significant discrepancies in the planet frequency between binary and single stellar systems.

Only high-contrast imaging studies have been able to access intermediate-separation (20 − 100 AU) binaries where the companion influence is the most expected. Several deep-imaging studies have revealed a number of additional close companions to known exoplanetary hosts (Patience et al. 2002; Chauvin et al. 2006a,b; Eggenberger et al. 2007a,b; Mugrauer et al. 2009). However, a dedicated survey using a reference sample was mandatory in order to conduct a proper multiplicity study to test the impact of duplicity on the occurrence of giant planet. Eggenberger et al. (2007a,b) observed two subsamples of more than 50 stars each. They find a lower corrected binary fraction for the planet-host subsample, particularly for physical separations shorter than 100 AU (Eggenberger et al. 2008). This statistical result corroborates the theoretical prediction that multiplicity has a negative effect on planetary formation and evolution at less than 100 AU (e.g. Nelson et al. 2000; Mayer et al. 2005; Thébault et al. 2006).

Binaries with small semi-major axes (≲20 AU) hosting a planetary system offer an ideal opportunity to characterize the dynamical impact of the binary companion on the inner circumstellar planet in more detail. They can also serve as a testbed for planet formation models, as they push many of these models parameters to their limits. We conducted such a study combining RV and AO imaging observations for the Gliese 86 system (Lagrange et al. 2006). We confirmed that the companion was a white dwarf identified in spectrocopy by Neuhäuser et al. (2005). We showed that the planetary system around Gliese 86 A had survived the later stages of evolutiion of the white dwarf progenitor, a probable late-F to early-K type star (i.e, the mass loss of the B component and a semi-major axis intially reduced to 13 AU compared with its 18 AU current value). In the course of the VLT/CFHT deep imaging surveys of exoplanet hosts (Chauvin et al. 2006a,b, 2007), we discovered a close (~20 AU) binary companion to HD 196885 (see Fig. 1). This system is well-suited to a detailed dynamical study. In this paper, we summarize the observations and the results of our recent imaging campaign aimed at monitoring the binary orbital motion. We report the best orbital adjustment to fit the combined imaging and RV observations of the complete system. Finally, we discuss the dynamical stability of the inner planetary system that has formed and survived despite the dynamical influence of the close binary companion.

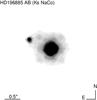thumbnail Fig. 1

VLT/NACO image obtained in Ks-band using the S27 CONICA platescale. The binary is clearly resolved.

Table 1

Relative astrometric position of the binary companion HD 196885 B to the exoplanet host star HD 196885 A.

2. The HD 196885 exoplanet host binary

HD 196885 is an F8V (V = 6.398, B − V = 0.559) star located at 33.0 ± 0.9 pc (Perryman et al. 1997). Based on CORALIE spectra, Sousa et al. (2006) derived a spectrocopic temperature, surface gravity, and metallicity of Teff = 6340 ± 39 K, log(g) = 4.46 ± 0.02 and [Fe/H] = 0.29    ±    0.05, respectively. The star vsini was estimated to 7.3    ±    1.5 km s-1 from ELODIE spectra (Correia et al. 2008). These results were recently supported by independent Lick observations reported by Fischer et al. (2009). The chromospheric activity level is relatively low. Bolometric luminosity correction and evolutionary model predictions lead to an estimate of the luminosity and the mass of 2.4   L⊙ and 1.3   M⊙, respectively. Finally, the corresponding stellar age derived from evolutionary tracks and from the activity level varies between 1.5 to 3.5 Gyr (see Correia et al. 2008; Fischer et al. 2009). As noted by Correia et al. (2008), HD 196885 might be part of a wider binary system with the star BD+104351 B1 located 192 ′′ north (which would correspond to a minimum physical separation of 6330 AU, Dommanget et al. 2002).

In 2004, an RV variation was measured and adjusted with a preliminary orbital period of P = 0.95 yr. The result was temporarily reported on the California Planet Search Exoplanet Web site and was thus withdrawn owing a significant residual drift in the orbital solution. Nevertheless, this star was included in our deep-imaging survey of stars hosting planets detected by RV observations (Chauvin et al. 2006a,b). Our imaging and spectroscopic observations led to detecting a co-moving M1 ± 1V dwarf companion located at only 0.7 ′′ (23 AU in projected physical separation) and likely to be responsible for the trend seen in the Lick RV residuals (Chauvin et al. 2007). Our two epochs of observations resolved the binary orbital motion confirming its physical nature.

Using a double-Keplerian model for the binary star and the planet to adjust their ELODIE, CORALIE, and CORAVEL observations spread over 14 years, Correia et al. (2008) derived a first range of orbital solutions. They revised the planet solution with a minimum mass of MAb   sini = 2.96 MJup, a period of P = 3.69    ±    0.03 yr, and an eccentricity of e = 0.462 ± 0.026. Moreover, they found additional constraints for the binary companion HD 196885 B with a period of P > 40 yr, a semi-major axis a > 14 AU, and a minimum mass of MB   sini > 0.28   M⊙. Based on Lick observations, Fischer et al. (2009) recently derived consistent results for both the inner planet and the binary companion. Nevertheless, in both studies a relatively wide range of masses and periods remains for the binary companion. Additional observing constraints are therefore needed to refine the binary companion properties and to understand how it could have affected the formation and the stability of the circumstellar planetary system around HD 196885 A.

thumbnail Fig. 2

VLT/NACO measurements with uncertainties in the offset positions of HD 196885 B relative to A, obtained on August 1, 2005, August 28, 2006, August 27, 2007, June 26, 2008 and August 27, 2009. The solid line gives the expected variation in the offset positions of B relative to A, if B is a background stationary object. This variation takes the initial offset position of B relative to A into account on August 1, 2005 and the proper and parallactic motions of HD 196885 A. After April 2006, the predicted offset positions go beyond the (Δα,Δδ) astrometric range considered for this figure.

3. Observation and data reduction

The orbit of HD 196885 AB was monitored with the NACO (NAOS-CONICA) high-contrast adaptive optics (AO) imager of the VLT-UT4. The NAOS AO system (Rousset et al. 2002) is equipped with a tip-tilt mirror, a 185 piezo actuator deformable mirror, and two wavefront sensors (Visible and IR). Attached to NAOS, CONICA (Lenzen et al. 1998) is the near infrared (1−5   μm domain) imaging, Lyot coronagraphic, spectroscopic, and polarimetric camera, equipped with a 1024 × 1024 pixels Aladdin InSb array. Observations were obtained at five different epochs on August 1, 2005, August 26, 2006, August 25, 2007, June 28, 2008 and August 27, 2009. Over the different observing campaigns, the atmospheric conditions were stable enough to close the AO loop and resolve both components. The offset position of HD 196885 B relative to A was monitored well at each epoch. The typical observing sequence included a set of five jittered images obtained with the Ks filter and the S27 camera CONICA (mean plate scale of 27.01 mas/pixel). This led to a total exposure time of  ~ 5 min on source. To calibrate the plate scale and the detector orientation, we observed the astrometric field of θ Ori 1 C (McCaughrean & Stauffer 1994). When not observable in June 2008, we used the astrometric binary IDS 21506S5133 as secondary calibrator (van Dessel & Sinachopoulos 1993), recalibrated with the θ Ori 1 C field.

thumbnail Fig. 3

NaCo astrometric observations and orbital solution of HD 196885 A and B. The full orbital solution is sketched in red and superimposed on the astrometric data points in blue. Predicted positions from the fit are shown in green. Left, full orbital solution. Right, zoomed on with the astometric data points and their uncertainties.

After cosmetic reductions (dead and hot pixels, dark and flat) using eclipse (Devillard 1997), we applied the deconvolution algorithm of Véran & Rigaut (1998) to obtain the offset position of HD 196885 B relative to A at each epoch. Single stars of similar brightness observed on the same night were used for point spread function (PSF) estimation. The results are reported in Table 1. The platescale and the true north orientation of the detector are given for each measurement. The relative positions are shown in Fig. 2. The expected variation in offset positions, if B is a background stationary object, is shown. It takes into account the initial offset position of B relative A and the proper ((μα,μδ) = (47.5 ± 0.9,83.1 ± 0.5) mas/yr) and parallactic (π = 30.31 ± 0.81 mas) motions of HD 196885 A. The orbital curvature is detected and the background stationary hypothesis for HD 196885 B is fully excluded.

4. Orbital solution

In an attempt to constrain the physical and orbital properties of the HD 196885 system, we simultaneously considered the astrometric data points listed in Table 1 and all data from past RV surveys: CORAVEL (9 RV measurements from June 1982 to August 1997), ELODIE (69 measurements from June 1997 to August 2006), CORALIE (33 measurements from April 1999 to November 2002) and Lick (75 measurements from 1998 to 2008) spanning more than 26 years (see Correia et al. 2008; Fischer et al. 2009). We used the iterative Levenberg-Marquardt χ2 minimization method (Press et al. 1992) to simultaneously fit both set of data and derive the characteristics of both orbits (the outer AB orbit between HD 196885 B and A, and the Ab orbit between the giant planet and HD 196885 A). The basic assumptions are that both orbits contribute to the RV signal and that only the AB orbit is seen in the astrometric motion. For the RV data, separate zero point velocities have been fitted for each set of data to account for instrumental shifts. The fitting routine turned out to rapidly converge towards a unique best solution reported in Table 2. This solution is also sketched in Figs. 3 and 4 and superimposed on the astrometric and RV data points.

Table 2

Fit and orbital parameters of HD 196885 Ab and B

With a minimum mass of MP   sini = 2.98 MJup, a period of P = 3.63 yr, and an eccentricity ofe = 0.48, the solution for the giant planet (Orbit Ab) is consistent with the orbital parameters found by Correia et al. (2008) and Fischer et al. (2009). The imaging data lift the degeneracy of orbital parameters for the stellar companion HD 196885 B. The mass of 0.45   M⊙ agrees with the companion photometry and the M1  ±  1V spectral type (Chauvin et al. 2007). With a period of P = 72.1 yr, our observations confirm a close orbit with a semi-major axis of just 21 AU. Together with Gl 86 (Queloz et al. 2000; Lagrange et al. 2006), γ Cep (Hatzes et al. 2003; Neuhäuser et al. 2007), and HD 41004 (Zucker et al. 2004), this system is among the closest binaries with one component hosting a giant planet.

5. Dynamical evolution and stability

We performed a preliminary numerical study of this system using the symplectic N-body package HJS (Beust 2003) optimized for hierarchical multiple systems. The study was started from the fitted solution of Table 2, considering that some free parameters in the Ab orbit remained (namely inclination i and the longitude of node Ω). Depending on the inclination assumed, the mass of the giant planet could range between the minimum value quoted in Table 2 and several tens of Jupiter masses. The angle Ω had no effect on the RV signal of the planet, but is related to the mutual inclination ir (mutual inclination between the two orbits) by 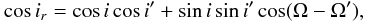cosir=cosicosi′+sinisini′cos(Ω−Ω′),\begin{equation} \cos i_r=\cos i\cos i'+\sin i\sin i'\cos (\Omega - \Omega') , \end{equation}(1)where i′ and Ω′ are the corresponding parameters for the AB orbit (listed in Table 2), and i and ir turn out to be the more relevant parameters for dynamically characterizing the system. We thus performed various integrations over 107   yr with different values of (i,ir) couples. Not all pairs were compatible with our constraints.

thumbnail Fig. 4

Radial velocity observations and orbital solution of HD 196885 AB based on the CORAVEL, ELODIE, CORALIE and Lick surveys. Top Left: radial velocity variation as a function of time with the best orbital solution overplotted presenting the complete set of RV observations. Top Right: zoom-in on the RV variation due to the giant planet HD 196885 Aa superimposed to the RV drift due to the companion HD 196885 B. Bottom Left: radial velocity variation of HD 196885 A due to the B component only as a function of the orbital phase. Bottom Right: radial velocity variation of HD 196885 A due to the Ab planet only as a function of the orbital phase.

thumbnail Fig. 5

Examples of integration runs for the HD 196885 3 body system. The evolution of the inner orbit Ab is shown over 107   yr. Top: a typical coplanar solution, with semi-major axis (left) and eccentricity (right) evolution; Bottom: same for a typical highly ir solution with kozai oscillations (see eccentricity).

Two main results were obtained from our simulations. The first result shows that in all cases the system appears chaotic with significant (more or less erratic) changes in the semi-major axis for the Ab orbit. The stability of the system therefore needs to be investigated on a much longer timescale. The second result shows that the mass of the giant planet HD 196885 Ab (hence the Ab orbit inclination i) does not significantly affect the stability of the system. Additional simulations with similar ir but different i show similar behaviours. This can be explained by the dominant influence of the higher mass companion HD 196885 B as the giant planet behaves almost like a massless test particle in this system. The mutual inclination ir is, however, a key parameter in the system’s stability. The behaviour of two different solutions (low and high ir) concerning the Ab orbit is shown on Fig. 5. The AB orbit remains slightly affected and is not considered here. In both cases, we note significant semi-major axis oscillations that reveal a chaotic regime. The eccentricity oscillations are high, especially in the high ir case. In fact, all high ir configurations fall in the Kozai resonance regime (Kozai 1962). Under the effect of secular perturbations by the outer body, the giant planet is subject to a periodic evolution that drives it to a lower inclination but very high eccentricity. This mechanism is active in non-coplanar hierarchical triple systems (Harrington 1968; Ford et al. 2000) and is therefore not surprising in our case. It was actually invoked to explain the high eccentricity of some extrasolar planets in binary systems (Mazeh 1997; Holman et al. 1997; Libert & Tsiganis 2009; Fabricky et al. 2007).

Surprisingly, our results show that the system is more stable in the Kozai regime. The Kozai resonance is an angular momentum exchange process. In a pure 3-body system, it does not affect the semi-major axis evolution and the system stability. Therefore the real level of instability can be read from the evolution of the semi-major axis, which is more stable in the Kozai configuration (see Fig. 5). This is a general trend present in all our simulations. For coplanar systems, only marginally stable solutions are found. Consequently, our results suggest that a non-coplanar configuration, which is characterized by a Kozai regime, is more probable for HD 196885. The high eccentricity of the Ab orbit fit is another strong indication of a Kozai regime. If confirmed, this system would constitute one of the most compact non-coplanar systems known so far. Deeper investigation will be needed to further constrain this issue and will be presented in a forthcoming paper.

6. Discussion

Stellar companions do influence the occurrence and the properties of planets in circumstellar orbits (i.e orbiting one of the binary compenent). Observations show that planets seem less frequent in close ( ≤ 100 AU) binaries (Eggenberger et al. 2007a,b, 2008) and that massive short-period planets mainly appear to be found orbiting one component of a multiple system (Zucker & Mazeh 2002; Eggenberger et al. 2004; Desidera & Barbieri 2007). Among the few tens of exoplanetary hosts, Gl 86, γ Cep, HD 41004, and HD 196885 are of particular interest as they are short period binaries with semi-major axis lower than  ~25 AU (see system properties in Table 3). In such close systems, we can wonder how their planets might have formed and survived the close interaction with the outer binary companion. The presence of a binary companion is expected to truncate the protoplanetary disk, affect its eccentricity, and affect the velocity dispersion and evolution of planetesimals that could lead to a planet formation hostile environment (e.g. Thébault et al. 2006; Paardekooper et al. 2008; Xie et al. 2008; Marzari et al. 2009; Cieza et al. 2009). In the context of γ Cep, Thébault et al. (2004) and Paardekooper et al. (2008) show that core-accretion formation of a giant planet is feasible, although it probably slows down (assuming coplanarity of the disk, planet, and binary). Jang-Condell et al. (2008) find that disk instability is in addition more unlikely, since a massive circumstellar disk and/or extremely high accretion rate as seen in FU Orionis events are required. Kley & Nelson (2008) then examined the dynamical evolution when a protoplanetary core has formed and begins the accretion phase. They constrain the initial semi-major axis of the giant planet to (ap ≤ 2.7 AU), which could lead to a stable solution surviving inward migration and eccentricity variation. HD 196885 closely resembles the γ Cep system. However, the higher mass ratio between the binary companion and the primary and the farther location of the inner planet makes it even more challenging for core-accretion planet formation theories.

Table 3

Orbital parameters of small separation (a ~ 20 AU) binaries with one exoplanet around one component.

Although coplanarity seems a reasonable assumption for the planet formation in close binaries (Hale 1994), our preliminary dynamical study shows that a non-coplanar configuration, characterized by a Kozai regime, is more probable for HD 196885. Its origin might therefore be questioned, as it seems difficult to build a non-coplanar system from a single disk. The giant planet has to form and survive in a non-coplanar system under the combination of the secular pertubation of the close binary companion and disk evolution. This has to be tested. An alternative scenario could be that the binary was less compact in the past. Close encounters with other young stars could have led its orbit to shrink (Malmberg et al. 2008). The companion may also have been captured after the formation of a giant planet around the primary in the birth cluster (Portegies Zwart & McMillan 2005; Pfahl & Muterspaugh 2006). We could even think of a capture of the giant planet itself. These are, of course, speculations but the high present-day eccentricity of HD 196885 B is also an indication of a chaotic past dynamical history for that system. Further investigation will be needed to constrain and test the system stability and origin over a broader parameter range.

7. Conclusion

We have reported the results of four years of astrometric monitoring of the planet-host binary system HD 196885 AB using NaCo at the VLT. Combined with RV observations, our imaging results enabled us to derive the inclination, the eccentricity, and the true mass of the B component, a low-mass star orbiting at 21 AU. We found solutions for the planet that are consistent with previously reported results. We also confirmed that HD 196885 AB belongs to the rare cases of close binaries with one component hosting a giant planet, offering an ideal labolatory for studying the formation and evolution processes in such extreme planetary systems. Finally, we ran N-body numerical simulations to test the system’s stability. The main result suggests that non-coplanarity and high mutual inclination, characterized by a Kozai regime, favour the system stability. If confirmed, HD 196885 would constitute one of the most compact non-coplanar systems hosting a circumstellar planetary system. How planet formation could have occurred in such an extreme and hostile environment remains a challenging question. In-situ formation of a non-coplanar system cannot be excluded and has to be tested; however, alternative scenarii, such as an external perturbation with stellar encounters modifying the binary properties or capture mechanisms, are likely to offer reasonable explanations.

1

And not BD+104251 B as mentionned by Correia et al. (2008).

Acknowledgments

We would like to thank the staff of ESO-VLT for their support at the telescope, and the Osservatorio di Arcetri and its director Francesco Palla for the visiting scientist stay of the author during the writing of this paper. We would like also to thank Philippe Thébault for his comments and suggestions on the article. Finally, this publication made use of the SIMBAD and VizieR database operated at the CDS, Strasbourg, France. And, we acknowledge partial financial support from the Programmes Nationaux de Planétologie et de Physique Stellaire (PNP & PNPS) and the Agence Nationale de la Recherche, in France. A.E. is also supported by a fellowship for advanced researchers from the Swiss National Science Foundation (grant PA00P2_126150/1).

References

  1. Beust, H. 2003, A&A, 400, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bonavota, M., & Desidera, S. 2007, A&A, 468, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Chauvin, G., Lagrange, A. M., Udry, S., et al. 2006a, A&A, 456, 1165 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
  4. Chauvin, G., Lagrange, A. M., Udry, S., et al. 2006b, A&A, 475, 723 [Google Scholar]
  5. Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  6. Cieza, L. A., Padgett, D. L., Allen, L. E., et al. 2009, ApJ, 696, 84 [Google Scholar]
  7. Correia, A. C. M., Udry, S., Mayor, M., et al. 2008, A&A, 479, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
  9. Desidera, S., & Barbieri 2007, A&A, 460, 349 [Google Scholar]
  10. Desidera, S., Gratton, R., Martinez Fiorenzano, A., et al. 2010, EAS, 42, 117 [EDP Sciences] [Google Scholar]
  11. Devillard, N. 1997, The messenger, 87 [Google Scholar]
  12. Döellinger, M. P., Hatzes, A. P., Pasquini, L., et al. 2009, A&A, 505, 1311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Dommanget, J., & Nys, 0. 2000, A&A, 363, 991 [NASA ADS] [Google Scholar]
  14. Eggenberger, A. 2010, EAS Proc., 42, 19 [CrossRef] [EDP Sciences] [Google Scholar]
  15. Eggenberger, P., Udry, S., & Mayor M. 2004, A&A 417, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Eggenberger, A., Udry, S., Chauvin, G., et al. 2007a, A&A, 474, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Eggenberger, A., Udry, S., Mayor, M., et al. 2007b, A&A, 466, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Fabrycky, D., & Tremaine, S. 2007, ApJ, 669, 1298 [NASA ADS] [CrossRef] [Google Scholar]
  19. Ford, E. B., Kozinsky, B., & Rasio, F. A. 2000, ApJ, 535, 385 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fischer, D., Driscoll, P., Isaacson, H., et al. 2009, ApJ, 703, 1545 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hale, A. 1994, AJ, 107, 306 [NASA ADS] [CrossRef] [Google Scholar]
  22. Harrington, R. S. 1968, AJ 73, 190 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  24. Holman, M., Touma, J., & Tremaine, S. 1997, Nature 386, 254 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jang-Condell, H., Mugrauer, M., & Schmidt, T. 2008, ApJ, 683, 191 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jorissen, A., Mayor, M., & Udry, S. 2001, A&A, 379, 992 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Kley, W., & Nelson, R. P. 2008, A&A, 486, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Konacki, M. 2005, ApJ, 626, 431 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  30. Lagrange, A.-M., Beust, H., Udry, S., et al. 2006, A&A, 459, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Lagrange, A.-M., Desort, M., Galland, F., et al. 2009, A&A, 495, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Lenzen, R., Hartung, M., Brandner, et al. 2002, SPIE, 4841 [Google Scholar]
  33. Libert, A.-S., & Tsiganis, K. 2009, A&A, 493, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Mayer, L., Wadsley, J., & Quinn, T. 2005, MNRAS, 363, 641 [NASA ADS] [Google Scholar]
  36. Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Marzari, F., Scholl, H., Thbault, P., & Baruteau, C. 2009, A&A, 508, 1493 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Mazeh, T., Krymolowski, Y., & Rosenfeld, G. 1997, ApJ, 477, 103 [Google Scholar]
  39. McCaughrean, M. J., & Stauffer, J. R. 1994, AJ, 108, 1382 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mugrauer, M., & Neuhäuser, R. 2009, A&A, 494, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Neuhäuser, R., & Mugrauer, M. 2005, MNRAS, 361, 15 [Google Scholar]
  42. Neuhäuser, R., Mugrauer, M., Fukagawa, M., Torres, G., & Scmidt, T. 2007, A&A, 462, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Nelson, A. 2000, ApJ, 537, 65 [Google Scholar]
  44. Paardekooper, S.-J., Thébault, P., & Mellema, G. 2008, MNRAS, 386, 973 [NASA ADS] [CrossRef] [Google Scholar]
  45. Patience, J., White, R. J., Ghez, A. M., et al. 2002, ApJ, 581, 654 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pfahl, E., & Muterspaugh, M. 2006, ApJ, 652, 1694 [NASA ADS] [CrossRef] [Google Scholar]
  47. Portegies Zwart, S. F., & McMillan, S. L. W. 2005, ApJ, 633, 141 [Google Scholar]
  48. Queloz, D., Mayor, M., Weber, L., et al. 2000, A&A, 354, 99 [NASA ADS] [Google Scholar]
  49. Raghavan, D., Henry, T. J., Mason, B. D., et al. 2006, ApJ, 646, 523 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  50. Rousset, G., Lacombe, F., Puget P., et al., 2002, SPIE, 4007 [Google Scholar]
  51. Setiawan, J., Henning, T., & Launhardt, R. 2008, Nature, 451, 38 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  52. Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2006, A&A, 458, 873 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Tamuz, O., Sgransan, D., Udry, S., et al. 2008, A&A, 480, 33 [Google Scholar]
  54. Thébault, P., Marzari, F., Scoll, H., Turrini, D., & Barbieri, M. 2004, A&A 427, 1097 [Google Scholar]
  55. Thébault, P., Marzari, F., & Scoll, H. 2006, Icarus, 183, 193 [NASA ADS] [CrossRef] [Google Scholar]
  56. Toyota, E., Itoh, Y., Ishiguma, S., et al. 2009, PASP, 61, 19 [Google Scholar]
  57. Udry, S., & Santos, N. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
  58. Véran, J.-P., & Rigaut, F. 1998, SPIE, 3353, 426 [Google Scholar]
  59. Watson, C. A., Littlefair, S. P., Collier Cameron, A., Dhillon, V. S., & Simpson, E. K. 2010, MNRAS, 408, 1606 [NASA ADS] [CrossRef] [Google Scholar]
  60. Xhie, J.-W., & Zhou, J.-L. 2008, ApJ, 686, 570 [NASA ADS] [CrossRef] [Google Scholar]
  61. Zucker, S., & Mazeh, T. 2002, ApJ, 568, 113 [Google Scholar]
  62. Zucker, S., Mazeh, T., Santos, N. C., Udry, S., & Mayor, M. 2004, A&A, 426, 695 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]

All Tables

Table 1

Relative astrometric position of the binary companion HD 196885 B to the exoplanet host star HD 196885 A.

In the text
Table 2

Fit and orbital parameters of HD 196885 Ab and B

In the text
Table 3

Orbital parameters of small separation (a ~ 20 AU) binaries with one exoplanet around one component.

In the text

All Figures

thumbnail Fig. 1

VLT/NACO image obtained in Ks-band using the S27 CONICA platescale. The binary is clearly resolved.
In the text
thumbnail Fig. 2

VLT/NACO measurements with uncertainties in the offset positions of HD 196885 B relative to A, obtained on August 1, 2005, August 28, 2006, August 27, 2007, June 26, 2008 and August 27, 2009. The solid line gives the expected variation in the offset positions of B relative to A, if B is a background stationary object. This variation takes the initial offset position of B relative to A into account on August 1, 2005 and the proper and parallactic motions of HD 196885 A. After April 2006, the predicted offset positions go beyond the (Δα,Δδ) astrometric range considered for this figure.
In the text
thumbnail Fig. 3

NaCo astrometric observations and orbital solution of HD 196885 A and B. The full orbital solution is sketched in red and superimposed on the astrometric data points in blue. Predicted positions from the fit are shown in green. Left, full orbital solution. Right, zoomed on with the astometric data points and their uncertainties.

In the text
thumbnail Fig. 4

Radial velocity observations and orbital solution of HD 196885 AB based on the CORAVEL, ELODIE, CORALIE and Lick surveys. Top Left: radial velocity variation as a function of time with the best orbital solution overplotted presenting the complete set of RV observations. Top Right: zoom-in on the RV variation due to the giant planet HD 196885 Aa superimposed to the RV drift due to the companion HD 196885 B. Bottom Left: radial velocity variation of HD 196885 A due to the B component only as a function of the orbital phase. Bottom Right: radial velocity variation of HD 196885 A due to the Ab planet only as a function of the orbital phase.

In the text
thumbnail Fig. 5

Examples of integration runs for the HD 196885 3 body system. The evolution of the inner orbit Ab is shown over 107   yr. Top: a typical coplanar solution, with semi-major axis (left) and eccentricity (right) evolution; Bottom: same for a typical highly ir solution with kozai oscillations (see eccentricity).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.