| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201015233 | |
| Published online | 17 March 2011 | |
Evolution of the binary population in young dense star clusters
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
e-mail: kaczmarek@ph1.uni-koeln.de
2
Astronomisches Rechen-Institut (ARI), Zentrum für Astronomie der
Universitaet Heidelberg (ZAH) Mönchhofstr. 12-14, 69120
Heidelberg,
Germany
3
Max-Planck-Institut für Astronomie (MPIA),
Königstuhl 17,
69117
Heidelberg,
Germany
4
National Astronomical Observatories of China (NAOC), Chinese
Academy of Sciences (CAS) 20A Datun Lu, Chaoyang District, 100012
Beijing, PR
China
5
The Kavli Institute for Astronomy and Astrophysics (KIAA), Peking
University (PKU) Yi He Yuan Lu 5, Hai Dian Qu, 100871
Beijing, PR
China
6
Max-Planck-Institut für Radioastronomie (MPIfR),
Auf dem Hügel 69,
53121
Bonn,
Germany
Received:
18
June
2010
Accepted:
2
February
2011
Context. Field stars are not always single stars, but can often be found in bound double systems. Since binary frequencies in the birth places of stars, young embedded clusters, are sometimes even higher than on average the question arises of how binary stars form in young dense star clusters and how their properties evolve to those observed in the field population.
Aims. We assess, the influence of stellar dynamical interactions on the primordial binary population in young dense cluster environments.
Methods. We perform numerical N-body simulations of the Orion nebula cluster like star cluster models including primordial binary populations using the simulation code nbody6++.
Results. We find two remarkable results that have yet not been reported: The first is that the evolution of the binary frequency in young dense star clusters is independent predictably of its initial value. The time evolution of the normalized number of binary systems has a fundamental shape. The second main result is that the mass of the primary star is of vital importance to the evolution of the binary. The more massive a primary star, the lower the probability that the binary is destroyed by gravitational interactions. This results in a higher binary frequency for stars more massive than 2 M⊙ compared to the binary frequency of lower mass stars. The observed increase in the binary frequency with primary mass is therefore most likely not due to differences in the formation process but can be entirely explained as a dynamical effect.
Conclusions. Our results allow us to draw conclusions about the past and the future number of binary systems in young dense star clusters and demonstrate that the present field stellar population has been influenced significantly by its natal environments.
Key words: binaries: general / galaxies: clusters: general / galaxies: clusters: individual: ONC / methods: numerical
© ESO, 2011
1. Introduction
Today the formation process of isolated single stars seems to be understood in principle. One remaining uncertainty, at least to some extent, concerns the formation of binary stars. There are several ways to form binary stars – the fragmentation of a collapsing cloud or core or the dynamical capture of a companion. However, determining the dominating process of binary formation requires knowledge of the parameters of the primordial binary population, i.e. the population as it appears just after star formation has finished.
Several surveys have been performed to determine the present-day parameters of binary populations in different kinds of environments. Observations of the field binary population have shown that the binary frequency is quite high, 60% for G-type dwarf stars (Duquennoy & Mayor 1991) and 35–42% for M-type dwarfs (Fischer & Marcy 1992; Reid & Gizis 1997). Both Duquennoy & Mayor (1991) and Fischer & Marcy (1992) determined the mass ratio and separation/period distributions of their samples. They found that the mass ratio distribution for G-type dwarfs increases as the mass ratios decreases while the mass ratio distribution for M-dwarfs is flat. The separation/period distributions for G-type and M-type dwarfs can be fitted by a Gaussian distribution in logarithmic space where both peak at nearly the same separation (~30 AU for G-type and 9–30 AU for M-type dwarfs) with the FWHM of both distributions spanning over three orders of magnitude (see Duquennoy & Mayor 1991, Fig. 7).
Another feature of binary populations is their dependence on the primary mass: observations indicate that the probability of finding a massive star in a binary system is higher than for low-mass stars. For OB stars, a binary frequency of ~70% is found (Preibisch et al. 2002), whereas for G-dwarfs a binary frequency of ~60% (Duquennoy & Mayor 1991) and for M-dwarfs a value as low as ~31% (Marchal et al. 2003) has been observed.
An understanding of the presently observed properties of evolved binary populations requires knowledge of the primordial binary population. To achieve this one has to look at sites where star formation has just happened, such as young star clusters. However, observations of binary populations in star clusters do not provide such a clear picture as the observations of the field binary population. While in dense star clusters such as the Orion nebula cluster (ONC) or NGC 2024 the observed binary frequency is similar to the field binary frequency (Köhler et al. 2006; Beck et al. 2003), sparse clusters such as the Taurus-Auriga association have much higher binary frequencies (see Duchêne 1999, and references therein). This leads to the question of what defines the binary frequency in the different environments. Possible explanations are differences in the temperatures of the parent clouds (Durisen & Sterzik 1994) or the dynamical evolution within the cluster (e.g. Kroupa et al. 1999). The latter possibility will be investigated in this study.
According to current knowledge, stars do not form in isolation, but in a clustered environment consisting of several tens to thousands of stars. Most of them possibly formed in clusters such as the ONC or even denser environments (Lada & Lada 2003; Pfalzner 2009). The stellar density in ONC-like clusters is sufficiently high to potentially affect the evolution of the binary population via gravitational interactions.
The gravitational interactions that alter binaries in a star cluster are mostly three- and four-body interactions between binary and single stars. Heggie (1975a,b) and Hills (1975) showed that three-body interactions are very effective in altering the parameters of binary systems. Both authors found that loosely bound binaries (also called soft) tend to become softer (meaning that their internal energy increases resulting in the widening of the binaries) owing to three-body interactions, while firmly bound (hard) binaries tend to become harder (Heggie-Hills law).
Four-body interactions (binary-binary encounters) become important in clusters that consist of a high number of binary stars (see for example Fig. 1 in Leigh & Sills 2010). In addition to three-body interactions, four-body interactions can form two “new” binary systems by exchanging the binary components, can destroy one or even both binary systems, or can lead to the formation of bound hierarchies of three or more stars. nbody6++ (Aarseth 2003; Spurzem 1999), the simulation code used for this study, uses several techniques such as the regularization of three-body interactions (Aarseth & Zare 1974) or the chain method (Mikkola & Aarseth 1993) to compute the evolution of these interactions correctly. However, in this study we only diagnose the evolution of the binary population.
Numerical investigations of the dynamical evolution of binaries in star clusters started in the 70’s with the development of the first N-body codes (e.g. Aarseth 1971). The early works concentrated on the formation of binaries in star clusters with initially pure single stellar systems. Only in recent years simulations have been performed to investigate the evolution of a primordial binary population. For example, Kroupa et al. (1999) simulated the evolution of ONC-like star cluster models where all stars initially were part of a binary system, i.e. a primordial binary frequency of 100%. They showed that the cluster evolution destroys wide binaries quite efficiently leading to a reduction in the initial binary fraction as the cluster evolves.
Here we also want to study the evolution of the primordial binary population of a young dense star cluster. In contrast to the previous studies, we investigate the effect of the initial binary frequency (0–100%) and a log-uniform semi-major axis distribution similar to that observed in very young star forming regions (e.g. Reipurth et al. 2007; Connelley et al. 2008). Because observations indicate that the binary frequency increases with stellar mass, we also focus on the dependence of the binary evolution on stellar mass.
This paper is structured in the following way. In Sect. 2 we define parameters that describe a binary population. Section 3 covers the setup of the simulations, including the generation of the cluster models and initialization of the primordial binary population. Finally in Sect. 4 we present the results obtained from the simulations.
2. Definitions
The most simple measure of the binary population of a star cluster is the number of binaries (Nb) within the cluster. Here, a pair of stars is called a binary system if the system is bound and the two stars are at the same time nearest neighbors. In this definition, a star that is part of a multiple system can be part of several “binary” systems simultaneously since two stars do not have to be mutually nearest neighbors. Hence triple or other higher order multiples are not handled separately by our diagnostic but are counted as multiple binary systems. In this study, we mostly use the normalized number of binary systems 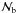 defined as
defined as 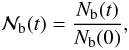 (1)where Nb(0) denotes the initial and Nb(t) the number of binary systems at time t within the cluster. The usual measure of binary populations in star clusters is the binary frequency bf
(1)where Nb(0) denotes the initial and Nb(t) the number of binary systems at time t within the cluster. The usual measure of binary populations in star clusters is the binary frequency bf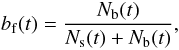 (2)where Ns(t) denotes the actual number of observed single stars and Nb(t) the actual number of binary systems. One major result of our work is that the normalized number of binary systems, Eq. (1), is the appropriate measure of a binary population.
(2)where Ns(t) denotes the actual number of observed single stars and Nb(t) the actual number of binary systems. One major result of our work is that the normalized number of binary systems, Eq. (1), is the appropriate measure of a binary population.
3. Method and cluster setup
Here the evolution of binary populations in young dense star clusters is studied using the parallized version nbody6++ of the high-accuracy N-body code nbody6 (Aarseth 2003; Spurzem 1999). The study presented can be understood as a follow up of Pfalzner & Olczak (2007). The main difference to Pfalzner & Olczak (2007) is that here the clusters contain a primordial binary population, with varying initial binary frequencies. In both studies, the ONC has been chosen as a model cluster because it is one of the most well-studied star forming regions for which many parameters are well constrained (see for example Prosser et al. 1994; Hillenbrand 1997; Hillenbrand & Hartmann 1998), in particular several surveys of its binary population (Petr et al. 1998; Preibisch et al. 1999; Köhler et al. 2006; Reipurth et al. 2007) exist. This allows a detailed comparison of the simulated binary populations with the observed ones.
Our simulations started with 4000 stellar systems, where stellar systems correspond to either single stars or binary systems. This means that for a simulation with a primordial binary frequency of 100% the dynamical evolution of 8000 stars is calculated. The masses M of the 4000 stellar systems were sampled from the initial mass function given by Kroupa (2002)![\begin{equation} \label{eq:kroupa-imf} \xi(M) = \begin{cases} \; M^{-1.3} \quad & \textrm{if} \quad 0.08 \leq M \left[ \Msun \right]< 0.5, \\ \; M^{-2.3} \quad & \textrm{if} \quad 0.5 \leq M \left[ \Msun \right]< 1.0, \\ \; M^{-2.3} \quad & \textrm{if} \quad 1.0 \leq M \left[ \Msun \right]< \infty. \end{cases} \end{equation}](/articles/aa/full_html/2011/04/aa15233-10/aa15233-10-eq19.png) (3)The minimum and maximum masses of the stellar systems have been chosen as Mmin = 0.08 M⊙, corresponding to the hydrogen-burning limit, and Mmax = 50 M⊙ the mass of the most massive stellar system in the ONC – θ1COri.
(3)The minimum and maximum masses of the stellar systems have been chosen as Mmin = 0.08 M⊙, corresponding to the hydrogen-burning limit, and Mmax = 50 M⊙ the mass of the most massive stellar system in the ONC – θ1COri.
Observations of the stellar content in the ONC have shown that the stellar radial density profile of the cluster can be approximated by an isothermal sphere (i.e. ρpresent ∝ 1/r2, see e.g. Jones & Walker 1988; Hillenbrand 1997) with the exception of the cluster core (Rcore ≈ 0.2pc), which has a much flatter density profile (ρpresent, core ∝ r-0.5, Scally et al. 2005). To account for this, we adopt an initial density profile of the form ![\begin{equation} \label{eq:initial_radial_density_profile} \rho_{0} (r) = \begin{cases} \rho_{0}\; (r/R_{\mathrm{core}} )^{-2.3},&\quad r\in (0,R_{\mathrm{core}}] \\ \rho_{0}\; (r/R_{\mathrm{core}} )^{-2.0},&\quad r\in (R_{\mathrm{core}}, R]\\ \qquad 0,& \quad r\in (R,\infty] \end{cases} \end{equation}](/articles/aa/full_html/2011/04/aa15233-10/aa15233-10-eq26.png) (4)where ρ0 = 3.1 × 103 pc-3, Rcore = 0.2 pc, and R = 2.9 pc. Olczak et al. (2010) demonstrated that this initial radial density profile evolves towards the currently observed one after about 1 Myr of dynamical evolution, the estimated age of the ONC (Hillenbrand 1997).
(4)where ρ0 = 3.1 × 103 pc-3, Rcore = 0.2 pc, and R = 2.9 pc. Olczak et al. (2010) demonstrated that this initial radial density profile evolves towards the currently observed one after about 1 Myr of dynamical evolution, the estimated age of the ONC (Hillenbrand 1997).
Observations of the ONC indicate that the cluster are mass-segregated (e.g. Hillenbrand 1997). Numerical simulations by Bonnell & Davies (1998) comparable to the cluster models studied here demonstrated that this mass segregation cannot be due to dynamical evolution of the cluster and therefore must be primordial. Following their suggestion, we initially place the most massive stellar system at the cluster centre and the three next most massive stars at random positions within a sphere of radius R = 0.6 Rhm centred on the cluster centre, where Rhm is the half-mass radius of the cluster.
The velocities of the stellar systems are sampled from a Maxwellian velocity distribution in virial equilibrium. The resulting velocity dispersion of our model is lower than the observational value (σ = 4.3 ± 0.5 km s-1: Jones & Walker 1988). However, because of significant mass of the molecular cloud associated with the ONC that was neglected in our numerical model, the observed velocity dispersion is consistent without any assumption about a stellar system in dynamical equilibrium. In future investigations of the binary populations, we plan to include the effect of the gas associated with the cluster.
For the primordial binary population, we chose the model described in Kouwenhoven et al. (2007). They compared observations of the Scorpius OB II association with simulated observations of their binary population model to eliminate observational selection effects and biases that affect real observations of star clusters. Their analysis shows that the binary frequency in Scorpius OB II is above 70% with a confidence of 3σ. The closest agreement with observations is obtained for models with a binary frequency of 100%. The model of Kouwenhoven et al. (2007) was chosen here since it is a well-studied binary population, close to its initial conditions. Scorpius OB II is a relatively young (about 5−20 Myr) and probably too sparse region to have undergone significant dynamical evolution.
In contrast to the field population that exhibits a log-normal period distribution of G and M-dwarf binaries (Duquennoy & Mayor 1991; Reid & Gizis 1997), the younger population in Sco OB II has a flat distribution of the semi-major axis in logarithmic space (Kouwenhoven et al. 2007) 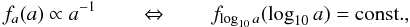 (5)where a is the semi-major axis of the binary system.
(5)where a is the semi-major axis of the binary system.
A flat distribution of the semi-major axes in logarithmic space corresponds to a similar distribution of periods P with the relation 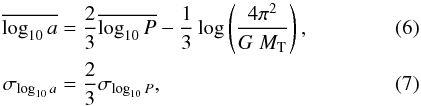 where G is the gravitational constant and MT the total mass of a binary system.
where G is the gravitational constant and MT the total mass of a binary system.
A flat binary period distribution has not only been observed in Sco OB II but also in other regions (e.g. Connelley et al. 2008; Reipurth et al. 2007) and has been used in several theoretical studies involving the evolution of primordial binary frequencies (Heggie & Aarseth 1992; Ivanova et al. 2005; Hurley et al. 2007).
 |
Fig. 1 Initial semi-major axis distribution for all simulated clusters. Crosses, stars, open and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
In addition to a log-uniform shape of the initial period distribution, other distributions have been used in numerical studies of the dynamical evolution of binary populations. For example, Kroupa (1995a) demonstrated that a dynamically evolved period distribution that is initially rising for short periods and nearly constant for long periods matches the observed period distribution of the field G-type dwarfs (Duquennoy & Mayor 1991). In contrast, this cannot be achieved with an initially log-uniform period distribution because of the much larger number of dynamically stable short-period binaries. However, physical processes that were not taken into account by Kroupa (1995a) could significantly lower the number of short period binaries. For example “the orbital decay of embedded binary stars” (Stahler 2010; Kroupa 1995b) is capable of reshaping a log-uniform binary period distribution within less than 1 Myr towards a log-normal distribution (Hövel et al., in prep.). Consequently, as the effect of different initial period distributions on the evolution of the binary population in star clusters is basically unknown we will explicitly focus on this topic in a future investigation. In this context the present study can be understood as preparatory work.
Figure 1 shows the initial semi-major axis distribution of our simulations. Although the semi-major axis distributions have been set up log-uniformly in the range 4.6 × 10-2 AU−4.6 × 104 AU, the distribution is only flat up to about 2 × 103 AU and declines afterwards to zero. The apparent lack of wide binary systems in the 2 × 103−4.6 × 104 AU range is due to the generating algorithm. In the code, binary systems are formed in isolation and then placed in the cluster environment. The wider a binary, the higher the probability that (at least) one of its components has a closer neighbour among the other cluster members. According to our definitions (see Sect. 2), this chance neighbour is now the potential companion and most probably not bound.
Kouwenhoven et al. (2007) also found the mass ratio distribution to have the form  (8)where q = Msec/Mprim is the mass-ratio of a binary with primary mass Mprim and secondary mass Msec. Adopting this functional form in our models, the binary system masses were sampled from the Kroupa (2002) IMF and then divided using Eq. (8). This approach, however, does not reproduce the observed stellar IMF as can be seen in Fig. 2 (thin lines), which displays the stellar IMFs produced in our simulations (filled squares, representing simulation with initially 100% binaries). For comparison, the standard IMF was included by setting up simulations using random pairing of the binary components instead of using Eq. (8) to pair the binary components. Random pairing has been shown to reproduce the stellar IMF (Leinert et al. 1993) and is here therefore used to represent the standard IMF. Using Eq. (8) to pair the binary components generates too few low-mass stars in the range 0.08−0.16 M⊙ and too many intermediate mass stars in the mass range 0.15−0.5 M⊙, where the deviations become larger the higher the initial binary frequency is. The number of stars generated with masses exceeding 0.5 M⊙ reproduces the Kroupa (2002) IMF quite well, although their numbers are slightly under-predicted.
(8)where q = Msec/Mprim is the mass-ratio of a binary with primary mass Mprim and secondary mass Msec. Adopting this functional form in our models, the binary system masses were sampled from the Kroupa (2002) IMF and then divided using Eq. (8). This approach, however, does not reproduce the observed stellar IMF as can be seen in Fig. 2 (thin lines), which displays the stellar IMFs produced in our simulations (filled squares, representing simulation with initially 100% binaries). For comparison, the standard IMF was included by setting up simulations using random pairing of the binary components instead of using Eq. (8) to pair the binary components. Random pairing has been shown to reproduce the stellar IMF (Leinert et al. 1993) and is here therefore used to represent the standard IMF. Using Eq. (8) to pair the binary components generates too few low-mass stars in the range 0.08−0.16 M⊙ and too many intermediate mass stars in the mass range 0.15−0.5 M⊙, where the deviations become larger the higher the initial binary frequency is. The number of stars generated with masses exceeding 0.5 M⊙ reproduces the Kroupa (2002) IMF quite well, although their numbers are slightly under-predicted.
The thick lines in Fig. 2 show the initial binary-system mass (mHy′s = Mprim + Msec) functions for the simulations used in this study and additionally the initial binary-system mass function if the binary components are drawn randomly from the stellar IMF. The binary system mass function in both cases is very similar. We do not expect the differences in the single-star IMFs to affect the evolution of the binary populations because it depends on the system masses as we show in Sect. 4.
 |
Fig. 2 Comparison of the stellar initial mass function (thin lines) and the initial binary-system mass function (thick lines). The open circles denote simulations that used random pairing to pair the binary components while the solid squares denotes simulations that used Eq. (8). |
The eccentricity of the binary systems in Sco OBII was found by Kouwenhoven et al. (2007) to be thermally distributed, in agreement with the eccentricities of long period binaries in the field. Following Kroupa & Burkert (2001) who illustrated that the dynamical evolution is not capable of changing the eccentricity distribution significantly, a thermal period distribution was applied to all of our simulations.
Observations show that the binary frequency varies among low-mass stars in the field (35–42%) (Fischer & Marcy 1992; Reid & Gizis 1997), Sun-like stars in the solar neighbourhood (~60%) (Duquennoy & Mayor 1991), and the high binary frequency in low-mass star-forming regions such as Taurus (~100%) (Duchêne 1999). We account for the large spread among the different environments by investigating cluster models initially with 30%, 50%, 75%, and 100% binary frequency.
To improve the statistical significance of our results, for each initial binary frequency 100 simulations were performed. Only those that fulfilled the following conditions were considered in the subsequent diagnostic process:
-
after 1 Myr of cluster evolution, the most massive stellar system in the simulations has to be within 1pc of the cluster centre.
-
the cluster density profile after 1 Myr of cluster evolution has to agree with the cluster density profiles observed by Hillenbrand (1997) and McCaughrean et al. (2002).
4. Results
Observations of binary populations in different environments usually use the binary frequency as the main observable of a binary population since it can easily be compared between different environments and different observing campaigns. Theoretical studies of the evolution of binary populations are unaffected by from this shortcoming but usually also use this simple observable for reasons of comparison with observational data (see for example Kroupa 1995a; Kroupa et al. 2001; Kroupa & Bouvier 2003; Ivanova et al. 2005; Hurley et al. 2007; Sollima 2008). If we also do this here, we obtain the result described by Fig. 3a. It shows the evolution of the normalized binary frequency during the first three Myr of cluster evolution in the simulations. The normalization is performed by dividing the given binary frequencies by the initial binary frequency and allows direct comparison of the evolution of the binary frequencies for simulations with different initial binary frequencies.
As expected from previous studies (Kroupa 1995a; Kroupa & Bouvier 2003; Parker et al. 2009), dynamical evolution reduces the binary frequency with time in all simulations. This can be explained by the destruction of wide binary systems by means of three body encounters (see Kroupa 1995a,b, for more details). Apart from this general trend, Fig. 3a shows that the evolution of the binary population depends on the initial binary frequency in the sense that the higher the initial binary frequency, the higher the fraction of binaries that are destroyed during cluster evolution. This finding could lead to the conclusion that the evolution of binary populations is stronger in clusters with a higher initial binary frequency. An analogous dependence was found by Sollima (2008), who investigated the evolution of the binary population in globular star clusters using an analytical approach.
 |
Fig. 3 Evolution of the normalized binary frequency, normalized number of binary systems and normalized number of single stars with time. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
In short, the evolution of the binary population in star clusters seems to depend on the initial binary frequency. However, because the calculation of the binary frequency depends on the number of single stars (see Eq. (2)) it is probably not an unbiased measure of the evolution of the binary population. We thus introduce the normalized number of binary systems 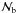 (see Eq. (1)) as the proper quantity and show its evolution in Fig. 3b.
(see Eq. (1)) as the proper quantity and show its evolution in Fig. 3b.
As expected from Fig. 3a, the normalized number of binaries also decreases with time. However, in contrast to the normalized binary frequency the evolution of the normalized number of binary systems with time does not depend on the initial binary frequency. The difference among the data of only 1% is of the order of the statistical error in the simulation. How can this difference in the evolution of the binary frequency and the binary population be explained? It is the evolution of the single star population in the star clusters that significantly affects the evolution of the binary frequency. Its evolution is show in Fig. 3c.
In contrast to the binary frequency and the number of binaries, the number of single stars in the star cluster obviously increases with time because the dissolution of a binary system creates two new single stars. The evolution of the normalized number of single stars, however, depends even more strongly on the initial binary frequency than the evolution of the binary frequency.
We show by means of simple arithmetic why the evolution of the single star population depends on the initial binary frequency while the evolution of the binary population does not. First, we assume that the evolution of the number of binary systems can be described by a function α(t,bf,... ) that may depend on the time of evolution, initial binary frequency, and other parameters, so that Nb(t) = α(t,bf,... )Nb(0), where Nb(t) is the number of binary systems at time t. Dividing this by the initial number of binary systems we obtain the evolution of the normalized number of binary systems 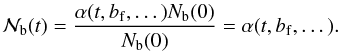 (9)If we also assume, based on the findings of Fig. 3b, that the evolution of the normalized number of binary systems does not depend on the initial binary frequency, the function α can be expressed as α(t,bf,...) ≈ α(t). Because the dissolution of a binary system leads to the generation of two new single stars, the evolution of the number of single stars can be written as
(9)If we also assume, based on the findings of Fig. 3b, that the evolution of the normalized number of binary systems does not depend on the initial binary frequency, the function α can be expressed as α(t,bf,...) ≈ α(t). Because the dissolution of a binary system leads to the generation of two new single stars, the evolution of the number of single stars can be written as ![\begin{equation} \label{eq:evolution_number_of_single_stars} \Nsing (t) = \Nsing (0) + 2\left[ 1-\alpha (t,\binaryfrequency,\dots) \right] \Nbin (0), \end{equation}](/articles/aa/full_html/2011/04/aa15233-10/aa15233-10-eq64.png) (10)where the first summand represents the initial number of single stars and the second summand gives the number of newly formed single stars. Applying the relation
(10)where the first summand represents the initial number of single stars and the second summand gives the number of newly formed single stars. Applying the relation 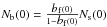 and dividing by the initial number of single stars Ns(0), we find that the evolution of the normalized number of binary systems is given by
and dividing by the initial number of single stars Ns(0), we find that the evolution of the normalized number of binary systems is given by 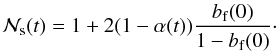 (11)Hence, in contrast to the normalized number of binary systems (Eq. (9)), which depends only on α, the normalized number of single stars depends explicitly on the initial binary frequency in the cluster. Consequently, using Eqs. (9) and (11), we derive an analogous dependence for the normalized binary frequency
(11)Hence, in contrast to the normalized number of binary systems (Eq. (9)), which depends only on α, the normalized number of single stars depends explicitly on the initial binary frequency in the cluster. Consequently, using Eqs. (9) and (11), we derive an analogous dependence for the normalized binary frequency 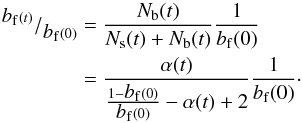 (12)In summary, our simple model (Eqs. (9)–(12)) describes the evolution presented in Fig. 3 very well: it is the evolution of the single star population that is very sensitive to the initial binary frequency, while the binary population evolves independently of the initial binary frequency. The normalized number of binary systems (Eq. (1)) introduced here is therefore the most simple measure of the evolution of a binary population independent of the initial binary frequency.
(12)In summary, our simple model (Eqs. (9)–(12)) describes the evolution presented in Fig. 3 very well: it is the evolution of the single star population that is very sensitive to the initial binary frequency, while the binary population evolves independently of the initial binary frequency. The normalized number of binary systems (Eq. (1)) introduced here is therefore the most simple measure of the evolution of a binary population independent of the initial binary frequency.
As a consequence, we can use Eq. (12) to calculate the initial binary frequency in young ONC-like star clusters from only a few observables. Solving Eq. (12) for bf(0) reveals that 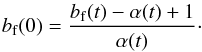 (13)This finding has a fundamental consequence: if we are able to determine the explicit form of the function α(t,bf,... ), we are able to predict the past and future number of binary systems from the present number of binaries in any cluster environment. If we again assume that α(t,bf,... ) = α(t), we find that αfit(t) = atb + ct + 1 with a = −0.35 ± 0.04,b = 0.89 ± 0.01, and c = 0.27 ± 0.04, provides an excellent fit to the data in Fig. 3b. However, we emphasize that our assumptions neglects the potential effects of other parameters such as the stellar density or distribution of binding energy, which will be investigated in a forthcoming paper.
(13)This finding has a fundamental consequence: if we are able to determine the explicit form of the function α(t,bf,... ), we are able to predict the past and future number of binary systems from the present number of binaries in any cluster environment. If we again assume that α(t,bf,... ) = α(t), we find that αfit(t) = atb + ct + 1 with a = −0.35 ± 0.04,b = 0.89 ± 0.01, and c = 0.27 ± 0.04, provides an excellent fit to the data in Fig. 3b. However, we emphasize that our assumptions neglects the potential effects of other parameters such as the stellar density or distribution of binding energy, which will be investigated in a forthcoming paper.
Nonetheless, for illustrative purposes we assume that the ONC has cluster age of 1 Myr Hillenbrand (1997) and obtain α(1 Myr) = 0.92 using the given fit. Assuming a present-day binary frequency of 60%, motivated by observations that find a consistency between the binary populations of field G dwarfs (Duquennoy & Mayor 1991) and the ONC (Petr et al. 1998; Köhler et al. 2006), we derive an initial binary frequency of 74%. This is clearly below the binary frequency observed in young sparse star-forming regions as Taurus-Auriga (Leinert et al. 1993; Ghez et al. 1993) and suggests that the initial binary frequency depends on the star-forming environment as stated by Durisen & Sterzik (1994).
 |
Fig. 4 Fraction of binary systems per semi-major axis bin that is destroyed after 1 Myr of cluster evolution. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
We note that this result is based on our specific cluster model, which does not include all the physical processes present in real star clusters. Thus, further investigations may alter the determined initial binary frequency to some extent. For example, including the gas the young clusters are embedded in would probably require a higher initial density since star clusters expand significantly after gas expulsion (e.g. Baumgardt & Kroupa 2007). Higher densities should increase the fraction of dynamically destroyed binary systems during cluster evolution, resulting in larger values of α. This means that the ONC could have been born with a higher initial binary frequency than estimated from our current simulations (as demonstrated by Kroupa et al. 2001).
We next use our homogeneous data set to investigate why the binary population evolves independently of the initial binary frequency. Figure 4 shows the fraction of binary systems per semi-major axis bin that is destroyed after 1 Myr of cluster evolution. It is evident that only binaries with semi-major axis wider than about ≈30 AU are destroyed during cluster evolution. This dependence on the semi-major axis was previously reported in other studies of the evolution of binary populations (e.g. Kroupa 1995b) and can be explained by the outcome of three body encounters (for details see Heggie 1975a): to dissolve a binary system in a three body interaction, the kinetic energy of the intruding star must exceed the binding energy of the binary system, or, in other words, the velocity of the intruder must be larger than the orbital velocity of the binary system. With this, we estimate a lower limit to the semi-major axis of destroyed binaries in the cluster. Following Kroupa & Bouvier (2003), we estimate the “thermal period” log 10Pth ≈ 4.75 at which destruction still is possible from 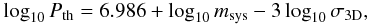 (14)using the least massive equal-mass system msys = 0.16 M⊙ and assuming a typical relative velocity equal to the cluster velocity dispersion in our simulations σ3D ≈ 3 km s-1. Our result, log 10Pth ≈ 4.75d, corresponds to a minimum semi-major axis of about 53 AU.
(14)using the least massive equal-mass system msys = 0.16 M⊙ and assuming a typical relative velocity equal to the cluster velocity dispersion in our simulations σ3D ≈ 3 km s-1. Our result, log 10Pth ≈ 4.75d, corresponds to a minimum semi-major axis of about 53 AU.
This estimate is in good agreement with the results of our simulations in Fig. 4. However, in our simulations, there is no sharp transition between stable and destroyed systems because the thermal period Pth depends strongly on the system mass (Eq. (14)). Since the periods of the binaries in the simulations have been sampled independently of the binary system masses the fraction of binaries destroyed by the dynamical evolution of the cluster decreases with binary mass. This is demonstrated in Fig. 5. The fraction of destroyed binaries clearly decreases with binary mass.
The solid line in Fig. 5 represents a fit of the function f(msys) = alog 10msys + b to the data of the simulations with initially 75% binaries in the range from msys = 0.16 M⊙ up to 10 M⊙. For higher masses, the results suffer from low number statistics and have therefore been excluded from the fit. We note that f(msys) also fits the data of the other simulations demonstrating that the evolution of the binary population is independent of the initial binary frequency.
 |
Fig. 5 Fraction of binaries per binary system mass bin that are destroyed after 1 Myr of cluster evolution. The solid line is the fit of the function f(msys) = alog 10msys + b to the data with initially 75% binaries. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
The strong mass dependence of the binary destruction is further illustrated in Fig. 6a. It shows the evolution of the normalized number of binaries with primary masses either exceeding 2 M⊙ (thin lines) and lower than 2 M⊙ (thick lines) in clusters with various initial binary frequencies. Clearly, a larger fraction of low-mass binaries is destroyed during the dynamical evolution of the cluster.
The boundary of 2 M⊙ between high and low-mass primaries was chosen in accordance with the study of Köhler et al. (2006), who performed a high spatial resolution infrared study of the binary population in the ONC. They found the frequency of binaries with high-mass primaries to be significantly higher. Figure 6a implies that this finding can be explained by the dynamical evolution of the cluster and does not depend on the initial binary frequency.
 |
Fig. 6 Panel a) evolution of the normalized number of binary systems with primary masses exceeding 2 M⊙ (thin lines) and binaries with masses below 2 M⊙ (thick lines) with time. Panel b) evolution of the normalized binary frequencies of binaries with high- (thin lines) and low-mass (thick lines) primaries with time. Panel c) evolution of the difference of the binary frequency of high- and low-mass stars with time. The difference at each time-step has been reduced by the initial difference of the binary frequencies to improve the readability. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
However, a consistent comparison of our simulation and the observations by Köhler et al. (2006) must focus on the frequency and not the number of binaries. Figure 6b shows the evolution of the frequency of binaries with high and low-mass primaries using the same symbols as in Fig. 6a. Clearly the binary frequencies of the high and low-mass primaries evolve quite differently. The former decreases much more slowly with time than the latter and does not depend on the initial binary frequency. In contrast, the evolution of binaries with low-mass primaries does depend on the initial binary frequency.
The differences in the evolution are explained by two mechanisms. First, binaries with low-mass primaries are preferentially destroyed by dynamical interactions in the cluster because of their lower binding energy (Fig. 6a). Secondly, the destruction of a binary by a high-mass primary can result in the generation of two new single high-mass stars or a high and a low-mass star. The latter possibility means that the number of single low-mass stars increases, hence the frequency of binaries with low-mass primaries decreases relative to the former case. Simultaneously, the frequency of binaries with a high-mass primary does not decrease as fast as implied by Eq. (12) because of the smaller increase in the number of single high-mass stars. Hence, the possible generation of a high- and a low-mass star in the destruction of a binary with a high-mass primary accelerates the reduction of the binary frequency of low-mass stars and decelerates the reduction of the binary frequency of high-mass stars.
We emphasize the different evolution of binaries with high and low-mass primaries in Fig. 6c. Here we show the difference between the binary frequencies of high and low mass stars over time, Δhlbf(t), relative to its initial value Δhl(t). This normalization accounts for the possible initial difference of the binary frequencies of high and low-mass stars, so that all values are zero initially.
In all simulations, the difference of the binary frequency of high and low-mass stars increases with time because the binary frequency of low-mass stars decreases faster than the binary frequency of high-mass stars (Fig. 6b). However, the amount of increase depends strongly on the initial binary frequency in the cluster with the lowest initial binary frequency (30%) resulting in the smallest increase of less than 2% after 3 Myr while in simulations with the maximum initial binary frequency (100%) the difference increases by more than 10%. Under the assumption that initially the frequency of binaries with low- and high-mass stars was the same in the ONC, the observational data from Köhler et al. (2006) imply that the binary frequency in the ONC initially was very high with values well above 75%. If the initial binary frequencies were lower initially the observed difference must have been part of the initial conditions of the binary population.
5. Conclusions
We have studied the dynamical evolution of the binary population in young dense ONC-like star-clusters using two different measures: the (normalized) binary frequency (Eq. (2)) and the normalized number of binary systems (Eq. (1)). As expected, the evolution of the binary frequency depends heavily on the initial binary frequency: the higher the initial binary frequency in a cluster, the stronger the decrease in the binary frequency during cluster evolution. However, our main result is that the evolution of the normalized number of binaries is independent of the initial binary frequency. During the first Myr of cluster evolution, the number of binary systems decreases by about 6–9% independent of the initial binary frequency in the clusters.
The reason for this discrepancy between the two measures is the dependence of the binary frequency on the population of single stars. Since the destruction of a binary system leads to the generation of two new single stars, the single star population can easily dominate the evolution of the binary frequency in a cluster, especially in the case of high initial binary frequencies (Eq. (12)). Hence, the number of binaries – unbiased by the evolution of the single star population – represents the proper measure of the evolution ofthe binary population. We can therefore conclude that the evolution of the binary population in ONC-like stars clusters is independent of the initial binary frequency, which is in striking contrast to what would be inferred from the evolution of the binary frequency.
This independence of the number of binaries has allowed us to determine the initial binary frequency and predict the evolution of the binary population in young ONC-like stars clusters from present-day observational data. For example, taking the observed binary frequency of the ONC of ~60% and its age of 1 Myr (Petr et al. 1998; Hillenbrand 1997), and estimating α(1 Myr) = 0.92 from our fit to the simulations, Eq. (13) provides an initial binary frequency of 74%. This binary frequency is significantly lower than the binary frequency observed in sparse star-forming regions such as Taurus-Auriga (e.g. Leinert et al. 1993; Ghez et al. 1993) and implies that the initial binary frequency depends on the star-forming region. This finding agrees well with the results of Durisen & Sterzik (1994), who claimed that the primordial binary frequency in star-forming regions depends on the temperature of the natal molecular cloud in which the stars are forming of. However, different initial conditions of the clusters (e.g. higher initial stellar densities) could possibly increase the amount of destroyed binary systems, which would further increase the estimated initial binary frequency (Kroupa et al. 2001). It is not trivial to quantify these effects, so further numerical studies are required.
In addition, our simulations show that the evolution of the binary populations depends crucially on the masses of the primary stars: the lower the mass of the primary, the more likely that the binaries are destroyed. Over time, this leads to a higher binary frequency for stars with masses exceeding 2 M⊙ than for lower mass stars. This is even so in the case where the binary frequencies of high and low-mass stars were initially the same. This finding is in good agreement with the observations of Köhler et al. (2006), who found a significantly higher binary frequency for high-mass stars than for low-mass stars in the ONC. Our results suggest that the difference in the binary frequencies of high- and low-mass stars are probably not the outcome of the binary formation process but rather the result of the dynamical evolution with time. A possible test of this hypothesis would be to compare the maxima of the period/semi-major axis distributions of high- and low-mass stars in young dense star clusters. Since the probability of destroying a binary in a three body encounter depends on the binding energy and therewith on the separation and mass of the binary, the maximum of the period and semi-major-axis distributions for massive stars should be at longer periods and wider semi-major axis than for lower mass stars. However, this test is not easy to be carried out since observations of the binary population in young dense star clusters usually only cover a small range of periods/separations of the binaries, and it is often not even possible to determine the physical orbital parameters based on the observations.
The simulations presented here were performed for ONC-like clusters only and used the specific binary population model of Kouwenhoven et al. (2007). We aim to generalise the present results by performing simulations with different cluster and binary population models for an forthcoming paper.
Acknowledgments
Simulations were performed at the Jülich Supercomputer Centre, Research Centre Jülich, Project HKU14.
References
- Aarseth, S. J. 1971, Ap&SS, 13, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Aarseth, S. J. 2003, Gravitational N-Body Simulations, ed. S. J. Aarseth [Google Scholar]
- Aarseth, S. J., & Zare, K. 1974, Celestial Mechanics, 10, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., & Kroupa, P. 2007, MNRAS, 380, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, T. L., Simon, M., & Close, L. M. 2003, ApJ, 583, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I. A., & Davies, M. B. 1998, MNRAS, 295, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Connelley, M. S., Reipurth, B., & Tokunaga, A. T. 2008, AJ, 135, 2526 [NASA ADS] [CrossRef] [Google Scholar]
- Duchêne, G. 1999, A&A, 341, 547 [NASA ADS] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Durisen, R. H., & Sterzik, M. F. 1994, A&A, 286, 84 [NASA ADS] [Google Scholar]
- Fischer, D. A., & Marcy, G. W. 1992, ApJ, 396, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Neugebauer, G., & Matthews, K. 1993, AJ, 106, 2005 [Google Scholar]
- Heggie, D. C. 1975a, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Heggie, D. C. 1975b, in Dynamics of the Solar Systems, ed. A. Hayli, IAU Symp., 69, 73 [Google Scholar]
- Heggie, D. C., & Aarseth, S. J. 1992, MNRAS, 257, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A. 1997, AJ, 113, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., & Hartmann, L. W. 1998, ApJ, 492, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Hills, J. G. 1975, AJ, 80, 809 [Google Scholar]
- Hurley, J. R., Aarseth, S. J., & Shara, M. M. 2007, ApJ, 665, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Belczynski, K., Fregeau, J. M., & Rasio, F. A. 2005, MNRAS, 358, 572 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jones, B. F., & Walker, M. F. 1988, AJ, 95, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Köhler, R., Petr-Gotzens, M. G., McCaughrean, M. J., et al. 2006, A&A, 458, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 1995a, MNRAS, 277, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 1995b, MNRAS, 277, 1507 [NASA ADS] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kroupa, P., & Bouvier, J. 2003, MNRAS, 346, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Burkert, A. 2001, ApJ, 555, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Petr, M. G., & McCaughrean, M. J. 1999, New Astron., 4, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Leigh, N., & Sills, A. 2010, MNRAS, 1645 [Google Scholar]
- Leinert, C., Zinnecker, H., Weitzel, N., et al. 1993, A&A, 278, 129 [NASA ADS] [Google Scholar]
- Marchal, L., Delfosse, X., Forveille, T., et al. 2003, in Brown Dwarfs, ed. E. Martín, IAU Symp., 211, 311 [Google Scholar]
- McCaughrean, M., Zinnecker, H., Andersen, M., Meeus, G., & Lodieu, N. 2002, The Messenger, 109, 28 [NASA ADS] [Google Scholar]
- Mikkola, S., & Aarseth, S. J. 1993, Celestial Mechanics and Dynamical Astronomy, 57, 439 [Google Scholar]
- Olczak, C., Pfalzner, S., & Eckart, A. 2010, A&A, 509, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, R. J., Goodwin, S. P., Kroupa, P., & Kouwenhoven, M. B. N. 2009, MNRAS, 397, 1577 [NASA ADS] [CrossRef] [Google Scholar]
- Petr, M. G., Coudé du Foresto, V., Beckwith, S. V. W., Richichi, A., & McCaughrean, M. J. 1998, ApJ, 500, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S. 2009, A&A, 498, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pfalzner, S., & Olczak, C. 2007, A&A, 475, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., Balega, Y., Hofmann, K., Weigelt, G., & Zinnecker, H. 1999, New A, 4, 531 [Google Scholar]
- Preibisch, T., Brown, A. G. A., Bridges, T., Guenther, E., & Zinnecker, H. 2002, AJ, 124, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Prosser, C. F., Stauffer, J. R., Hartmann, L., et al. 1994, ApJ, 421, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, I. N., & Gizis, J. E. 1997, AJ, 113, 2246 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., Guimarães, M. M., Connelley, M. S., & Bally, J. 2007, AJ, 134, 2272 [NASA ADS] [CrossRef] [Google Scholar]
- Scally, A., Clarke, C., & McCaughrean, M. J. 2005, MNRAS, 358, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Sollima, A. 2008, MNRAS, 388, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Spurzem, R. 1999, J. Comput. Appl. Math., 109, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Stahler, S. W. 2010, MNRAS, 402, 1758 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Initial semi-major axis distribution for all simulated clusters. Crosses, stars, open and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
| In the text | |
 |
Fig. 2 Comparison of the stellar initial mass function (thin lines) and the initial binary-system mass function (thick lines). The open circles denote simulations that used random pairing to pair the binary components while the solid squares denotes simulations that used Eq. (8). |
| In the text | |
 |
Fig. 3 Evolution of the normalized binary frequency, normalized number of binary systems and normalized number of single stars with time. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
| In the text | |
 |
Fig. 4 Fraction of binary systems per semi-major axis bin that is destroyed after 1 Myr of cluster evolution. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
| In the text | |
 |
Fig. 5 Fraction of binaries per binary system mass bin that are destroyed after 1 Myr of cluster evolution. The solid line is the fit of the function f(msys) = alog 10msys + b to the data with initially 75% binaries. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
| In the text | |
 |
Fig. 6 Panel a) evolution of the normalized number of binary systems with primary masses exceeding 2 M⊙ (thin lines) and binaries with masses below 2 M⊙ (thick lines) with time. Panel b) evolution of the normalized binary frequencies of binaries with high- (thin lines) and low-mass (thick lines) primaries with time. Panel c) evolution of the difference of the binary frequency of high- and low-mass stars with time. The difference at each time-step has been reduced by the initial difference of the binary frequencies to improve the readability. Crosses, stars, open, and filled squares denote simulations with initially 30%, 50%, 75%, and 100% binaries, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


