| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014501 | |
| Published online | 15 March 2011 | |
Magnetic flux generation and transport in cool stars⋆
1
Max-Planck-Institut für Sonnensystemforschung,
37191 Katlenburg-Lindau, Germany
e-mail: schmitt@mps.mpg.de; schuessler@mps.mpg.de
2
Department of Physics, Faculty of
Science & Letters, İstanbul Kültür University, Ataköy Campus, Bakırköy
34156
İstanbul,
Turkey
e-mail: e.isik@iku.edu.tr
Received: 25 March 2010
Accepted: 13 January 2011
Context. The Sun and other cool stars harbouring outer convection zones manifest magnetic activity in their atmospheres. The connection between this activity and the properties of a deep-seated dynamo generating the magnetic flux is not well understood.
Aims. By employing physical models, we study the spatial and temporal characteristics of the observable surface field for various stellar parameters.
Methods. We combine models for magnetic flux generation, buoyancy instability, and transport, which encompass the entire convection zone. The model components are: (i) a thin-layer αΩ dynamo at the base of the convection zone; (ii) buoyancy instabilities and the rise of flux tubes through the convection zone in 3D, which provides a physically consistent determination of emergence latitudes and tilt angles; and (iii) horizontal flux transport at the surface.
Results. For solar-type stars and rotation periods longer than about 10 days, the latitudinal dynamo waves generated by the deep-seated αΩ dynamo are faithfully reflected by the surface distribution of magnetic flux. For rotation periods of the order of two days, however, Coriolis acceleration of rising flux loops leads to surface flux emergence at much higher latitudes than the dynamo waves at the bottom of the convection zone reach. A similar result is found for a K0V star with a rotation period of two days. In the case of a rapidly rotating K1 subgiant, overlapping dynamo waves lead to noisy activity cycles and mixed-polarity fields at high latitudes.
Conclusions. The combined model reproduces the basic observed features of the solar cycle. The differences between the latitude distributions of the magnetic field at the bottom of the convection zone and the emerging surface flux grow with increasing rotation rate and convection zone depth, becoming quite substantial for rapidly rotating dwarfs and subgiants. The dynamical evolution of buoyantly rising magnetic flux should be considered as an essential ingredient in stellar dynamo models.
Key words: Sun: activity / Sun: dynamo / stars: interiors / stars: late-type / stars: activity / stars: magnetic field
3 movies are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
It is commonly accepted that the large-scale magnetic field of the Sun is maintained by a hydromagnetic dynamo process, which operates in the convective envelope and leads to an oscillatory magnetic field with an average period of 11 years. Among the processes considered in the current theoretical context for the magnetic activity cycle (see reviews by Ossendrijver 2003; Charbonneau 2005; Fan 2009) are: (1) generation of toroidal magnetic field from poloidal field by differential rotation (Ω-effect); (2) formation and instabilities of toroidal magnetic flux tubes; (3) buoyant rise of toroidal magnetic flux; (4) generation of poloidal from toroidal magnetic field by helical convection or through twisting of rising flux loops by the Coriolis force (α-effect); and (5) transport of magnetic flux by meridional flow.
In rapidly rotating stars with outer convection zones, manifestations of magnetic activity are observed throughout the electromagnetic spectrum. Distribution and coverage of starspots can be quite different from the solar activity patterns (Strassmeier 2009): spots near the rotational poles, and high UV and X-ray fluxes indicative of a large surface coverage of magnetic regions. Observations of stellar magnetic activity provide constraints of stellar dynamo models (see e.g., Strassmeier 2005; Schüssler 2005; Berdyugina 2005). Hence, it is necessary to investigate the links between magnetic flux generation and transport, as well as the effects of stellar structure and rotation on the spatio-temporal distribution of the surface field.
It is often tacitly assumed that the latitudinal distribution of toroidal magnetic fields generated in stellar interiors can be taken to represent the surface emergence patterns. However, the correspondence between the latitudinal distribution of the dynamo-generated field and the emergence pattern is not self-evident, because (a) the stability properties of flux tubes at the bottom of the convection zone depend sensitively on field strength and their position in latitude (Ferriz-Mas & Schüssler 1993, 1995), and (b) rising flux tubes in a rotating star are deflected towards the poles, owing to angular momentum conservation (Choudhuri & Gilman 1987; Schüssler & Solanki 1992; Granzer et al. 2000).
Numerical simulations of the rise of flux tubes in the convection zone (e.g., D’Silva & Choudhuri 1993; Fan et al. 1994; Caligari et al. 1995, 1998) have successfully reproduced many observed properties of sunspot groups, among which the tilt angle (the angle between the line connecting the opposite polarity regions and the local latitudinal circle) is of particular importance for Babcock-Leighton-type dynamos (e.g., Dikpati & Charbonneau 1999). Here, we consider the connection between the dynamo mechanism operating in the stellar interior, the transport of toroidal magnetic flux through the convection zone, and the emerged flux evolving under the effects of near-surface flows. We combine models for three processes: (1) a dynamo operating in the overshoot layer at the bottom of the convection zone; (2) the magnetic buoyancy instability and rise of magnetic flux tubes through the convection zone; (3) the transport of magnetic flux at the surface. In this first exploratory study we have used a very simple one-dimensional dynamo model that yields the time-latitude characteristics of the solar cycle. A more complete two-dimensional dynamo model will be employed in a forthcoming study.
Preliminary results obtained with our combined model were presented by Işık et al. (2007a). In this paper, we give a detailed account of the model setup, discuss the effects of different rotation rates in Sun-like stars, and apply the model to a rapidly rotating K0-type main sequence star, and a K1-type subgiant star.
2. Dynamo model
We consider the generation of magnetic flux in the overshoot layer at the bottom of the convection zone (at radius r0 ≃ 0.73 R⊙). We assume a kinematic αΩ dynamo operating in a thin layer (Schmitt & Schüssler 1989). The model is based on the assumption that the radial diffusion of magnetic flux out of the layer is partly compensated by downward flux pumping by convective flows. This thin-layer αΩ dynamo exhibits magnetic cycles and latitudinal propagation of dynamo waves based upon a radial gradient of the rotational angular velocity. Differential rotation in latitude and meridional circulation, although probably relevant for the operation of solar/stellar dynamos cannot be consistently incorporated into this simple model. We chose to use this model as a simple means of obtaining solar-like time-latitude behaviour of the toroidal field at the bottom of the convection zone and to avoid overloading this exploratory study with the complications (and uncertain parameters) of a more complex model. These models can of course be incorporated into our model framework, as we intend to do in future studies.
2.1. Dynamo equations
We use spherical polar coordinates (r,θ,φ) and decompose the azimuthally averaged magnetic field, B, into a toroidal component, 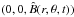 , and a poloidal component described by the vector potential, A = (0,0,Â(r,θ,t)), yielding
, and a poloidal component described by the vector potential, A = (0,0,Â(r,θ,t)), yielding 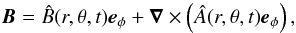 (1)where eφ is the unit vector in the azimuthal direction. Following Hoyng et al. (1994), the radial dependence of  and
(1)where eφ is the unit vector in the azimuthal direction. Following Hoyng et al. (1994), the radial dependence of  and 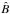 is assumed to have the form of a spherical wave
is assumed to have the form of a spherical wave 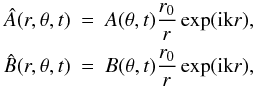 (2)reflecting flux loss from the thin dynamo layer at r = r0 by magnetic diffusion in the radial direction. The mean magnetic field at r = r0 as a function of the colatitude, θ, and time, t, is governed by the dynamo equations for A(θ,t) and B(θ,t), viz.
(2)reflecting flux loss from the thin dynamo layer at r = r0 by magnetic diffusion in the radial direction. The mean magnetic field at r = r0 as a function of the colatitude, θ, and time, t, is governed by the dynamo equations for A(θ,t) and B(θ,t), viz. ![\begin{eqnarray} \frac{\partial B}{\partial t} &=& \Omega^\prime(\theta)\frac{\partial}{\partial\theta}(A\sin\theta) +\frac{B_0}{\tau}f\left(B\over B_0\right) \nonumber \\ \label{eq:dyn-d-t} & & +\frac{\eta}{r_0^2}\left[\frac{1}{\sin\theta}\frac{\partial}{\partial\theta} \left(\sin\theta\frac{\partial B}{\partial\theta}\right)-\frac{B}{\sin^2\theta} -(kr_0)^2 B \right], \\ \label{eq:dyn-d-p} \frac{\partial A}{\partial t} &=& \alpha(\theta)B + \frac{\eta}{r_0^2}\left[\frac{1}{\sin\theta}\frac{\partial}{\partial\theta} \left(\sin\theta\frac{\partial A}{\partial\theta}\right)-\frac{A}{\sin^2\theta} -(kr_0)^2 A \right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq22.png) where η is the turbulent magnetic diffusivity, Ω′(θ) is the radial gradient of the angular velocity at r = r0, and α(θ) represents the α-effect. For the Sun, we take r0 = 5.07 × 1010 cm, which corresponds to the middle of the convective overshoot layer (according to the stratification model used in Sect. 3), and kr0 = 3, so that a quarter of the wavelength of the radial dependence of the magnetic field corresponds roughly to the thickness of the convection zone. The second term on the r.h.s. of Eq. (3) represents the buoyant loss of toroidal magnetic flux from the dynamo layer. The quantity B0 is the critical mean field strength, above which the flux is lost from the layer with a characteristic timescale τ, corresponding to the growth time of the magnetic buoyancy instability of toroidal flux tubes (Sect. 3.2). The value of B0 scales with the critical field strength for the instability (average value between 0° and 40° latitude), which depends on the given stellar model and rotation rate (see Figs. 5a, 7a, 9a, 10a, 12a). The nonlinear function f describes the B-dependence of the flux loss in the form
where η is the turbulent magnetic diffusivity, Ω′(θ) is the radial gradient of the angular velocity at r = r0, and α(θ) represents the α-effect. For the Sun, we take r0 = 5.07 × 1010 cm, which corresponds to the middle of the convective overshoot layer (according to the stratification model used in Sect. 3), and kr0 = 3, so that a quarter of the wavelength of the radial dependence of the magnetic field corresponds roughly to the thickness of the convection zone. The second term on the r.h.s. of Eq. (3) represents the buoyant loss of toroidal magnetic flux from the dynamo layer. The quantity B0 is the critical mean field strength, above which the flux is lost from the layer with a characteristic timescale τ, corresponding to the growth time of the magnetic buoyancy instability of toroidal flux tubes (Sect. 3.2). The value of B0 scales with the critical field strength for the instability (average value between 0° and 40° latitude), which depends on the given stellar model and rotation rate (see Figs. 5a, 7a, 9a, 10a, 12a). The nonlinear function f describes the B-dependence of the flux loss in the form 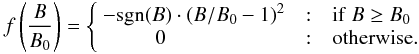 (5)We rewrite the dynamo equations in nondimensional form by taking r0 as our unit of length, the diffusion time,
(5)We rewrite the dynamo equations in nondimensional form by taking r0 as our unit of length, the diffusion time, 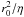 , as the unit of time, B0 as the unit field strength, α0 as the maximum absolute magnitude of the α-effect, and r0B0 as the unit of the vector potential. Using the same symbols as before, (A,B), for the nondimensional quantities, Eqs. (3) and (4) transform into
, as the unit of time, B0 as the unit field strength, α0 as the maximum absolute magnitude of the α-effect, and r0B0 as the unit of the vector potential. Using the same symbols as before, (A,B), for the nondimensional quantities, Eqs. (3) and (4) transform into 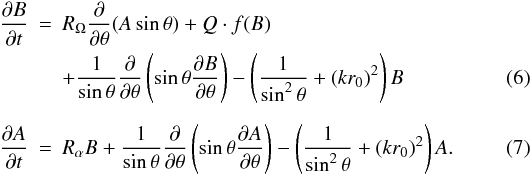 The induction effects are characterised by two dimensionless numbers, namely a Reynolds number for the α-effect
The induction effects are characterised by two dimensionless numbers, namely a Reynolds number for the α-effect 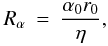 (8)which represents the efficacy of induction by the α-effect, and a Reynolds number for the radial shear (Ω-effect)
(8)which represents the efficacy of induction by the α-effect, and a Reynolds number for the radial shear (Ω-effect) 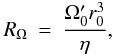 (9)which represents the efficacy of induction by the differential rotation. The dimensionless number Q, which determines the strength of the flux-loss nonlinearity is given by the ratio of the timescales for diffusion and flux loss
(9)which represents the efficacy of induction by the differential rotation. The dimensionless number Q, which determines the strength of the flux-loss nonlinearity is given by the ratio of the timescales for diffusion and flux loss 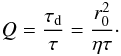 (10)In the dynamo model, we consider only one hemisphere and assume dipolar parity for the magnetic field, i.e., antisymmetry with respect to equatorial plane. The boundary conditions at the pole and at the equator are thus given by
(10)In the dynamo model, we consider only one hemisphere and assume dipolar parity for the magnetic field, i.e., antisymmetry with respect to equatorial plane. The boundary conditions at the pole and at the equator are thus given by 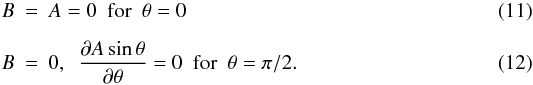 We set the turbulent diffusivity to η ≃ 2.96 × 1011 cm2 s-1. For the solar-type model, α0 ≃ − 11.7 cm s-1 leads to a magnetic cycle period of 22 years.
We set the turbulent diffusivity to η ≃ 2.96 × 1011 cm2 s-1. For the solar-type model, α0 ≃ − 11.7 cm s-1 leads to a magnetic cycle period of 22 years.
Equations (6), (7) with the boundary conditions Eqs. (11), (12) are numerically solved with an implicit finite-difference method (cf. Schmitt & Schüssler 1989) using 90 grid points in latitude.
2.2. Differential rotation and α-effect
The radial rotational shear in the dynamo layer, Ω′(θ) = dΩ(r,θ) / dr | r = r0, is taken in the form 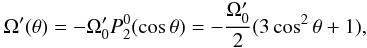 (13)where
(13)where 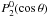 is the associated Legendre polynomial. Equation (13) with
is the associated Legendre polynomial. Equation (13) with 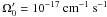 roughly represents the shear profile in the solar tachocline as determined by helioseismology (Schou et al. 1998).
roughly represents the shear profile in the solar tachocline as determined by helioseismology (Schou et al. 1998).
The latitudinal dependence of the α-effect is assumed as ![\begin{eqnarray} \alpha(\theta) = \left\{ \begin{array}{r@{\quad:\quad}l} \alpha_0\sin\left[ \pi \left(\theta-\theta_0\right)/\left(\pi/2-\theta_0\right)\right] & {\rm for}~\theta \geqslant \theta_0 \\ 0~~~~~~~~~~~~~~~~~~~~~~~ & {\rm for}~\theta < \theta_0, \end{array} \right. \label{eq:alpha} \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq54.png) (14)where α0 is the amplitude, and θ0 = 55°, which corresponds to the zero crossing of the function Ω′(θ). The functions α(θ) and Ω′ (θ), normalised to their amplitudes, are shown in Fig. 1. In order for the dynamo waves to propagate equatorward, one must have αΩ′ < 0. To fulfil this criterion, α0 has been chosen to be negative, because the sign of radial shear in the solar tachocline is positive for θ > 55°. The choice of Eq. (14) and the sign of α0 are motivated by the α-effect driven by magnetic flux tube instabilities (Ferriz-Mas et al. 1994) and unstable magnetostrophic waves (Schmitt 2003).
(14)where α0 is the amplitude, and θ0 = 55°, which corresponds to the zero crossing of the function Ω′(θ). The functions α(θ) and Ω′ (θ), normalised to their amplitudes, are shown in Fig. 1. In order for the dynamo waves to propagate equatorward, one must have αΩ′ < 0. To fulfil this criterion, α0 has been chosen to be negative, because the sign of radial shear in the solar tachocline is positive for θ > 55°. The choice of Eq. (14) and the sign of α0 are motivated by the α-effect driven by magnetic flux tube instabilities (Ferriz-Mas et al. 1994) and unstable magnetostrophic waves (Schmitt 2003).
3. Emergence of magnetic flux
We assume that (1) the toroidal magnetic field in the dynamo layer undergoes a magnetic Rayleigh-Taylor instability, which leads to the formation of magnetic flux tubes (Fan 2001, 2009); (2) the flux tubes reach a mechanical equilibrium state by developing an internal flow (Moreno-Insertis et al. 1992); and (3) their equilibrium location is at the middle of the overshoot region. The flux tubes become subject to the undulatory (Parker) instability once their field strength exceeds a critical value, Bcr, which is a function of latitude. We determine the linear stability properties following Ferriz-Mas & Schüssler (1995) and carry out numerical simulations of the nonlinear evolution of the unstable flux tubes and their rise towards the surface.
3.1. MHD equations for magnetic flux tubes
The equation of motion for the material inside a flux tube, in a reference frame rotating with the angular velocity of the tube, Ω, can be written as (Ferriz-Mas & Schüssler 1993) ![\begin{eqnarray} \rho_i\frac{{\rm D}{\vec\varv}_i}{{\rm D}t} &=& -\vec\nabla\Big(p_i+\frac{B^2}{8\pi}\Big) + \frac{({\vec B\cdot\vec\nabla}){\vec B}}{4\pi} \nonumber \\ & & + \rho_i\big[{\vec g - \vec\Omega\times(\vec\Omega\times \vec r)}\big] + 2\rho_i{\vec \varv}_i\times\vec{\Omega} + {\vec F}_{\rm D}, \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq60.png) (15)where D / Dt ≡ ∂ / ∂t + 3·∇ is the Lagrangian derivative. The subscript i denotes quantities inside the flux tube and, in the following, the subscript e denotes external quantities. The terms on the right hand side of the equation are, respectively, the total pressure force (gas and magnetic), magnetic tension force, effective gravity (including the centrifugal force), Coriolis force, and hydrodynamic drag force. For the drag force, we use the expression for a flow past a straight spherical cylinder,
(15)where D / Dt ≡ ∂ / ∂t + 3·∇ is the Lagrangian derivative. The subscript i denotes quantities inside the flux tube and, in the following, the subscript e denotes external quantities. The terms on the right hand side of the equation are, respectively, the total pressure force (gas and magnetic), magnetic tension force, effective gravity (including the centrifugal force), Coriolis force, and hydrodynamic drag force. For the drag force, we use the expression for a flow past a straight spherical cylinder, 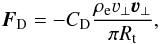 (16)where
(16)where 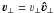 is the perpendicular component of the relative velocity of the tube with respect to the external medium,
is the perpendicular component of the relative velocity of the tube with respect to the external medium, 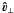 is the unit vector along 3 ⊥ , CD is the hydrodynamic drag coefficient which we take as unity (Batchelor 1967), ρe is the density of the external medium, and Rt is the cross-sectional radius of the tube.
is the unit vector along 3 ⊥ , CD is the hydrodynamic drag coefficient which we take as unity (Batchelor 1967), ρe is the density of the external medium, and Rt is the cross-sectional radius of the tube.
The combination of the equations for continuity and magnetic induction in ideal MHD leads to Walén’s equation 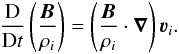 (17)For the energy equation, we assume that the mass elements of the flux tube evolve isentropically. This is justified because the timescale for heat exchange by radiation in the deep convection zone is much longer than the timescale of flux tube motions (Moreno-Insertis 1986). The system of equations is closed by the equation of state for an ideal gas and the condition of magnetic flux conservation.
(17)For the energy equation, we assume that the mass elements of the flux tube evolve isentropically. This is justified because the timescale for heat exchange by radiation in the deep convection zone is much longer than the timescale of flux tube motions (Moreno-Insertis 1986). The system of equations is closed by the equation of state for an ideal gas and the condition of magnetic flux conservation.
We consider the equations given above in the framework of the thin flux tube approximation (Spruit 1981), in the form given by Ferriz-Mas & Schüssler (1993).
3.2. The escape of magnetic flux tubes from the dynamo layer
Magnetic flux tubes leave the dynamo layer owing to the undulatory buoyancy instability, which sets in for B > Bcr and leads to flux loops rising through the convection zone. To determine the number, field strength, and latitude of unstable flux tubes, we assign a probability, p, for a flux loop to start rising at a given latitude and time.
 |
Fig. 1 Normalised latitudinal profiles of α and the radial shear Ω′. |
In the case of the Sun, we have Bcr ≃ 105 G in the middle of the convective overshoot layer (Schüssler et al. 1994). The corresponding magnetic energy density is about 100 times higher than the kinetic energy density of convective motions. We assume that the shear-generated mean toroidal field, B, is fragmented by the magnetic Rayleigh-Taylor instability into flux tubes of strength BFT, such that 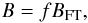 (18)where f is the filling factor of flux tubes contributing to the mean field. For BFT = 105 G and f = 0.1, we have B ≃ 104 G, which is of the order of the equipartition field strength, Beq = (4πρ)1 / 23c, where 3c is the convective velocity determined by using a mixing length model. The individual flux tubes are considered to be intensified to field strengths of the order of 105 G by a combination of rotational shear and the conversion of potential energy in the external stratification as suggested by Rempel & Schüssler (2001).
(18)where f is the filling factor of flux tubes contributing to the mean field. For BFT = 105 G and f = 0.1, we have B ≃ 104 G, which is of the order of the equipartition field strength, Beq = (4πρ)1 / 23c, where 3c is the convective velocity determined by using a mixing length model. The individual flux tubes are considered to be intensified to field strengths of the order of 105 G by a combination of rotational shear and the conversion of potential energy in the external stratification as suggested by Rempel & Schüssler (2001).
Latitudes and number of erupting flux tubes
We assume the emergence rate of flux tubes to be proportional to the mean toroidal field given by the dynamo model, 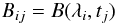 (19)for a given latitude, λi, and time, tj, which are discretised into time intervals, Δt = tj + 1 − tj, and latitude intervals, Δλ = λi + 1 − λi, with λ = π / 2 − θ and
(19)for a given latitude, λi, and time, tj, which are discretised into time intervals, Δt = tj + 1 − tj, and latitude intervals, Δλ = λi + 1 − λi, with λ = π / 2 − θ and 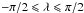 . The probability of a flux tube at λi and tj to start rising is assumed to be proportional to the local mean field, so that we have
. The probability of a flux tube at λi and tj to start rising is assumed to be proportional to the local mean field, so that we have 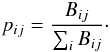 (20)We denote the number of flux tubes emerging at time tj with nj. To determine the initial latitudes of flux tubes at the bottom of the convection zone, nj pseudo-random numbers taken from a uniform distribution in the interval [ 0,1 ] are mapped via the cumulative probability distribution function (PDF), Qij, based on pij:
(20)We denote the number of flux tubes emerging at time tj with nj. To determine the initial latitudes of flux tubes at the bottom of the convection zone, nj pseudo-random numbers taken from a uniform distribution in the interval [ 0,1 ] are mapped via the cumulative probability distribution function (PDF), Qij, based on pij: 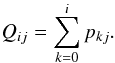 (21)The mapping for a sample PDF is illustrated in Fig. 2.
(21)The mapping for a sample PDF is illustrated in Fig. 2.
 |
Fig. 2 A sample cumulative probability distribution function, Qij, as a function of latitude, λi, at a given time tj. For each erupting flux tube, a pseudo-random number is chosen in the interval [0, 1]. The latitude λi at which the flux tube erupts is then obtained by the mapping shown by the arrows. |
The number of emerging tubes, nj, is chosen to be proportional to the total toroidal flux density at that time, ∑ iBij, requiring that a total number of N tubes emerge per activity cycle, viz. ![\begin{eqnarray} n_j= \left[N\cdot\frac{\sum_i B_{ij}}{\sum_{i,j} B_{ij}}+0.5\right]. \label{eq:nofts} \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq98.png) (22)Here the brackets denote the nearest integer to the value of the expression they enclose. For the case of the Sun, N is set to 2100, which constrains the total flux emerging over an activity cycle to be of the order of 1025 Mx, which is comparable with observations.
(22)Here the brackets denote the nearest integer to the value of the expression they enclose. For the case of the Sun, N is set to 2100, which constrains the total flux emerging over an activity cycle to be of the order of 1025 Mx, which is comparable with observations.
 |
Fig. 3 Number of flux tubes per time interval of 7 days, nj, as a function of time. The dashed line shows the value in brackets of Eq. (22), and the full line shows nj. |
Figure 3 shows nj as a function of time, with B(λ,t) taken from the solar dynamo model given in Sect. 2.
Field strengths of unstable flux tubes
To determine the field strength BFT, we consider the stability properties of flux tubes (Ferriz-Mas & Schüssler 1995) in the middle of the overshoot region (5000 km above the upper boundary of the radiative zone), using the non-local mixing length model of Skaley & Stix (1991). We consider a rotation profile similar to that obtained using helioseismic data (e.g., Schou et al. 1998) ![\begin{eqnarray} \frac{\Omega(r,\theta)}{\Omega_0} &=& 0.9635 - \left[1+{\rm erf}\left(\frac{r-r_0}{d_0}\right)\right] \nonumber \\ \label{eq:introt} & & \cdot\left(0.0876\cos^4\theta+0.0535\cos^2\theta-0.0182\right), \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq101.png) (23)where Ω0 is the equatorial rotation rate at the surface, and d0 = 0.075 R⊙ is taken as the half-thickness of the tachocline. Lines of constant angular velocity are shown in Fig. 4.
(23)where Ω0 is the equatorial rotation rate at the surface, and d0 = 0.075 R⊙ is taken as the half-thickness of the tachocline. Lines of constant angular velocity are shown in Fig. 4.
 |
Fig. 4 Meridional profile of internal rotation used in the stability analysis and flux tube simulations. Contours denote angular velocity, normalised to the equatorial value at the surface. |
This 2D profile is consistent with the latitude dependence of the radial shear given in Eq. (13), which we use in the dynamo model.
 |
Fig. 5 a) Stability diagram for thin magnetic flux tubes in the middle of the solar overshoot region, for Sun-like differential rotation (given by Eq. (23)). White regions represent stable flux tubes, while shaded areas indicate instability. For light-shaded areas, the fastest growing mode has azimuthal wave number m = 1, while for dark-shaded areas it is m = 2. Contours show lines of constant growth times (e-folding times), labelled in units of days. b) Time-latitude diagram of the dynamo-generated mean toroidal magnetic field B(λ,t) at the bottom of the convection zone (contours at ± 0.04, ± 0.1, ± 0.3, ± 0.5, ± 0.7, ± 0.9 of the maximum value of B, solid for positive and dashed for negative values) and of the flux loops emerging at the surface (dots) for a Sun-like star. c) Time-latitude diagram of the longitudinally averaged radial surface magnetic field for the solar model. d) Time variation of the total unsigned surface magnetic flux. The values are averaged over 27-day time intervals. |
Figure 5a shows the stability diagram in a plane defined by flux tube latitude and field strength. We define Bτ(λ) to be the field strength of unstable flux tubes as a function of latitude, corresponding to a certain growth time, τ, of the instability. In the course of the amplification of the toroidal magnetic field, instability sets in when BFT exceeds a critical value. This value also defines the mean field strength B0 in Eq. (5), at which the dynamo saturates, taking into account the scaling given by Eq. (18). In most parts of the stability diagram, τ decreases with increasing field strength. In the αΩ dynamo model, the toroidal field amplification occurs on the timescale of the rotational shear in the tachocline, which is about a few years. As long as the growth time of the flux tube instability is longer than the shearing timescale, the toroidal field continues to be amplified without the flux tube leaving the shear region (Işık & Holzwarth 2009). As the field strength reaches a level of the order 105 G, the two timescales become comparable and the flux tube is lost from the layer. Therefore, we do not consider unstable tubes with growth times much longer than the amplification timescale and choose the field strengths of the emerging flux tubes given by the curve B200(λ), corresponding to τ = 200 days. Choosing a growth time exceeding this value leads to almost identical results since the curves of constant growth time become very close to each other near the stability limit (Fig. 5a). We consider the contour line B200(λ) of the main region of instability in Fig. 5a, which is a single-valued function of latitude. Taking field strengths corresponding to the low-latitude “island” to the left of the diagram does not lead to a significant difference in the emergence latitudes and tilt angles (Caligari et al. 1995). To avoid the occasional emergence of flux loops at unrealistically high latitudes in the case of the Sun, we assume that unstable flux tubes only form if the local mean toroidal field exceeds 400 G (4% of the equipartition field strength).
3.3. The rise of flux loops
Having determined the times of emergence, initial latitudes, and the corresponding field strengths of unstable flux tubes, we simulate their rise through the convection zone using the code developed by Moreno-Insertis (1986) and extended to three dimensions and spherical geometry by Caligari et al. (1995). In the numerical scheme, the thin flux tube is described by a string of Lagrangian mass elements.
The initial value for the cross-sectional radius of each flux tube is taken to be Rt = 1000 km. For B = 105 G, this corresponds to a magnetic flux of about 3 × 1021 Mx, which is typical of a bipolar magnetic region (hereafter BMR) of moderate size at the solar surface. The tube radius is large enough for the rising flux loops to be largely unaffected by the drag force (D’Silva & Choudhuri 1993; Caligari et al. 1995), so that differential rotation and meridional circulation do not influence their motion. Therefore, the dynamics of flux tubes with Rt ≳ 1000 km is independent of their radius, as long as the thin flux tube approximation remains valid.
The fastest growing modes of unstable flux tubes have azimuthal wavenumbers m = 1 or m = 2. On the other hand, the angular separation of large BMRs on the Sun corresponds to much larger azimuthal wavenumbers (m = 10 − 60). A possible mechanism for limiting the longitudinal separation of BMRs is the dynamical disconnection from their magnetic roots at depths of a few Mm below the surface soon after emergence (Schüssler & Rempel 2005).
To determine the emergence latitudes and tilt angles, we use a table derived from a number of simulations of rising unstable flux tubes for various initial latitudes and magnetic field strengths. The initial latitudes are in steps of 5° and the corresponding field strengths are obtained from the curve B200(λ). Linear interpolation is used to obtain the emergence latitudes and tilt angles at intermediate values of initial latitude and field strength. Figure 5b shows a comparison of the dynamo-generated toroidal field in the overshoot layer (contour lines) and the surface emergence pattern of rising flux loops (dots). The overall emergence pattern coincides with the dynamo waves, since the poleward deflection of rising flux tubes with field strength of the order of 105 G by the Coriolis force is small for solar rotation rates. This result is consistent with the implicit assumption often made when interpreting solar dynamo models, namely that the surface activity pattern closely reflects the dynamo wave pattern.
4. Surface flux transport
Times, latitudes, and tilt angles of emerging flux loops obtained with the procedures described so far determine the flux input into the surface flux transport model, which we consider in this section. The model describes the subsequent evolution of magnetic flux at the stellar surface.
4.1. The surface evolution of magnetic flux
We follow the evolution of the surface field governed by the emergence of BMRs and flux transport by differential rotation, meridional flow, and (turbulent) diffusion due to convective flows. In contrast to the big flux tubes rising through the convection zone, the large-scale surface field described by the flux transport model is highly fragmented into small-scale flux concentrations. These magnetic elements are vertically oriented (owing to buoyancy) and sufficiently small to be passively transported by the surface flows via the drag force.
We therefore assume that the surface field has only a radial component, Br, whose evolution as a function of latitude, λ, longitude, φ, and time, t, is described by the magnetic induction equation in the form (cf. Baumann et al. 2004) 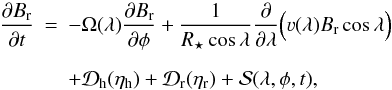 (24)where R ⋆ is the stellar radius,
(24)where R ⋆ is the stellar radius, 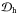 is the term for horizontal diffusion with uniform turbulent diffusivity ηh = 600 km s-1,
is the term for horizontal diffusion with uniform turbulent diffusivity ηh = 600 km s-1, 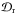 denotes the radial diffusion term with uniform radial diffusivity ηr = 100 km s-1 (Baumann et al. 2006). In addition,
denotes the radial diffusion term with uniform radial diffusivity ηr = 100 km s-1 (Baumann et al. 2006). In addition, 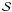 is the source term describing the newly emerging BMRs and Ω is the surface angular rotation rate as a function of latitude λ
is the source term describing the newly emerging BMRs and Ω is the surface angular rotation rate as a function of latitude λ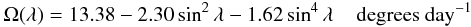 (25)(Snodgrass 1983). The meridional flow velocity 3 (Snodgrass & Dailey 1996; Hathaway 1996) is assumed to be
(25)(Snodgrass 1983). The meridional flow velocity 3 (Snodgrass & Dailey 1996; Hathaway 1996) is assumed to be 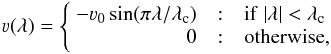 (26)where 30 = 11 m s-1 and λc = ± 75° (cf. van Ballegooijen et al. 1998; Baumann et al. 2004).
(26)where 30 = 11 m s-1 and λc = ± 75° (cf. van Ballegooijen et al. 1998; Baumann et al. 2004).
The numerical solution of Eq. (24) is carried out by representing the magnetic field as an expansion in terms of spherical harmonics with a maximum degree of ℓ = 63 (Baumann et al. 2004). This corresponds approximately to the observed size of the supergranules (~30 Mm) on the Sun.
4.2. Treatment of source BMRs
The flux density of a newly emerged BMR is written in the form 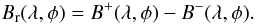 (27)The emergence longitudes of the BMRs are randomly distributed. Following van Ballegooijen et al. (1998) and Baumann et al. (2004), we assume that the unsigned field strength of the two polarities is given by
(27)The emergence longitudes of the BMRs are randomly distributed. Following van Ballegooijen et al. (1998) and Baumann et al. (2004), we assume that the unsigned field strength of the two polarities is given by ![\begin{eqnarray} \label{eq:gaudist} B^{\pm}(\lambda,\phi) = B_0 \exp\left[- \frac{ 2\left[ 1-\cos\beta_{\pm}(\lambda,\phi) \right]}{\delta_{\rm in}^2}\right], \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq140.png) (28)where β ± (λ,φ) are the heliocentric angles between a given position (λ,φ) and the centres of the positive and negative polarities, (λ ± ,φ ± ). The initial characteristic angular width of each polarity, δin, and the angular separation of the centres of the two poles, Δβ, are related by δin = 0.4Δβ. The maximum field strength B0 is set to 250 G (see Baumann et al. 2004).
(28)where β ± (λ,φ) are the heliocentric angles between a given position (λ,φ) and the centres of the positive and negative polarities, (λ ± ,φ ± ). The initial characteristic angular width of each polarity, δin, and the angular separation of the centres of the two poles, Δβ, are related by δin = 0.4Δβ. The maximum field strength B0 is set to 250 G (see Baumann et al. 2004).
The BMRs, which are smaller than the grid cell size (~1 square degree) of the simulations, are taken into account by considering these regions only at a later stage in their evolution, after having expanded (by turbulent diffusion) to an angular width of δ0 = 4°. The description of the two polarities for such a BMR is thus given by ![\begin{eqnarray} B^{\pm}(\lambda,\phi) = B_0 \Bigg(\frac{\delta_{\rm in}}{\delta_0}\Bigg)^2\exp\left[- \frac{ 2\left[ 1-\cos\beta_{\pm}(\lambda,\phi) \right]}{\delta_0^2}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq149.png) (29)In our numerical treatment, the spherical harmonic coefficients defining the field distribution of the newly emerged BMRs are multiplied by a spatial filter of the form
(29)In our numerical treatment, the spherical harmonic coefficients defining the field distribution of the newly emerged BMRs are multiplied by a spatial filter of the form ![\hbox{$\mathrm{exp}\big[-\beta_\pm^2 l(l+1)/4\big]$}](/articles/aa/full_html/2011/04/aa14501-10/aa14501-10-eq150.png) (van Ballegooijen et al. 1998), in order to diminish the effect of ringing (Gibbs phenomenon) caused by the truncation of the expansion in spherical harmonics.
(van Ballegooijen et al. 1998), in order to diminish the effect of ringing (Gibbs phenomenon) caused by the truncation of the expansion in spherical harmonics.
 |
Fig. 6 Time variation of the emerging magnetic flux integrated over the surface, and summed over 27-day time intervals. The corresponding average unsigned field strength is indicated on the right-hand vertical axis. |
4.3. Size distribution and the emerging magnetic flux
The total size of a newly emerged BMR is related to the heliocentric angular separation of the centres of the two poles, Δβ, which, in our model, ranges from 3.5° to 10° in steps of 0.1°. The corresponding range of areas is 30 − 250 square degrees, and the resulting range of magnetic flux is 2.3 × 1021 − 3.5 × 1022 Mx. The areas A of the bipolar source regions are determined randomly with a number distribution derived from solar observations, N(A) ~ A-2 (Schrijver & Harvey 1994).
For the solar model, the time series of emerging magnetic flux, summed over 27 days (one full solar rotation), is given in Fig. 6. It shows a cyclic variation with a period of about 11 years, closely following the underlying oscillatory dynamo model.
The evolution of the surface flux is given in a supplementary animation (see the online appendix, Fig. A.1, top panels), which shows the weakening and cancellation of the polar field, and the gradual build-up of the polar field of the following cycle. The time-latitude diagram of the longitudinal average of the signed flux density is shown in Fig. 5c. The extreme values of the unsigned flux density are lower than those found by Baumann et al. (2004) for a similar model. The reason is that the tilt angles resulting from the simulated rise of flux tubes are systematically smaller than the latitude dependence assumed by Baumann et al. (2004), but actually provide a better match to the observations (see Caligari et al. 1995, Fig. 12). The corresponding time variation in the total unsigned flux (and the equivalent average unsigned field strength) is shown in Fig. 5d. The activity minima are less marked than those of the emerging flux (Fig. 6); this is due to the phase difference of about half a period between the variations in the polar flux and the flux emerging at low latitudes.
5. Rapidly rotating Sun-like stars
As a first non-solar application of the combined model of magnetic flux generation and transport, we consider rapidly rotating stars of solar internal structure.
For simplicity (and due to lack of information), we assume the same values for the turbulent magnetic diffusivities for the dynamo region, the convection zone, and the surface as in the solar model discussed in the previous sections. We also use the same profiles for the rotational shear, i.e., we assume that the difference between the minimum and maximum angular velocities in the convective envelope, ΔΩ, is independent of the equatorial rotation rate at the surface, Ω ⋆ . This is motivated by observations of cool stars indicating a rather weak dependence of ΔΩ at the stellar surface on Ω ⋆ (e.g., Barnes et al. 2005; Donahue et al. 1996). This assumption corresponds to a decrease in ΔΩ / Ω ⋆ by a factor Ω⊙ / Ω ⋆ with respect to the solar value, so that the constants on the right hand side of Eq. (23) have to be multiplied by Ω⊙ / Ω ⋆ . Because ΔΩ is kept constant, the surface flux transport equation (Eq. (24)), the rotation profile (Eq. (25)), and RΩ (Eq. (9)) remain unchanged. We also adopt a solar-type internal rotation profile in the present section, owing to the lack of observational information on stellar internal rotation profiles. When results from asteroseismology become available, they can be directly incorporated into the model.
In the dynamo model, we assume that α0 scales with Ω ⋆ (Krause & Rädler 1980), so that Rα ∝ Ω ⋆ in Eq. (8), because η is not changed. The dynamo cycle period, Pcyc, then decreases with increasing Ω ⋆ . We note, however, that this scaling might not be valid for the very most rapid rotators since the α-effect driven by helical turbulence saturates when the cyclonic rotation of rising fluid parcels exceeds π / 2 (Parker 1982; Rüdiger & Kitchatinov 1993).
The total number of erupting flux tubes per activity cycle, N, is also scaled with Ω ⋆ , in accordance with the observed relation between the rotation rate and the level of magnetic activity (e.g., Montesinos et al. 2001).
5.1. The case of Prot = 9 d
We first consider a Sun-like star with an equatorial rotation rate of Ω ⋆ = 2.7 Ω⊙, corresponding to a period of about 9 d. Figure 7a shows the stability diagram of flux tubes located in the middle of the overshoot region.
The critical field strength for the Parker instability is larger than in the solar case, since rotation has a stabilising effect on the flux tubes. With increasing Ω ⋆ , angular momentum conservation suppresses the tube displacements perpendicular to the rotation axis, so that the magnetic buoyancy needs to be stronger than in a similar situation in the Sun.
In determining the function B200(λ), we excluded the “islands” of instability seen in Fig. 7a. Test simulations showed that the emergence latitudes and tilt angles of rising flux tubes do not differ significantly between the islands and the neighbouring part of the main region of instability.
The time-latitude diagram of the dynamo-generated toroidal field at the bottom of the convection zone and the locations of flux emergence are combined in Fig. 7b. They show a cyclic variation with the dynamo period of about five years. The poleward deflection of rising flux tubes is slightly stronger than in the case of solar rotation. The effect responsible is the component of the Coriolis acceleration directed towards the rotation axis (resulting from a retrograde flow along the flux tube required by angular momentum conservation), which is proportional to the rotation rate.
The emerging magnetic flux, summed over one-month intervals is shown in Fig. 8. While the total flux emerging per cycle is about five times higher than in the solar case, the relative variation between the minima and maxima of the emerging flux is considerably weaker. This is due to the larger overlap between consecutive cycles, which is a consequence of stronger dynamo excitation. Figure 7c shows that also the polar field maxima are higher than in the case of solar rotation (note the different saturation level of the colour table from Fig. 5c). This is due to 1) a higher flux emergence rate and 2) the bigger tilt angles of the emerging BMRs because of the stronger Coriolis force experienced by the horizontally expanding crest of the rising tubes. The animation of the surface field distribution is given in a supplementary animation (see the online appendix, Fig. A.1, middle panels). Figure 7d shows that the cycle signal introduced by the underlying dynamo is largely washed out in the time evolution of the total magnetic flux at the surface. This is caused by 1) a larger overlap between consecutive cycles owing to a stronger α-effect; and 2) strong polar magnetic fields in antiphase with the cycle of emerging flux.
5.2. The case of Prot = 2 d
 |
Fig. 9 Same as Fig. 5, but for a Sun-like star with Prot = 2 d. In panel b), the dots are shown at one-month intervals for clarity. |
For a star with a rotation rate of Ω ⋆ = 13 Ω⊙, corresponding to a period of two days, the stabilising effect of rotation on the flux tubes is even stronger than in the previous case. The stability diagram given in Fig. 9a shows that the critical field strength increased to a few times 105 G. As before, we exclude the instability islands in determining the field strengths of rising flux tubes.
For such a large rotation rate, the flux tubes rise almost parallel to the rotation axis and emerge at a significantly higher latitude than their starting location (Schüssler & Solanki 1992). The initial latitudes are in the range of roughly 0°−25°, while the emergence latitudes are about 23°−40°, so that there is no flux emergence in an “avoided zone” up to ± 23° latitude from the equator. Figure 9b shows the dynamo-generated toroidal magnetic field at the bottom of the convection zone together with the distribution of flux tubes emerging at the surface. It is evident that the poleward deflection of flux tubes causes a significant deviation between the dynamo waves in the interior and the pattern of surface emergence.
For such a rapidly rotating star, the tilt angles of emerging bipolar regions are much larger (around 35°) than in the solar case. The relatively narrow latitudinal extension of flux emergence and the large tilt angles lead to a pair of almost non-migrating latitudinal belts of opposite magnetic polarity in each hemisphere (see Fig. 9c and the supplementary animation in the online appendix, Fig. A.1, bottom panels). The net poleward transport of flux from the higher-latitude bands produces polar fields reaching field strengths of up to 35 G. Compared to the Prot = 9 d case, there is smaller overlap between the emergence patterns of consecutive cycles. Consequently, the corresponding surface-integrated unsigned magnetic flux (Fig. 9d) shows a clearer cycle (mainly determined by the activity bands), with a period of about two years, an amplitude of about 1.5 × 1024 Mx, and a minimum-to-maximum flux variation by a factor of about two.
6. Rapidly rotating K stars
6.1. K0 dwarf
We consider a K0V star at the zero-age main sequence, with a rotation period of 2 days. Such a star has a smaller radius and a relatively deeper convection zone than the Sun. We use a stellar model with R ⋆ = 0.735 R⊙ and the bottom of the convection zone located at 0.677 R ⋆ (Holzwarth & Schüssler 2001).
The Reynolds numbers for differential rotation, RΩ, and the α-effect, Rα, have to be adapted to the new value of the length scale, namely the radial distance of the convection zone lower boundary from the center. Scaling with Ω ⋆ / Ω⊙, we obtain α0 = 152 cm s-1. The resulting dynamo number RαRΩ is about a factor of four smaller than in the case of the Sun-like star with Prot = 2 d (Sect. 5.2), which leads to a somewhat longer magnetic cycle period of about 6.5 years. The number of emerging flux tubes per cycle is set to the same value as in the Sun-like star with the same rotation period. The emergence latitudes and tilt angles of the BMRs are determined with the same procedure as in the previous sections, considering the stability properties of flux tubes in the mid-overshoot region of the K0V star (Fig. 10a).
The comparison of the dynamo waves of the deep-seated toroidal field with the emergence pattern at the surface is shown in Fig. 10b. The difference between the emergence latitudes and the initial latitudes of flux tubes is larger by about 10° than for the solar-type star with the same rotation rate. This is due to a simple geometric effect: the K0V star has a deeper convection zone (in terms of fractional radius), so that a flux loop rising parallel to the rotation axis emerges at a higher latitude than in the case of a shallower convection zone.
The time-latitude diagram of the longitudinally averaged magnetic field and the time variation of the integrated unsigned surface flux are shown in Fig. 10c. Owing to the rapid rotation, the emerging BMRs have large tilt angles between 40° and 55°. This leads to pronounced branches of follower polarity drifting poleward via diffusion and meridional circulation. The cycle signal is similar in strength to the corresponding Sun-like case (Sect. 5.2), again due to the small cycle overlap of the emergence patterns and the large tilt angles leading to the formation of activity bands (Fig. 10d).
Three snapshots of the flux distribution at the stellar surface are shown in Fig. 11. Near an activity minimum (left panel), mid-latitude BMRs of the newly started cycle lead to an uneven longitudinal distribution of magnetic flux, owing to the relatively low emergence frequency. In the maximum phase (middle panel), highly tilted BMRs lead to the formation of a pair of latitudinal belts of opposite polarity in each hemisphere. The higher-latitude belt provides the source for the respective polar field of the same polarity. After seven months (right panel), flux emergence has decreased in parallel to the evolution of the deep-seated toroidal field generated by the dynamo, while the polar field has reached its maximum strength. As a result, the surface-integrated unsigned magnetic flux exhibits a cyclic variation with a period of about 2.75 yr (Fig. 10d).
6.2. K1 subgiant
As a further example, we consider a K1 subgiant rotating with a period of 2.8 days. A star of this type is the magnetically active component of HR 1099, the most thoroughly studied RS CVn-type binary system. In the structure model adopted here (Holzwarth & Schüssler 2001), the stellar mass is 1.5 M⊙, the age is about 2.4 Gyr, the stellar radius is R ⋆ = 3.44 R⊙, and the bottom of the convection zone is at 0.35 R ⋆ . These parameters still allow flux tubes to rise up to the surface. If the bottom of the convection zone were located deeper than about 0.30 R ⋆ , buoyant flux tubes entering the convection zone would be trapped within the star as a consequence of the magnetic curvature force (Holzwarth & Schüssler 2001).
 |
Fig. 11 Snapshots of the magnetic field distribution at the surface of the K0V star with Prot = 2 d. The colour table shows the field strength with a saturation level at ± 500 G. Left: the activity minimum phase. Middle: the activity maximum phase. Right: the beginning of the decay phase following the activity maximum, when the polar field reaches its maximum strength. The inclination of the rotation axis with respect to the line of sight is 30°. |
We assumed rigid rotation in the calculations regarding the instability and the rise of magnetic flux tubes, and the surface flux transport. This assumption is supported by the very weak surface shear observed in HR 1099 (Donati et al. 2003; Petit et al. 2004). Furthermore, the effects on flux tube dynamics of differentially rotating convection zones in post-main sequence stars is yet to be explored, as an extension of the work by Holzwarth & Schüssler (2001). The linear stability diagram for flux tubes in the middle of the overshoot region (about 0.33 R ⋆ ) is shown in Fig. 12a.
For the dynamo model, RΩ has been rescaled using the radius r0 = 1.1 R⊙ of the star’s radiative core and the surface latitudinal shear of about 0.87° d-1, following the measured value with the lowest variance, as given by Petit et al. (2004). The resulting dynamo number leads to an activity cycle with a period of about 4 yr, compared to the observed cycle periods of 5.3 yr and 16 yr (Berdyugina & Henry 2007).
Figure 12b shows that the dynamo waves and the emergence pattern have no spatial correlation. As a result of the deep convection zone and the geometric effect described in Sect. 6.1, the average latitude of emergence is shifted to even higher latitudes than in the case of main-sequence stars. The emergence belt centred around λ ≃ 62° has a latitudinal width of only about 7 degrees. This is caused by the projection of a low-latitude angular range at the bottom of the convection zone, onto the surface and along the direction parallel to the rotation axis, producing a much narrower range at high-latitudes.
Emerging BMRs have tilt angles between 5° and 8°, which are significantly smaller than those for the rapidly rotating main-sequence stars considered in the previous sections. This can be explained in the present case by the rising flux tubes spending a much longer time (about five years) in the convection zone, so that the magnetic tension force can more efficiently act against the twisting effect of the Coriolis force on the horizontally expanding loop.
The time-latitude diagram of the longitudinally averaged magnetic field strength (Fig. 12c) is similar to that of the rapidly rotating Sun-like star, apart from a shift of the patterns to higher latitudes. The total unsigned surface flux variation (Fig. 12d) shows a rather weak cyclic signal upon which irregular variations are superimposed. The narrow latitude range of flux emergence, as well as the weak transport effects by surface flows and diffusion in this region, amplify the effect of the random component of the surface flux injection process. This results in rather large fluctuations of the total unsigned surface flux.
Figure 12c also indicates a rather weak field in the polar caps above ~75° latitude, although polarity reversals still occur. This weakness is due to the relatively small tilt angles of the BMRs and the long diffusion timescale (proportional to 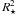 ): the meridional flow vanishes beyond ± 75°, so that further poleward flux transport occurs only by means of the relatively inefficient diffusion process. Inefficient diffusion and small tilt angles lead to an intermingling of polarities in the narrow flux emergence belts, as shown in Fig. 13. Therefore, the resulting poloidal field produced by the diffusing BMRs is weak and far from a simple dipole configuration.
): the meridional flow vanishes beyond ± 75°, so that further poleward flux transport occurs only by means of the relatively inefficient diffusion process. Inefficient diffusion and small tilt angles lead to an intermingling of polarities in the narrow flux emergence belts, as shown in Fig. 13. Therefore, the resulting poloidal field produced by the diffusing BMRs is weak and far from a simple dipole configuration.
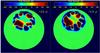 |
Fig. 13 Field strength distribution at an activity minimum (left panel), and at a maximum (right panel), for the K1 subgiant star. The inclination of the rotation axis with respect to the line of sight is 30°. The colour table shows the field strength with a saturation level at ± 300 G. |
7. Discussion
The combined model of magnetic field generation and transport provides two major improvements compared to previous models (e.g., Baumann et al. 2004; Holzwarth et al. 2006):
-
1.
the cycle properties are determined by an underlying dynamomodel, whereas in previous studies either the butterfly diagramswere prescribed arbitrarily, or observed emergence patternswere used. We thus establish the nontrivial link between thedeep-seated field generation and surface flux transport;
-
2.
the tilt angles and emergence latitudes of bipolar magnetic regions at the surface are not prescribed, but consistently determined from simulations of rising flux tubes. This may strongly affect the surface distribution of magnetic flux, and particularly the strength of the polar magnetic fields.
In this first exploratory study, our main motivation was to evaluate the effects of combining models for the dynamo, flux tube stability and dynamics, and surface transport, rather than to constrain dynamo models for cool stars. We therefore adopted a rather simple thin-layer dynamo model with differential rotation in radius, which does not include the probably important effects of latitudinal differential rotation and meridional circulation. We note also that Spruit (2010) argues that the radial angular velocity gradient in the solar tachocline is not capable of building up a sizeable toroidal field. Our model can certainly be utilised to test more elaborate dynamo models, such as Babcock-Leighton-type flux transport dynamos (Charbonneau 2005).
For solar-type and K0 main-sequence stars, we find that the polar magnetic fields for rotation periods of 10 d and 2 d are stronger than in the solar case, indicating the importance of surface transport effects (Schrijver & Title 2001; Işık et al. 2007b): the emergence and meridional transport of BMRs at mid-latitudes with tilt angles as high as 35° lead to strong (in comparison to the Sun) unipolar flux regions around the poles.
For the solar-type model with Prot = 10 d, the surface flux transport blurs the periodic signal of the oscillatory dynamo in the surface-integrated unsigned flux. This suggests that for rapid rotators, a cyclic dynamo may actually underly an apparently irregular variation in activity indicators. This could possibly be the case for HD 190771, a Sun-like star with Prot = 8.8 d observed by Petit et al. (2009). Using the Doppler-imaging technique, they report that the total magnetic energy at the surface does not change over the observed period, although global polarity reversals in the radial and azimuthal field components occur. Although considering only a radial field at the surface, our models show that a roughly constant total magnetic flux at the surface may arise from the combined effects of dynamo cycle overlap, large tilt angles, high flux emergence frequency, and meridional transport.
For all models with Prot = 2 d, we found that the dynamo wave pattern and the emerging surface flux are completely different from each other, owing to the strong poleward deflection of rising flux loops by the Coriolis force. Consequently, for rapid rotators the observed activity patterns on the surface may not necessarily be taken to represent the spatio-temporal distribution of magnetic field in the deep interior.
The results presented here are certainly rather preliminary, owing to the very simple dynamo model used and the insufficient information we have at present about various important parameters:
-
the dependence on rotation rate and stellar structure of α-effect, internal rotation profile, and the meridional flow velocity are largely unknown;
-
various complications regarding the formation of flux tubes, the growth of the buoyancy instability, and the rise through the convection zone are omitted, because the connection between dynamo-generated field and flux tube dynamics is not well understood (e.g., Schüssler & Ferriz-Mas 2003);
-
reliable models for the structure of convective overshoot regions do not exist;
-
it is unclear whether the solar value of ηh = 600 km2 s-1 for the turbulent surface diffusivity is valid for stars of different structure, rotation, and fraction of surface covered by magnetic flux.
Our assumption that the number of flux tubes emerging per activity cycle is proportional to the rotation rate is qualitatively consistent with our scaling of the α-effect with rotation rate. However, there are energetic and geometrical constraints on the maximum amount of magnetic flux that can be generated in rapid-rotator convection zones with the known mechanisms (Rempel 2008).
8. Conclusions
We have presented a combined model including 1) a thin-layer dynamo with an α-effect due to magnetic buoyancy instability and radial shear according to helioseismic results; 2) the stability analysis and dynamical simulation of flux tubes rising through the convection zone; and 3) surface flux transport by differential rotation, meridional flow, and turbulent diffusion that reproduce the basic observed features of the solar cycle (such as the butterfly diagram of flux emergence, the evolution of the large-scale surface flux distribution, and the polar field reversals).
Extending the model to rapidly rotating Sun-like and K-type main-sequence stars, we have found that the latitude distribution of emerging flux at the surface may differ significantly from that of the deep-seated toroidal field generated by the dynamo process. A strong overlap of the cycles may hide the cyclic signal in activity indicators related to the integrated total surface flux. Low- to mid-latitude flux emergence and activity can co-exist with strong polar fields (“polar spots”) arising from poleward surface flux transport.
In the case of a K1 subgiant, we have found that the large depth of the convection zone and long diffusion time lead to belts of intermingled mixed-polarity field at high latitudes and relatively weak polar field.
For improved realism of the model, a two-dimensional flux-transport dynamo model will be incorporated at our next proposed developed stage. Information about the stellar interior and the surface differential rotation, meridional flow, and internal structure can be included in the model as it becomes available by means of asteroseismology.
Online material
Movie 1
Access here
Movie 2
Access here
Movie 3
Access hereReferences
- Barnes, J. R., Cameron, A. C., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Batchelor, G. K. 1967, Fluid dynamics (Cambridge, England: Cambridge University Press) [Google Scholar]
- Baumann, I., Schmitt, D., Schüssler, M., & Solanki, S. K. 2004, A&A, 426, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baumann, I., Schmitt, D., & Schüssler, M. 2006, A&A, 446, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 http://www.livingreviews.org/lrsp-2005-8 [Google Scholar]
- Berdyugina, S. V., & Henry, G. W. 2007, ApJ, 659, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995, ApJ, 441, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Caligari, P., Schüssler, M., & Moreno-Insertis, F. 1998, ApJ, 502, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, P. 2005, Liv. Rev. Sol. Phys., 7, 3 http://www.livingreviews.org/lrsp-2010-3 [Google Scholar]
- Choudhuri, A. R., & Gilman, P. A. 1987, ApJ, 316, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Dikpati, M., & Charbonneau, P. 1999, ApJ, 518, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, R. A., Saar, S. H., & Baliunas, S. L. 1996, ApJ, 466, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Collier Cameron, A., & Petit, P. 2003, MNRAS, 345, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- D’Silva, S., & Choudhuri, A. R. 1993, A&A, 272, 621 [NASA ADS] [Google Scholar]
- Fan, Y. 2001, ApJ, 546, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, Y. 2009, Liv. Rev. Sol. Phys., 6, 4 http://www.livingreviews.org/lrsp-2009-4 [Google Scholar]
- Fan, Y., Fisher, G. H., & McClymont, A. N. 1994, ApJ, 436, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Ferriz-Mas, A., & Schüssler, M. 1993, Geophys. Astrophys. Fluid Dynamics, 72, 209 [Google Scholar]
- Ferriz-Mas, A., & Schüssler, M. 1995, Geophys. Astrophys. Fluid Dynamics, 81, 233 [Google Scholar]
- Ferriz-Mas, A., Schmitt, D., & Schüssler, M. 1994, A&A, 289, 949 [NASA ADS] [Google Scholar]
- Granzer, T., Schüssler, M., Caligari, P., & Strassmeier, K. G. 2000, A&A, 355, 1087 [NASA ADS] [Google Scholar]
- Hathaway, D. H. 1996, ApJ, 460, 1027 [Google Scholar]
- Holzwarth, V., & Schüssler, M. 2001, A&A, 377, 251 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holzwarth, V., Mackay, D. H., & Jardine, M. 2006, MNRAS, 369, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyng, P., Schmitt, D., & Teuben, L. J. W. 1994, A&A, 289, 265 [NASA ADS] [Google Scholar]
- Işık, E., & Holzwarth, V. 2009, A&A, 508, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Işık, E., Schmitt, D., & Schüssler, M. 2007a, Astron. Nachr., 328, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Işık, E., Schüssler, M., & Solanki, S. K. 2007b, A&A, 464, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jouve, L., Brown, B. P., & Brun, A. S. 2010, A&A, 509, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, F., & Rädler, K. H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
- Montesinos, B., Thomas, J. H., Ventura, P., & Mazzitelli, I. 2001, MNRAS, 326, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F. 1986, A&A, 166, 291 [NASA ADS] [Google Scholar]
- Moreno-Insertis, F., Schüssler, M., & Ferriz-Mas, A. 1992, A&A, 264, 686 [NASA ADS] [Google Scholar]
- Ossendrijver, M. 2003, A&AR , 11, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1982, Geophys. Astrophys. Fluid Dynamics, 20, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Donati, J., Wade, G. A., et al. 2004, MNRAS, 348, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, P., Dintrans, B., Morgenthaler, A., et al. 2009, A&A, 508, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rempel, M. 2008, J. Phys. Conf. Ser., 118, 012032 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Schüssler, M. 2001, ApJ, 552, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Rüdiger, G., & Kitchatinov, L. L. 1993, A&A, 269, 581 [NASA ADS] [Google Scholar]
- Schmitt, D. 2003, in Advances in Nonlinear Dynamos, ed. A. Ferriz-Mas, & M. Núñez (London: Taylor and Francis), 83 [Google Scholar]
- Schmitt, D., & Schüssler, M. 1989, A&A, 223, 343 [NASA ADS] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Harvey, K. L. 1994, Sol. Phys., 150, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., & Title, A. M. 2001, ApJ, 551, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M. 2005, Astron. Nachr., 326, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M., & Ferriz-Mas, A. 2003, in Advances in Nonlinear Dynamos, ed. A. Ferriz-Mas, & M. Núñez (London: Taylor and Francis), 123 [Google Scholar]
- Schüssler, M., & Rempel, M. 2005, A&A, 441, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schüssler, M., & Solanki, S. K. 1992, A&A, 264, L13 [NASA ADS] [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., & Moreno-Insertis, F. 1994, A&A, 281, L69 [Google Scholar]
- Skaley, D., & Stix, M. 1991, A&A, 241, 227 [NASA ADS] [Google Scholar]
- Snodgrass, H. B. 1983, ApJ, 270, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Snodgrass, H. B., & Dailey, S. B. 1996, Sol. Phys., 163, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
- Spruit, H. C. 2010, [arXiv:1004.4545] [Google Scholar]
- Strassmeier, K. G. 2005, Astron. Nachr., 326, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G. 2009, A&ARv, 17, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., & Bartus, J. 2000, A&A, 354, 537 [NASA ADS] [Google Scholar]
- van Ballegooijen, A. A., Cartledge, N. P., & Priest, E. R. 1998, ApJ, 501, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Vogt, S. S., Hatzes, A. P., Misch, A. A., & Kürster, M. 1999, ApJS, 121, 547 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Animations
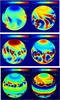 |
Fig. A.1 The surface distributions of magnetic flux for the Sun-like star with Prot = 27 d (top panels), Prot = 9 d (middle panels), and Prot = 2 d (bottom panels), near the activity minimum (left panels) and the maximum phases (right panels). The colour scale for the magnetic field strength saturates at ± 5,30, and 75 G for top, middle, and bottom panels, respectively. The corresponding time-latitude diagrams for the azimuthally averaged magnetic field strength are shown in Figs. 5c, 7c, and 9c. |
We provide three animated GIF files showing the simulated evolution of surface magnetic flux for three rotation rates of the Sun-like star, available on-line.
The animation Bsurf_27d.gif shows the evolution of magnetic field at the surface for the Sun-like model (Sect. 4.3). Still frames from the animation are shown in Fig. A.1 (top panels). The simulation begins at a cycle phase close to the polar field maximum with negative polarity at the north pole. The overlapping of two activity cycles is visible, i.e., high-latitude BMRs of the next cycle emerge, while BMRs of the ending cycle continue to emerge at low latitudes. In the course of the cycle, the polar field is weakened by cancellation with opposite-polarity (negative) flux transported from the active lower latitudes and eventually reverses around activity maximum. Afterwards, BMRs of the new cycle gradually build up positive flux at the north pole.
The animation Bsurf_9d.gif shows the variation in magnetic field at the surface of the Sun-like star with Prot = 9 d (Sect. 5.1). Still frames from the animation are shown in Fig. A.1 (middle panels). Although the flux emerges within a rather restricted latitude range, it is spread over the entire stellar surface by diffusion and the large-scale flows. There are unipolar magnetic regions near the poles and mixed-polarity regions at low to middle latitudes.
The animation Bsurf_2d.gif shows the evolution of magnetic field at the surface of the Sun-like star with Prot = 2 d (Sect. 5.2). Still frames from the animation are shown in Fig. A.1 (bottom panels). The latitude range of flux emergence is smaller than in the previous cases, and the tilt angle is significantly larger. As a result, two bands of magnetic regions of opposite polarity form, predominantly during the activity maximum.
All Figures
 |
Fig. 1 Normalised latitudinal profiles of α and the radial shear Ω′. |
| In the text | |
 |
Fig. 2 A sample cumulative probability distribution function, Qij, as a function of latitude, λi, at a given time tj. For each erupting flux tube, a pseudo-random number is chosen in the interval [0, 1]. The latitude λi at which the flux tube erupts is then obtained by the mapping shown by the arrows. |
| In the text | |
 |
Fig. 3 Number of flux tubes per time interval of 7 days, nj, as a function of time. The dashed line shows the value in brackets of Eq. (22), and the full line shows nj. |
| In the text | |
 |
Fig. 4 Meridional profile of internal rotation used in the stability analysis and flux tube simulations. Contours denote angular velocity, normalised to the equatorial value at the surface. |
| In the text | |
 |
Fig. 5 a) Stability diagram for thin magnetic flux tubes in the middle of the solar overshoot region, for Sun-like differential rotation (given by Eq. (23)). White regions represent stable flux tubes, while shaded areas indicate instability. For light-shaded areas, the fastest growing mode has azimuthal wave number m = 1, while for dark-shaded areas it is m = 2. Contours show lines of constant growth times (e-folding times), labelled in units of days. b) Time-latitude diagram of the dynamo-generated mean toroidal magnetic field B(λ,t) at the bottom of the convection zone (contours at ± 0.04, ± 0.1, ± 0.3, ± 0.5, ± 0.7, ± 0.9 of the maximum value of B, solid for positive and dashed for negative values) and of the flux loops emerging at the surface (dots) for a Sun-like star. c) Time-latitude diagram of the longitudinally averaged radial surface magnetic field for the solar model. d) Time variation of the total unsigned surface magnetic flux. The values are averaged over 27-day time intervals. |
| In the text | |
 |
Fig. 6 Time variation of the emerging magnetic flux integrated over the surface, and summed over 27-day time intervals. The corresponding average unsigned field strength is indicated on the right-hand vertical axis. |
| In the text | |
 |
Fig. 7 Same as Fig. 5, but for a Sun-like star with Prot = 9 d. |
| In the text | |
 |
Fig. 8 Same as Fig. 6, but for a Sun-like star with Prot = 9 d. |
| In the text | |
 |
Fig. 9 Same as Fig. 5, but for a Sun-like star with Prot = 2 d. In panel b), the dots are shown at one-month intervals for clarity. |
| In the text | |
 |
Fig. 10 Same as Fig. 5, but for a K0V star with Prot = 2 d. |
| In the text | |
 |
Fig. 11 Snapshots of the magnetic field distribution at the surface of the K0V star with Prot = 2 d. The colour table shows the field strength with a saturation level at ± 500 G. Left: the activity minimum phase. Middle: the activity maximum phase. Right: the beginning of the decay phase following the activity maximum, when the polar field reaches its maximum strength. The inclination of the rotation axis with respect to the line of sight is 30°. |
| In the text | |
 |
Fig. 12 Same as Fig. 5, but for a K1 subgiant star with Prot = 2.8 d and rigid rotation. |
| In the text | |
 |
Fig. 13 Field strength distribution at an activity minimum (left panel), and at a maximum (right panel), for the K1 subgiant star. The inclination of the rotation axis with respect to the line of sight is 30°. The colour table shows the field strength with a saturation level at ± 300 G. |
| In the text | |
 |
Fig. A.1 The surface distributions of magnetic flux for the Sun-like star with Prot = 27 d (top panels), Prot = 9 d (middle panels), and Prot = 2 d (bottom panels), near the activity minimum (left panels) and the maximum phases (right panels). The colour scale for the magnetic field strength saturates at ± 5,30, and 75 G for top, middle, and bottom panels, respectively. The corresponding time-latitude diagrams for the azimuthally averaged magnetic field strength are shown in Figs. 5c, 7c, and 9c. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


