EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 527 (March 2011) A&A, 527 (2011) A123 Full HTML
Highlight
Free Access
Issue
A&A
Volume 527, March 2011
Article Number A123
Number of page(s) 10
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201015973
Published online 08 February 2011

© ESO, 2011

1. Introduction

This paper is the third in a series dedicated to reconsidering the modelling of dust evolution in shocks in molecular clouds (Guillet et al. 2007, 2009, hereafter Papers I and II). Shocks are violent events generated in the ISM by supernova explosions, supersonic collisions between clumps, or by a jet entering a cloud. They are routinely observed around YSOs where jets and outflows emitted by the new-born star penetrate the surrounding molecular gas. Millimeter and infrared observations of these shocked regions reveal the presence of species like SiO or Fe+ which are usually highly depleted from the gas in quiescient regions. As Si and Fe are known constituents of dust grains this attests to the destruction of dust in these shocks. In Paper II, we presented a model calculating the degree of grain destruction in mono-fluid MHD, J-type shocks, which are relevant to the hot shocked gas where Fe+ is observed. In this paper, we study the evolution of dust in multi-fluid MHD C-type shocks for which models predict lower peak gas temperatures (typically a few thousand K).

In hydrodynamical or J-type shocks the shock energy is dissipated on the mean free path scale by the fluid viscosity, which suddenly heats the gas to high temperatures with later cooling. In C-type shocks, the energy is dissipated on a much larger scale through friction between two fluids which are decoupled: the neutral gas and the charged fluid (ions, electrons and dust grains). On this large scale, the heating and cooling of the gas occur at the same time, which results in a much lower temperature in a C shock than in a J shock of the same energy. C shocks are limited in velocity because the magnetosonic waves, pressure waves in the charged fluid, must travel faster than the shock itself to form a magnetic precursor that accelerates, heats and compresses ions, electrons and dust ahead of the neutral gas. Unlike J-type shocks, C-type shocks can only propagate in weakly ionised gases, i.e. in diffuse and molecular clouds. First, the decoupling of the neutral fluid from the charged fluid only exists if the friction between the two fluids is weak enough, i.e. where the ionisation fraction is low (<10-4) as it is in diffuse or dense clouds. Second, for the decoupling to persist, the gas temperature must also remain low enough (below 104 K) to prevent the appearance of a viscous subshock in the gas. This condition exists only if the dominant molecular coolant H2 is not fully dissociated by the shock itself, which imposes a second limit on the velocity of C shocks. For more details on the physics of C and J shocks, see Draine & McKee (1993).

The processes leading to dust destruction and the evolution of its size distribution are quite general and do not automatically involve shocks (e.g. Draine & Salpeter 1979; Hirashita & Yan 2009). Dust is subject to destruction in gas-grain and grain-grain collisions. High-velocity impacts of gas particles on a grain lead to the progressive removal of atoms and molecules from its surface, a processed called sputtering. For icy mantles on grain surfaces, this occurs for temperature higher than 6000 K or for impact velocities 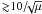≳10/μ\hbox{${\gtrsim} 10/\!\!\sqrt{\mu}$} km s-1 with μ the reduced mass of the impactor relative to hydrogen. For the more refractory cores, the threshold is higher:  ~25 km s-1 or 5 × 105 K (Tielens et al. 1994; May et al. 2000). Grain-grain collisions at low impact velocities ( ≳ 1 − 2 km s-1) shatter grains into very small fragments and can vaporise part or all of the colliding grains at higher velocities ( ≳ 20 km s-1, Tielens et al. 1994; Jones et al. 1996). At lower velocities ( ≲ 1 km s-1, a limit which is size and material dependent), grains can stick together (Chokshi et al. 1993; Dominik & Tielens 1997).

Gas-grain destructive processes (sputtering) in C-type shocks have been extensively studied in order to confront shock models with line measurements of tracers such as SiO, H2O and CH3OH in molecular flows around YSOs (e.g. Schilke et al. 1997; Jiménez-Serra et al. 2008; Gusdorf et al. 2008). Few studies have so far attempted to model the destruction of dust in vaporising grain-grain collisions (e.g. Caselli et al. 1997), a destructive process that is usually considered less efficient than sputtering. Shattering, which always accompagnies vaporisation, but which has no direct impact on the release of species into the gas phase, has usually been ignored, aside from simple estimates (Caselli et al. 1997; Flower & Pineau des Forêts 2003). However studies of dust dynamics in C shocks demonstrate that grains in C shocks do not behave as a single fluid (Chapman & Wardle 2006; Paper I). At high densities large grains tend to decouple from small grains and so we expect grain-grain processing in high-velocity collisions between large and small grains.

Based on our previous multi-fluid modelling of grain charge and dynamics (Paper I), this article describes how we model all the relevant dust processes in C-type shocks, including the effect of vaporisation on the dust destruction efficiency and, for the first time, the effect of grain shattering on the dust size distribution. We also take into account the feedback of these processes on the shock dynamics. By self-consistently coupling the dust physics with the physics and chemistry ruling C-type shocks, we show that shattering and vaporisation are important at high densities (nH ≥ 105 cm-3), both for the evolution of the dust and for the shock structure itself, but are negligible at lower densities (nH ≤ 104 cm-3).

The paper is structured as follows. In Sect. 2, we describe the physics of grain charge and dynamics in C-type shocks. Sect. 3 presents the modelling of gas-grain and grain-grain processes, and how we couple them to the shock physics. Our results are presented in Sect. 4. Section 5 discusses our critical assumptions relating to the charging, dynamics and processing of very small fragments which control the feedback of dust onto the shock ionisation and dynamics. Finally, we summarize our results in Sect. 6.

2. C-type shocks with dust dynamics

Our shock code is an updated version of that of Flower & Pineau des Forêts (2003), a 2-fluid shock model which solves for the shock dynamics, the ionisation, chemical composition and temperature of the gas, the population of H2 ro-vibrationnal levels, as well as the release of dust core and mantle species (e.g. Si, Fe and CH3OH) into the gas through sputtering. The Flower & Pineau des Forêts (2003) shock model applies to transverse shocks where the magnetic field remains perpendicular to the shock propagation direction (for oblique C-type shocks, see e.g. Chapman & Wardle 2006). This simplification allows for an elaborate description of the chemical network in the shock, which includes more than 130 species and 900 reactions. Our recent extension of this code (see Paper I) allows us to study the charge and dynamics of numerous silicate and carbonaceous grain fluids.

In this section, we define our standard critical C shock that will be our reference throughout the paper, and briefly summarise the charge and dynamics of dust grains in C shocks (see Paper I for more details).

2.1. C shocks propagating at the critical velocity

As mentioned in the introduction the velocity of steady-state C-type shocks is limited by two critical velocities, the velocity at which the main coolant H2 is fully dissociated and the velocity of magnetosonic waves. The magnetosonic velocity is a function of the magnetic field intensity B and of the total mass density, ρc, of species coupled to the magnetic field in the preshock (i.e. unshocked) gas: 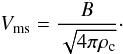Vms=B4πρc·\begin{equation} V_{\rm ms}=\frac{B}{\sqrt{4\pi\rho_{\rm c}}}\cdot \end{equation}(1)In dense clouds the magnetic field intensity B is related to the proton density nH = n(H) + 2n(H2) through the scaling law (Crutcher 1999): 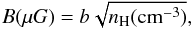B(μG)=bnH(cm-3),\begin{equation} B(\mu G)=b\sqrt{\nH({\rm cm^{-3}})}, \end{equation}(2)with b close to unity. The mass density ρc includes that of the ions and electrons (which are strongly coupled to the magnetic field) but only a fraction of the dust mass density because large grains may be only partially coupled to the magnetic field in the preshock gas due to their low charge to mass ratio. We refer the reader to Paper I for the way we calculate ρc.

C-type shocks of a given velocity, Vs, can exist for a wide range of magnetic field intensities as long as the shock velocity is smaller than the magnetosonic velocity and the H2 dissociation velocity. First, we limit our study to low velocity shocks ( ≤ 50 km s-1) which do not fully dissociate H2. Second, to limit the number of free parameters in our study, we calibrate the magnetic field intensity in the preshock gas, hence the factor b, to study only C-type shocks propagating at a velocity close to the critical velocity: Vs  ≃  Vcrit. Studying critical C shocks is justified by the fact that the observed shocks will be dominated by the brightest ones, i.e. the fastest.

thumbnail Fig. 1

(Top) Temperature, density and (bottom) velocity profiles in the shock frame for our standard 30 km s-1 C shock, propagating in a molecular cloud of preshock density nH0 = 105 cm-3 and transverse magnetic field B = 417   μG (b = 1.32). As in Paper I, grain-grain processing is ignored.

Table 1

Parameter 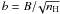b=B/nH\hbox{$b=B/\!\sqrt{\nH}$} relating the preshock magnetic field to the preshock proton density, and the corresponding magnetic field intensity (shown as b/B   (μG)), as a function of shock velocity Vs and preshock density nH for our critical shocks. Our standard model is framed.

Table 1 presents the intensity of the preshock transverse magnetic field for critical shocks, tabulated as a function of the shock velocity and preshock proton density. A 30 km s-1critical shock propagating through a molecular cloud of density 105 cm-3 and magnetic field intensity B = 417   μG (b = 1.32) will be our standard reference shock throughout this article. Figure 1 presents the gas temperature, density and velocity1 profiles for this standard shock, in a model where dust evolution is ignored, as in Paper I. The peak of the gas temperature is of the order of a few thousand K, much lower than the temperature of the charged fluid2. The gas compression is ultimately limited by the magnetic pressure which increases as the square of the density.

2.2. Grain charge and dynamics

The dynamics of a dust particle in a MHD shock is primarly determined by the evolution of its electric charge. Grains get their charge from electron attachment, ion recombination on their surface, photoelectric electron emission and, at high energies, the ejection of secondary electrons by the impact of primary electrons or ions (e.g. Draine & Salpeter 1979). In molecular outflows around YSOs, the dense gas is generally screened from the interstellar and stellar radiation field by dust extinction and so we can ignore grain charging by photoelectric effects. In Paper I we demonstrated that grain charging by cosmic ray-induced secondary photons can be neglected for the modelling of grain dynamics in C shocks3. Secondary electron emission occurs for high electron/ion impact energies (higher than  ~10 eV, Draine & Salpeter 1979; Jurac et al. 1995), which are never encountered in C shocks. Grain charge in C-type shocks is therefore controled by the competition between electron attachment and ion recombination on the grain surface.

As in Paper I, the silicate and carbon dust size distributions of grains are modelled by 8 size bins ranging from 100 Å to 3000 Å with an initial (preshock) MRN size distribution (dn(a) ∝ a-3.5   da, Mathis et al. 1977). Carbon grains initially represent  ~0.2% of the gas mass, silicate grains  ~0.4%, and ice mantles  ~0.3% (a mass fraction of the chemical species composing grain mantles that is compatible with observations, see Table 2 in Flower et al. 2003). The ice mantle covering grain cores in the preshock gas is  ~150 Å thick whatever the core size (see Paper I).

Our shock code follows the evolution of the charge distribution of each grain size through the shock. This costly numerical method, which accounts for  ~1000 of the integration variables, is necessary to the calculation of the ionisation state of the gas when the shattering of dust grains is included. We refer the reader to Paper I for the full description of our grain charge numerical model.

thumbnail Fig. 2

(Top) Average charge in our standard shock for large and small grains, with the ion-electron temperature superimposed. (Bottom) Fractional density of ions Xions = ni/nH (red curve), free electrons Xe −  = ne/nH (blue curve) and negative charge on the dust surface per proton (black curve). Grain-grain processing is ignored.

thumbnail Fig. 3

Silicate grain velocities along (top) and perpendicular (bottom) to the shock propagation direction of our standard shock, for large charged grains and one small neutral grain size. Horizontal axis is linear at flow time  < 10 yr to zoom onto the grain motion, then logarithmic to show the whole shock. Grain-grain processing is ignored.

Figure 2 presents the resulting average charge of silicate grains in our standard shock without grain-grain processing, as well as the detailed ionisation balance between ions, electrons and grains. Grain charge is negative and proportional to the grain radius and to the electron-ion temperature (Fig. 2a), as expected (e.g. Spitzer 1941; Draine & Sutin 1987). The ionisation fraction of the gas is very low and so the increase in grain charge in the shock depletes electrons from the gas relative to ions (Fig. 2b). This effect is even more dramatic when the fragmentation of grains is included, as we show below.

Figure 3 presents the 2D dynamics of the grains through the shock, in the shock propagation direction z and along the shock front y, without grain-grain processing. As shown in Paper I, one must distinguish between large grains ( ≳ 100 Å) for which charge fluctuations can be ignored and small grains (≲100 Å) for which the stochastic dynamics is entirely controled by charge fluctuations. Large grains follow, on average, the motion of ions while gyrating around the magnetic field lines. Their gyration is rapidly damped by gas drag early in the shock, after which they essentially follow the motion of the ions4. Very small grains (40 Å in Fig. 3) are almost inertia-free and we can neglect their gyration phase. Through the shock their charge is close to zero: they follow the ions when they are charged (not shown here) and tend to almost follow the gas when they are neutral, as presented in Fig. 3 (see Paper I for a complete description of the stochastic dynamics of very small grains in C shocks). As we will demonstrate, very small neutral grains play an important role in the processing of grains in C shocks.

3. Dust processing model

Can we now simply derive the evolution of the dust size distribution and the degree of dust destruction in the shock from the dynamics of small and large grains presented in Fig. 3? The answer is no, unfortunately we can not: in weakly ionised clouds grain shattering has such a tremendous effect on the ionisation state of the gas and on the coupling between the gas and the magnetic field that the charge, the dynamics, the processing of all grain sizes and the shock dynamics are affected by the feedback onto the shock of the evolution of the dust size distribution throughout the shock.

In order to self-consistently calculate the impact of C-type shocks on the dust size distribution, one has to fully couple the charge, dynamics and processing of dust grains with solving for the shock structure. In this section we describe how we model grain shattering, vaporisation and sputtering, and how we handle their effects on the physical conditions of the shock.

3.1. Gas-grain processing

The sputtering of grain mantles and cores was already included in the shock model by Flower et al. (2003), using the sputtering yields from May et al. (2000) for grain cores (here graphite and silicate) and Barlow (1978) for icy mantles. The adsorption of icy molecules by accretion from the gas onto the grain surfaces is also included but is only efficient at high densities, i.e. in the shock tail.

The mantle thickness remains independent of the grain size in the shock because all grains approximately follow on average the same dynamics, that of ions (see Paper I for more details). If we ignore the impact of shattering and vaporisation on grain icy mantles, the evolution of mantle thickness can be followed numerically throughout the shock by integrating the rates for the adsorption and desorption processes on a unique effective grain. This numerical simplification is justified by the fact that the processing of mantles and cores occur in distinct regions of the shock (see Sect. 4).

3.2. Grain-grain processing

When two grains collide at velocities greater than  ~1 km s-1, shock waves propagate in the grains thereby compressing both solids. When the high pressure of the shock wave is released, a fraction of the mass is vaporised5, another fraction is shattered into a size distribution of fragments in the excavation flow. We use the model by Tielens et al. (1994) and Jones et al. (1996) to calculate these fractions. In this model, the shattering threshold for carbon grains (1.2 km s-1) is lower than for silicate grains (2.7 km s-1). The vaporisation threshold, i.e. the impact velocity at which dust material starts to be vaporised in the collision and returned to the gas, is almost the same for both silicate and carbon grains (~19 km s-1).

Following Jones et al. (1996), we assume a power-law size distribution of spherical fragments in shattering events, with an exponent of  − 3.3: 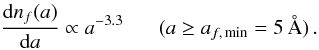dnf(a)da∝a-3.3(a≥af, min=5 Å) .\begin{equation} \frac{\d n_{ f}(a)}{\d a} \propto a^{-3.3} \hspace{0.6 cm} ( a \ge a_{f,\,{\rm min}}=5\,\AA )\,. \end{equation}(3)The radius of the smallest fragments is af,   min = 5 Å (a critical parameter, see Sect. 5.1 for a discussion), which corresponds to the average size of PAHs. The radius of the largest fragment, af,   max, is a function of the target radius a and of the mass fraction f of the target material which is shattered (Jones et al. 1996): 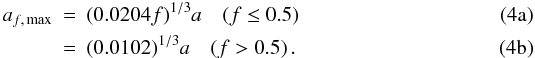af, max=(0.0204f)1/3a (f≤0.5)=(0.0102)1/3a (f>0.5) .\begin{subequations} \begin{eqnarray} a_{f,\,{\rm max}} &=& (0.0204 f)^{1/3} a \quad{ (f \le 0.5)} \\ & =& (0.0102)^{1/3} a \quad{ (f > 0.5)}\,. \end{eqnarray} \end{subequations}af,   max is always at least 5 times smaller than the target grain and is not a critical parameter. Dust fragmentation is followed numerically by adding 7 bins for grains smaller than 100 Å to the already existing 8 bins for larger grains. These bins are initially empty and are progressively filled by the fragments resulting from the shattering of larger grains. In particular, the fragments in the smallest carbon dust size bin can be regarded as PAHs. They are initially depleted from the preshock gas, accreted onto the surface of larger grains, and are then produced in huge quantities in the shock by fragmentation.

Shattering is intimately coupled to the ionisation state of the gas through the charging of fragments. To let the integrator solve for the ionisation state of the gas, we ensure that the total electric charge is conserved during the shattering of grains, i.e. that shattering does not immediately affect the ionisation of the gas (through the release of electrons or ions into the gas for example). The total charge initially carried by the target and projectile grains is therefore set equal to the electric charge carried by the fragments and what remains of the target and projectile grains after the collision. As the total number of fragments usually exceeds the number of negative charge (electrons) carried by the target and projectile grains, this means that the fragmentation must produce positively charged fragments to compensate for the charge taken by negatively charged fragments. Our code handles this by shifting the charge distribution for each fragment (usually towards positive values); this allows for the conservation of the total charge during the collision. The charge of fragments subsequently evolves in the shock as described in Paper I, thus affecting the ionisation state of the gas.

4. Results

Our shock model self-consistently couples the dust physics (charge, dynamics and evolution) with the shock dynamics and chemistry. We are thus able to follow the destruction of grains and the evolution of the dust size distribution through the shock at the same time as we calculate the feedback of dust evolution on the shock dynamics.

4.1. Impact of the shock on the dust size distribution

thumbnail Fig. 4

Initial (black) and final core size distributions (mantles not included) for silicate (red) and carbon (blue) grains in our standard C shock.

thumbnail Fig. 5

Evolution of the total grain cross-section  ⟨ nσ ⟩  carried by dust in our standard shock model, with (red) and without (black) taking into account grain mantles, normalised by flux to its preshock value ( ⟨ nσV ⟩ / ⟨ nσ ⟩ 0Vs), with (solid) and without (dashed) shattering.

Figure 4 presents the initial and final size distributions of carbon and silicate grains once our standard shock has passed. Large grains have been shattered into smaller grains (<100 Å), an effect more acute for the carbon than for the silicate distribution6.

Small fragments have considerably increased the total geometrical cross-section carried by dust grains. Figure 5 shows that the total dust surface generally evolves in three distinct phases when shattering is included: 1) a decrease by a factor  ~3 during the erosion of icy mantles (t < 7 yr); 2) a factor  ~10 increase through the shattering of grain cores (4 < t < 10 yr); and 3) another factor  ~5 with the re-accretion of molecular species onto the surface of fragments in the postshock gas (20 < t < 100 yr). Due to the increased total cross-section carried by grain cores, the final mantle thickness is only  ~20 Å, although all the gas neutral species (except H2 and He) are now depleted onto grains. This maximal depletion in the postshock gas also explains why the mantle is thicker in the postshock gas (~230 Å) than in the preshock gas (~150 Å) when shattering is ignored (dashed curve).

4.2. Feedback of shattering on the shock

thumbnail Fig. 6

Temperature, density (top) and velocity profiles in the shock frame (bottom) for our standard 30 km s-1 C shock, with (solid) and without shattering (dashed). The dotted line shows a model with shattering when accretion is turned off.

thumbnail Fig. 7

Evolution of the fractional abundances of ions (red), free electrons (blue), positive (pink) and negative (black) charges on dust grains, as a function of flow time in our standard shock, with (solid) and without (dashed) shattering. Horizontal axis: see caption of Fig. 3.

The huge production of very small fragments presented in Fig. 4 has a strong impact on the shock itself. It does this in two ways.

First, shattering reinforces the collisional coupling between the gas and the charged fluid by increasing the collisional dust cross-section7 (see Fig. 5). Figure 6 compares the shock profiles when shattering is included with the Paper I model presented in Fig. 1 where shattering was ignored. Shattering reduces the shock length by a factor  ~3−5, thus raising the peak temperature of the shock by a factor  ~2 (from  ~3200 K to  ~6100 K). Whereas the activation or de-activation of accretion does not modify the temperature profile when shattering is ignored, it has a slight effect on the temperature tail (below 100 K) when shattering is introduced. Accretion takes coolants like H2O from the gas phase: the gas is then cooled only by collisions with dust.

Second, as shown in Fig. 7, shattering accelerates the recombination of ions on the grain surfaces, thus strongly lowering the ionisation fraction of the gas compared to a model without shattering. By charging negatively, very small fragments also deplete electrons from the gas faster than they deplete ions. Charged grains therefore become the dominant charge carrying species in this weakly ionised plasma, similar to what happens in dusty plasmas studied in laboratories (for a review of the subject see Fortov et al. 2005).

4.3. Feedback of shattering on grain charge and dynamics

thumbnail Fig. 8

Evolution of the average electric charge carried by silicate grains in our standard shock, with (solid) and without (dashed) shattering. Horizontal axis: see caption of Fig. 3.

Shattering would not be so important in C shocks if it had no feedback on the ionisation fraction of the gas, which in turn affects the charge and dynamics of grains and increases the level of shattering and vaporisation. As shown in Fig. 8, the evolution of grain charge differs depending on whether dust evolution and its feedback on the shock structure is ignored or not. A striking effect happens when the numerous fragments produced by grain shattering deplete electrons from the gas: the current of electrons onto the grains, which sustains their high negative charge, suddenly drops. Due to their larger cross-section, large grains are affected faster than smaller grains by this change in the ionisation properties of the gas8: grains do not react randomly to the change in the ionisation conditions but in order of decreasing radius. In Fig. 8, the charge of the 1600 Å grain is the first to flip to positive values, followed by that of the 800 Å grain, whereas the average charge of the 400 Å grain does not flip but remains negative. This situation, where large positive grains and small negative grains coexist and are the dominant charge carriers (not the ions and electrons), persists in the shock tail.

thumbnail Fig. 9

Grain velocities along (top) and perpendicular (bottom) to the shock propagation direction, for 4 silicate grain sizes, in our standard shock with shattering. Horizontal axis: see caption of Fig. 3. The dashed line represents the neutral gas velocity when shattering is ignored as in Fig. 1.

thumbnail Fig. 10

Average velocity of neutral grains in the shock direction (top) and fraction of neutral grain in the shock (bottom) for 3 grains sizes in our standard shock with shattering and vaporisation. Horizontal axis: see caption of Fig. 3.

Shattering is self-reinforced in two ways. First, charge flips sign when the depletion of electrons occurs and this has a direct impact on the dynamics of the large grains (Fig. 9). As their charge goes through zero toward positive values (Fig. 8), their coupling to the magnetic field lines weakens and is briefly overcome by gas drag: large grains then decouple from the ions. They start gyrating again when their charge reaches high positive values (Fig. 9). This new gyration phase is rapidly stopped by the gas drag due to the high density of the postshock gas but provides high-velocity, grain-grain collisions that fragment large grains that would otherwise have been protected by their strong coupling to the magnetic field. Second, the depletion of electrons increases the lifetime of very small neutral grains by delaying their capture of electrons. Small neutral grains have enough time to couple to the gas before being charged again, even for sizes close to 100 Å (see Fig. 10). Electron depletion also increases their fractional abundance, relative to charged grains, by moving the average grain charge toward zero. The presence of very small, fast-moving neutral grains enhances the destruction of large grains by cratering9 their surface, which in turn re-injects a large quantity of small grains. Shattering is therefore self-reinforced, a positive feedback which can only stop when the neutral and charged fluids re-couple, i.e. when the shock ends, a condition that is met sooner when shattering is active (Fig. 6).

As can be seen in Fig. 10, small grains are mainly neutral in the postshock gas, unlike in the preshock gas where they were mostly negatively charged. This well-known effect of dusty plasma physics is due to the depletion of electrons from the gas, which is itself triggered by the overpopulation of small grains.

4.4. Dust destruction by vaporisation and sputtering

thumbnail Fig. 11

Fractional destruction for (left) silicate and (right) carbonaceous grains in C shocks propagating in a cloud of preshock density 104 cm-3 (top) and 105 cm-3 (bottom). In the 105 cm-3 case, the dashed line represents the destruction by sputtering when grain-grain processing, i.e. shattering and vaporisation, is ignored. The intensity of the preshock magnetic field is scaled to obtain critical shocks (see Sect. 2.1 and Table 1).

Figure 11 displays the degree of dust destruction predicted by our model arising from the sputtering and vaporisation of silicate and carbon grains. At a preshock density of 104 cm-3, vaporisation is negligible compared to sputtering. At a higher preshock density of 105 cm-3, vaporisation is significant at all shock velocities and dominates over sputtering. At low shock velocities grain-grain impact collisions are close to the vaporisation threshold, a highly non-linear regime. In that shock velocity range vaporisation is dominated by collisions between large grains during their gyration phase. As the gas drag damps more rapidly the gyration of carbon grains than that of silicates grains (their specific density is only 2.2 g cm-3, compared to 3.3 g cm-3 for silicates), we find that carbon grains experience less destruction by vaporisation than silicate grains. In higher-velocity shocks shattering is more intense, which in turn has a feedback on vaporisation: high-velocity ( ≥ 20 km s-1) collisions between very small neutral grains (which follow the gas) and other grains (which are coupled to the ions) leads to significant vaporisation. As shattering is more important for carbon grains than for silicate grains (see Fig. 4), this results in a higher destruction of carbon grains than silicate grains by vaporisation for high-velocity shocks.

The degree of dust destruction obtained with our shock model when grain-grain processing is ignored is also displayed in Fig. 11 (dashed lines). We can see that the degree of sputtering is different with and without grain shattering, especially for carbon grains. This is a consequence of the large increase of the total dust cross-section due to dust fragmentation, which increases the sputtering rate by the same factor. This result is not straightforward: to have a feedback at the level of sputtering, shattering must significantly increase the total cross-section before sputtering ends, i.e. before the gas has been slowed down to a velocity equal to the sputtering threshold. This feedback is therefore important in high-velocity shocks and for carbon grains which have a low shattering threshold (1.2 km s-1) and are therefore easily fragmented early in the shock.

When comparing our sputtering results with those of Gusdorf et al. (2008), a model also based on the Flower & Pineau des Forêts (2003) shock code, one should keep in mind that sputtering is strongly influenced by the preshock magnetic field intensity, which is different in the two studies (see Table 1).

4.5. The higher the density, the more the shattering

There is a general trend for stronger shattering at higher densities because the ratio of the drag force to the Lorentz force increases with the density (e.g. Chapman & Wardle 2006). Large grains ( ≫ 100 Å) tend to decouple from the magnetic field in the shock at high densities (~106 cm-3). The predicted dust dynamics present a large velocity dispersion in the early phase of the shock, from the smaller charged grains which remain strongly coupled to the ions to the larger grains that first follow the gas because of their high inertia and then couple to the ions once they have started their gyration or become partially coupled to both fluids (see Paper I for more details). This large velocity dispersion in the hottest part of the shock is optimal for the fragmentation of grains10. So even without the feedback of shattering onto the shock dynamics and ionisation, we expect shattering to become more important at higher densities.

When the feedback due to shattering on the ionisation state of the gas is introduced, the tendency for more shattering at high densities is reinforced. Higher density gas has a lower ionisation fraction and is therefore more sensitive to the presence of small fragments which capture electrons: the depletion of free electrons from the gas is such that more and more grains tend toward zero charge, and decouple from the magnetic field, providing more impactors for fragmentation.

thumbnail Fig. 12

Initial (black) and final core size distributions (mantles not included) for silicate (red) and carbon (blue) dust in C shocks propagating at various velocities in a cloud of preshock density 104 cm-3 (top) and 105 cm-3 (bottom).

Modelling dust fragmentation in C shocks therefore leads to the conclusion that fragmentation is more important at high densities. Figure 12 compares the final size distribution for silicate and carbon grains at a preshock density of 104 and 105 cm-3, for increasing shock velocities. At 104 cm-3, the shattering intensity is weak because grains are strongly coupled to the magnetic field lines (see Paper I, Fig. 3) and because the higher ionisation fraction at this density limits the feedback of grain shattering on the ionisation state of the gas, thus breaking the positive feedback of shattering. Higher shock velocities also mean larger charges for grains, therefore a better coupling of large grains to the magnetic field and less small neutral grains, resulting in less shattering. In this case grain fragmentation mainly occurs during the short grain gyration phase early in the shock. At a density of 104 cm-3 C shock models can therefore safely ignore fragmentation. At 105 cm-3, shattering is more important because its range of action extends well beyond the gyration phase. Grains are less coupled to the magnetic field lines compared to the 104 cm-3 case because the Lorentz force11 has increased by a factor 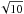10\hbox{$\sqrt{10}$}, whereas the drag force has increased by a factor 10. The preshock ionisation fraction is also lower (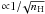∝1/nH\hbox{${\propto} 1{/}\!{\sqrt{\nH}}$}, e.g. Hartquist et al. 1992), thus favouring electron depletion and consequently the decoupling of large grains and very small neutral grains from the magnetic field. For high shock velocities, shattering “digs a deeper hole” in the size distribution close to 100 Å for silicate grains and 300 Å for carbon grains. This feature is characteristic of the shattering by very small grains (a few nanometers in radius) which are very abundant and efficient at breaking grains  ~10 times larger than themselves (see Jones et al. 1996). At higher densities (106 cm-3), our steady-state shock code does not converge because the feedback of shattering on the shock is too strong, even at a velocity of 20 km s-1. As we show below, the threshold density at which shattering starts to be non-negligible is model-dependent. Figure 12 is presented here only for illustration purposes. However, this threshold density probably lies between 104 and 105 cm-3.

5. Discussion

In this section, we discuss how our results depend on our model and assumptions. Our general argument is that some model-dependent effects, that tend to limit the effects of shattering, are counteracted by the trend of more shattering at higher densities as discussed above. The question is not therefore whether this effect happens but at what density does it start to become important.

5.1. Which model for the very small fragments?

In our model shattering in C shocks can become self-enhanced: the more small fragments the shock produces, the more small neutral grains become decoupled from the magnetic field lines, which results in more shattering. This positive feedback of the shattering process on itself can only stop when the shock ends, a process that shattering accelerates by increasing the coupling between the charged and neutral fluids. Our results therefore depend on the physical model for the fragments: their smallest size (5 Å here), their size distribution, their initial charge distribution and the capability of small fragments to craterize other grains.

The smallest grains control the depletion of electrons from the gas, and because their size distribution is a power-law with index  −3.3 (see Sect. 3.2), the smaller their minimum size, the higher their number density and the stronger their feedback onto the ionisation of the gas. By choosing a larger minimum size for fragments (e.g.  10 Å) or smaller index (e.g.   −3.0), the feedback of shattering on the shock becomes less important at densities (here e.g.  105 cm-3) where it was dominant with a smaller minimum fragment size (here 5 Å).

The charge distribution of the fragments at the time they are produced by the excavation flow is unknown. Unfortunately, it has major consequences for their future dynamics because their charge fluctuation time is not negligible compared to the flow time. In our model we decided to choose a charge distribution which minimizes the effect of shattering in the shock. This can be done by imposing the condition that no neutral fragments are produced (neutral fragments would immediatly and efficiently craterize grains by following the gas). Any other hypothesis on the charge distribution of fragments leads to a stronger, or even catastrophic, effect of shattering on the dust size distribution. Numerically, once the charge distribution of fragments is set, we simply share the possible neutral grains equally between charge Z =  −1 and Z =  +1. Charged fragments may become subsequently neutral by the charging process. We have also minimized the effects of shattering in shocks by ignoring fragmentation (but not vaporisation) in collisions involving very small grains (the last two bins: 5−8 Å, and 8–12 Å). These fragments, however, still have an impact on the ionisation state of the gas by capturing electrons. With this conservative hypothesis, we still find an important effect of shattering at preshock densities relevant to astrophysical observations such as molecular outflows. Thus, here we minimise the effects of shattering in all of our models.

5.2. What is the influence of the ionisation model for the gas?

thumbnail Fig. 13

Initial (black) and final size distributions (mantles not included) for silicate (red) and carbon (blue) dust (mantles not included) for our standard shock model (30 km s-1, 105 cm-3) varying the cosmic ray ionisation rate ζ.

The ionisation of the gas is an important ingredient in our model because the grain charge, combined with the gas drag, determines the coupling of grains to the magnetic field. When the ionisation fraction is large (≫10-7), the grain charge is found to be proportional to the grain radius and the electron/ion temperature (Spitzer 1941). When the ionisation fraction is low, grain charge feeds back onto the ionisation state and the resulting grain charge is lower due to the electron depletion from the gas (Pilipp et al. 1990; Paper I). This results in a weaker coupling of grains to the magnetic field.

The ionisation fraction depends on the density, the cosmic ray ionisation rate per H nucleus, ζ, and the radiation field. In this article we ignore the radiation field because of the large extinction found in dense clouds. The dependence on the density was presented in Sect. 4.5. Figure 13 compares the final dust size distribution with various ζ: 10-17 s-1, 5 × 10-17 s-1 and 10-16 s-1, for our standard shock model (30 km s-1, 105 cm-3). The impact of cosmic-ray ionisation on the shattering of grains in the shock only weakly increases with ζ as the ionisation fraction in the shock is primarly determined by the friction between the neutral and charged fluids and not by ζ. With a similar degree of shattering, these shocks also share the same temperature profile (shown in Fig. 6) so the effect of ζ on shattering can be ignored.

Grain charge, and therefore grain coupling to the magnetic field, also depend on the electron temperature. In our model, we imposed the same temperature for electrons and ions, unlike in Paper I and in other C shock models (Draine et al. 1983; Flower & Pineau des Forêts 2003) where the electron temperature is lower than the ion temperature. The reason for this restriction is numerical: the shortage of electrons that appears in the shock (see Fig. 7) prevents the calculation of an independent electron temperature when no more electrons are present in the gas. In this article, we therefore decided to impose a common temperature for the electrons and ions. If however the electron temperature is lower than the ion temperature, the grain charge would be lower12, and grains would be less coupled to the magnetic field lines. We would therefore expect more shattering, which also means that the importance of shattering would start at lower densities. An electron temperature higher than the ion temperature would have the opposite effect.

5.3. Could coagulation compensate for the shattering?

thumbnail Fig. 14

Initial (black) and final (red) silicate dust size distributions (mantles not included) for our standard shock at a flow time of 1000 yr, with (solid) and without (dashed) grain coagulation included.

When two grains collide at low velocities (<1 km s-1), they can stick to each other and form an aggregate. Such conditions are not present in the hottest parts of the shock but are present in the shock tail where the charged and neutral fluids are almost recoupled. To check if coagulation is able to couterbalance the effects of shattering in C shocks, we implemented a simplified coagulation model. We assume that coagulation between two grains only happens if the impact velocity is lower than a critical velocity: ΔV < 0.4   a − 5/6 (in cgs units) where a is the reduced radius of the colliding grains (Chokshi et al. 1993; Poppe & Blum 1997). For simplicity, the resulting coagulated grain is assumed to be spherical, compact and pure. These restrictions are imposed by our numerical model and result from our inability to model the coagulation between carbonaceous and silicate grains. This leads to an underestimate of the rate of coagulation by a factor of  ~2, which is not critical here. Our adapted coagulation method will be presented in a forthcoming paper.

The coulombian interaction is usually thought to prevent coagulation (e.g. Okuzumi 2009) because large grains are negatively charged in normal plasmas. The situation is different in dusty plasmas like C shocks, where the electron depletion produces positive grains (Fig. 7), as well as neutral grains. Following the model by Ossenkopf (1993), we include the effect of charge attraction and repulsion in the collisional cross-section between charged grains, and induced-dipole attraction between charged and neutral grains. The results for our standard shock is displayed in Fig. 14, where we have stopped the integration at a time of 1000 yr (a time rather long for this shock, see Fig. 1). We find that coagulation diminishes the abundance of very small grains (5–10 Å) but is unable to remove grains of a few nanometers in radii, or to rebuild large grains. There is even an interplay between coagulation and grain charging which leads to the paradoxical result that large grains are more shattered when coagulation is activated. This happens because coagulation between oppositely charged grains is favoured by the coulombian interaction and tends to drive grain charge toward zero earlier in the shock than without coulombian-enhanced coagulation. Large grains then decouple from the magnetic field lines and shattering starts again earlier.

5.4. Vaporisation

thumbnail Fig. 15

Fractional abundances of Si (blue) and SiO (red) through our standard (30 km s-1, 105 cm-3) C shock when shattering and vaporisation are ignored (top) or taken into account (bottom), together with the corresponding temperature profile of the neutrals (black). Vaporisation produces warm SiO whereas sputtering produces cold SiO.

An important result of our study, shown in Fig. 11, is that vaporisation may be the dominant destructive process for dust in C shocks at high densities (nH ≥ 105 cm-3). We currently lack laboratory constraints on the vaporisation of sub-microns grains, but this process has nevertheless interesting observational consequences. As discussed in Paper II, vaporisation probably produces SiO directly upon collision, unlike sputtering which releases atomic Si which later reacts with OH or O2 to produce SiO. As shown in Fig. 15b, vaporisation therefore produces warm SiO early in the shock, when the gas is at a thousand K. In contrast, sputtering is only the first step in the production of a cold SiO through the reactions of Si with O2 or OH (Fig. 15a). SiO forms later in the shock when the gas temperature is a few hundreds K because of the characteristical time of those reactions (Gusdorf et al. 2008). However, as the C shock is shorter when the feedback of fragmentation onto the shock is included, there is also a lower column density of warm gas in the shock. It therefore remains to be calculated how the inclusion of shattering and vaporisation in C shocks models will affect the SiO lines profiles.

6. Conclusions

In this article, we have studied the evolution of dust in C-type shocks. We include the sputtering of grain cores and mantles and, for the first time, shattering and vaporisation in grain-grain collisions. Our shock code self-consistently couples the evolution of the size distributions of silicate and carbon grains with the shock dynamics, ionisation state and chemistry.

We first stress the strong impact of shattering in C shocks, both on the dust size distribution and the shock dynamics. Shattering in grain-grain collisions, by breaking up the larger grains, produces a high density of very small fragments, which in return make the shock hotter and shorter because of the increased collisional coupling between the charged and neutral fluids. This effect is important for preshock densities greater than  ~105 cm-3  but is negligible at lower densities ( ≲ 104 cm-3).

Our second major result is that dust destruction by grain-grain collisions (vaporisation) dominates over that by gas-grain

collisions (sputtering) at high densities (nH ≳ 105 cm-3), but is negligible at lower densities (nH ≲ 104 cm-3), like shattering. Dust grains can also be destroyed through vaporisation for a range of shock velocities (20−25 km s-1) where sputtering is not efficient. Vaporisation directly produces SiO in the hottest part of the shock, whereas the production of SiO from the sputtering of Si and the subsequent chemical reactions with O-bearing species such as O2 and OH only appears in the colder part of the shock. Vaporisation could therefore be discernable from sputtering in the predicted SiO line profiles. This will be the subject of a forthcoming paper.

Our detailed results depend on the choice of parameters for the shattering and charging models of small grains, but the general trend of a higher shattering, vaporisation and stronger feedback onto the shock dynamics at higher densities seems inescapable for the steady-state transverse C shock model studied here. The effect should even be enhanced in oblique shocks where grains collide at higher velocities because of out-of-shock-plane motion (Wardle 1998; Chapman & Wardle 2006).

1

All velocities are measured in the shock frame, a frame moving toward the preshock gas at the shock velocity.

2

Unlike in Paper I, here the electrons and ions share a common temperature (see Sect. 5.2).

3

Our assumed cosmic-ray ionisation rate per H nucleus is ζ    =    10-17   s-1.

4

As justified in Paper I, betatron acceleration (Spitzer 1976) can be ignored in C shocks propagating in dense clouds.

5

As justified in Paper II, we assume that the vaporisation of silicate grain cores directly produces SiO molecules from olivine-type silicates (i.e. with a stoechiometry MgFeSiO4).

6

Carbon grains are more fragile to shattering than silicate grains (see Sect. 3). However, this will depend upon the nature of the carbon in the grains, see e.g. Serra Díaz-Cano & Jones (2008).

7

Dust grains dominate the ions in their coupling with the neutral gas in C-type shocks at high densities (Draine et al. 1983).

8

The characteristical time for a grain to reach its equilibrium charge is inversely proportional to its radius (e.g. Horanyi 1996). It can be of the order of the shock dynamical time for very small grains and a very low ionisation level, as it happens here.

9

A process which may be closer to sputtering than shattering.

10

It is also optimal for coagulation, but only in the shock tail where the velocity dispersion does not exceed  ~1 km s-1 (see Sect. 5.3).

11

The Lorentz force is proportional to the magnetic field intensity B which, in the preshock gas, scales as the square root of the density nH, see Sect. 2.1.

12

Grain charge is proportional to the electron temperature, not to the ion temperature (Draine & Sutin 1987).

Acknowledgments

We would like to thank the referee for a careful reading of the manuscript and useful comments. The authors also thank Antoine Gusdorf, Sylvie Cabrit and Alexei Ivlev for interesting discussions and suggestions. This research acknowledges the support of the french Agence Nationale de la Recherche (ANR) through the program Cold dust (ANR-07-BLAN-0364-01).

References

  1. Barlow, M. J. 1978, MNRAS, 183, 367 [NASA ADS] [CrossRef] [Google Scholar]
  2. Caselli, P., Hartquist, T. W., & Havnes, O. 1997, A&A, 322, 296 [NASA ADS] [Google Scholar]
  3. Chapman, J. F., & Wardle, M. 2006, MNRAS, 371, 513 [NASA ADS] [CrossRef] [Google Scholar]
  4. Chokshi, A., Tielens, A. G. G. M., & Hollenbach, D. J. 1993, ApJ, 407, 806 [Google Scholar]
  5. Crutcher, R. M. 1999, ApJ, 520, 706 [NASA ADS] [CrossRef] [Google Scholar]
  6. Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
  7. Draine, B. T., & McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS] [CrossRef] [Google Scholar]
  8. Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
  9. Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
  10. Draine, B. T., Roberge, W. G., & Dalgarno, A. 1983, ApJ, 264, 485 [NASA ADS] [CrossRef] [Google Scholar]
  11. Flower, D., & Pineau des Forêts, G. 2003, MNRAS, 343, 390 [NASA ADS] [CrossRef] [Google Scholar]
  12. Flower, D., Bourlot, J. L., Pineau des Forêts, G., & Cabrit, S. 2003, MNRAS, 341, 70 [NASA ADS] [CrossRef] [Google Scholar]
  13. Fortov, V. E., Ivlev, A. V., Khrapak, S. A., Khrapak, A. G., & Morfill, G. E. 2005, Phys. Rep., 421, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  14. Guillet, V., Pineau des Forêts, G., & Jones, A. P. 2007, A&A, 476, 263 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Guillet, V., Jones, A. P., & Pineau des Forêts, G. 2009, A&A, 497, 145 (Paper II) [Google Scholar]
  16. Gusdorf, A., Cabrit, S., Flower, D., & Pineau des Forêts, G. 2008, A&A, 482, 809 [Google Scholar]
  17. Hartquist, T. W., Havnes, O., & Morfill, G. E. 1992, Fund. Cosm. Phys., 15, 107 [NASA ADS] [Google Scholar]
  18. Hirashita, H., & Yan, H. 2009, MNRAS, 233 [Google Scholar]
  19. Horanyi, M. 1996, ARA&A, 34, 383 [NASA ADS] [CrossRef] [Google Scholar]
  20. Jiménez-Serra, I., Caselli, P., Martín-Pintado, J., & Hartquist, T. W. 2008, A&A, 482, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
  22. Jurac, S., Baragiola, R. A., Johnson, R. E., & Sittler, E. C. 1995, J. Geophys. Res., 100, 14821 [NASA ADS] [CrossRef] [Google Scholar]
  23. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  24. May, P. W., Pineau des Forêts, G., Flower, D., et al. 2000, MNRAS, 318, 809 [NASA ADS] [CrossRef] [Google Scholar]
  25. Okuzumi, S. 2009, ApJ, 698, 1122 [NASA ADS] [CrossRef] [Google Scholar]
  26. Ossenkopf, V. 1993, A&A, 280, 617 [NASA ADS] [Google Scholar]
  27. Pilipp, W., Hartquist, T. W., & Havnes, O. 1990, MNRAS, 243, 685 [NASA ADS] [Google Scholar]
  28. Poppe, T., & Blum, J. 1997, Adv. Space Res., 20, 1595 [NASA ADS] [CrossRef] [Google Scholar]
  29. Schilke, P., Walmsley, M., Pineau des Forêts, G., & Flower, D. 1997, A&A, 321, 293 [NASA ADS] [Google Scholar]
  30. Serra Díaz-Cano, L., & Jones, A. P. 2008, A&A, 492, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Spitzer, L. J. 1941, ApJ, 93, 369 [NASA ADS] [CrossRef] [Google Scholar]
  32. Spitzer, L. J. 1976, Comm. Astrophys., 6, 177 [Google Scholar]
  33. Tielens, A. G. G. M., McKee, C. F., Seab, G. C., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
  34. Wardle, M. 1998, MNRAS, 298, 507 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Parameter 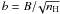b=B/nH\hbox{$b=B/\!\sqrt{\nH}$} relating the preshock magnetic field to the preshock proton density, and the corresponding magnetic field intensity (shown as b/B   (μG)), as a function of shock velocity Vs and preshock density nH for our critical shocks. Our standard model is framed.

In the text

All Figures

thumbnail Fig. 1

(Top) Temperature, density and (bottom) velocity profiles in the shock frame for our standard 30 km s-1 C shock, propagating in a molecular cloud of preshock density nH0 = 105 cm-3 and transverse magnetic field B = 417   μG (b = 1.32). As in Paper I, grain-grain processing is ignored.
In the text
thumbnail Fig. 2

(Top) Average charge in our standard shock for large and small grains, with the ion-electron temperature superimposed. (Bottom) Fractional density of ions Xions = ni/nH (red curve), free electrons Xe −  = ne/nH (blue curve) and negative charge on the dust surface per proton (black curve). Grain-grain processing is ignored.
In the text
thumbnail Fig. 3

Silicate grain velocities along (top) and perpendicular (bottom) to the shock propagation direction of our standard shock, for large charged grains and one small neutral grain size. Horizontal axis is linear at flow time  < 10 yr to zoom onto the grain motion, then logarithmic to show the whole shock. Grain-grain processing is ignored.
In the text
thumbnail Fig. 4

Initial (black) and final core size distributions (mantles not included) for silicate (red) and carbon (blue) grains in our standard C shock.
In the text
thumbnail Fig. 5

Evolution of the total grain cross-section  ⟨ nσ ⟩  carried by dust in our standard shock model, with (red) and without (black) taking into account grain mantles, normalised by flux to its preshock value ( ⟨ nσV ⟩ / ⟨ nσ ⟩ 0Vs), with (solid) and without (dashed) shattering.
In the text
thumbnail Fig. 6

Temperature, density (top) and velocity profiles in the shock frame (bottom) for our standard 30 km s-1 C shock, with (solid) and without shattering (dashed). The dotted line shows a model with shattering when accretion is turned off.
In the text
thumbnail Fig. 7

Evolution of the fractional abundances of ions (red), free electrons (blue), positive (pink) and negative (black) charges on dust grains, as a function of flow time in our standard shock, with (solid) and without (dashed) shattering. Horizontal axis: see caption of Fig. 3.
In the text
thumbnail Fig. 8

Evolution of the average electric charge carried by silicate grains in our standard shock, with (solid) and without (dashed) shattering. Horizontal axis: see caption of Fig. 3.
In the text
thumbnail Fig. 9

Grain velocities along (top) and perpendicular (bottom) to the shock propagation direction, for 4 silicate grain sizes, in our standard shock with shattering. Horizontal axis: see caption of Fig. 3. The dashed line represents the neutral gas velocity when shattering is ignored as in Fig. 1.
In the text
thumbnail Fig. 10

Average velocity of neutral grains in the shock direction (top) and fraction of neutral grain in the shock (bottom) for 3 grains sizes in our standard shock with shattering and vaporisation. Horizontal axis: see caption of Fig. 3.
In the text
thumbnail Fig. 11

Fractional destruction for (left) silicate and (right) carbonaceous grains in C shocks propagating in a cloud of preshock density 104 cm-3 (top) and 105 cm-3 (bottom). In the 105 cm-3 case, the dashed line represents the destruction by sputtering when grain-grain processing, i.e. shattering and vaporisation, is ignored. The intensity of the preshock magnetic field is scaled to obtain critical shocks (see Sect. 2.1 and Table 1).

In the text
thumbnail Fig. 12

Initial (black) and final core size distributions (mantles not included) for silicate (red) and carbon (blue) dust in C shocks propagating at various velocities in a cloud of preshock density 104 cm-3 (top) and 105 cm-3 (bottom).
In the text
thumbnail Fig. 13

Initial (black) and final size distributions (mantles not included) for silicate (red) and carbon (blue) dust (mantles not included) for our standard shock model (30 km s-1, 105 cm-3) varying the cosmic ray ionisation rate ζ.
In the text
thumbnail Fig. 14

Initial (black) and final (red) silicate dust size distributions (mantles not included) for our standard shock at a flow time of 1000 yr, with (solid) and without (dashed) grain coagulation included.
In the text
thumbnail Fig. 15

Fractional abundances of Si (blue) and SiO (red) through our standard (30 km s-1, 105 cm-3) C shock when shattering and vaporisation are ignored (top) or taken into account (bottom), together with the corresponding temperature profile of the neutrals (black). Vaporisation produces warm SiO whereas sputtering produces cold SiO.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.