EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 527 (March 2011) A&A, 527 (2011) A33 Full HTML
Free Access
Issue
A&A
Volume 527, March 2011
Article Number A33
Number of page(s) 7
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201015573
Published online 21 January 2011

© ESO, 2011

1. Introduction

Observable matter in galaxies and in clusters of galaxies cannot produce sufficient gravity to explain their dynamics. Cold dark matter (CDM) scenarios or alternative theories of gravitation are therefore invoked to resolve the problem. Nowadays, the CDM hypothesis is the dominant paradigm. This hypothetical matter does not interact with electromagnetic radiation and only shows its presence through its gravitational interaction. Even though the dark matter hypothesis has successfully explained the internal dynamics of galaxy clusters, gravitational lensing, and the standard model of cosmology within the framework of general relativity (GR) (Spergel 2003), much experimental effort has failed to yield a detection of dark matter particles. Moreover the results of high-resolution simulations of structure formation do not reproduce some observations on galactic scales, such as the central structures of rotation curves, the prevalence of low bulge-to-disc ratios, and the numbers and spatial distribution of the subhalos (Klypin et al. 1999; Moore et al. 1999; Metz et al. 2008; Kroupa et al. 2010). Even the ability of the dark matter theory to account for the Tully-Fisher and Freeman relations is controversial (Bosch & Dalcanton 2000; Governato et al. 2010). These shortcomings have not led to the rejection of the theory only because on galactic scales baryons are at least non-negligible contributors to the mass density, consequently simulations that include the complex physics of star formation are essential for reliable predictions. Currently such simulations are still at an experimental stage and are usually substituted by “semi-analytic” arguments that have weak theoretical underpinnings.

One of the alternative theories to CDM is the so-called modified Newtonian dynamics (MOND) theory, which was originally proposed by Milgrom (1983) to explain the flat rotation curves of spiral galaxies at large distances by a modification of Newton’s second law of acceleration below a characteristic scale of a0 ≃ 1.2 × 10-10 m s-2 = 3.6 pc/(Myr)2 without invoking dark matter (Bekenstein & Milgrom 1984). In MOND, Newton’s second law is modified to μ(a/a0)a = aN + ∇ × H, where ρ is the mass-density distribution, aN is the Newtonian acceleration vector, a is the MONDian acceleration vector, a = |a| is the absolute value of MONDian acceleration, μ is an interpolating function for the transition from the Newtonian to the MONDian regime, which runs smoothly from μ(x) = x at x ≪ 1 to μ(x) = 1 at x ≫ 1 (Bekenstein & Milgrom 1984). Different interpolating functions have been suggested, such as the simple function, μ(x) = x/(1 + x) (Famaey & Binney 2005) and the standard interpolation function, 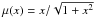μ(x)=x/1+x2$\mu(x)=x/\sqrt{1+x^2}$ (Milgrom 1983). Because the simple function fits galactic rotation curves better than the standard function (Gentile et al. 2011), in this paper we use the simple function. The value of the curl field H depends on the boundary conditions and the spatial mass distribution and vanishes only for some special symmetries (Bekenstein & Milgrom 1984). The non-linearity of the MOND field equation leads to difficulties for standard N-body codes and makes the use of the usual Newtonian N-body simulation codes impossible in the MOND regime.

It has been shown that on galactic scales MOND can explain many phenomena better than CDM (Begmann 1989; Begmann et al. 1991; Sanders & McGaugh 2002; Sanchez-Salcedo & Hernandez 2007; Haghi et al. 2006; Malekjani et al. 2009; Gentile et al. 2007; Milgrom 1994; Brada & Milgrom 2000; Milgrom 1995; Wu et al. 2008; Zhao & Famaey 2006; Tiret & Combes 2007; Hasani et al. 2010). MOND has been generalized to a general-relativistic version (Bekenstein 2004; Sanders 2005; Zlosnik et al. 2007; Milgrom 2009), making it possible to test its predictions for gravitational lensing. Dynamics of galaxies in clusters (2002) and the merging of galaxy clusters, where the baryonic mass is clearly separated from the gravitational mass (Clowe et al. 2006) cannot be completely explained by MOND without invoking some kind of hot dark matter, perhaps in the form of massive (active or sterile, 2 to 11 eV) neutrinos (Angus et al. 2006, 2010).

In order to decide whether MOND is a comprehensive theory to explain the dynamics of the universe, it is desirable to study MOND for objects in which no dark matter is supposed to exist and where the characteristic acceleration of the stars is less than the MOND critical acceleration parameter a0. Globular clusters (GCs) are a perfect candidate since they are the largest virialized structure that do not contain dark matter (Moore 1996).

In the distant halo of our Milky Way there exist several low-mass GCs where both internal and external accelerations of stars are significantly below the critical acceleration parameter a0 of MOND. Because GCs are assumed to be dark-matter-free, if MOND is true, the motions of stars must deviate from the standard Newtonian dynamics. It has been proposed by Baumgardt (2005) that some of these distant Galactic GCs are perfect tools to test gravitational theories in the regime of very weak accelerations. For MOND, the internal velocity dispersion among the stars in these clusters would be significantly higher than in Newtonian dynamics.

The mean velocity dispersion of stellar systems for the two extreme cases of internal (ai ≫ ae) or external (ae ≫ ai) field domination have been derived analytically by Milgrom (Milgrom 1986, 1994), assuming that the systems are everywhere in the deep-MOND regime (ae,ai ≪ a0). Many systems that can be used to test MOND are not completely either internally or externally dominated. Globular clusters or dwarf galaxies of the Milky Way for example have internal and external accelerations that are of the same order (Baumgardt et al. 2005), consequently one has to determine the velocity dispersion numerically for intermediate cases. Sollima & Nipoti (2010) constructed self-consistent, spherical models for stellar systems in MOND, neglecting the external field effect and presented a dynamical model for six galactic GCs. The presence of the external field effect breaks the spherical symmetry and validity of their model. Recently Haghi et al. (2009, hereafter HBK09) investigated the dynamics of star clusters by numerically modeling them in MOND, assuming circular orbits. They performed N-body simulations and presented analytical formulae for the velocity dispersion of stellar systems in the intermediate MOND regime, which are useful for a comparison with observational data of several GCs and dSph galaxies (for details on the numerical calculations see HBK09). In a follow-up paper, Jordi et al. (2009) determined the velocity dispersion (using 17 stars) and mass-function slope of Pal 14 and showed that MOND can hardly explain the low-velocity dispersion of this system. However, Gentile et al. (2010) showed that with the currently available data, the Kolmogorov-Smirnov (KS) test is still unable to exclude MOND with a sufficiently high confidence level. Moreover, the low density of Pal 14 suggests that binary stars may be an important issue for interpreting its measured velocity dispersion (Küpper & Kroupa 2010), and the true velocity dispersion of Pal 14 could be much lower than the value reported by Jordi et al. (2009), thereby possibly posing an even larger challenge for MOND, but also for Newtonian gravity and for any understanding of the dynamics of this object as being in equilibrium.

In this paper we calculate the prediction of MOND and Newtonian dynamics on the velocity dispersion of six other distant clusters of the MW (Table 1). In order to see the pure MONDian effects, we concentrate on systems in which the tidal radius is much larger than the gravitational radius1 and therefore tidal effects are unimportant. In other words, this paper provides the basis for further observational efforts. The measurements of a low- (Newtonian) velocity dispersion would mean that MOND in its present form is in severe trouble and that globular clusters do not possess dark matter. In contrast, a high-velocity dispersion would either favor MOND or could be a hint to the existence of dark matter in GCs (Baumgardt et al. 2009).

The paper is organized as follows: in Sect. 2 we give a brief review of the external field effect (EFE) in MOND. The simulation setup is explained in Sect. 3. The numerical results for six clusters are discussed in Sect. 4. We present our conclusions in Sect. 5.

2. External field effect in MOND

In classical Newtonian dynamics, a uniform external field does not affect the internal dynamics of a stellar system. In other words, in the frame of the system relative motions of objects are the same as in an isolated system.

In MOND, the situation is entirely different. Owing to the non-linearity of Poisson’s equation, the strong equivalence principle (SEP) is violated (Bekenstein & Milgrom 1984), and consequently the internal properties and the morphology of a stellar system are affected by both the internal and external field. This so-called external field effect (EFE) significantly affects non-isolated systems and can provide a strict test for MOND.

The EFE is indeed a phenomenological requirement of MOND and was postulated by Milgrom (1983) to explain the dynamical properties of open clusters in the MW that do not show MONDian effects. The EFE allows high-velocity stars to escape from the potential of the Milky Way (Famaey et al. 2007; Wu et al. 2007) and implies that rotation curves of spiral galaxies should fall where the internal acceleration becomes equal to the external acceleration (Gentile et al. 2007; Wu et al. 2008).

For a star cluster with a density distribution ρc, which is embedded in a host galaxy with a density distribution ρext, the acceleration of stars in the cluster satisfies the modified Poisson equation ∇.[μ(∇Φa0)∇Φ]=4πG(ρc+ρext),\begin{equation} \nabla.\left[\mu\left(\frac{\nabla\Phi}{a_{0}}\right)\nabla\Phi\right] = 4\pi G (\rho_{\rm c}+\rho_{\rm ext}), \label{mon1} \end{equation}(1)where ∇Φ is the MONDian potential generated by the total matter density. For star clusters or dwarf galaxies far out in the halo of the Milky Way the local density of the Milky Way is negligible (i.e. ρext ≪ ρc). One way to solve Eq. (1) is then to assume that the total acceleration is the sum of the internal ai and the external ae acceleration, which both satisfy the modified Poisson equation as (Bekenstein & Milgrom 1984; Wu et al. 2007, 2008; Angus 2008) ∇.[μ(|ae+ai|a0)(ae+ai)]=4πGρc.\begin{equation} \nabla.\left[\mu\left(\frac{|\vec{a}_{\rm e}+\vec{a}_{\rm i}|}{a_{0}}\right)({\vec a_{\rm e}}+{\vec a_{\rm i}})\right] = 4\pi G \rho_{\rm c}. \label{mon2} \end{equation}(2)In Eq. (2), the direction of the external acceleration is important for the dynamics of stars in the clusters. For example, for two stars the acceleration would be different if ae is parallel or anti-parallel to their internal acceleration.

Several attempts have been made considering the EFE. Wu et al. (2007) simulated an isolated object with a static MONDian potential solver, but changed the boundary condition on the outermost grid point to be nonzero. Famaey et al. (2007) estimated the escape velocity of galaxies in MOND and assumed μ(|ae + ai|/a0)ai = aN. As a first order test they replaced |ae + ai| with (ae + ai), or 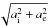ai2+ae2$\sqrt{a_{\rm i}^2+a_{\rm e}^2}$. This is an approximation, since they neglected the direction of ae (i.e. a possible angular difference between ai and ae).

In order to study the evolution of the systems we need to calculate the acceleration at each step by adding the constant external gravitational field to the internal acceleration inside the μ-function, considering the different angle between external and internal acceleration for all stars throughout the evolution.

3. Simulation setup

We performed a large set of N-body simulations of star clusters with the N-MODY code, which has been developed by Ciotti et al. (2006). N-MODY is a parallel, three-dimensional particle-mesh code for the time-integration of collision-less N-body systems (Londrillo & Nipoti 2009). The code numerically solves the non-linear MOND field equations, which can be used to perform numerical experiments in either MONDian or Newtonian dynamics. The potential solver of N-MODY is based on a grid in spherical coordinates and is best suited for modeling isolated systems. N-MODY uses the leap-frog method to advance the particles. The code and the potential solver have been presented and tested by Ciotti et al. (2006) and Nipoti et al. (2007).

In the present study we used a spherical grid (r,θ,ϕ) made of Nr × Nθ × Nϕ = 128 × 128 × 128 grid cells for the integration. The total number of particles is Np = 105. The details of the scaling of the numerical MOND models and code units are discussed in Nipoti et al. (2007).

Our treatment of the external field effect is based on the idea that the star clusters we study are much smaller than they are distant from the Milky Way, so the external field is nearly constant over the cluster area. We carry out the simulations in a rotating reference frame centered on the cluster. We also assume that the clusters are on a circular orbit, so the external field of the Milky Way is also constant with time in the clusters frame.

We assume that tidal forces arising from a gradient of the external field and the Coriolis acceleration caused by the rotating reference frame can be neglected. This is justified as long as the size of the cluster is much smaller than the tidal radius. We then solve Eq. (2) numerically with N-MODY, using a constant acceleration ae as the boundary condition.

In order to include the EFE for non-isolated systems, we applied several changes to the N-MODY code. The changes were encoded in the source file mond-lib.f90, which contains all relevant routines implementing the MOND potential solver. The Mondian potentials and accelerations are assigned to stars in subroutines: “gmond” and “mond-acc”, and we placed the vector of ae in the interpolating function for all stars, i.e., ae is added to ai via vector summation and the code solves Eq. (2) by iteration. At each step of potential solving, we added the constant external field for all grid points according to Eq. (2). This is a first approximation that allows us to focus on the effects of a constant external field, which in turn allows us to deal with the intermediate MOND regime. We would like to stress that our numerical solution agrees very well with analytic ones for the extreme cases ai ≪ ae ≪ a0, ae ≪ ai ≪ a0 and ae,ai ≫ a0 (HBK09).

Our method is a first attempt to take into account the constant EFE in N-MODY, in order to avoid solving the modified Poisson equation for the large area including both galaxy and cluster, which is impossible with the current version of N-MODY. This can only be studied with a realistic, high-resolution MOND simulation that includes the density distribution causing the external field.

In this work we start from Newtonian equilibrium Plummer models and produce MONDian equilibrium initial systems. In order to have a MONDian equilibrium initial system, we increased the initial velocity of the particles. This method is useful when the external field is important. The details of the method are described in HBK09.

thumbnail Fig. 1

Line-of-sight velocity dispersion for clusters listed in Table 1 for various masses as found by N-MODY. In order to compare with the real cluster, the half-mass radii of all models are fixed. For low masses, which mean low internal accelerations, the prediction of Newtonian dynamics differs from the numerical solution. As the mass increases (at about 106 M⊙), the internal acceleration grows and the system enters the Newtonian regime and the numerical solutions get close to the Newtonian prediction. In order to focus on a reasonable range of mass for these clusters, we show the results in the range of 500−2 × 105. Dashed vertical lines show the expected cluster mass, calculated from the absolute luminosity by assuming a stellar mass-to-light ratio of M/LV = 2. This value agrees with observed mass-to-light ratios of galactic GCs (Mieske et al. 2008).

Table 1

Globular clusters modeled in this paper.

4. Modeling the distant globular clusters

We calculated the velocity dispersion for the Galactic GCs mentioned in Table 1. These clusters are best suited for testing MOND. A large set of dissipationless N-MODY computations with MONDian equilibrium initial conditions were performed for stellar systems that are embedded in the outer MW halo and affected by different values of the external field. Clusters in Table 1 are generally far out in the Galactic halo so that the external acceleration caused by the MW is small. In order to produce different internal acceleration regimes, we changed the cluster mass from 500 M⊙ to 107 M⊙ and assume the half-mass radius to be constant. The models are evolved for several crossing times to reach the equilibrium state. The EFE on the predicted line-of-sight velocity dispersion for non-isolated stellar systems with different internal accelerations have been carried out in HBK09.

For the GCs listed in Table 1, observational efforts are underway to determine their velocity dispersion and to constrain their mass (Grebel et al. 2009). Because the half-mass relaxation times of most clusters in Table 1 are on the order of a Hubble time or even larger, dynamical evolution does not play an important role for these clusters, therefore we can assume that the half-light radius is equal to the half-mass radius. The projected half-mass radii, Rhp, and galactocentric distances, RG, are taken from Harris (1996). The projected half-mass radii relate to the three-dimensional half-mass radii as Rhp = γRh with γ ≈ 0.74. For all clusters in Table 1, the tidal radii are larger than the half-mass radii by a factor of 5 to 10, which means that tidal effects play no significant role for the internal dynamics of the clusters in our sample. We perform numerical modeling to obtain the mean velocity dispersion.

thumbnail Fig. 2

Top panel: the ratio of the velocity dispersion in the direction of the external field compared to the perpendicular direction for Pal 3 as an example plotted against the radius. The system is isotropic throughout the cluster. Bottom panel: the anisotropy profile, β, for Pal 3 as an example plotted against the radius. The system is isotropic throughout the cluster.

thumbnail Fig. 3

Upper panel: radial velocity distribution of stars for a Newtonian (red triangles) and MONDian (black dots) system in which both have the same internal velocity dispersion. The smoothed line shows a Gaussian fitted to the distributions. Both distributions follow the Gaussian fit very closely. Lower panel: the relative difference between Newtonian and Mondian velocity distributions. There is a difference between the two models, but it is too small (less than 1%) to be detected observationally.

Because the cluster masses are not known from observations, it is useful to calculate line-of-sight velocity dispersions for different values of cluster mass. If the velocity dispersion is determined observationally, one can constrain the cluster mass. In Fig. 1 the resulting global line-of-sight velocity dispersion as a function of mass is plotted for the six stellar clusters and is compared with the Newtonian results. The black line shows the Newtonian prediction for the velocity dispersion, which we calculate using 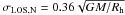σLOS,N=0.36GM/Rh$\sigma_{\rm LOS,N}=0.36\sqrt{GM/R_{\rm h}}$ (Haghi et al. 2009). The red line shows the numerical calculation of the velocity dispersion in the MONDian regime. For each cluster the external acceleration of the Galaxy is given in Table 1. All clusters are in the intermediate regime, for which there is no analytical prediction in MOND. In the low-acceleration region, the numerical solutions show a considerable relative difference with Newtonian results. As the mass increases, the internal acceleration grows and then gets close to the Newtonian results (at about M = 106 M⊙). The vertical dashed lines show the expected mass for each cluster calculated from the absolute luminosities by assuming a stellar mass-to-light ratio of M/L = 2 (Mieske et al. 2008). It should be noted that in the simulations we do not assume any M/L, but we vary the mass and therefore the M/L ratio of the clusters. The velocity dispersions corresponding to this mass for both cases are indicated in Table 1. The M/L ratio of 2 is only used in Table 1 to illustrate there is a MOND effect, which makes a difference for the studied clusters. Our predictions for the MONDian case are lower than those by Baumgardt et al. (2005). The absolute differences between MONDian and Newtonian results are largest for the clusters Pal 4, Pal 3, AM 1, and Eridanus. Therefore these clusters would be the best cases to test MOND. The same qualitative results were also obtained by Sollima & Nipoti (2009), who have studied some of the clusters of our list (i.e., Eridanus, AM1, Pal 3, Pal 4, and Pal 14, which we have studied in HBK09). They have obtained the cluster’s velocity dispersion profile. Their predictions for the velocity dispersion are generally higher than ours. For AM1 for example, the mean value of the velocity dispersion is ~1.7 km s-1 since the predicted MOND velocity dispersion profile is flat throughout the cluster area (Fig. 5 of Sollima & Nipoti 2009). This is higher than the value of 1.5 km s-1 we find, which is to be expected because they did not include the EFE. If we take the EFE into account, the systems tend to be in the quasi-Newotonian regime, where the gravity is weaker than in the deep-Mondian regime (HBK09).

In MOND the external field introduces an anisotropy so that clusters could in principle become elongated. In order to test for a possible elongation of the velocity dispersion in the direction of the external field (σx), we define the parameter 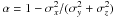α=1−σx2/(σy2+σz2)$\alpha=1-\sigma_x^2/(\sigma_y^2+\sigma_z^2)$. Figure 2 shows that the line-of-sight velocity dispersion in the direction of the external field differs only randomly compared to that perpendicular to the external field. This small a difference would be unobservable.

thumbnail Fig. 4

Mean P-value vs. number of stars in the sample for a number of random realizations of distributions of stars following a Gaussian with a standard deviation of σN for clusters listed in Table 1. The minimum number of stars necessary to reject MOND is defined where the mean P-value drops below 0.05.

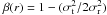In order to show the situation of the isotropy in the velocity dispersion, the anisotropy profile, β(r)=1−(σt2/2σr2)$\beta(r)=1- (\sigma_{\rm t}^2 /2 \sigma_{\rm r}^2)$ for one cluster is plotted in Fig. 2, where, σt is the tangential velocity dispersion and σr is the radial velocity dispersion.

Figure 3 shows the distribution of radial velocities of the Ntotal = 105 stars in the velocity range –10 to +10 km s-1 for both Newtonian (red triangles) and Mondian (black dots) cases together with the best Gaussian fit to this distribution using the least square method. We created the Newtonian model with a mass of 177 000 M⊙ and the Mondian one with a mass of 320 00 M⊙, so that the velocity dispersions are the same. The bottom panel shows the relative deviation, (NNewtonian − NMond)/Ntotal, where N is the number of stars in a velocity bin. Evidently the observed radial velocity distribution is well approximated by this Gaussian. The Newtonian one is slightly different from the Mondian distribution, but the relative difference is very small (less than 1%), therefore it is impossible to find a detectable deviation observationally.

5. Distinguishing between MOND and Newtonian gravity models

Usually, it is not feasible to measure the velocity dispersion of a large sample of stars in distant and low-mass GCs. If only a few stars are measured, the observed velocity dispersion has a large error, which makes it difficult to distinguish between MOND and Newtonian dynamics. Recently, Gentile et al. (2010) have shown that the small sample size for Pal 14 (i.e., radial velocity of 17 stars were used to determine the observed velocity dispersion) can only reject MOND with a low confidence level.

In order to see how many stars are necessary to reject MOND with high statistical confidence if the underlying velocity dispersion is Newtonian, we created artificial data sets of increasing sample size from the Newtonian simulations for each of the six clusters. For each sample size we produced 20 random realizations of a mock sample, and each time applied a KS test with the null hypothesis being that MOND is correct (thus comparing the mock data set from the Newtonian simulation with the velocity dispersion of the MONDian simulation, σMOND). We approximate the cluster mass from the V-band luminosity by assuming a stellar mass-to-light ratio of M/L = 2 (vertical dashed line in Fig. 1). Figure 4 shows the mean P-value from the KS test as a function of the number of stars in the sample. The number of stars changes in the range of [10–160]. For any given cluster and a fixed number of stars a 1-sigma range of P-values are shown as error bars. The minimum number of stars, Nmin, which is necessary to achieve P < 0.05 (i.e. exclusion confidence of 95%), are obtained for each cluster and are given in Table 1. Measurement of Nmin stars should therefore be enough to rule out MOND if the cluster mass is simultaneously determined by independent measurements, possibly through e.g. star counts.

6. Conclusions

We compared global line-of-sight velocity dispersions of six distant low-density GCs of the Milky Way in MONDian and Newtonian dynamics and showed that they have a significantly higher velocity dispersion in MOND than the prediction of Newtonian dynamics.

Using the N-MODY code, we obtained a large set of dissipationless numerical solutions for GCs with the MONDian initial conditions as end-products of the N-body computations by adding the external field. In order to produce different internal acceleration regimes, we changed the mass of the system over a wide range for each cluster. In addition, our results show that the clusters Pal 4, Pal 3, AM 1, and Eridanus are the best cases to test MOND owing to their larger absolute difference between MONDian and Newtonian velocity dispersions. These results will allow us to test MOND more rigorously than was possible so far, and this will enable us to compare MOND with observational data in the future.

Recently Sollima & Nipoti (2010) have performed a test for MOND by constructing self-consistent dynamical models for outer galactic clusters. These authors neglected the external field effect of the Milky Way, and hence obtained higher estimates for the velocity dispersion of clusters compared with our results. This difference is reasonable. Indeed, the external field in MOND is leading the system to move from the deep-MONDian regime toward the quasi-Newtonian regime, and thus to reduce the velocity dispersion. In other words, the larger the external field, the smaller the internal acceleration, which implies a lower velocity dispersion for the cluster (Haghi et al. 2009).

It should be noted that the clusters could be on eccentric orbits, which means that the MOND predictions would be different because of the variation of the external field (in direction and amplitude) along the orbit.

Using a KS test, we calculated the minimum number of stars that are sufficient to exclude MOND (under the hypothesis that these GCs are on circular orbits) at the 95% confidence level. We found that between 30 to 80 stars are necessary for most clusters to distinguish between both cases. This number of stars can be observed with current 8 m class telescopes. Additional observational efforts to determine the velocity dispersions of these clusters and constraining the mass of the clusters by star counts would be highly important and provide a strict test of MOND. On the other hand, if MOND is the correct theory, these observations could be used to constrain the external field and consequently to put constraints on the potential in which the systems are embedded. According to the anisotropy profile, the simulated systems are isotropic throughout.

1

The gravitational radius is a measure of the size of the system and is related to the mass and potential energy as given in Eqs. (2)–(132) in Binney & Tremaine (1987). In many stellar systems the gravitational radius can be approximated by the three-dimensional half-mass radius rh as rg = 1.25rh if the assumption of virial equilibrium is valid.

Acknowledgments

We would like to thank C. Nipoti for providing us with the N-MODY code and his help in using it. H.H. thanks the stellar dynamics group of the Argelander Institute for Astronomy for giving financial support for this research. H.B. acknowledges support from the German Science foundation through a Heisenberg Fellowship and from the Australian Research Council through Future Fellowship grant FT0991052.

References

  1. Angus, G. W. 2008, MNRAS, 387, 1481 [NASA ADS] [CrossRef] [Google Scholar]
  2. Angus, G. W., Famaey, B., & Zhao, H. S. 2006, MNRAS, 371, 138 [NASA ADS] [CrossRef] [Google Scholar]
  3. Angus, G.W., Famaey, B., & Diaferio, A. 2010, MNRAS, 402, 395 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baumgardt, H., Grebel, E. K., & Kroupa, P. 2005, MNRAS, 359, L1 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baumgardt, H., Cote, P., Hilker, M., et al. 2009, MNRAS, 396, 205 [Google Scholar]
  6. Begmann, K. G. 1989, A&A, 233, 47 [NASA ADS] [Google Scholar]
  7. Begmann, K. G., Broeils, A. H., & Sanders, R. H. 1991, MNRAS, 249, 523 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bekenstein, J. 2004, PRD, 70, 083509 [Google Scholar]
  9. Bekenstein, J. D., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
  10. Binney, S., & Tremaine, S. 1987, Galactic Dynamics (Princeton, NJ: Princeton Univ. Press) [Google Scholar]
  11. Bosch, V. D., & Dalcanton, J. J. 2000, ApJ, 534, 146 [NASA ADS] [CrossRef] [Google Scholar]
  12. Brada, R., & Milgrom, M. 2000, ApJ, 541, 556 [NASA ADS] [CrossRef] [Google Scholar]
  13. Clowe, D., Brada, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
  14. Ciotti, L., Londrillo, P., & Nipoti, C. 2006, ApJ, 640, 741 [NASA ADS] [CrossRef] [Google Scholar]
  15. Famaey, B., & Binney, J. 2005, MNRAS, 361, 633 [NASA ADS] [CrossRef] [Google Scholar]
  16. Famaey, B., Bruneton, J., & Zhao, H. S. 2007, MNRAS, 377, L79 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gentile, G., Famaey, B., Combes, F., et al. 2007, A&A, 472, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Gentile, G., Famaey, B., Angus, G., & Kroupa, P. 2010, A&A, 509, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gentile, G., Famaey, B., & de Blok, W. J. G. 2011, A&A, in press [arXiv:1011.4148] [Google Scholar]
  20. Governato, F., Brook, C., & Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Haghi, H., Rahvar, S., & Hasani Zonoozi, A. 2006, ApJ, 652, 354 [NASA ADS] [CrossRef] [Google Scholar]
  22. Haghi, H., Baumgardt, H., Kroupa, P., et al. 2009, MNRAS, 395, 1549 (HBK09) [NASA ADS] [CrossRef] [Google Scholar]
  23. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hasani Zonoozi, A., & Haghi, H. 2010, A&A, 524, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Jordi, K., Grebel, E. K., Hilker, M., et al. 2009, AJ, 137, 4586 [NASA ADS] [CrossRef] [Google Scholar]
  26. Klypin, A., Kravtsov, A. V., Valenzuela, O., & Prada, F. 1999, ApJ, 522, 82 [Google Scholar]
  27. Kroupa, P., Famaey, B., de Boer, K. S., et al. 2010, A&A, 523, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Küpper, A. H. W., & Kroupa, P. 2010, ApJ, 716, 776 [NASA ADS] [CrossRef] [Google Scholar]
  29. Londrillo, P., & Nipoti, C. 2009, MSAIS, 13, L89 [NASA ADS] [Google Scholar]
  30. Malekjani, M., Rahvar, S., & Haghi, H. 2009, ApJ, 694, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  31. Metz, M., Kroupa, P., & Libeskind, N., 2008, ApJ, 680, 287 [NASA ADS] [CrossRef] [Google Scholar]
  32. Mieske, S., Hilker, M., Jordán, A., et al. 2008, A&A, 487, 921 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Milgrom, M. 1983, ApJ, 270, 365 [NASA ADS] [CrossRef] [Google Scholar]
  34. Milgrom, M. 1986, ApJ, 302, 617 [NASA ADS] [CrossRef] [Google Scholar]
  35. Milgrom, M. 1994, ApJ, 429, 540 [NASA ADS] [CrossRef] [Google Scholar]
  36. Milgrom, M. 1995, ApJ, 455, 439 [NASA ADS] [CrossRef] [Google Scholar]
  37. Milgrom, M. 2009, PRD, 80, 123536 [Google Scholar]
  38. Moore, B. 1996, ApJ, 461, L13 [NASA ADS] [CrossRef] [Google Scholar]
  39. Moore, B., Ghigna, S., Governato, F., et al. 1999, ApJ, 524, L19 [Google Scholar]
  40. Nipoti, C., Londrillo, P., & Ciotti, L. 2007, ApJ, 660, 256 [NASA ADS] [CrossRef] [Google Scholar]
  41. Sanchez-Salcedo, F. J., & Hernandez, X. 2007, ApJ, 667, 878 [NASA ADS] [CrossRef] [Google Scholar]
  42. Sanders, R. H. 2005, MNRAS, 363, 459 [NASA ADS] [Google Scholar]
  43. Sanders, R. H., & McGaugh, S. 2002, ARA&A, 40, 263 [NASA ADS] [CrossRef] [Google Scholar]
  44. Sollima, A., & Nipoti, C. 2010, MNRAS, 401, 131 [NASA ADS] [CrossRef] [Google Scholar]
  45. Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
  46. Tiret, O., & Combes, F. 2007, A&A, 464, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Wu, X., Zhao, H. S., Famaey, B., et al. 2007, ApJ, 665, L101 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wu, X., Famaey, B., Gentile, G., Perets, H., & Zhao, H. 2008, MNRAS, 386, 2199 [NASA ADS] [CrossRef] [Google Scholar]
  49. Zhao, H.S, & Famaey, B. 2006, ApJ,638, L9 [NASA ADS] [CrossRef] [Google Scholar]
  50. Zlosnik, T. G., Ferreira, P. G., & Starkman, G. D. 2007, PRD, 75, 044017 [Google Scholar]

All Tables

Table 1

Globular clusters modeled in this paper.

In the text

All Figures

thumbnail Fig. 1

Line-of-sight velocity dispersion for clusters listed in Table 1 for various masses as found by N-MODY. In order to compare with the real cluster, the half-mass radii of all models are fixed. For low masses, which mean low internal accelerations, the prediction of Newtonian dynamics differs from the numerical solution. As the mass increases (at about 106 M⊙), the internal acceleration grows and the system enters the Newtonian regime and the numerical solutions get close to the Newtonian prediction. In order to focus on a reasonable range of mass for these clusters, we show the results in the range of 500−2 × 105. Dashed vertical lines show the expected cluster mass, calculated from the absolute luminosity by assuming a stellar mass-to-light ratio of M/LV = 2. This value agrees with observed mass-to-light ratios of galactic GCs (Mieske et al. 2008).
In the text
thumbnail Fig. 2

Top panel: the ratio of the velocity dispersion in the direction of the external field compared to the perpendicular direction for Pal 3 as an example plotted against the radius. The system is isotropic throughout the cluster. Bottom panel: the anisotropy profile, β, for Pal 3 as an example plotted against the radius. The system is isotropic throughout the cluster.

In the text
thumbnail Fig. 3

Upper panel: radial velocity distribution of stars for a Newtonian (red triangles) and MONDian (black dots) system in which both have the same internal velocity dispersion. The smoothed line shows a Gaussian fitted to the distributions. Both distributions follow the Gaussian fit very closely. Lower panel: the relative difference between Newtonian and Mondian velocity distributions. There is a difference between the two models, but it is too small (less than 1%) to be detected observationally.
In the text
thumbnail Fig. 4

Mean P-value vs. number of stars in the sample for a number of random realizations of distributions of stars following a Gaussian with a standard deviation of σN for clusters listed in Table 1. The minimum number of stars necessary to reject MOND is defined where the mean P-value drops below 0.05.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.