| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 5 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015388 | |
| Published online | 08 February 2011 | |
Photospheric Hanle diagnostic of weak magnetic dipoles in stars
1
THEMIS – CNRS UPS 853,
C/ vía Láctea s/n,
38200
La Laguna,
Spain
e-mail: Arturo.Lopez@themis.iac.es
2
Instituto de Astrofísica de Canarias, C/ vía Láctea s/n, 38200 La Laguna,
Tenerife,
Spain
3
Departamento de Física, Ingeniería de Sistemas y Teoría de la
Señal, Universidad de Alicante, Apdo. 99, 03080
Alicante,
Spain
Received: 13 July 2010
Accepted: 23 November 2010
Aims. We propose and explore a new diagnostic technique based upon the linear polarization emitted in Hanle-sensitive lines in disk-integrated stars where a dipolar magnetic field breaks the rotational symmetry of the resonance scattering polarization
Methods. A star with a simple dipolar field and a 1–0 spectral line were used to compute polarization amplitudes and angles.
Results. Predicted amplitudes are low but within reach of present instruments
Conclusions. A new application of the Hanle effect is proposed and analyzed as a tool that allows measuring of some of the weakest stellar magnetic fields.
Key words: techniques: polarimetric / techniques: spectroscopic / methods: observational / stars: magnetic field
© ESO, 2011
1. Introduction
Magnetic fields accompany stars from the cradle to the grave. They have been detected in hot molecular cores (Girart et al. 2009), they are known to be responsible for the electromagnetic emission of pulsars (Ferrario & Wickramasinghe 2008), and they also have long been detected in other stellar remnants such as white dwarfs (Kemp et al. 1970). Magnetic fields influence diverse physical processes, such as mass accretion and loss, stellar rotation, or elemental diffusion, which critically affect the evolution of their host stars. And yet we lack a proper explanation of their origin, and our understanding of their evolution along the HR diagram is still fragmentary.
Outside our Sun, the vast majority of the direct information (i.e. excluding indirect indexes of magnetic activity such as X-ray emission) that we possess on stellar magnetic fields comes from exploiting the various observational features associated with the Zeeman effect. These appear in intensity (line broadening) and in polarized light (as signatures in linear and circular polarization). Magnetic line broadening is very weak, even for strong fields, and competes with other processes such as thermal and rotational broadening. Polarization measurements, on the other hand, are much richer in information and sensitive to weaker fields (a few G, according to Donati & Landstreet 2009), although they often require the use of specialized instrumentation such as Balmer-line Zeeman analyzers (Angel & Landstreet 1970) or high-resolution echelle spectropolarimeters (as those developed by Semel et al. 1993; or Donati 2003). But these polarimetric instruments also open the door to diagnostics based upon other physical phenomena also affecting polarization and dependent on magnetic fields. With this paper we aim to provide the theoretical background to a new tool for detecting even weaker magnetic fields, based on the measurement of the Hanle effect, that will complement the existing techniques. in sensitivity and information content.
2. Disk-integrated polarization from a magnetic dipole
Resonance scattering polarization is the result of an anisotropic illumination of emitting atoms. Spectral lines formed in a stellar atmosphere can show resonance scattering polarization if their region of formation is high enough for the radiation field to be anisotropic. Limb-darkening contributes to increase the anisotropy. The emitted light is linearly polarized, and its degree of polarization depends on the scattering angle. In the classical approximation, the polarization will be zero in forward scattering and maximum at 90 degrees scattering. Resonance scattering is, however, a quantum phenomenon, and the classical view only provides a rough approximation to the actual degree of polarization, though one that serves the purpose of illustrating the main issue with the stellar observation of resonance scattering polarization. The linear polarization emitted will be maximum at the limb of the stellar disk and zero at the center. From pure symmetry considerations, the direction of polarization will be tangent to the stellar limb at every position angle. As we integrate over all position angles, the resultant polarization will be zero if the star presents a spherical aspect.
Rotationally deformed stars, non spherical stellar envelopes or winds constitute examples in which the spherical symmetry has been broken, and the integral over all the emitting points may end up being different from zero. These cases have been extensively studied in the past by Ignace and collaborators (Ignace 2001a; Ignace et al. 2009; Ignace & Gayley 2008).
But here we want to concentrate on the case of stellar photospheres with spherical symmetry. And with that aim we turn our attention to the fact that resonance scattering polarization is also modified by magnetic fields. This is the so-called Hanle effect. It is commonly used in solar physics to measure magnetic fields in prominences (Casini et al. 2003) and in the quiet solar photosphere (Stenflo 1982; Faurobert et al. 2001). Generally speaking, the Hanle effect induces two primary modifications of the resonance scattering polarization arising from a single scattering event: it depolarizes the emitted light and it rotates its plane of polarization. The amount of depolarization and rotation will depend on the strength of the field, but also on the geometry of the three distinctive directions present in the problem: the direction of preferential illumination of the atom (usually the local vertical), the magnetic field and the line of sight. Calculating the polarization in a spectral line from a nonresolved star then requires adding all the scattering events in its atmosphere as the line-of-sight changes in direction with respect to the two other directions. The theory describing those dependencies has been completely developed for spectrally resolved lines (Landi Degl’Innocenti & Landolfi 2004). In this work we use the full theory, but in the following paragraphs and in the sake of illustration, we voluntarily simplify our description of the Hanle effect and limit it to just those two modifications of the polarization generated at every single scattering event. Even further, rather than going into a detailed description of those two modifications, we first take the opposite direction and make use of a widely known geometric property of the Hanle effect. A magnetic field perfectly aligned with the direction of illumination produces no effect on the resonance scattering polarization. Such simplifications capture still the essence of the Hanle effect in the case under study without burdening it with details, unnecessary at this point and incorporated nevertheless in the computations below.
It is time now to set the example that will explain our proposed diagnostic. We suppose a spherical star rotating around an axis in the plane of the sky, that is, with the equator seen edge-on. The density and temperature of the star are spherically symmetric, and it presents limb darkening. We are interested in relatively weak photospheric lines for which the last scattering approximation applies (Stenflo 1982). We assume a global dipolar field with strength B0 at the equator of the stellar surface. We further suppose in our first example that the dipole is perfectly aligned with the rotation axis. For rays from most of the equator line, the dipolar field will primarily induce a depolarization of the background resonance scattering polarization. At the poles, however, the dipolar field will be strictly aligned with the vertical direction of illumination and will result in no modification of the resonance scattering polarization. The three inset images of Fig. 1 show the polarization degree at every point in the resolved disk and illustrate the loss of symmetry described at two different dipole field strengths. It can be seen that the polarization amplitude in the poles is no longer compensated for by the diminished polarization at the equator and the integral around the limb will not be zero. Explained in such simple terms, a dipolar field results in measurable linear polarization from the star.
To estimate the expected polarization degree from this effect, we use a spectral line arising from an atomic system with angular momenta Ju = 1 for the upper level and Jl = 0 for the lower level. This simplification allows us to use the analytic results of Casini (2002) for this atomic system1 in our computations. All lines that can be acceptably simulated by such an atomic system are characterized by a critical Hanle field Bc, defined as the field at which the Zeeman splitting of the sublevels equals the natural width of the level 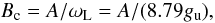 (1)where ωL is the Larmor frequency of a 1 G field, A the Einstein coefficient of the level in MHz, and gu the Landé factor of the upper level. With the dipole field strength put in terms of this critical Hanle field, the Hanle behavior of all such spectral lines is identical. Figure 1 shows the linear polarization of such lines in the presence of a dipolar field integrated over the observable stellar disk. At zero field we are in the conditions of resonance scattering polarization that cancels out over the disk for symmetry reasons. As the magnetic field increases, depolarization at the equator happens, but not at the poles, as described. Cancellation is not complete and a linear net polarization appears over the star. The effect grows for increasing field strengths and then saturates beyond the Hanle critical field. The reason is that Hanle effect can only take place while the Zeeman sublevels are not separated in energy more than their natural width. When the sublevels reach this critical field the quantum interference between the sublevels drops and the magnetic field cannot modify them any further. For reference, Fig. 2 shows the value in G of the Hanle critical field for about 500 Hanle-sensitive lines in the visible and near-IR spectral region (0.4 through 2.5 microns), extending previous compilations (Ignace 2001a).
(1)where ωL is the Larmor frequency of a 1 G field, A the Einstein coefficient of the level in MHz, and gu the Landé factor of the upper level. With the dipole field strength put in terms of this critical Hanle field, the Hanle behavior of all such spectral lines is identical. Figure 1 shows the linear polarization of such lines in the presence of a dipolar field integrated over the observable stellar disk. At zero field we are in the conditions of resonance scattering polarization that cancels out over the disk for symmetry reasons. As the magnetic field increases, depolarization at the equator happens, but not at the poles, as described. Cancellation is not complete and a linear net polarization appears over the star. The effect grows for increasing field strengths and then saturates beyond the Hanle critical field. The reason is that Hanle effect can only take place while the Zeeman sublevels are not separated in energy more than their natural width. When the sublevels reach this critical field the quantum interference between the sublevels drops and the magnetic field cannot modify them any further. For reference, Fig. 2 shows the value in G of the Hanle critical field for about 500 Hanle-sensitive lines in the visible and near-IR spectral region (0.4 through 2.5 microns), extending previous compilations (Ignace 2001a).
 |
Fig. 1 Total polarization emitted from a star in a Hanle-sensitive line for a dipolar field, aligned with the axis of rotation and included in the plane of the sky. Field strength of the dipole at the stellar surface is given in terms of the critical Hanle field of the observed line. The vertical axis is scaled in terms of the polarization Q0 emitted by the atom at 90-degree scattering in the absence of magnetic fields. The three inset images show the Q and U polarizations (Q defined positive tangent to the local meridian) in the disk-resolved star for a dipole field strength of 0, 40, and 80% of the critical Hanle field of the spectral line. |
 |
Fig. 2 Critical Hanle field (Bc in G) of about 500 lines sensitive to the Hanle effect in the visible and near-IR spectrum. |
The computed polarization in Fig. 1 is given in terms of the zero-field polarization amplitude Q0 of the line. Unfortunately the actual value of Q0 is unknown for most (if not all) spectral lines. The reason for this is that it strongly depends on the actual anisotropy of the radiation field that illuminates the scattering atom. This anisotropy may depend on the formation height of the line in each stellar atmosphere, on the limb darkening conditions and on the pattern of intensities in the photosphere below the line. For example granulation in solar-like stars is known to influence this anisotropy and modifies the zero-field polarization Q0 in these atmospheres (Trujillo Bueno & Shchukina 2007).
Although line-ratio techniques may sometimes overcome the problem of ignoring the value of Q0, in general one is bound to estimate it by indirect reasonings. Examination of the solar spectra provides some clues to the value of Q0. The scattering polarization of the visible spectra has been measured and is available in atlas (Gandorfer 2000). Its spectral variation is very intriguing, and it is so different from the intensity spectra that it is referred to as the second solar spectrum (Stenflo & Keller 1997). In it we can see that the Sr i line at 460.7 nm, a paradigmatic 1–0 transition, presents a polarization level of 0.013 the intensity of the surrounding continuum. But this value is not the Q0 amplitude we are seeking. The solar photosphere is believed to be permeated by a turbulent and therefore random magnetic field that effectively depolarizes all Hanle-sensitive lines in the second-solar spectrum. The value of 0.013 corresponds to a Hanle-depolarized emission. The solar literature does not yet agree on how much depolarized the Hanle-sensitive lines are. Mean field strengths from 20 to 150 G are suggested, depending on the authors, with the most precise studies (Trujillo Bueno et al. 2004) pointing toward the higher value. Depending on the assumptions, this may translate into a depolarization of up to 80% in the case of the Sr line. Therefore Q0 is anywhere in the range of 0.013 to 0.06 times the intensity of the continuum.
Limb darkening is a major ingredient for computing the anisotropy of the radiation field, hence the actual value of Q0. Since stars of different spectral classes present a variation in their limb darkening, we estimated the dependence of Q0 with the spectral class. The result is a mere factor 3 of variation (from 0.005 through 0.015) between the coldest and hottest stars, assuming the line forms in all those atmospheres, with higher Q0 values for cooler stars.
In conclusion, and despite our ignorance of the actual value of the Q0 zero-field polarization amplitude, we can safely assume it is in the range of a few percent. The proposed diagnostic results in integrated values (Fig. 1), which are consequently of a few percent of a few percent, in other words at the level of 10-4 to 10-3 times the intensity of the line. This sets the feasability and the observing requirements for this diagnostic tool yet to be exploited.
3. Oblique magnetic rotators and temporal modulation of the signal
In general the magnetic dipole will not be aligned with the rotation axis of the star. The rotation of the dipole around the rotation axis will result in a temporal modulation of the observed linear polarization. This is very interesting since the shape of the temporal variation of polarization carries precious information on the orientation of the dipole in the star. To illustrate this, we consider a star in which, as before, the rotation axis is on the plane of the sky and it sets our preferred direction of polarization Q. A magnetic dipole of B = 0.7Bc is assumed with a constant astrographic latitude. It rotates around the rotation axis. Figure 3 shows three cases of modulation of the amplitude with rotational phase, and the angle of polarization (0 degrees meaning the preferred direction of polarization Q), for latitudes of 30, 45 and 60 degrees. In the description of the Hanle effect made above we mentioned that depolarization was accompanied by a rotation of the plane of polarization. Such rotation can be seen as a nonzero value of the Stokes U polarization with non-zero magnetic field, and so is seen in the inset images of Fig. 1 where the Stokes U amplitude is plotted in the hemisphere of the disk at 0, 50 and 100 G dipole field strength. The angle of polarization in Fig. 3 is defined as half the arctangent of the ratio of Q and U polarization amplitudes.
Both the polarization amplitude and angle show a strong asymmetric behavior with rotational phase. The absence of symmetry with respect to the central meridian of the star is due to the dependence of the polarization with twice the position angle, and not the angle itself. Because of this lack of hemispheric symmetry, the signal from an oblique rotator should allow the geometry of the magnetic dipole to be determined with great precision (signal-to-noise levels allowing). In this aspect the proposed Hanle diagnostic outperforms similar diagnostics based upon the integrated circular polarization, not just for its sensitivity to weaker fields, but also for the amount of topological information encoded in its temporal variation, assuming the dipole is not aligned with the rotation axis. It can be speculated that not only can the relative angle between the rotation and dipole axis be ascertained, but also the inclination of the rotation axis with respect to the plane of the sky, independently of the rotation period, which is a result already pointed out by Ignace (2001b).
 |
Fig. 3 Total linear polarization (in terms of Q0)and plot of Q vs. U (defined with respect to a fixed direction in the sky corresponding to U = 0 when perpendicular to the rotation axis) with varying rotational phase. The magnetic dipole strength has been fixed at 70% of the critical Hanle field, and the fixed astrographic latitude of the magnetic pole is 30, 45, and 60 degrees for the dashed (crosses), continuous (stars), and dotted (diamond) lines respectively. |
4. Spectral lines apt for the measurement and line addition techniques
Zeeman diagnostics of stellar fields made a huge leap forward when it was proposed that thousands of spectral lines across the spectrum could be coherently added (Semel & Li 1996; Donati et al. 1997; Semel et al. 2009). Individual lines present circular polarization levels below noise. But when many different lines are appropriately added, noise will add up incoherently, thereby diminishing in amplitude as the square root of the number of lines added with respect to the Zeeman signal. Signals meanwhile will add up coherently, maintaining its amplitude. With this technique signal-to-noise ratios of 105 are routinely achieved in many stars by the foremost instruments in this field: EsPadons and Narval (Donati 2003; Manset & Donati 2003; Donati et al. 2006a; Aurière 2003).
The amplitudes of linear polarization expected from the diagnostic proposed in this paper are of the level of 10-4 to 10-3 at its best. Its measurement requires long integration times, unless we can make use of a similar line-addition technique. The issue with the Hanle effect is that many lines do not form in regions where the anisotropy of the radiation field is sufficient to introduce resonance scattering polarization. Furthermore, the actual level of zero-field polarization Q0 is highly dependent on the quantum numbers of the transitions (Landi Degl’Innocenti & Landolfi 2004). Also it cannot be known a priori in what plane the polarization signal will be maximum, and therefore both Q and U need to be measured at the telescope before being able to add the lines. Finally the last difficulty is that the spectral shape of the resonance scattering polarization is not standard for all lines, contrary to the Zeeman effect, which induces a similar spectral shape of circular polarization to any Zeeman-sensitive line. All these are factors that make it difficult adding lines in the Hanle case. Belluzzi & Landi Degl’Innocenti (2009) examined and classified the spectral signatures and amplitudes of all lines in the second solar spectrum. The 1–0 atomic model we have used in the present work results systematically in a Gaussian-like profile. Belluzzi & Landi Degl’Innocenti (2009) refer to lines with that spectral signature as belonging to class S and identify a large total of 80 lines in the solar spectrum belonging to this class. From the point of view of stellar observations and line-addition techniques, this means that in solar-like stars up to 80 lines, including the Sr i line, are susceptible of being coherently added, and a corresponding increase of a factor 9 in signal-to-noise ratio can be expected.
Following the practice in the LSD treatment of Zeeman-Doppler Imaging (Brown et al. 1991), we can further propose that the lines of class S to be added can be weighted to improve their contribution to the integrated mean pseudo-line. Let us stress here an important point: in the usual spatially-resolved Hanle diagnostics (e.g. solar applications) the lines present a linear polarization at zero magnetic field. Adding up lines in this scenario will just result in a dilution of the magnetic signal rather than a reinforcement. At first sight, line addition would appear to be counterproductive. But in the stellar non-resolved case, the integral for all position angles at zero field results in a cancellation of the zero-field signal. Therefore in the stellar observation, the Hanle effect is also characterized by a zero signal for zero field and non-zero signal for growing magnetic field. This unexpected fact is what permits proposing line addition: the individual line signals are all signatures of a non-zero field. And in analogy to the weighting of lines by their Landé factor in the Zeeman case, it appears as judicious to weight lines by the quotient of the line polarizability over the critical Hanle field of each line.
In summary, the use of lines of class S opens the possibility to add lines coherently and to build up the signal-to-noise ratio in the measurement of linear polarization signature of disk-integrated Hanle effect of photospheric lines. We wish to leave this as a proposition for further work, since many other aspects need to be worked out to put in practice any line addition scheme for Hanle signatures, aspects that are beyond the scope of the present work.
5. Interest as a diagnostic
A dipolar magnetic field breaks the rotational symmetry in the direction of linear polarization from resonance scattering. An immediate result is that a Hanle-induced linear polarization signal appears even in disk-integrated stellar observations. Its amplitude is directly related to the dipole field strength, although highly influenced by the geometry of the field and its variation in time with respect to the observer. As with any Hanle diagnostics, it is sensitive to very weak fields, which opens new observational windows in stellar magnetism. But, also as with any Hanle diagnostics, the expected signals are of low amplitude. Such low amplitudes set strong limitations in terms of signal-to-noise ratios for the observation. However, we estimate that they are not beyond the reach of present spectropolarimetric instruments.
The small amplitudes can be partially overcome by line addition, similar to the Zeeman case. About 80 lines can be identified in the visible spectra of solar-type stars ready for addition and potentially affording a factor 9 increase in the signal-to-noise ratio for fixed exposure time and instrument. Colder stars may present a higher number of lines ready for addition, including molecular lines. They also present an enlarged anisotropy in the line formation due to its stronger limb darkening that results in stronger resonance scattering polarization.
The method works best for stars with simple dipolar topologies that simplify the analysis. These fields are to be found in several stages of stellar evolution. Upper main sequence stars (with masses above 1.5 M⊙) are known to host them, and while solar-type stars are dominated by fields with a very complicated geometry, mostly dipolar structures reappear in later stages of stellar evolution, in fully convective stars with spectral types later than M3 (Donati & Landstreet 2009).
Regarding field strengths, our method would prove useful in the study of several populations: Herbig Ae/Be stars, mostly in a pre-main sequence stage, have large-scale fields in the range 0.5–5 kG (Alecian et al. 2009). Into the main sequence, the few O stars with field measurements are θ1 Ori (Donati et al. 2002), sporting a ~1 kG field, HD 19161, with ~200 G (Donati et al. 2006b) and the supergiant ζ Ori A, with a field within 50 to 100 G (Bouret et al. 2008); in fact, the Hanle effect will be one of the diagnostics used in the UV by FUSP (Fast Ultraviolet Spectro-Polarimeter, Nordsieck 1999). Peculiar Ap and Bp stars are known to have fields up to several tens of kG with a minimum around 300 G (Aurière et al. 2009), so they fall beyond our reach, but their normal A, B and F counterparts have no measurable fields to date, down to errors from 10 to 100 G (Donati & Landstreet 2009). Our diagnosis could lower these detectability thresholds. Field intensity seems to decay with stellar type, so G giants show fields with poloidal structure and strength of several tens to 100 G (Aurière et al. 2009; Lèbre et al. 2009).
Although fields below 1 G have been detected in Pollux, a K0II star (Aurière et al. 2009), little is known about more evolved giants. The detection of the 1 G field in Pollux required the combination of more than 90 spectra taken during 18 months and with S/N > 1000, a prohibitive amount of observational time. In contrast, having a tool sensitive enough to infer the properties of dipolar fields below the actual sensitivity limits would provide very useful information on the evolution of magnetic fields. Particularly in high-mass stars, as in these giants, the magnetic fluxes will be smaller than their dwarf counterparts. This population is of particular interest, as they are the progenitors of neutron stars, and thus necessary for the whole picture of the evolution of magnetic fields.
A general transition or multi-level atom has been described and can also be adequately computed (Landi Degl’Innocenti & Landolfi 2004).
Acknowledgments
A.A.R. gratefully acknowledges financial support from the Consolider-GTC (CSD2006-00070) project and Spanish Ministerio de Ciencia e Innovación (MICINN) under grant AYA2007-63881. C.G.F. gratefully aknowledges financial support from the Consolider-GTC (CSD2006-00070) project and Spanish Ministerio de Ciencia e Innovación (MICINN) under grant AYA2008-06166-C03-03.
References
- Alecian, E., Catala, C., Wade, G. A., et al. 2009, in Stellar Magnetism, ed. C. Neiner, & J.-P. Zahn, EAS Pub. Ser., 39, 121 [Google Scholar]
- Angel, J. R. P., & Landstreet, J. D. 1970, ApJ, 160, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Aurière, M. 2003, in Magnetism and Activity of the Sun and Stars., Proc. Conf. held 17–21 September, 2002 in Toulouse, France, ed. J. Arnaud, & N. Meunier, EAS Publ. Ser., 9, 105 [Google Scholar]
- Aurière, M., Wade, G. A., Konstantinova-Antova, R., et al. 2009, A&A, 504, 231 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belluzzi, L., & Landi Degl’Innocenti, E. 2009, A&A, 495, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouret, J., Donati, J., Martins, F., et al. 2008, MNARS, 389, 75 [Google Scholar]
- Brown, S. F., Donati, J., Rees, D. E., & Semel, M. 1991, A&A, 250, 463 [NASA ADS] [Google Scholar]
- Casini, R. 2002, ApJ, 568, 1056 [NASA ADS] [CrossRef] [Google Scholar]
- Casini, R., Ariste, A. L., Tomczyk, S., & Lites, B. W. 2003, ApJ, 598, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J. 2003, in Solar Polarization, Proc. Conf. held 30 September–4 October, 2002 at Tenerife, Canary Islands, Spain, ed. J. T. Bueno, & J. S. Almeida, ASP Conf. Proc., 307, 41 [Google Scholar]
- Donati, J., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997, MNARS, 291, 658 [Google Scholar]
- Donati, J., Babel, J., Harries, T. J., et al. 2002, MNARS, 333, 55 [Google Scholar]
- Donati, J., Catala, C., Landstreet, J. D., & Petit, P. 2006a, in Solar Polarization 4, ed. R. Casini, & B. W. Lites, ASP Conf. Ser., 358, 362 [Google Scholar]
- Donati, J., Howarth, I. D., Bouret, J., et al. 2006b, MNARS, 365, L6 [Google Scholar]
- Faurobert, M., Arnaud, J., Vigneau, J., & Frisch, H. 2001, A&A, 378, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrario, L., & Wickramasinghe, D. 2008, MNARS, 389, L66 [Google Scholar]
- Gandorfer, A. 2000, The Second Solar Spectrum: A high spectral resolution polarimetric survey of scattering polarization at the solar limb in graphical representation, Volume I: 4625 Å to 6995 Å (vdf Hochschulverlag) [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ignace, R. 2001a, ApJ, 547, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Ignace, R. 2001b, in Advanced Solar Polarimetry – Theory, Observation, and Instrumentation – 20TH NSO/Sac Summer Workshop, ASP Conf. Proc., 236, 227 [NASA ADS] [Google Scholar]
- Ignace, R., & Gayley, K. G. 2008, in Clumping in hot-star winds: Proc. international workshop held in Potsdam, Germany, 18–22 June 2007, ed. W.-R. Hamann, A. Feldmeier, & L. M. Oskinova, 137 [Google Scholar]
- Ignace, R., Al-Malki, M. B., Simmons, J. F. L., et al. 2009, A&A, 496, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kemp, J. C., Swedlund, J. B., Landstreet, J. D., & Angel, J. R. P. 1970, ApJ, 161, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines, 307 (Kluwer) [Google Scholar]
- Lèbre, A., Palacios, A., Nascimento, J. D. D., et al. 2009, A&A, 504, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manset, N., & Donati, J. 2003, in Polarimetry in Astronomy, Proc. SPIE, 4843, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Nordsieck, K. H. 1999, in Ultraviolet-Optical Space Astronomy Beyond HST, ed. J. A. Morse, J. M. Shull, & A. L. Kinney, ASP Conf. Ser., 164, 268 [Google Scholar]
- Semel, M., & Li, J. 1996, Sol. Phys., 164, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Semel, M., Donati, J., & Rees, D. E. 1993, A&A, 278, 231 [NASA ADS] [Google Scholar]
- Semel, M., Vélez, J. C. R., González, M. J. M., et al. 2009, A&A, 504, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stenflo, J. O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O., & Keller, C. U. 1997, A&A, 321, 927 [NASA ADS] [Google Scholar]
- Trujillo Bueno, J., & Shchukina, N. 2007, ApJ, 664, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo Bueno, J., Shchukina, N., & Asensio Ramos, A. 2004, Nature, 430, 326 [Google Scholar]
All Figures
 |
Fig. 1 Total polarization emitted from a star in a Hanle-sensitive line for a dipolar field, aligned with the axis of rotation and included in the plane of the sky. Field strength of the dipole at the stellar surface is given in terms of the critical Hanle field of the observed line. The vertical axis is scaled in terms of the polarization Q0 emitted by the atom at 90-degree scattering in the absence of magnetic fields. The three inset images show the Q and U polarizations (Q defined positive tangent to the local meridian) in the disk-resolved star for a dipole field strength of 0, 40, and 80% of the critical Hanle field of the spectral line. |
| In the text | |
 |
Fig. 2 Critical Hanle field (Bc in G) of about 500 lines sensitive to the Hanle effect in the visible and near-IR spectrum. |
| In the text | |
 |
Fig. 3 Total linear polarization (in terms of Q0)and plot of Q vs. U (defined with respect to a fixed direction in the sky corresponding to U = 0 when perpendicular to the rotation axis) with varying rotational phase. The magnetic dipole strength has been fixed at 70% of the critical Hanle field, and the fixed astrographic latitude of the magnetic pole is 30, 45, and 60 degrees for the dashed (crosses), continuous (stars), and dotted (diamond) lines respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


