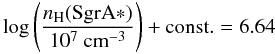| Issue |
A&A
Volume 527, March 2011
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201015323 | |
| Published online | 20 January 2011 | |
Low-luminosity AGNs
1
PN Lebedev Physical Institute,
Leninsky Prospect 53,
119991
Moscow,
Russia
e-mail: istomin@lpi.ru
2
LUTH, Observatoire de Paris, CNRS, Université Paris Diderot,
Place J. Janssen,
92195
Meudon,
France
e-mail: helene.sol@obspm.fr
Received:
1
July
2010
Accepted:
9
November
2010
Context. We propose that low-luminosity AGNs (LLAGNs), or some of them, are sources extracting their energy from the black hole rotation by the Blandford-Znajek mechanism.
Aims. It is shown that almost all energy of the black hole rotation is converted to relativistic protons in a jet. Owing to the high magnetic-field magnitude near the black hole, required for the Blandford-Znajek mechanism, electrons are not strongly accelerated because of their high synchrotron losses. Conversely, protons gain energies on the order of (104 − 105)mpc2 when crossing the light cylinder surface. Protons are also accelerated in a disk by 2D turbulent motion of the disk matter.
Methods. We calculate the luminosity of the synchrotron radiation by fast protons in the disk, the frequencies of this radiation being in the infrared band, and the luminosities corresponding to LLAGNs. We measure the very high energy (VHE) radiation luminosities from the disk and the jet, finding that VHE radiation is produced by collisions of accelerated protons with surrounding matter.
Results. We predict a correlation between the infrared luminosity
LIR and the VHE luminosity LVHE
of the disk,  ,
where M is the mass of a black hole. Two low-luminosity sources Sgr A*
and M 87, for which luminosities LIR and
LVHE are known, appear to follow this scheme.
,
where M is the mass of a black hole. Two low-luminosity sources Sgr A*
and M 87, for which luminosities LIR and
LVHE are known, appear to follow this scheme.
Conclusions. The discovery of new bright VHE sources from LLAGNs could confirm our hypotheses that they are energy sources powered by the Blandford-Znajek mechanism.
Key words: galaxies: active / acceleration of particles / accretion, accretion disks / gamma rays: galaxies
© ESO, 2011
1. Introduction
The common point of view about active galactic nuclei (AGN) is that they are massive black
holes placed in the galactic center surrounded by an accretion disk. Energy-release
mechanisms that have been proposed up to now are the transformation of the gravitation
energy of accreting matter into heat and radiation, and the extraction of energy from the
black hole rotation. The latter is known as the Blandford-Znajek mechanism (1977). The former mechanism gives an AGN luminosity
L = ηrṀc2,
which is proportional to the mass rate accretion Ṁ,
ηr being the radiative efficiency (the standard value of which
is ηr ≃ 0.1 for bright AGNs). For the Eddington luminosity
LEdd = 4πGMmpc2/σT = 1.3 × 1038(M/M⊙) erg/s,
the accretion rate is  ,
where G is the gravitational constant, mp is
the proton mass, c is the speed of light, and
σT is the Thomson cross-section. The value M
is the black hole mass, and M⊙ is the solar mass. Accretion of
the interstellar gas into a black hole is defined by its gravitational radius
,
where G is the gravitational constant, mp is
the proton mass, c is the speed of light, and
σT is the Thomson cross-section. The value M
is the black hole mass, and M⊙ is the solar mass. Accretion of
the interstellar gas into a black hole is defined by its gravitational radius
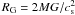 , at which the
gravitational energy of a particle in the field of a black hole equals the particle thermal
energy. The value of cs is the gas sound velocity. In this case,
the accretion rate is equal to
, at which the
gravitational energy of a particle in the field of a black hole equals the particle thermal
energy. The value of cs is the gas sound velocity. In this case,
the accretion rate is equal to 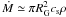 , where ρ is the
gas density. The gravitational radius RG is much larger than the
radius of the horizon of a Schwarzchild black hole
rH = 2MG/c2,
RG = rH(c/cs)2.
Nevertheless, the accretion rate of interstellar gas into a black hole is small because of
the low gas density,
, where ρ is the
gas density. The gravitational radius RG is much larger than the
radius of the horizon of a Schwarzchild black hole
rH = 2MG/c2,
RG = rH(c/cs)2.
Nevertheless, the accretion rate of interstellar gas into a black hole is small because of
the low gas density, 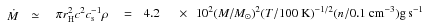 ,
where T is the gas temperature and n is the gas
concentration
n = ρ/mp.
If the accretion is fed by a dense molecular cloud or a disrupted star, then the accretion
flow has the form of an accretion disk, which possesses a large angular momentum. The
accretion rate Ṁ for disks can be as high as the Eddington rate
ṀEdd and depends on the disk structure. The bolometric
luminosity of AGN Lb is often less than the Eddington
luminosity LEdd by a factor 10-3 − 10-1.
A noticeable fraction of nearby galaxies do not contain bright AGNs, but instead contain
low-luminosity AGNs (LLAGNs) for which
Lb ≈ (10-5 − 10-3)LEdd.
The center of our Galaxy Sgr A* is dimmer, its bolometric luminosity being only
Lb ≈ 1036 erg/s ≈ 2 × 10-9 LEdd(M ≈ 3.6 × 106 M⊙).
The reason for this low luminosity is the low value of the radiative
efficiency ηr or low value of the accretion mass
rate Ṁ. Low radiative efficiency is inherent to the advection-dominated
accretion flow (ADAF) (Narayan 1994). At low
accretion mass rates of Ṁ ≪ ṀEdd, the radiative
cooling of the disk becomes inefficient. These accretion flows are generally called
radiatively inefficient accretion flows (RIAFs) (Narayan 2002). This class of disk flow also includes ADAFs. The accretion mechanism of the
energy release is ineffective for LLAGNs.
,
where T is the gas temperature and n is the gas
concentration
n = ρ/mp.
If the accretion is fed by a dense molecular cloud or a disrupted star, then the accretion
flow has the form of an accretion disk, which possesses a large angular momentum. The
accretion rate Ṁ for disks can be as high as the Eddington rate
ṀEdd and depends on the disk structure. The bolometric
luminosity of AGN Lb is often less than the Eddington
luminosity LEdd by a factor 10-3 − 10-1.
A noticeable fraction of nearby galaxies do not contain bright AGNs, but instead contain
low-luminosity AGNs (LLAGNs) for which
Lb ≈ (10-5 − 10-3)LEdd.
The center of our Galaxy Sgr A* is dimmer, its bolometric luminosity being only
Lb ≈ 1036 erg/s ≈ 2 × 10-9 LEdd(M ≈ 3.6 × 106 M⊙).
The reason for this low luminosity is the low value of the radiative
efficiency ηr or low value of the accretion mass
rate Ṁ. Low radiative efficiency is inherent to the advection-dominated
accretion flow (ADAF) (Narayan 1994). At low
accretion mass rates of Ṁ ≪ ṀEdd, the radiative
cooling of the disk becomes inefficient. These accretion flows are generally called
radiatively inefficient accretion flows (RIAFs) (Narayan 2002). This class of disk flow also includes ADAFs. The accretion mechanism of the
energy release is ineffective for LLAGNs.
We discuss the situation when the energy release due to accretion into the black hole of an AGN is small, and the energy activity is determined generally by the Blandford-Znajek mechanism. As we see below, the main energy output from a rotating black hole is in a relativistic jet. Thus, we mean LLAGNs with a jet. They are low-luminosity Seyfert galaxies and LINERs, the central source of which is a low luminosity AGN. A LINER is the low-ionization nuclear emission-line region at the center of a bright galaxy. LINERs are characterized by collisionally excited lines of neutral and singly ionized gas (Maoz 2007).
We first describe in Sect. 2 how the Blandford- Znajek mechanism operates. We describe configurations of the magnetic field and electric currents in both a disk and the black hole magnetosphere above a disk. We also show how the energy and angular momentum are transmitted from the black hole rotation to a jet. In Sect. 3, we calculate the synchrotron radiation of fast protons in a disk. The production of high energy γ-rays by relativistic protons is presented in Sect. 4. The observational consequences of the suggested scheme are described in the last section.
2. Blandford-Znajek mechanism
The Blandford-Znajek mechanism assumes that energy and angular momentum are extracted from
the black hole rotation. The rotation energy Erot stored in the
black hole rotation is large, for slow rotation being
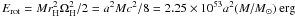 . Here we introduce the
dimensionless parameter of rotation,
a = Jc/M2G,
where J is the angular momentum of the black hole. For a black hole,
a < 1. The value of ΩH is the angular
velocity of black hole rotation,
ΩH = ac/2rH.
The extraction of the rotation energy is possible if there exists a poloidal magnetic
field B near the black hole horizon. The black hole in this case works as
a dynamo machine, creating the voltage U,
U = ΩHfH/2πc
(Landau & Lifshitz 1984; Thorne et al. 1986), where fH is the flux
of the magnetic field reaching the horizon,
. Here we introduce the
dimensionless parameter of rotation,
a = Jc/M2G,
where J is the angular momentum of the black hole. For a black hole,
a < 1. The value of ΩH is the angular
velocity of black hole rotation,
ΩH = ac/2rH.
The extraction of the rotation energy is possible if there exists a poloidal magnetic
field B near the black hole horizon. The black hole in this case works as
a dynamo machine, creating the voltage U,
U = ΩHfH/2πc
(Landau & Lifshitz 1984; Thorne et al. 1986), where fH is the flux
of the magnetic field reaching the horizon, 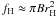 . The voltage
generates the electric current
I = U/(R + RH),
which on one side is closed at the black-hole horizon surface of resistivity
RH = 4π/c ≈ 377 ohms
(Thorne et al. 1986). The resistivity of the outer
part of the system is R. Thus, the extracted power is
. The voltage
generates the electric current
I = U/(R + RH),
which on one side is closed at the black-hole horizon surface of resistivity
RH = 4π/c ≈ 377 ohms
(Thorne et al. 1986). The resistivity of the outer
part of the system is R. Thus, the extracted power is
 . The
power L reaches its maximum value Lm when
R = RH,
. The
power L reaches its maximum value Lm when
R = RH,
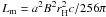 . This value is proportional to the
square of the black hole mass,
Lm ∝ M2, and for large enough
magnetic fields can exceed the Eddington luminosity,
B > BEdd = 5.5 × 109a-1(M/M⊙)−1/2 Gauss.
For high masses of AGN black holes, the value of the magnetic field
BEdd is quite moderate,
BEdd ≃ 105 Gauss (a ≃ 1).
. This value is proportional to the
square of the black hole mass,
Lm ∝ M2, and for large enough
magnetic fields can exceed the Eddington luminosity,
B > BEdd = 5.5 × 109a-1(M/M⊙)−1/2 Gauss.
For high masses of AGN black holes, the value of the magnetic field
BEdd is quite moderate,
BEdd ≃ 105 Gauss (a ≃ 1).
We note that to ensure in general that the gravitation energy release is extremely efficient, there must be a high mass accretion rate Ṁ on to the massive black hole and a high radiative efficiency ηr, whereas the Blandford-Znajek mechanism provides such efficiencies when there is black hole rotation, ΩH ≠ 0, and a strong enough magnetic field B near the black hole horizon. Formally, the Blandford-Znajek mechanism does not need accretion. In addition, the accumulation of a strong magnetic field requires some accretion process, but accretion is not a source of energy.
2.1. Magnetic field and electric current configurations
For disk accretion, the magnetic field inside the disk and nearby must have no component that is perpendicular to the disk (Istomin & Sol 2009). In the axisymmetric stationary electromagnetic field, a charged particle conserves the generalized angular momentum, ρpφ + qf/c = const., where ρ is the cylindrical distance from the center, f is the flux of the poloidal magnetic field, and q is the charge of a particle. However, two terms in this relation are practically not commensurable in the case of disk accretion. The first one is proportional to the frequency of rotation of a particle in the disk vφ/ρ, the second one is proportional to the cyclotron frequency, ωc = qBz/mc, of the particle rotation in the perpendicular magnetic field Bz. A charged particle then can move in the radial direction if it is not magnetized, ωc ≃ vφ/ρ, i.e. in a practically zero perpendicular magnetic field. The radial Bρ and the azimuthal Bφ components can be arbitrary. We see that the accretion of matter provides only the radial component of the poloidal magnetic field towards the black hole vicinity. And the magnetic field in the expression for the Blandford-Znajek luminosity is the radial magnetic field B = Bρ produced by the conducting matter of the accretion disk. For there to be a zero component of the magnetic field perpendicular to the disk, an electric current Iρ must flow through the disk, which is just the current I = −Iρ generated by the voltage U. The accretion disk is not only the origin of the flux of the matter on to the black hole, but also conducts the electric current. This current then flows onto the black hole horizon and closes through a jet in outer space. Owing to the spiral motion of charged particles in the disk, there exist not only a radial current jρ but also an azimuthal current jφ. Only the azimuthal current creates the radial magnetic field. The ratio of the radial current to the azimuthal one αj = jρ/jφ can be found by considering that from one side the current I is produced by the black hole rotation, I = U/(R + RH) = (a/16π)BρrHc [ RH/(R + RH) ] , and from another side the Maxwell equation determines the radial magnetic field through the azimuthal current, I = αjrHcBρ. We obtain αj = (a/16π) [ RH/(R + RH) ] ≪ 1, which shows that the toroidal magnetic field Bφ is much less than the radial magnetic field Bρ, Bφ = αjBρ.
2.2. Jet power
The radial magnetic field at the black hole horizon allows the transfer of energy and
angular momentum from the black hole rotation to particles of the black hole magnetosphere
and to particles leaving the accretion disk. The lines of the radial magnetic field begin
to rotate with the angular velocity
ΩF < ΩH, ΩF = ΩHR/(R + RH)
(Thorne et al. 1986). For the optimal condition
R = RH,
ΩF = ΩH/2 (Blandford & Znajek 1977). Forced by the centrifugal acceleration towards
the light cylinder surface
(rL = c/ΩF = 2a-1rHR/(R + RH)),
particles achieve azimuthal velocities, which are close to the speed of light, and
significant energies. The main energy is in protons because of their low synchrotron
losses in the strong magnetic field. The Lorentz factor γ of protons on
the light cylinder surface is
γ = (ωcL/ΩF)1/2
(Istomin & Sol 2009), where
ΩcL = eBL/mpc
is the non – relativistic proton cyclotron frequency in the magnetic field
BL on the light cylinder surface. Taking into account that
the radial magnetic field falls as ρ-1, we obtain
γ = (ωcHrH/c)1/2,
where ωcH is the proton cyclotron frequency near a black hole.
Almost all particle energy is in the azimuthal motion,
pφ ≃ mpγc,
and only a small part is in the radial one,
pρ ≃ mpγ1/2c
(Istomin & Sol 2009). Thus, rotating
energetic protons slowly flow outside the light cylinder surface,
vρ ≃ cγ−1/2,
forming the relativistic jet. The energy density of particles on the light cylinder is
equal to the density of the electromagnetic energy 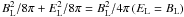 (Istomin 2010). We can then calculate the jet luminosity
(Istomin 2010). We can then calculate the jet luminosity
 . The
total Blandford-Znajek luminosity L must, of course, be higher than the
jet luminosity LJ. This implies the definite condition for the
magnetic field stress near the black hole
. The
total Blandford-Znajek luminosity L must, of course, be higher than the
jet luminosity LJ. This implies the definite condition for the
magnetic field stress near the black hole
![\begin{equation} \frac{\omega_{\rm cH}r_{\rm H}}{c}\ge(128\pi)^4 a^{-8}\left[\frac{(R+R_{\rm H})^2}{4RR_{\rm H}}\right]^4, \end{equation}](/articles/aa/full_html/2011/03/aa15323-10/aa15323-10-eq97.png) (1)or for
R = RH
(1)or for
R = RH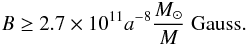 (2)For AGN black-hole
masses of M ≃ 108 M⊙, this
condition (B > 3 × 103 Gauss) is not
onerous and AGN with such moderate magnetic fields can produce a relativistic jet. Less
massive black holes must have higher magnetic fields. At the center of our Galaxy, for
example, there must be B ≈ 105 Gauss. However, a magnetic
field of the order of 1011 Gauss for micro-quasars seems problematic when
producing relativistic jets. However, Karitskaya et al. (2009) measured the disk magnetic field to be 600 Gauss at a distance
2 × 105rH in Cygnus X-1. We see in Eqs. (1)
and (2) a strong dependence of the magnitude of the magnetic field near the black
hole B on the black hole rotation,
B ∝ a-8. This increases the value of
magnetic fields for slowly rotating black holes. We note, however, that the rotation
cannot be too slow: the light cylinder surface must be inside the jet radius for producing
a relativistic jet,
rJ > rL, a > 4rH/rJ.
(2)For AGN black-hole
masses of M ≃ 108 M⊙, this
condition (B > 3 × 103 Gauss) is not
onerous and AGN with such moderate magnetic fields can produce a relativistic jet. Less
massive black holes must have higher magnetic fields. At the center of our Galaxy, for
example, there must be B ≈ 105 Gauss. However, a magnetic
field of the order of 1011 Gauss for micro-quasars seems problematic when
producing relativistic jets. However, Karitskaya et al. (2009) measured the disk magnetic field to be 600 Gauss at a distance
2 × 105rH in Cygnus X-1. We see in Eqs. (1)
and (2) a strong dependence of the magnitude of the magnetic field near the black
hole B on the black hole rotation,
B ∝ a-8. This increases the value of
magnetic fields for slowly rotating black holes. We note, however, that the rotation
cannot be too slow: the light cylinder surface must be inside the jet radius for producing
a relativistic jet,
rJ > rL, a > 4rH/rJ.
2.3. The resistivity R
The effective work done by the Blandford-Znajek mechanism depends on the value of
resistivity R. The maximum output is for
R = RH. However, the real resistivity of
the system can differ from this value. We now estimate the resistivity
Rc of the current loop created by the unipolar inductor
voltage U. The current resistivity, of course, is determined by the
electron motion. We assume the conducting system to be a box with the
cross-section S and the length l along the direction
of the electric current. The resistivity of this system is then
Rc = l/Sσ,
where σ is the electron conductivity,
σ = ne2τe/me,
n is the electron density, me and
e are its mass and charge, and τe is the
relaxation time of electrons. Coulomb collisions of electrons dominate even in a low
ionized plasma, and we can write the electron conductivity in the form
 (3)We
introduce the coefficient
ησ < 1, which takes
into account the possible abnormal electron conductivity due to turbulent or another
processes decreasing the electron conductivity. The other parameters
are ε the mean electron energy, and Λ the Coulomb logarithm,
Λ ≈ 15−20. Thus, the electron resistivity is
(3)We
introduce the coefficient
ησ < 1, which takes
into account the possible abnormal electron conductivity due to turbulent or another
processes decreasing the electron conductivity. The other parameters
are ε the mean electron energy, and Λ the Coulomb logarithm,
Λ ≈ 15−20. Thus, the electron resistivity is
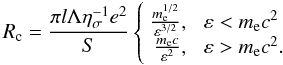 (4)The
electron resistivity strongly depends on the electron energy, decreasing as the energy
increases. The energy ε can be estimated from the bolometric luminosity
Lb in a continuous spectrum,
Lb = S1σSε4,
where S1 is the surface of the current system,
S1 ≈ 2S + 4S1/2l.
The constant σS is the Stefan-Boltzmann constant in energetic
units,
σS = π2/60ħ3c2 = 1.6 × 1059 erg-3 cm-2 s-1.
Substituting the expression
ε = (Lb/S1σS)1/4
into Eq. (4), we get
(4)The
electron resistivity strongly depends on the electron energy, decreasing as the energy
increases. The energy ε can be estimated from the bolometric luminosity
Lb in a continuous spectrum,
Lb = S1σSε4,
where S1 is the surface of the current system,
S1 ≈ 2S + 4S1/2l.
The constant σS is the Stefan-Boltzmann constant in energetic
units,
σS = π2/60ħ3c2 = 1.6 × 1059 erg-3 cm-2 s-1.
Substituting the expression
ε = (Lb/S1σS)1/4
into Eq. (4), we get 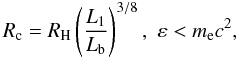 (5)
(5)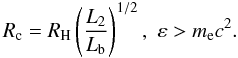 (6)Characteristic
luminosities L1 and L2 are defined
as
(6)Characteristic
luminosities L1 and L2 are defined
as 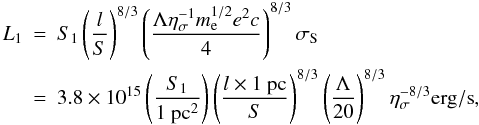 (7)
(7) (8)Equations
(7) and (8) show that for the real bolometric luminosities of AGN and LLAGN the
resistivity Rc is very small,
Rc ≪ RH, and the current system
is far from the optimal condition
Rc = RH. We note that for
relativistic electrons the characteristic luminosity L2 does
not depend on the size of the system, and the factor
l2S1/S2
is only the geometric factor which is of the order of unity. In contrast, the
luminosity L1 for non-relativistic electrons is inversely
proportional to the system size l,
L1 ∝ l−2/3.
According to this estimation, we can conclude that the Blandford-Znajek mechanism for
extracting energy from rotating black holes is ineffective for Ohmic heating of outer
space. The only possible way to extract power by means of the Blandford-Znajek mechanism
is to transform it into relativistic jet luminosity LJ. We can
attribute to the jet some value of the resistivity RJ using
the relation
LJ = RJI2.
Neglecting the electron resistivity, we have
L = LJ. This implies that the equation for
determining the jet resistivity is
(8)Equations
(7) and (8) show that for the real bolometric luminosities of AGN and LLAGN the
resistivity Rc is very small,
Rc ≪ RH, and the current system
is far from the optimal condition
Rc = RH. We note that for
relativistic electrons the characteristic luminosity L2 does
not depend on the size of the system, and the factor
l2S1/S2
is only the geometric factor which is of the order of unity. In contrast, the
luminosity L1 for non-relativistic electrons is inversely
proportional to the system size l,
L1 ∝ l−2/3.
According to this estimation, we can conclude that the Blandford-Znajek mechanism for
extracting energy from rotating black holes is ineffective for Ohmic heating of outer
space. The only possible way to extract power by means of the Blandford-Znajek mechanism
is to transform it into relativistic jet luminosity LJ. We can
attribute to the jet some value of the resistivity RJ using
the relation
LJ = RJI2.
Neglecting the electron resistivity, we have
L = LJ. This implies that the equation for
determining the jet resistivity is  (9)Denoting the
quantity
κ = a2(ωcHrH/c)1/4/128π, (κ ≥ 1),
we find that
(9)Denoting the
quantity
κ = a2(ωcHrH/c)1/4/128π, (κ ≥ 1),
we find that ![\begin{equation} R_{\rm J}=R_{\rm H}[2\kappa-1\pm 2(\kappa^2-\kappa)^{1/2}]. \end{equation}](/articles/aa/full_html/2011/03/aa15323-10/aa15323-10-eq142.png) (10)Only for
κ = 1 do we achieve the optimal efficiency of the central machine,
R = RH. For
κ > 1, we can assign to the jet two values of
resistivity, one greater than RH (the sign + in Eq. (10)),
another less than RH (the sign – in Eq. (10)). For both
values, the jet luminosity is the same. However, the solution in Eq. (10) with the
negative sign is unstable because a fluctuation of the magnetic field δB
in this case results in a negative feedback with the power of the central machine,
δL/δB < 0,
while the value
δLJ/δB
is always positive since
δLJ/δB = 7LJ/4B.
(10)Only for
κ = 1 do we achieve the optimal efficiency of the central machine,
R = RH. For
κ > 1, we can assign to the jet two values of
resistivity, one greater than RH (the sign + in Eq. (10)),
another less than RH (the sign – in Eq. (10)). For both
values, the jet luminosity is the same. However, the solution in Eq. (10) with the
negative sign is unstable because a fluctuation of the magnetic field δB
in this case results in a negative feedback with the power of the central machine,
δL/δB < 0,
while the value
δLJ/δB
is always positive since
δLJ/δB = 7LJ/4B.
3. Acceleration of protons in accretion disk: proton synchrotron radiation
Producing a relativistic jet, a rotating black hole transmits an electric
current I of high magnitude through an accretion disk. This current
creates the magnetic field not only outside the disk, but also inside. Internal magnetic
fields Bρ and
Bφ, such that
Bφ ≪ Bρ,
are of the same order as that above the disk, except that they are equal to zero at the disk
equator. Fields are frozen to the disk plasma motion. Therefore, a turbulent motion in the
disk induces a turbulent electric field ![$\vec{\tilde{{E}}}=- [\vec{\tilde{{u}}}\vec{B}]/c$](/articles/aa/full_html/2011/03/aa15323-10/aa15323-10-eq151.png) , where
, where
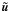 is the turbulent plasma velocity. This stochastic electric field accelerates disk particles.
This scenario of particle acceleration by large-scale 2D turbulence in a disk was discussed
by Istomin & Sol (2009). They found that
protons are indeed accelerated by this mechanism up to high energies. The maximum value of
the proton Lorentz factor γm ≫ 1. Electrons are almost not
accelerated at all because of large synchrotron losses (Istomin & Sol 2009). Thus, for the pure Blandford-Znajek mechanism
almost no non-thermal high-energy radiation is produced by disk electrons because of the
strong magnetic field and, connected with this, large synchrotron losses in any acceleration
process.
is the turbulent plasma velocity. This stochastic electric field accelerates disk particles.
This scenario of particle acceleration by large-scale 2D turbulence in a disk was discussed
by Istomin & Sol (2009). They found that
protons are indeed accelerated by this mechanism up to high energies. The maximum value of
the proton Lorentz factor γm ≫ 1. Electrons are almost not
accelerated at all because of large synchrotron losses (Istomin & Sol 2009). Thus, for the pure Blandford-Znajek mechanism
almost no non-thermal high-energy radiation is produced by disk electrons because of the
strong magnetic field and, connected with this, large synchrotron losses in any acceleration
process.
In contrast, fast disk protons can radiate the synchrotron emission in strong magnetic
fields. The distribution function of fast protons follows a power-law function
fp = bγ−β.
The index β is the ratio of the loss energy rate to the rate of
acceleration by stochastic electric field (Istomin & Sol 2009) 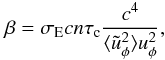 (11)where n is
the proton density, σE is the cross-section of the proton-proton
collisions in the disk σE ≈ 10-26 cm2,
and the time τc is the correlation time of the turbulence. We
consider that relativistic protons have energies in the range
10 < γ < 108 eV/Td,
where the pricipal means of energy loss for fast protons is in their collisions with disk
protons and Td is the disk temperature in eV units. The
correlation time τc is of the order of the time of the azimuthal
gyration of the matter in the disk,
τc ≃ ρ/uφ ∝ ρ3/2.
We consider the velocity uφ to be
uφ ∝ ρ−1/2,
as in the Keplerian disk. The same law applies to the turbulent motion,
(11)where n is
the proton density, σE is the cross-section of the proton-proton
collisions in the disk σE ≈ 10-26 cm2,
and the time τc is the correlation time of the turbulence. We
consider that relativistic protons have energies in the range
10 < γ < 108 eV/Td,
where the pricipal means of energy loss for fast protons is in their collisions with disk
protons and Td is the disk temperature in eV units. The
correlation time τc is of the order of the time of the azimuthal
gyration of the matter in the disk,
τc ≃ ρ/uφ ∝ ρ3/2.
We consider the velocity uφ to be
uφ ∝ ρ−1/2,
as in the Keplerian disk. The same law applies to the turbulent motion,
 , and the disk density is
n ∝ ρ-2. We see that the power-law
index β increases with the radius ρ as
ρ3/2, β = βH(ρ/rH)3/2,
where βH is the index value near the black hole. The density of
energetic protons is determined by the condition that their energy density is of the order
of the energy density of the stochastic electric field
, and the disk density is
n ∝ ρ-2. We see that the power-law
index β increases with the radius ρ as
ρ3/2, β = βH(ρ/rH)3/2,
where βH is the index value near the black hole. The density of
energetic protons is determined by the condition that their energy density is of the order
of the energy density of the stochastic electric field
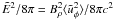 . Therefore, the
distribution function of fast protons is
. Therefore, the
distribution function of fast protons is
 (12)We see that the fast
proton density decreases as ∝ ρ-3. Substituting this function
into the well known expression for synchrotron radiation of one particle
P1 = 2(e2/mpc2)2cB2γ2/3
and integrating over γ up to γm, we find that
the density of the synchrotron power W is
(12)We see that the fast
proton density decreases as ∝ ρ-3. Substituting this function
into the well known expression for synchrotron radiation of one particle
P1 = 2(e2/mpc2)2cB2γ2/3
and integrating over γ up to γm, we find that
the density of the synchrotron power W is
 (13)The total synchrotron
luminosity Ls is the integral of Eq. (13) over the disk volume
(13)The total synchrotron
luminosity Ls is the integral of Eq. (13) over the disk volume
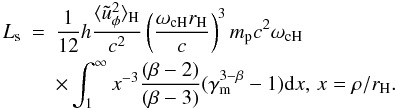 (14)Here
we introduce the dimensionless disk width near the black hole,
h = H/rH.
Because the index β increases with distance from the black hole, i.e.,
β = βHx3/2,
the main contribution to the total synchrotron luminosity comes from the inner part of the
disk,
x < x1 = (3/βH)2/3
if βH < 3. For
βH > 3, the luminosity is lower. For
lnγm ≫ 1, the result of the integration in Eq. (14) with
logarithmic accuracy is
(14)Here
we introduce the dimensionless disk width near the black hole,
h = H/rH.
Because the index β increases with distance from the black hole, i.e.,
β = βHx3/2,
the main contribution to the total synchrotron luminosity comes from the inner part of the
disk,
x < x1 = (3/βH)2/3
if βH < 3. For
βH > 3, the luminosity is lower. For
lnγm ≫ 1, the result of the integration in Eq. (14) with
logarithmic accuracy is  (15)
(15)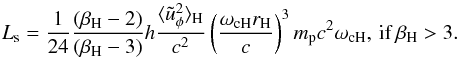 (16)To generate a
relativistic proton jet, an AGN must have a strong magnetic field near the central black
hole. This condition is given by Eq. (1),
ωcHrH/c ≥ (128π)4a-8.
Using that, we obtain
(16)To generate a
relativistic proton jet, an AGN must have a strong magnetic field near the central black
hole. This condition is given by Eq. (1),
ωcHrH/c ≥ (128π)4a-8.
Using that, we obtain  (17)
(17)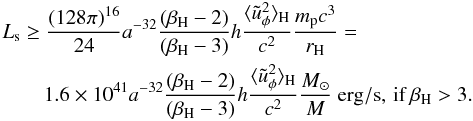 (18)For
our Galaxy, the estimated synchrotron luminosity of the disk is
Ls ≃ 1035 erg/s, which is
close to its bolometric luminosity
Lb ≃ 1036 erg/s. In any case,
the synchrotron luminosity from a turbulent disk given by Eqs. ((15), (16)) is always much
less than the total power extracted from a AGN rotating black hole.
(18)For
our Galaxy, the estimated synchrotron luminosity of the disk is
Ls ≃ 1035 erg/s, which is
close to its bolometric luminosity
Lb ≃ 1036 erg/s. In any case,
the synchrotron luminosity from a turbulent disk given by Eqs. ((15), (16)) is always much
less than the total power extracted from a AGN rotating black hole.
The frequencies of radiation are in the range 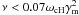 . According to Eq. (1)
ωcH ≥ (128π)4a-8c/rH,
we estimate that
. According to Eq. (1)
ωcH ≥ (128π)4a-8c/rH,
we estimate that 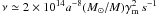 .
For γm ≃ 103 − 104, frequencies are in the
infrared band for AGNs
(M ≃ 108 M⊙). Observed LLAGNs
with radiatively inefficient accretion flow indeed show a peak in infrared emission (Maoz
2007). The center also radiates infrared light, and
according to observations (Genzel et al. 2003;
Nishiyama et al. 2009), this emission comes from the
rotating accretion disk. We suggest that this infrared emission is due to the proton
synchrotron radiation from the disk. The emitted spectrum of radiation is locally a power
law
F(ν) ∝ ν−(β−1)/2
because the fast proton distribution function is a power law with index β.
However, β changes in the disk since
β = βH(ρ/rH)3/2.
The integration over the disk gives the following dependence
F(ν) ∝ ν−(βH−1)/2/ln(ν),
which is almost a power law, but corrected by the logarithmic function. We note that the
observed power-law index of the infrared radiation from the Galactic center is −0.6 (Meyer
et al. 2009), implying that index of the proton
distribution is βH ≃ 2.2.
.
For γm ≃ 103 − 104, frequencies are in the
infrared band for AGNs
(M ≃ 108 M⊙). Observed LLAGNs
with radiatively inefficient accretion flow indeed show a peak in infrared emission (Maoz
2007). The center also radiates infrared light, and
according to observations (Genzel et al. 2003;
Nishiyama et al. 2009), this emission comes from the
rotating accretion disk. We suggest that this infrared emission is due to the proton
synchrotron radiation from the disk. The emitted spectrum of radiation is locally a power
law
F(ν) ∝ ν−(β−1)/2
because the fast proton distribution function is a power law with index β.
However, β changes in the disk since
β = βH(ρ/rH)3/2.
The integration over the disk gives the following dependence
F(ν) ∝ ν−(βH−1)/2/ln(ν),
which is almost a power law, but corrected by the logarithmic function. We note that the
observed power-law index of the infrared radiation from the Galactic center is −0.6 (Meyer
et al. 2009), implying that index of the proton
distribution is βH ≃ 2.2.
4. Very high energy radiation
In the Blandford-Znajek mechanism, almost all energy is transformed into protons, a jet, or
a disk. Thus, it appears to be a barionic scenario for the very high energy (VHE) photon
production. VHE photons are measured by Cherenkov telescopes and have energy in the TeV
band. Energetic protons collide with the ambient matter and produce pions and then gamma
quanta. Sources of the VHE radiation can be in the disk and the jet. We first calculate the
VHE radiation from a disk. The spectrum of photons reproduces the spectrum of fast protons
in Eq. (12), γ ≫ 1, and is equal to
 (19)where n
is the disk proton density, γph is the photon energy
Eph in units of the proton rest energy,
γph = Eph/mpc2.
The integration in Eq. (19) is over the disk volume. The quantities
(19)where n
is the disk proton density, γph is the photon energy
Eph in units of the proton rest energy,
γph = Eph/mpc2.
The integration in Eq. (19) is over the disk volume. The quantities
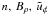 ,
and β depend on the radial distance ρ as we have
discussed. The result of the integration with logarithmic accuracy,
lnγph > 1, is
,
and β depend on the radial distance ρ as we have
discussed. The result of the integration with logarithmic accuracy,
lnγph > 1, is
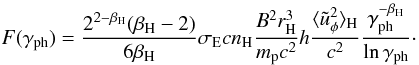 (20)We obtain the total
luminosity of VHE radiation from the disk by integrating the spectrum given by Eq. (19) over
photon energies
mpc2γph
(20)We obtain the total
luminosity of VHE radiation from the disk by integrating the spectrum given by Eq. (19) over
photon energies
mpc2γph (21)We see that the VHE
luminosity is proportional to the energy of the magnetic field near the black hole,
LVHE ∝ B2M3,
and increases with the black hole mass. Substituting the condition in Eq. (2) in to the
expression (21), we get
(21)We see that the VHE
luminosity is proportional to the energy of the magnetic field near the black hole,
LVHE ∝ B2M3,
and increases with the black hole mass. Substituting the condition in Eq. (2) in to the
expression (21), we get  (22)which implies that
(22)which implies that
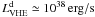 for
M ≃ 108 M⊙. We note that the
luminosity of VHE photons from the disk increases with the black hole mass in Eq. (22),
while the bolometric luminosity of the proton synchrotron radiation in the disk represented
by Eqs. (17) and (18) decreases with mass because of the different dependences of
luminosities on the magnetic field B,
Ls ∝ B4,
LVHE ∝ B2. The magnetic field must
be stronger for low-mass black holes (see Eq. (2)).
for
M ≃ 108 M⊙. We note that the
luminosity of VHE photons from the disk increases with the black hole mass in Eq. (22),
while the bolometric luminosity of the proton synchrotron radiation in the disk represented
by Eqs. (17) and (18) decreases with mass because of the different dependences of
luminosities on the magnetic field B,
Ls ∝ B4,
LVHE ∝ B2. The magnetic field must
be stronger for low-mass black holes (see Eq. (2)).
Fast protons of the jet can also produce VHE photons. Their energy density on the light
cylinder surface,
ρ = rL = c/ΩF ≃ 4a-1rH,
is equal to the energy density of the electromagnetic field near this surface
 (Istomin 2010). Thus, the jet proton density on the light cylinder surface is
nL = a2B2/64πmpc2γ.
Moving further away the light surface, protons diminish in density
nJ in line with the jet poloidal magnetic field to which they
are frozen,
nJ = nL(RL/ρ)2.
The total luminosity of the jet in γ-rays is
(Istomin 2010). Thus, the jet proton density on the light cylinder surface is
nL = a2B2/64πmpc2γ.
Moving further away the light surface, protons diminish in density
nJ in line with the jet poloidal magnetic field to which they
are frozen,
nJ = nL(RL/ρ)2.
The total luminosity of the jet in γ-rays is
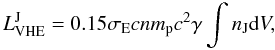 where
n is the density of the interstellar gas inside the jet
and V is the jet volume. The integration provides a simple formula
analogous to Eq. (21)
where
n is the density of the interstellar gas inside the jet
and V is the jet volume. The integration provides a simple formula
analogous to Eq. (21)  (23)where l is
the jet length and rJ is the outer radius of the jet at its
base. Comparing Eqs. (21) and (23), we conclude that they are similar and that both contain
the column density of the matter, which for the disk is
nHH and the jet is nl. We
assume an angular resolution Δφ. In the field of the central source, there
is a contribution of the jet emission along its length
l = DΔφ, where D is
the distance to the source. For a resolution
Δφ < (rH/D)(nH/n),
this means that the VHE luminosity of the disk dominates over the observed flux of the
central source. In contrast, for a resolution
Δφ > (rH/D)(nH/n)
we will observe only the radiation of the jet. Using the condition given by Eq. (2), the
expression in Eq. (23) becomes
(23)where l is
the jet length and rJ is the outer radius of the jet at its
base. Comparing Eqs. (21) and (23), we conclude that they are similar and that both contain
the column density of the matter, which for the disk is
nHH and the jet is nl. We
assume an angular resolution Δφ. In the field of the central source, there
is a contribution of the jet emission along its length
l = DΔφ, where D is
the distance to the source. For a resolution
Δφ < (rH/D)(nH/n),
this means that the VHE luminosity of the disk dominates over the observed flux of the
central source. In contrast, for a resolution
Δφ > (rH/D)(nH/n)
we will observe only the radiation of the jet. Using the condition given by Eq. (2), the
expression in Eq. (23) becomes 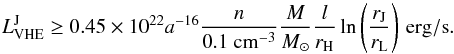 (24)If the jet length
l does not depend on the black-hole scale
length rH, as it occurs over the accretion disk
width H, then the VHE luminosity of the jet does not depend on the black
hole mass and is defined only by the column density nl,
(24)If the jet length
l does not depend on the black-hole scale
length rH, as it occurs over the accretion disk
width H, then the VHE luminosity of the jet does not depend on the black
hole mass and is defined only by the column density nl,
 .
.
5. Discussion
It seems that LLAGNs are good candidates in which to observe the Blandford-Znajek
mechanism. Accreting matter onto a black hole in LLAGNs is a weak source of energy because
of either the low accretion mass rate or low radiative efficiency. It may then be possible
to observe a black hole operating like a dynamo machine. The accretion disk would play the
role of a conductor through which the electric current would flow and the electric current
would then follow a jet. For jet creation, a strong magnetic field near the black hole is
needed. For AGNs of mass 108 M⊙, this field
should not be too high, B ≥ 3 × 103 Gauss. The magnetic field
could be accumulated during previous epochs of high accretion rate. The rotating black hole
loses its rotation energy and angular momentum, which are both transmitted to the jet.
Rotating with the black hole, the radial magnetic field transfers its rotation to the
surrounding matter, which leeds to relativistic energies being attained on the light
surface. The energy is mainly in protons, which form the relativistic jet. The accretion
disk around the black hole can be observed in millimetre and infrared bands. To accrete
matter, the disk must be turbulent (abnormal transport coefficients). The turbulent motion
in the strong magnetic field generates a turbulent electric field, which accelerates disk
ions. Electrons are not accelerated to relativistic energies because of their large
synchrotron losses. Disk fast protons radiate synchrotron emission in the infrared range.
The high proton energies should correspond to a high disk luminosity in the very high energy
(VHE) photon range, and that a correlation exists between the infrared luminosity
Ls of the disk and its VHE luminosity
 . Using Eqs. (15)
and (21), and excluding the unknown value of the magnetic field, we find the correlation
. Using Eqs. (15)
and (21), and excluding the unknown value of the magnetic field, we find the correlation
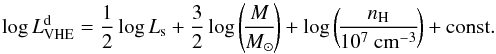 (25)We can check the
validity of this relation for low-luminosity AGNs with known luminosities
LVHE and Ls, namely the Galactic
center (Sgr A*), M 87, and Centaurus A. The nucleus of Centaurus A has a high bolometric
luminosity Lb ≃ 1.3 × 1041 erg/s
(Meisenheimer et al. 2009). At this luminosity, a
high density of infrared photons of energy εph ≃ 0.1 eV in the
central source prevents the free escape of VHE photons due to photon-photon collisions and
the production of electron-positron pairs. The simple estimate
Lb < εphcd/σT,
where σT is the Thomson cross-section and d is
the length scale of the central engine
d ≃ 102rH = 1.5 × 1015cm
for Centaurus A for which
M = 5 × 107 M⊙, gives the
condition
Lb < 1.1 × 1037 erg/s
at which the photon-photon annihilation is ineffective. The absorption of VHE quanta and the
generation of e + e − pairs result in the re-radiation of VHE
emission, as described by Stawarz et al. (2006), for
the interaction of VHE radiation with the starlight radiation from stars of the host galaxy.
Thus, for Centaurus A the observed luminosity LVHE does not
reflect the direct VHE radiation from the black hole vicinity.
(25)We can check the
validity of this relation for low-luminosity AGNs with known luminosities
LVHE and Ls, namely the Galactic
center (Sgr A*), M 87, and Centaurus A. The nucleus of Centaurus A has a high bolometric
luminosity Lb ≃ 1.3 × 1041 erg/s
(Meisenheimer et al. 2009). At this luminosity, a
high density of infrared photons of energy εph ≃ 0.1 eV in the
central source prevents the free escape of VHE photons due to photon-photon collisions and
the production of electron-positron pairs. The simple estimate
Lb < εphcd/σT,
where σT is the Thomson cross-section and d is
the length scale of the central engine
d ≃ 102rH = 1.5 × 1015cm
for Centaurus A for which
M = 5 × 107 M⊙, gives the
condition
Lb < 1.1 × 1037 erg/s
at which the photon-photon annihilation is ineffective. The absorption of VHE quanta and the
generation of e + e − pairs result in the re-radiation of VHE
emission, as described by Stawarz et al. (2006), for
the interaction of VHE radiation with the starlight radiation from stars of the host galaxy.
Thus, for Centaurus A the observed luminosity LVHE does not
reflect the direct VHE radiation from the black hole vicinity.
For Sgr A*, we have LVHE = 3 × 1034 erg/s (Aharonian et al. 2009a) and Ls = LIR = 1036 erg/s (Yuan et al. 2003), M = 3.6 × 106 M⊙, and for M 87 LVHE = 3 × 1040 erg/s (Aharonian et al. 2006) and Ls = LIR = 1039 erg/s (Perlman et al. 2007), M = 3 × 109 M⊙. Substituting these values in to Eq. (25), we find
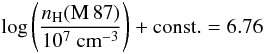 for M 87. These data do
not contradict our model. To reach this conclusion, we must be sure that the observed VHE
luminosity LVHE comes from the disk, and not the jet. For the
angular resolution of current VHE instruments, this requires that
nH/n > 10-3(D/rH).
For M 87, the argument in favor of a disk origin of the VHE radiation is its short time
variability, which excludes the large scale jet of 2 kpc length (Aharonian et al. 2006). On the basis of our estimate of the VHE luminosity
of the total jet given by Eq. (21),
for M 87. These data do
not contradict our model. To reach this conclusion, we must be sure that the observed VHE
luminosity LVHE comes from the disk, and not the jet. For the
angular resolution of current VHE instruments, this requires that
nH/n > 10-3(D/rH).
For M 87, the argument in favor of a disk origin of the VHE radiation is its short time
variability, which excludes the large scale jet of 2 kpc length (Aharonian et al. 2006). On the basis of our estimate of the VHE luminosity
of the total jet given by Eq. (21), 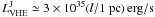 , the jet is less
luminous than the luminosity observed, while
, the jet is less
luminous than the luminosity observed, while 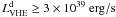 from Eq. (22). For the
region of Sgr A*, the origin of the VHE emission is not quite clear (HESS collaboration
2010). One argument in favor of a disk origin of the
VHE radiation is that the observed spectral index and the cut-off energy of VHE radiation
(Aharonian et al. 2009a), β ≃ −2.1
and Ec ≃ 16 TeV, are close to the values that follow from the
observation of IR radiation from the disk, β ≃ −2.2,
γm ≃ 104, and
Em ≃ 10 TeV. The argument of Aharonian et al. (2008) that VHE radiation from Sgr A* is likely from the
jet rather than the disk is based on the assumptions that the X-ray emission originates in
the disk and there is no time variability in the VHE flux during the X-ray flare. However,
we discuss below another possible origin of X-ray radiation in the Blandford-Znajek
mechanism, which is not in the disk.
from Eq. (22). For the
region of Sgr A*, the origin of the VHE emission is not quite clear (HESS collaboration
2010). One argument in favor of a disk origin of the
VHE radiation is that the observed spectral index and the cut-off energy of VHE radiation
(Aharonian et al. 2009a), β ≃ −2.1
and Ec ≃ 16 TeV, are close to the values that follow from the
observation of IR radiation from the disk, β ≃ −2.2,
γm ≃ 104, and
Em ≃ 10 TeV. The argument of Aharonian et al. (2008) that VHE radiation from Sgr A* is likely from the
jet rather than the disk is based on the assumptions that the X-ray emission originates in
the disk and there is no time variability in the VHE flux during the X-ray flare. However,
we discuss below another possible origin of X-ray radiation in the Blandford-Znajek
mechanism, which is not in the disk.
Although Centaurus A is unsuitable for a comparison of the discussed model with observations, substituting its data into Eq. (25) provides values of the VHE luminosity not far from previous estimates, i.e.,
 where
LVHE = 2.6 × 1039 erg/s
(Aharonian 2009b),
LIR = 1.3 × 1041 erg/s, and
M = 5 × 107 M⊙. This implies
that the re-radiation of VHE emission does not strongly affect its power.
where
LVHE = 2.6 × 1039 erg/s
(Aharonian 2009b),
LIR = 1.3 × 1041 erg/s, and
M = 5 × 107 M⊙. This implies
that the re-radiation of VHE emission does not strongly affect its power.
We should also consider whether the observed infrared radiation from Sgr A* and M 87 might originate in the disk. For Sgr A*, the short time variability of the NIR emission, which has a period of the order of 20 min, is strong evidence that it originates in the disk (Genzel et al. 2003; Nishiyama et al. 2009). The measured period corresponds to the rotation of a hot spot on the disk around the black hole at distances close to the black hole horizon. We recall that M 87 is a LINER. Apart from the thermal component of its mid-infrared emission, we also observe its power law synchrotron-like emission of similar intensity ≃1039 erg/s (Perlman et al. 2007). The thermal component of temperature ≃50 K is the radiation of the dust around the central energy source. The power-law component is thought to be the radiation from the disk.
LLAGNs also radiate significant power in the X-ray band (Maoz 2007). Because the Thomson cross-section of the scattering of the
electromagnetic radiation for protons is
(me/mp)2
times less than that for electrons the process of the inverse Compton scattering, which is
important to models of standard AGN radiation, can not be applied to explain the X-ray
radiation of LLAGNs in the scheme suggested here. However, a second component of fast
protons exists in the jet formed by the Blandford-Znajek mechanism. These are protons
accelerated in the disk, then ejected into the black hole magnetosphere that obtain
additional energy while crossing the light cylinder surface. This two-step mechanism of
proton acceleration up to very high energies was suggested by Istomin & Sol (2009). The Lorentz factor of these particles is
γ = (γdωcL/ΩF)1/2.
We recall that ωcL is the non-relativistic proton cyclotron
frequency at the light surface, ΩF is the angular frequency of rotation of
magnetic field lines, ΩF ≃ ΩH/2, and
γd is the Lorentz factor of disk fast protons. The ratio
ωcL/ΩF is a very large number,
≫ γd, and the energy of these particles is much greater than
the energy of fast particles in the disk. They radiate synchrotron emission in the region
behind the light surface above the outer part of the disk near the base of the jet. The
ratio of frequencies of the synchrotron radiation in both this region and the inner disk is
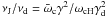 , where
, where
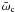 is the proton cyclotron frequency at the jet base averaged over the volume from
rL to rJ. In the jet behind the
light surface, the poloidal magnetic field weakens like ∝ ρ-2,
the toroidal field decreases more slowly, ∝ ρ-1, but initially
at
ρ = rLBφ
is small,
Bφ ≪ Bρ.
Because of this we can consider
B(ρ) = BL(rL/ρ)2
out to the outer jet radius rJ and
is the proton cyclotron frequency at the jet base averaged over the volume from
rL to rJ. In the jet behind the
light surface, the poloidal magnetic field weakens like ∝ ρ-2,
the toroidal field decreases more slowly, ∝ ρ-1, but initially
at
ρ = rLBφ
is small,
Bφ ≪ Bρ.
Because of this we can consider
B(ρ) = BL(rL/ρ)2
out to the outer jet radius rJ and
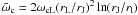 .
As a result, we obtain
.
As a result, we obtain
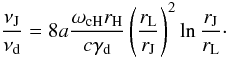 Using the
expression in Eq. (1) for the ratio
ωcHrH/c ≃ 3 × 1010
and the estimates γd ≃ 104 and
rJ/rL ≃ 10−102,
we obtain
νJ/νd ≃ 104−105,
which corresponds to νJ frequencies in the X-ray band when
νd is in the IR band. Unfortunately, we cannot estimate the
X-ray luminosity from the jet base because we do not know the fraction of fast protons
escaping the disk and being collected by the jet, which depends on the disk model. The
variability of this X-ray emission is expected from plasma instabilities in the jet (Istomin
2010).
Using the
expression in Eq. (1) for the ratio
ωcHrH/c ≃ 3 × 1010
and the estimates γd ≃ 104 and
rJ/rL ≃ 10−102,
we obtain
νJ/νd ≃ 104−105,
which corresponds to νJ frequencies in the X-ray band when
νd is in the IR band. Unfortunately, we cannot estimate the
X-ray luminosity from the jet base because we do not know the fraction of fast protons
escaping the disk and being collected by the jet, which depends on the disk model. The
variability of this X-ray emission is expected from plasma instabilities in the jet (Istomin
2010).
In conclusion, we can say that LLAGNs, or at least some of them, could be be extracting the
energy from the black hole rotation by means of the Blandford-Znajek mechanism. The black
hole spends almost all its energy on the jet production and proton acceleration. These
LLAGNs are probably sources of high-energy cosmic rays. Their VHE luminosity should reflect
the intensive process of proton acceleration. Our scenario predicts that the value of
LVHE increases with the black hole mass as
M3/2 and with the infrared luminosity of
the disk as  (see Eq. (25)). The discovery of new bright VHE sources from LLAGNs could confirm our
hypotheses.
(see Eq. (25)). The discovery of new bright VHE sources from LLAGNs could confirm our
hypotheses.
Acknowledgments
We acknowledge support from the Observatoire de Paris and the LEA ELGA. This work also was partially supported by the Russian Foundation for Basic Research (grant No. 08-02-00749) and the State Agency for Science and Innovation (state contract No. 02.740.11.0250).
References
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al., HESS Collaboration 2006, Science, 314, 1424 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al., HESS Collaboration 2008, A&A, 492, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al., HESS Collaboration 2009a, A&A, 503, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Anton, G., et al., HESS Collaboration 2009b, ApJ, 695, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 423 [Google Scholar]
- Genzel, R., Schödel, R., Ott, T., et al. 2003, Nature, 425, 924 [Google Scholar]
- HESS Collaboration,Acero, F., Aharonian, F., Akhperjanian, A. G., et al. 2010, MNRAS, 402, 1877 [NASA ADS] [CrossRef] [Google Scholar]
- Istomin, Ya. N. 2010, MNRAS, 408, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Istomin, Ya. N., & Sol, H. 2009, Ap&SS, 321, 57 [Google Scholar]
- Karitskaya, E. A., Bochkarev, N. G., Hubbrig, S., et al. 2009 [arXiv:0908.2719v1] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1984, in Course of Theoretical Physics, Electrodynamics of Continuous Media, Oxford, 8 [Google Scholar]
- Maoz, D. 2007, MNRAS, 377, 1696 [NASA ADS] [CrossRef] [Google Scholar]
- Meisenheimer, K., Tristam, K. R. W., Jaffe, W., et al. 2007, A&A, 472, 453 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, L., Do, T., Ghez, A., et al. 2009, ApJ, 694, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R. 2002, in Lighthouses of the Universe: The Most Luminous Celestial Objects and Their Use for Cosmology, ed. M. Gilfanov, R. Sunyaev, & E. Churazov (Berlin: Springer), 405 [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 702, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E.S., Mason, R. E., Packman, C., et al. 2007, ApJ, 663, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Stawarz, L., Aharonian, F., Wagner, S., & Ostrowski, M. 2006, MNRAS, 371, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Thorne, K. S., Price, R. H., & MacDonald, D. A. 1986, Black Holes: the Membrane Paradigm (Yale University Press) [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [NASA ADS] [CrossRef] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.