| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A99 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201015646 | |
| Published online | 05 January 2011 | |
Spectroscopic characterization of a sample of metal-poor solar-type stars from the HARPS planet search program⋆
Precise spectroscopic parameters and mass estimation⋆⋆
1
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas,
4150-762
Porto,
Portugal
e-mail: sousasag@astro.up.pt
2
Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
3
Geneva Observatory, Geneva University,
51 Ch. des Mailletes,
1290
Sauverny,
Switzerland
4 Departamento de Física e Astronomia, Faculdade de Ciências da
Universidade do Porto, Portugal
5
Departamento de Astrofisica, Universidade de La
Laguna, 38205
La Laguna, Tenerife,
Spain
Received: 26 August 2010
Accepted: 3 November 2010
Stellar metallicity strongly correlates with the presence of planets and their properties. To check for new correlations between stars and the existence of an orbiting planet, we determine precise stellar parameters for a sample of metal-poor solar-type stars. This sample was observed with the HARPS spectrograph and is part of a program to search for new extrasolar planets.
The stellar parameters were determined using an LTE analysis based on equivalent widths (EW) of iron lines and by imposing excitation and ionization equilibrium. The ARES code was used to allow automatic and systematic derivation of the stellar parameters.
Precise stellar parameters and metallicities were obtained for 97 low metal-content stars. We also present the derived masses, luminosities, and new parallaxes estimations based on the derived parameters, and compare our spectroscopic parameters with an infra-red flux method calibration to check the consistency of our method in metal poor stars. Both methods seems to give the same effective temperature scale.
Finally we present a new calibration for the temperature as a function of B − V and [Fe/H]. This was obtained by adding these new metal poor stars in order to increase the range in metallicity for the calibration. The standard deviation of this new calibration is ~50 K.
Key words: stars: fundamental parameters / planetary systems / stars: abundances / stars: statistics
Based on observations collected at the La Silla Parana Observatory, ESO (Chile) with the HARPS spectrograph at the 3.6-m telescope (ESO runs ID 72.C-0488, 082.C-0212, and 085.C-0063).
Tables 1–3 are only available in electronic form at http://www.aanda.org
© ESO, 2011
1. Introduction
The discovery of exoplanets continues at a very high rate and has recently passed the 450th detection. The radial velocity technique gives strong input for this number, supported by the several dedicated observing programs that almost continually observe stellar spectra in different high-resolution instruments spread across the world. The HARPS spectrograph is one of the leading instruments that over the past five years has alone spotted more than 85 of the exoplanets now known to orbit stars other than the Sun.
All of these new discoveries are providing new clues for the formation and evolution of stars and planets. One of these clues is the very well known and established correlation between the metallicity of the stars and the presence of an orbiting giant planet (Gonzalez 1997; Gonzalez et al. 2001; Santos et al. 2001, 2004; Fischer & Valenti 2005; Udry et al. 2006; Udry & Santos 2007). This observational correlation suggests that giant planets are more easily formed around metal-rich stars, supporting the core accretion idea as the main mechanism in the formation of giant planets (Ida & Lin 2004; Benz et al. 2006) instead of the alternative model focused on the idea of the disk instability (Boss 2002).
Although this correlation seems to be true for giant planets, it might not be so for lower mass planets. With the new discoveries reaching lower and lower masses, the new “lighter systems” are starting to reveal that these new planet-host stars present a different and wider metallicity distribution (Sousa et al. 2008). That can also be explained by recent models of the core accretion idea (Mordasini et al. 2009).
Several programs have been compiled to try to understand the distribution of the planets and the metallicity correlation. In particular, some are focused on metal-poor stars with the goal of not only checking the frequency of giants and low-mass planets in these stars, but also of measuring the lower limit in metallicity where it is possible to form and find gi ant planets. One of these programs is part of the HARPS GTO planet search program (Mayor et al. 2003). In this paper we present the precise derivation of fundamental spectroscopic stellar parameters and make an estimate of the masses for the stars in this sample.
We present a catalog of spectroscopic stellar parameters for the metal-poor sample observed with HARPS to search planets. In Sect. 2 we describe the observations with the HARPS spectrograph. Section 3 describes the procedure used to derive precise spectroscopic stellar parameters and to estimate for the stellar masses and new spectroscopic parallaxes based on the derived parameters. In Sect. 4, we compare our temperature values with the ones obtained with an IRFM (infra-red flux method) calibration to check for consistency. In Sect. 5 we redo a calibration for the temperature as a function of B − V and [Fe/H] using the new parameters derived in this work that were added to data from a previous work. Finally in Sect. 6 we summarize the work presented here.
2. The sample & observations
The sample of metal-poor stars, part of the HARPS GTO planet search program, is composed of a total of 104 stars. This sample was compiled from the catalog of Nordström et al. (2004): late-F, G, and K stars (with b − y > 0.33) with declination lower than +10 ° and visual V magnitude brighter than 12. All known visual and spectroscopic binaries were excluded, as were giants and stars that present a projected rotational velocity vsini greater than 6 Km s-1 (to avoid active stars that normally rotate faster). The final selection of the targets was made by considering only the targets with photometric [Fe/H] between –0.5 and –1.5. We direct the reader to Santos et al. (2011) for more details on the sample and a complete list of targets.
The data was collected between October 2003 and April 2010 with the HARPS spectrograph mounted in the ESO 3.6m telescope at La Silla, Chile. Since this sample was part of the HARPS GTO planet search program, most of the stars in this sample have several individual spectra collected through the duration of all the runs. The individual spectra of each star were reduced using the HARPS pipeline and then combined with IRAF1 after correcting for its radial velocity. The final spectra have very good quality with a resolution of R ~ 110 000 and S/N that vary from ~30 to ~2000, depending on the amount and quality of the original spectra. Figure 1 shows the distribution of the final signal-to-noise ratio where ~92% of the sample has S/N > 100 and ~68% has S/N > 200.
3. Stellar parameters
The spectroscopic stellar parameters and metallicities were derived following the same procedure as used in previous works (Santos et al. 2004; Sousa et al. 2008). The method is based on the equivalent widths of Fe I and Fe II weak lines, by imposing excitation and ionization equilibrium assuming LTE. For this task we used the 2002 version of the code MOOG (Sneden 1973) and a grid of Kurucz Atlas 9 plane-parallel model atmospheres (Kurucz 1993). [Fe/H] is used as a proxy for the metallicity in this procedure.
The equivalent widths were automatically measured with the ARES2 code (Automatic Routine for line Equivalent widths in stellar Spectra – Sousa et al. 2007) which reproduces the common manual EWs measurements with success. The procedure used in Sousa et al. (2008) was closely followed, and the same input parameters were used for ARES in this work. Since in this sample there is a significant number of stars with S/N lower than 100 and even a couple of spectra with S/N lower than 50, we present an empirical formula that upgrades Table 2 presented in Sousa et al. (2008) for low S/N levels of the spectra. This formula can be used to obtain the recommended values for the ARES parameter rejt for low S/N values. These values can be obtained with the empirical equation 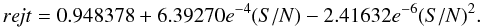 (1)This empirical relation between the S/N and the rejt parameter was obtained by considering a subsample of 6 HARPS spectra selected from the metal poor sample studied in this work. The spectra were selected in a way to represent different low S/N values, ranging between 30 and 100, and then setting for each spectra, by eye, the best value of rejt that would fit correctly the local continuum. To verify this task we selected a few isolated lines and set the ARES code to allow the presentation of plots for the local automatic normalization and also automatic determination of the continuum. These subjective values were then used to adjust a simple polynomial of second order. With this equation and the previous recommended values for the rejt parameter for S/N over 100, we are ready to measure automatically and in a systematic way the equivalent widths for the several absorption lines in the stellar spectra. These values and this new equation are valid for HARPS spectra; however, these values can be used as a first approach and a similar procedure should be made to obtain compatible values to be used for other resolution spectrographs.
(1)This empirical relation between the S/N and the rejt parameter was obtained by considering a subsample of 6 HARPS spectra selected from the metal poor sample studied in this work. The spectra were selected in a way to represent different low S/N values, ranging between 30 and 100, and then setting for each spectra, by eye, the best value of rejt that would fit correctly the local continuum. To verify this task we selected a few isolated lines and set the ARES code to allow the presentation of plots for the local automatic normalization and also automatic determination of the continuum. These subjective values were then used to adjust a simple polynomial of second order. With this equation and the previous recommended values for the rejt parameter for S/N over 100, we are ready to measure automatically and in a systematic way the equivalent widths for the several absorption lines in the stellar spectra. These values and this new equation are valid for HARPS spectra; however, these values can be used as a first approach and a similar procedure should be made to obtain compatible values to be used for other resolution spectrographs.
 |
Fig. 1 Distribution of the signal-to-noise ratio of the final spectra compilation. |
The spectroscopic parameters are presented in Table 2. We compared these values with the ones we could find in the work of Fischer & Valenti (2005). From the 9 stars we found in common we observe a mean difference of −95 ± 90 K, −0.03 ± 0.15 dex, and −0.06 ± 0.05 for temperature, surface gravity, and [Fe/H], respectively.
3.1. Precision errors vs. acuracy errors
Table 2 also presents the errors determined following the same procedure as described in previous works (Sousa et al. 2008; Santos et al. 2004). These values are indeed precision errors that are intrinsic to the spectroscopic method used in this work. These values are typically very small, especially for the stars more like the Sun. This comes directly from the method itself since a differential analysis is performed with the Sun as a reference. Stars that are significantly cooler or hotter than the Sun will have larger intrinsic errors. If the reader is interested in accurate errors, then we also estimate possible systematic errors. These systematic errors can be estimated when comparing the parameters derived using a given method with others derived from different methods. Using the comparison plots in Sousa et al. (2008), we can assume a systematic error of 60 K coming from the comparison between our method temperatures and the ones derived with the IRFM (Fig. 3, (g) and (h)). For the surface gravity we can consider a systematic error of 0.1 dex coming from an average of the comparison of the different methods (Fig. 4). Similarly, an average of 0.04 dex extracted from the different methods in Fig. 5 of the same work can be used for the systematic error for [Fe/H].
These values can be quadratically added to the precision errors. For the stars below 5000 K the systematic values should be higher. As discussed before, these stars are farthest from the Sun, so any systematic will be more significant. As an example, for stars below 5000 K a more appropriate typical systematic error will be closer to 100 K for the temperature.
 |
Fig. 2 Comparison between the estimated masses using the Hipparcos parallaxes and the estimated masses using the iterative procedure. the mean diference and dispersion are also shown for stars with mass greater than 0.9 solar masses. |
3.2. Masses and parallaxes
Stellar masses were estimated as in previous works (e.g. Santos et al. 2004; Sousa et al. 2008). In this case we applied the stellar evolutionary models from the Padova group, computed using the web interface dealing with stellar isochrones and their derivatives (http://stev.oapd.inaf.it/cgi-bin/cmd) to the stars of our sample. For this task we used the Hipparcos parallaxes and V magnitudes (van Leeuwen 2007), a bolometric correction from Flower (1996), and the effective temperature derived from the spectroscopic analysis. The errors presented for the masses were also given by the web interface.
Since the parallaxes for most of these stars present large erros (~10–20%) and for some cases they even present absolute errors of the same order of magnitude as the parallaxes, we used an iterative process to derive new values for the parallaxes and therefore also for the masses. This iterative process was already used in Santos et al. (2010) where it was applied for a single star.
The iterative procedure in this work makes use of Eq. (1) in Santos et al. (2004), the relation between luminosity, radius, and parallax, and the Padova web-interface to derive the masses.
-
1.
First, we fixed the bolometric correction and the visualmagnitude of the star to the values derived by the calibration ofFlower (1996) and the value listed in the Hipparcos catalog,respectively. An initial value for the stellar mass was alsoobtained using the Hipparcos parallax, the V magnitude, the metallicity, and the temperature derived from spectroscopy. However, since in our sample there are some stars without measured Hipparcos parallaxes (HD 62849, HD 75745, HD 95860, HD 123517, HD 144589, HD 149747, HD 171028, CD-45 12460, and CD-452997), it was not possible to estimate the mass to initiate the first step of the procedure. To overcome this problem we alternatively used the calibration presented in the work of Torres et al. (2010) to derive the initial guess for the mass for each star and then allowed initiation of iterative process with this value instead.
-
2.
The second step is to obtain a new value for the parallax that is used in the next iteration to derive a new mass using the web interface from Padova.
This procedure is then followed iteratively until we find a convergence for both the mass and parallax. On average, for all the stars we found a convergence after only three iterations.
In Fig. 2 a comparison is presented between the masses derived using the Hipparcos parallaxes and the mass estimated using the iterative procedure. From this figure we can see that both mass values are compatible within the errors with a increased dispersion for higher values where the errors also increase significantly. The final value for the parallax can be significantly different from the one measured by Hipparcos. There were a few stars (4) for which it was not possible to derive any value for the mass and/or parallax since the web interface would not return any values. The reason for this is unknown to us.
 |
Fig. 3 In the top panel, we present the distribution of the sample stars in the H − R diagram. We also plot some evolutionary tracks computed with CESAM for a 0.8, 0.9 and 1.0 M⊙ assuming the mixing length parameter as 1.4, the initial Helium ratio Y = 0.26 and for [Fe/H] ~ –0.5. In the bottom panel, we present the metallicity distribution of this sample. |
The luminosity was computed by considering the estimated Hipparcos parallaxes, V magnitude and the bolometric correction. Its error is derived from the parallax errors that are the main source of uncertainty in calculating luminosity. The typical error for the luminosity is ~0.04, which is obtained by assuming the mean parallax for the stars (~20 mas) and a typical error for the estimated parallaxes of 1 mas.
Figure 3 presents some characteristics of the sample. The top plot shows the distribution of the sample on the Hertzsprung-Russell diagram, where we represent evolutionary tracks for 0.8, 0.9, and 1.0 M⊙, computed with the CESAM code (Morel 1997) using the mixing length parameter with the value 1.4, the initial helium content as Y = 0.26 and assuming a Z that corresponds to the mean observed metallicity for the stars corresponding to [Fe/H] ~ –0.5. For this plot we made use of the estimated paralaxes because we have these values for a higher number of stars in the sample. The typical error boxes are also presented in this specific diagram, where the error in the luminosity is the same as described before, and the error in the temperature is derived from the spectroscopic method. This plot shows that the sample is composed mainly of main-sequence solar-type stars. We can see a dispersion in this figure that can be explained by the uncertainty of the parallaxes that are very small and can lead to larger errors on the luminosity. In the bottom plot we present the metallicity distribution that has a mean value of about –0.65 dex. This shows that these stars belong to an excellent sample that is perfectly complementary in terms of metallicity to the other samples used to search for planets. As a reference, the mean metallicity of the stars in the main HARPS GTO planet search program is –0.09 (Sousa et al. 2008). This sample is ideal for probing and testing the connection between metal-poor stars and the existence of planets around them.
In Table 2 we present the derived spectroscopic parameters for 97 stars, together with the determined parallaxes and masses. The absent stars are explained in the next section.
3.3. Special cases
There are 7 stars for which we were unable to derive spectroscopic stellar parameters. HD161265, BD-032525, HD164500, and HD187151 were excluded because they are double-line spectroscopic binaries SB2 stars. BD-004234 is suspected of also being a spectroscopic binary, so, it was also removed from the observation list from the runs. HD197890 was observed a few times but presents a strange spectrum. This could possibly be an active star. HD128575 was observed 2 times, also indicating strange spectral features, possibly an active star. Both these stars do not allow combining the individual spectra, so the parameters were not derived. A complete description of these special cases can be found in Santos et al. (2010).
HD967 is a target also present in the main HARPS GTO program with the parameters derived in Sousa et al. (2008). The parameters presented before (Teff: 5568 K; log g: 4.51; [Fe/H]: –0.68) are extremely consistent with the ones presented in this work, proving that the spectrocopic analysis performed by our team is precise and systematic.
3.4. High surface gravity
In Table 2 we observe that there are a few stars (6) with high surface gravity values (log g > 4.7). These kinds of values are not expected, and stellar interior models may encounter dificulties when trying to fit this kind of surface gravity for dwarf stars. A more attentive reader can find out that these high values are more or less correlated with the low metallicity for these stars. In fact, from these stars only BD+063077 is above [Fe/H] ~ –1. For this specific star we may explain that the high value of gravity comes from the very low S/N of the spectrum.
For the rest of these stars, they all have [Fe/H] < −1. We do not rule out that there might be some systematic result of our spectroscopic method. For these stars the lines are all typically very weak, some even undetected due to the low amount of iron. Therefore for these stars we have on average fewer lines used for determining the stellar parameters. Moreover, since the lines are typically weaker, they propagate higher errors coming from the equivalent width measurements. For these stars we compared the stellar parameters directly with others in the literature. As an example, for 4 of these 6 stars, that we found in common in the work of Casagrande et al. (2010), we see a mean difference of −28 ± 76 K for temperature. Although there is a large dispersion for all the different methods, the values are mostly consistent and within the errors. Even for surface gravity we typically found high values for these stars in the other methods. Although considering that the gravity may be overestimated using our method for these low metal stars, the other parameters seems to be reliable. A more complete comparison is made in the next section, which shows that there is no clear metallicity correlation in the comparison. Nevertheless the reader should take possible systematics into account for these high surface gravity stars.
 |
Fig. 4 Comparison between the derived spectroscopic temperatures and the ones derived using an IRFM calibration. |
4. IRFM calibration comparison
To check the consistency of the derived parameters we compared the derived spectroscopic temperatures and the ones derived using an IRFM calibration presented in the work of Casagrande et al. (2010). To perform this comparison we first need to obtain the values of the several photometric colors required for the IRFM calibration. These colors were compiled from different sources. The U was obtained from the SKY2000 Catalog, Version 4 (Myers et al. 2001), and the B, V, R were obtained from the NOMAD catalog (Zacharias et al. 2004). The I was calculated from the index V − I obtained in the Hipparcos catalog (van Leeuwen 2007). Finally the JHK colors were obtained from the 2MASS catalog (Cutri et al. 2003). The list of the colors used in this work are presented in Table 3.
For each of the stars, and considering the available colors, we derived several values for the absolute flux calibration and the angular diameter calibrations from the coefficients presented in both Tables 5 and 6 from the work of Casagrande et al. (2010). These values were then average-weighted considering the errors in the tables for each color calibration to obtain both fbolmean and θradmean. With this it is possible to compute the calibrated effective temperature (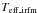 ) using the equation
) using the equation 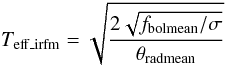 (2)where σ is the StefanBoltzmann constant.
(2)where σ is the StefanBoltzmann constant.
Figure 4 shows the comparison between the derived spectroscopic temperatures and the temperatures obtained with this IRFM calibration. The comparison is consistent when presenting a mean difference of 3 ± 125 K. This shows that both the spectroscopic temperatures and the temperatures derived from this IRFM are on the same scale of temperature.
In the bottom plot of Fig. 4 we present the difference between the derived effective temperatures as a function of metallicity. We cannot see any clear metallicity effect in this plot, meaning that any NLTE effect for low metallicity is not significant for deriving of the temperature. The high dispersion may be explained by the possibly bad quality of the photometry used for the IRFM calibration.
 |
Fig. 5 Calibration of the effective temperature as a function of the color index B − V and [Fe/H]. The 4 fitted lines correspond to lines with constant values of [Fe/H] (–1.0, –0.5, 0.0, 0.5). The bottom panel presents the direct comparison between the spectroscopic temperatures and the calibration. The filled line is the identity line. |
5. A new calibration for effective temperature
In this section we present a new calibration for the effective temperature as a function of B − V and [Fe/H]. This kind of calibration was already presented in Sousa et al. (2008). Here we derive a new calibration by adding the data derived for the metal-poor sample. This will increase not only the number of stars but, more importantly, widen the metallicity range for the calibration. Therefore by adding these new metal-poor stars we achieve a new metallicity interval that ranges from the values –1.5 to 0.5.
This new calibration made use of the spectroscopic parameters derived in both works, and used the B − V value taken from the Hipparcos catalog (ESA 1997). The result is illustrated in Fig. 5, and the calibration is then expressed by ![\begin{eqnarray} \label{eqcal} T_{\mathrm{eff}} &=& 8939 - 6395(B{-}V) + 2381(B{-}V)^2 \nonumber \\ && + 451{\rm [Fe/H]} + 154{\rm [Fe/H]}^2. \end{eqnarray}](/articles/aa/full_html/2011/02/aa15646-10/aa15646-10-eq38.png) (3)The final coefficients were obtained after removing an outlier, i.e., after the first fit to all the stars, we removed the stars that presented a difference greater than 4 sigma of the fit. There were 6 outliers, HD 62849, HD 88474, HD 119949, HD 128340, BD-084501, and CD-452997. The reasons for these outliers maybe errors in the the color index B − V and/or the errors in the derived effective temperature, especially for the cases of BD-084501 (lower number of analyzed lines and one of the most metal-poor stars in the sample) and CD-452997 (S/N of the spectra is ~25).
(3)The final coefficients were obtained after removing an outlier, i.e., after the first fit to all the stars, we removed the stars that presented a difference greater than 4 sigma of the fit. There were 6 outliers, HD 62849, HD 88474, HD 119949, HD 128340, BD-084501, and CD-452997. The reasons for these outliers maybe errors in the the color index B − V and/or the errors in the derived effective temperature, especially for the cases of BD-084501 (lower number of analyzed lines and one of the most metal-poor stars in the sample) and CD-452997 (S/N of the spectra is ~25).
The standard deviation for the fit is only 52 K, illustrating the good quality of the relation. This result is similar to the previous calibration presented in Sousa et al. (2008). and the calibration can be useful and be applied to stars without the need for a detailed spectroscopic analysis, with the guarantee that the result will lie on the same effective temperature scale. This calibration is valid in the following intervals: 4500 K < Teff < 6400 K, −1.5 < [Fe/H] < 0.50, and 0.40 < B − V < 1.20.
6. Conclusions
In this work we presented precise stellar parameters for a sample of metal-poor stars. The stellar parameters were derived in a consistent way following the same method as in previous works. It is crucial that the spectroscopic parameters for these stars are derived precisely and in a systematic way to allow correct comparison between stars. This is very useful when searching for clues for the stellar and planet formations that are typically done by comparing the stars with detected planets to the single stars that do not show any evidence of hosting any planet. These parameters and abundances will be used to study the frequency of planets as a function of the stellar parameters, but this is beyond the scope of this paper.
ARES is a very important tool for this task, not only because it is an automatic tool that allows faster and more completely analysis of the spectra of many stars, but more importantly, because it clearly allows eliminating of most of the human factor that was creating larger errors in the spectral analysis (more specifically the subjective position of the continuum located by eye when measuring the EWs of the lines with interactive routines).
We also present estimations for the mass of these stars using similar procedures as in previous works. Here it was necessary to overtake the problem of the high errors in the Hipparcos parallaxes presented for most of the stars in the sample. Therefore we estimated a second value for the mass by assuming a different parallax based on the derived spectroscopic parameters.
The effective temperature for these metal-poor stars was tested and compared against an IRFM calibration. The comparison between the two different approaches to derive the effective temperature are consistent, meaning that our spectroscopic method is still valid for lower metallicity stars.
Finally a new calibration for the effective temperature as a function of the color index B − V and [Fe/H] is presented where the metallicity range is now wider thanks to using the parameters derived in this work.
Online material
Details of the spectral data for each star.
Stellar parameters and respective errors derived for the metal poor sample.
List of the photometry used for the use of the IFRM calibration.
The ARES code can be downloaded at http://www.astro.up.pt/~sousasag/ares
Acknowledgments
S.G.S acknowledges the support from the Fundação para a Ciência e Tecnologia (Portugal) in the form of grant SFRH/BPD/47611/2008. NCS thanks for the support by the European Research Council/European Community under the FP7 through a Starting Grant, as well as the support from the Fundação para a Ciência e a Tecnologia (FCT), Portugal, through program Ciência 2007. We also acknowledge support from the FCT in the form of grants reference PTDC/CTE-AST/098528/2008, PTDC/CTE-AST/66181/2006, and PTDC/CTE-AST/098604/2008.
References
- Benz, W., Mordasini, C., Alibert, Y., & Naef, D. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, ed. L. Arnold, F. Bouchy, & C. Moutou, 24 [Google Scholar]
- Boss, A. P. 2002, ApJ, 567, L149 [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, 2MASS All Sky Catalog of point sources., ed. Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. [Google Scholar]
- ESA. 1997, The Hipparcos and Tycho Catalogues [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1997, MNRAS, 285, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G., Laws, C., Tyagi, S., & Reddy, B. E. 2001, AJ, 121, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 616, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid. Kurucz CD-ROM No. 13. Cambridge, Mass.: Smithsonian Astrophysical Observatory, 13 [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Myers, J. R., Sande, C. B., Miller, A. C., Warren, Jr., W. H., & Tracewell, D. A. 2001, VizieR Online Data Catalog, 5109, [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Benz, W., et al. 2010, A&A, 512, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Bonfils, X., et al. 2011, A&A, in press [Google Scholar]
- Sneden, C. 1973, PhD Thesis, Univ. of Texas [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Udry, S., & Santos, N. C. 2007, ARA&A, 45, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Udry, S., Mayor, M., Benz, W., et al. 2006, A&A, 447, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, BAAS, 36, 1418 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distribution of the signal-to-noise ratio of the final spectra compilation. |
| In the text | |
 |
Fig. 2 Comparison between the estimated masses using the Hipparcos parallaxes and the estimated masses using the iterative procedure. the mean diference and dispersion are also shown for stars with mass greater than 0.9 solar masses. |
| In the text | |
 |
Fig. 3 In the top panel, we present the distribution of the sample stars in the H − R diagram. We also plot some evolutionary tracks computed with CESAM for a 0.8, 0.9 and 1.0 M⊙ assuming the mixing length parameter as 1.4, the initial Helium ratio Y = 0.26 and for [Fe/H] ~ –0.5. In the bottom panel, we present the metallicity distribution of this sample. |
| In the text | |
 |
Fig. 4 Comparison between the derived spectroscopic temperatures and the ones derived using an IRFM calibration. |
| In the text | |
 |
Fig. 5 Calibration of the effective temperature as a function of the color index B − V and [Fe/H]. The 4 fitted lines correspond to lines with constant values of [Fe/H] (–1.0, –0.5, 0.0, 0.5). The bottom panel presents the direct comparison between the spectroscopic temperatures and the calibration. The filled line is the identity line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


