| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201015219 | |
| Published online | 22 December 2010 | |
Near-infrared absorption properties of oxygen-rich stardust analogs
The influence of coloring metal ions
1
Astrophysikalisches Institut,
Schillergässchen 2-3,
07745
Jena,
Germany
e-mail: sz@astro.uni-jena.de; mutschke@astro.uni-jena.de
2
Institut für Astronomie, Türkenschanzstraße 17, 1180
Wien,
Austria
e-mail: thomas.posch@univie.ac.at; hannes.richter@univie.ac.at
3
Institut für Optik und Quantenelektronik,
Max-Wien-Platz 1,
07743
Jena,
Germany
e-mail: ortrud.wehrhan@uni-jena.de
Received: 16 June 2010
Accepted: 15 October 2010
Context. Several astrophysically relevant solid oxides and silicates have extremely small opacities in the visual and near-infrared in their pure forms. Datasets for the opacities and for the imaginary part k of their complex indices of refraction are hardly available in these wavelength ranges.
Aims. We aimed at determining k for spinel, rutile, anatase, and olivine, especially in the near-infrared region. Our measurements were made with impurity-containing, natural, and synthetic stardust analogs.
Methods. Two experimental methods were used: preparing small sections of natural minerals and synthesizing melt droplets under the electric arc furnace. In both cases, the aborption properties of the samples were measured by transmission spectroscopy.
Results. For spinel (MgAl2O4), anatase, rutile (both TiO2), and olivine ((Mg,Fe)2SiO4), the optical constants have been extended to the visual and near-infrared. We highlight that the individual values of k(λ) and the absorption cross section Qabs(λ) depend strongly on the content in transition metals like iron. Based on our measurements, we infer that k values below 10-5 are very rare in natural minerals including stardust grains, if they occur at all.
Conclusions. Data for k and Qabs(λ) are important for various physical properties of stardust grains such as temperature and radiation pressure. With increasing Qabs(λ) due to impurities, the equilibrium temperature of small grains in circumstellar shells increases as well. We discuss why and to what extent this is the case.
Key words: circumstellar matter / infrared: stars / methods: laboratory
© ESO, 2010
1. Introduction
Most studies of the absorption properties of stardust analogs are focused on those wavelength ranges where the respective minerals or glasses have strong resonance features. This is usually the case in the ultraviolet range, on the one hand, and in the mid-infrared (MIR) range, on the other. Between these two ranges – i.e. between the range of strong electronic resonances and the range of strong lattice vibration resonances – there is frequently a lack of data for the complex index of refraction m(λ) = n(λ) + i k(λ). This is especially true for those insulator materials that are highly transparent in the visible and near infrared (NIR), such as magnesium and aluminum silicates and oxides, since their k(λ)-values tend towards values that are too small to be measured with respect to several standard methods of spectroscopy. For example, the k(λ)-values of pure MgAl2O4-spinel would decrease from 10-3 at about 7 μm to 2.2 × 10-13 at about 2 μm according to Tropf and Thomas (1991). For λ < 2 μm, no k-data are available at all from this source.
The importance of k(λ)-data characterizing stardust in the visual and NIR region becomes clear by the following argument. Dust in circumstellar shells mostly absorbs ultraviolet, visual, and NIR radiation from the stellar radiation field, thermalizes it via its internal degrees of freedom and re-emits it at mid-, as well at far-infrared wavelengths. Consider an asymptotic giant branch (AGB) star with an effective photospheric temperature of 2500–4000 K: such an object will emit most of its radiation energy close to 1 μm. Having no information on k(λ) for λ ≈ 1 μm means nothing else than being unable to calculate the energy budget of a dust-enriched stellar atmosphere. Therefore, efforts should be made to close the gaps in k(λ) – which are usually much wider than eventual gaps in n(λ) – where they show up in optical databases for stardust components.
For a very limited number of potential cosmic dust minerals – namely for spinel, rutile, anatase, and olivine – this task will be approached in the present paper by measuring the absorption properties depending on their content of transition metal ions as “impurities” (colouring and absorption-enhancing).
Why do standard optical databases – especially those used in astronomical modeling – often lack absorption data for the transparency regions? Reflectance spectroscopy on bulk surfaces, which is very helpful for deriving MIR optical constants, hardly deliver any reliable constraints on k(λ) in the transparency regime. Here, absorption coefficients based on reflection measurements are usually nothing more than the results of extrapolations. A proper determination of the usually small absorption coefficients in the near-infrared range require transmission measurements at high column densities. Since scattering losses may compete with the effects of absorption in the visual and NIR region, homogeneous (bulk) samples are needed, i.e. sections of millimeter or tenths of millimeter thickness. These are not easy to obtain whether synthetically or from natural sources.
This paper intends to provide a guideline of how to improve k(λ) data for the task of modeling dust absorption in the visual and NIR wavelength regions. The paper is structured in the following way. Section 2 aims at characterizing some of the absorption processes relevant to these regions. In Sect. 3, we describe our measurements on individual stardust analogs, namely spinel, rutile, anatase, and olivine. We present the spectra and optical constants derived for these materials, focusing on their transparency regimes. In the final section, we discuss a specific astrophysical implication of our work, the influence of the derived k(λ)-values on dust temperatures in a radiative equilibrium.
2. The concept of the “transparency regime”
2.1. Definition and illustration
 |
Fig. 1 Absorption indices k(λ) for glassy SiO2, crystalline Mg0.5Fe0.5O, and crystalline MgO from the ultraviolet to the far infrared. The gray area illustrates the “transparency regime” as defined by Mitra (1985) and by Eq. (2). The sources of the data sets are [1] Philipp (1985), [2] Henning et al. (1995), and [3] Roessler & Huffman (1991). |
Figure 1 shows k(λ) for glassy SiO2 according to Philipp (1985), for Mg0.5Fe0.5O according to Henning et al. (1995), and for MgO according to Roessler & Huffman (1991), from the ultraviolet to the far infrared (FIR). Between the two ranges of strong absorption, where k(λ) reaches and exceeds unity, a large region in the visual and near-infrared (NIR) can be seen, where k(λ) drops to very low values both for SiO2 and MgO, while this is not the case for the iron-rich material Mg0.5Fe0.5O. Recalling that the absorption coefficient α(λ) of a solid, which enters into Lambert-Beer’s law, is  (1)we can quantitavely define, following Mitra (1985), the “transparency regime” of a crystalline or amorphous solid as the region where
(1)we can quantitavely define, following Mitra (1985), the “transparency regime” of a crystalline or amorphous solid as the region where  (2)At a thickness of 1 mm, a window in this regime would transmit more than about 90% of the light entering at normal incidence; at 1 cm thickness, it would still transmit at least 1/e or 37% of the radiation (neglecting reflection losses). In terms of k(λ), Eq. (2) defines a wavelength-dependent limit as shown in Fig. 1 (border between the gray and white areas). At λ = 1 μm, for example, we may call a solid “ransparent” if k < 8 × 10-6. This is definitely the case for pure MgO and SiO2. It is also true for pure crystalline MgAl2O4, α-Al2O3, Fe-free Mg-silicates and indeed most oxygen-rich stardust analogs without impurities. We note that for the visible/near-infrared, our transparency criterion is consistent with the statement by Bohren & Huffman (1983) who point out that already for k-values amounting to kvis ≈ 10-4 bulk materials appear black, even in small pieces.
(2)At a thickness of 1 mm, a window in this regime would transmit more than about 90% of the light entering at normal incidence; at 1 cm thickness, it would still transmit at least 1/e or 37% of the radiation (neglecting reflection losses). In terms of k(λ), Eq. (2) defines a wavelength-dependent limit as shown in Fig. 1 (border between the gray and white areas). At λ = 1 μm, for example, we may call a solid “ransparent” if k < 8 × 10-6. This is definitely the case for pure MgO and SiO2. It is also true for pure crystalline MgAl2O4, α-Al2O3, Fe-free Mg-silicates and indeed most oxygen-rich stardust analogs without impurities. We note that for the visible/near-infrared, our transparency criterion is consistent with the statement by Bohren & Huffman (1983) who point out that already for k-values amounting to kvis ≈ 10-4 bulk materials appear black, even in small pieces.
While the transparency regime is limited towards shorter wavelengths in the UV/visible by the edge of electronic interband transitions and possibly excitonic transitions (we give the energies and wavelengths at which strong absorption sets in Table 1), in the infrared it is limited by the energetically highest lattice vibration mode. As a rule of thumb, if a solid has a transparency region, it sets in at wavelengths shorter than  (3)where ωLO denotes the highest longitudinal optical frequency (in wavenumbers) and λLO denotes the corresponding wavelength (cf. Barker 1975; however, Barker uses a different criterion for the transparency and therefore derives other values for λ*). Physically, this upper frequency limit corresponds to the limit up to which two-phonon absorption processes can be excited. Photons of shorter wavelengths (i.e. in the transparency region) can be absorbed by higher overtones, i.e. the simultaneous excitation of three or more phonons, which is less likely and does usually not lead to k values above the transparency limit. As can be seen from Table 1, transparent materials like MgO, amorphous SiO2, MgAl2O4, and TiO2 have two properties in common: their highest energy LO mode is located at 700 to 1400 cm-1, and accordingly, their transparency regime sets in at wavelengths below 7.1 to 3.6 μm. This is also the wavelength region where many sets of optical constants derived from infrared measurements come to an end because there is a lack of physically meaningful k values (as mentioned above).
(3)where ωLO denotes the highest longitudinal optical frequency (in wavenumbers) and λLO denotes the corresponding wavelength (cf. Barker 1975; however, Barker uses a different criterion for the transparency and therefore derives other values for λ*). Physically, this upper frequency limit corresponds to the limit up to which two-phonon absorption processes can be excited. Photons of shorter wavelengths (i.e. in the transparency region) can be absorbed by higher overtones, i.e. the simultaneous excitation of three or more phonons, which is less likely and does usually not lead to k values above the transparency limit. As can be seen from Table 1, transparent materials like MgO, amorphous SiO2, MgAl2O4, and TiO2 have two properties in common: their highest energy LO mode is located at 700 to 1400 cm-1, and accordingly, their transparency regime sets in at wavelengths below 7.1 to 3.6 μm. This is also the wavelength region where many sets of optical constants derived from infrared measurements come to an end because there is a lack of physically meaningful k values (as mentioned above).
For nonconducting materials, there is an FIR transparency regime as well. At wavelengths greater than a few hundred micrometers, k again drops to values lower than 10-3 to 10-2, which are low enough to fulfill (2). Measurements in this wavelength range, therefore, bear some similarities to near-infrared measurements, although wavelengths and absorption mechanisms are different. Data in this wavelength range are additionally limited by the availability of FIR-spectrometers.
2.2. Causes of transparency and of absorption in the NIR region
It can furthermore be seen from Fig. 1 that there are materials without any transparency regime within the wavelength range shown. Mg0.5Fe0.5O – a solid solution of MgO and FeO – is an example of such a material. FeO is a semiconductor, in contrast to MgO and SiO2. Actually, it is a nonstoichiometric compound, its sum formula should better be written as Fe1−xO. Therefore, it contains both Fe2+ and Fe3+ ions, the content of Fe3+ is 0.09 according to Henning et al. (1995). These two properties lead to various absorption mechanisms for wavelengths in the visible and near infrared, as well as the FIR, which are not present or occur at different wavelengths for the previously discussed iron-free oxides, but are efficient in all the members of the series MgxFe1−xO (x < 1). Among these mechanisms are
-
1.
the fundamental interband absorption edge occurring in thevisible wavelength range (band gap 2.3 eV forFeO, according to Park et al. 1999);
-
2.
free electron excitations causing the increase of k(λ) towards the FIR. For FeO, this absorption mechanism should be weak, but a part of the material, which is metastable at room temperature, may be decomposed into Fe and Fe3O4, which both have high free-electron densities (at room temperature for Fe3O4);
-
3.
charge transfer transitions between the orbitals of Fe3+ and those of other metal or ligand ions, that are an important source of strong absorption in the visible extending into the near infrared;
-
4.
the splitting of the d-electron energy levels in transition metal ions, depending on their coordination by oxygen ions. In case of lower symmetry, transitions between these d-electron states can lead to moderately strong absorption bands (so-called crystal field bands, Burns 1993).
The last three mechanisms can obviously enhance the absorption in otherwise transparent wavelength ranges above the transparency limit. All three of them and even more absorption mechanisms, such as vibrational excitation, can be introduced by impurities.
Electronic band edges including strong excitons in terms of energy Eg, wavelength λg, longitudial optical lattice frequencies ωLO, and onset wavelengths λ* for the transparency regions for different materials (see text for more details).
If a (stardust) mineral is transparent at near-infrared and visual wavelengths in its pure, ideal, stoichiometric form, it may in reality contain “impurities” that strongly increase k(λ). This phenomenon is well known in geochemistry and mineralogy, but rarely accounted for in astromineralogical applications. The most efficient “enhancers” of k(λ), consequently of mass absorption coefficients (opacities), are transition metals: Sc, Ti, V, Cr, Mn, Fe, Co, and Ni. Among them, Fe, Ni, Cr, and Mn are probably the most relevant for stardust minerals considering the mean cosmic elemental abundances (Burns 1993).
Any significant inclusion of transition metal ions into an originally transparent mineral will turn its appearance in the visual spectral range from colorless to colored or even black. At present, it is hardly known which amounts of transition metal ions are actually present in stardust minerals as “impurities”, but it is unrealistic to expect impurity-free minerals in circumstellar and interstellar environments.
Even though several visually transparent oxides such as spinel and Al2O3 have been identified in presolar grains, it has not yet been possible to determine the transition metal content of these minerals; in other words, their “color” has not been quantitatively measured. Spectroscopic methods determining the transition metal content of cosmic dust by “remote sensing” are restricted, up to now, to reflectance spectroscopy of lunar and planetary surfaces (Burns 1993).
Therefore, in the present paper, we chose the following approach when synthetically including transition metals into oxides: We based our measurements of k(λ) partly on natural terrestrial samples, which always contain impurities to some extent, and we were partly able to widen the range of possible inclusions of transition metals by producing synthetic samples. For one of our samples, spinel, it was thus possible to create a series of samples and corresponding sets of optical constants such as exploring the possible range of absorption that may occur in samples of cosmic elemental composition.
3. Individual measured stardust analogs
3.1. Derivation of k(λ) from the transmission spectra
The method we applied to derive k(λ) was transmission spectroscopy of small sections of our materials. For producing these sections we embedded pieces of our materials with sufficient size (diameter > 0.5 mm) into resin and cut and abraded the resin slabs to thicknesses between 80 and 1100 μm. After that, the samples were just polished to have an even and smooth surface.
Some of the examined materials are crystals of non-cubic symmetry and therefore optically anisotropic; i.e. their optical constants depend on their orientation relative to the polarization direction of the light. For these materials, it has been necessary to perform measurements with polarized radiation. An overview of the sample properties such as chemical composition determined by energy-dispersive X-ray analysis (EDX), crystal symmetry, and slab thickness is given in Table 3 (the oxygen content is not a direct result of the EDX measurements, but has been inserted according to stoichiometry).
Compositions of the samples and thicknesses of the platelets examined in this paper.
For the spectroscopic measurements, the following spectrometers have been used: a Perkin Elmer Lambda 19 (for the wavelength range from 0.275 to 2 μm), a Bruker FTIR 113v (for the wavelength range from 1.6 to 25 μm), and a single-beam optical absorption spectrometer constructed on the basis of a SpectraPro-275 triple-grating monochromator. The actual range of the transmission measurements is limited by the wavelengths at which the samples become opaque. For a typical sample thickness of 300 μm, this happens for a k value of about 10-3 on the short-wavelength side and at a few 10-2 on the long-wavelength side. The transmittance values (transmitted intensity normalized by incident intensity) were converted in k(λ) using the relation  (4)where d is the thickness of the small section and the reflectance R is given as
(4)where d is the thickness of the small section and the reflectance R is given as  (5)For very small values of k(λ) this equation reduces to
(5)For very small values of k(λ) this equation reduces to  (6)While using n(λ) values from Palik (1985–98) we were able to derive values for k(λ) for various samples.
(6)While using n(λ) values from Palik (1985–98) we were able to derive values for k(λ) for various samples.
The following subsections contain a presentation and discussion of our results for the individual materials. The derived k values for the NIR will be made publicly available on the Jena Database of Optical Constants, http://www.astro.uni-jena.de/Laboratory/Database/databases.html.
3.2. Spinels
3.2.1. Material properties, sample preparation and analysis
Spinel is an abundant component of presolar grains from meteorites (e.g. Hoppe 2004) and has been proposed as the carrier of mid-infrared emission bands observed in the spectra of circumstellar dust shells (e.g. Posch et al. 1999; Fabian et al. 2001). Pure stoichiometric spinel (MgAl2O4) has an elementary cell that consists of 32 O anions, 16 Al, and 8 Mg cations. In the ideal crystal lattice, the trivalent Al cations are octahedrally coordinated by oxygen ions, while the bivalent Mg cations are tetrahedrally coordinated. The cubic lattice symmetry of this mineral make it optically isotropic.
While many previous publications refer to impurity-free spinels, the measurements presented in this paper refer to a series of spinels that contain impurities (mainly chromium and iron). The Cr ions partly substitute Al, so they occupy a part of the octahedral sites. The Fe ions partly substitute Al, partly Mg. Because the lattice structure of the Cr-containing spinels is unambiguous (since Cr is not polyvalent in contrast to Fe), we have chosen synthetic Cr-doped spinels as a representative of the effect of impurities on k, even though in cosmic environments, it is much more likely to have Fe impurities in spinels due to the much higher stellar abundance of Fe compared to Cr as given in Table 2.
Additionally, a dark-red natural spinel crystal from Burma was examined. Apart from a very small amount of Si, it contains traces of both Fe and Cr. The exact chemical composition of the sample is given in Table 3.
 |
Fig. 2 Section of the spinel crystal from Burma used for deriving k(λ) from transmission spectroscopy. From bottom to top this crystal has a size of around 3 mm. |
The synthesis of the Cr-doped spinels was performed in the following way (see also Richter et al. 2005). We used a tungsten electric-arc furnace with a water-cooled copper baseplate. Powders of Mg oxide, Al oxide, and Cr(III) oxide have been mixed in corresponding proportions so as to obtain the basic material for the melting procedure. After being homogenized, the mixture was pressed into several pellets of 150–300 mg mass each and a diameter of 1.3 cm each. This densification of the powder was necessary to avoid electrostatic interactions between the tungsten pike in the furnace and the powder particles when starting the melting process. Since Mg oxide in particular is a hardly fusable material, the pellets were broken again into several pieces (4–7 for each pellet) to facilitate the melting process. After putting several pieces into the furnace, the melting process started under a 1 bar argon atmosphere. The samples were exposed to the electric arc until they were fully melted. The formation temperature should be close to the melting point of spinel (about 2400 K), and it probably increased with the Cr content (the melting point of Cr2O3 is about 2700 K). After cooling to subliquidous temperature within a few seconds and subsequent cooling to room temperature, we obtained melt-droplets that were 3–5 mm in size and had colors ranging from light red in the most Cr-poor spinel to dark red (almost black) in the most Cr-rich sample. The theoretical compositions of the samples are given by MgAl(2−x)CrxO4, with x amounting to 0.02, 0.03, 0.12, and 0.23.
The exact chemical compositions were derived from EDX analyses, where several (typically 12) spots for each of the Cr-spinel droplets were scanned and investigated for inhomogeneities and variations in the Mg/Al/Cr ratios. Tab. 3 gives the resulting mean stoichiometries – also for the TiO2 and olivine samples discussed in Sects. 3.3 and 3.4.
3.2.2. Measured transmission spectra and derived k(λ) values
 |
Fig. 3 Absorption indices k(λ) of different spinels derived from transmission spectroscopy. For the interpretation of the different bands seen in the spectra, see text. |
We now present and interpret the results of the transmission spectroscopy performed on the above-mentioned samples at UV-, visual, near-infrared, and mid-infrared wavelengths.
The measured transmittances were converted into k(λ) values by applying (4) and Fig. 3 shows the derived results. The dashed line represents k(λ) for pure stoichiometric spinel according to Tropf and Thomas (1991). The mid infrared maxima of k(λ) – between 10 and 40 μm – correspond to three vibrational modes of the lattice structure: The origin of the 31–32 μm band is an Mg–O vibration, while the remaining two maxima originate from Al–O vibrations. For further details see Fabian et al. (2001).
It can be clearly seen from Fig. 3 that for the impurity-free spinel – and only for this one – a very steep decrease of k(λ) with decreasing wavelength occurs at λ < 7 μm.
The solid line denotes k(λ) for our natural sample from Burma which contains about 1% iron and approximately as much chromium. This k(λ)-curve begins to deviate from the corresponding line for pure spinel at 6–7 μm and never drops below the limit of the transparency regime, in accordance with the opaque character of the 0.25 mm thick sample. Within the range of rough agreement between the two curves (> 7 μm), there is some structure in our new data, especially a peak at ~7 μm, which is likely an overtone of the 13–14 μm lattice vibration band.
Between 4 and 1.5 μm, a broad maximum occurs with its origin in the Fe2+ and OH− content of the sample. Even though the OH content is very small (definitely below 1%), it is sufficient for the O–H stretching vibration band to appear in the spectrum as a narrow band at 2.8 μm. Then k(λ) approaches values even close to 10-3 at the center of this band. The same holds true for the maximum of the Fe2+ band, which is located at 2.0 μm. A detailed interpretation of the Fe2+ and OH− bands in natural and synthetic spinels can be found in a recent paper by Lenaz et al. (2008). A comparison between our data and those published by Lenaz et al. (2008) is shown in Fig. 4.
 |
Fig. 4 Comparison between the absorption indices derived for spinels with different transtion metal content. The solid line refers to our sample – with an Fe content of 1.2% and a Cr content of 0.87%. The dotted line refers to a very Fe-rich sample (Fe-content of 11.1%), the dashed line denotes an Fe-poor sample (both according to Lenaz et al. 2008). The Fe content of the samples clearly correlates with the respective k-values at 2 μm. |
The region below 1 μm is characterized by further electronic absorption mechanisms. In this region, the k(λ) spectra strongly depend on the Cr content of spinel. This can be nicely seen by comparing the solid line with the dotted lines, which represent the Cr-doped synthetic spinels.
The Al to Cr substitution in the samples results in a generally increased visual and UV absorption. Additionally, two distinct absorption bands occur around 0.550 μm and 0.387 μm. The positions and shapes of these bands accordance well with the band positions in spectra of low-Cr Mg-Al- spinels – both natural and synthetic ones – published by Wood et al. (1968), Taran et al. (1994), and Ikeda et al. (1997). These bands originate from crystal field electronic transitions, namely 4T2g ← 4A2g for the 0.550 μm maximum and 4T1g ← 4A2g for the 0.387 μm maximum. Of course, the intensity of the Cr electronic absorption bands is higher for the synthetic Cr-doped samples, and k-values up to 2 × 10-3 are reached at 0.550 μm for 12% Cr content.
3.3. Rutile and anatase (TiO2)
Together with Ca and Al oxides, Ti oxides are considered as candidates for the very first condensates in oxygen-rich circumstellar shells, notwithstanding that titanium is rather rare according to its mean cosmic elemental abundance (2.5 orders of magnitude less abundant than Si and Mg). With respect to dust formation in circumstellar shells, it is noteworthy that molecular TiO is extremely prominent in the atmospheres of M- and S-stars. Furthermore, titanium is heavily depleted in the interstellar gas, indicating that it is indeed consumed by previous dust formation processes.
Jeong et al. (2003) predict that TiO2 is the most promising candidate for the first (seed-)condensate in oxygen-rich circumstellar shells. There is also evidence from meteoritics that Ti compounds form in circumstellar shells and a presolar meteoritic TiO2 grain has been tentatively identified (Nittler 2003).
We examined the two most common terrestrial species of TiO2 with respect to their near infrared absorption properties, namely anatase and rutile. Both materials have a tetragonal crystal symmetry, hence only one optical axis. Consequently, the measurements for the polarization directions parallel and perpendicular to this optical axis could be performed on a single sample cut along this axis by rotating the polarizer by 90 degrees.
k(λ)NIR is not unmeasurably small in the case of our samples due to their Fe and V contents. The Fe- and V- contents of our TiO2 samples have been determined by energy-dispersive X-ray measurements and are summarized in Table 3
3.3.1. Rutile
Rutile is the most abundant modification of titanium dioxide on the Earth. It has tetragonal symmetry like anatase, but is characterized by a higher density, a greater Ti-Ti distance, and a shorter Ti-O distance than the latter. As for rutile’s ultraviolet and mid-infrared properties, Ribarsky (1985) compiled a rather comprehensive table of optical constants. However, for wavelengths between 0.4 μm and 11.2 μm, data for k(λ) are largely missing.
We were able to measure k for a natural rutile sample from 0.5 to 8 μm, based on a section with a thickness of d = 155 μm (see Figs. 5 and 6). The most significant feature in the NIR k-spectrum of rutile is a sharp peak at 3.03 μm. This peak, which becomes especially prominent when the electric field vector of the polarized radiation is perpendicular to the c-axis of the crystal, is due to an OH stretching mode (see Maldener et al. 2001). It is explained by the presence of H2O in natural rutile. The 3.03 μm band of our sample may be explained with an H2O content of the order of magnitude of 300 weight ppm, based on the spectra and analytical results by Maldener et al. (2001).
 |
Fig. 5 Section of the rutile crystal used for deriving k(λ) from transmission spectroscopy. The crystal has a width of about 1.5 mm. |
 |
Fig. 6 Absorption index k(λ) for rutile (TiO2) derived from transmission measurements on a small section of 155 μm diameter. The k(λ) values in the UV and MIR are from Palik (1985–98). The sharp peak in k(λ) comes from a small crystal water content of the natural sample. |
3.3.2. Anatase
Anatase is a modification of tetragonal Ti oxide with a TiO6 octahedron structure consisting of one Ti4+ and six O2− ions. It can be transformed to rutile by heating above 1200 K. Its mid-infrared optical constants have been published by Posch et al. (2003).
For anatase we used a section of d = 255 μm thickness to perform transmittance measurements between 0.7 and 8 μm. The transmittance spectra obtained for the individual orientations of the sample relative to the polarized radiation did not differ within the measurement’s accuracy, therefore only one curve is plotted in Fig. 7.
The most conspicuous feature in the k(λ) spectrum of anatase is the broad double-peaked band 2–3 μm. Maximum k values of more than 0.001 are reached in this range. The second of the two peaks, located at 3.0 μm, corresponds to an O–H stretching mode at 3389.7 cm-1. It is an indirect consequence of the V content of our sample, since V-containing TiO2 has a stronger hydroxyl content (Zhou et al. 2010). The primary peak in the absorption, located at 2.0 μm, may be directly caused by the V content of the sample.
 |
Fig. 7 Absorption index k(λ) of the TiO2 modification anatase derived from transmission spectroscopy. The values for λ > 10 μm are from Posch et al. (2003). |
3.4. Olivine
Olivine is, together with pyroxene, the most abundant crystalline silicate in space. Its prominent bands are observed in many spectra of accretion disks around young stars and in the outflows of AGB stars (Henning 2003a,b). Olivine also occurs in our solar system in the form of cometary dust (Hanner 2003), as interplanetary dust particles (Bradley 2003), and on planetary surfaces (e.g. Hartmann 2005).
Olivine has the general sum formula (Mg, Fe)2SiO4 with its Mg end member forsterite and the rarer Fe end member fayalite. On Earth, olivine is the most abundant material in the upper lithosphere. In general, more Mg-rich and less Fe-rich olivines are found. It crystallizes in orthorhombic symmetry with isolated [SiO4]4− tedrahedra surrounded by metal cations (Fe2+, Mg2+), each in coordination to six oxygen atoms. There are two different types of these coordinations, both slightly distorted from the octahedral symmetry. One is centrosymmetric and elongated along one of the O-O axes (cation sites in this coordination are called “M1”), and the other is non-centrosymmetric and irregular (“M2”; cf. Burns 1993).
Olivine crystals usually have a greenish to yellowish color, which can turn into brown when it contains traces of Fe3+ ions. The greenish coloring is caused by a crystal field band of Fe around 1 μm wavelength, which leads to an increased opacity for red light and an increased transmittance of yellow and green light. The brownish coloring comes from charge transfer processes toward the Fe3+ ions leading to absorption increasing throughout the visible wavelength range towards the ultraviolet. This kind of absorption has been detected in the central parts of our Sri Lanka olivine sample (see below), where cracks may have given rise to oxidation of Fe2+ in interface regions.
In the present paper, we compare near-UV to MIR absorption spectra of k(λ) of San Carlos olivine single crystals with spectra of an Fe-rich variety of olivine obtained from Ratnapura (Sri Lanka) (Fe contents: 8% and 20%, respectively – see Table 3). Since olivine crystals have non-cubic symmetry, the polarization of the incoming radiation relative to the three crystallographic axes x, y, and z plays an important role in the resulting spectra. Several platelets of the San Carlos olivine have been prepared to have a surface perpendicular to one of these axes. Two of them, denoted as C and D1, have been chosen to represent the properties of oriented olivine in polarized light due to the quality of their spectra. Sample C has been cut along the y-z plane, sample D1 along the x-y plane, so all three crystallographic axes were available for the measurements. The thicknesses are 1063 μm for sample C and 1115 μm for sample D1. For the Sri Lanka olivine, only measurements of light polarized along the y- and z-axes (E||y and E||z) were possible, since only one platelet (thickness: 300 μm) could be prepared. The sample is shown in Fig. 8. For these measurements we chose an area of about 1 mm diameter without cracks, which can be seen in the figure. This area is also free of brownish colouring which occurs along the major cracks in the middle of the sample. The surface of this platelet is also not perfectly oriented perpendicular to the x-axis, because an inclination of approximately 20° could be measured by X-ray diffraction.
The most important differences in the absorption spectra between the different oriented samples of San Carlos olivine are found in the bands caused by transitions of the metal cations, located around 0.7–1.5 μm. While E||y and E||z polarized light creates broad structures with peaks around 1.056 μm and 1.108 μm, light polarized along the x-axis creates a more prominent band around 1.073 μm. Shoulders appear in all three polarizations on both sides of the main peak around 0.87 μm and between 1.25 and 1.35 μm. The value of k in the maxima of this band reaches ~1.8 × 10-4 for both E||y and E||z, while k reaches a value of ~4 × 10-4 for E||x. The corresponding values for the Sri Lanka olivine are given in Table 4. The k values of this band are increased compared to the measurements of the San Carlos olivine in the same polarization (in its maxima by a factor of ≈2) and also the particular positions of band and shoulders are shifted to longer wavelengths, except for the short-wavelength shoulder that shifts to shorter wavelengths.
 |
Fig. 8 Platelet of the Fe-rich Sri Lanka sample used for transmission measurements under polarized light. The sample has a width of 4 mm and a length of 6 mm. The black circle features the spot of the measurements. |
Specific positions and k values for the main peaks (‘mp’) and shoulders (“sh I” and “sh II”) of the crystal field band caused by Fe ions of the San Carlos (SC) and Sri Lanka olivines (SL), respectively.
The continuum k values are in general relatively independent of the polarization and increases constantly towards longer wavelengths (see Fig. 9). Toward shorter wavelengths we cannot see an absorption increase, which indicates noticeable charge transfer processes. The sharp increase in k at around 0.4 μm, which becomes more pronounced with increasing Fe content, is due to the onset of intrinsic transitions of the Fe2+ ions. The continuum k value is independent of the Fe content of the olivine, which is remarkable.
Towards longer and towards shorter wavelengths from the crystal field band at around 1 μm, several very weak bands appear. The bands at shorter wavelengths are comparatively sharp and appear independently of the polarization at 0.65, 0.49, 0.47, and 0.45 μm. These bands come from the spin forbidden transitions in the Fe2+ ions (Burns 1993). In contrast to that, the structures at longer wavelengths show a polarization dependence. For the Sri Lanka sample in E||y polarization, a broad and relatively strong band can be seen at 3 μm, which is due to the stretching vibrations of OH groups. For the E||z polarization this band is much sharper, similar to the corresponding band in the rutile. Around the 5.5 μm wavelength, another band is located, which is likely an overtone of the 10 μm stretching vibration band of the SiO4-tetrahedron.
 |
Fig. 9 Spectra of oriented San Carlos olivine in polarized light. The spectra were measured from samples C and D1 (see text for further details). |
 |
Fig. 10 Spectra of oriented San Carlos and Sri Lanka olivines in polarized light for E||y. For the San Carlos olivine spectra of sample D1 are shown. |
 |
Fig. 11 Spectra of oriented San Carlos and Sri Lanka olivines in polarized light for E||z. For the San Carlos olivine, spectra of sample C are shown. |
4. The influence of k(λ) on the temperature of small grains
In the present section, we apply our results for the magnitude of k(λ) to the calculation of the radiative equilibrium temperature of dust grains, which is an important parameter characterizing the conditions in dust-forming regions like circumstellar shells, and it indeed depends on absorption and emission properties. In the case of a thermodynamical equilibrium between the stellar radiation field (assuming a star with radius R∗ with an effective temperature T∗) and the dust grains in an optically thin circumstellar shell, it is possible to derive the dust temperature Td for a given distance from the star from the energy balance. The radiative energy absorbed by an individual dust grain is then given by 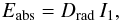 (7)where
(7)where  (8)and Drad, the radial dilution factor of the stellar radiation field, is defined as
(8)and Drad, the radial dilution factor of the stellar radiation field, is defined as ![\begin{equation} \label{drad} D_\mathrm{rad} = 2 \left[1-\sqrt{1-\frac{R_\mathrm{*}^2}{R_\mathrm{d}^2}}\right]\cdot \end{equation}](/articles/aa/full_html/2011/02/aa15219-10/aa15219-10-eq113.png) (9)Here, R∗ denotes the effective stellar radius, and Rd is the distance of a dust grain from the star’s center. Eq. (9) is based on the so-called Lucy-approximation (Lucy 1971), according to which the star is not considered as a point source, but its spatial extension is taken into account, which is important for small distances of the dust grains from the star. Already for a distance of 3 stellar radii, the dilution factor Drad may be simplified to
(9)Here, R∗ denotes the effective stellar radius, and Rd is the distance of a dust grain from the star’s center. Eq. (9) is based on the so-called Lucy-approximation (Lucy 1971), according to which the star is not considered as a point source, but its spatial extension is taken into account, which is important for small distances of the dust grains from the star. Already for a distance of 3 stellar radii, the dilution factor Drad may be simplified to  /
/ .
.
The radiative energy emitted by a single (spherical) dust grain with the radius a is given by  (10)Numerically, the integrals I1 and I2 can not (and don’t need to) be calculated from zero to infinity as Eqs. (8) and (10) suggest. It is sufficient to integrate over those wavelengths where the star emits a significant fraction of it total radiative energy. On the other hand, the energy balance of the dust cannot be calculated correctly if optical constants (and hence Qabs-values) are lacking even at NIR wavelegths where the maximum of the stellar radiation field is located.
(10)Numerically, the integrals I1 and I2 can not (and don’t need to) be calculated from zero to infinity as Eqs. (8) and (10) suggest. It is sufficient to integrate over those wavelengths where the star emits a significant fraction of it total radiative energy. On the other hand, the energy balance of the dust cannot be calculated correctly if optical constants (and hence Qabs-values) are lacking even at NIR wavelegths where the maximum of the stellar radiation field is located.
The combination of Eqs. (8), (10) leads to Eq. (11), which allows calculating the dependence of the dust temperature Td on the distance from the star Rd: ![\begin{equation} \label{rlucy} R_\mathrm{d}(T_\mathrm{d}) = \frac{R_\mathrm{*}}{\sqrt{1-[1-\frac{2I_2}{I_1}]^2}}\cdot \end{equation}](/articles/aa/full_html/2011/02/aa15219-10/aa15219-10-eq122.png) (11)For the simplified dilution factor
(11)For the simplified dilution factor  /
/ , the previous equation can also be simplified, namely to
, the previous equation can also be simplified, namely to  (12)For very small dust grains (with sizes amounting to 0.01 μm or less), the relation between Td and Rd becomes independent of the grain size (which enters into the absorption efficiency Qabs(λ), in both the integrals I1 and I2; see Krügel 2003). In this case, the influence of the optical constants on Qabs(λ) becomes most decisive for the dust temperature. Again in the small particle limit (also called Rayleigh limit), the relation between Qabs and the optical constants n and k is given by
(12)For very small dust grains (with sizes amounting to 0.01 μm or less), the relation between Td and Rd becomes independent of the grain size (which enters into the absorption efficiency Qabs(λ), in both the integrals I1 and I2; see Krügel 2003). In this case, the influence of the optical constants on Qabs(λ) becomes most decisive for the dust temperature. Again in the small particle limit (also called Rayleigh limit), the relation between Qabs and the optical constants n and k is given by
 (13)from which it follows that in those regions where n(λ) is approximately constant, such as in the NIR region for the oxide species discussed in this paper, k(λ) becomes the decisive quantity for Qabs(λ), hence decisive for the dust temperature as well.
(13)from which it follows that in those regions where n(λ) is approximately constant, such as in the NIR region for the oxide species discussed in this paper, k(λ) becomes the decisive quantity for Qabs(λ), hence decisive for the dust temperature as well.
More precisely, it is the magnitude of k(λ) and Qabs(λ) in the visual and NIR relative to the respective MIR/FIR-values that determines the dust temperature. Consequently, dust species that have small k(λ), corresponding to their high transparency in the optical and NIR – such as transition metal free oxides and silicates – will be much less heated by the stellar radiation than absorbing grain species. This can be seen most clearly from Fig. 12. For MgO, the lack of absorption mechanisms operating at short wavelegths leads to inefficient radiative heating, such that the dust temperature Td drops below 500 K already at two stellar radii. For Mg0.5Fe0.5O, on the other hand, Td amounts to 2000 K close to 2 R∗. Furthermore, Td(Rd) drops much more steeply for MgO than for Mg0.5Fe0.5O.
The difference between MgO and Mg0.5Fe0.5O with respect to NIR absorbance and radiative equilibrium temperature is obviously an extreme case. Smaller, but still significant differences in Td(r) show up for the other dust species discussed in the present paper, e.g. for spinel (see Fig. 13).
As a consequence of the differences in the absorption efficiency factors calculated according to Eq. (13) for small spherical grains – see insert in Fig. 13 – a difference in Td results. In this case, it amounts to about 25% at 2 R∗ (the precise values are 850 K vs. 625 K at 2 R∗). While Qabs calculated according to Eq. (13) for small spherical grains (Fig. 13 insert) increases linearly with k, the increase in Td in this case appears to be relatively weak, the gradient of Td with R remains steep for the Cr-containing spinel.
Notwithstanding, it is important to take the effect of kvis/NIR into account, since when it comes to condensation or evaporation, a few degrees Kelvin may decide about the existence or nonexistence of grains in a particular zone around a dust-forming star. Furthermore, there is still another parameter that linearly increases with k in the small particle limit, namely the radiation pressure efficiency factor Qpr. For particles that are smaller than the wavelength, Qpr ≈ Qabs, and thus an increase in k leads, via Eq. (13), to a corresponding increase in Qpr. The more efficiently a dust grain absorbs radiation around 1 μm, the larger the radiation pressure it experiences and the velocity it can reach in a radiation-pressure driven stellar wind. For a detailed discussion of the influence of absorption and scattering on the radiation pressure acting on dust grains, we refer to Höfner (2008).
 |
Fig. 12 Comparison of the radiative equilibrium temperature of MgO (characterized by extremely low k(λ) values in the NIR region) with the equilibrium temperature of Mg0.5Fe0.5O (its k(λ) value is more than seven orders of magnitude larger in the NIR). The stellar effective temperature has been set to 3000 K. |
 |
Fig. 13 The radiative equilibrium temperature of natural (terrestrial) spinel dust containing impurities compared to the temperature of impurity-free Mg-Al-spinel according to Palik (1985–98). The stellar effective temperature has been set to 4000 K. |
5. Conclusions
We examined the near-infrared and visual absorption properties of several stardust analogs. Our focus has been on materials for which extremely low k values – or no k values at all – can be found in the literature for the above-mentioned wavelength range: spinel, rutile, anatase, and olivine.
The examined samples were either natural terrestrial ones or synthetic crystals with a defined amount of absorption-enhancing impurities. In all cases, the impurity contents were such as to be compatible with cosmic elemental abundances, and in all cases, the derived k values were 1-2 orders of magnitude higher than the limit of the “transparency regime” defined at the beginning of this paper (Eq. (1)).
We suggest that even for cosmic dust grains which have smaller impurity contents than our analogs, k values below the limit of transparency will rarely be reached. In cases where no appropriate k data are available, the limit of the “transparency regime” (k ≈ 10-5 at 1 μm and k ≈ 10-4 at 10 μm) may serve as a heuristic lower limit for the absorption of natural materials including stardust grains, although certain circumstances can produce very transparent natural minerals.
Even though the “real” k values of cosmic dust grains still has to be determinated by further investigations (e.g. on presolar grains), the above constraint seems more realistic than adopting k values dropping to 10-8 and below, which can be found in the solid-state physics literature and which mostly refer to synthetic, impurity-free materials.
As an example, we showed that using k data for spinel taken from Palik (1985–98) can lead to underestimating the equilibrium temperature reached by this oxygen-rich dust species in a circumstellar radiation field. More realistic results can be obtained if optical constants with k values above the transparency limit are used. The same holds true for olivine, which is a much more abundant component of circumstellar dust.
The magnitude of absorption also has an important influence on other quantities characterizing an expanding circumstellar shell, such as the radiation pressure. This is, however, beyond the scope of the present paper.
Acknowledgments
Comments by an anonymous referee helped us to improve the structure of our paper. Gabriele Born, Jena, kindly did the sample preparation and helped with the EDX measurements. We are grateful to Prof. A. Tsuchiyama, Osaka University, for providing the Sri Lanka olivine. H. M. and S. Z. acknowledge support by DFG grant Mu 1164/7 within SPP 1385 “The first ten Million Years of the Solar System – a Planetary Materials Approach”. T.P. acknowledges support by the Austrian “Fonds zur Förderung der wissenschaftlichen Forschung” (FWF; project number P18939-N16). HR is a member of the IK I033-N “Cosmic Matter Circuit” at the University of Vienna.
References
- Barker, A. J., Wilkinson, G. R., Massa, N. E., et al. 1975, in Optical Properties of Highly Transparent Solids (New York: Plenum), ed. S. S. Mitra, & B. Bendow [Google Scholar]
- Bohren, C. F., & Huffman D. R. 1983, Absorption and Scattering of Light by Small Particles (New York: John Wiley) [Google Scholar]
- Bradley, J. 2003, in Astromineralogy (Berlin and Heidelberg: Springer-Verlag), ed. Th. Henning, 225 [Google Scholar]
- Burns, R. G. 1993, Mineralogical Applications of Crystal Field Theory, 2nd edn. (Cambridge University Press) Cambridge Topics in Mineral Physics and Chemistry, 19 [Google Scholar]
- Fabian, D., Posch, Th., Mutschke, H., Kerschbaum, F., & Dorschner, J. 2001, A&A, 373, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanner, M. S. 2003, in Astromineralogy (Berlin and Heidelberg: Springer-Verlag), ed. Th. Henning, 173 [Google Scholar]
- Hartmann, W. K. 2005, Moons and Planets, 5th edn. (Belmont, CA), 239 [Google Scholar]
- Henning, Th., & Mutschke, H. 1997, A&A, 327, 743 [NASA ADS] [Google Scholar]
- Henning, Th., Begemann, B., Mutschke, H., & Dorschner, J. 1995, A&AS, 112, 143 [NASA ADS] [Google Scholar]
- Henning, T., Il’in, V. B.,Krivova, N. A., et al. 1999, A&AS, 136, 405 [Google Scholar]
- Henning, Th. 2003a, in Solid-State Astrochemistry, ed. V. Pirronello, J. Krelowski, & L. Manico (Dordrecht: Kluwer) [Google Scholar]
- Henning, Th. 2003b, Astromineralogy, Lecture Notes in Physics (Berlin and Heidelberg: Springer-Verlag), 609 [Google Scholar]
- Höfner, S. 2008, A&A, 491, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoppe, P., 2004, in: ASP Conf. Ser., 309, 265 [Google Scholar]
- Ikeda, K., Nakamura, Y., Masumoto, K., & Shima, H. 1997, J. Amer. Cer. Soc. 80, 2672 [CrossRef] [Google Scholar]
- Jeong, K. S., Winters, J. M., LeBertre, T., & Sedlmayr, E. 2003 A&A, 407, 191 [Google Scholar]
- Krügel, E. 2003, The Physics of Interstellar Dust (Bristol and Philadelphia: Institute of Physics Publishing) [Google Scholar]
- Lenaz, D., Skogby, H., Nestola, F., & Princivalle, F. 2008, GCA, 72, 475 [NASA ADS] [Google Scholar]
- Lucy, L. B. 1971, ApJ, 163, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Maldener, J., Rauch, F., Gavranic, M., & Beran, A. 2001, Mineralogy & Petrology, 71, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mitra, S. S. 1985, in Handbook of Optical Constants of Solids I (Boston: Academic Press), ed. E. D. Palik, 213 [Google Scholar]
- Nittler, L. R. 2003, EPSL, 209, 259 [Google Scholar]
- Palik, E. D. 1985–1998, Handbook of Optical Constants of Solids, 3 vols. (Boston: Academic Press) [Google Scholar]
- Palme H., & Beer H. 1993, in Landolt-Börnstein, Group VI: Astronomy and Astrophysics, ed. O. Madelung, 3, 205 [Google Scholar]
- Park, J.-C., Kim, D., Lee, Ch.-S., & Kim, D.-K. 1999, Bull. Korean Chem. Soc. 20, 1005 [Google Scholar]
- Philipp, H. R. 1985, in Handbook of Optical Constants of Solids I (Boston: Academic Press), ed. E. D. Palik, 749 [Google Scholar]
- Posch, Th., Kerschbaum, F., Mutschke, H., et al. 1999, A&A, 352, 609 [NASA ADS] [Google Scholar]
- Posch, Th., Kerschbaum, F., Mutschke, H., Dorschner, J., & Jäger, C. 2002, A&A, 393, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posch, Th., Kerschbaum, F., Fabian, D., et al. 2003, Ap&SS, 149, 437 [Google Scholar]
- Ribarsky, M. W. 1985, in Handbook of Optical Constants of Solids I (Boston: Academic Press), ed. E. D. Palik, 795 [Google Scholar]
- Richter, H., Posch, Th., Taran, M., & Mutschke, H. 2005, Mineralogy & Petrology, 85, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Roessler, D. M., & Huffmann, D. R. 1991, in Handbook of Optical Constants of Solids II (Boston: Academic Press), ed. E. D. Palik, 919 [Google Scholar]
- Shankland, T. J. 1968, Science, 161, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sogawa, H., Koike, C., Chihara, H., et al. 2006, A&A, 451, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, H., Berger, H., Schmid, P. E., & Lévy, F. 1993, Solid State Communications, 87, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Taran, M. N., Langer, K., Platonov, A. N., & Indutny, V. V. 1994, Phys. Chem. Minerals, 21, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Tropf, W. J., & Thomas, M. E. 1991, in Handbook of Optical Constants of Solids II (Boston: Academic Press), ed. E. D. Palik, 883 [Google Scholar]
- Wood, D. L., Imbusch, G. F., MacFarlane, R. M., Kisliuk, P., & Larkin, P. M. 1968, J. Chem. Phys., 48, 5255 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, W., Liu, Q., Zhu, Z., & Zhang, J. 2010, J. Phys. D: Appl. Phys., 43, 035301 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Electronic band edges including strong excitons in terms of energy Eg, wavelength λg, longitudial optical lattice frequencies ωLO, and onset wavelengths λ* for the transparency regions for different materials (see text for more details).
Compositions of the samples and thicknesses of the platelets examined in this paper.
Specific positions and k values for the main peaks (‘mp’) and shoulders (“sh I” and “sh II”) of the crystal field band caused by Fe ions of the San Carlos (SC) and Sri Lanka olivines (SL), respectively.
All Figures
 |
Fig. 1 Absorption indices k(λ) for glassy SiO2, crystalline Mg0.5Fe0.5O, and crystalline MgO from the ultraviolet to the far infrared. The gray area illustrates the “transparency regime” as defined by Mitra (1985) and by Eq. (2). The sources of the data sets are [1] Philipp (1985), [2] Henning et al. (1995), and [3] Roessler & Huffman (1991). |
| In the text | |
 |
Fig. 2 Section of the spinel crystal from Burma used for deriving k(λ) from transmission spectroscopy. From bottom to top this crystal has a size of around 3 mm. |
| In the text | |
 |
Fig. 3 Absorption indices k(λ) of different spinels derived from transmission spectroscopy. For the interpretation of the different bands seen in the spectra, see text. |
| In the text | |
 |
Fig. 4 Comparison between the absorption indices derived for spinels with different transtion metal content. The solid line refers to our sample – with an Fe content of 1.2% and a Cr content of 0.87%. The dotted line refers to a very Fe-rich sample (Fe-content of 11.1%), the dashed line denotes an Fe-poor sample (both according to Lenaz et al. 2008). The Fe content of the samples clearly correlates with the respective k-values at 2 μm. |
| In the text | |
 |
Fig. 5 Section of the rutile crystal used for deriving k(λ) from transmission spectroscopy. The crystal has a width of about 1.5 mm. |
| In the text | |
 |
Fig. 6 Absorption index k(λ) for rutile (TiO2) derived from transmission measurements on a small section of 155 μm diameter. The k(λ) values in the UV and MIR are from Palik (1985–98). The sharp peak in k(λ) comes from a small crystal water content of the natural sample. |
| In the text | |
 |
Fig. 7 Absorption index k(λ) of the TiO2 modification anatase derived from transmission spectroscopy. The values for λ > 10 μm are from Posch et al. (2003). |
| In the text | |
 |
Fig. 8 Platelet of the Fe-rich Sri Lanka sample used for transmission measurements under polarized light. The sample has a width of 4 mm and a length of 6 mm. The black circle features the spot of the measurements. |
| In the text | |
 |
Fig. 9 Spectra of oriented San Carlos olivine in polarized light. The spectra were measured from samples C and D1 (see text for further details). |
| In the text | |
 |
Fig. 10 Spectra of oriented San Carlos and Sri Lanka olivines in polarized light for E||y. For the San Carlos olivine spectra of sample D1 are shown. |
| In the text | |
 |
Fig. 11 Spectra of oriented San Carlos and Sri Lanka olivines in polarized light for E||z. For the San Carlos olivine, spectra of sample C are shown. |
| In the text | |
 |
Fig. 12 Comparison of the radiative equilibrium temperature of MgO (characterized by extremely low k(λ) values in the NIR region) with the equilibrium temperature of Mg0.5Fe0.5O (its k(λ) value is more than seven orders of magnitude larger in the NIR). The stellar effective temperature has been set to 3000 K. |
| In the text | |
 |
Fig. 13 The radiative equilibrium temperature of natural (terrestrial) spinel dust containing impurities compared to the temperature of impurity-free Mg-Al-spinel according to Palik (1985–98). The stellar effective temperature has been set to 4000 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


