| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 7 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201014961 | |
| Published online | 14 December 2010 | |
Reconsidering the Galactic coordinate system
1
Department of AstronomyNanjing University,
Nanjing
210093,
PR China
e-mail: jcliu;zhuzi@nju.edu.cn; zhangh@nju.edu.cn
2
Key Laboratory of Modern Astronomy and Astrophysics (Nanjing
University), Ministry of
Education, Nanjing
210093, PR
China
Received:
10
May
2010
Accepted:
18
October
2010
Initially defined by the IAU in 1958, the Galactic coordinate system was thereafter transformed in 1984 from the B1950.0 FK4-based system to the J2000.0 FK5-based system. In 1994, the IAU recommended that the dynamical reference system FK5 be replaced by the ICRS, which is a kinematical non-rotating system defined by a set of remote radio sources. However the definition of the Galactic coordinate system was not updated at that time. We consider that the present Galactic coordinates may be problematic because of the unrigorous transformation method from the FK4 to the FK5 and of the non-inertiality of the FK5 system with respect to the ICRS. This has led to some confusion when applying of the Galactic coordinates. We tried to find the transformation matrix in the framework of the ICRS after carefully investigating the definition of the Galactic coordinate system and transformation procedures, but we could not find a satisfactory Galactic coordinate system that is connected steadily to the ICRS. To avoid unnecessary misunderstandings, we suggest reconsidering the definition of the Galactic coordinate system which should be directly connected with the ICRS for highly precise observations at the micro-arcsecond level.
Key words: astrometry / Galaxy: general / reference systems
© ESO, 2010
1. Introduction
For studies of Galactic structure, kinematics, and dynamics, it is important to establish the Galactic coordinate system with its equatorial plane in the Galactic plane and with the pole coinciding with the Galactic pole. The definition of the system of Galactic coordinates, which is based on the FK4 system at the epoch of B1950.0, was announced by the International Astronomical Union (IAU) Sub-Commission 33b in the late 1950s (Blaauw et al. 1960). It is a barycentric rectangular system with three main axes in the direction of Galactic center, Galactic rotation, and north Galactic pole. Following the recommendation of the Sixteenth General Assembly of the IAU in Grenoble in 1976, the previous fundamental reference system FK4 has been replaced by FK5 at the epoch of J2000.0. In addition, the IAU adopted the new system of astronomical constants and time units in order to construct an inertial framework from observed materials. The transformation procedures from the FK4 based reference system to the FK5 reference system were developed by Standish (1982) and Aoki et al. (1983). The transformation matrix from the equatorial coordinate system to a Galactic coordinate system at the epoch of J2000.0 was derived by Murray (1989) under the assumption that the FK4 and FK5 systems only have orientation offsets due to both the precession motion from B1950.0 to J2000.0 and the equinox bias.
The fundamental celestial reference system for astronomical application is now the International Celestial Reference System (ICRS) as specified in the IAU Res. B2 of 1997. To establish the ICRS as a practical system, the IAU provided a set of distant benchmark radio sources, by whose coordinates the direction of the ICRS axes are defined (Ma et al. 1998). The ICRS is realized optically, but with lower accuracy, by the star positions and proper motions of the Hipparcos Catalog (ESA 1997). However, the Galactic coordinate system is still based on the observations in the FK4 system at the epoch of B1950.0 or more recently, transformed to the FK5 system in a loose sense. The FK5 system is non-inertial based on the comparison between the FK5 and Hipparcos proper motion systems. In other words, the Galactic coordinate system is rotating with respect to the ICRS, whether its principal axes are in the FK4 system at B1950.0 or in the FK5 system at J2000.0. This can lead to some confusions or misunderstandings. Considering a submilliarcsecond or even micro-arcsecond astrometric accuracy, the Galactic coordinate system should be directly connected to the ICRS for uniform practical applications and for an exact definition of the coordinate system. We suggest that a new definition of the Galactic coordinate system be considered.
In Sects. 2 and 3 of the present work we review the definition of the Galactic coordinate system as well as the confusion in astronomical applications. In Sect. 4 a suggestion of the new definition is presented and some conclusions are given in Sect. 5.
2. History of the development of the Galactic coordinate system
2.1. IAU 1958 Galactic coordinate system
From the time of William Herschel in the 1780s until 1932, various Galactic coordinate
systems that differ from one another by one or two degrees were used. Ohlsson (1932) summarized extensive observations at
Harvard Observatory and adopted a position of the north Galactic pole at right ascension
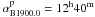 and declination
and declination
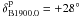 . With the
development of radio astronomy in the 1950s, it became evident that the old Galactic
coordinate system did not serve its purpose any longer and was seriously in error for many
observations, especially in the radio specturm. In 1958 the IAU Sub-Commission authorized
a new definition of the Galactic coordinate system, according to which the equatorial
plane was defined by the flat HI principal plane and the zero point of the system by the
direction of the Galactic center.
. With the
development of radio astronomy in the 1950s, it became evident that the old Galactic
coordinate system did not serve its purpose any longer and was seriously in error for many
observations, especially in the radio specturm. In 1958 the IAU Sub-Commission authorized
a new definition of the Galactic coordinate system, according to which the equatorial
plane was defined by the flat HI principal plane and the zero point of the system by the
direction of the Galactic center.
Radio continuum observations gave strong support to a pole based on the HI observations,
and optical data were used as a check. The Sun is effectively defined to be in the plane
even though it is thought to be some 10−20 pc above the HI principal plane (Zhu 2009). The revision and reconstruction of the
Galactic coordinate system was presented in a series of five papers (Blaauw et al. 1960; Gum et al.
1960; Gum & Pawsey 1960; Blaauw 1960; Oort
& Rougoor 1960). The system was defined by three main values:
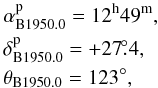 (1)where
(1)where
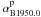 ,
,
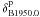 are the right
ascension and declination of the north Galactic pole,
and θB1950.0 is the position angle of the Galactic center
from the equatorial pole. The three main values defining the Galactic coordinate system
are based on the FK3 system, because at that time in 1958 the FK4 catalog had not been
published yet. Nevertheless, the equinox and equator were not changed in the FK4 with
respect to the FK3, so it should be justified to assume that the defining values are based
on the equator and equinox of the FK4 system at the epoch of B1950.0. These numbers in
Eq. (1) should be used as a strict definition with infinite accuracy or, in other words,
as one valid to an infinite number of decimals. Users are supposed to quote the definition
correctly rather than copy computer algorithms in order to avoid inconsistency in the
forward-backward conversion between equatorial (α, δ)
and Galactic (ℓ, b) coordinate systems (Lane 1979).
are the right
ascension and declination of the north Galactic pole,
and θB1950.0 is the position angle of the Galactic center
from the equatorial pole. The three main values defining the Galactic coordinate system
are based on the FK3 system, because at that time in 1958 the FK4 catalog had not been
published yet. Nevertheless, the equinox and equator were not changed in the FK4 with
respect to the FK3, so it should be justified to assume that the defining values are based
on the equator and equinox of the FK4 system at the epoch of B1950.0. These numbers in
Eq. (1) should be used as a strict definition with infinite accuracy or, in other words,
as one valid to an infinite number of decimals. Users are supposed to quote the definition
correctly rather than copy computer algorithms in order to avoid inconsistency in the
forward-backward conversion between equatorial (α, δ)
and Galactic (ℓ, b) coordinate systems (Lane 1979).
Establishing of the Galactic coordinate system does not require the same degree of precision as the equatorial reference system, which is realized by the fundamental catalogs (FK4, FK5), because it is constructed based on the concentration of HI gas in a statistical sense. Although the requirements for establishing of the Galactic coordinate system are less drastic, it must be fixed in the fundamental reference system of the time, say, aligned with FK4, FK5, or ICRS.
2.2. Principal Galactic axes in the FK5 system at J2000.0
The new fundamental stellar catalog FK5 and the IAU (1976) system of astronomical constants were introduced in 1 January 1984. The transformation from the FK4 to the FK5 includes the following changes
-
the E-term of aberration was removed from the mean places andproper motions;
-
the Newcomb’s precession constants were replaced by the IAU 1976 astronomical constants (Lieske et al. 1977);
-
the bias between FK4 equinox and the dynamical equinox (equinox correction) was eliminated;
-
the time unit was changed from tropical to Julian centuries;
-
the standard coordinate system was precessed from the equinox and equator at B1950.0 to that of J2000;
-
the positions of the stars were presented at the epoch of J2000.0 by adding their proper motions;
-
the systematic differences (FK5−FK4) were corrected, when known.
The so-called E-term of aberration depends explicitly on the eccentricity of the Earth orbit around the Sun and represents the components of the displacement due to the departure of the elliptic orbital motion from a circle. During the process of transforming the Galactic coordinates from the FK4 system (B1950.0) to the FK5 system (J2000.0), the impure rotation related to the E-term of aberration has consequently led to an unacceptable nonorthogonal system of axes if those axes are considered to be defined by specific objects in the three main directions (Murray 1989). Accordingly, Murray proposed that the axes of IAU 1958 Galactic coordinate system be considered as absolute directions, unaffected by the E-term of aberration.
To understand the transformation, we consider the column unit vector (3 × 1) of a certain
absolute direction or a fictitious distant extragalactic source at the epoch of B1950.0,
AB and
GB, and at the epoch of
J2000.0, AJ
and GJ. For brevity,
the subscript B stands for the epoch of B1950.0 and J
stands for J2000.0. The characters A
and G denote the unit vectors in the equatorial and
Galactic systems, so they can be expressed as 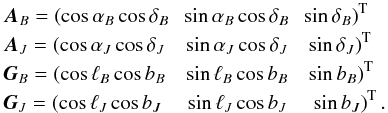 Let
Let
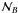 and
and  be the 3 × 3 matrices that convert the position vector from the equatorial system to the
Galactic system, i.e.,
be the 3 × 3 matrices that convert the position vector from the equatorial system to the
Galactic system, i.e.,  Suppose
that
Suppose
that 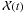 is the transformation matrix of position vector from J2000.0 system to that of
B1950.0 system at some epoch of t, so that
is the transformation matrix of position vector from J2000.0 system to that of
B1950.0 system at some epoch of t, so that
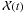 can be computed from the following formula:
can be computed from the following formula:
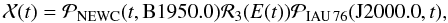 (4)where
t is reckoned from B1950.0 in tropical centuries.
(4)where
t is reckoned from B1950.0 in tropical centuries.
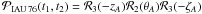 is the precession matrix from the epoch of t1
to t2 based on the IAU (1976) constant system
and
is the precession matrix from the epoch of t1
to t2 based on the IAU (1976) constant system
and 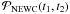 the precession matrix based on Newcomb’s precession formulae. The precession matrices were
constructed for the transformation of coordinates from one
epoch (t1) to another (t2).
For the equinox correction, Fricke (1982) pointed
out that the equinox correction E(t) at any epoch can be
expressed as
the precession matrix based on Newcomb’s precession formulae. The precession matrices were
constructed for the transformation of coordinates from one
epoch (t1) to another (t2).
For the equinox correction, Fricke (1982) pointed
out that the equinox correction E(t) at any epoch can be
expressed as 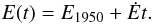 (5)We assume here that
(5)We assume here that
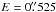 at the epoch of J1950.0 and
at the epoch of J1950.0 and 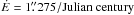 as Aoki et al. (1983) did for the consistency of the
new formula for the sidereal time.
as Aoki et al. (1983) did for the consistency of the
new formula for the sidereal time.
According to Sôma & Aoki (1990)’s method,
the E-term in aberration and the systematic and individual corrections are ignored, thus
the equatorial position is only affected by the precession motion from B1950.0 to J2000.0
and the equinox correction: 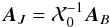 (6)where
the matrix
(6)where
the matrix 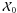 is the constant term in the expanded polynomial of
is the constant term in the expanded polynomial of 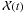 :
:
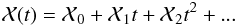 We can see from
Eq. (6) that in current problems the transformation is unrelated to the
epoch t.
We can see from
Eq. (6) that in current problems the transformation is unrelated to the
epoch t.
Because the Galactic coordinate system must be regarded as absolute in the celestial
sphere, the Galactic coordinates (ℓ,b) of a given direction (or a distant
radio source) will not change, although its equatorial coordinates refer to the FK4 system
and are then transformed to the FK5 system. The transformation only takes the orientation
difference between the FK4 and the FK5 into account, as if they were both inertial. We
therefore have 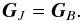 (7)Finally we obtain
from Eqs. (3), (6), and (7) the transformation matrix based on the FK5 system at the epoch
of J2000.0:
(7)Finally we obtain
from Eqs. (3), (6), and (7) the transformation matrix based on the FK5 system at the epoch
of J2000.0: 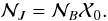 (8)The numerical matrices,
printed to 0.1 milli-arcsec accuracy of the precession formulae in the IAU (1976)
system, are
(8)The numerical matrices,
printed to 0.1 milli-arcsec accuracy of the precession formulae in the IAU (1976)
system, are 
 and
and
 (9)Such
a procedure guarantees that the Galactic coordinate system is orthogonal and does not
rotate with respect to the FK5 system at the epoch of J2000.0.
(9)Such
a procedure guarantees that the Galactic coordinate system is orthogonal and does not
rotate with respect to the FK5 system at the epoch of J2000.0.
Inserting (b = 90°) and (ℓ = 0,b = 0),
respectively, in Eq. (3), we can obtain the direction of the Galactic pole and the
position angle in the J2000.0 equatorial system (also at 0.1 milli-arcsec level):
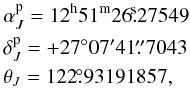 (10)and
the equatorial coordinates of the Galactic center:
(10)and
the equatorial coordinates of the Galactic center:
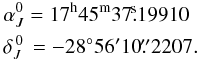 (11)Murray (1989) and Miyamoto & Sôma (1993) have also obtained coincidental results using a
slightly different method with only a few tenth of milli-arcsecond discrepancy. It is
worth noting that if we set t = 0 (i.e. transformation at the epoch
of B1950.0) in Eq. (4) and its expanded form, the transformation matrix is given by
(11)Murray (1989) and Miyamoto & Sôma (1993) have also obtained coincidental results using a
slightly different method with only a few tenth of milli-arcsecond discrepancy. It is
worth noting that if we set t = 0 (i.e. transformation at the epoch
of B1950.0) in Eq. (4) and its expanded form, the transformation matrix is given by
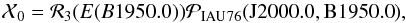 (12)which was adopted by
Murray (1989).
(12)which was adopted by
Murray (1989).
The transformation between equatorial and Galactic coordinate systems in the
Hipparcos system (ESA 1997)
adopted Murray’s method during the conversion from the equatorial to Galactic coordinates
in which the difference between the FK5 and the Hipparcos is ignored. The
Hipparcos transformation matrix is numerically different from ours at
the milli-arcsecond level because it is calculated by
adopting 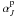 ,
,
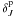 and θJ as defining values. There is a
possible loss of precision during the computing procedure, as adopted by
Hipparcos, from the truncated value of
and θJ as defining values. There is a
possible loss of precision during the computing procedure, as adopted by
Hipparcos, from the truncated value of
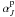 ,
,
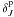 ,
θJ to the
matrix
,
θJ to the
matrix 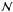 :
:
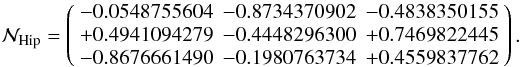
3. Confusions and misunderstandings in applying of the Galactic coordinate system
As mentioned in the preceding sections, the present Galactic coordinates may be problematic because of the inaccurate transformation from one fundamental reference system to another. Consequently, some confusion in applications of Galactic coordinates and misunderstandings in the concept of the reference system can be found.
3.1. Conversion of Galactic coordinates from the FK4 to the FK5 system
According to the IAU resolutions adopted in 1976 (Trans. IAU 16B), in 1979 (Trans. IAU 17B) and in 1982 (Trans. IAU 18B), new methods and astronomical constants system are used for computing of the positions and proper motions of stars. Conversion processes of mean positions and proper motions of stars from the FK4 system (B1950.0) to the FK5 system (J2000.0) had been proposed by Standish (1982) and Aoki et al. (1983) and subsequently reviewed by Smith et al. (1989), Yallop et al. (1989), Murray (1989), and Sôma & Aoki (1990). The methods for calculating the apparent places in the new IAU system were also developed by Lederle & Schwan (1984).
The rigorous method of converting the position and proper motion of a celestial object at
B1950.0 to those at J2000.0 contains two major steps: (i) remove the E-terms of aberration
and their variations’ effect; (ii) transfer the position and proper motion vector using
a 6 × 6 matrix to the new IAU system. When adopting the notations given by Standish (1982), the 6-space transformation matrix
operated on 1984 January 1.0 (Aoki et al. 1983) is
described as  (13)where
G1 and G2 are the time
intervals 1984.0−B1950.0 and J2000.0−1984.0, respectively. For details of the notions
in Eq. (13) and the constructing procedure of ℳ1984.0, readers are referred to
Standish (1982) and Aoki et al. (1983). The numerical form of our matrix ℳ1984.0
shows consistency with other authors’ except the difference in the last digit. Based on
the transformation matrix, we converted the positions and proper motions of 1535 FK4
bright stars from B1950.0 to J2000.0. Figure 1
displays the position’s difference of corresponding stars in the FK4 and FK5 catalog at
the epoch of J2000.0. The top panels show the position difference in the sense of
FK4(J2000.0)−FK5 for right ascensions and the bottom panels for declinations. The
position differences in the southern hemisphere are more pronounced because of the lower
quality observations of the stars. Likewise, the plots show residual systematic difference
versus declinations, which imply the imperfection of the transformation procedure from the
FK4 to the FK5 reference frames. On the other hand, the differences for most stars are
less than 0.3 arcsec in right ascension and declination, which shows that the
transformation is correct in the range of the error of the FK4 system.
(13)where
G1 and G2 are the time
intervals 1984.0−B1950.0 and J2000.0−1984.0, respectively. For details of the notions
in Eq. (13) and the constructing procedure of ℳ1984.0, readers are referred to
Standish (1982) and Aoki et al. (1983). The numerical form of our matrix ℳ1984.0
shows consistency with other authors’ except the difference in the last digit. Based on
the transformation matrix, we converted the positions and proper motions of 1535 FK4
bright stars from B1950.0 to J2000.0. Figure 1
displays the position’s difference of corresponding stars in the FK4 and FK5 catalog at
the epoch of J2000.0. The top panels show the position difference in the sense of
FK4(J2000.0)−FK5 for right ascensions and the bottom panels for declinations. The
position differences in the southern hemisphere are more pronounced because of the lower
quality observations of the stars. Likewise, the plots show residual systematic difference
versus declinations, which imply the imperfection of the transformation procedure from the
FK4 to the FK5 reference frames. On the other hand, the differences for most stars are
less than 0.3 arcsec in right ascension and declination, which shows that the
transformation is correct in the range of the error of the FK4 system.
 |
Fig. 1 Position differences between the FK4-based and FK5 bright stars. The subscript 1984.0 indicates that the transformation is operated at the epoch of 1984.0 by the matrix ℳ1984.0. |
During the transformation, a correction of the time derivative of the E-term would
produce an additional effect on the proper motions in comparison to the pure rotations.
In fact, if we assume that the position of an extragalactic object referred to the FK4
(or FK5) system is fixed (because its proper motion is zero), then it has non-zero
fictitious proper motion with respect to the FK5 (or FK4) system, by the corresponding
total amount of difference in derivative of the E-term. Reid & Brunthaler (2004) give out the coordinates of the north Galactic
pole in J2000.0 system, 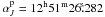 ,
,
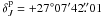 , and of the Galactic center,
, and of the Galactic center,
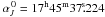 ,
,
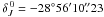 , as well as the position angle
of the direction of the Galactic center,
, as well as the position angle
of the direction of the Galactic center, 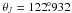 (see their Appendix). We tried to transform the IAU 1958 version of the definition
in Eq. (1), using the rigorous method (two steps described above), from B1950.0 to that
of J2000.0 and found identical values to the results derived by Reid & Brunthaler (2004). As a byproduct, the proper motions of
both points are
(see their Appendix). We tried to transform the IAU 1958 version of the definition
in Eq. (1), using the rigorous method (two steps described above), from B1950.0 to that
of J2000.0 and found identical values to the results derived by Reid & Brunthaler (2004). As a byproduct, the proper motions of
both points are 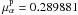 ,
,
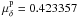 ,
,
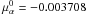 and
and
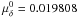 in arcsecond per century, which can be attributed to the derivative of the E-term in
aberration. Such a transformation procedure would be problematic for calculating the
orientation of the new Galactic coordinate system. First, the x- and
z-axes, which point to the Galactic center and north Galactic pole, are
not perpendicular to each other with a mismatch of 0.377 arcsec at the epoch of J2000.0.
The discrepancy will accumulate as the time interval gets longer (see Fig. 2). Second, the points, like the intersections of the
coordinate axes and celestial sphere, and circles like the Galactic equator, which must be
fixed in the FK5 system at J2000.0 are going to move at the rate of their “fictitious
proper motions”. Figure 3 describes the distortion of
the Galactic plane in the FK5 reference system if it is transformed from B1950.0, when it
was a rigorous great circle on the celestial sphere. The vectors denote the “proper
motions” coming from the non-pure-rotation transformation. The reduced Galactic plane is a
time-dependent curve. This incoherence is attributed to the adoption of definitional
values, as in Eq. (1), as the coordinates of specific objects.
in arcsecond per century, which can be attributed to the derivative of the E-term in
aberration. Such a transformation procedure would be problematic for calculating the
orientation of the new Galactic coordinate system. First, the x- and
z-axes, which point to the Galactic center and north Galactic pole, are
not perpendicular to each other with a mismatch of 0.377 arcsec at the epoch of J2000.0.
The discrepancy will accumulate as the time interval gets longer (see Fig. 2). Second, the points, like the intersections of the
coordinate axes and celestial sphere, and circles like the Galactic equator, which must be
fixed in the FK5 system at J2000.0 are going to move at the rate of their “fictitious
proper motions”. Figure 3 describes the distortion of
the Galactic plane in the FK5 reference system if it is transformed from B1950.0, when it
was a rigorous great circle on the celestial sphere. The vectors denote the “proper
motions” coming from the non-pure-rotation transformation. The reduced Galactic plane is a
time-dependent curve. This incoherence is attributed to the adoption of definitional
values, as in Eq. (1), as the coordinates of specific objects.
 |
Fig. 2 The relationship between λxz − 90° and
time interval since J2000.0. The
symbol λxz is the angular separation
between the x- and z-axes, which is computed
backward and forward from J2000.0 using constant proper motion
|
On the other hand, Eq. (4) is not a rigorous transfer equation from the FK4 to the
FK5 systems, which would cause confusion in observations in the Galactic coordinate
system. For instance, supposing an object was observed to coincide with the Galactic
center at the epoch of B1950.0 in the FK4 system
(ℓB = 0,
bB = 0), its Galactic coordinates cannot
correspond to the Galactic center at J2000.0
(ℓJ ≠ 0,
bJ ≠ 0), if the equatorial position was
transformed using the rigorous method from B1950.0 to J2000.0 and then
using 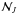 from equatorial to Galactic coordinate system at the epoch of J2000.0. In other words, the
direction
(ℓJ = 0,bJ = 0)
would not correspond to the original object in the Galactic center. Any other stars on the
celestial sphere will suffer this effect (tenth of arcsecond level) if related to the
transformation of the Galactic coordinates from the FK4 to FK5 systems. Therefore the
transformed Galactic coordinate system (Murray
1989) does not coincide with the physical features as in the 1958 definitions. One
may have doubts about where the actual Galactic center and Galactic plane are. For other
applications of the conversion, Aoki et al. (1986)
discussed the optical observation and the difficulties in observing the radio sources.
According to their study, specified reference framework and constant system are essential
for avoiding unnecessary confusion.
from equatorial to Galactic coordinate system at the epoch of J2000.0. In other words, the
direction
(ℓJ = 0,bJ = 0)
would not correspond to the original object in the Galactic center. Any other stars on the
celestial sphere will suffer this effect (tenth of arcsecond level) if related to the
transformation of the Galactic coordinates from the FK4 to FK5 systems. Therefore the
transformed Galactic coordinate system (Murray
1989) does not coincide with the physical features as in the 1958 definitions. One
may have doubts about where the actual Galactic center and Galactic plane are. For other
applications of the conversion, Aoki et al. (1986)
discussed the optical observation and the difficulties in observing the radio sources.
According to their study, specified reference framework and constant system are essential
for avoiding unnecessary confusion.
 |
Fig. 3 The distortion of the Galactic plane (the solid curve) in the FK5 system at J2000.0. The vectors denote the proper motions of certain points, although they should be fixed in the FK4 system at B1950.0. The solid line is the nominal Galactic plane with ℓ = 0. |
3.2. Conversion of Galactic coordinates from the FK5 system to the ICRS
The establishment of the ICRS as the fundamental celestial reference system was described by Arias et al. (1995) and Feissel & Mignard (1998). It is a coordinate system whose origin is at the barycenter of the Solar System and whose axis directions are effectively defined by the adopted 212 extragalactic radio sources observed by the VLBI technique (Ma et al. 1998). Although the ICRF-2 (Boboltz et al. 2010) which includes 3414 extragalactic radio sources was put into effect on January 1, 2010, the definition of the ICRS was not changed. The orientation of the ICRS was designed to be consistent with the dynamical equator and equinox (realized by the FK5 catalog) at the epoch of J2000.0.
Systematically, a frame bias matrix ℬ is needed to convert ICRS data to
the dynamical equator and equinox of J2000.0. It is a fixed set of very small rotations
and can be used as follows: 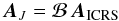 (14)where
the column vector A has the similar form as before except
for the subscripts, which denote the benchmark reference system or epoch. The matrix ℬ is,
to the first order (IERS Conventions 2003),
(14)where
the column vector A has the similar form as before except
for the subscripts, which denote the benchmark reference system or epoch. The matrix ℬ is,
to the first order (IERS Conventions 2003),
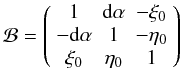 (15)where
the angles η0 = −6.819 ± 0.0015 mas and
ξ0 = −16.6171 ± 0.0080 mas are the ICRS pole offsets
in x, y directions, and dα = 14.6 ±
0.5 mas is the offset in the equinox between the ICRS and J2000.0 dynamical system
(Chapront et al. 2002). See Hilton & Hohenkerk (2004) for a detailed description. To the
second order, the more precise format is
(15)where
the angles η0 = −6.819 ± 0.0015 mas and
ξ0 = −16.6171 ± 0.0080 mas are the ICRS pole offsets
in x, y directions, and dα = 14.6 ±
0.5 mas is the offset in the equinox between the ICRS and J2000.0 dynamical system
(Chapront et al. 2002). See Hilton & Hohenkerk (2004) for a detailed description. To the
second order, the more precise format is
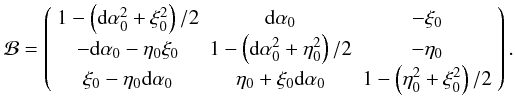 (16)The above matrix can also
be used to transform vectors from ICRS to the FK5 system at the epoch of J2000.0 by simply
substituting dα0 = −22.9,
η0 = −19.9 and ξ0 = 9.1 mas
(Mignard & Frœschlé 1997).
(16)The above matrix can also
be used to transform vectors from ICRS to the FK5 system at the epoch of J2000.0 by simply
substituting dα0 = −22.9,
η0 = −19.9 and ξ0 = 9.1 mas
(Mignard & Frœschlé 1997).
For the Galactic coordinate system, we can use Murray’s method to construct the
equatorial-Galactic transformation matrix in the ICRS. Neglecting the relative rotation
between the FK5 system and the ICRS and assuming the axes of the Galactic coordinate
system are absolute, we get the relation between 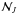 and
and 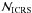 :
:
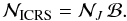 (17)The numerical form
of the matrix
(17)The numerical form
of the matrix 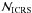 is
is  (18)by
adopting ℬ as in Eq. (16). The direction of the Galactic pole and the position angle in
the ICRS should be
(18)by
adopting ℬ as in Eq. (16). The direction of the Galactic pole and the position angle in
the ICRS should be 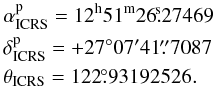 (19)The
difference between Eqs. (10) and (19) is on the order of several milli-arcseconds. The
above discussion only considered the orientation bias between the FK5 and the ICRS. In the
sense of inertia, the Galactic coordinates have a slow spin, as well as regional
distortion with respect to the ICRS due to the imperfections in the FK5 system. Such a
derived Galactic coordinate system is still an expediency because it is not fixed in
the ICRS.
(19)The
difference between Eqs. (10) and (19) is on the order of several milli-arcseconds. The
above discussion only considered the orientation bias between the FK5 and the ICRS. In the
sense of inertia, the Galactic coordinates have a slow spin, as well as regional
distortion with respect to the ICRS due to the imperfections in the FK5 system. Such a
derived Galactic coordinate system is still an expediency because it is not fixed in
the ICRS.
In order to reveal the systematic difference between the FK5 and ICRS, which is optically realized by the Hipparcos catalog, various authors (Zhu & Yang 1999; Mignard & Frœschlé 2000; Zhu 2000; Walter & Hering 2005) have intensively compared the proper motion systems of the two catalogs. To summarize the studies, the global rotation between the FK5 and ICRS, which is derived from the comparison of the proper motion systems of FK5 and Hipparcos show obvious inconsistencies (approximately −1.3 mas yr-1 by rotational offsets of the Hipparcos and FK5 proper motion systems), compared to what is predicted by the precession correction, Δp, and correction of the fictitious motion of the equinox, Δe + Δλ, from the unprecedented-accurate VLBI and LLR observations (Charlot et al. 1995; Capitaine et al. 2004). The mismatch is probably caused by the error and nonrigid nature of the FK5 proper-motion system and this strongly implies the existence of non-inertiality of the FK5 system. Directly speaking, the FK5 is rotating with respect to the distant radio sources even if the precession correction is applied to the IAU (1976) precession constants. Furthermore, the region-, magnitude-, and color-dependent systematic errors between the FK5 and Hipparcos prevent us from perfectly aligning of the FK5 system with the ICRS by using simple rotation matrices. Sôma (2000) analyzed Lunar occultations and found much larger errors in the rotation of the Hipparcos reference frame than those given by the Hipparcos team, which suggests the possibility of a non-inertiality of the Hipparcos system. Therefore we come to the conclusion that the Galactic coordinate system derived from a transformation is neither space-fixed nor time-independent. The system is rotating with respect to the distant extragalactic objects even if it is exactly fixed to the FK5 system.
4. Reconsidering the definition of the Galactic coordinate system
The present Galactic coordinate system does not meet the defining criterion of the
fundamental reference system, namely, non-rotating with respect to the ensemble of distant
extragalactic objects by using the transformation method we can not tie the Galactic
coordinate system, which was originally defined in 1958, uniquely to the ICRS. There must be
residual rotation (slow spin) due to the non-inertial property of the FK5 system, which is
unacceptable for high-precision observations at the level of one micro-arcsecond. There
actually exist several different Galactic coordinate systems, based on the FK4, the FK5,
or the ICRS, showing orientation offsets and relative rotation. The smallest (relative
rotation neglected) differences (between Eqs. (19) and (10)) in the main values that define
the Galactic coordinate system in the sense of ICRS−FK5 are, roughly,
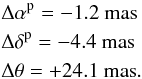 These
offsets are much greater than the axes stability of the ICRS (≃ 20 μas),
so the old definition is not appropriate in the current fundamental reference system.
To avoid confusion in choosing the Galactic coordinate system, we think that a new
definition is needed. Since more and more important astrometric data, such as UCAC3 (Zacharias et al. 2010), PPMX (Röser et al. 2008), and PPMXL (Roeser
et al. 2010), are presented in the ICRS framework, the Galactic coordinate system
should be directly connected to the ICRS for practical observations and studies of the
Galactic structure, kinematics, and dynamics, especially for the Galactic center.
These
offsets are much greater than the axes stability of the ICRS (≃ 20 μas),
so the old definition is not appropriate in the current fundamental reference system.
To avoid confusion in choosing the Galactic coordinate system, we think that a new
definition is needed. Since more and more important astrometric data, such as UCAC3 (Zacharias et al. 2010), PPMX (Röser et al. 2008), and PPMXL (Roeser
et al. 2010), are presented in the ICRS framework, the Galactic coordinate system
should be directly connected to the ICRS for practical observations and studies of the
Galactic structure, kinematics, and dynamics, especially for the Galactic center.
To successfully achieve the objective of establishing a Galactic coordinate system fixed to
the ICRS, which was originally defined in the radio bandpass, the principal plane and the
Galactic center should likewise be observed using radio techniques. For example, direct
observation of the compact radio source Sagittarius A* (Sgr A*) at the dynamical center of
the Milky Way (Reid et al. 2009) might give the
starting point of the Galactic longitude. With measurements using the Very Long Baseline
Array (VLBA), the best estimation of the absolute position (J2000.0) of Sgr A* (Reid & Brunthaler 2004) is
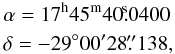 (20)and
the proper motion of Sgr A* is
μℓ = −6.379 ± 0.026 mas yr-1
and μb = −0.202 ±
0.019 mas yr-1 which may reflect the Galactic rotation and the peculiar
motion of the Sun. The uncertainty of the position (± 10 mas) is dominated by the position
of J1745-2820. Considering that the proper motion of Sgr A* is nonzero, the observational
position should be reduced to the fixed epoch J2000.0. Suppose that Sgr A*, whose position
in the ICRS is given by Eq. (20), is at the Galactic center (i.e. the Sgr A* is regarded as
the zero point of the system), we can find the position of the corresponding Galactic
pole
(20)and
the proper motion of Sgr A* is
μℓ = −6.379 ± 0.026 mas yr-1
and μb = −0.202 ±
0.019 mas yr-1 which may reflect the Galactic rotation and the peculiar
motion of the Sun. The uncertainty of the position (± 10 mas) is dominated by the position
of J1745-2820. Considering that the proper motion of Sgr A* is nonzero, the observational
position should be reduced to the fixed epoch J2000.0. Suppose that Sgr A*, whose position
in the ICRS is given by Eq. (20), is at the Galactic center (i.e. the Sgr A* is regarded as
the zero point of the system), we can find the position of the corresponding Galactic
pole 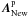 from following
equations:
from following
equations: 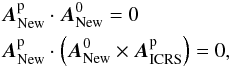 (21)where
(21)where
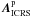 is the unit column
vector along the Galactic pole derived from Eq. (19)
and
is the unit column
vector along the Galactic pole derived from Eq. (19)
and 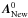 the position vector
of the new Galactic center defined by Eq. (20). This new Galactic pole is located closest to
the old one (
the position vector
of the new Galactic center defined by Eq. (20). This new Galactic pole is located closest to
the old one (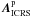 ). The resulting
equatorial coordinates of the new Galactic pole in the ICRS are (printed to one
micro-arcsecond accuracy):
). The resulting
equatorial coordinates of the new Galactic pole in the ICRS are (printed to one
micro-arcsecond accuracy): 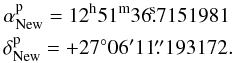 (22)Accepting
the coordinates in Eq. (20) as a new definition of the zero point of the Galactic coordinate
systems, and the position described in Eq. (22) as the position of the new Galactic pole, we
obtain the transformation matrix
(22)Accepting
the coordinates in Eq. (20) as a new definition of the zero point of the Galactic coordinate
systems, and the position described in Eq. (22) as the position of the new Galactic pole, we
obtain the transformation matrix  (23)as
well as the position angle:
(23)as
well as the position angle: 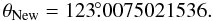 (24)These values are
not consistent with those in previous sections because we adopted different coordinates for
the Galactic center, which disagree by several arcminutes.
(24)These values are
not consistent with those in previous sections because we adopted different coordinates for
the Galactic center, which disagree by several arcminutes.
As for the formal definition of the Galactic reference system in the ICRS, re-observation of the Galactic center and the HI principal plane in the radio bandpass is necessary, and multi-wavelength observations may be needed for practical application purposes. Because the height of the Sun above the Galactic plane z0 is not zero, the equatorial plane of the Galactic coordinate system, which should theoretically pass through the Sun and the Galactic center, should be set as close to the HI principal plane as possible. Then the obtained Galactic orientation parameters should be regarded as the definition of the new Galactic coordinate system. Since the Galactic coordinate system is fixed in the ICRS, there is no epoch associated with a Galactic coordinate, so it is technically incorrect to say that the Galactic coordinate system is a “J2000.0 system”.
As the newly defined Galactic coordinate system should become effective, the data in the old (FK5) Galactic coordinate system could be calculated at the epoch of J2000.0 by multiplying the bias matrix ℬ where high accuracy is not required. In the optical frequency range, the new Galactic coordinate system should be fixed in the Hipparcos celestial reference system (HCRS), which is aligned to the ICRS using various methods (Kovalevsky et al. 1997). The estimated uncertainty of the link corresponds to a standard error of 0.6 mas in axes alignment and 0.25 mas yr-1 in the rate of rotation.
The Galactic coordinate system that we considered is a convenient barycentric system. If we know the accurate distance of the Sun out of the Galactic plane, one could consider rotating the system to what would be observed by an observer exactly in the plane. This would be approximately a 0.1 degree rotation (the angle of the Sun with respect to the Galactic plane viewed from the Galactic center) so that the origin of the reference system is certainly in the Galactic plane. Kovalevsky (2003) points out that a Galactocentric rather than a barycentric reference frame should be used because upcoming space astrometric missions Gaia (ESA 2000) and SIM (Danner & Unwin 1999) will drastically improve the astrometric accuracy to a micro-arcsecond level. If one wishes to define a reference system centered at on Galactic center, one needs to know the exact Galactic constants such as the Galactocentric distance of the Sun (R0), Oort constants (A, B), the vertical distance of the Sun above the Galactic plane (z0), and any other parameters that define the position and the motion of the Sun, but all these values are estimated and still open for research; there is no official resolution about the definite values of Galactic constants – different Galactic constants would lead to different reference systems. The definition of a Galactocentric reference system is at risk and uneconomical even if the Galactic constants are authorized because all observations were made in a barycentric system. The astrometric data (positions, proper motions and parallaxes of celestial bodies) must be converted from a barycentric to Galactocentric reference system by some more complicated transformation, and the transformation is related to the Galactic constants, rather than to ordinary rotation once such a coordinate system is defined.
5. Conclusion
We reviewed the history of the Galactic coordinate system, which was originally defined by the IAU in 1958. The efforts of transforming the Galactic coordinate system from the FK4 to the FK5, and from the FK5 to the currently used fundamental reference system – ICRS, have led to some confusions and misunderstandings. The Galactic coordinate system is rotating with respect to the ICRS, and the effect cannot be eliminated by simple rotation owing to the complexity of the fundamental catalogs (FK4, FK5). As a temporary expedient, we derived the rotation matrix from the equatorial to the Galactic coordinate system in the framework of the ICRS using the bias matrix, and this can only be used when high accuracy is not needed. Our proposal for the new definition of the Galactic coordinate system makes use of current observations of the supermassive black hole Sgr A* and is, of course, still open for discussion. With the development of radio astronomy to an unprecedented accuracy, we suggest that the Galactic coordinate system be directly connected to the ICRS by observing the Galactic center and plane. Therefore, it is recommended that the definition of the Galactic coordinate system be reconsidered by the relevant IAU Commissions.
Acknowledgments
This work was funded by the National Natural Science Foundation of China (NSFC) under No. 10973009. The authors wish to thank Drs. L. Chen, D. L. Kong, and Prof. M. Miyamoto for their interest and encouragement. We are grateful to Prof. W. J. Jin, M. Reid, Dr. E. Høg, and in particular, to M. Sôma for their valuable comments, suggestions and discussions. Some points have been revised according to their suggestions. We are also indebted to Prof. W. F. van Altena for his very careful correction of the language.
References
- Arias, E. F., Charlot, P., Feissel, M., & Lestrade, J.-F. 1995, A&A, 303, 604 [NASA ADS] [Google Scholar]
- Aoki, S., Soma, M., Kinoshita, H., & Inoue, K. 1983, A&A, 128, 263 [NASA ADS] [Google Scholar]
- Aoki, S., Sôma, M., Nakajima, K., et al. 1986, IAUS, 109, 123 [NASA ADS] [Google Scholar]
- Blaauw, A. 1960, MNRAS, 121, 164 [NASA ADS] [Google Scholar]
- Blaauw, A., Gum, C. S., Pawsey, J. L., & Westerhout, G. 1960, MNRAS, 121, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Boboltz, D. A., Gaume, R. A., Fey, A. L., et al. 2010, BAAS, 41, 512 [NASA ADS] [Google Scholar]
- Capitaine, N., Wallace, P. T., & Chapront, J. 2004, A&A, 421, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapront, J., Chapront-Touzé, M., & Francou, G. 2002, A&A, 387, 700 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charlot, P., Sovers, O. J., Williams, J. G., & Newhall, X. X. 1995, AJ, 109, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Danner, R., & Unwin, S. 1999, Space Interferometry Mission, Jet Propulsion Laboratory, JPL 400-811, 3/99, 70 [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues (Noordwijk: ESA), ESA SP-1200 [Google Scholar]
- ESA 2000, GAIA, Composition, Formation and Evolution of the Galaxy, ESA Report ESA-SCI (200) 4, 100 [Google Scholar]
- Feissel, M., & Mignard, F. 1998, A&A, 331, L33 [NASA ADS] [Google Scholar]
- Fricke, W. 1982, A&A, 107, L13 [NASA ADS] [Google Scholar]
- Gum, C. S., & Pawsey, J. L. 1960, MNRAS, 121, 150 [NASA ADS] [Google Scholar]
- Gum, C. S., Kerr, F. J., & Westerhout, G. 1960, MNRAS, 121, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, J. L., & Hohenkerk, C. Y. 2004, A&A, 413, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 743, 747 [Google Scholar]
- Kovalevsky, J., Lindegren, L., Perryman, M. A. C., et al. 1997, A&A, 323, 620 [NASA ADS] [Google Scholar]
- Lane, A. P. 1979, PASP, 91, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Lederle, T., & Schwan, H. 1984, A&A, 134, 1 [NASA ADS] [Google Scholar]
- Lieske, J. H., Lederle, T., Fricke, W., & Morando, B. 1977, A&A, 58, 1 [NASA ADS] [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, D. D., & Petit, G. 2003, IERS Conventions, IERS Tech Note32, available at URL: http://tai.bipm.org/iers/conv2003/conv2003.html [Google Scholar]
- Miyamoto, M., & Sôma, M. 1993, AJ, 105, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F., & Frœschlé, M. 1997, Linking the FK5 to the ICRS, JD12, 23rd IAU General Assembly, August, Highlights in Astronomy [Google Scholar]
- Mignard, F., & Frœschlé, M. 2000, A&A, 354, 732 [NASA ADS] [Google Scholar]
- Murray, C. A. 1989, A&A, 218, 325 [NASA ADS] [Google Scholar]
- Ohlsson, J. 1932, Ann. Lund. Obs., 3 [Google Scholar]
- Oort, J. H., & Rougoor, G. W. 1960, MNRAS, 121, 171 [NASA ADS] [Google Scholar]
- Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Roeser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Röser, S., Schilbach, E., Schwan, H., et al. 2008, A&A, 488, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwan, H. 2001, A&A, 367, 1078 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, C. A., Kaplan, G. H., Hughes, J. A., et al. 1989, AJ, 97, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sôma, M. 2000, IAU Coll., 180, 115 [Google Scholar]
- Sôma, M., & Aoki, S. 1990, A&A, 240, 150 [NASA ADS] [Google Scholar]
- Standish, E. M., Jr., 1982, A&A, 115, 20 [NASA ADS] [Google Scholar]
- Walter, H. G., & Hering, R. 2005, A&A, 431, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yallop, B. D., Hohenkerk, C. Y., Smith, C. A., et al. 1989, AJ, 97, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C., Girard, T., et al. 2010, AJ, 139, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z. 2000, PASP, 112, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z. 2009, RAA, 9, 1285 [Google Scholar]
- Zhu, Z., & Yang, T. 1999, AJ, 117, 1103 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Position differences between the FK4-based and FK5 bright stars. The subscript 1984.0 indicates that the transformation is operated at the epoch of 1984.0 by the matrix ℳ1984.0. |
| In the text | |
 |
Fig. 2 The relationship between λxz − 90° and
time interval since J2000.0. The
symbol λxz is the angular separation
between the x- and z-axes, which is computed
backward and forward from J2000.0 using constant proper motion
|
| In the text | |
 |
Fig. 3 The distortion of the Galactic plane (the solid curve) in the FK5 system at J2000.0. The vectors denote the proper motions of certain points, although they should be fixed in the FK4 system at B1950.0. The solid line is the nominal Galactic plane with ℓ = 0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


