| Issue |
A&A
Volume 526, February 2011
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014728 | |
| Published online | 11 January 2011 | |
Analyzing X-ray pulsar profiles: geometry and beam pattern of A 0535+26
1
CEA Saclay, DSM/IRFU/SAp – UMR AIM (7158) CNRS/CEA/Université P.
Diderot,
Orme des Merisiers, Bât. 709,
91191
Gif-sur-Yvette,
France
e-mail: isabel.caballero@cea.fr
2
Institut für Physik und Technik, Universität
Hildesheim, Marienburger Platz
22, 31141
Hildesheim,
Germany
3
Institute für Astronomie und Astrophysik, Kepler Center for Astro
and Particle Physics, Eberhard Karls Universität Tübingen,
Sand 1, 72076
Tübingen,
Germany
4
ISOC, European Space Astronomy Centre (ESAC), PO Box
78, 28691
Villanueva de la Cañada,
Spain
Received: 2 April 2010
Accepted: 28 October 2010
Aims. We applied a decomposition method to the energy dependent pulse profiles of the accreting binary pulsar A 0535+26, in order to identify the contribution of the two magnetic poles of the neutron star and to obtain constraints on the geometry of the system and on the beam pattern.
Methods. We analyzed pulse profiles obtained from RXTE observations in the X-ray regime. Basic assumptions of the method are that the asymmetry observed in the pulse profiles is caused by non-antipodal magnetic poles and that the emission regions have axisymmetric beam patterns.
Results. Constraints on the geometry of the pulsar and a possible solution of the beam pattern are given. We interpreted the reconstructed beam pattern in terms of a geometrical model of a hollow column plus a halo of scattered radiation on the neutron star surface, which includes relativistic light deflection.
Key words: X-rays: binaries / pulsars: individual: A 0535+26
© ESO, 2011
1. Introduction
The Be/X-ray binary A 0535+26 was discovered by Ariel V in 1975 (Rosenberg et al. 1975) during a giant outburst. The system consists of a neutron star orbiting the optical companion HDE 245770 on an eccentric orbit (e = 0.47 ± 0.02) of orbital period Porb = 111.1 ± 0.3 d (Finger et al. 2006). The source presents quiescent X-ray emission with a luminosity of LX ≲ 1035−36 erg s-1, sometimes interrupted by “normal” outbursts (LX ≈ 1037 erg s-1) linked to the periastron passages of the neutron star, and less frequent “giant” outbursts (LX > 1037 erg s-1) of longer duration and less clearly related to the orbital phase (see, e.g., Giovannelli & Graziati 1992; Kendziorra et al. 1994; Finger et al. 1996). The system presents two cyclotron resonant scattering features at E ~ 45 keV and E ~ 100 keV, from which a magnetic field strength of B ~ 4 × 1012 G is inferred (Kendziorra et al. 1994; Grove et al. 1995; Kretschmar et al. 2005; Caballero et al. 2007).
Pulsations are observed to have a period of Pspin ~ 103 s, typically with spin-up during stronger outbursts and spin-down during quiescent periods1. The pulse profile evolves from a complex profile at lower energies to a simpler, two-peaked structure at higher energies. This behavior is observed in several accreting X-ray pulsars. Similar to other sources (e.g., Staubert et al. 1980), individual pulses show strong pulse-to-pulse variations, while the average pulse profile is rather stable, with slower variations over the course of an outburst (Caballero et al. 2008b).
The basic concept of pulsed emission is well understood. Pulsed emission originates in regions close to the magnetic poles of a rotating neutron star with the magnetic axis misaligned with respect to the rotation axis. In contrast, physical modeling of the pulsed emission turns out to be a complex task. Many processes are in fact involved in modeling pulse profiles, from the modeling of the emission regions and their local emission pattern to the formation of the pulse profiles seen by a distant observer. Comparison of model calculations with observations has been performed for instance by Wang & Welter (1981), Meszaros & Nagel (1985), and Leahy (1991).
A proper model calculation should include relativistic light deflection, which has a significant effect on the pulse shape2 (Riffert & Meszaros 1988). For slowly rotating neutron stars, the metric around a neutron star can be approximated by the Schwarzschild metric (see, e.g., Pechenick et al. 1983). Due to the strong gravitational field around the neutron star, the X-rays will be observed at red-shifted energies. Geometrical models of filled and hollow accretion columns of accreting neutron stars, including relativistic light deflection, were computed in Kraus (2001) and Kraus et al. (2003). These models give the beam pattern or energy-dependent flux of one emission region as a function of the angle, as seen by a distant observer. Introducing the rotation of the pulsar and its geometry, i.e., the orientation of the rotation axis with respect to the direction of observation and the location of the two poles, the pulsed emission from each of the two poles (single-pole pulse profiles) observed by a distant observer can be modeled. The sum of the single-pole contributions gives the total pulse profile.
An alternative method of analyzing pulse profiles is to start from the observed pulse profiles and, based on symmetry considerations, decompose the pulse profile into single-pole contributions. This is then transformed into the visible section of the beam pattern. This method has been successfully applied to the accreting X-ray binary pulsars Cen X-3, Her X-1 and EXO 2030+375 (Kraus et al. 1996; Blum & Kraus 2000; Sasaki et al. 2010, respectively) and is applied in this work to A 0535+26. Preliminary results were presented in Caballero et al. (2008a).
2. Method
2.1. Assumptions
A major goal of this work is to reconstruct the beam pattern of the neutron star in the binary system A 0535+26. By beam pattern we refer to the emission of one magnetic pole, as seen by a distant observer, as a function of the angle θ between the direction of observation and the magnetic axis (see Fig. 1). The basic assumption made in this work, which is often adopted in model calculations, is that the emission regions at the magnetic poles are axisymmetric. The magnetic axis is therefore a symmetry axis of the emission from the neutron star. Under this assumption, the beam pattern from one pole is only a function of angle θ, and therefore the pulsed emission of each magnetic pole or single-pole pulse profile has to be symmetric. One of the symmetry points will be the instant when the magnetic axis is closest to the line of sight, and the other symmetry point will be half a period later, with the magnetic axis pointing away from the observer.
In the case of an ideal dipole field, the sum of the two single-pole pulse profiles will give a symmetric pulse profile because the two single-pole pulse profiles have the same symmetry points. However, the observed pulse profiles of accreting X-ray pulsars are generally asymmetric. To explain the asymmetry observed in the pulse profiles, we assume a dipole magnetic field with a small offset from an ideal dipole field (see Fig. 2). A small deviation of one of the magnetic poles from the antipodal position makes the symmetry points of the two single-pulse profiles different, causing the asymmetry in the total pulse profile.
Another assumption made in this work is that the two emission regions are the same, i.e., have the same beam pattern. This implies that each of the two poles will make one section of the same beam pattern visible. Depending on the geometry of the neutron star and the angle of observation, those two sections will have coincident parts in some cases. This assumption was tested with the accreting pulsars Cen X-3 (Kraus et al. 1996) and Her X-1 (Blum & Kraus 2000). In these cases an overlapping region was found, in agreement with the assumption of two equal emission regions.
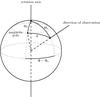 |
Fig. 1 Schematic view of a rotating neutron star from Kraus et al. (1995). A spherical coordinate system is used, with the rotation axis as polar axis. Θi is the polar angle of the ith pole. Θ0 is the polar angle of the direction of observation. The angle θ between the magnetic pole and the direction of observation changes with the rotation angle Φ. |
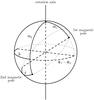 |
Fig. 2 Intrinsic geometry of the pulsar. With the rotation axis as polar axis, the magnetic poles are located at polar angles Θ1 and Θ2. The angular distance δ between the second magnetic pole and the point that is antipodal to the first magnetic pole gives the deviation from an ideal dipole field. Figure from Kraus et al. (1995). |
2.2. Decomposition into single-pole pulse profiles
The first step of the analysis is to express the original pulse profile as a Fourier series. The total pulse profile F is written as ![\begin{equation} F(\Phi)=\frac{1}{2}u_{0}+\displaystyle\sum_{k=1}^{n/2-1} [u_{k}\cos(k\Phi) +v_{k}\sin(k\Phi)]+u_{n/2}\cos\left(\frac{n}{2}\Phi\right) \label{eq:fourier} \end{equation}](/articles/aa/full_html/2011/02/aa14728-10/aa14728-10-eq18.png) (1)where n is the number of bins of the original pulse profile, Φ the phase, and uk, vk are given by
(1)where n is the number of bins of the original pulse profile, Φ the phase, and uk, vk are given by 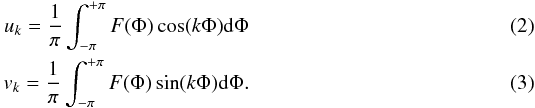 Equation (1) gives a valid representation of the original pulse profile at all phases if the Fourier transform of F approaches zero as the frequency approaches n/2.
Equation (1) gives a valid representation of the original pulse profile at all phases if the Fourier transform of F approaches zero as the frequency approaches n/2.
The single-pole pulse profiles f1 and f2 are described by the following symmetric functions: ![\begin{equation} f_{1}(\Phi)=\frac{1}{2}c_{0}+\displaystyle\sum_{k=1}^{n/2} c_{k}\cos[k(\Phi-\Phi_{1})] \label{eq:f1} \end{equation}](/articles/aa/full_html/2011/02/aa14728-10/aa14728-10-eq26.png) (4)
(4)![\begin{equation} f_{2}(\Phi)=\frac{1}{2}d_{0}+\displaystyle\sum_{k=1}^{n/2} d_{k}\cos\{k[\Phi-(\Phi_{2}+\pi)]\}, \label{eq:f2} \end{equation}](/articles/aa/full_html/2011/02/aa14728-10/aa14728-10-eq27.png) (5)where Φ1 and Φ2 are the symmetry points of f1(Φ) and f2(Φ), respectively. Formally, a decomposition of F into two symmetric functions exists for every choice of their symmetry points Φ1 and Φ2. For convenience, we use the parameter Δ: = π − (Φ1 − Φ2), which represents the azimuthal displacement of one pole with respect to the antipodal position (see Sect. 2.2.1). All formal decompositions will be contained in the parameter space Φ1 − Δ, with 0 ≤ Φ1 ≤ π and 0 ≤ Δ ≤ π/2. Once the formal decompositions are calculated, the following criteria are applied to reduce the number of decompositions to physically meaningful ones:
(5)where Φ1 and Φ2 are the symmetry points of f1(Φ) and f2(Φ), respectively. Formally, a decomposition of F into two symmetric functions exists for every choice of their symmetry points Φ1 and Φ2. For convenience, we use the parameter Δ: = π − (Φ1 − Φ2), which represents the azimuthal displacement of one pole with respect to the antipodal position (see Sect. 2.2.1). All formal decompositions will be contained in the parameter space Φ1 − Δ, with 0 ≤ Φ1 ≤ π and 0 ≤ Δ ≤ π/2. Once the formal decompositions are calculated, the following criteria are applied to reduce the number of decompositions to physically meaningful ones:
-
positive criterion: both f1(Φ) and f2(Φ) must be positive, since they represent photon fluxes;
-
non-ripple criterion: the single-pole contributions f1(Φ) and f2(Φ) should not be much more complicated than the original pulse profile. Individual pulse profiles with many peaks that cancel out in the sum are not accepted;
-
the same symmetry points Φ1 and Φ2 must give valid decompositions in all energy bands.
Once a possible decomposition is found, the symmetry points for each of the two poles Φ1 and Φ2, and the parameter Δ, related to the position of the emission regions on the neutron star, are determined.
2.2.1. From single-pole pulse profiles to beam pattern
In Fig. 1 a schematic view of a rotating neutron star is shown. A spherical coordinate system is used with the rotation axis as polar axis. As explained above, the beam pattern is assumed to be axisymmetric, hence to only depend on the angle between the direction of observation and the magnetic axis θ. The value of θ changes with the rotation angle Φ. Depending on the position of the poles with respect to the rotation axis and depending on the direction of observation with respect to the magnetic axis, we only observe a section of the beam pattern for each pole.
Applying the cosine formula to the spherical triangle in Fig. 1, we obtain θ as a function of the phase Φ: 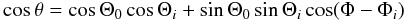 (6)where Θ0 is the polar angle of the direction of observation, Θi the polar angle of the ith pole, and Φi one symmetry point for the ith pole.
(6)where Θ0 is the polar angle of the direction of observation, Θi the polar angle of the ith pole, and Φi one symmetry point for the ith pole.
The intrinsic pulsar geometry is shown in Fig. 2. A complete description of the pulsar can be given in terms of the polar angles Θ1 and Θ2, and the difference in their azimuthal angles Φ1 − Φ2 = π − Δ. The angular distance δ between the location of the second magnetic pole and the point that is antipodal to the first magnetic pole can be used as a measure for the deviation from an ideal dipole field. From Fig. 2 comes 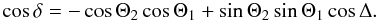 (7)Considering the beam pattern as a function of cosθ and the single-pole pulse profiles as functions of cos(Φ − Φi), there is no distortion between the two functions because the relation between cosθ and cos(Φ − Φi) is linear (Eq. (6)). Therefore, once we have the single-pole pulse profiles, by plotting them as a function of cos(Φ − Φi) we obtain two different sections of the same beam pattern. These two sections are different because we see a different interval of θ for each of the two magnetic poles. Depending on the geometry, these two ranges of θ can overlap, so there will be an overlapping region in the beam pattern. In this region, at an instant Φ, the first pole will be seen at an angle θ. At another instant
(7)Considering the beam pattern as a function of cosθ and the single-pole pulse profiles as functions of cos(Φ − Φi), there is no distortion between the two functions because the relation between cosθ and cos(Φ − Φi) is linear (Eq. (6)). Therefore, once we have the single-pole pulse profiles, by plotting them as a function of cos(Φ − Φi) we obtain two different sections of the same beam pattern. These two sections are different because we see a different interval of θ for each of the two magnetic poles. Depending on the geometry, these two ranges of θ can overlap, so there will be an overlapping region in the beam pattern. In this region, at an instant Φ, the first pole will be seen at an angle θ. At another instant 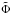 , the second pole will be seen at the same angle θ. We can use Eq. (6) to express the relation between Φ and
, the second pole will be seen at the same angle θ. We can use Eq. (6) to express the relation between Φ and 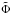 in terms of the geometric parameters
in terms of the geometric parameters 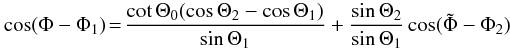 (8)that we write as
(8)that we write as 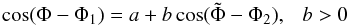 (9)where the parameter a represents the shift between the two single-pole pulse profiles.
(9)where the parameter a represents the shift between the two single-pole pulse profiles.
The sections that the single-pole pulse profiles have in common can be found by representing them as a function of cos(Φ − Φi), so the values of a and b can be determined. Once this is done, both sections of the beam pattern can be represented as a function of the same variable q, defined as 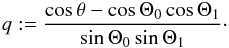 (10)Using Eqs. (6) and (9):
(10)Using Eqs. (6) and (9): 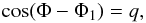 (11)
(11)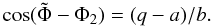 (12)Since the relation between q and cosθ is linear, by plotting the two single-pole pulse profiles as a function of q we obtain the total visible part of the beam pattern without distortion. If the values of a and b have been determined, by comparing Eqs. (8) and (9) we obtain two equations relating the three geometric parameters Θ0, Θ1, and Θ2. They can be solved for Θ1 and Θ2 as a function of Θ0:
(12)Since the relation between q and cosθ is linear, by plotting the two single-pole pulse profiles as a function of q we obtain the total visible part of the beam pattern without distortion. If the values of a and b have been determined, by comparing Eqs. (8) and (9) we obtain two equations relating the three geometric parameters Θ0, Θ1, and Θ2. They can be solved for Θ1 and Θ2 as a function of Θ0: 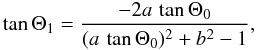 (13)
(13)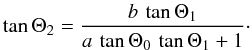 (14)To obtain the location of the magnetic poles Θ1 and Θ2, an independent determination of the direction of observation Θ0 is necessary. If Θ0 is known, the position of the two magnetic poles can be obtained from Eqs. (13) and (14). The pulsar geometry is then completely determined: the location of the poles Θ1 and Θ2, their displacement from the antipodal position Δ, and the direction of observation Θ0. Once the geometric parameters of the system are known, the single-pole pulse profiles can be expressed as a function of θ using Eq. (6). The observable part of the beam pattern is in this way completely reconstructed. Further details can be found in Kraus et al. (1995).
(14)To obtain the location of the magnetic poles Θ1 and Θ2, an independent determination of the direction of observation Θ0 is necessary. If Θ0 is known, the position of the two magnetic poles can be obtained from Eqs. (13) and (14). The pulsar geometry is then completely determined: the location of the poles Θ1 and Θ2, their displacement from the antipodal position Δ, and the direction of observation Θ0. Once the geometric parameters of the system are known, the single-pole pulse profiles can be expressed as a function of θ using Eq. (6). The observable part of the beam pattern is in this way completely reconstructed. Further details can be found in Kraus et al. (1995).
2.3. Application to A 0535+26
Our analysis is based on RXTE-HEXTE observations of A 0535+26 during its August/September 2005 normal outburst. Pointed observations performed between MJD 53614.66–53615.6 were used (observation IDs 91085-01-01-03, -01-01-05, -01-02-00, -01-02-01, -01-02-02, -01-02-03, for a total exposure time of ~20 ks). We extracted RXTE-HEXTE background-substracted light curves in the energy ranges 18.27−30.90 keV, 30.90−44.53 keV, 44.53−59.07 keV, 59.07−99.85 keV. After applying barycentric and orbital correction to the light curves (ephemeris from Finger et al. 2006), we folded them with 30 bins, using the best pulse period from Caballero et al. (2008b). An example of the energy-dependent pulse profiles is given in Fig. 3. The pulse profiles selected for the analysis correspond to the main part of the outburst, as those profiles remain stable during the outburst and also during historical observations (see, e.g., Frontera et al. 1985; Kendziorra et al. 1994; Finger et al. 1996). The flux during the observations was F(3−50) keV ≈ (1.66−1.85) × 10-8 erg cm-2 s-1, giving a luminosity of L(3−50) keV ≈ (0.79−0.885) × 1037 erg s-1 assuming a distance of d = 2 kpc (Steele et al. 1998). The flux was determined from PCA and HEXTE spectra, that we modeled with a power law with a high-energy cutoff plus two Gaussian absorption lines at ~45 and ~100 keV. Details of the spectral and timing analysis of the observations can be found in Caballero et al. (2007, 2008b).
 |
Fig. 3 Example of A 0535+26 original pulse profiles used in the decomposition analysis, obtained from RXTE-HEXTE observations performed during its August/September 2005 normal outburst (MJD 53614.66), in the energy ranges (18.27−30.90) keV, (30.90−44.53) keV, (44.53−59.07) keV, (59.07−99.85) keV from top to bottom. The fluxes have been normalized to unity. Two pulse cycles are shown for clarity. |
2.3.1. Search for acceptable decompositions
The energy-dependent pulse profiles are expressed as Fourier series using an FFT algorithm. Twenty Fourier coefficients out of the 30 sampled points are enough to properly describe the original profiles. The highest frequency terms are not considered in order to avoid aliasing (see e.g. Press et al. 1992). These functions are then written as the sum of two symmetric functions f1(Φ) and f2(Φ). The condition F(Φ) = f1(Φ) + f2(Φ) allows us to obtain the coefficients ck and dk (Eqs. (4), (5)) as a function of uk and vk (Eqs. (2), (3)). To search for physically meaningful decompositions, the Φ1 − Δ parameter space is divided in 1° × 1° boxes. All the formal decompositions are represented in this plane. First we apply the non-negative criterion. This criterion is more restrictive when the minimum of the pulse profile is close to zero. Knowledge of the background level is particularly important in this step. A small amount of negative flux is allowed to account for the ~1% uncertainty of the HEXTE background (Rothschild et al. 1998). The non-negative criterion reduces the number of acceptable decompositions considerably, which are mainly driven by the higher energy pulse profiles (E = 59.1−99.8 keV) that have a pulsed fraction of ~79%. The result of applying this criterion, which requires each decomposition to be valid at all energy ranges, can be seen in the Φ1 − Δ plane in Fig. 4 (left). The black regions indicate where positive decompositions have been found. We limit the search of physically acceptable decompositions to those regions.
 |
Fig. 4 Left: result of applying the non-negative criterion: decompositions outside the black area are discarded. Right: highest ranked decompositions according to the non-ripples criterion grouped in five regions A, B, C, D, and E. The different symbols represent different energy ranges: +(18.3−30.9) keV, × (30.9–44.5) keV, △ (44.5–59.1) keV, Λ (59.1–99.8) keV. |
The non-ripples criterion is then applied. The original pulse profiles in the considered energy ranges have two main peaks. We expect the single-pole contributions not to have many more peaks than the original one. The number of peaks of the single-pole pulse profiles are counted. A quality function is defined as the inverse of the total number of peaks. With this method we obtain the decompositions sorted according to their quality function. Higher values of the quality function correspond to decompositions that are simpler and not much more complicated than the original pulse profile.
For each decomposition, there is a certain region in the Φ1 − Δ plane that contains other qualitatively similar decompositions. To handle the large amount of possible decompositions that have to be studied, similar ones are grouped together into types. A decomposition belongs to a certain type if its square deviation with respect to the chosen representative decomposition of that type is smaller than a certain χ2 = 10-3. Grouping them into types considerably reduces the number of decompositions that are left to study, since we only consider one representative of each type. For instance, in the 18.27−30.90 keV range, 1863 decompositions are grouped into 286 types. Figure 4 (right) shows where the highest ranked profile representatives were found, grouped into types. We examined all these decompositions in different energy ranges, dividing the parameter space in five regions A, B, C, D, and E, shown in Fig. 4 (right).
 |
Fig. 5 Left: original pulse profiles described with a Fourier series, normalized to unity in four different energy ranges. Right: best decomposition of the original pulse profiles in two symmetric functions, corresponding to region A. The vertical lines indicate the ranges for the symmetry points for both single-pole pulse profiles, Φ1 (dashed lines) and Φ2 (dash-dotted lines). The dotted horizontal lines represent the unmodulated flux left available to distribute between the two functions. |
 |
Fig. 6 Left: original pulse profiles described with a Fourier series, normalized to unity in four different energy ranges. Right: “second best” decomposition of the original pulse profiles in two symmetric functions, corresponding to region E. Dashed and dash-dotted lines have the same meaning as in Fig. 5. |
As discussed in detail below, by combining different energy ranges and different observations, we find the best decomposition of the original pulse profiles for the parameters of Region A. They are shown in Fig. 5, with the remaining unmodulated flux available to distribute between the two symmetric functions that cannot be determined from the decomposition. The minima of the two symmetric functions have been shifted to zero, so that the sum of the two symmetric functions plus the unmodulated flux reproduces the original pulse profile. As expected, the single-pole pulse profiles at all energy ranges are not much more complicated than the sum. The symmetry points obtained for this best decomposition, calculated as the average from the different energy ranges, are given in Table 1. We take 5° as the estimate for the uncertainty in the symmetry points, which is the approximate range in region A for which the decompositions are similar.
Symmetry points and azimuthal displacement of one pole with respect to the antipodal position for the best decomposition of the A 0535+26 pulse profiles.
The decompositions in Region C are discarded because they present a very strong anti-correlation in the main peaks which seems artificial, not expected from two independent emission regions. The single-pole pulse profiles are generated independently, so they should not have features that match exactly and cancel out in the sum. Decompositions in Regions B and D have also been discarded, because the single-pole pulse profiles present an anti-correlation in many small features that cancel out in the sum, which is also not expected from two independent emission regions. In Region E we find the “second best” decomposition for Φ1 = 82 ° ± 5 ° and Δ = 63 ° ± 2 °. The single-pole pulse profiles are not much more complicated than the sum, and present an energy evolution similar to that of the total pulse profile. However, we favor the solution in Region A compared to Region E because the single-pole pulse profiles in Region E present a strong anti-correlation in the main features, not expected from a physical point of view. Another argument for rejecting decompositions in Regions C, D, and E is that they all present higher values of Δ. Under the assumption of slightly displaced magnetic poles, lower values of Δ are more likely to be real. This was the case in the analysis of the accreting pulsars Cen X-3 (Kraus et al. 1996) and Her X-1 (Blum & Kraus 2000), where the best decompositions were found for low values of Δ. A further argument against decompositions in Regions B, C, and D emerges in the reconstruction of the beam pattern from the single-pole contributions (see Sect. 2.3.2). This argument does not emerge for Region E, and therefore the beam pattern obtained for Region E is also discussed below.
2.3.2. From single-pole pulse profiles to geometry and beam pattern
In the previous Sect. (2.3.1) we obtained a decomposition of the pulse profiles of A 0535+26 in two single-pole components. We therefore have the pulse profile for each magnetic pole for a given energy range as a function of the rotation angle Φ. As shown in Sect. 2.2.1, using Eq. (6), by representing the single-pole pulse profiles as a function of cos(Φ − Φi), we obtain two sections of the same beam pattern. We performed this transformation to the single-pole pulse profiles of A 0535+26. In contrast to the accreting pulsars Her X-1 and Cen X-3, an overlapping region is not observed for A 0535+26.
However, under the assumption of two identical emission regions, the two sections can almost be connected to each other, with a small gap in between in the beam pattern that remains unobservable to us. This means that, owing to the geometry of the neutron star and to its rotation, we are observing two different sections of the same beam pattern. However, unlike the case of an overlapping region, we cannot determine the parameters a and b of Eq. (9) from a fit. But we can estimate their values. We combined the sections of the beam pattern in all energy ranges using different values of a, which represents the shift between the two single-pole pulse profiles. The best estimate for the parameter a is a = 2.2 ± 0.1. In the case of antipodal poles, b = 1 (Kraus et al. 1995). Since we are assuming a small distortion, b should be close to 1, so we make the assumption b = 1.
With these estimates for a and b plus the direction of observation Θ0, it is possible to obtain the location of the poles Θ1 and Θ2. The angular distance between the location of the second pole and the point that is antipodal to the first pole δ can be estimated using Eq. (7). In Fig. 7 the constraints on the geometry of the pulsar are shown. The values of Θ1, Θ2 and δ are represented for all possible values of the direction of observation Θ0. The mass transfer from the optical companion is expected to align the rotation axes of the binary system on a shorter timescale than the system’s lifetime. Assuming that the rotation axis of the neutron star is perpendicular to the orbital plane, the inclination of the system is identical to the direction of observation i = Θ0. Giovannelli et al. (2007) determined an inclination for the system of i = 37 ± 2 °. We can therefore obtain the location of the poles Θ1 and Θ2. Table 2 gives the estimated values we find for the position of the magnetic poles and the offset.
 |
Fig. 7 Constraints on the pulsar geometry. The vertical lines indicate the orbital inclination (solid line) and its error range (dashed lines). |
It is then possible to plot the reconstructed sections of the beam pattern as a function of θ. The two sections of the beam pattern are reconstructed for θ ∈ (13°,87°) and θ ∈ (93°,167°). Figure 8 (left panels) shows the reconstructed beam pattern or emission of one magnetic pole as a function of θ, with θ = 0° meaning the distant observer is looking down onto the magnetic pole, and θ = 180° meaning the observer looks at the pole from the antipodal position. Figure 8 (right) shows the same beam pattern in polar representation.
For regions B, C, and D, it was not possible to connect the two single pole contributions, providing a further argument for discarding them. For the “second best” decomposition (Region E), it has been possible to connect the reconstructed sections of the beam pattern in a similar way as for Region A, also suggesting that the two emission regions are the same. We can connect them with the same values of a and b as in Region A. This implies the same values for the polar angles of the magnetic poles Θ1 and Θ2. The value of Δ is higher than in region A, so that the offset from an ideal dipole field is also higher, δ ≈ 48°. In Fig. 8 left (right panels) the beam patterns for the best decompositions in region E are represented for comparison. They differ slightly from those in Region A, but the main features of the two functions are similar. The single-pole pulse profiles also had very similar shapes, just different symmetry points.
 |
Fig. 8 Left: reconstructed beam pattern of A 0535+26 or emission of one magnetic pole as a function θ, as seen by a distant observer. The beam pattern is shown in linear representation for Regions A (left panels) and E (right panels) for different energy ranges. Right: reconstructed beam pattern for Region A in polar representation, for the energy ranges 18.27−30.90 keV (solid line) and 59.07−99.85 keV (dashed line). θ = 0° means that the distant observer is looking down onto the magnetic pole, and θ = 180° means that the observer looks at the pole from the antipodal position. |
2.3.3. Interpretation and modeling of the beam pattern
A characteristic feature of the reconstructed beam pattern is a minimum observed in the flux between θ ≈ 30°−40° (Fig. 8 left). This feature is present at all energies, leading us to believe that it could be related to the geometry of the accretion. Filled column models give a beam pattern in which the flux decreases at low values of θ, corresponding to the instant when the observer looks along the accretion stream (Kraus et al. 2003). Introducing a hollow column plus a halo created on the neutron star surface around the column walls from scattered radiation emitted from the walls would explain the increase in flux at low values of θ and the minimum as θ increases when the observer looks directly into the column.
Another characteristic feature of the reconstructed beam patterns at all energies is a steep increase in flux at high values of θ (θ > 120°, meaning the observer looks at one pole of the neutron star from the antipodal position). This can be due to gravitational light bending, making the emission from one pole visible from all directions and brightest from the antipodal position. Such a steep increase in flux at high values of θ has been observed in model calculations, producing a maximum in the flux at θ = 180° (Kraus et al. 2003). This feature has also been observed in the reconstructed beam patterns of other X-ray pulsars (Her X-1 and EXO 2030+375, see Blum & Kraus 2000; Sasaki et al. 2010).
To obtain estimates on the size of the accretion column, we applied a phenomenological model of a hollow column to the case of A 0535+26. The model has been computed for values of θ ∈ [0,40] °, to try to reproduce the minimum observed in the reconstructed beam patterns of A 0535+26 for low values of θ (Fig. 8, left). The applied model describes medium-luminosity pulsars for which the local luminosity per pole is on the order of 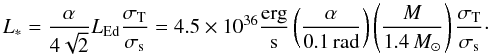 (15)Here, α is the half opening angle of the base of the accretion funnel, LEd = 4πcmpGM/σT the Eddington luminosity, M the mass of the neutron star, σT the Thomson scattering cross section, and σs the magnetic scattering cross section averaged over direction and frequency. In this case a radiative shock is expected to occur at a height that is a small fraction of the stellar radius. The shock separates a region of freely falling plasma above from a settling region of nearly stagnant plasma below, with radiation mainly originating in the shock and the settling region and escaping from the sides of the subshock column or mound (Basko & Sunyaev 1976).
(15)Here, α is the half opening angle of the base of the accretion funnel, LEd = 4πcmpGM/σT the Eddington luminosity, M the mass of the neutron star, σT the Thomson scattering cross section, and σs the magnetic scattering cross section averaged over direction and frequency. In this case a radiative shock is expected to occur at a height that is a small fraction of the stellar radius. The shock separates a region of freely falling plasma above from a settling region of nearly stagnant plasma below, with radiation mainly originating in the shock and the settling region and escaping from the sides of the subshock column or mound (Basko & Sunyaev 1976).
The modeling is performed as in Kraus et al. (2003) and includes a small accretion column, the formation of a halo on the neutron star surface, an accretion funnel delimited by magnetic field lines, magnetic scattering in the accretion stream, and relativistic light deflection. This is an extension of the purely geometric hollow column models presented in Kraus (2001). A detailed study of this model will be presented in Kraus et al. (2010).
Beam patterns were computed in the range θ < 40° for accretion onto a neutron star with the canonical values of mass M = 1.4 M⊙ and radius rn = 10 km. According to the observations of A 0535+26, we take an asymptotic luminosity per pole of L∞ = 8 × 1036 erg s-1, corresponding to a local luminosity per pole of L = L∞/(1 − rs/rn) = 1.4 × 1037 erg s-1 that is close to the limiting luminosity in Eq. (15) for typical values of α as studied below. The radiation is emitted from the side of the column below a radiative shock set at rt = 10.5 km, and the local emission is taken to be an isotropic blackbody at the effective temperature of the column wall. This simple emission pattern is based on more detailed studies that have shown that the bulk of the radiation is expected to escape from the side of the accretion funnel (Wang & Frank 1981) and that, in static columns, the local emission in many circumstances is close to isotropic (Mészáros & Nagel 1985).
The inner and outer half opening angles αi and αo of the hollow accretion funnel (see Fig. 9) were varied as listed in Table 3. The table also lists the effective temperature of the column wall and the density that the accreting material has at the base of the free fall column. These parameters follow from the assumed geometry and the prescribed luminosity as described in Kraus et al. (2003). The effective temperature of the column walls, when assuming an isotropic black body, is derived from 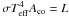 , where σ is the Stefanà-Boltzmann constant, Aco the emitting area, and L the local luminosity per pole. The free-fall density in the plasma rest frame at the base of the free fall column (at r = rn) is taken to be homogeneous over the polar cap, and derives from ρ0c3βγ(γ − 1)Acap = L, where β = v/c and
, where σ is the Stefanà-Boltzmann constant, Aco the emitting area, and L the local luminosity per pole. The free-fall density in the plasma rest frame at the base of the free fall column (at r = rn) is taken to be homogeneous over the polar cap, and derives from ρ0c3βγ(γ − 1)Acap = L, where β = v/c and 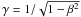 are evaluated at r = rn (see Kraus et al. 2010, for more details).
are evaluated at r = rn (see Kraus et al. 2010, for more details).
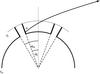 |
Fig. 9 Geometrical model of hollow column (Kraus 2001). |
The results of the modeled beam patterns in the θ ∈ [0°,40°] range for different values of the inner and outer half opening angles, for a photon energy of E = 7.6 keV for a distant observer (E = 10 keV at the neutron star surface) are shown in Fig. 10. As in Fig. 8, θ = 0° means the distant observer looks down onto the magnetic pole. The minimum in the computed beam patterns is caused by the passage of the accretion stream through the line of sight. These modeled beam patterns reproduce the shape of the reconstructed beam pattern of A 0535+26 for low values of θ well (Fig. 8). In Fig. 10 (left) computed beam patterns for different values of the opening angle are shown. The position of the minimum moves to higher values of θ when the opening angle of the funnel increases. In Fig. 10 (right) computed beam patterns for different values of the column thickness are shown. The width of the minimum increases for thicker columns. By comparing the reconstructed beam patterns of A 0535+26 in Fig. 8 (left) for low value of θ with the modeled beam patterns in Fig. 10, we estimate the half-opening angle of the accretion stream in the case of A 0535+26 to be αo = 0.2 rad or ~11.5° and the wall thickness to be αo − αi = 0.06 rad or ~3.4°. We used these estimates for the half-opening angle and for the wall thickness to investigate the energy dependence of the computed beam patterns. We calculated beam patterns for photon energies E = 10 keV, E = 20 keV, E = 30 keV, and E = 40 keV at the neutron star surface (or E = 7.6 keV, E = 15.2 keV, E = 22.8 keV, and E = 30.4 keV for a distant observer). The computed beam patterns for different photon energies are shown in Fig. 11. The passage of the accretion stream through the line of sight produces a distinct minimum that only weakly depends on the photon energy as expected from a geometric signature.
Model parameters used in the computation of beam patterns for A 0535+26, for θ ∈ [0°,40°] .
3. Summary and conclusions
In this work, a decomposition analysis was applied to the A 0535+26 energy-dependent pulse profiles. A dipole magnetic field is assumed with axisymmetric emission regions. The asymmetry in the total pulse profiles is explained with a small offset from one of the magnetic poles from the antipodal position. We find a physically acceptable decomposition of the pulse profiles that allows us to extract information on the geometry of the pulsar. We obtain Θ1 ≈ 50° and Θ2 ≈ 130° for the position of the magnetic poles, and an offset of δ ≈ 25°.
 |
Fig. 10 Beam pattern models for a hollow column with a halo of scattered radiation on the neutron star surface. θ has the same meaning as in Fig. 8. The minimum is produced when observer looks in the direction of the accretion stream. Left: fixed column thickness αo − αi = 0.06 rad and different opening angles αo = 0.2 rad (solid line), αo = 0.15 rad (dashed line), αo = 0.1 rad (dotted line). Right: fixed outer opening angle αi = 0.1 rad and different column thickness αo − αi = 0.02 rad (solid line), αo − αi = 0.04 rad (dashed line) and αo − αi = 0.06 rad (dotted line). |
 |
Fig. 11 Computed beam patterns for different photon energies for an outer opening angle αo = 0.2 rad and a column thickness αo − αi = 0.06 rad. θ has the same meaning as in Fig. 8. |
The visible section of the beam pattern was reconstructed. A characteristic feature of the reconstructed beam pattern at all energies is a minimum observed in the flux between θ ≈ 30°−40°, where θ is the angle between the direction of observation and the magnetic axis. This was interpreted in terms of a simple geometrical model that includes relativistic light deflection. The model includes a hollow column emitting isotropically black body radiation, plus a thermal halo created on the neutron star surface around the column from scattered radiation emitted from the column walls. Another characteristic feature of the reconstructed beam pattern is a steep increase in flux at high values of θ (θ > 120°). This could come from gravitational light bending, which produces a similar feature in model calculations.
We performed model calculations for different column thicknesses and opening angles, and we found the best estimates of the half-opening angle and column thickness to be αo = 0.2 rad, αo − αi = 0.06 rad. We would like to stress, however, that this model is simplified, and we do not claim it is true in all details, but it does reproduce the basic shape of the energy-dependent reconstructed beam pattern of A 0535+26 for values of θ < 40° well. Computation of beam patterns at different energies has revealed a weak dependence of the minimum and its depth with the energy, suggesting that the minimum is mainly an effect of the geometry of the system, produced when the observer looks directly onto the accretion stream. This weak energy dependence on the minimum is also found in the reconstructed beam patterns of A 0535+26.
See, e.g., the results of Fermi-GBM monitoring at http://gammaray.nsstc.nasa.gov/gbm/science/pulsars/
The importance of relativistic light deflection in model calculations can be visualized in http://www.spacetimetravel.org/xpulsar06/xpulsar06.html
Acknowledgments
We thank the referee for providing helpful and constructive comments. Part of this work was supported by the Bundesministerium für Wirtschaft und Technologie through the German Space Agency (DLR) under contract No. 50 OR 0302. I.C. acknowledges both support and hospitality of the ESAC faculty, and financial support from the French Space Agency CNES through CNRS.
References
- Basko, M. M., & Sunyaev, R. A. 1976, MNRAS, 175, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, S., & Kraus, U. 2000, ApJ, 529, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, I., Kretschmar, P., Santangelo, A., et al. 2007, A&A, 465, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero, I., Kraus, U., Postnov, K., et al. 2008a, in Proc. 7th INTEGRAL Workshop [Google Scholar]
- Caballero, I., Santangelo, A., Kretschmar, P., et al. 2008b, A&A, 480, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finger, M. H., Wilson, R. B., & Harmon, B. A. 1996, ApJ, 459, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Finger, M. H., Camero-Arranz, A., Kretschmar, P., Wilson, C., & Patel, S. 2006, BAAS, 38, 359 [NASA ADS] [Google Scholar]
- Frontera, F., dal Fiume, D., Morelli, E., & Spada, G. 1985, ApJ, 298, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Giovannelli, F., & Graziati, L. S. 1992, Space Sci. Rev., 59, 1 [Google Scholar]
- Giovannelli, F., Bernabei, S., Rossi, C., & Sabau-Graziati, L. 2007, A&A, 475, 651 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grove, J. E., Strickman, M. S., Johnson, W. N., et al. 1995, ApJ, 438, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Kendziorra, E., Kretschmar, P., Pan, H. C., et al. 1994, A&A, 291, L31 [NASA ADS] [Google Scholar]
- Kraus, U. 2001, ApJ, 563, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Nollert, H.-P., Ruder, H., & Riffert, H. 1995, ApJ, 450, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Blum, S., Schulte, J., Ruder, H., & Meszaros, P. 1996, ApJ, 467, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Zahn, C., Weth, C., & Ruder, H. 2003, ApJ, 590, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, U., Zahn, C., & Santangelo, A. 2010, A&A, submitted [Google Scholar]
- Kretschmar, P., Kreykenbohm, I., Pottschmidt, K., et al. 2005, ATel, 601 [Google Scholar]
- Leahy, D. A. 1991, MNRAS, 251, 203 [NASA ADS] [Google Scholar]
- Meszaros, P., & Nagel, W. 1985, ApJ, 299, 138 [CrossRef] [Google Scholar]
- Pechenick, K. R., Ftaclas, C., & Cohen, J. M. 1983, ApJ, 274, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Flannery, B. P., Teukolsky, & S. T. V. W. 1992, Numerical Recipes in FORTRAN 77: The Art of Scientific Computing (ISBN 0 521 43064 X, Cambridge University Press) [Google Scholar]
- Riffert, H., & Meszaros, P. 1988, ApJ, 325, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, F. D., Eyles, C. J., Skinner, G. K., & Willmore, A. P. 1975, Nature, 256, 628 [Google Scholar]
- Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Sasaki, M., Klochkov, D., Kraus, U., Caballero, I., & Santangelo, A. 2010, A&A, 517, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Staubert, R., Kendziorra, E., Pietsch, W., et al. 1980, ApJ, 239, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Steele, I. A., Negueruela, I., Coe, M. J., & Roche, P. 1998, MNRAS, 297, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Welter, G. L. 1981, A&A, 102, 97 [NASA ADS] [Google Scholar]
All Tables
Symmetry points and azimuthal displacement of one pole with respect to the antipodal position for the best decomposition of the A 0535+26 pulse profiles.
Model parameters used in the computation of beam patterns for A 0535+26, for θ ∈ [0°,40°] .
All Figures
 |
Fig. 1 Schematic view of a rotating neutron star from Kraus et al. (1995). A spherical coordinate system is used, with the rotation axis as polar axis. Θi is the polar angle of the ith pole. Θ0 is the polar angle of the direction of observation. The angle θ between the magnetic pole and the direction of observation changes with the rotation angle Φ. |
| In the text | |
 |
Fig. 2 Intrinsic geometry of the pulsar. With the rotation axis as polar axis, the magnetic poles are located at polar angles Θ1 and Θ2. The angular distance δ between the second magnetic pole and the point that is antipodal to the first magnetic pole gives the deviation from an ideal dipole field. Figure from Kraus et al. (1995). |
| In the text | |
 |
Fig. 3 Example of A 0535+26 original pulse profiles used in the decomposition analysis, obtained from RXTE-HEXTE observations performed during its August/September 2005 normal outburst (MJD 53614.66), in the energy ranges (18.27−30.90) keV, (30.90−44.53) keV, (44.53−59.07) keV, (59.07−99.85) keV from top to bottom. The fluxes have been normalized to unity. Two pulse cycles are shown for clarity. |
| In the text | |
 |
Fig. 4 Left: result of applying the non-negative criterion: decompositions outside the black area are discarded. Right: highest ranked decompositions according to the non-ripples criterion grouped in five regions A, B, C, D, and E. The different symbols represent different energy ranges: +(18.3−30.9) keV, × (30.9–44.5) keV, △ (44.5–59.1) keV, Λ (59.1–99.8) keV. |
| In the text | |
 |
Fig. 5 Left: original pulse profiles described with a Fourier series, normalized to unity in four different energy ranges. Right: best decomposition of the original pulse profiles in two symmetric functions, corresponding to region A. The vertical lines indicate the ranges for the symmetry points for both single-pole pulse profiles, Φ1 (dashed lines) and Φ2 (dash-dotted lines). The dotted horizontal lines represent the unmodulated flux left available to distribute between the two functions. |
| In the text | |
 |
Fig. 6 Left: original pulse profiles described with a Fourier series, normalized to unity in four different energy ranges. Right: “second best” decomposition of the original pulse profiles in two symmetric functions, corresponding to region E. Dashed and dash-dotted lines have the same meaning as in Fig. 5. |
| In the text | |
 |
Fig. 7 Constraints on the pulsar geometry. The vertical lines indicate the orbital inclination (solid line) and its error range (dashed lines). |
| In the text | |
 |
Fig. 8 Left: reconstructed beam pattern of A 0535+26 or emission of one magnetic pole as a function θ, as seen by a distant observer. The beam pattern is shown in linear representation for Regions A (left panels) and E (right panels) for different energy ranges. Right: reconstructed beam pattern for Region A in polar representation, for the energy ranges 18.27−30.90 keV (solid line) and 59.07−99.85 keV (dashed line). θ = 0° means that the distant observer is looking down onto the magnetic pole, and θ = 180° means that the observer looks at the pole from the antipodal position. |
| In the text | |
 |
Fig. 9 Geometrical model of hollow column (Kraus 2001). |
| In the text | |
 |
Fig. 10 Beam pattern models for a hollow column with a halo of scattered radiation on the neutron star surface. θ has the same meaning as in Fig. 8. The minimum is produced when observer looks in the direction of the accretion stream. Left: fixed column thickness αo − αi = 0.06 rad and different opening angles αo = 0.2 rad (solid line), αo = 0.15 rad (dashed line), αo = 0.1 rad (dotted line). Right: fixed outer opening angle αi = 0.1 rad and different column thickness αo − αi = 0.02 rad (solid line), αo − αi = 0.04 rad (dashed line) and αo − αi = 0.06 rad (dotted line). |
| In the text | |
 |
Fig. 11 Computed beam patterns for different photon energies for an outer opening angle αo = 0.2 rad and a column thickness αo − αi = 0.06 rad. θ has the same meaning as in Fig. 8. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


