EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 525 (January 2011) A&A, 525 (2011) L11 Full HTML
Free Access
Issue
A&A
Volume 525, January 2011
Article Number L11
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201016017
Published online 07 December 2010

© ESO, 2010

1. Introduction

Many indirect observations indicate that magnetic fields should be present around massive stars (Henrichs et al. 2005; Hubrig 2008), and recently a few direct detections have been made via the Zeeman effect (see the recent review by Donati & Landstreet 2009). For instance, direct measurements have been obtained for a handful of O stars, among them θ1 Ori C and HD 191612, with values of a few hundred G (Donati et al. 2002, 2006a). This last star is a member of the class of Of?p stars, of which only 5 are known in the Galaxy. Of these, three have been observed in detail and all three have detectable magnetic fields (Wade et al. 2010).

Among early B-type stars, a magnetic field has been discovered in the B0.2V star τ Sco (Donati et al. 2006b, ~0.5 kG) and in three β Cepheid stars: ξ1 CMA (Hubrig et al. 2006, B0.7IV, 300 G), β Cep (Henrichs et al. 2000, B2III, less than 100 G), and V2052 Oph (Neiner et al. 2003b, B2IV, less than 100 G). Neiner et al. (2003a) and Hubrig et al. (2006) have discovered magnetic fields of the order of a few hundred G in slowly pulsating B-type stars. Magnetic fields have been detected around a few Be stars (Yudin et al. 2009; Hubrig et al. 2007; Neiner & Hubert 2005), and these fields are of the order of 100 G or less.

The origin of these magnetic fields is still unknown. It might be fossil fields (e.g. the spectral characteristics of Of?p stars are indicative of organized magnetic fields, most likely of a fossil origin according to Wade et al. 2010), or fields produced through a dynamo mechanism. Recent simulations by Cantiello et al. (2010) of subsurface convective zone in massive stars show dynamo-generated magnetic fields of the order of one kG. According to these authors, these magnetic fields might reach the surface of OB stars.

In the Sun, magnetic braking results from solar wind material following the magnetic field lines that extend well beyond the stellar surface. This coupling exerts a torque on the surface layers of the Sun, and this slows down its rotation. Could such a process also be active in massive stars showing a sufficiently strong surface magnetic field? Townsend et al. (2010) has recently discovered that σ Ori E (B2Vpe, ~10 kG) is undergoing rotational braking. The spin-down time of 1.34 Myr is in good agreement with theoretical predictions based on magnetohydrodynamical simulations of angular momentum loss from a magnetized line-driven wind. This gives some support to the hypothesis that at least a few massive stars may indeed suffer magnetic braking.

Such an effect has for the moment never been included in massive star models; however, by modifying the internal distribution of Ω, the angular velocity, magnetic braking can significantly change the mixing of the elements inside the star, as well as the evolution of its angular momentum content.

Although rotating models have improved the agreement between models and theory, some points remain to be clarified. A small subset of stars exhibit surface properties, such as low surface velocities and strong surface enrichments, which, when the star is not a giant or a supergiant, cannot be explained by current rotating stellar models for single stars (see discussions in Brott et al. 2009; Hunter et al. 2009). Although the fraction of these stars is small and some may be stars at the end of the MS phase (Maeder et al. 2009), it is worthwhile investigating what the physical cause of this behaviour could be.

Theoretical models with rotation also predict rotation velocities that are too high for the young pulsars (see the discussion in Heger et al. 2004, 2005). Thus it does appear interesting to study any effects that can remove angular momentum from the star. Can magnetic braking be an interesting explanation for the strongly mixed, slow rotators? Can it help in reducing the angular momentum of the core? In this first paper, we want to study these questions by presenting a first series of computations accounting for this effect. In Sect. 2 we present the formalism we used to account for the magnetic braking effect, as well as the physical ingredients of the models. The results are discussed in Sects. 3 and 4 and conclusions are given in Sect. 5.

2. Physics of the stellar models

The formalism of the magnetic braking law used here follows theoretical developments first made for the Sun, starting with Weber & Davis (1967) who used an idealized monopole field to model the angular momentum loss in the solar wind 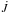\hbox{$\dot J$}. They found that 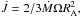J̇=2/3ṀΩRA2,\hbox{$ \dot J={2/3} \dot M \Omega R^2_{\rm A},$} where Ṁ is the mass loss rate and RA the Alfvén radius, defined as the point where the ratio between the magnetic field energy density and the kinetic energy density of the wind is equal to 1. ud-Doula & Owocki (2002) and ud-Doula et al. (2008) have examined the angular momentum loss from magnetic hot stars with a line-driven stellar wind and a rotation-aligned dipole magnetic field using 2-D numerical MHD simulations. They find that the total angular momentum loss follows the expression given above, but with a smaller RA than in the monopole case. 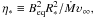They find that dJdt=23ṀΩR∗2[0.29+(η∗+0.25)1/4]2,\begin{equation} {{\rm d}J\over {\rm d}t} = {2 \over 3}\dot M \Omega R^2_*\left[0.29+(\eta_* + 0.25)^{1/4}\right]^2, \label{ma} \end{equation}(1)where η∗ is the magnetic confinement parameter (ud-Doula & Owocki 2002) defined by η∗≡Beq2R∗2/Ṁυ∞,\hbox{$\eta_* \equiv {B^2_{\rm eq} R^2_* / \dot M \upsilon_\infty}, $} where R∗ is the stellar radius, Beq, the magnetic field at the equator and at the surface of the star, and υ∞ the wind velocity at infinity. Very interestingly, when applied to the case of σ Ori E, Eq. (1) gives a spin-down timescale of the order of 1 Myr (ud-Doula et al. 2009), quite in agreement with the observed spin-down timescale for this star (Townsend et al. 2010).

thumbnail Fig. 1

Evolution of the N/C ratio (in number) as a function of the gravity at the surface of 10 M⊙ stellar models with υini = 200 km s-1. The value of the magnetic field is indicated. Continuous (dashed) lines are for models with interior differential (solid body) rotation. In the shaded areas, models with differential rotation predict surface velocities inferior to 50 km s-1 during the MS phase. The full circle and square correspond to HD 16582 and HD 3360 (ζ Cas) respectively (see text for references).

We have implemented in the Geneva evolution code (Eggenberger et al. 2008) Eq. (1) for the loss of the angular momentum. Various values of Beq are used between 0.1 and 10 kG. In the present exploratory work, we suppose that the magnetic field keeps a constant value during the MS phase. We computed the evolution of 10 M⊙ stellar models at solar metallicity with υini = 200 km s-1. In the context of shellular rotation (Zahn 1992), the vertical transport of chemicals through the combined action of vertical advection and strong horizontal diffusion can be described as a pure diffusive process (Chaboyer & Zahn 1992). The advective transport is then replaced by a diffusive term, with an effective diffusion coefficient Deff = |rU(r)|2/30Dh, where r is the characteristic radius of the isobar, U(r) the vertical component of the meridional circulation velocity (Maeder & Zahn 1998) and Dh the diffusion coefficient associated to horizontal turbulence as given by Zahn (1992). The vertical transport of chemical elements then obeys a diffusion equation, which in addition to this macroscopic transport, also accounts for (vertical) turbulent transport with the same coefficient Dshear as for the transport of angular momentum (Maeder & Meynet 2001).

The effects of magnetic braking depend a lot on how angular momentum, hence the chemical species, is transported inside the star. Here we consider two limiting cases:

  • Differential rotation: the angular momentum transport isdriven by the meridional currents and the shear instabilities.These two effects are not efficient enough to produce solid bodyrotation. A moderate differential rotation is therefore presentduring the whole MS phase, and the mixing of the chemicalspecies is mainly due to shear instabilities.

  • Solid body rotation: when the transport of the angular momentum is very efficient, then solid body rotation is maintained during the whole MS phase1. The chemical species are transported by the meridional currents.

At the present time it is not known which is the most frequent situation in nature, so we explore these two possibilities, which represent some limiting cases hopefully framing the real world.

3. Models with magnetic braking and interior differential rotation

In Figs. 1–3 (look at the continuous lines) are shown the evolutions of the abundances and of the (equatorial) velocities at the surface of models computed with different values of the magnetic field. We see that, compared with the model without magnetic braking, models with magnetic braking present stronger changes of the surface abundances. This comes from the fact that magnetic braking creates strong differential rotation in the outer layers and thus triggers mixing by shear. At the same time the surface velocity rapidly decreases.

More quantitatively, we see that, at 100 G, the effects on N/C remain modest (increase by about 20% at the end of the MS phase with respect to the model without magnetic braking) but are already significant for the surface velocity, which is decreased from 168 to 115 km s-1 at the blue turnoff of the MS band. For a 500 G magnetic field, the effects are very strong: increase by more than a factor 2.2 of the N/C ratio at the end of the MS phase. The surface velocity reaches values around 19 km s-1 at the end of the MS phase. Surface abundances of boron provide a very sensitive test of how mixing occurs in the outer layers of the star. Indeed, that element already begins to be destroyed at temperatures between 5–6 × 106 K. From Fig. 2, we see that in models with magnetic braking, boron is much more rapidly depleted at the surface.

thumbnail Fig. 2

Same as Fig. 1 for the evolution of the abundance of B at the surface.

thumbnail Fig. 3

Same as Fig. 1 for the evolution of the surface velocity at the equator.

Stars in the hatched zone of Figs. 1 and 2 present strong signs of mixing during the main sequence and have surface velocities inferior to 50 km s-1. Typically, one would expect that at least some LMC stars in group 2 of Fig. 5 in Hunter et al. (2009) would be in this region. We defer a detailed comparison with the data of Hunter et al. (2009) to a later paper where models with the LMC metallicity will be computed. In Figs. 1–3, we have indicated the positions of the two known stars having initial masses between 9 and 11 M⊙ and showing boron depletion by more than an order of magnitude (data taken from Tables 3 and 4 of Frischknecht et al. 2010, see detailed references therein). We see that current models with magnetic braking although not providing a perfectly consistent fit to the data2, appear to be promising for explaining stars with strong signs of mixing, low surface velocities, and high gravities. It is interesting to mention that the star corresponding to the square (ζ Cas) has a detected magnetic polar field of 335(+120−65) G (Neiner et al. 2003a).

Can this process extract angular momentum from the core region? In Fig. 4, the specific angular momentum inside the central 2 M⊙ at the end of the MS phase is shown for various models. We recall that the reduction between the angular momentum of the core on the ZAMS and at the presupernova stage occurs for a significant part during the MS phase. Typically about 70% of the total angular momentum lost by the core during the whole stellar lifetime is lost during the MS phase (see Fig. 7 in Hirschi et al. 2004). In models with differential rotation, a magnetic field of about 100 G reduces the specific angular momentum by about 25% (0.1 dex) with respect to the values obtained in the model without magnetic braking. When a magnetic field between 500 G and 1 kG is considered, j is on average decreased by slightly more that 0.3 dex, which means by a factor between 2 and 2.2 with respect to the model with no magnetic braking. Thus magnetic braking in differentially rotating models has an impact on the evolution of core angular momentum content.

4. Models with magnetic braking and interior solid body rotation

thumbnail Fig. 4

Variation in the specific angular momentum as a function of the Lagrangian mass inside the cores of different models.

The case of solid body rotation is quite different from the one of differential rotation as can be seen in Figs. 1–4. This is expected since the physical processes responsible for the transport mechanisms are quite different. For the angular momentum, a strong coupling is imposed in the model. The chemical elements are no longer transported by shear turbulence as in the previous case, but by meridional currents.

Whenever meridional currents are responsible for the transport of the chemical species, the key factor governing chemical element mixing is Ω, which decreases rapidly in the whole interior when magnetic braking is exerted at the surface. When magnetic braking is accounted for, mixing is much weaker than in the case without magnetic braking. For a magnetic field equal to or larger than 0.5 kG, no nitrogen enrichment is predicted by the models during the whole MS phase. Boron depletions are not as strong in models with magnetic braking.

From Fig. 3, we can see that for models with magnetic braking and solid body rotation, the surface rotation decreases much more rapidly than in the case of differential rotation (for a given value of Beq). Thus such models would predict stars at the end of the MS phase with low surface velocity and weak or even nonexistent surface enrichments. Such stars can also result from the evolution of progenitors starting with low initial rotational velocities. However, the internal structure at the end of the MS will be different if the star has ever been a slow rotator or has come from a slowed down, initially rapid rotators. Typically the star with a fast-rotating progenitor will have a larger core.

Solid body rotation alone (without magnetic braking) is already an interesting way to evacuate the angular momentum enclosed in the core. For instance, it has been shown by Heger et al. (2005, 2004), who computed models where solid body rotation is imposed during the MS phase by the action of the Tayler-Spruit dynamo (Spruit 2002), that these models could produce neutron stars with rotational velocities at birth in the upper range values given by observations. As can be seen from Fig. 4 (lower panel), magnetic braking with solid body rotation has a dramatic effect on the angular momentum content of the core. We see that, already with a value of Beq = 100 G, j is decreased by more than one dex with respect to the corresponding solid-body rotation with no magnetic braking. For magnetic fields of 1 kG, j is decreased by more than 4 orders of magnitude! In that last model, the specific angular momentum in the core at the end of the MS phase has the same order of magnitude as the one required for explaining the long-period (150 ms) young pulsar PSR B1509-58 (see Table 3 in Heger et al. 2004).

5. Conclusions

The main results in this paper are the following. Models with differential rotation and magnetic braking may produce strongly mixed stars with low surface velocities during the MS phase. Some of the stars discussed by Hunter et al. (2009,see their Group 2 stars in their Fig. 5) as well as some stars showing very strong boron depletion with no N-enhancement (Venn et al. 2002; Mendel et al. 2006; Frischknecht et al. 2010), might be stars that suffered magnetic braking. Models with solid-body rotation and magnetic braking produce stars that at the end of the MS phase have low surface velocities and none or very weak changes in the surface abundances. Magnetic braking reduces the angular momentum content of the core, even for moderate values of the magnetic field when solid body rotation is considered.

Present models are of course quite preliminary and have to be improved in the future. For instance, the coexistence of a large-scale/dipolar magnetic field (as adopted here) with internal differential rotation may be problematic. If the field is of fossil origin, it will likely pervade the whole star and may induce strong coupling, thus reducing or even removing any differential rotation. In that case, our models with solid-body rotation would apply. In these models, magnetic braking is so efficient that the slow down occurs before any significant changes in the surface abundances. If the surface magnetic fields are produced by a dynamo (see for instance the suggestion by Cantiello et al. 2010), differential rotation may still be present in the interior, and changes in the surface abundances are quite rapid. However, one may question whether it is justified to assume a constant value for Beq as we did here. More quantitative estimates need detailed understanding of the dynamo process and of its dependence on rotation. Finally let us stress that in the Hunter diagram most stars follow the predictions of rotating models (Maeder et al. 2009) without magnetic braking. This is consistent with the weak magnetic fields of OB stars.

1

We do not invoke any specific mechanism here. Solid-body rotation might be due to a fossil magnetic field for instance or to a dynamo driven by shear such as the one proposed by Spruit (2002).

2

All our models start their evolution with a velocity of 200 km s-1, which may not be adequate for these stars.

References

  1. Brott, I., Hunter, I., de Koter, A., et al. 2009, Commun. Asteroseismol., 158, 55 [Google Scholar]
  2. Cantiello, M., Braithwaite, J., Brandenburg, A., et al. 2010, [arXiv:1009.4462] [Google Scholar]
  3. Chaboyer, B., & Zahn, J.-P. 1992, A&A, 253, 173 [NASA ADS] [Google Scholar]
  4. Donati, J., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  5. Donati, J., Babel, J., Harries, T. J., et al. 2002, MNRAS, 333, 55 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  6. Donati, J., Howarth, I. D., Bouret, J., et al. 2006a, MNRAS, 365, L6 [NASA ADS] [CrossRef] [Google Scholar]
  7. Donati, J., Howarth, I. D., Jardine, M. M., et al. 2006b, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
  8. Eggenberger, P., Meynet, G., Maeder, A., et al. 2008, Ap&SS, 316, 43 [NASA ADS] [CrossRef] [Google Scholar]
  9. Frischknecht, U., Hirschi, R., Meynet, G., et al. 2010, A&A, 522, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Heger, A., Woosley, S. E., Langer, N., & Spruit, H. C. 2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens, IAU Symp., 215, 591 [Google Scholar]
  11. Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
  12. Henrichs, H. F., de Jong, J. A., Donati, J., et al. 2000, in The Be Phenomenon in Early-Type Stars, ASP Conf. Ser. 214, ed. M. A. Smith, H. F. Henrichs, & J. Fabregat, IAU Colloq., 175, 324 [Google Scholar]
  13. Henrichs, H. F., Schnerr, R. S., & ten Kulve, E. 2005, in The Nature and Evolution of Disks Around Hot Stars, ed. R. Ignace, & K. G. Gayley, ASP Conf. Ser., 337, 114 [Google Scholar]
  14. Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Hubrig, S. 2008, in Rev. Mex. Astron. Astrofis. Conf. Ser., 27, 33 26 [Google Scholar]
  16. Hubrig, S., Briquet, M., Schöller, M., et al. 2006, MNRAS, 369, L61 [NASA ADS] [CrossRef] [Google Scholar]
  17. Hubrig, S., Yudin, R. V., Pogodin, M., et al. 2007, in VI Reunion Anual Sociedad Chilena de Astronomia (SOCHIAS), 21 [Google Scholar]
  18. Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
  21. Maeder, A., Meynet, G., Ekström, S., & Georgy, C. 2009, Commun. Asteroseismol., 158, 72 [NASA ADS] [Google Scholar]
  22. Mendel, J. T., Venn, K. A., Proffitt, C. R., Brooks, A. M., & Lambert, D. L. 2006, ApJ, 640, 1039 [NASA ADS] [CrossRef] [Google Scholar]
  23. Neiner, C., & Hubert, A. M. 2005, in The Nature and Evolution of Disks Around Hot Stars, ed. R. Ignace, & K. G. Gayley, ASP Conf. Ser., 337, 275 [Google Scholar]
  24. Neiner, C., Geers, V. C., Henrichs, H. F., et al. 2003a, A&A, 406, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Neiner, C., Henrichs, H. F., Floquet, M., et al. 2003b, A&A, 411, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Townsend, R. H. D., Oksala, M. E., Cohen, D. H., Owocki, S. P., & ud-Doula, A. 2010, ApJ, 714, L318 [NASA ADS] [CrossRef] [Google Scholar]
  28. ud-Doula, A., & Owocki, S. P. 2002, ApJ, 576, 413 [NASA ADS] [CrossRef] [Google Scholar]
  29. ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2008, MNRAS, 385, 97 [NASA ADS] [CrossRef] [Google Scholar]
  30. ud-Doula, A., Owocki, S. P., & Townsend, R. H. D. 2009, MNRAS, 392, 1022 [NASA ADS] [CrossRef] [Google Scholar]
  31. Venn, K. A., Brooks, A. M., Lambert, D. L., et al. 2002, ApJ, 565, 571 [NASA ADS] [CrossRef] [Google Scholar]
  32. Wade, G. A., Grunhut, J. H., Marcolino, W. L. F., et al. 2010, [arXiv:1009.3564] [Google Scholar]
  33. Weber, E. J., & Davis, Jr., L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] [Google Scholar]
  34. Yudin, R., Hubrig, S., Pogodin, M., et al. 2009, in IAU Symp., 259, 397 [Google Scholar]
  35. Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

All Figures

thumbnail Fig. 1

Evolution of the N/C ratio (in number) as a function of the gravity at the surface of 10 M⊙ stellar models with υini = 200 km s-1. The value of the magnetic field is indicated. Continuous (dashed) lines are for models with interior differential (solid body) rotation. In the shaded areas, models with differential rotation predict surface velocities inferior to 50 km s-1 during the MS phase. The full circle and square correspond to HD 16582 and HD 3360 (ζ Cas) respectively (see text for references).

In the text
thumbnail Fig. 2

Same as Fig. 1 for the evolution of the abundance of B at the surface.

In the text
thumbnail Fig. 3

Same as Fig. 1 for the evolution of the surface velocity at the equator.

In the text
thumbnail Fig. 4

Variation in the specific angular momentum as a function of the Lagrangian mass inside the cores of different models.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.