| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | L7 | |
| Number of page(s) | 3 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201016012 | |
| Published online | 06 December 2010 | |
Letters to the Editor
A weakly random Universe?
1 Yerevan Physics Institute and Yerevan State University,
Yerevan, Armenia
2
School of Mathematical Sciences, Monash University,
Clayton,
Australia
3
Dipartimento di Fisica “E.R. Caianiello”, Universita’ degli Studi
di Salerno, Fisciano,
Italy
4
Institute of Theoretical Physics, University of Zurich,
Zurich,
Switzerland
5
Salento University and INFN, Sezione di Lecce, Lecce, Italy
Received: 27 October 2010
Accepted: 16 November 2010
Cosmic microwave background (CMB) radiation is characterized by well-established scales, the 2.7 K temperature of the Planckian spectrum and the 10-5 amplitude of the temperature anisotropy. These features were instrumental in indicating the hot and equilibrium phases of the early history of the Universe and its large-scale isotropy, respectively. We now reveal one more intrinsic scale in CMB properties. We introduce a method developed originally by Kolmogorov, which quantifies a degree of randomness (chaos) in a set of numbers, such as measurements of the CMB temperature in a given region. Considering CMB as a composition of random and regular signals, we solve the inverse problem of recovering of their mutual fractions from the temperature sky maps. Deriving the empirical Kolmogorov’s function in the Wilkinson Microwave Anisotropy Probe’s maps, we obtain the fraction of the random signal to be about 20 per cent; i.e., the cosmological sky is a weakly random one. The paper is dedicated to the memory of Vladimir Arnold (1937–2010).
Key words: cosmic background radiation
© ESO, 2010
The high-accuracy Planckian spectrum, the quadrupole anisotropy, and the acoustic peaks of the power spectrum (Mather 1994; Smoot et al. 1992; de Bernardis et al. 2000) of the cosmic microwave background (CMB) appear to be carriers of valuable information on the early Universe. Among other peculiarities of the CMB signal is that it is described well by a Gaussian distribution of initial fluctuations. This is remarkable at least for two reasons. Gaussian fluctuations follow from the simplest single scalar field version of inflation. The Gaussian is also a limiting distribution, in accordance with the central limit theorem, as the sum of many independent random variables of finite variance. CMB fitting the Gaussian certainly does not reveal its randomness, as it might arise from both random and regular distributions.
Is it possible to reveal the fractions of random and regular signals in the CMB?
One can deal with this problem using the Kolmogorov distribution and the stochasticity parameter as a rigorous measure of randomness (Kolmogorov 1933; Arnold 2008a). Arnold applied this technique to arithmetical and geometrical progressions and to number sequences (Arnold 2008a,b,c, 2009a,b), and it has also been applied to CMB temperature datasets (Gurzadyan et al. 2009). Now, based on the 7-year CMB data obtained by the Wilkinson Microwave Anisotropy Probe (WMAP) (Jarosik et al. 2010) we have derived a general result, i.e., that the random signal yields about 0.2 fraction in the CMB total signal.
We start by briefly outlining the approach. We consider a sequence { X1,X2,...,Xn } of a random variable X ordered in an increasing manner X1 ≤ X2 ≤ ··· ≤ Xn. Cumulative distribution function of X is defined as the probability of the event X ≤ x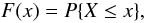 and an empirical distribution function Fn(x) as
and an empirical distribution function Fn(x) as 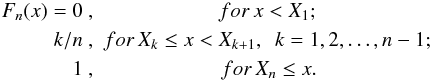 Then the Kolmogorov’s stochasticity parameter λn, which is also a random quantity, is defined as the normalized deviation of those two distribution functions
Then the Kolmogorov’s stochasticity parameter λn, which is also a random quantity, is defined as the normalized deviation of those two distribution functions 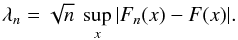 (1)Here, the multiplier
(1)Here, the multiplier 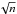 appears to account for the deviation expected for n independent observations of a genuinely random variable.
appears to account for the deviation expected for n independent observations of a genuinely random variable.
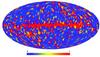 |
Fig. 1 The Kolmogorov map of cosmic microwave background radiation, i.e. the distribution of Kolmogorov’s function Φ over the sky for the Wilkinson Microwave Anisotropy Probe’s 7-year W-band temperature dataset. |
The remarkable result is Kolmogorov’s (1933) proof (“the astonishing Kolmogorov’s theorem” as Arnold 2008b, called it), concerning the asymptotic behavior of the distribution of λ for any continuous F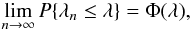 where the limiting distribution for any real λ > 0 is
where the limiting distribution for any real λ > 0 is 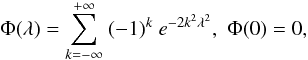 (2)the convergence is uniform, and Φ, the Kolmogorov’s distribution, is independent of the distribution F of the initial random variable X. The interval of probable values of λ yields 0.3 ≤ λn ≤ 2.4 (Kolmogorov 1933). This universality of Kolmogorov’s distribution marks it as a measure of a stochasticity degree of datasets (Arnold 2008a,b,c, 2009a,b).
(2)the convergence is uniform, and Φ, the Kolmogorov’s distribution, is independent of the distribution F of the initial random variable X. The interval of probable values of λ yields 0.3 ≤ λn ≤ 2.4 (Kolmogorov 1933). This universality of Kolmogorov’s distribution marks it as a measure of a stochasticity degree of datasets (Arnold 2008a,b,c, 2009a,b).
This objective measure enables one to consider the composition of signals of various randomness; e.g., the behavior of λn and Φ was studied at numerical simulations of sequences (Ghahramanyan et al. 2009; Mirzoyan & Poghosian 2009).
Within this remarkable system, an approach to apply is the CMB dataset, just because its cumulative distribution function happens to be known, and it is close to Gaussian! Then for Gaussian distribution function F and via a properly developed strategy (for algorithmic and numerical details see Gurzadyan & Kocharyan 2008; Gurzadyan et al. 2009) one can obtain the distribution of Φ for CMB, the Kolmogorov map for WMAP’s temperature data, as shown in Fig. 1. Not only is the non-cosmological signal, the Galactic disk, clearly outlined, which was not at all trivial a priori, but also a non-Gaussian feature such as the Cold Spot also appears to be outlined by a specific behavior by the function Φ that is compatible with its void nature (Gurzadyan & Kocharyan 2008, 2009; Gurzadyan et al. 2005, 2009). The Gaussian nature of CMB is characterized by certain correlations studied by traditional methods, i.e. the harmonic analysis, correlations functions, and power spectrum, which were particularly informative due to the structures of the acoustic peaks. Application of Kolmogorov’s approach will complement those studies by quantifying the cumulative degree of correlations in the CMB signal. Kolmogorov’s parameter is also efficient in detecting point sources, radio and Fermi/LAT gamma-ray, and other anomalies in CMB maps (Gurzadyan et al. 2010; Gurzadyan et al. 2008); i.e., this method enables the separation of the cosmological signal from non-cosmological ones.
In the present paper, for the first time, we undertake a novel analysis of the cosmological CMB signal revealed by the Φ distribution. First, we obtain the Kolmogorov distribution Φ(λ) for different regions of sky and WMAP’s 7-year W-band data (Jarosik et al. 2010) in HEALPix representation (Gorski et al. 2005). The procedure was as follows. Circles of radii 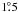 were considered to have enough pixels to estimate the mean Φ(λ), given that the λ itself is a random parameter. The variance of the Gaussian then was estimated for each circle region containing around 540 pixels on average. Then the resulting frequency distribution vs. Φ was obtained, and it appears to be decaying, corresponding to 10 000 2D-balls randomly distributed over the sky with the consequent elimination of belts of coordinates |b| < 20°, |b| < 30°, |b| < 40°, in order to evaluate the role of the contamination of the Galactic disk. Figure 2 shows the plot for |b| < 30°. The 2D-balls obviously also cover the cold spot regions studied in (Jarosik et al. 2010; Gurzadyan et al. 2009). The point sources revealed in CMB maps (Gurzadyan et al. 2010) are also covered; however, they cannot contribute to the distribution of Φ, not only because of their small quantity but also mainly because of their point-like feature, i.e. small number pixelization.
were considered to have enough pixels to estimate the mean Φ(λ), given that the λ itself is a random parameter. The variance of the Gaussian then was estimated for each circle region containing around 540 pixels on average. Then the resulting frequency distribution vs. Φ was obtained, and it appears to be decaying, corresponding to 10 000 2D-balls randomly distributed over the sky with the consequent elimination of belts of coordinates |b| < 20°, |b| < 30°, |b| < 40°, in order to evaluate the role of the contamination of the Galactic disk. Figure 2 shows the plot for |b| < 30°. The 2D-balls obviously also cover the cold spot regions studied in (Jarosik et al. 2010; Gurzadyan et al. 2009). The point sources revealed in CMB maps (Gurzadyan et al. 2010) are also covered; however, they cannot contribute to the distribution of Φ, not only because of their small quantity but also mainly because of their point-like feature, i.e. small number pixelization.
 |
Fig. 2 The empirical frequency distribution of Kolmogorov’s function Φ in the CMB map with the extracted Galactic disk region |b| < 30° and the generated signal zn for the fraction of the random sequence α = 0.19. |
The first conclusion drawn from Fig. 2 is expected. The CMB signal is certainly not purely random Gaussian; otherwise, the stochasticity parameter, hence the function Φ, would have a uniform distribution, i.e. constant, as follows from Kolmogorov theorem.
Once Kolmogorov theorem enables estimation of the randomness Φ for a given sequence, with the empirical distribution of Φ in Fig. 2, one can inquire into the inverse problem of reconstructing the initial signal to result in that distribution.
To solve this inverse problem, we consider a regular sequence represented in the form (cf. Arnold 2008c) 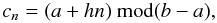 (3)i.e. as an arithmetical progression repeated within an interval [a,b] , and where h is an arbitrary constant.
(3)i.e. as an arithmetical progression repeated within an interval [a,b] , and where h is an arbitrary constant.
Since the sequence (3) corresponds to a uniform distribution, one can use von Neumann’s method (von Neumann 1951) to extract a Gaussian nonrandom sequence of standard deviation σ and mean value m from it. The latter we consider within the adopted interval a = m − 10σ and b = m + 10σ.
Von Neumann’s method enables generating of sequences with any differential distribution f(x) and extracting of sequences with the desired distribution from a uniform one. The method is particularly efficient when no explicit form of F(x), i.e. of the integral of f(x), is available. The procedure is as follows. First, we consider a uniform sequence an and a distribution f(x) having minimal and maximal values ymin and ymax. Then, to extract a sub-sequence from an one has to go through all elements of an and, for each ai, generate a random uniform number z within the interval (ymin,ymax); if z < f(ai), one assigns ai to a new sequence and skips it otherwise. The extracted subsequence will have a distribution f(x). We used this procedure to generate random and regular sequences with Gaussian distribution, i.e. when f(x) is a Gaussian. If the original sequence an is a random one, then one gets a random Gaussian sequence, and a regular one otherwise.
By generating many regular sequences with a Gaussian distribution of mean and standard deviations corresponding to the WMAP’s CMB signal and calculating the Kolmogorov parameter for each of them, we were able to construct the empirical distribution of Φ at the best choice of the parameter h = 7.342....
 |
Fig. 3 The confidence level in χ2 vs. the parameter α, i.e. the fraction of the random component, for the WMAP7 CMB maps with extracted Galactic disk regions: |b| < 20°,30°,40°. |
As the next step, the following sequence was considered, 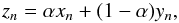 (4)where xn is a random Gaussian sequence with the same m and σ as the regular von Neumann-Gaussian sequence yn, i.e. the one derived by means of the von Neumann method. Thus, we have a sum of random and regular sequences with their varying proportion defined by the parameter α ∈ [0,1] : for α = 0 we have a regular sequence, while for α = 1 it is random.
(4)where xn is a random Gaussian sequence with the same m and σ as the regular von Neumann-Gaussian sequence yn, i.e. the one derived by means of the von Neumann method. Thus, we have a sum of random and regular sequences with their varying proportion defined by the parameter α ∈ [0,1] : for α = 0 we have a regular sequence, while for α = 1 it is random.
It can be shown that zn also has a Gaussian distribution with mean m and standard deviation 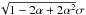 . While varying α from 0 to 1 we see, as expected, the distribution of Φ gradually changing from the form in Fig. 2 to a uniform one. At some value of α, we get the closest fit evaluated in confidence levels for distribution of Φ of zn to WMAP’s sequences. Figure 3 shows the behavior of χ2 vs. the α for the CMB maps with extracted regions |b| < 20°, |b| < 30°, |b| < 40°, and as seen, the results of the last two maps are identical. We see that the minimal values of χ2, so the highest confidence levels are reached for 0.15 and 0.19 values of α for the 20° and 30° disks, respectively.
. While varying α from 0 to 1 we see, as expected, the distribution of Φ gradually changing from the form in Fig. 2 to a uniform one. At some value of α, we get the closest fit evaluated in confidence levels for distribution of Φ of zn to WMAP’s sequences. Figure 3 shows the behavior of χ2 vs. the α for the CMB maps with extracted regions |b| < 20°, |b| < 30°, |b| < 40°, and as seen, the results of the last two maps are identical. We see that the minimal values of χ2, so the highest confidence levels are reached for 0.15 and 0.19 values of α for the 20° and 30° disks, respectively.
The resulting α distributions are shown in Fig. 2 along with WMAP’s frequency plot for the CMB map with extracted Galactic disk of |b| < 30°. If the small difference, a few per cent, between the values of α of the CMB maps with extracted |b| < 20° and |b| < 30° regions stems from the Galactic disk contamination, then one can state that the latter contributes to a slight regularization of the CMB signal.
The methodology of Kolmogorov’s approach is based on studying statistical properties, namely, the degree of randomness of the signal via the stochasticity parameter and the distribution Φ. As it appears, those characteristics are informative enough to distinguish one signal from another, for example, the
cosmological CMB and the Galactic synchrotron one. Although the photons of such different origins can have the same temperature, they differ in their degree of randomness, hence in their correlation properties; e.g., the synchrotron is characterized by a power-law spectrum, and the CMB by a Planckian one. This difference is reflected in the statistical analysis. However, here we went further to quantify the contribution of the correlations and of chaotic components. The correlations in the CMB signal are carriers of information on various processes, from primordial, through the last scattering and reionization epochs, up to the integrated Sachs-Wolfe and Sunyaev-Zeldovich effects. Revealing the degree of correlations in CMB signal, particularly, reflects the cumulative contribution and properties of those processes.
Thus, considering CMB as a composition of signals, we showed that the random component is a minor perturbation of mostly regular signal. The model-independent character of this result comes from the universality of the Kolmogorov theorem that we used in analyzing real datasets, the WMAP’s 7-year CMB maps. We solved the inverse problem by numerical methods and recovered the mutual fractions of random and regular signals which would lead to the empirical Kolmogorov’s distribution.
That the CMB sky is a weakly random one and the derived 0.2 fraction of the random signal in CMB by their intrinsic statistical content may be compared with other scales of CMB, the 2.7 K temperature of the Planckian spectrum, and the 10-5 amplitude of the quadrupole anisotropy, indicating the hot equilibrium history of the Universe and the isotropy of the Universe, respectively. If the Planckian spectrum and the anisotropy amplitude do reflect and do scale certain correlations in CMB signal, the obtained fraction scales the correlations in the cosmological Gaussian perturbations.
What insights will the new scaling open to the early Universe?
Acknowledgments
We dedicate this paper to the memory of Vladimir Arnold (1937–2010), recalling the memorable discussions (V.G., A.A.K.) with him.
References
- Arnold, V. I. 2008a, Nonlinearity, 21, T109 [NASA ADS] [CrossRef] [Google Scholar]
- Arnold, V. I. 2008b, ICTP/2008/001, Trieste [Google Scholar]
- Arnold, V. I. 2008c, Uspekhi Mat. Nauk, 63, 5 [CrossRef] [Google Scholar]
- Arnold, V. I. 2009a, Trans. Moscow Math. Soc., 70, 31 [CrossRef] [Google Scholar]
- Arnold, V. I. 2009b, Funct. Anal. Other Math., 2, 139 [Google Scholar]
- de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2000, Nature, 404, 955 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ghahramanyan, T., Mirzoyan, S., Poghosian, E., & Yegorian, G. 2009, Mod. Phys. Lett., A24, 1187 [Google Scholar]
- Gorski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, V.G., de Bernardis, P., et al. 2005, Mod. Phys. Lett., A20, 893 [Google Scholar]
- Gurzadyan, V. G. & Kocharyan, A. A. 2008, A&A, 492, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G. & Kocharyan, A. A. 2009, A&A, 493, L61; Europhys. Lett., 86, 29002 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Starobinsky, A. A., et al. 2008, A&A, 490, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Allahverdyan, A. E., et al. 2009, A&A, 497, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Kashin, A. L., Khachatryan, H. G., et al. 2010, Europhys. Lett., 91, 19001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jarosik, N., Bennett, C. L., et al. 2010, ApJS, submitted [arXiv:1001.4744] [Google Scholar]
- Kolmogorov, A. N. 1933, Giorn. Ist. Ital. Attuari, 4, 83 [Google Scholar]
- Mather, J. C., Cheng, E. S., Cottingham, D. A., et al. 1994, ApJ, 420, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Mirzoyan, S., & Poghosian, E. 2009, Mod. Phys. Lett., A24, 3091 [NASA ADS] [Google Scholar]
- Neumann von, J. 1951, Monte Carlo Methods, AMS, 36, National Bureau of Standards [Google Scholar]
- Smoot, G. F., Bennett, C. L., Kogut, A., et al. 1992, ApJ, 396, L1 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The Kolmogorov map of cosmic microwave background radiation, i.e. the distribution of Kolmogorov’s function Φ over the sky for the Wilkinson Microwave Anisotropy Probe’s 7-year W-band temperature dataset. |
| In the text | |
 |
Fig. 2 The empirical frequency distribution of Kolmogorov’s function Φ in the CMB map with the extracted Galactic disk region |b| < 30° and the generated signal zn for the fraction of the random sequence α = 0.19. |
| In the text | |
 |
Fig. 3 The confidence level in χ2 vs. the parameter α, i.e. the fraction of the random component, for the WMAP7 CMB maps with extracted Galactic disk regions: |b| < 20°,30°,40°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


