| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A111 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015556 | |
| Published online | 06 December 2010 | |
Achromatic late-time variability in thermonuclear X-ray bursts
An accretion disk disrupted by a nova-like shell?
1
SRON Netherlands Institute for Space Research,
Sorbonnelaan 2,
3584 CA
Utrecht,
The Netherlands
e-mail: jeanz@sron.nl
2
Center for Stellar and Planetary Astrophysics & School of
Physics, Monash University, VIC
3800, Australia
3
Center for Relativistic Astrophysics, School of Physics, Georgia
Institute of Technology, Atlanta, GA
30332,
USA
Received: 10 August 2010
Accepted: 5 October 2010
An unusual Eddington-limited thermonuclear X-ray burst was detected from the accreting neutron star in 2S 0918-549 with the Rossi X-ray Timing Explorer. The burst commenced with a brief (40 ms) precursor and maintained near-Eddington fluxes during the initial 77 s. These characteristics are indicative of a nova-like expulsion of a shell from the neutron star surface. Starting 122 s into the burst, the burst shows strong (87 ± 1% peak-to-peak amplitude) achromatic fluctuations for 60 s. We speculate that the fluctuations are caused by Thompson scattering by fully-ionized inhomogeneities in a resettling accretion disk that was disrupted by the effects of super-Eddington fluxes. An expanding shell may be the necessary prerequisite for the fluctuations.
Key words: accretion, accretion disks / X-rays: binaries / X-rays: bursts / X-rays: individuals: 2S 0918-549
© ESO, 2010
1. Introduction
Close to one hundred accreting low-magnetic-field neutron stars (NSs) in our galaxy are known to exhibit X-ray bursts from time to time1 (e.g., Cornelisse et al. 2003; Galloway et al. 2008). These bursts, lasting roughly 1 min and with a kT ≈ 1 keV thermal spectrum, originate in thermonuclear shell flashes of hydrogen and helium accreted in the top ~108 g cm-2 (or ~1 m) of the NS (Woosley & Taam 1976; Maraschi & Cavaliere 1977; Lamb & Lamb 1978). The burst recurrence time depends on the rate of fuel supply, in other words the mass accretion rate, and the fuel mixture (e.g., Fujimoto et al. 1981; Lewin et al. 1993; Bildsten 1998; Strohmayer & Bildsten 2006). For 96% of all 3387 cases studied by Keek et al. (2010), the recurrence time ranges from 1 hr upward. A few percent of all X-ray bursts are longer than usual (e.g., Keek & in ’t Zand 2008), because of larger ignition depths. These events include “intermediate duration” bursts (in ’t Zand et al. 2005; Cumming et al. 2006; Falanga et al. 2008), with durations of the order of half an hour, and superbursts (Cornelisse et al. 2000; Cumming & Bildsten 2001; Strohmayer & Brown 2002), with durations of the order of 1 d. These durations are thought to be due to thick (~1010 g cm-2) helium piles in low-Ṁ systems and deep (~1012 g cm-2) ignition of carbon, respectively.
Helium burning through the 3α process is faster than hydrogen burning. Therefore, if the fuel consists predominantly of helium, the energy release is more likely to give rise to super-Eddington fluxes. The resulting radiation pressure will expand the photosphere which is easily measurable through a combination of spectral cooling and increasing emission areas, combined with a more or less constant bolometric flux. Photospheric radius-expansion (PRE) bursts comprise about 20% of all bursts (Galloway et al. 2008). Most intermediate-duration bursts, if not all, are of the PRE kind.
The prototype of the intermediate duration burst is from the low-mass X-ray binary 2S 0918-549 (in ’t Zand et al. 2005). This binary is thought to be ultracompact in nature with an orbital period of 1 h or less, a hydrogen-deficient donor star to the NS and a distance of 5.4 kpc (Nelemans et al. 2004; in ’t Zand et al. 2007). The ultracompact nature was recently supported by the tentative measurement of the orbital period of 17.4 min (Zhong & Wang 2010). The burst was detected with the BeppoSAX Wide Field Cameras and lasted approximately 40 min. Here we report a detection of a similar burst from the same system, but this time with the much more sensitive Proportional Counter Array (PCA) on the Rossi X-ray Timing Explorer (RXTE). We identify a new type of X-ray variability in the late stages of the burst decay, which we refer to as achromatic late-time variability. We describe the properties of this variability and speculate on its origin.
2. Observations
Until May 2010, 2S 0918-549 was observed for 520 ks with the PCA (Jahoda et al. 2006), an instrument consisting of five co-aligned non-imaging proportional counter units (PCUs) that combine to an effective area of 6500 cm2 at 6 keV, have a bandpass of 2 to 60 keV with a typical spectral resolution of 20% and are collimated to a field of view of 2° × 2° (full-width at zero response). No other X-ray sources are known within the field of view around 2S 0918-549. Five X-ray bursts were detected, two of which have an uncertain thermonuclear origin (Galloway et al. 2008). The first four occurred in 2000–2004. On 2008 February 8, the PCA detected the fifth X-ray burst when two PCUs were active, numbers 0 and 2. The relevant RXTE observation identification is 93416-01-05-00. The decay of the fifth burst is seven times longer and 20% brighter (in photon count rate per PCU) than the next longest/brightest first burst (Jonker et al. 2001).
3. Analysis
3.1. Lightcurves
 |
Fig. 1 PCA lightcurves of long burst from 2S 0918-549 in two bandpasses and over the two active PCUs (top two panels) and the hardness ratio between both (third panel). The time resolution is 0.1 s for times earlier than 1 s, and 1.0 s for later times. The inset in the first panel shows the full-bandpass lightcurve for the first 60 ms at a time resolution of 1 ms with a rate in units of 104 c s-1. |
 |
Fig. 2 Top: full bandpass PCA lightcurve of a part of the burst that exhibits fluctuations, at 1 s resolution. The dashed line shows the extrapolation of an exponential function fitted to data beyond 190 s. The e-folding decay time fitted is 124.8 ± 0.8 s. The inset zooms in on the chirp. Two PCUs were active. Bottom: Fourier power spectrum of same lightcurve, but at 0.5 ms resolution. |
Figure 1 presents the lightcurves of the fifth burst in two bandpasses and the (hardness) ratio of both. Many aspects of the burst are similar to what has been observed before in this and other sources. The rise of the burst is very fast. In fact, a precursor can be distinguished that merely lasts 0.04 s. This duration is similar to that of the record holder (the precursor to a burst from 4U 0614+09; Kuulkers et al. 2009). The start of the main event is 1.2 s after that of the precursor. The precursor signifies that superexpansion happens in this burst, which is presumably the result of an optically thick shell being expelled by strong radiative driving (in ’t Zand & Weinberg 2010). The time scales are identical to the record burst from 4U 0614+09. The hardness peaks 77 s after burst onset. This identifies the so-called “touch down” point (see spectroscopic analysis below). It coincides with a local minimum (30% below the trend) in the photon count rate for energies below 4 keV. Such a decrease is hardly seen above 4 keV.
One aspect about this burst is very unusual and is the focus of the present paper. At 122 s, a strong variability starts that lasts 66 s and has a ~87% peak-to-peak amplitude. Interestingly, the hardness ratio is unaffected: there are no hardness fluctuations corresponding to the intensity fluctuations. After this phase, the burst decays in an orderly fashion until the end of the observation at 313 s, when the flux is approximately 10% of the peak value. The exponential decay times during this orderly phase are 149.3 ± 3.1 and 113.4 ± 1.2 s for the low (i.e., below 4 keV) and high-energy (above 4 keV) lightcurves, respectively.
Figure 2 shows a detailed lightcurve of the variable phase and a Fourier power spectrum of the same data. A number of features to note here are:
-
the typical time scale is 1 s. There is no variabilitybelow 0.2 s; the Fourier power density above5 Hz is consistent with statistical (white) noise withan upper limit on the fractional rms of about 1.2% atthe frequency resolution applied in Fig. 2;
-
a cross-correlation analysis between the low (<4 keV) and high energy (>4 keV) lightcurves shows no time lags in excess of 0.01 s;
-
no burst oscillations were detected in any time segment, with 3σ upper limits on the fractional rms amplitude (cf., Strohmayer & Bildsten 2006) of 3.9% in 4 s time segments and 6.9% in 1 s segments;
-
most dip ingresses are shorter than a few tenths of a second. Egresses are almost always longer;
-
dip durations range from 0.2 to 9 s. Dips tend to become longer at later times;
-
fluctuations upward are limited to a factor of 1.6 with respect to the general decay trend (dashed line in Fig. 2). Fluctuations downward are as deep as a factor of 3. The peak-to-peak amplitude for the whole period of fluctuations is 87 ± 1%;
-
all upward fluctuations are left and right accompanied by downward fluctuations, most clearly for the features at 124 and 134 s. The converse does not apply;
-
between 138 and 140 s, 4 dips at progressively shorter intervals are seen, giving the appearance of a chirp.
3.2. Spectra
 |
Fig. 3 Time-resolved spectroscopy of the burst from 2S 0918-549. The top panel shows the full bandpass lightcurve of the xenon layers, the second panel the bolometric flux (early values suffer from statistical errors between 10 and 20%), the third panel the blackbody temperature in terms of kTeff, the fourth panel the blackbody radius for a distance of 5.4 kpc, and the bottom panel the reduced χ2 for the fits per time bin. |
We employed event mode data that have a time resolution of 125 μs and bin the photon energy in 64 channels. Data from all Xenon detector layers and the two active PCUs were combined. Spectra were extracted in time bins that are sufficiently small to follow the variations in hardness (see Fig. 1), with bin sizes measuring 2 ms (until 6 ms after precursor onset; see Fig. 3), 12 ms (until 1 s), 0.1 s (until 2 s), 1 s (until 200 s) and 5 s (beyond 200 s). The particle and cosmic background were modeled per time bin as prescribed by pcabackest with the minimum allowed sample time of 16 s. A response matrix was calculated through pcarmf version 11.7. Exposure times were corrected for detector dead time following the RXTE Cook Book2. Because the time resolution for this correction is limited to 0.125 s, interpolation was necessary for the precursor. The spectra were analyzed between 3 and 30 keV with XSPEC version 12.5.0 (Arnaud 1996). A systematic error of 0.5% was assumed per photon energy channel. All spectra were corrected for the modeled particle and cosmic background.
A pre-burst spectrum of 2S 0918-549 was acquired from 672 s of standard-2 data that are available up to 100 s before the burst onset. The shape of the pre-burst spectrum is within 3 to 30 keV consistent with the broadband 0.1–200 keV spectrum that was measured by in ’t Zand et al. (2005). The extrapolated 0.1–200 keV unabsorbed flux is 50% larger at 5.5 × 10-10 erg cm-2 s-1 than the absorbed 3 to 30 keV flux. This is 0.5% of the bolometric peak flux of the burst (see below). For a canonical 1.4 M⊙/R = 10 km NS, this translates to a mass accretion rate of 1.0 × 1016 g s-1. Allowance was made for the accretion radiation in the spectral analysis of the burst data by including a fixed pre-burst model, thus indirectly subtracting the background. This was not done for the precursor data since it is expected that the accretion flow is significantly disturbed (i.e., the flux during superexpansion is lower than before the precursor). Although the accretion radiation was accounted for, it was found that neglecting this did not make a significant difference for any of the spectral results. The accretion flux is always much lower than the burst flux for data with a meaningful statistical significance.
The time-resolved burst spectra were modeled by simple blackbody radiation with interstellar absorption. The absorbing column was fixed at NH = 3 × 1021 cm-2 (in ’t Zand et al. 2005), which is hardly detectable within the bandpass of the PCA. The results are shown in Fig. 3, in both logarithmic (left panel; to focus on the early part of the burst) and linear scales (right panel; to focus on the part where the fluctuations occur). The bolometric fluence over the measurements of the burst is (1.58 ± 0.11) × 10-5 erg cm-2. Extrapolating the decay beyond the end of the observation (through an exponential function with an e-folding decay time of 120 s) predicts that 20% of fluence is likely to have been missed in the observation. For 5.4 kpc, this translates to a total radiative energy output of about 7 × 1040 erg, which is consistent with an ignition depth of 4 × 109 g cm-2 if the pre-burst layer is pure helium (see Fig. 8 in in ’t Zand et al. 2005).
The precursor shows a rapid photospheric expansion driven by radiation pressure because the burst emission is super-Eddington. Within 30 ms, the photosphere expands to about 103 km, with an average velocity of approximately 0.1c. We do not believe this is an optical depth effect, because prior to the burst no gas of sufficient density is expected up to that height around the NS. It would fall onto the NS within a dynamical time scale of 1 ms. The measured average velocity is about 20% of the escape velocity from a canonical NS, so this shows that the photosphere is strongly driven by radiation for as long as it is visibly expanding. Otherwise it would return to the NS already within a height of less than 1 km. The photosphere is probably on a shell of thickness 106−7 g cm-2 (cf., in ’t Zand & Weinberg 2010). At the end of the precursor the shell radiation moves out of the PCA bandpass so that it becomes undetectable. After 1.2 s the burst emission reappears. Probably the shell at that time diffused so much that it became optically thin and uncovered the underlying radiating NS. The radiation is still super-Eddington with high temperatures (>2 keV), moderately increased levels of blackbody radius and a more or less constant bolometric flux. After 70 s the flux starts to decrease, signifying the end of the Eddington-limited phase. At that time the spectrum shows a hardening lasting approximately 40 s, which may be caused by Comptonization of the thermal photons against a hot receding atmosphere (London et al. 1986; Madej et al. 2004). The simultaneous radius measurements are most probably biased by this systematic effect and do not represent true variations of the photospheric size. This “touch-down” phase is often seen in Eddington-limited bursts (Damen et al. 1990; Galloway et al. 2008; Steiner et al. 2010). Subsequently ordinary NS cooling sets in, until the fluctuations start at 122 s. As for the hardness ratio in Fig. 1, the evolution of the blackbody temperature is largely unaffected by the fluctuations. The root mean square of the temperature variations with respect to a fitted exponential function is 1.0 ± 1.6% before the fluctuations (i.e., between 80 and 120 s) and 2.3 ± 2.3% during (i.e., between 120 and 190 s). We conclude that the fluctuations are achromatic.
4. Achromatic late-time variability in other bursts
Achromatic late-time variability was also seen in the previous long burst detected from 2S 0918-549 with BeppoSAX-WFC (in ’t Zand et al. 2005, referred to in Sect. 1). Indeed, that looks very similar, but with worse statistical quality (the effective area of BeppoSAX-WFC is 45 times smaller than of the PCA). The fluctuations started 135 s after burst onset, lasted 50 s and the amplitudes reach factors of up to 3. Additionally, a very long dip was detected, starting 200 s after burst onset. The flux decreased by a factor of 4 for 70 s. The burst decay is followed during the dip. We could not detect a spectral change for this dip either.
The WFC burst was probably also a superexpansion burst, because it shows a rapid decline in the blackbody radius at the onset. A definitive identification of superexpansion is not possible because no precursor is detected, but this is not unexpected because there would be too few photons in the precursor to be able to detect it with the moderately sensitive WFC. The WFC burst has within 20% the same near-Eddington duration and decay time as the PCA burst. These similarities are unlikely to be a coincidence and point to the burst as the initiator of the variability.
Achromatic variability was also detected in two other long superexpansion bursts, from SLX 1735-269 (Molkov et al. 2005) and 4U 1820-30 (Strohmayer & Brown 2002; Ballantyne & Strohmayer 2004; in ’t Zand & Weinberg 2010). In the former, detected with JEM-X on INTEGRAL, the fluctuations lasted between 700 and 1300 s after burst onset, with a touch-down at 400 s. The burst from 4U 1820-30 was a superburst detected with the PCA. Fluctuations in that burst have varying time scales, but those at ~10 s time scale are also energy-independent (see Fig. 4). The fluctuations started 3365 s after burst onset and lasted until 7200 s, while the touch-down for that burst is at 1100 s.
Finally, achromatic variability was seen in a burst from M15 X-2 (van Paradijs et al. 1990) between 127 and 156 s after burst onset, with a touch down time of 94 s. They were attributed to dipping activity, although it was not understood why the non-burst emission failed to exhibit dips.
Achromatic variability was not seen in shorter bursts from 2S 0918-549 that are Eddington-limited but lack superexpansion (Jonker et al. 2001; in ’t Zand et al. 2005).
Fluctuations downward were seen in a burst from A 1246-58 (in ’t Zand et al. 2008). A number of intermediate duration bursts, which (are likely to) have a precursor, did not show fluctuations (e.g., in ’t Zand et al. 2007; in ’t Zand & Weinberg 2010).
In conclusion, based on the aforementioned six fluctuating bursts, the necessary conditions for fluctuations seem to be the presence of superexpansion (i.e., the expulsion of a shell), a burst duration in excess of 120 s (although that is susceptible to selection effects), and the termination of the Eddington-limited phase. Because some long and probably superexpansion bursts lack fluctuations, another parameter may be at work, perhaps the inclination angle. Since none of the above bursters show dipping or eclipsing behavior in the persistent emission, the inclination angle must be smaller than i = 70° (White et al. 1995). It seems plausible that in bursters that fail to show fluctuations in superexpansion bursts, the inclination angle is smaller again, so that a disrupted disk does not extend into the line of sight.
5. Discussion
 |
Fig. 4 PCA lightcurve of the part of the superburst from 4U 1820-30 that shows achromatic variability. For panel explanation, see Fig. 1. The time resolution is 1.0 s throughout. |
We presented an analysis of a type of X-ray intensity variation seen in some long intense X-ray bursts with superexpansion. These variations have not been reported previously in such detail; here we discuss possible origins.
5.1. Origin of fluctuations
The fluctuations are achromatic and go factors above and below the decay trend of the burst. The latter rules out a thermonuclear origin, because then the flux would not undercut the decaying trend of the initial flash. An example of thermonuclear variability is millihertz oscillatory behavior in the non-burst emission of some bursters (4U 1608-52 and 4U 1636-536; Revnivtsev et al. 2001; Heger et al. 2007; Altamirano et al. 2008). The characteristics of these oscillations are different from the achromatic variability reported here, both in time scales and spectral behavior.
The fluctuations downward point to something occasionally and partly obscuring the line of sight to the NS. Because the NS is small and the dips are ≈ 70% deep, the obscuration appears to be due to clouds of optical depth τ ≈ 1. That the fluctuations are achromatic suggests that the cloud plasma is in thermal balance with the radiation field, so that the scattering of the photons is elastic (i.e., Thompson scattering). The column density of the electrons in the clouds for a uniform density would be Ne = τ/σT = 1.7 × 1024 cm-2 (with σT the Thompson cross section). Because the clouds need to be larger than the L = 20 km size of the NS, the electron density is inferred to be ne < Ne/L ≈ 1018 cm-3.
The picture arises that hot plasma clouds move around the NS and Thompson scatter the burst photons. If a cloud is in front of the NS, burst emission is scattered out of the line of sight. If it is at the other side of the NS, but visible to the observer, it is scattered backward into the line of sight. Because we see basically unaffected burst emission between upward and downward fluctuations (for instance at 125–129 s, 134–136 s, 162–166 s), only a few clouds would be responsible for the fluctuations and there would hardly be any sideways scattering. The latter would be consistent with Thompson scattering, since that is predominantly in the forward and backward direction. Still, the flux level between fluctuations appears to be somewhat increased. This may be the result of some sideways scattering or to backward scattering of clouds with smaller angular sizes.
The fluctuations downward are reminiscent of dips as seen in the out-of-burst radiation of low-mass X-ray binaries with inclination angles higher than about 70°. Those are thought to be caused by splashes off the accretion disk that result from the impact of the mass stream from the donor star on the disk (Parmar et al. 1986; Armitage & Livio 1998). The splashes usually populate a small range of orbital phases and return to the line of sight periodically, obscuring the inner (X-ray radiating) disk, resulting in dips in the lightcurve with typical durations of a few tens of seconds. The dip spectrum can be modeled by a combination of energy-dependent absorption by cold matter and energy-independent absorption by warm photoionized matter with a photo-ionization parameter of ξ = L/ner2 ~ 102.5−3 erg s-1 cm (Boirin et al. 2005; Díaz Trigo et al. 2006). The dips reported here are not connected to certain orbital phases, but to certain phases in long bursts. A simple estimate for the probability that the two long bursts occur at the same orbital phase by chance is 1 min/17.4 min, which is only 6%. Also, classical dips in the non-bursting emission would also have to occur, but have never been reported for 2S 0918-549. Still, our dips are energy-independent like part of the classical dips. For log ξ ≳ 3, L ≈ 2 × 1038 erg s-1 and ne ≲ 1018 cm-3, the distance of the scattering medium to the NS would be of the order of r ≲ 104 km.
The first down-up-down fluctuation at 122 s appears to be the effect of a single cloud that first is in front of the NS, 1 s later behind, then again in front and subsequently gone, possibly accreted. Almost the same happens at 130 s. This suggests a 2 s Keplerian period, which would translate into a typical cloud distance from the NS of 3 × 103 km, which is approximately consistent with the photo-ionizing argument above. The chirp at 139 s could be explained similarly, with a progressively shorter orbital period. Later dips appear to become progressively longer, but peaks stay as long and disappear. In the other superexpansion burst detected from 2S 0918-549 by the WFC, one dip lasted as long as 70 s. An explanation may be that the clouds extend over larger azimuthal ranges as time progresses and obscure backscattering. Either the clouds become larger in linear size, or they remain as large, but come closer to the NS.
Warping of accretion disks may be strengthened by irradiation from a central source. Previous studies (Petterson 1977; Pringle 1996, 1997; Wijers & Pringle 1999; Ogilvie & Dubus 2001) assumed the central source to be the inner accretion disk, but a bursting neutron star would seem viable as well. However, the time scales of the radiation are totally different (weeks versus minutes), and it is questionable whether burst radiation will be as effective in warping the disk. Furthermore, radiative warping would occur irrespective of the presence of superexpansion, in contrast to what we observe.
5.2. Accretion disk disruption
Where would the cloud structure come from? An obvious possibility is that the clouds arise from material in the inner accretion disk. Theoretical investigations have shown that it is possible for Eddington-limited X-ray bursts to disrupt the inner accretion disk. Ballantyne & Everett (2005) treated this issue in an attempt to explain spectroscopic measurements of the 4U 1820-30 superburst (not the aforementioned fluctuations); earlier discussions may be found in Fukue (1983), Walker & Meszaros (1989), Walker (1992) and Fukue & Umemura (1995). Five mechanisms are discussed by Ballantyne & Everett (2005), four of which are concerned with the interaction between the radiation from the NS with the accretion disk: radiatively and thermally driven winds, increased inflows as a result of radiation drag (i.e., the Poynting-Robertson effect), and X-ray heating of the disk. It is clear that thermally driven winds are ineffective because of the large gravitation field near the NS. Radiation pressure is more effective, but it is not obvious that it can sweep the inner accretion because the optical depth of the disk is large along the radial travel direction of the burst radiation. Radiation drag is probably only important in the innermost region of the accretion disk (cf., Miller & Lamb 1996), at radii smaller than 20 Rg ≈ 40 km with Rg = GM/c2. The final radiative disruption mechanism, X-ray heating of the disk surface, may change the disk structure for example through puffing up the surface on a dynamical time scale and settling it on viscous time scales. A non-radiative fifth mechanism is concerned with the mechanical interaction between the radiatively driven outflow and the accretion disk. This effect was dismissed by Ballantyne & Everett (2005) for a radiation-driven wind because that carries insufficient kinetic energy to overcome the potential energy of the wind. However, the circumstances may be different for superexpansion bursts where the shell carries much more density than the previously considered wind. In Sects. 5.2.1 and 5.2.2 we concentrate on the two most likely mechanisms for disrupting the disk.
5.2.1. Disruption by shell
The geometrically thin but optically thick shell expands at a velocity of the order of 10% of the speed of light. The column thickness of the shell at launch is at maximum ~1% of the ignition depth or y ≲ 106−7 g cm-2 and diffuses as R-2. The radial profile of the density of the accretion disk at mid plane, for a gas-supported disk (as applicable for an accretion rate of ~1% of Eddington) with electron-scattering opacity (Shakura & Sunyaev 1973; Svensson & Zdziarski 1994; Ballantyne & Everett 2005) and assuming a Gaussian vertical density profile, is given by 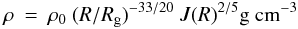 (1)with Rg = 2M1.4 km (M1.4 is the NS mass in units of 1.4 M⊙),
(1)with Rg = 2M1.4 km (M1.4 is the NS mass in units of 1.4 M⊙), 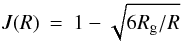 (2)and
(2)and 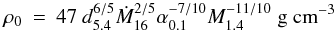 (3)(d5.4 is the distance in units of 5.4 kpc, Ṁ16 the accretion rate in units of 1016 g s-1 and α0.1 the disk viscosity parameter in units of 0.1). The mean molecular weight is assumed to be μ = 1.3. For α = 0.1, Ṁ16 between 1 and 10 (for radiation efficiencies of η = 1 and 0.1, respectively) and y = 106 g cm-2, the mass column swept up by the diffusing shell will have reached the shell’s own diminished column mass at 50 to 150 km above the NS surface. For y = 107 g cm-2 this range becomes 110–440 km. We assume here that the disk is magnetically truncated at
(3)(d5.4 is the distance in units of 5.4 kpc, Ṁ16 the accretion rate in units of 1016 g s-1 and α0.1 the disk viscosity parameter in units of 0.1). The mean molecular weight is assumed to be μ = 1.3. For α = 0.1, Ṁ16 between 1 and 10 (for radiation efficiencies of η = 1 and 0.1, respectively) and y = 106 g cm-2, the mass column swept up by the diffusing shell will have reached the shell’s own diminished column mass at 50 to 150 km above the NS surface. For y = 107 g cm-2 this range becomes 110–440 km. We assume here that the disk is magnetically truncated at 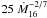 km from the NS (for a canonical NS with B = 108 G; this does not have to be accompanied by pulsations, see Frank et al. 2002). Away from the mid plane the disk density is lower. At 3–4 scale heights above or below the disk (this is approximately equivalent to the τ = 1 level), the shell may be able to disrupt the disk up to a distance of ~3000 km. Thus, the shell appears able to blast away a small radial part of the disk, out to perhaps a few tens of NS radii, and ablate the surface of the disk up to distances of 103−4 km. Note that with a suggested orbital period of 17.4 min (Zhong & Wang 2010), the accretion disk has a size of 1.7 × 105 km.
km from the NS (for a canonical NS with B = 108 G; this does not have to be accompanied by pulsations, see Frank et al. 2002). Away from the mid plane the disk density is lower. At 3–4 scale heights above or below the disk (this is approximately equivalent to the τ = 1 level), the shell may be able to disrupt the disk up to a distance of ~3000 km. Thus, the shell appears able to blast away a small radial part of the disk, out to perhaps a few tens of NS radii, and ablate the surface of the disk up to distances of 103−4 km. Note that with a suggested orbital period of 17.4 min (Zhong & Wang 2010), the accretion disk has a size of 1.7 × 105 km.
It is difficult to determine whether the energy and momentum are conserved in the the disk/shell interaction. The apparent expansion velocity of the shell is only ~20% of the escape velocity at the NS surface, which allows to bridge only 4% of the potential energy required to escape, while the shell is observed to bridge 99% (i.e., the maximum photospheric radius is 103 km). Obviously, the transformation of radiation to kinetic energy is a dominant term in the energy balance. An assessment of that is beyond the scope of the present observational paper. Conservation of momentum is roughly upheld. The ram pressure of the shell at 100 km is ρv2 = y(R/RNS)2(0.1c)2/D ≈ 1017 dyne cm-2 with D = 1 m the thickness of the shell or perhaps a few orders of magnitude smaller if the shell thickness grows with the shell radius. The density of the disk at 100 km is of the order of 10-3 g cm-3 (Eq. (1)). From Ṁ = 2πRHρv this results in a radial inward velocity of ≈ 20 km s-1. The ram pressure of the disk3 then is ≈ 107 dyne cm-2 at 100 km. However, the gas pressure of the disk is larger and will take over counteracting the shell. For an ideal gas it is ~1015 dyne cm-2 for a disk temperature of 107 K. This order-of-magnitude calculation shows that the shell may have enough momentum to sweep the inner 100 km of the accretion disk.
5.2.2. Disruption by radiation pressure
In the previous section we showed that in the first 10-1 s the shell may disrupt the accretion disk over the inner 103−4 km, possibly even clearing it completely over the inner 102 km. Thus, an environment is created that is more susceptible to the near-Eddington fluxes that ensue for 70 s. Ballantyne & Everett (2005) modeled the effects of super-Eddington fluxes on the accretion disk without the preceding shell disruption, but with otherwise similar circumstances (same burst flux that stays near-Eddington for at least 70 s; same type of binary orbit). They find that the gas in the surface layers of the disk with ne = 1017 cm-3 is accelerated radially to ≈ 0.1 c within at most ≈ 30 s. Thus, the radiation is likely to clear the parts of the disk that are already disrupted by the shell even more or, at least, prevent it from falling back. The effect may even be greater, because the shell will likely puff up the disk, increasing the solid angle of accretion disk material as seen from the NS so that a larger portion of the burst luminosity will be involved in the radiative disruption.
5.3. Accretion disk resettlement
If the disk is disrupted, it is plausible that it deviates considerably from cylindrical symmetry. The push by the shell and its lateral expansion will likely puff up the disk, as will the radiation pressure owing to turbulence. If the effect of super-Eddington radiation subsides, the accretion disk is expected to return to the immediate surroundings of the NS, because the feeding of the disk by the donor star continues. We speculate that it is this return of the disk that is responsible for the achromatic fluctuations.
How can we then explain the delay time of 45 s between the end of the Eddington-limited phase and the onset of achromatic variability? The free-fall time over 103 km of 0.5 s is much shorter, so it involves something else than a straightforward fall back of disk material. Could it be the viscous dissipation time scale of the disk? This time scale is for a gas-pressure dominated accretion disk given by (Svensson & Zdziarski 1994; Ballantyne & Everett 2005) 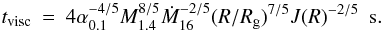 (4)At 100 km, tvisc ranges between 60 and 960 s. This is close to the measured delay time of 45 s. However, not so for the 2000 s delay time for the superburst from 4U 1820-30. Ṁ16 is 11 times larger and tvisc 2.5 times smaller, while the measured value is 50 times higher.
(4)At 100 km, tvisc ranges between 60 and 960 s. This is close to the measured delay time of 45 s. However, not so for the 2000 s delay time for the superburst from 4U 1820-30. Ṁ16 is 11 times larger and tvisc 2.5 times smaller, while the measured value is 50 times higher.
Instead of the time it takes the disk to respond to changes in the environment, the onset of the fluctuations may be determined by the level of irradiation (see Sect. 5.2.2). The radiation pressure is equal to L/4πR2c. The disk will be disrupted as long as L > 4πR2cPram with Pram the (uncertain) ram pressure of the in-flowing accretion disk. For L = 2 × 1038 erg s-1 and R = 100 km, Pram would have to be 5 × 1013 dyne cm-2. The uncertainties are large in the disk parameters (Ṁ, T, R, Pram) and the physics employed may be oversimplified. Therefore, it is difficult to judge the validity of this effect.
The duration of the achromatic variability, 66 s, may be related to the radial extent over which the clouds reside when they start to fall back. The longer the near-Eddington phase lasts, the farther away disk material is blown away by the radiation pressure. Indeed, there is a relation between the duration of the variability and that of near-Eddington fluxes of the cases discussed in Sect. 4 (approximately linear).
6. Summary and outlook
We report achromatic late-time variability in thermonuclear X-ray bursts from 2S 0918-549 and a few other low-mass X-ray binaries, and suggest it may be explained by the settlement of the accretion disk near the NS that is disrupted by the combination of a shell expulsion and a near-Eddington flux. Order-of-magnitude calculations of the effect of the various disruption mechanisms suggest that this explanation is plausible, although there is a need for follow-up by numerical time-dependent calculations of the dynamical response of the accretion disk to the expanding shell and wind, the near-Eddington radiation and the subsequent settling disk. We note that this numerical investigation may also be interesting for the study of less energetic classical novae on massive white dwarfs where the shell is expected to be less massive so that the disk may survive the explosion (Sokoloski et al. 2008). Apart from these theoretical investigations, detecting more bursts with this variability with a variety of burst durations would be constraining, particularly from X-ray binaries with known orbital periods. An observation that would reject our hypothesis would be achromatic variability in bursts without superexpansion with a device that is sensitive enough to detect 10 ms precursors. Finally, we note that our findings imply a warning: not all features in X-ray burst lightcurves originate on the neutron star (see also Shaposhnikov et al. 2003) and in some cases these additional effects can be significant.
For a list, see http://www.sron.nl/~jeanz/bursterlist.html
Note that the higher disk ram pressures calculated in Frank et al. (2002) are for azimuthal motion instead of radial, as is applicable for balancing magnetic pressure.
Acknowledgments
We sincerely thank Jean-Pierre Lasota, Laurens Keek, Dimitrios Psaltis, Jennifer Sokoloski, and Nevin Weinberg for useful discussions.
References
- Altamirano, D., van der Klis, M., Wijnands, R., & Cumming, A. 2008, ApJ, 673, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J., & Livio, M. 1998, ApJ, 493, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Ballantyne, D. R., & Everett, J. E. 2005, ApJ, 626, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R., & Strohmayer, T. E. 2004, ApJ, 602, 105 [Google Scholar]
- Bildsten, L. 1998, in The many faces of neutron stars, ed. A. Alpar, L. Buccheri, & J. van Paradijs, NATO ASI (Dordrecht: Kluwer), 419 [Google Scholar]
- Boirin, L., Méndez, M., Díaz Trigo, M., Parmar, A. N., & Kaastra, J. S. 2005, A&A, 436, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornelisse, R., Heise, J., Kuulkers, E., Verbunt, F., & in ’t Zand, J. J. M. 2000, A&A, 357, L21 [NASA ADS] [Google Scholar]
- Cornelisse, R., in ’t Zand, J. J. M., Verbunt, F., et al. 2003, A&A, 405, 1033 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cumming, A., & Bildsten, L. 2001, ApJ, 559, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Macbeth, J., Zand, J. J. M. I., & Page, D. 2006, ApJ, 646, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Damen, E., Magnier, E., Lewin, W. H. G., et al. 1990, A&A, 237, 103 [NASA ADS] [Google Scholar]
- Díaz Trigo, M., Parmar, A. N., Boirin, L., Méndez, M., & Kaastra, J. S. 2006, A&A, 445, 179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falanga, M., Chenevez, J., Cumming, A., et al. 2008, A&A, 484, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: third edition, ed. J. Frank, A.King, & D. J. Raine [Google Scholar]
- Fujimoto, M. Y., Hanawa, T., & Miyaji, S. 1981, ApJ, 247, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Fukue, J. 1983, PASJ, 35, 355 [NASA ADS] [Google Scholar]
- Fukue, J., & Umemura, M. 1995, PASJ, 47, 429 [NASA ADS] [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Cumming, A., & Woosley, S. E. 2007, ApJ, 665, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- in ’t Zand, J. J. M., & Weinberg, N. N. 2010, A&A, 520, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Bassa, C. G., Jonker, P. G., et al. 2008, A&A, 485, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Cornelisse, R., & Méndez, M. 2005, A&A, 440, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- in ’t Zand, J. J. M., Jonker, P. G., & Markwardt, C. B. 2007, A&A, 465, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Jonker, P. G., van der Klis, M., Homan, J., et al. 2001, ApJ, 553, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Keek, L., & in ’t Zand, J. J. M. 2008, in 7th INTEGRAL Workshop – An INTEGRAL View of Compact Objects, Proceedings of Science [Google Scholar]
- Keek, L., Galloway, D. K., in’t Zand, J. J. M., & Heger, A. 2010, ApJ, 718, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Kuulkers, E., in ’t Zand, J. J. M., Atteia, J., et al. 2010, A&A, 514, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, D. Q., & Lamb, F. K. 1978, ApJ, 220, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Lewin, W. H. G., van Paradijs, J., & Taam, R. E. 1993, Space Sci. Rev., 62, 223 [NASA ADS] [CrossRef] [Google Scholar]
- London, R. A., Taam, R. E., & Howard, W. M. 1986, ApJ, 306, 170 [Google Scholar]
- Madej, J., Joss, P. C., & Różańska, A. 2004, ApJ, 602, 904 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Cavaliere, A. 1977, in X-ray Binaries and Compact Objects, 127 [Google Scholar]
- Miller, M. C., & Lamb, F. K. 1996, ApJ, 470, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- Molkov, S., Revnivtsev, M., Lutovinov, A., & Sunyaev, R. 2005, A&A, 434, 1069 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Jonker, P. G., Marsh, T. R., & van der Klis, M. 2004, MNRAS, 348, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ogilvie, G. I., & Dubus, G. 2001, MNRAS, 320, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Parmar, A. N., White, N. E., Giommi, P., & Gottwald, M. 1986, ApJ, 308, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Petterson, J. A. 1977, ApJ, 216, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E. 1996, MNRAS, 281, 357 [NASA ADS] [Google Scholar]
- Pringle, J. E. 1997, MNRAS, 292, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Churazov, E., Gilfanov, M., & Sunyaev, R. 2001, A&A, 372, 138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N., & Sunyaev, R. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shaposhnikov, N., Titarchuk, L., & Haberl, F. 2003, ApJ, 593, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Sokoloski, J. L., Rupen, M. P., & Mioduszewski, A. J. 2008, ApJ, 685, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Strohmayer, T., & Bildsten, L. 2006, New views of thermonuclear bursts (Compact stellar X-ray sources), 113 [Google Scholar]
- Strohmayer, T. E., & Brown, E. F. 2002, ApJ, 566, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Svensson, R., & Zdziarski, A. A. 1994, ApJ, 436, 599 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J., Dotani, T., Tanaka, Y., & Tsuru, T. 1990, PASJ, 42, 633 [NASA ADS] [Google Scholar]
- Walker, M. A. 1992, ApJ, 385, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, M. A., & Meszaros, P. 1989, ApJ, 346, 844 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Nagase, F., & Parmar, A. N. 1995, in X-ray Binaries, ed. W. H. G. Lewin, J. van Paradijs, & E. P. J. van den Heuvel, 1 [Google Scholar]
- Wijers, R. A. M. J., & Pringle, J. E. 1999, MNRAS, 308, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Taam, R. E. 1976, Nature, 263, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Zhong, J., & Wang, Z. 2010, ApJ, submitted [arXiv:1006.3980] [Google Scholar]
All Figures
 |
Fig. 1 PCA lightcurves of long burst from 2S 0918-549 in two bandpasses and over the two active PCUs (top two panels) and the hardness ratio between both (third panel). The time resolution is 0.1 s for times earlier than 1 s, and 1.0 s for later times. The inset in the first panel shows the full-bandpass lightcurve for the first 60 ms at a time resolution of 1 ms with a rate in units of 104 c s-1. |
| In the text | |
 |
Fig. 2 Top: full bandpass PCA lightcurve of a part of the burst that exhibits fluctuations, at 1 s resolution. The dashed line shows the extrapolation of an exponential function fitted to data beyond 190 s. The e-folding decay time fitted is 124.8 ± 0.8 s. The inset zooms in on the chirp. Two PCUs were active. Bottom: Fourier power spectrum of same lightcurve, but at 0.5 ms resolution. |
| In the text | |
 |
Fig. 3 Time-resolved spectroscopy of the burst from 2S 0918-549. The top panel shows the full bandpass lightcurve of the xenon layers, the second panel the bolometric flux (early values suffer from statistical errors between 10 and 20%), the third panel the blackbody temperature in terms of kTeff, the fourth panel the blackbody radius for a distance of 5.4 kpc, and the bottom panel the reduced χ2 for the fits per time bin. |
| In the text | |
 |
Fig. 4 PCA lightcurve of the part of the superburst from 4U 1820-30 that shows achromatic variability. For panel explanation, see Fig. 1. The time resolution is 1.0 s throughout. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


