| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201014544 | |
| Published online | 01 December 2010 | |
Dynamics of braided coronal loops
II. Cascade to multiple small-scale reconnection events
1
Division of MathematicsUniversity of Dundee,
Nethergate,
Dundee,
DD1 4HN,
UK
e-mail: dpontin@maths.dundee.ac.uk
2
Niels Bohr Institute, Blegdamsvej 17, 2100
Copenhagen Ø,
Denmark
Received:
30
March
2010
Accepted:
18
October
2010
Aims. Our aim is to investigate the resistive relaxation of a magnetic loop that contains braided magnetic flux but no net current or helicity. The loop is subject to line-tied boundary conditions. We investigate the dynamical processes that occur during this relaxation, in particular the magnetic reconnection that occurs, and discuss the nature of the final equilibrium.
Methods. The three-dimensional evolution of a braided magnetic field is followed in a series of resistive MHD simulations.
Results. It is found that, following an instability within the loop, a myriad of thin current layers forms, via a cascade-like process. This cascade becomes more developed and continues for a longer period of time for higher magnetic Reynolds number. During the cascade, magnetic flux is reconnected multiple times, with the level of this “multiple reconnection” positively correlated with the magnetic Reynolds number. Eventually the system evolves into a state with no more small-scale current layers. This final state is found to approximate a non-linear force-free field consisting of two flux tubes of oppositely-signed twist embedded in a uniform background field.
Key words: Sun: corona / magnetohydrodynamics (MHD) / magnetic reconnection
© ESO, 2010
1. Introduction
The braiding of magnetic loops in the solar corona, via convective motions at the solar surface, has long been suggested as a potential mechanism for heating the corona. Parker (1972) proposed that in response to arbitrary footpoint motions at the photosphere, the coronal magnetic field will ideally relax towards a force-free equilibrium containing tangential discontinuities, corresponding to current sheets. Therefore, it was argued, as such a singular state is approached during the relaxation, the diffusivity of the plasma must always become important, leading to magnetic reconnection and plasma heating. Since this idea was first proposed, there have been many arguments for and against its validity (e.g., van Ballegooijen 1985; Longcope & Strauss 1994; Ng & Bhattacharjee 1998).
In Parker’s original “topological dissipation” model, an initially uniform magnetic field is taken between two perfectly conducting parallel plates. Then random (smooth) motions are applied on the perfectly conducting plates. A number of attempts have been made to simulate such a scenario numerically, using a variety of numerical approaches. Craig & Sneyd (2005) employed an ideal relaxation scheme which includes a fictitious frictional term in the equation of motion (Craig & Sneyd 1986). They applied various complex deformations at the boundaries of the domain. They found that regardless of the nature or extent of the deformation, no tangential discontinuities developed in the relaxed state, with the current concentrations remaining large-scale in all cases. Mikić et al. (1989) employed a slightly different approach. They began with a uniform field and then sequentially applied large-scale shear flows of random orientation on one boundary (while the field at the other boundary was held fixed). In the time between each boundary shear, they solved the ideal MHD equations (neglecting the pressure and advective terms in the equation of motion), including a large spatially-uniform viscosity in order to relax the magnetic field towards equilibrium. They found, once again, that no discontinuities were formed during any of these relaxation processes. However, progressively smaller scale current structures were found to develop as the number of shear disturbances increased. The implication is therefore that after a sufficient length of time, the scales would reach those appropriate for dissipation in the corona. They found, furthermore, that the current density in the domain increased exponentially in time, which is consistent with the earlier analysis of van Ballegooijen (1985), who predicted thin non-singular current layers rather than tangential discontinuities.
Galsgaard & Nordlund (1996) employed a further different approach to those discussed above, solving the full set of resistive MHD equations without employing any artificial force (such as enhanced viscosity) to inhibit the plasma dynamics. They applied a similar sequence of large-scale shearing motions as Mikić et al. (1989), this time at both driving boundaries. The amplitude and orientation of the shearing were chosen at random (from a normal distribution). The results were similar to those of Mikić et al. (1989), in that after only a few Alfvén crossing times, multiple small-scale current filaments were found to form in the domain. However, with the shearing applied on both boundaries, exponentially growing currents were already obtained after the second shear motion due to the interlocking of the field lines, with the tension force setting up a stagnation flow. Due to the finite resistivity in their simulations, magnetic reconnection and Joule dissipation occurred in these filaments. This energy release was found to be intermittent or “bursty” when the time scale for energy input (via the boundary shearing) was long compared with the Alfvén crossing time. The work was extended by Galsgaard (2002) with the inclusion of a stratified atmosphere. Furthermore, the generation and properties of turbulence in Parker’s model have been studied in the framework of reduced MHD by a number of authors. In the initial studies, two-dimensional simulations were performed, with imposed “forcing terms” taking the place of the boundary driving (e.g., Einaudi et al. 1996; Dmitruk & Gómez 1997; Georgoulis et al. 1998). More recently, three-dimensional simulations of Parker’s model with the reduced MHD equations have been performed (e.g., Dmitruk et al. 2003; Rappazzo et al. 2008), and the resulting energy spectra and heating event statistics investigated.
In the present work, we approach the topological dissipation problem discussed above from a different angle to previous studies. We take a braided magnetic field that is close to force-free as an initial condition, and concentrate on the details of the subsequent evolution, including current sheet formation. In general, braided force-free fields could arise in the solar corona either through the emergence of braided flux from the interior or through random footpoint motions at the solar surface, accompanied by some intermediate relaxation processes. The ideal relaxation of this field towards a force-free state was considered in Wilmot-Smith et al. (2009a) where only large-scale current features were found in the end state.We now follow the evolution of the system in a resistive MHD simulation. In a previous paper (Wilmot-Smith et al. 2010, hereafter referred to as Paper I) we described how during the early evolution an instability occurs which moves the system away from equilibrium, leading to the formation of current sheets and thus the onset of magnetic reconnection. In the present paper we address the following key questions:
-
1.
as the plasma seeks a new equilibrium, what is the nature of theresistive relaxation process?
-
2.
in particular what are the properties of the magnetic reconnection processes that take place?
-
3.
what is the nature of the final state of the relaxation?
-
4.
what is the dependence of each of the above on the magnetic Reynolds number?
In Sect. 2 we introduce the numerical method and summarise the results of our previous investigations. In Sect. 3 we describe qualitatively the evolution of the system, and in Sect. 4 we discuss the nature of the final state. In Sect. 5 we investigate the reconnection in the system in more detail, and then in Sect. 6 discuss the dependence on the plasma resistivity. Finally in Sect. 7 we present our conclusions.
2. Numerical method and early evolution
2.1. Numerical scheme
The numerical scheme employed in the simulations that follow is described briefly below
(further details may be found in Nordlund &
Galsgaard (1997) and at http://www.astro.ku.dk/~kg). We solve
the three-dimensional resistive MHD equations in the form 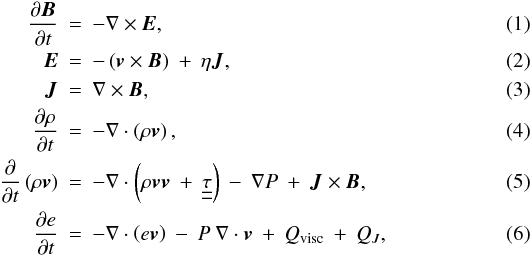 where
B is the magnetic field, E
the electric field, v the plasma velocity,
ρ the density, η the resistivity,
J the electric current density,
where
B is the magnetic field, E
the electric field, v the plasma velocity,
ρ the density, η the resistivity,
J the electric current density,
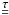 the viscous stress tensor, P the pressure, e the thermal
energy, Qvisc the viscous dissipation and
QJ the Joule dissipation. An ideal gas is
assumed, and hence
the viscous stress tensor, P the pressure, e the thermal
energy, Qvisc the viscous dissipation and
QJ the Joule dissipation. An ideal gas is
assumed, and hence 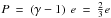 . The equations above have
been non-dimensionalised by setting the magnetic permeability
μ0 = 1, and the gas constant equal to the mean molecular
weight. The result is that for a volume in which
|ρ| = |B| = 1, time units are
such that an Alfvén wave would travel one space unit in one unit of time.
. The equations above have
been non-dimensionalised by setting the magnetic permeability
μ0 = 1, and the gas constant equal to the mean molecular
weight. The result is that for a volume in which
|ρ| = |B| = 1, time units are
such that an Alfvén wave would travel one space unit in one unit of time.
In all simulation runs we employ an explicitly prescribed, spatially uniform resistivity, and thus we have simply QJ = ηJ2. Viscosity is calculated using a combined second-order and fourth-order method (sometimes termed “hyper-viscosity”), which is capable of providing sufficient localised dissipation where necessary to handle the development of numerical instabilities (Nordlund & Galsgaard 1997). The effect is to “switch on” the viscosity where very short length scales develop in v, while maintaining a minimal amount of viscous dissipation where the velocity field is smooth. As such, the total viscous dissipation in the domain is negligible when compared with the Joule dissipation. All simulations are carried out on a grid with 5123 nodes. The dimensionless plasma density is initialised to have value ρ = 1 throughout the domain, while the thermal energy is initialised with value e = 0.1. The result is a plasma-β that varies throughout the domain between 0.10 and 0.14 at t = 0.
We have checked our numerical results by repeating the standard run described below (with η = 10-3) using the Lare3d MHD code (Arber et al. 2001). The qualitative results described in Sects. 3 − 6 have been verified with this different scheme, demonstrating their robustness.
2.2. Initial conditions and early time evolution
We use as an initial condition for our resistive MHD simulations a magnetic field that is close to being force-free (Wilmot-Smith et al. 2009a), and that is obtained via an ideal Lagrangian relaxation scheme (Craig & Sneyd 1986; Pontin et al. 2009). This is explained in detail in Paper I. In what follows, we term the input field for the ideal relaxation scheme the “pre-initial” magnetic field. The final state of this relaxation, which is the initial condition for the resistive MHD simulations described herein, is termed the “initial” magnetic field. The pre-initial and initial magnetic fields have the same braided magnetic topology (as the relaxation is exactly ideal). The magnetic field is modelled on the so-called pigtail braid, with a subset of the field lines being linked in a non-trivial way – see Fig. 1a. The pre-initial structure consists of six localised regions of twisted flux in an otherwise homogeneous field. These twists are of equal magnitude, but with opposite sign in three of the regions, such that the net current density and net helicity in the computational volume are both zero. (To be precise we calculate the relative helicity (Berger & Field 1984) using the potential field (Bp = [0,0,1] ) as the reference field. In our case we can choose a gauge such that Ap = A on the boundary so that the relative helicity reduces to an integral over A·B only.) In the initial magnetic field used for our MHD simulations, there are two large-scale, diffuse current structures within the domain, but no thin current layers – see Fig. 1b and Wilmot-Smith et al. (2009a,b) for a full description.
 |
Fig. 1 a) Three representative magnetic field lines from the initial magnetic field (t = 0) which demonstrate the braiding present in the field. b) Isosurface of current density |J| at t = 0, at 25% of its maximum value. |
The numerical domain has dimensions [x,y,z] ∈ [±6, ±6, ±24] . The magnetic field is line-tied on z = ±24, where the plasma velocity is fixed at zero for the whole experiment, while the x and y boundary conditions are periodic. Since B = [0,0,1] at the x- and y-boundaries, these boundaries are closed with respect to the magnetic field at t = 0. We find that the dynamics is confined within the domain (x,y ∈ [−4,4] ) and, with the confining background field, field lines do not leave the numerical box through the side boundaries at any stage of the simulation. We note finally that the simulations are run for a sufficient time that in the final state the resistive dissipation is occurring on the global length scale of the regions of twist that were present in the pre-initial field (see below).
The evolution of the system at early stages can be summarised as follows, and is described in detail in Paper I. The system initially remains relatively stationary, being close to a force-free equilibrium. However, at approximately t = 8 an instability sets in, and the current intensifies in two thin layers. At present the nature of this instability is not fully understood, though we propose that it may be a resistive instability analogous to the internal kink instability. This time interval corresponds to the Alfvén travel time between two of the imposed regions of twist in the pre-initial magnetic field. We go on below to investigate the continued evolution of the system.
3. Long time evolution
3.1. Qualitative behaviour
Following the instability which gives rise to the initial current layers, the system goes on to develop an increasing number of thin current layers, as illustrated in Fig. 2 where isosurfaces of current density at 50% of the domain maximum are shown. It is worth noting that the two initial current layers are stronger than any of those that form in the subsequent evolution (see the following section and Fig. 4). The development of a highly fragmented current structure means that magnetic reconnection also occurs in a highly fragmented portion of the domain. This magnetic reconnection is investigated in detail in Sect. 5. The evolution resembles qualitatively the onset of a turbulent-like behaviour, with the current layers forming a highly disordered pattern which fills the central portion (in xy) of the computational domain (the region in which the initial field line mapping is non-trivial). Investigating the power spectra of relevant physical quantities to ascertain whether indeed true turbulence develops is beyond the scope of this paper. It is in any case likely to require higher numerical resolution (and the lower value of imposed η that this permits) in order to resolve a sufficient number of decades of spatial scales. Thus, in the remainder of this paper we use the terms turbulence and cascade only in a very loose sense.
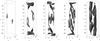 |
Fig. 2 Isosurfaces of the current density |J| at t = 15,27.5,35,50,290, at 50% of the corresponding maximum value of |J| . For the run with η = 10-3. |
In Paper I, it was shown that the locations where the first pair of current sheets form
are well predicted by analysing in combination the squashing factor Q of
the field line mapping (Titov et al. 2002; Titov 2007) and the integrated parallel current along
field lines, 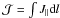 . The
initial current layers form in regions threaded by field lines with high values of both
quantities (for an explanation of the importance of
. The
initial current layers form in regions threaded by field lines with high values of both
quantities (for an explanation of the importance of
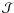 see Wilmot-Smith et al. 2009a). The question
naturally arises: do the secondary, tertiary and subsequent current layers form in
response to the dynamics that are set in motion by the initial instability and
reconnection process? Or are they the result of multiple instabilities which occur
throughout the domain with different growth rates – with the initial current sheets that
we observe being simply those associated with the fastest growing instabilities? The
myriad of thin layers of high Q and
see Wilmot-Smith et al. 2009a). The question
naturally arises: do the secondary, tertiary and subsequent current layers form in
response to the dynamics that are set in motion by the initial instability and
reconnection process? Or are they the result of multiple instabilities which occur
throughout the domain with different growth rates – with the initial current sheets that
we observe being simply those associated with the fastest growing instabilities? The
myriad of thin layers of high Q and
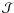 found in the domain would support the latter idea. The evidence suggests that neither of
these alternatives is solely responsible, but rather a combination of the two. However,
this is another aspect of the simulations that warrants further investigation.
found in the domain would support the latter idea. The evidence suggests that neither of
these alternatives is solely responsible, but rather a combination of the two. However,
this is another aspect of the simulations that warrants further investigation.
In an attempt to gain some insight, one can look at individual reconnection events in the domain. One can identify the outflow from certain current layers with the inflow to another reconnection process (this being one typical picture of how a multitude of current layers may form, where one reconnection process drives the next and so on, see e.g., Galsgaard & Nordlund 1996; Watson & Craig 2003; Hood et al. 2009). However, there are many other current layers for which this is clearly not the case. Moreover, determining the local relationship between reconnection processes is not straightforward – in three dimensions reconnection need not necessarily occur in a region of hyperbolic field, and is also not always associated with a hyperbolic flow structure with well-defined inflow and outflow. In fact, in three dimensions the characteristic property for reconnection in the absence of null points is a counter-rotational plasma flow on either side (with respect to the direction of B) of the diffusion region (Hornig & Priest 2003). Thus, determining the dynamic interaction between different reconnection processes within the volume is a non-trivial problem.
The increase in the complexity of the current distribution continues until around t = 80, after which the number of current layers begins to decrease. Eventually, the current concentrations again attain large scales (see Figs. 2 and 3). The properties of the final state of the simulation are considered in detail in Sect. 4. The extent and duration of the fragmentation of the current layers – and the subsequent time taken to return to a configuration with currents on system-size scales – is found to be dependent on the value taken for the resisitvity, η. This is discussed in Sect. 6.
 |
Fig. 3 Current density |J| at z = 0 for [x,y] ∈ [±3.5, ±3.5] every t = 20 units from t = 0 to t = 340 (top-left to bottom-right). The shading intensity is scaled individually to the maximum at each time, for clarity. For the run with η = 10-3. |
3.2. Relaxation properties
 |
Fig. 4 From top to bottom: time evolution of the spatial maximum of |J| ; the Joule dissipation ηJ2 per unit volume, the magnetic energy per unit volume, and the thermal energy per unit volume, for the run with η = 10-3. |
 |
Fig. 5 Total per unit volume of the kinetic energy plus the magnetic energy in excess of that of the background field, plotted on a log -log scale, for the run with η = 10-3. |
As noted above the relaxation process has a turbulent appearance. However, due to the moderate Reynolds numbers that we are able to use with the present resolution, the system is unlikely to be in a state of fully developed turbulence, though we anticipate that such a state would be reached were we able to perform simulations with lower values of the resistivity. In terms of the categorisation described by Biskamp (2003), the system would then be described as undergoing decaying turbulence, since the additional energy in the system is included as excess magnetic energy in the system at large scales at t = 0 (in contrast with the forced turbulence simulations in which a mechanical stressing is continually applied, e.g., Einaudi et al. 1996; Dmitruk & Gómez 1997; Georgoulis et al. 1998; Dmitruk et al. 2003; Rappazzo et al. 2008). The sum of the magnetic and kinetic energies is expected to decay exponentially in time during decaying turbulence (Biskamp 2003). In Fig. 5 this quantity is plotted versus time on a log-log scale, where we have subtracted the constant contribution to the magnetic energy arising from the uniform background field, for clarity. The dashed line shows a least-squares fit for the data points between t = 20 and t = 180 when the current distribution contains small scales. It is clear that we do indeed see a power law dependence during this time, which is suggestive that we are at least approaching a regime of decaying turbulence. It is also apparent from the plot that after t ≈ 180 (after which physical quantities vary on system-size scales), this power law is no longer followed, with a steepening of the curve suggesting a possible transition towards an exponential decay.
While the simulation has been run to t = 350, it is found that after t ≈ 200 the topology of the magnetic field changes only due to diffusion in the two tubular current structures which have system-size dimensions both along B and perpendicular to B (see Figs. 2 and 3, and Fig. 9 bottom panel). Owing to the enormous diffusive timescale in the corona, this diffusive evolution is not relevant for the coronal field. We therefore consider the state reached at the end of our simulations to characterise the physically relevant final state. We therefore take t = 290 as the final state of the simulation for our investigations into its nature that follow. It should be noted that this final state is not an exact force-free equilibrium, due to the finite plasma pressure, as well the residual Alfvénic oscillation of the structure about its equilibrium (our use of a hyper viscosity means that these oscillations are damped only very slowly). However, it is close to force-free, in that in terms of the dimensionless measure of the proximity to a force-free field, ϵl, given in Wilmot-Smith et al. (2009a), we have ϵl ≈ 6 × 10-3 (where ϵl ∈ [0,1] and ϵl = 0 for a perfectly force-free field).
4. Nature of the final state
4.1. Properties of the relaxation
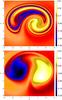 |
Fig. 6 The mean value of α∗ along field lines shown on a section of the lower boundary (z = −24) of the domain in the initial (top, t = 0) and final (bottom, t = 290) states showing a smoothing of α∗ during the resistive relaxation with η = 10-3. |
In order to investigate the nature of the final state, we take a grid of starting points
on the lower boundary z = −24 (taking 1602 points over the
region [−3,3] 2) and trace field lines through the volume to the upper
boundary. For each field line, we calculate 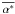 ,
the mean value along the field line of the quantity
α∗ = (J·B)/(B·B).
Note that for a perfectly force-free field this simply reduces to the force-free parameter
α (where
J = αB)
which is constant along field lines. Figure 6 shows
contours of
,
the mean value along the field line of the quantity
α∗ = (J·B)/(B·B).
Note that for a perfectly force-free field this simply reduces to the force-free parameter
α (where
J = αB)
which is constant along field lines. Figure 6 shows
contours of 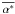 found in this way for the initial state (top panel) and the final state
(t = 290, lower panel). In both cases the sum
of
found in this way for the initial state (top panel) and the final state
(t = 290, lower panel). In both cases the sum
of 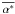 over all field lines in the domain is zero. In the final state the small scales in
over all field lines in the domain is zero. In the final state the small scales in
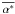 have been smoothed out leaving two large-scale patches of opposite signs. Note in addition
that the extremes of the value of
have been smoothed out leaving two large-scale patches of opposite signs. Note in addition
that the extremes of the value of 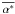 have been reduced.
have been reduced.
The two patches of 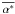 shown in Fig. 6 are signatures of the separation of
the braided field during the relaxation into a simpler structure consisting of two weakly
twisted magnetic flux tubes of oppositely signed twist, embedded in an approximately
uniform field. Here we provide two simple visualizations of the field structure in order
to demonstrate this process. In Fig. 7 we show sample
magnetic field lines in the initial (left) and final (right) states. In each case two sets
of field lines are shown. First, a set of field lines is traced from three circles of
radius 0.1, 0.3 and 0.5 lying in the z = −24 plane and centered at
x1 = (1.415, −0.4875, −24). A second set of
field lines is traced from three circles of the same radii centered at
x2 = (−1.06,0.0375, −24). The centers
x1 and
x2 of the two flux tubes have been chosen to
lie at the maximum and minimum values of
shown in Fig. 6 are signatures of the separation of
the braided field during the relaxation into a simpler structure consisting of two weakly
twisted magnetic flux tubes of oppositely signed twist, embedded in an approximately
uniform field. Here we provide two simple visualizations of the field structure in order
to demonstrate this process. In Fig. 7 we show sample
magnetic field lines in the initial (left) and final (right) states. In each case two sets
of field lines are shown. First, a set of field lines is traced from three circles of
radius 0.1, 0.3 and 0.5 lying in the z = −24 plane and centered at
x1 = (1.415, −0.4875, −24). A second set of
field lines is traced from three circles of the same radii centered at
x2 = (−1.06,0.0375, −24). The centers
x1 and
x2 of the two flux tubes have been chosen to
lie at the maximum and minimum values of 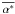 (at z = −24) in the final state.
(at z = −24) in the final state.
 |
Fig. 7 Above: field lines traced from fixed locations on the lower boundary (and coloured according to location on the lower boundary). Below: locations of intersection with the plane z = +24 of field lines traced from a regular grid in the plane z = −24. Field lines traced from locations x ≥ 0 on the lower boundary are coloured white, from x < 0 black. Plots are made for t = 0 (left) and t = 290 (right) for the run with η = 10-3. |
In the lower panels of Fig. 7 a two dimensional representation of this separation is shown. We trace field lines from a regular grid of points (over the region [x,y] ∈ [±6, ±6] ) on the lower boundary. In the figure we plot the intersections of these field lines with the upper boundary z = 24, colour-coded such that those field lines that begin at x ≥ 0 at z = −24 are coloured white, while those with x < 0 at z = −24 are coloured black. The left panel demonstrates the complexity of the footpoint mapping generated by the braided field in the initial state. The right panel shows the much simpler mapping obtained in the final state.
In summary, we have found that in the final state of our simulation the magnetic field has two important properties:
-
1.
the magnetic field has been “unbraided”, becoming much moretopologically simple;
-
2.
the field relaxes towards a non-linear, rather than a linear, force-free field.
4.2. Discussion
The nature of the relaxed state following the resistive relaxation of astrophysical magnetic fields (such as found in the Solar corona) is an important and unresolved issue. A linear force-free field is often conjectured to be the end-state of general turbulent relaxation processes. This notion was put forward by Taylor (1974) to explain the turbulent relaxation of a reversed field pinch (RFP), and was applied to the corona by Heyvaerts & Priest (1984, 1992). Noting that the full set of invariants of ideal MHD do not hold in a resistive situation, Taylor suggested that as the magnetic field of an RFP decays toward a state of minimum energy, a single invariant – the total magnetic helicity (H = ∫A·B dV) – will serve as a constraint on the minimization. Formulating this as a variational problem the end state of relaxation is found to be a linear force-free field, which matches experimental data of the RFP rather well (e.g., Taylor 1986). In the solar coronal case, on the other hand, it is not yet known whether the total helicity is the only constraint on relaxation. It is certainly true that there are fundamental differences between the two plasma environments, the most obvious being that field lines in the solar corona do not close there, but rather can be considered to be anchored in the solar photosphere.
In a series of numerical simulations Browning and coworkers (Browning & Van der Linden 2003; Browning et al. 2008; Hood et al. 2009) have followed the development of the kink instability in an initially non-linear force-free cylindrical loop. In their simulations, various initial distributions of α take the form of cylindrically symmetric step-functions with different profiles. The authors find the end-state of relaxation to be a linear force-free field. By contrast, Amari & Luciani (2000) – who also tracked a turbulent resistive evolution subsequent to a kink instability – found as an end state a non-linear force-free field containing two distinct flux tubes.
Hood et al. (2009) have suggested that a smoothing of α over the full domain is natural in the presence of fully developed turbulence, i.e. with reconnection regions sufficiently spatially overlapping (in the case in which a dominant vertical magnetic field Bz is present this implies an overlapping of current sheets when projected along field lines onto the xy plane). However, as we proceed to demonstrate below, our study indeed satisfies such a criterion, though we do not obtain a linear force-free field, as discussed above. We have recently discovered one additional constraint on the resistive relaxation of line-tied magnetic flux tubes, which demonstrates why a Taylor relaxation to the linear force-free state is prohibited in the braided field studied here (Yeates et al. 2010). It is clear that further studies are necessary to determine the end state of relaxation even in isolated flux tubes or braids.
To qualify the above discussion, it is worth emphasising at this point that the final state of our simulations is not an exact force-free field, due to the finite plasma pressure and residual oscillations, as discussed above. Within each twisted flux tube, there is a balance between magnetic tension associated with their internal twist, and a combination of magnetic and plasma pressure. That the plasma pressure is enhanced in the central part of the domain is not a surprise, since the plasma has been heated there by a multitude of reconnection events. Although the Taylor relaxation scenario assumes a very small plasma-β, and we have used a plasma-β of order 0.1, we do not expect that the plasma pressure plays a crucial role in determining the qualitative properties of the final state. We have repeated the simulation run with η = 10-3 with the plasma-β reduced by a factor of 10 with no change in the qualitative results.
5. Magnetic reconnection
5.1. Introduction
In order for the magnetic field to resistively relax, it is necessary that magnetic
reconnection occurs, since a subset of the field lines in the volume have a non-trivial
topology – see Fig. 1a. Reconnection allows a change
of the magnetic topology, and thus release of the energy stored in the magnetic field. It
is becoming apparent that magnetic reconnection processes are fundamentally different in
two dimensions (2D) and three dimensions (3D, clearly the regime applicable to the solar
corona). In 2D, the rate at which the magnetic flux is transferred from one flux domain to
another (through a magnetic X-point) is given by the value of the electric field evaluated
at the null point. However, in 3D, the electric field E and
magnetic field B are no longer perpendicular, and it is the
component of E parallel to B
(denoted E ∥ ) that is the crucial quantity. More
specifically, magnetic reconnection can be defined to occur within a region in which
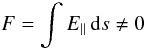 (7)where
s is a parameter that runs along magnetic field lines, and where the
quantity E ∥ should be spatially localised (Schindler et al. 1988; Hesse & Schindler 1988). The rate of reconnection in this case is given
by the maximum value of F over all field lines threading the diffusion
region. Thus, the efficiency of the reconnection process is determined not by a local
quantity evaluated at a given point, but rather by a “global” property of the field in the
vicinity of the diffusion region. Furthermore, the interpretation of this reconnection
rate is far more complicated in 3D. The way in which the magnetic flux evolves during the
reconnection process has been shown to be fundamentally different in 2D and 3D (Priest et al. 2003; Hornig & Priest 2003; Pontin et al.
2005a). One crucial difference is that the magnetic field lines change their
connectivity continuously throughout the diffusion region. A key result of this property
is that magnetic field lines do not reconnect in a one-to-one “cut and paste” fashion, as
in simple 2D models. This has a profound effect on the way that the magnetic flux is
restructured by the reconnection process. The issue is further complicated by the fact
that many different modes of magnetic reconnection may occur in 3D, depending on the local
magnetic field structure in the vicinity of the diffusion region, with each having
different characteristic behaviour in terms of the evolution of the flux (e.g., Hornig & Priest 2003; Pontin et al. 2004, 2005b; Wilmot-Smith & De Moortel 2007; Parnell et al. 2010).
(7)where
s is a parameter that runs along magnetic field lines, and where the
quantity E ∥ should be spatially localised (Schindler et al. 1988; Hesse & Schindler 1988). The rate of reconnection in this case is given
by the maximum value of F over all field lines threading the diffusion
region. Thus, the efficiency of the reconnection process is determined not by a local
quantity evaluated at a given point, but rather by a “global” property of the field in the
vicinity of the diffusion region. Furthermore, the interpretation of this reconnection
rate is far more complicated in 3D. The way in which the magnetic flux evolves during the
reconnection process has been shown to be fundamentally different in 2D and 3D (Priest et al. 2003; Hornig & Priest 2003; Pontin et al.
2005a). One crucial difference is that the magnetic field lines change their
connectivity continuously throughout the diffusion region. A key result of this property
is that magnetic field lines do not reconnect in a one-to-one “cut and paste” fashion, as
in simple 2D models. This has a profound effect on the way that the magnetic flux is
restructured by the reconnection process. The issue is further complicated by the fact
that many different modes of magnetic reconnection may occur in 3D, depending on the local
magnetic field structure in the vicinity of the diffusion region, with each having
different characteristic behaviour in terms of the evolution of the flux (e.g., Hornig & Priest 2003; Pontin et al. 2004, 2005b; Wilmot-Smith & De Moortel 2007; Parnell et al. 2010).
5.2. Method of measurement
Thus far we have described the formation of multiple current sheets during our
simulations. We now examine the properties of the magnetic reconnection that occurs in
these current sheets, in particular the rate of the reconnection. Due to the strong
background (“guide”) field in the z-direction, there are no null points
or closed field lines in our volume. The magnetic reconnection takes place in the absence
of such topological features, as described for example in the models of Hesse & Schindler (1988); Priest & Forbes (1992); Hornig
& Priest (2003); Wilmot-Smith et al.
(2006, 2009c). As discussed above, the
rate of reconnection is determined, for an isolated diffusion region in 3D, by the maximum
value of 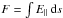 attained along any field line
threading the diffusion region.
attained along any field line
threading the diffusion region.
It is clear from Sect. 3.1 that there are multiple diffusion regions, at which reconnection is occurring, during the simulations. Therefore the first step towards calculating the reconnection rate is to first identify all of the individual reconnection regions that exist at each time. The global reconnection rate is then obtained by summing the moduli of the maxima of F (see Eq. (7)) over all such regions.
At periodic intervals during the simulations, the data of all physical fields is output, providing a “snapshot” of the evolution. We proceed as follows, treating each individual snapshot in turn.
-
1.
Integrate E ∥ along a set of field lines which intersect the z = 0 plane in arectangular grid with resolution approximately twice that of thecomputational mesh (to ensure that no information is lost in areaswhere the field line mapping shows expansion). For clarity weintegrate field lines only over the positive half-space, with thedomain having symmetry about the z = 0 plane. This yields atwo-dimensional quantity
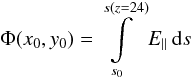 (8)subject to
(x,y,z) = (x0,y0,0)
at s = s0, i.e.
(x0,y0) is the
intersection of the appropriate field line with the z = 0 plane.
(8)subject to
(x,y,z) = (x0,y0,0)
at s = s0, i.e.
(x0,y0) is the
intersection of the appropriate field line with the z = 0 plane.
-
2.
Search for the maxima and minima of Φ. We want to count only the reconnection rate for “isolated” diffusion regions, and so we require that Φ falls below some threshold between peaks in order to class two regions as corresponding to separate reconnection processes. The threshold we choose to class two given maxima as “separate” is that Φ must drop below 60% of the lower of the two peak values between the peaks. (In principle we would like Φ to fall to zero, but the effect of projecting along the field lines is likely to mean that regions that may be isolated in 3D overlap to some extent in the 2D projection. In addition, numerical quantities are never exactly zero in practice, so it is not realistic to enforce such a condition.)
-
3.
To be classed as a reconnection region, maxima/minima are required to contain at least 500 field lines. This corresponds to a cross-sectional area of around 0.02, or around 40 grid cells. (This does not dramatically alter the reconnection rate obtained. However, it discounts large numbers of false positives in the algorithm used to identify isolated maxima, which otherwise selects many peaks which are sufficiently small (both in spatial coverage and modulus) to be close to the noise threshold.)
-
4.
To obtain the global reconnection rate, sum the moduli of the identified peak values, and multiply by 2 to obtain a value for the whole domain (since the above procedure is only implemented on the positive half-space in z).
Below we present the results of implementing this procedure for the standard run with η = 10-3, before going on in the next section to describe the effect of varying the value of η. As a frame of reference for the numerical values obtained for the reconnection rate, we note the following characteristic values in our simulations. Since ρ ≈ 1 and the equations have been non-dimensionalised by setting μ0 = 1, we have |vA| ≈ |B| ≈ 1. The “guide field” Bz has magnitude of order 1 for all time, and at t = 0 for example we have peak values of Bx,By of approximately 0.3, and rms values of approximately 0.05.
 |
Fig. 9 Plots of Φ for Φ < 0 only, at times t = 0,15,50,140,290, for the run with η = 10-3. |
5.3. Nature and rate of reconnection process
A sample Φ plot is presented in Fig. 8, where the shading intensity shows the value of Φ. It is clear that there exist multiple distinct reconnection regions, which is consistent with the 3D visualisation of the current density presented in Fig. 2. We now consider the qualitative evolution of Φ in time, shown in Fig. 9. For clarity only one sign of Φ is shown (Φ < 0). At t = 0 only a single reconnection region exists, which we see split and then intensify (t = 15) as time progresses, consistent with the formation of the initial pair of current sheets. As the evolution continues we see the formation of multiple distinct reconnection regions which fill the majority of the central portion of the x0y0-plane where the twisted and braided flux is located (this filling is even more apparent when Φ of both signs is plotted, see Fig. 8). As the simulation continues, and the current again assumes a large-scale structure as described above, the number of distinct reconnection regions diminishes once more.
Quantitative measures of the behaviour described above are presented in Fig. 10. The global reconnection rate – plotted as the solid curve in the left panel of Fig. 10 – is defined by 2 × ∑ |Φmax| , as discussed above, where we multiply by 2 to take into account the lower half-space z < 0. The plot shows that initially the reconnection rate grows steadily, peaking at t = 35. There is then a gradual decay until t = 170 when the rate settles to an approximately constant value (representing large-scale diffusion). The first thing to note is that the time of the peak reconnection rate (t = 35) does not coincide with the time of the peak current in the domain (t = 15). Furthermore, it does not occur at the time when the reconnection rate for any given single region is a maximum (t = 15). Rather, the reconnection rate continues to increase after this time, as a result of the fragmentation of the spatial location of the reconnection process. So the reconnection rate grows not because of an intensification of the current or an increase of the rate in any one region, but because of an increase in the fragmentation of the volume in which reconnection processes take place. This is demonstrated by the dashed line in the left panel of Fig. 10, which shows the maximum rate for the fastest reconnection process (of either sign), defined by |Φ| global max, multiplied again by 2 for consistency. The number of individual reconnection regions identified throughout the simulation is shown by the dashed line in the top panel of Fig. 12.
 |
Fig. 10 Left: reconnection rate versus time (solid line) for the run with η = 10-3, defined by 2 × ∑ |Φmax| . Also plotted (dashed line) is 2 × (absolute maximum of |Φ| ). Right: cumulative reconnected flux versus time, for the same run. |
The reconnection rate as calculated above is of course only an estimation. We would argue that it provides a lower bound on the reconnection rate for the system. There are a number of reasons why it should give a conservative estimate:
-
finite spatial resolution of the simulation grid, which will ingeneral underestimate the true current maxima;
-
finite spatial resolution of the field line grid means the actual peak Φ will not be exactly obtained;
-
finite temporal resolution will mean that we fail to capture the highest global peak value;
-
partial cancellation of positive/negative E ∥ along some field lines will degrade some maxima;
-
exclusion of small regions (step 3 above);
-
projection along field lines may lead to regions distinct in 3D failing the test for separate regions, criterion described in step 2 above.
5.4. Reconnected flux
It is straightforward to estimate the total reconnected magnetic flux from the reconnection rate obtained as described in the previous section, by performing a simple time integral. The cumulative reconnected flux is plotted against time in the right panel of Fig. 10. It turns out that the total number of (non-dimensional) units of flux reconnected during the simulation is ≈41.2. It is revealing to compare this figure with the total poloidal flux in the initial state, which is 30 units. (During the ideal relaxation used to define the initial condition for the present resistive MHD simulations, this quantity is conserved. In the symmetric pre-initial field, which is known in closed form, the poloidal flux is equivalent to the total flux of either sign passing through the y = 0 plane.) Furthermore, as we saw in Sect. 4, the final state of the relaxation is not the homogeneous field, but rather contains a finite amount of twist and thus poloidal flux. Due to the high degree of symmetry in the final state, the remaining poloidal flux may be estimated by integrating the positive (say) flux B through the y = 0 plane. The result that we obtain is 15.3 units, indicating that around half of the initial poloidal flux has been cancelled.
To recap then, beginning with 30 units of poloidal flux, 41.2 units are reconnected and 15.3 remain. So the total reconnected flux is greater than the quantity that would appear to be available. The only conclusion is that (at least some of) this flux is reconnected multiple times, most likely in different reconnection regions, during the relaxation and “unbraiding” of the field. On average, each unit of flux is reconnected around 2.8 times. This demonstrates the highly complex nature of the reconnection process that occurs in complex (realistic) magnetic fields such is the one considered here.
The result should be compared with that of Parnell et al. (2008), who observed what they termed “recursive reconnection” in a numerical simulation in which two opposite-polarity flux sources were driven past one another in the presence of an overlying field. In their simulation, a number of separator lines (field lines connecting one magnetic null point to another) were formed through which the reconnection took place. Thus the reconnection regions were long-lived and individually identifiable from one time-frame of their simulation to another. They calculated that the magnetic flux was reconnected on average 1.8 times, and argued that this occurred cyclically around the same circuit of reconnection regions (separators). It is clear that we observe a very similar phenomenon occurring here, even though the magnetic field configuration is completely different (and, additionally, isn’t continually being driven). The difference in the present case is that due to the lack of topological features present in the magnetic field and the high degree of complexity, it is difficult to label individual reconnection processes and follow them in time. The magnetic flux undergoing the reconnection process described above then may be best described as being “multiply” rather than “recursively” reconnected. Given that such similar processes occur in such vastly different configurations, this suggests that such “multiple” or “recursive” reconnection is likely to be ubiquitous in astrophysical magnetic fields.
6. Dependence on resistivity
 |
Fig. 11 Plots of Φ for Φ < 0 only, at times t = 50,140,290, for the run with η = 2 × 10-4. |
 |
Fig. 12 Number of identified reconnection regions (upper panel), reconnection rate (middle panel) and cumulative reconnected flux (lower panel) for runs with η = 10-2 (grey solid line), η = 10-3 (black, dashed) and η = 2 × 10-4 (black, solid). |
Qualitatively, the differences between the simulation runs can be described as follows. The initial magnetic field loses stability at a time that is independent of η, with two current layers forming at locations that are also independent of η (see Paper I). However, the subsequent evolution does vary greatly between the simulation runs. First, the lower the value of η used, the greater the degree of fragmentation of the current structure. This is quantified below where we also discuss the reconnection rate and evolution of the magnetic flux. It can also be seen by comparison of the frames showing one sign of Φ in Figs. 9 and 11. The second main effect of reducing η is to increase the timescale of the relaxation process. In other words, the plasma resistivity acts to inhibit the tendency to form an increasingly complex system of current layers, such that for larger η the system transitions to a diffusive-timescale evolution in a shorter period of time (again, compare Figs. 9 and 11).
The above description can be quantified by analysing the global reconnection rate in the same way as before. First, in Fig. 12 (top panel) we plot the time evolution of the number of individual localised reconnection processes within the domain, for the runs with different η. It is clear that for lower η not only is the peak number higher, but the period over which the reconnection process occurs in a fragmented volume is significantly longer. Of course our algorithm is not sufficiently robust for the exact numbers of regions identified to have any physical meaning – however, we are confident that the trends that are demonstrated when varying η are physical. Next, in the middle panel of Fig. 12 we compare the measured global reconnection rate versus time. The plots indicate that there is a dependence of reconnection rate on resistivity – albeit a rather weak one. However, once again the robustness of our algorithm for calculating Φ could be questioned here. It is also possible that if some small amount of numerical dissipation is present for the low η run, then we may under-estimate the reconnection rate by under-estimating η.
The greatest insight into the changing nature of the relaxation process is gained by plotting the cumulative reconnected flux versus time for the different simulation runs – see the lower panel of Fig. 12. Here we see that the lower η becomes, the greater the total amount of flux reconnected in the cascade phase of our simulations. This in itself is not an absolute quantity (there is no precise criterion that we can apply for the transition from a fast, “reconnective” evolution to a slow diffusive evolution), but we can compare this number both with the initial poloidal flux and with the net twist remaining in the field at the end of our runs. Note that in the final state of each simulation the field has the same structure as described in Sect. 4 of two oppositely twisted flux tubes. In the run with η = 10-2 our measured cumulative reconnected flux is 24.5 units while 13.1 units remain (compare this with the 30 units of poloidal flux in the initial condition). As discussed in Sect. 5.4, for η = 10-3 we measure 41.2 units reconnected and 15.3 units remaining. Finally, for the run with η = 2 × 10-4 we measure 61.8 total units reconnected, while 16.2 units remain. We observe that there is a clear trend as η is reduced for more reconnection to be required to “unbraid” the field: the flux is reconnected on average 1.4 times for η = 10-2, 2.8 times for η = 10-3 and 4.4 times for η = 2 × 10-4. We would expect this trend to continue, at least until η has a sufficiently low value that structures on the scale of the initial field line mapping are resolved. As noted by Wilmot-Smith et al. (2009b), these length scales decrease exponentially with increasing braid complexity. Therefore in a true braided coronal loop we would expect a highly complex network of current sheets threading the loop, in which the flux is multiply reconnected to a high degree.
7. Conclusions
We have described a series of numerical experiments in which we considered the resistive MHD evolution of a braided magnetic field between two perfectly conducting parallel plates. Although the magnetic field in the simulations is initially approximately force-free, it was described in Paper I that the field experiences an instability on some characteristic time-scale. Here we considered the subsequent evolution of the system, which is best described as a resistive relaxation. The route taken to find a new equilibrium involves the formation of a complex array of current sheets which are scattered throughout the domain. The current sheets have a ribbon-like appearance, tending to be highly elongated in the direction along the loop, i.e. parallel to the strong axial field. The formation of this myriad of current layers suggests that a turbulent cascade may develop for higher Reynolds numbers than we have been able to use. Due to the absence of boundary forcing, this turbulence would fall under the heading of decaying turbulence. It would be of interest to push the spatial resolution of our simulations (thus allowing the reduction of η) to investigate whether a regime of fully-developed turbulence arises, by examining spectral properties of the magnetic and velocity fields. This is beyond the scope of this paper, and we leave it to a future investigation.
The relaxation process as described above results in a simplification of the magnetic field structure as demonstrated by the mapping of field lines from one line-tied boundary to the other (Fig. 7). The magnetic field lines are untangled, such that no three field lines are braided about one another any longer in the final state. The final state in fact consists of two (weakly) twisted flux tubes, of oppositely signed twist, embedded in an approximately uniform field. This final state approximates a force-free field, ∇ × B = αB, in which field lines in one twisted flux tube have positive α and in the other negative α. Thus thesystem approaches a non-linear force-free field, which is not consistent with the Taylor relaxation picture put forward by Heyvaerts & Priest (1984). In principle since the net current in the system is zero, a Taylor relaxation would lead to a final state with α = 0 on every field line, i.e. the homogeneous potential field. Clearly the single constraint (global helicity conservation) of the Taylor hypothesis is not sufficient to describe this relaxation. Extra constraints on the relaxation which prevent some of the helicity cancellation must be present. Although it is always dangerous to place too much trust in the extrapolation of simulation results to the extremely high Reynolds number coronal plasma, it appears unlikely that the cause could be related to the “turbulence” in the system not being sufficiently developed. In fact we retain more twist in our flux tubes in the final state for lower η, where the turbulence is better developed. In fact, an additional constraint on the relaxation has recently been discovered (Yeates et al. 2010).
The “unbraiding” of the magnetic flux during the relaxation to a non-linear force-free field occurs by magnetic reconnection. This reconnection occurs in the absence of magnetic nulls or closed field lines (note the presence of a strong background field throughout the domain). Furthermore, reconnection occurs in a multitude of regions that are spread throughout the volume. In order to determine the efficiency of the reconnection process, we must therefore sum the reconnection rate over all reconnection diffusion regions within the volume. The outcomes of performing such an analysis are as follows:
-
1.
The global reconnection rate continues to grow for some timeafter the peak current in the domain begins to fall. That is, duringthe intermediate stages of the simulations, the reconnection rategrows not because of an intensification of the current or anincrease of the rate in any one region, but rather because of anincrease in the fragmentation of the volume in which thereconnection processes take place.
-
2.
The peak value of the global reconnection rate is at most weakly dependent on the resistivity.
-
3.
The number of identifiable reconnection regions increases as the resistivity is decreased.
-
4.
The total quantity of magnetic flux that is reconnected is greater than the total poloidal flux present. This implies that the magnetic flux is “multiply-reconnected” in the complex array of reconnection regions.
-
5.
As the resistivity is decreased – resulting in an increase in the complexity of the multitude of current layers – the average number of reconnections for each unit of flux increases.
In summary, the loss of stability and subsequent relaxation of braided coronal loops results in a complex array of current layers which permit a dissipation of the stored magnetic energy and the attainment of a lower energy non-linear force-free field. These results yield a new and intriguing potential resolution to the long-standing debate over the validity of Parker’s model of coronal heating by topological dissipation. Specifically, while current singularities are not an inevitable result of random field line tangling, once the field line mapping becomes sufficiently complex, an instability will be triggered, causing the electric current structures to collapse to small scales. The complexity that is inherent in the field then results in the formation of a fragmented system of current layers (the sum of the associated reconnection processes being “fast” in the sense that the rate of energy release is only weakly dependent on the magnetic Reynolds number). The global result is a turbulent dissipation of the excess magnetic energy stored in the field, ultimately in the form of heat. There are many interesting aspects of the above study that warrant further investigation, such as determining what parameters and physical quantities govern the nature of the final state, the possible turbulence properties of the relaxation, and the spatial and temporal distribution of the resulting heating in the loop.
Acknowledgments
The simulations described were carried out on the DCSC at University of Copenhagen, and on the STFC and SFC (SRIF) funded linux clusters of the UKMHD consortium. A.W.S. and G.H. acknowledge financial support from the UK’s STFC.
References
- Amari, T., & Luciani, J. F. 2000, Phys. Rev. Lett., 84, 119 [Google Scholar]
- Arber, T. D., Longbottom, A. W., Gerrard, C. L., & Milne, A. M. 2001, J. Comp. Phys., 171, 151 [Google Scholar]
- Berger, M. A., & Field, G. B. 1984, J. Fluid Mech., 147, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Biskamp, D. 2003, Magnetohydrodynamic turbulence (Cambridge: Cambridge University Press) [Google Scholar]
- Browning, P. K., & Van der Linden, R. A. M. 2003, A&A, 400, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Browning, P. K., Gerrard, C., Hood, A. W., Kevis, R., & van der Linden, R. A. M. 2008, A&A, 485, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Craig, I. J. D., & Sneyd, A. D. 1986, ApJ, 311, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Sneyd, A. D. 2005, Sol. Phys., 232, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Dmitruk, P., & Gómez, D. O. 1997, ApJ, 484, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Dmitruk, P., Gómez, D. O., & Matthaeus, W. H. 2003, Phys. Plasmas, 10, 3584 [NASA ADS] [CrossRef] [Google Scholar]
- Einaudi, G., Velli, M., Politano, H., & Pouquet, A. 1996, ApJ, 457, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K. 2002, Flux braiding in a stratified atmosphere, SOLMAG 2002, Proc. Magnetic Coupling of the Solar Atmosphere Euroconference, ed. H. Sawaya-Lacoste, ESA SP, 505, 269 [NASA ADS] [Google Scholar]
- Galsgaard, K., & Nordlund, A. 1996, J. Geophys. Res., 101, 13445 [NASA ADS] [CrossRef] [Google Scholar]
- Georgoulis, M. K., Velli, M., & Einaudi, G. 1998, ApJ, 497, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Hesse, M., & Schindler, K. 1988, J. Geophys. Res., 93, 5558 [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1984, A&A, 137, 63 [NASA ADS] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1992, ApJ, 390, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Browning, P. K., & van der Linden, R. A. M. 2009, A&A, 506, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hornig, G., & Priest, E. R. 2003, Phys. Plasmas, 10, 2712 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., Strauss, H. R. 1994, ApJ, 437, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Mikić, Z., Schnack, D. D., & van Hoven, G. 1989, ApJ, 338, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Ng, C. S., & Bhattacharjee, A. 1998, Phys. Plasmas, 5, 4028 [Google Scholar]
- Nordlund, A., & Galsgaard, K. 1997, A 3d mhd code for parallel computers, Technical report, Astronomical Observatory, Copenhagen University [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Haynes, A. L., & Galsgaard, K. 2008, ApJ, 675, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., Haynes, A. L., & Galsgaard, K. 2010, J. Geophys. Res., 115, A02102 [Google Scholar]
- Pontin, D. I., Hornig, G., & Priest, E. R. 2004, Geophys. Astrophys. Fluid Dynamics, 98, 407 [Google Scholar]
- Pontin, D. I., Galsgaard, K., Hornig, G., & Priest, E. R. 2005a, Phys. Plasmas, 12, 052307 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Hornig, G., & Priest, E. R. 2005b, Geophys. Astrophys. Fluid Dynamics, 99, 77 [CrossRef] [Google Scholar]
- Pontin, D. I., Hornig, G., Wilmot-Smith, A. L., & Craig, I. J. D. 2009, ApJ, 700, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Forbes, T. G. 1992, J. Geophys. Res., 97, 1521 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Hornig, G., & Pontin, D. I. 2003, J. Geophys. Res., 108, 1285 [Google Scholar]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, K., Hesse, M., & Birn, J. 1988, J. Geophys. Res., 93, 5547 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. B. 1974, Phys. Rev. Lett., 33, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. B. 1986, Rev. Mod. Phys., 58, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, V. S. 2007, ApJ, 660, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, V. S., Hornig, G., & Démoulin, P. 2002, J. Geophys. Res., 107, SSH 3–1 [Google Scholar]
- van Ballegooijen, A. A. 1985, ApJ, 298, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, P. G., & Craig, I. J. D. 2003, ApJ, 590, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., Hornig, G., & Priest, E. R. 2006, Proc. R. Soc. A, 462, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., & De Moortel, I. 2007, A&A, 473, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilmot-Smith, A. L., Hornig, G., & Pontin, D. I. 2009a, ApJ, 696, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., Hornig, G., & Pontin, D. I. 2009b, ApJ, 704, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., Hornig, G., & Priest, E. R. 2009c, Geophys. Astrophys. Fluid Dynamics, 103, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Wilmot-Smith, A. L., Pontin, D. I., & Hornig, G. 2010, A&A, 516, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yeates, A. R., Hornig, G., & Wilmot-Smith, A. L. 2010, Phys. Rev. Lett., 105, id. 085002 [Google Scholar]
All Figures
 |
Fig. 1 a) Three representative magnetic field lines from the initial magnetic field (t = 0) which demonstrate the braiding present in the field. b) Isosurface of current density |J| at t = 0, at 25% of its maximum value. |
| In the text | |
 |
Fig. 2 Isosurfaces of the current density |J| at t = 15,27.5,35,50,290, at 50% of the corresponding maximum value of |J| . For the run with η = 10-3. |
| In the text | |
 |
Fig. 3 Current density |J| at z = 0 for [x,y] ∈ [±3.5, ±3.5] every t = 20 units from t = 0 to t = 340 (top-left to bottom-right). The shading intensity is scaled individually to the maximum at each time, for clarity. For the run with η = 10-3. |
| In the text | |
 |
Fig. 4 From top to bottom: time evolution of the spatial maximum of |J| ; the Joule dissipation ηJ2 per unit volume, the magnetic energy per unit volume, and the thermal energy per unit volume, for the run with η = 10-3. |
| In the text | |
 |
Fig. 5 Total per unit volume of the kinetic energy plus the magnetic energy in excess of that of the background field, plotted on a log -log scale, for the run with η = 10-3. |
| In the text | |
 |
Fig. 6 The mean value of α∗ along field lines shown on a section of the lower boundary (z = −24) of the domain in the initial (top, t = 0) and final (bottom, t = 290) states showing a smoothing of α∗ during the resistive relaxation with η = 10-3. |
| In the text | |
 |
Fig. 7 Above: field lines traced from fixed locations on the lower boundary (and coloured according to location on the lower boundary). Below: locations of intersection with the plane z = +24 of field lines traced from a regular grid in the plane z = −24. Field lines traced from locations x ≥ 0 on the lower boundary are coloured white, from x < 0 black. Plots are made for t = 0 (left) and t = 290 (right) for the run with η = 10-3. |
| In the text | |
 |
Fig. 8 Plot of Φ(x0,y0) (as defined in Eq. (8)) for t = 50 for the run with η = 10-3. |
| In the text | |
 |
Fig. 9 Plots of Φ for Φ < 0 only, at times t = 0,15,50,140,290, for the run with η = 10-3. |
| In the text | |
 |
Fig. 10 Left: reconnection rate versus time (solid line) for the run with η = 10-3, defined by 2 × ∑ |Φmax| . Also plotted (dashed line) is 2 × (absolute maximum of |Φ| ). Right: cumulative reconnected flux versus time, for the same run. |
| In the text | |
 |
Fig. 11 Plots of Φ for Φ < 0 only, at times t = 50,140,290, for the run with η = 2 × 10-4. |
| In the text | |
 |
Fig. 12 Number of identified reconnection regions (upper panel), reconnection rate (middle panel) and cumulative reconnected flux (lower panel) for runs with η = 10-2 (grey solid line), η = 10-3 (black, dashed) and η = 2 × 10-4 (black, solid). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


