| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014207 | |
| Published online | 29 November 2010 | |
The γ Doradus CoRoT target HD 49434
II. Frequency analysis of the CoRoT data ⋆,⋆⋆
1
UMR 6525 H. Fizeau, UNS, CNRS, OCA,
Campus Valrose, 06108
Nice Cedex 2,
France
2
Instituto de Astrofísica de Andalucía, CSIC,
PO Box 3004, 18080
Granada,
Spain
e-mail: eloy@iaa.es
3
LESIA, Observatoire de Paris, CNRS, Université Paris
Diderot, 5 pl. Jules
Janssen, 92190
Meudon,
France
4
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot;
CEA, IRFU, SAp, centre de Saclay, 91191
Gif-sur-Yvette,
France
5
Laboratoire d’Astrophysique de Toulouse-Tarbes, Université de
Toulouse, CNRS, 57 avenue
d’Azereix, 65000
Tarbes,
France
e-mail: Philippe.Mathias@ast.obs-mip.fr
6
INAF - Osservatorio Astronomico di Brera, via E. Bianchi
46, 23807
Merate,
Italy
7
Institut für Astronomie, Universität Wien,
Türkenschanzstr. 17,
1180
Wien,
Austria
8
Observatoire de Genève, Université de Genève,
1290
Sauverny,
Switzerland
9
Konkoly Observatory, PO Box 67, 1525
Budapest,
Hungary
10
Institut d’Astrophysique Spatiale, CNRS, Université Paris XI UMR
8617, 91405
Orsay,
France
Received: 5 February 2010
Accepted: 15 July 2010
Context. HD 49434 is a bright (V = 5ṃ75) and multiperiodic γ Dor-type pulsator that has been selected for the asteroseismic core programme of the CoRoT satellite.
Aims. An extensive and detailed study has been carried out to investigate the pulsational content of this object on the basis of the 136.9 d (331291 useful datapoints) time series collected by the CoRoT satellite during the long-run LRa01 (October 2007–March 2008).
Methods. The frequency analysis was carried out using the recently available software package SigSpec and Period04.
Results. The results confirm HD 49434 as a complex pulsator with a very dense pulsation spectrum. A total of 1686 significant peaks are formally detected, essentially in the region below 15 d-1. No significant pulsation peaks are detected for frequencies higher than 30 d-1. Solar-type oscillations are not detected in this star. The reliability of such a high number of detected peaks has been investigated on the basis of two independent methods. As a result, we propose a total of 840 frequencies that can be assumed to be intrinsic to the star.
Conclusions. The CoRoT mission provides very high-quality light curves and datasets, which are excellent for asteroseismic studies of complex pulsating stars beacause they allow investigation of the frequency content down to amplitude levels of a few μmag, unattainable with ground-based observations. In this way, hundreds of excited modes were detected in HD 49434. This is the first time that so many frequencies have been found in a γ Dor-type pulsator.
Key words: stars: variables: general / stars: individual: HD 49434 / stars: oscillations / techniques: photometric
The CoRoT space mission was developed and it is operated by the French space agency CNES, with participation of ESA’s RSSD and Science Programmes, Austria, Belgium, Brazil, Germany, and Spain.
Tables 2, 3, 6–9, 11–14, 16–19, and 21–23 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/525/A23
© ESO, 2010
1. Introduction
Asteroseismic tools allow one to derive, for a low-amplitude pulsator, essential constraints on its internal structure, such as the internal rotation, metallicity, location of convective zones and core boundary. This task is achieved through determining the frequency spectrum, the associated mode identification, and modelling.
The primary work inherent to any asteroseismic study is to detect frequencies from time series data. Space missions such as CoRoT (Baglin et al. 2006), MOST (Walker et al. 2003), KEPLER (Borucki et al. 1997; Christensen-Dalsgaard et al. 2008), and soon PLATO (e.g. Roxburgh et al. 2007) open a new era in these studies. Indeed, time series of unprecedented time span (resulting in strong damping of the aliases) and precision (access to very low-amplitude modes) result in better defined frequency spectra. To illustrate the power of space data in comparison to ground-based data, Appendix A presents the results of simulations carried out with different examples of time series, comparing the expected noise and significant levels.
From an extensive ground-based photometric and spectroscopic campaign concerning HD 49434, Uytterhoeven et al. (2008, hereafter Paper I) performed a frequency analysis that revealed at least four frequencies in the 0.2–1.7 d-1 interval, as well as six frequencies in the 5–12 d-1 domain. Some of the spectroscopically detected pulsation modes were identified with degrees up to ℓ = 8. Because two frequency domains were identified, corresponding to the range typical of γ Dor and δ Sct stars, respectively, this star is a candidate for this hybrid status. However, due to the ambiguity of the real classification of the higher-frequency mode, and because the observed frequencies might strongly deviate from the co-rotating ones, this hybrid status has not been confirmed yet. It has also been suggested that the frequency spectrum, showing large residuals after the prewhitening of these frequencies, contained additional modes that could not be sorted out owing to both the relatively short timespan of the dataset and the low precision of the individual datapoints, which are limitations inherent to ground-based observations.
The present paper deals with the frequency analysis of the 5-month long run CoRoT dataset collected for the γ Dor-type pulsator HD 49434 (V = 5ṃ75, F1V), while forthcoming papers will concern mode identification and modelling of this star. In Sect. 2, we present the results of the frequency analysis performed on the CoRoT dataset. Section 3 deals with the reliability of the detected peaks. The frequency spectrum is discussed in Sect. 4. Finally, conclusions are derived in Sect. 5.
2. Frequency analysis of the CoRoT dataset
HD 49434 is the first γ Doradus variable of the CoRoT asteroseismic core programme, and it was observed from space from October 2007 to March 2008 (LRa01). The timespan of the collected dataset is ΔT = 136.9 d, with a sampling rate of 32 s. After removal of unreliable points (essentially those flagged by the reduction pipeline), the final dataset consisted of 331 291 datapoints. The associated Rayleigh frequency resolution is (1/ΔT) = 0.0073 d-1. The corresponding Nyquist frequency, i.e. the maximum limit to investigate the possible detection of significant peaks, is fNyq = 1350 d-1.
The present analysis is performed in the CoRoT JD frame, where the CoRoT JD corresponds to HJD 2445545.0 (January 1st, 2000 at UT 12:00:00). First, the data were detrended performing a linear fit to the light curves. Long-term trends were expected due to the ageing of the CCDs (Auvergne et al. 2009). In our analysis, a linear fit was chosen as the best option among the possible low-order polynomial fittings. No jumps were found in the CoRoT light curves of HD 49434. Nevertheless, an independent analysis was also performed in Sect. 2.5. A sine-fit with a few low-frequencies was applied for detrending the original light curves, but no significant differences were found in the results. Second, Period04 (Lenz & Breger 2005) was used for a preliminary inspection of the periodograms and one peak close to zero in the frequency domain (f = 0.0049 d-1, A = 1.36 mmag) was removed from the data. Then, the resulting residual time series was analysed using the computer program package SigSpec (Reegen 2007).
As a further check, the 50 first peaks in the residual time series were calculated with both Period04 and SigSpec and compared. The resulting peaks were identical. A similar test was successfully carried out for the CoRoT target HD 50844 (Poretti et al. 2009) with ΔT = 56.7 d and 140 016 useful datapoints. In that case, Period04 was used to investigate the first 200 peaks. The agreement between the two methods was successful for 99% of the cases.
 |
Fig. 1 Spectral window of the long-run CoRoT dataset on HD 49434. |
Main aliases in the spectral window.
2.1. Spectral window
Figure 1 shows the spectral window of HD 49434, which is typical of all the targets observed by the CoRoT satellite in the same run. As can be seen, the spectral window shows neither the typical aliases at 1 d-1 nor the harmonics that are common for ground-based data. On the contrary, all the aliases are related to effects produced by the satellite and its orbital frequency (fs = 13.972 d-1). Their amplitudes are much lower than the usual ones found for ground-based time series. Table 1 lists the main aliases in the figure and their corresponding relative amplitudes. The alias peaks at 2.005 (=2fsid) and 4.011 d-1 are due to the South Atlantic Anomaly (SAA) crossing, which occurred twice each sidereal day1.
2.2. Periodograms: region below 30 d-1
As mentioned above, mainly the program SigSpec (Reegen 2007) was used to study the pulsational content of HD 49434. In order to avoid problems with power of frequencies close to 0 d-1, the analysis was carried out in the range 0.05–30 d-1. In the case of Period04, the limit commonly used to consider a peak as significant is the amplitude signal-to-noise ratio S/N ≥ 4.0 (Breger et al. 1993; Kuschnig et al. 1997). In the case of SigSpec, the significance parameter is “sig” (=spectral significance), with default limit sig = 5.0. This limit is equivalent to S/N = 3.8 (and sig = 5.46 is approximately equivalent to S/N = 4.0) (Reegen 2007; Kallinger et al. 2008). Nevertheless, we used the much more conservative limit sig = 20.0 because the periodograms at this stage show forests of peaks, and the corresponding S/N values, determined using Period04 on the residuals, are much lower than expected. This is probably caused by a high number of true peaks still remaining among the residuals in the region of interest.
SigSpec computes the spectral significance levels for the discrete Fourier transform (DFT) amplitude spectrum of a time series at arbitrarily given sampling. It evaluates the probability density function (PDF) of a given DFT amplitude level analytically. Similar to Period04, the process is iterative, and when a new peak is found, the program fits all the frequencies, amplitudes, and phases detected so far, simultaneously. The main advantage of this method is that the process is fully automatic.
The limit of sig = 20 was achieved after removing 1686 peaks. This corresponds to a level of 5.4 μmag for the lowest amplitudes. The frequencies are listed in Table 2, together with the most relevant parameters (amplitude, phase, sig, S/N, residuals, and errorbars). Column 6 lists the S/N values corresponding to each peak, calculated by Period04 on the residual file provided by SigSpec. Each S/N value was calculated from a box of width 5 d-1 centred on the corresponding peak, as usual for this type of variables (Rodríguez et al. 2006a,b).
 |
Fig. 2 Top panel: amplitude spectrum of the original data of HD 49434. Bottom panel: amplitude spectrum after removing the first 10 main peaks. |
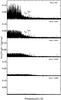 |
Fig. 3 Amplitude spectra of the residuals of HD 49434 at different stages of the frequency analysis. |
The last column of Table 2 lists the possible identification of harmonics or combination frequencies within a range of ±0.005 d-1. Peaks that possibly are related with the orbital frequency of the satellite, fs = 13.972 d-1 (harmonics and sidelobes) are also taken into account. Moreover, we have also considered the possibility of interaction of fs with peaks remaining in the very low-frequency domain (lower than 0.05 d-1, see Sect. 2.5). The main peak in this low frequency region is fl = 0.01104 d-1 with an amplitude of 0.257 mmag. As shown in Table 2, several peaks with very low amplitudes seem to be produced by these last interactions. Table 3 summarizes the combinations successfully identified in Table 2. We considered 663 possible combination frequencies, 481 identifications were detected, but only 312 of them are really independent. Moreover, a number of them are probably only “casual coincidences”.
To improve the consistency of our analysis with SigSpec, the original datapoints were binned every five consecutive points, resulting in a new time series with 66256 datapoints. SigSpec was used again and a new list with 1742 frequencies was obtained in excellent agreement with the list of 1686 peaks obtained before: we find 95% and 93% of “real” matches within a frequency error range of 0.005 and 0.001 d-1, respectively, using the same criteria as in Sect. 3.1. Elsewhere in the paper, the frequency analysis was performed on the initial set of 331 291 datapoints.
Figures 2 and 3 show the amplitude spectra of HD 49434 at different stages of the frequency analysis. There is a difference in Y-axis scale between the two figures. In the first two panels of Fig. 3, two clearly isolated and significant peaks f320 = 12.0330 d-1 (A = 47 μmag) and f410 = 10.2540 d-1 (A = 37 μmag) are marked. The frequency f320 was already detected in Paper I via spectroscopy and identified as a high-degree mode. Note the different spectral patterns of the γ Doradus star HD 49434 and the δ Scuti star HD 50844 (Fig. 3 in Poretti et al. 2009): the spectrum of the δ Scuti star shows a step at 30 d-1, while this step occurs below 10 d-1 for the γ Doradus star. This indicates that the two stars have different pulsational regimes. Figure 4 shows the original light curves of HD 49434 and residuals at different stages of the frequency analysis. The rms of the residuals at the bottom panel is of 0.228 mmag.
Since this value is higher than the dispersion σ ~ 0.12 mmag estimated from the original light curves, we suspect that a number of peaks still remain among the residuals. Another indication of additional peaks is that the noise level in the low-frequency domain is much larger than that in the domain where no frequencies are expected, e.g., 1.97 μmag near 5 d-1 versus 0.41 μmag near 150 d-1. In the region around 50 d-1, the noise level is slightly higher (~0.72 μmag) because of a number of peaks related to the harmonics of the CoRoTs orbital frequency (see Table 4). The contribution of these peaks to the noise level is much less in the region higher than 100 d-1 (see Table 5).
 |
Fig. 4 Example of the original light curves of HD 49434 and residuals at different stages of the frequency analysis. |
2.3. Periodograms: region higher than 30 d-1
We also investigated the frequency domain above 30 d-1 (until 700 d-1). In this region, the periodograms show few isolated peaks well-above the white noise level. We considered iterations until a spectral significance limit of sig = 5.5. In the interval 30–100 d-1 and, with much lower amplitudes, a number of significant peaks appear in the region 100–400 d-1. All these frequencies can be related to high-order harmonics of fs and/or with interactions of them with frequencies in the region <0.05 d-1; in particular with fl = 0.01104 d-1. Tables 4 and 5 list the ten main peaks detected in these two regions. Only one peak, seemingly unrelated to other frequencies, is found to be significant in the interval 400–700 d-1: f = 599.99 d-1 with sig = 5.8 and amplitude of only 2.9 μmag. This peak, well below the Nyquist frequency, is still unexplained.
Solar-like oscillations expected for a star as HD 49434 (Teff = 7300 K, M = 1.55 M⊙, R = 1.60 R⊙ (Paper I)) could reach ~16 μmag in the region around 140 d-1 (Kjeldsen & Bedding 1995). Using the scaling law of Samadi et al. (2007), together with the new estimates of the maximum bolometric amplitude of the Sun (Michel et al. 2009), the expected amplitudes for HD 49434 are around 6 μmag. However, this frequency region shows an amplitude level of about 2 μmag both in the residuals and when the peaks related to fs are removed. Therefore, solar-like oscillations are not detected in HD 49434.
First ten significant peaks in the region 30–100 d-1. sig = spectral significance.
First ten significant peaks in the region 100–400 d-1.
2.4. Distribution of the peaks
Figure 5 shows the frequency and amplitude distributions of the peaks detected in HD 49434. Figure 6 gives the amplitude of the peaks as a function of the frequency for different amplitude intervals. The relevant peaks f68 = 9.3069 d-1, f320 = 12.0330 d-1 (already detected in Paper I via spectroscopy) and f529 = 12.5485 d-1 (detected in new spectroscopy data, Uytterhoeven et al., in preparation), are marked. The peaks a–d are related to fs, but f410 (mentioned above) and f702 = 13.7725 d-1 (A = 21 μmag) do not seem to be related to instrumental effects.
The first panel of Fig. 5 shows that the number of peaks increases very quickly as the amplitude decreases. Only 15 peaks are found with amplitudes higher than 0.5 mmag, but below the threshold of about 0.2 mmag, the number of detected peaks increases steeply in a nearly exponential way. This behaviour agrees with what is found by Breger et al. (2005) for FG Vir, using the dataset provided by the longest ground-based photometric multisite campaign carried out to date for a δ Sct-type pulsator. However, in that case, the detection limit was only about 0.2 mmag. We used a significance threshold of sig = 20. If we adopt the spectral significance sig = 5.5 instead, i.e. the “theoretical” equivalent of S/N = 4.0, about 1000 additional peaks would be added to Fig. 5, with an amplitude level of 2.5 μmag for the lowest amplitudes.
The second panels of Figs. 5 and 6 show that the location of the peaks in the frequency domain spread towards higher frequencies. However, there are only seven frequencies higher than 15.0 d-1 that are not related to fs (see Table 2). The first of them is f1432 with an amplitude of 7.1 μmag.
 |
Fig. 5 Amplitude (top panel) and frequency (bottom panel) distributions of the peaks detected in HD 49434. |
 |
Fig. 6 Amplitude of the detected peaks as a function of frequency for different intervals of amplitude in the region 0.05–18 d-1. The peaks a–d are related to fs: a = f504 = fs − 1 − fl, b = f636 = fs − 1 + fl, c = f572 = fs + 1 + fl, and d = f634 = fs + 1 − fl. |
2.5. Comparison with Period04 analysis
To improve the results obtained with SigSpec, the whole data set was reanalysed with the Period04 software. The analysis was performed up to 500 frequencies from 0 to 30 d-1 with, each 100 frequencies, extension of the frequency domain at up to 200 d-1. After 500 frequencies, the residual is equal to 0.3685 mmag compared to 0.432 mmag derived from the 500 first SigSpec frequencies. This significant drop of the residual signal is probably caused by additional low frequencies between 0 and 0.05 d-1. The SigSpec analysis considered only the range 0.05–30 d-1. Indeed, comparing the two frequency sets, five additional frequencies between 0 and 0.05 d-1 are detected with Period04. Comparing the results from the two methods, 461 Period04 frequencies are found in the first 500 SigSpec frequencies, 484 within the first 600 SigSpec frequencies. All 495 frequencies between 0.05 and 30 d-1 derived by Period04 are also present among the 1686 SigSpec frequencies. Since there is no significant difference between the two frequency analysis methods, and considering the difficulty of computing each frequency with Period04 manually, the analysis was only performed up to the first 500 frequencies. However, considering the lower residual found with Period04, the original data set was prewhitened with the five additional frequencies found between 0 and 0.05 d-1. Then, the 1686 SigSpec frequencies were imposed in Period04. The resulting residual is only 0.1655 mmag, compared to 0.228 mmag obtained with SigSpec. A further frequency analysis showed additional low frequencies. After a prewhitening with 13 of these low frequencies, the residual in Period04 falls to 0.1484 mmag.
We cannot be certain that the frequencies obtained from the Period04 software (after the first 500 ones) would have been exactly the same as the 1686 obtained from the SigSpec software. Indeed, whereas results are very close for the first 500 frequencies, eventual accumulation of small differences in the iterative process could lead to a slow divergence for the whole list of used frequencies. However, the difference between both methods, based on the same Fourier algorithm, should be negligible.
3. Reliability of the detected frequencies
The list of the 1686 “formally” significant peaks presented in Table 2 is based on the frequency analysis carried out using SigSpec, with sig = 20 as significance threshold. As said above, this is a very conservative limit compared to sig = 5.5 proposed by Reegen (2007) as “theoretically” equivalent of S/N = 4.0. However, when using Period04 (Breger & Lenz 2005) to calculate the S/N value for each peak, the last 300 peaks of Table 2 do not satisfy the S/N ≳ 4.0 criterion. This can be explained by the presence of many additional peaks in the residuals, which causes the noise level to increase and the S/N values to decrease. Consequently, the criterion to define the noise level should be adapted to both the method and the dataset considered.
In a first attempt to evaluate the reality of the 1686 formally significant peaks, we use a simple and conservative procedure: we take out the peaks that do not satisfy the limit of S/N ≥ 4.0. This reduces our set of frequencies by about 300 peaks. Then, we use the residuals corresponding to this set and recalculate the noise level and S/N values corresponding to each peak. A new set of “not significant peaks” appears. We repeat the process until all the peaks are significant. However, our final set of “significant” peaks is reduced to less than 100, whereas the real number of peaks is obviously much higher.
This means that we need a different approach to evaluate the reliability of our set of frequencies. The way to confirm a peak as a true pulsation peak is the following. First, the peak must be present in the spectrum of the whole dataset and not induced by the frequency analysis method (true peak). Second, the peak must be intrinsic to the star and not an artifact of the reduction procedure (real peak). Third, the nature of the peak must be evaluated: related or not to pulsation. The last point is beyond the scope of this work, but some suggestions are given below in Sect. 4. We restrict this discussion to the two first items.
3.1. Reliability of true peaks
To evaluate whether a peak is a true peak, we compare the results obtained from the same dataset with different methods. Such a comparison has already been carried out for other CoRoT targets with very satisfactory results. In the case of HD 50844 (Poretti et al. 2009), the results from SigSpec were checked with those obtained using the iterative sine-wave fitting (Vaniček 1971) routine. The agreement was excellent (99% agreement for the first 500 peaks). Here, the comparison between SigSpec and Period04 (Sect. 2.5) leads to similar conclusions. This suggests that the great majority of the peaks in Table 2 are “true peaks”, and really exist in the spectrum of the whole HD 49434 dataset.
3.2. Reliability of real peaks
A true peak might be intrinsic to the star or an artefact of the reduction procedure. Indeed, inaccuracies in the reduction procedure can produce distortions in the light curves leading to “false” peaks in the spectra. In SigSpec, or any other automatic program package, any significant peak is interpreted as a “real” peak.
To investigate the nature of the true peaks, we compared the results obtained from the analysis of two independent data subsets S1 and S2 extracted from the whole dataset W. By construction, S1 consists of the first part of the HD 49434 CoRoT run, from day 0.0 to 70.0 with 166089 datapoints, while S2 consists of days 70.0 to 136.9 with 165202 datapoints. S1 and S2 were analysed in the same way as the whole dataset W, using SigSpec with iterations until the limit of sig = 20.0 was reached.
The results are listed in Tables 6 and 7 with the same format as Table 2. Now, the number of significant peaks is reduced to 978 and 896 for S1 and S2, respectively. This reduction relative to the 1686 peaks presented in Table 2 can be explained in terms of a higher noise level (by a factor 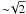 ) and a poorer frequency resolution (by a factor of 2) than for the whole dataset.
) and a poorer frequency resolution (by a factor of 2) than for the whole dataset.
The reliability of the different peaks detected in S1, S2, and W is evaluated using two different and independent methods. First, a comparison of the corresponding three frequencies per resolution bin, the “matching frequency” (mf) method. Second, a comparison of the phases derived from a sine-fit associated to a given frequency in the different datasets, the “phase constancy” (pc) method.
3.3. The matching frequency method
We first considered the results obtained from S1 and S2. Two peaks are considered “a match” when they differ less than 0.005 d-1 (Table 8) or 0.010 d-1 (Table 9) in the two datasets. The 0.005 and 0.010 d-1 values have been chosen in order to surround the Rayleigh frequency (0.073 d-1). After inspection of the frequency lists resulting from S1 and S2, we conclude that an appropriate length for the bins is about 0.005 d-1. Nevertheless, we also found that a number of pairs of peaks with differences larger than 0.005 d-1, but closer than 0.010 d-1, can also be considered as the same peak. Both criteria are more restrictive than the corresponding associated Rayleigh resolutions (0.0143 and 0.0149 d-1 for S1 and S2, respectively).
To consider matching frequencies as “real”, we also require that the two peaks must satisfy two other conditions: a) the order of detection in the two lists must be close enough and b) the amplitudes must be similar2. If two peaks satisfy these two conditions, the matching frequency is considered as “real”; if not, it is considered as “casual”. We also define an intermediate level as “casual?” (see last column of Tables 8 and 9).
Results are summarised in Table 10, where “probable” means “real” or “casual?”. Thus, 334 (resp. 539) “probable” coincidences are found between S1 and S2, assuming an errorbar of 0.005 d-1 (resp. 0.010 d-1), which are considered as “real peaks”, hence intrinsic to the star. The last column refers to the number of “probable” matching frequencies among the first 300 peaks. Obviously, a few remaining peaks associated to the satellite orbital frequency must be removed from both datasets.
Summary of matching frequencies between the peaks obtained in the analysis of S1 and S2, where the last column refers to the “probable” coincidences among the first 300 peaks.
We now compare S1 and S2 with the dataset W. Results are listed in Tables 11 to 14. The former (latter) two tables give the matching frequencies within a range of 0.005 d-1 (0.010 d-1). Results are summarised in Table 15. The last column refers to “probable” coincidences among the first 300 peaks. Interestingly, the results for the two subsets are very similar. This indicates a very good consistency in both the datasets and the method used for the analysis.
As seen in Table 15, 646 (66%) “probable” matching frequencies are found between S1 and W, and 600 (67%) for S2 and W, if we assume an errorbar of 0.005 d-1. The corresponding values largely increase up to 871 (89%) and 790 (88%), respectively, if we consider a range of validation of 0.010 d-1, or 93%, for both subsets and the first 300 peaks.
Finally, we selected from Tables 11 and 12 frequencies that are not obviously linked to the satellite orbit. Only the “real” and “casual?” cases were considered. In addition, when more than one of these frequencies were within a given bin, only the frequency corresponding to the largest amplitude was retained. The resulting frequency list, the final result of the mf method, is given in Table 23, which has the same format as Tables 11 and 12 with an additional column mentioning if the retained frequency was also selected from the pc method (see Sect. 3.2). Therefore, 281 frequencies result from the mf method, which is a very poor number compared to the initial 1686 frequencies that were detected.
Summary of the matching frequencies detected in the S1 and S2 subsets versus the whole dataset W within a range of 0.005 and 0.010 d-1.
How can we explain the frequency peaks that do not appear simultaneously in the spectra of the two data subsets? We can distinguish two types: peaks that appear in either S1 or S2, but also in the whole dataset W, and peaks detected in either S1 or S2, but not in the whole dataset. A possible explanation for the first type is that they are related to frequencies that show amplitude and/or phase variations with short timescales (up to weeks), which produce different peak strengths at different epochs. The second type might be explained in terms of short-term, low-level inaccuracies, introduced by the reduction procedure or instrumental effects, which lead to distortions in the light curves and even to fictitious peaks in the spectrum.
On the other hand, we can also analyse the differences between peaks detected in S1 or S2 and the W dataset, Tables 16 and 17 (resp. 18 and 19) list the differences for S1 and S2 within a range of 0.005 d-1 (resp. 0.010 d-1). The results are summarised in Table 20. It is shown that there is a number of peaks in the subsets that are not found in the W dataset. However, this number largely decreases when we increase the range of validity from 0.005 to 0.010 d-1. Moreover, the results are excellent if we only consider the first 300 peaks.
Nevertheless, we feel that the frequency resolution ΔF = 1/ΔT of the present dataset can be an important source of misidentifications. In the present case, ΔF = 0.0073 d-1 and 777 frequency pairs are found closer than ΔF among our 1686 peaks (and 307 ones among the first 1000 peaks). The situation will not be so drastic in the case of a typical δ Sct pulsator where the frequency range for detection of excited modes is much larger. In the case of HD 49434, this problem might largely be improved if the timespan is increased up to, for example, two years. If ΔF = 0.0014 d-1, only 25 close pairs exist among the first 1000 peaks. Table 21 lists the uncontaminated peaks for HD 49434 assuming ΔF = 0.0073 d-1.
Peaks detected in subset S1 (or S2), but not in the whole dataset W. The last column refers to the first 300 peaks.
3.4. The phase constancy method
The above results suggest that several hundred detected peaks are intrinsic to the star. Nevertheless, the peak density between 0.05 and 4 d-1 is so high that there is a high probability of finding two frequencies closer than 0.010 d-1 in S1 and S2 and even closer than 0.005 d-1. In the previous section, the discrimination relied mainly on the amplitude values associated to each frequency present in the different subsets. Unfortunately, amplitude variations have been detected in many pulsation stars due either to intrinsic variations or the beat phenomenon. From the study of an artificial dataset having similar characteristics as the CoRoT dataset, containing several hundred frequencies, we found large differences between the equivalent S1 and S2 subsets. Thus, it may be that many rejected frequencies from the mf method can actually be real.
In the following, we used another method based on the hypothesis that an intrinsic frequency keeps the same phase value ϕ in each subset. We imposed the 1686 frequencies on the two subsets S1 and S2 with the Period04 software (Lenz & Breger 2005). To avoid accumulative errors from too many cycles, the date of the first observation was used as time reference T0. The phase difference 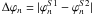 was computed for each frequency n. Figure 7 shows the histogram of the phase differences. It becomes immediately clear that most of the phase differences are relatively small, implying that most of the frequencies are real (according to our hypothesis). A total of 1235 frequencies have a phase difference smaller than 0.1 P and 762 smaller than 0.05 P, where P is the period value associated to the frequency used in the sine fit. Two groups can be distinguished when examining the frequencies with large phase differences: a group of very low frequencies, corresponding to trends in the CoRoT observations, and a group of low amplitude frequencies located close to (i.e., inside the Rayleigh criterion) larger amplitude frequencies. Therefore, the pc method automatically rejects the two types of frequencies that cannot be attributed to the stellar variations. The most difficult question remains: what is the limit in phase difference that is acceptable? Considering the phase uncertainties given by Breger (2008), we obtained a 3-σ uncertainty of 0.0651 P for the lowest amplitude frequencies. A total of 949 frequencies is thus retained within the 3-σ uncertainty. A further inspection of this list shows that a few frequencies are so close in value that they cannot be separated by our relatively short time basis. They are selected by chance, their phase differences being unexpectedly small. Frequencies obviously linked to the satellite orbital period are also detected from this list. Finally, the retained intrinsic frequencies, a total of 840, are provided in Table 22.
was computed for each frequency n. Figure 7 shows the histogram of the phase differences. It becomes immediately clear that most of the phase differences are relatively small, implying that most of the frequencies are real (according to our hypothesis). A total of 1235 frequencies have a phase difference smaller than 0.1 P and 762 smaller than 0.05 P, where P is the period value associated to the frequency used in the sine fit. Two groups can be distinguished when examining the frequencies with large phase differences: a group of very low frequencies, corresponding to trends in the CoRoT observations, and a group of low amplitude frequencies located close to (i.e., inside the Rayleigh criterion) larger amplitude frequencies. Therefore, the pc method automatically rejects the two types of frequencies that cannot be attributed to the stellar variations. The most difficult question remains: what is the limit in phase difference that is acceptable? Considering the phase uncertainties given by Breger (2008), we obtained a 3-σ uncertainty of 0.0651 P for the lowest amplitude frequencies. A total of 949 frequencies is thus retained within the 3-σ uncertainty. A further inspection of this list shows that a few frequencies are so close in value that they cannot be separated by our relatively short time basis. They are selected by chance, their phase differences being unexpectedly small. Frequencies obviously linked to the satellite orbital period are also detected from this list. Finally, the retained intrinsic frequencies, a total of 840, are provided in Table 22.
 |
Fig. 7 Histogram of the phase differences |
We point out that this method is very efficient in getting rid of the CoRoT trends as well as frequencies associated to the satellite orbit.
4. Discussion
A total of 1686 frequencies were detected in the CoRoT data of the γ Dor star HD 49434 using SigSpec up to spectral significance sig = 20. The density of frequencies is very high, especially between 0 and 8 d-1. In this region, the mean separation is equal to 0.00658 -1 which is lower than ΔF = 0.0073 -1. Among the 1686 frequencies, 777 pairs of frequency are closer than ΔF, so the number of separate frequencies falls down to 909. To verify the reality of this large amount of frequencies, we used two different methods, both based on the division of the whole data set into two equivalent subsets S1 and S2.
The first method, the mf method, is based on the hypothesis that the amplitude of a given frequency is relatively constant during the observing run. The advantage of this method is that we perform an independent frequency analysis on the two subsets. The inconvenience is that since S1 and S2 have a timespan half as long as the whole dataset, the width of the peaks doubles and the number of detected peaks decreases by a factor of 2. Another problem is that beating effects produce artificial amplitude variations that lead to the rejection of real frequencies. The first ten peaks coincide almost perfectly in the different datasets. Then, the amplitude decreases and the peak density increases, which makes it more and more difficult to decide which frequencies coincide. Finally, the result of the mf method consists of a list of 281 frequencies (Table 23) common to the two data sets and separated by more than 0.005 -1.
The second method, the pc method, is based on the hypothesis that the pulsation phase is constant during the whole observing period for any intrinsic frequency. The advantage of this method is that all the 1686 frequencies are tested. The inconvenience is that a few false frequencies are accidentally retained, if they by chance have small phase differences. Using the 3-σ criterion, the pc method results in a list of 949 frequencies. An important by-product of this method is the identification and removal of most of the frequencies corresponding to trends or harmonics and aliases of higher amplitude peaks. The frequencies closer than 0.005 -1 to a larger amplitude frequency, as well as frequencies close to harmonics of the orbital frequencies, are rejected. The final list includes 840 frequencies considered as intrinsic to the star (Table 22). Figure 8 summarizes the two lists of frequencies provided by both the mf and the pc methods.
 |
Fig. 8 Distribution of the detected frequencies from the frequency constancy method (upper panel) and the matching frequency method (lower panel). |
From the results presented above, it is evident that a large part of the significant peaks are intrinsic to HD49434, as they do not seem to depend on the frequency-analysis method used, nor are a consequence of instrumental effects or artifacts producing distortions in the light curves and fictitious peaks in the spectra.
What is the nature of the detected peaks? Do all these peaks correspond to an excited pulsation mode? If so, we are detecting photometrically excited modes corresponding to high (or very high)-degree ℓ-modes. In fact, modes up to ℓ = 14 have been successfully photometrically detected in the CoRoT dataset of the multiperiodic δ Sct target HD 50844 (Poretti et al. 2009). Moreover, Figs. 5 and 6 suggest that the threshold for such detections is about 0.2 mmag. This agrees with the results for HD 50844 or for the δ Sct-type pulsator FG Vir by Breger et al. (2005). It seems that the number of detected peaks highly increases in a near exponential way below this limit. This confirms the results of Daszyńska-Daskiewicz et al. (2006), who predict that high-degree ℓ-modes can be detected in high-accuracy photometric datasets, as the amplitude contrast is enhanced.
An important criterion concerns the definition of the spectral significance. We found 1686 peaks when assuming the limit sig = 20. The periodogram of the residuals after prewhitening 1686 frequencies is given in Fig. 9. Obviously, we did not deal with white noise, and frequencies still remain in the low-frequency domain. Considering sig = 5.5, the number of detected peaks increases to more than 2500. This huge amount of peaks can be explained in different ways. a) A large fraction of the peaks (mainly those with the highest amplitudes) are true pulsational peaks that correspond to excited modes with high-degree ℓ-modes. b) Some of the remaining peaks (mainly those with the lowest amplitudes) can also be residuals, resulting from an inexact extraction of the high-amplitude peaks in the prewhitening process. Consequently, later extractions of these residuals most likely introduce numerous new low-amplitude residual peaks.
 |
Fig. 9 Periodogram obtained from the residuals after prewhitening of 1686 detected frequencies using sig = 20. The red line represents the average considering an arbitrary frequency bin of 2 d-1. |
One way to investigate the genuineness of a low-amplitude peak is to search for low-amplitude peaks before extracting the high-amplitude ones. However, this method is limited, as it is very difficult to investigate the existence of a peak ranked at the low end of the list without extracting first several of its predecessors. A different procedure is needed.
To test the possibility that numerous frequencies of low amplitude are residuals in the prewhitening process, we searched for short-period fluctuations in the original data. To increase the precision of the curves, we smoothed the data with a sliding window over 5 points. In the region where the curve is relatively flat, small and rapid fluctuations with time scales around 0.01 d and amplitudes up to 0.2 mmag are easily seen (Fig. 10). The amplitudes of these irregular fluctuations are 30 times greater than the lowest amplitude peaks found in the frequency analysis of the global data set. These fluctuations are present everywhere in the observations and do not seem to be an effect of the smoothing. We tested different bins sizes (between 2 and 7 points) and found that the fluctuations are always present, and that their visibility increases with the quantity of points in the considered bin. As these fluctuations are not found in the analysis of the global data set, we searched for them in subsets. We studied the residuals obtained from the analysis of a subset of length 13.6 d prewhitened with up to 200 frequencies. We binned 5 points and searched for frequencies in the region 50–200 d-1. The highest peaks have an amplitude lower than 5 μmag, most of them lower than 3 μmag. When smaller parts of the set are analysed, the amplitude of the highest peaks increases from 8 to 15 μmag and up to 19 to 46 μmag for subsets of length 3 d and 0.5 d, respectively. A complete analysis (between 0 and 200 -1) was also performed on subsets with a sampling rate of 2 s. The fluctuations have frequencies between 30 and 120 -1, concentrated around 45–70 -1. But even with 50 frequencies, the fit remains very bad. It is only in very small subsets (of 0.05 d) that the fit is satisfactory: with fitting only 6 to 10 frequencies, the residuals decrease to 25 μmag. Clearly, we cannot represent the fluctuations as a sum of sinusoids, as we used to do with classical pulsations. They must be either irregular or of very short lifetime (of the orders of a few hours).
 |
Fig. 10 Zoom over a small region (0.1 d) of the original data set binned over 5 points. Rapid fluctuations are easily seen. |
5. Conclusions
In this work we present the results of the frequency analysis performed on the 5-month long-run CoRoT data of the target HD 49434. This star is a complex γ Dor-type pulsator with a very dense frequency spectrum. The frequency analysis was carried out using the computer program package SigSpec in a first step, and the results then refined with the package Period04. We identified significant peaks that may be harmonics or combination frequencies and frequencies of a possible instrumental nature or related with CoRoT’s orbital frequency.
A total of 1686 significant peaks are formally detected in the periodogram, essentially in the region below 15 d-1 using a formal conservative limit of spectral significance sig = 20 (limit in amplitude of 5.4 μmag). The frequency domain from 30 to 700 d-1 has also been investigated. Here, iterations were performed up to spectral significance sig = 5.5 (A ~ 3.0 μmag). However, no significant peaks have been found in this region, with the exception of high-order harmonics of the orbital frequency fs of the satellite or interactions between fs and remaining peaks in the very low-frequency domain. Solar-type oscillations are not detected in this star. Nevertheless, rapid fluctuations are present (Sect. 4), and their lack of coherence from one day to the next implies a very short lifetime of a few hours. Considering different scaling laws (e.g. Chaplin et al. 2009), p-mode lifetimes are a few days, hence longer than what is observed here. Therefore, the nature of the rapid fluctuations (also present in the CoRoT light curves of another γ Doradus candidate in the sismo-field, HD 171834, in preparation) remains unknown.
To study the reliability of such a high number of detected peaks, two independent methods were applied: the matching frequency (mf) and the phase constancy (pc) methods. After discussing the advantages and disadvantages of both methods, we retained the results provided by the pc method, as they seem more efficient for this case. Finally, we retained 840 peaks that are intrinsic to the star (Table 22).
Examples of time series simulations and expected noise and spectral significances.
Because of the γ Dor character of this star, the main modes are located mainly in the low-frequency region. As shown in Fig. 6, the number of peaks at higher frequencies increase as the amplitude decreases. The location of peaks in the frequency domain spread towards higher frequencies, up to about 14 d-1 for a limit in amplitude of ~5.5 μmag. Some peaks exist beyond 15 d-1, using both mf and pc methods. Only seven peaks are found with a frequency higher than 15.0 d-1 and not related to fs (Table 2). The one with the higher amplitude is f1432 = 20.6992 d-1 (A = 7.1 μmag). The six other peaks are f1488, f1510, f1570, f1584, f1631, and f1660 (four of them in the interval 15.0–15.6 d-1).
The nature of the modes still needs clarification. Assuming a pulsation constant of Q = 0.033 d (Handler & Shobbrook 2002), the fundamental mode of HD 49434 corresponds to a frequency of 18.4 d-1; i.e., all modes having a co-rotating frequency above this value are p-modes. The crucial problem here is the role of the rotation that leads to an apparent displacement of the mode by a quantity ∝ m Ω (1 − Cn,ℓ) at first order, where Ω is the rotation frequency and Cn,ℓ a term that depends on the structure of the star, a good approximation being 1 for p-modes and scaling as [ℓ(ℓ + 1)] -1 for g-modes. Owing to the relatively high rotation of HD 49434 (vsini = 84 km s-1, Paper I), the first-order approximation is not justified, and a more complete treatment should be applied. In the case of HD 49434, most of the modes are in the low frequency domain, and therefore should correspond to g- modes, as expected in γ Doradus stars. From Fig. 8 for instance, there is a clear distribution in the frequency density that is quite flat until about 8 d-1 and then decreases monotonically. The frequency 2.666 d-1 is a candidate for the rotation frequency3 (Paper I), and the corresponding shift is m × 1.333 d-1. For high m-values, some g-modes frequencies could indeed be shifted above the limit of 18.4 d-1 and could therefore mimic p-modes. Conversely, if p-modes are present in HD 49434, they can be spread towards the low-frequency region by the quantity m × 2.666 d-1, but also towards the higher frequency region, which is not observed. Finally, only one mode is unambiguously in the p-mode frequency region, f1432. It is also possible that if p-modes are excited, their amplitudes are so low that they remain undetected due to the conservative sig-parameter used in the present study. As shown in Fig. 9, the frequency amplitudes decrease very slowly towards higher frequency values (up to 30 d-1). The peaks in this region can be explained both through high m-values associated to g-modes (typically m ~ 20) and low-amplitude p-modes. At this point, we cannot classify the star as a hybrid γ Doradus star.
To summarise, this work confirms that the CoRoT mission can provide excellent datasets that are very suitable for asteroseismic studies of complex pulsating stars. Formally, we can perform a frequency analysis down to a limit of only a few μmag. In this way, hundreds of excited modes can be detected. This level of precision has never been reached to date, as it is impossible to achieve from ground-based observations.
Two questions remain: first, what is the real amplitude limit for a reliable detection? And, second, assuming that all the formally significant peaks detected are intrinsic to the star: do all the detected peaks correspond to stellar pulsation modes? From an energetic point of view, Moya & Rodríguez-López (2010) have shown that the star has enough energy to excite thousands of modes. In this context, the reality of many detected frequencies, as well as the automated processes used to detect them, may benefit greatly from observing the star again in the same conditions (i.e. long run) a few years later. Indeed, a larger timespan will strongly improve the frequency resolution, and would avoid part of the discussion concerning the matches of frequencies within too large a frequency bin. This objective will be at least partly fulfiled with the Kepler satellite that will observe the same stellar field for 3.5 years, containing many γ Dor variables, but unfortunately not HD 49434. In addition, the reality of eventual amplitude modulation of a given frequency will be studied in a safer way.
With the very first detection of several hundred frequencies in the γ Doradus star HD 49434, we took the first step in the challenging task of trying to understand the complex pulsational behaviour of this class of pulsators. The frequency input from this work will be the starting point for the ambitious project of mode identification and modelling of the star. A forthcoming paper will show that most (if not all) the peaks detected from ground-based data (photometry and spectroscopy) are recovered in the CoRoT light curve (Uytterhoeven et al., in preparation).
Because of their very low amplitudes (Table 1), aliases do not play a big role in our study. For example, fs ± 1 produces an amplitude level that corresponds to the peaks detected above the ~1300th rank in Table 2 (i.e. amplitudes lower than 8 μmag).
In some cases the comparison of both subsets suggests the presence of amplitude variations during the 150 d CoRoT run. For instance, the ground-based detected frequency F7 = 5.583 d-1, identified in the CoRoT dataset as f65 = 5.5838 d-1 (A = 0.139 mmag), corresponds to f41 = 5.5862 d-1 (A = 0.215 mmag) in subset S1 and as f213 = 5.5837 d-1 (A = 0.058 mmag) in subset S2. However, the apparent amplitude modulation might be a by-product of the frequency analysis: because both subsets do not have the same global multi-beat phases, any algorithms will modify the relative importance of any frequency peak.
Acknowledgments
This research was partially supported by the Junta de Andalucía and the Dirección General de Investigación (DGI) under projects AYA2006-06375 and ESP2004-03855-C03-01. P.J.A. acknowledges financial support from a “Ramon y Cajal” contract of the Spanish Ministry of Education and Science. E.P. and M.R. acknowledge financial support from the Italian ESS project, contract ASI/INAF I/015/07/0, WP 03170. The authors are very grateful to P. Lenz, M. Breger, and P. Reegen for making the computer programs Period04 and SigSpec available, essential for carrying out this work. E.R. is also in debt with M. Breger and P. Reegen for very useful comments. This research has made use of both the Simbad database, operated at CDS, Strasbourg, France, and the Astrophysics Data System, provided by NASA, USA.
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Michel, E., Auvergne, M., et al. 2006, ESASP, 624E, 34B [Google Scholar]
- Breger, M. 2008, Comm. Asteroseismol., 6, 156 [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Breger, M., Lenz, P., Antoci, V., et al. 2005, A&A, 435, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Dunham, E. W., & Jenkins, J. M. 1997, ASP Conf. Ser. 119, ed. D. Soderblom, 153 [Google Scholar]
- Chaplin, W. J., Houdek, G., Karoff, C., Elsworth, Y, & New, R. 2009, A&A, 500, 21 [Google Scholar]
- Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al., 2008, J. Phys. Conf. Ser., 118, 012039 [NASA ADS] [CrossRef] [Google Scholar]
- Daszyńska-Daskiewicz, J., Dziembowski, W. A., & Pamyatnykh, A. A. 2006, Mem. S.A.It., 77, 113 [Google Scholar]
- Handler, G., & Shobbrook, R. R. 2002, MNRAS, 333, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., Reegen, P., & Weiss, W. W. 2008, A&A, 481, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Kuschnig, R., Weiss, W. W., Gruber, R., et al. 1997, A&A, 328, 544 [NASA ADS] [Google Scholar]
- Lenz, P., & Breger, M. 2005, CoAst, 146, 5 [Google Scholar]
- Michel, E., Samadi, R., Baudin, F., et al. 2009, A&A, 495, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moya, A., & Rodríguez-López, C. 2010, ApJ, 710, 7 [Google Scholar]
- Poretti, E., Michel, E., Garrido, R., et al. 2009, A&A, 506, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez, E., Amado, P. J., Suárez, J. C., et al. 2006a, A&A, 450, 715 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodríguez, E., Costa, V., Zhou, A.-Y., et al. 2006b, A&A, 456, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roxburgh, I., Catala, C., & the Plato Consortium 2007, CoAst, 150, 357 [Google Scholar]
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Uytterhoeven, K., Mathias, P., Poretti, E., et al. 2008, A&A, 489, 1213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaniček, P. 1971, Ap&SS, 12, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, G., Matthews, J. M., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Time Series simulations
This Appendix illustrates the power of space data compared to what can be achieved from the ground through the results of simulations carried out with different examples of time series by comparing the expected noise and spectral significances.
We considered two types of ground-based photometric campaigns, mono- and multi-observatory runs. For the monosite observations we assumed 10 h of data collected every night, while we assume continuous data over 24 h every day for the multisite campaigns. Evidently, in this simulation we considered the ideal case of perfect campaigns without gaps due to bad photometric conditions or any other reason. We also considered runs for two different types of stars, one faint and one bright, with V = 9ṃ0 and V = 6ṃ0, respectively. The results are presented in Table A.1. The spectral significances are assumed as those corresponding to S/N = 4.0. For ground-based data, the estimation of precision and sampling interval between two consecutive datapoints is based on a typical case of Johnson V-filter differential photometry collected with a 75 cm telescope in an observational sequence with one main target and two check stars. The noise level is determined in each case in a box of width = 5 d-1 centred at frequency f = 20 d-1.
The results of the simulations are supported by those obtained from CoRoT satellite data. For instance, run number 7 can be compared with the CoRoT datastring of the star HD 50170 (V = 6ṃ82), which seems to be a constant star. The results from simulation and observational data are in very good agreement. On the other hand, run number 3 can be compared with the CoRoT time series of the multiperiodic δ Sct variable HD 50844 (V = 9ṃ10) (Poretti et al. 2009). The noise level of the CoRoT time series of this star in the region below 50 d-1, after removing 200 peaks, is about one order of magnitude higher than expected from the simulation. However, both noise levels agree for the region above 150 d-1.
Run number 6 can be compared with the multisite campaign carried out for the star FG Vir by Breger et al. (2005), the longest ground-based photometric campaign carried out up-to-date, hence probably the best dataset that one could expect from the ground. Table A.1 shows that the noise levels expected from runs 4 and 8 (the best ones from CoRoT) are about 25–30 times better than those expected from runs 2 and 6 (the best ones from the ground). Finally, from Table A.1 we can also see how the expected noise level approximately decreases as 1/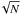 when the number N of the collected datapoints increases, or as ∝ σ, when the precision σ of the individual datapoints also decreases.
when the number N of the collected datapoints increases, or as ∝ σ, when the precision σ of the individual datapoints also decreases.
In the present case of HD 49434, for a datapoint distribution similar to the one collected by the CoRoT satellite, and assuming a precision σ ~ 0.12 mmag for the individual datapoints (as estimated from the original light curves), the noise level expected from our simulations is 0.36 ppm (that is, spectral significances of 1.44 ppm). This agrees with what we find in the present work in the out-of-interest region (frequency domain above 100 d-1).
All Tables
First ten significant peaks in the region 30–100 d-1. sig = spectral significance.
Summary of matching frequencies between the peaks obtained in the analysis of S1 and S2, where the last column refers to the “probable” coincidences among the first 300 peaks.
Summary of the matching frequencies detected in the S1 and S2 subsets versus the whole dataset W within a range of 0.005 and 0.010 d-1.
Peaks detected in subset S1 (or S2), but not in the whole dataset W. The last column refers to the first 300 peaks.
Examples of time series simulations and expected noise and spectral significances.
All Figures
 |
Fig. 1 Spectral window of the long-run CoRoT dataset on HD 49434. |
| In the text | |
 |
Fig. 2 Top panel: amplitude spectrum of the original data of HD 49434. Bottom panel: amplitude spectrum after removing the first 10 main peaks. |
| In the text | |
 |
Fig. 3 Amplitude spectra of the residuals of HD 49434 at different stages of the frequency analysis. |
| In the text | |
 |
Fig. 4 Example of the original light curves of HD 49434 and residuals at different stages of the frequency analysis. |
| In the text | |
 |
Fig. 5 Amplitude (top panel) and frequency (bottom panel) distributions of the peaks detected in HD 49434. |
| In the text | |
 |
Fig. 6 Amplitude of the detected peaks as a function of frequency for different intervals of amplitude in the region 0.05–18 d-1. The peaks a–d are related to fs: a = f504 = fs − 1 − fl, b = f636 = fs − 1 + fl, c = f572 = fs + 1 + fl, and d = f634 = fs + 1 − fl. |
| In the text | |
 |
Fig. 7 Histogram of the phase differences |
| In the text | |
 |
Fig. 8 Distribution of the detected frequencies from the frequency constancy method (upper panel) and the matching frequency method (lower panel). |
| In the text | |
 |
Fig. 9 Periodogram obtained from the residuals after prewhitening of 1686 detected frequencies using sig = 20. The red line represents the average considering an arbitrary frequency bin of 2 d-1. |
| In the text | |
 |
Fig. 10 Zoom over a small region (0.1 d) of the original data set binned over 5 points. Rapid fluctuations are easily seen. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


