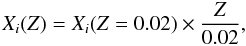| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015518 | |
| Published online | 23 November 2010 | |
Research Note
Convective overshooting and production of s-nuclei in massive stars during their core He-burning phase⋆
1
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio
5,
35122
Padova,
Italy
e-mail: mlpumo@oact.inaf.it
2
INAF – Osservatorio Astrofisico di Catania, via S. Sofia 78,
95123
Catania,
Italy
3
Università di Catania, Dip. di Fisica e Astronomia (Sez. Astrofisica), via S. Sofia
78, 95123
Catania,
Italy
Received: 3 August 2010
Accepted: 18 October 2010
Context. Many studies on the s-process and, more specifically, on the s-process weak component have been performed so far, but a detailed scrutiny of the impact of the stellar evolution modeling uncertainties on the efficiency of this nucleosynthesis process is still missing.
Aims. We analyze the role of convective overshooting on the production of s-nuclei in massive stars during their core He-burning phase.
Methods. With the “post-processing” technique we explore the role of the convective overshooting on the production of s-nuclei in stellar models of different initial mass and metallicity (15 ≤ MZAMS/M⊙ ≤ 25; 10-4 ≤ Z ≤ 0.02), considering a range of values for the parameter f, which determines the overall efficiency of convective overshooting.
Results. We find enhancements in the production of s-nuclei until a factor ~ 6 (measured as the average overproduction factor of the 6 s-only nuclear species with 60 ≲ A ≲ 90) in all our models of different initial mass and metallicity with f in the range 0.01 − 0.035 (i.e. models with overshooting) compared to the production obtained with “no-overshooting” models (i.e. models with the same initial mass and metallicity, but f = 10-5). Moreover the results indicate that the link between the overshooting parameter f and the s-process efficiency is essentially monotonic in all our models of different initial mass and metallicity. Also evident is the higher s-process efficiency when we progressively increase for a given f value both the mass of the models from 15 M⊙ to 25 M⊙ and the Z value from 10-4 to 0.02. We also briefly discuss the possible consequences of these results for some open questions linked to the s-process weak component efficiency, as well as a “rule of thumb” to evaluate the impact of the convective overshooting on the yields of a generation of stars.
Key words: nuclear reactions, nucleosynthesis, abundances / convection / stars: evolution / stars: interiors
Tables A.1 and A.2 are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/524/A45
© ESO, 2010
1. Introduction
As first pointed out by Burbidge et al. (1957), it is now widely accepted that about half of the elements between Fe and Bi are formed via the so-called s-process, through neutron capture reactions and beta decays along the “valley of stability”. It is also known that more than one s-process “component” (i.e. an event with a single set of physical conditions like neutron exposure, initial abundances and neutron density) is required in order to explain the observed solar distribution of s-nuclei abundances.
Current views on the subject suggest the existence of two components (so-called main and weak component of s-process, respectively) that, in terms of stellar environments, correspond to two distinct categories of stars in different evolutionary phases (e.g. Käppeler 1999). In particular, the main component is associated with low-mass stars (MZAMS ~ 1.5−3 M⊙) during their asymptotic giant branch (AGB) phase, and the main neutron source is the 13C(α,n)16O reaction; while the other one occurs in massive stars (MZAMS ≳ 13 M⊙) primarily during their core He-burning phase, and the main neutron source is the 22Ne(α,n)25Mg reaction.
In addition to these two components, other kinds of stars, such as massive AGB (MZAMS ~ 4−7 M⊙) and super-AGB stars ending their life as NeO white dwarfs (MZAMS ~ 7.5−10 M⊙; for details see e.g. Fig. 1 in Pumo et al. 2009b; but also Pumo & Siess 2007 or Pumo 2007, and references therein), could also contribute to the nucleosynthesis of s-species, but this hypothesis still needs further investigation (Pumo et al. 2009a, and references therein). Moreover, some studies (Gallino et al. 1998; Busso et al. 1999; Lugaro et al. 2003; Goriely & Siess 2004) suggest the existence of a “strong” component, which occurs in low-metallicity stars of low-intermediate mass during the AGB phase, and which is supposed to be responsible for the synthesis of “massive” (around 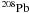 ) s-species. Furthermore, Travaglio et al. (2004) propose the existence of an additional component referred to as lighter element primary s-process (LEPP), but its nature is still unclear and under debate (e.g. Tur et al. 2009; Pignatari et al. 2010, and references therein).
) s-species. Furthermore, Travaglio et al. (2004) propose the existence of an additional component referred to as lighter element primary s-process (LEPP), but its nature is still unclear and under debate (e.g. Tur et al. 2009; Pignatari et al. 2010, and references therein).
Concerning the weak component, there is a wide consensus about the main characteristics of this nucleosynthesis process and, in particular, about its sensitivity to stellar mass and metallicity (e.g. Käppeler 1999). As for the dependence on the stellar mass, quantitative studies (see e.g. Prantzos et al. 1990; Käppeler et al. 1994; Rayet & Hashimoto 2000; The et al. 2000, 2007) show that the s-process weak component efficiency decreases with decreasing initial stellar mass, and that the shape of the distribution of the overproduction factors as a function of the mass number essentially does not depend on the initial stellar mass value. This behavior is connected to the fact that the reaction becomes efficient only for T ≳ 2,5 × 108 K, so the production of s-nuclei is more and more efficient when the initial stellar mass is increased, because more massive models burn helium at a “time averaged” higher temperature; however the ratio of the overproduction factor Fi of a given s-only nucleus i to the average overproduction factor F0 (see Sect. 4 for details on Fi and F0) remains fairly constant irrespective of the stellar mass, so the shape of the distribution of the overproduction factors does not change when the initial stellar mass is increased. As for the effect of metallicity, the s-process weak component efficiency depends on the so-called source/seed ratio1 (see e.g. Prantzos et al. 1990; Rayet & Hashimoto 2000). If the source/seed ratio is
constant with the metallicity Z, the efficiency is expected to increase
when increasing the Z value, because the effect of the
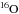 primary poison becomes less important
when the abundances of the source nuclei increase with Z,
For a non-constant source/seed ratio that increases when
decreasing Z, the efficiency (measured in terms of the number of neutrons
captured per initial
primary poison becomes less important
when the abundances of the source nuclei increase with Z,
For a non-constant source/seed ratio that increases when
decreasing Z, the efficiency (measured in terms of the number of neutrons
captured per initial 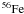 seed
nucleus nc; see also Sect. 4) has a non-linear behavior with Z, which reflects the interplay
between two opposite factors: from one hand, the aforementioned role of the
seed
nucleus nc; see also Sect. 4) has a non-linear behavior with Z, which reflects the interplay
between two opposite factors: from one hand, the aforementioned role of the
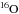 primary poison, which tends to
decrease nc with decreasing Z, because its
abundance remains the same independently of Z, so its relative importance
increases as Z decreases; on the other hand the effect of the increased
source/seed ratio, which tends to increase nc
with decreasing Z, because the number of available neutrons per nucleus
seed increases as Z decreases.
primary poison, which tends to
decrease nc with decreasing Z, because its
abundance remains the same independently of Z, so its relative importance
increases as Z decreases; on the other hand the effect of the increased
source/seed ratio, which tends to increase nc
with decreasing Z, because the number of available neutrons per nucleus
seed increases as Z decreases.
Although the general features of the s-process weak component seem to be well established therefore, there are still some open questions linked to the nuclear physics, the stellar evolution modeling, and the possible contribution to the s-nucleosynthesis from post-He-burning stellar evolutionary phases (see e.g. Woosley et al. 2002; Pumo et al. 2006, hereafter Paper I; Costa et al. 2006, hereafter Paper II).
Many works (see e.g. Meynet & Arnould 1993; Käppeler et al. 1994; Rayet & Hashimoto 2000; The et al. 2000, 2007; Hoffman et al. 2001; Tur et al. 2007, 2009; Pignatari et al. 2010; Bennett et al. 2010) have been devoted to analyze the uncertainties due to nuclear physics, linked both with the reaction rates of reactions affecting the stellar structure evolution (as, for example, the triple-alpha, the 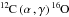 and the
and the 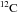 +
+ 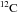 reactions) and with reaction rates on which the so-called “neutron economy” (i.e. the balance between neutron emission and captures) is based. The contribution to the synthesis of s-nuclei during the post-core-He-burning evolutionary phases was also explored by many authors (see e.g. Arcoragi et al. 1991; Raiteri et al. 1993; The et al. 2000, 2007; Hoffman et al. 2001; Rauscher et al. 2002; Limongi & Chieffi 2003; Tur et al. 2007, 2009), including in some cases the explosive burning (see e.g. Hoffman et al. 2001; Rauscher et al. 2002; Limongi & Chieffi 2003; Tur et al. 2007, 2009).
reactions) and with reaction rates on which the so-called “neutron economy” (i.e. the balance between neutron emission and captures) is based. The contribution to the synthesis of s-nuclei during the post-core-He-burning evolutionary phases was also explored by many authors (see e.g. Arcoragi et al. 1991; Raiteri et al. 1993; The et al. 2000, 2007; Hoffman et al. 2001; Rauscher et al. 2002; Limongi & Chieffi 2003; Tur et al. 2007, 2009), including in some cases the explosive burning (see e.g. Hoffman et al. 2001; Rauscher et al. 2002; Limongi & Chieffi 2003; Tur et al. 2007, 2009).
As for the impact of uncertainties owing to stellar evolution modeling, the determination of the size of the convective core and, more in general, of the mixing regions represents one of the major problems in calculating stellar structure and its evolution (see e.g. Zahn 1991; Young et al. 2003), which may directly affect the efficiency of the s-process nucleosynthesis by influencing the chemical and local temperature stratification (see e.g. Canuto 1997; Molawi & Forestini 1994; Deng & Xiong 2008), by determining the amount of stellar material which experiences neutron irradiation (see e.g. Langer et al. 1989), and by giving rise to a variation of the s-process lifetime2 (see e.g. Paper II). The convective core’s extension of a star with a given initial mass and metallicity is determined in turn by a series of physical parameters such as the choice of the convective instability criterion (Schwarzschild’s or Ledoux’s criteria), the extra mixing processes induced by axial rotation and convective overshooting (see e.g. Chiosi et al. 1992; Woosley et al. 2002).
A series of studies have been devoted to analyze the effects of these physical parameters on the evolution of massive stars (see e.g. Meynet & Maeder 1997, 2000; Heger et al. 2000; Woosley et al. 2002; Hirschi et al. 2004; Limongi & Chieffi 2006; El Eid et al. 2009) and to examine the corresponding impact on the s-process weak component (see e.g. Langer et al. 1989; Paper I; Paper II; Pignatari et al. 2008). As far as the convective overshooting is concerned, one finds that this extra mixing process leads to an increase of the convective core mass and to a variation of the chemical and temperature stratification that in turn tend to enhance the s-process weak component efficiency by giving rise to an increase of the amount of material that experiences neutron irradiation and to a variation of the s-process lifetime (see e.g. Paper II, for more details); however, a detailed scrutiny of the role of convective overshooting on the production of s-nuclei in massive stars is still missing.
In the light of our preparatory studies on this topic (Paper I and Paper II), which show a not negligible impact of the convective overshooting on the s-process during core He-burning in a 25 M⊙ star (ZAMS mass) with an initial metallicity of Z = 0.02, we believe it is worthwhile examining this issue further by analyzing the s-process efficiency in stellar models of different initial mass and metallicity (15 ≤ MZAMS/M⊙ ≤ 25; 10-4 ≤ Z ≤ 0.02).
We are aware that a full understanding of how the convective overshooting affects the s-nucleosynthesis process efficiency requires studies on the stellar evolution (possibly including explosive burning), fully describing the correlated nucleosynthesis processes. Nevertheless, we believe that the first step is an analysis of the impact of the convective overshooting on the s-process during core He-burning, which represents the primary evolutionary phase where the physical conditions are suitable for the neutron capture nucleosynthesis in massive stars.
To perform this analysis, as we did already in Paper I and Paper II, we use a diffusive approach to model the convective overshooting. According to this approach (for details see e.g. Freytag et al. 1996; Herwig et al. 1997, and reference therein), a free parameter – the so-called overhooting parameter f – determines the efficiency of the extra mixing due to the convective overshooting, so that a higher value of f implies a bigger extension of the extra mixing outside the convective region (see also Sect. 2.1). Salasnich et al. (1999) give some indications on how to fix the parameter f in stellar models of massive stars and, in particular, claim a setting of this parameter to a value of ~0.015 in order to reproduce the observed distribution of massive stars across the HR diagram; however, other works (see e.g. Young et al. 2001; Deng & Xiong 2008) indicate that massive starts could have a more extended overshooting region (compared to what is obtained using f = 0.015), that the f value may be mass dependent and, consequently, that a higher f value cannot be excluded for massive stars. Thus, since the proper f value is still widely debated, we prefer to consider a whole range of its possible values (f3 = 0.01, 0.02 and 0.035 for models with overshooting, and f = 10-5 for models without overshooting).
2. Input physics
2.1. The stellar evolution code
The stellar data were calculated starting from ZAMS until the end of core He-burning with the same stellar evolution code described in Paper I and Paper II (see also Weiss & Schlattl 2000; Bonanno et al. 2002, for details), but with the 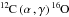 reaction rate taken from NACRE (Nuclear Astrophysics Compilation of REaction rates, Angulo et al. 1999). A complete description of the input physics used for calculating the stellar models can be found in Paper II; however we recall the main features concerning the treatment of the mixing here.
reaction rate taken from NACRE (Nuclear Astrophysics Compilation of REaction rates, Angulo et al. 1999). A complete description of the input physics used for calculating the stellar models can be found in Paper II; however we recall the main features concerning the treatment of the mixing here.
The mixing is treated as a diffusive process, and accordingly nuclear species abundance changes are calculated with the equation ![\begin{equation} \label{diffusion} \frac{{\rm d}X}{{\rm d}t} = \left(\frac{\partial X}{\partial t}\right)_{\rm nuc} + \frac{\partial}{\partial m_r}\left[\left(4\pi r^2 \rho\right)^2 D \frac{\partial X}{\partial m_r} \right]_{\rm mix}, \end{equation}](/articles/aa/full_html/2010/16/aa15518-10/aa15518-10-eq41.png) (1)where the first term on the right is the time derivative of a given isotopic abundance (mass fraction) owing to nuclear reactions, while the second is the diffusive term that describes mixing.
(1)where the first term on the right is the time derivative of a given isotopic abundance (mass fraction) owing to nuclear reactions, while the second is the diffusive term that describes mixing.
The difference among convective, overshooting, and radiative regions lies in the relation used to evaluate the value of the diffusion coefficient D. In convective zones (established through the Schwarzschild criterion) D is given by 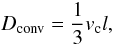 (2)where vc is the average velocity of convective elements derived according to the mixing length theory and l = α × Hp is the mixing length (Hp is the pressure scale height and α is mixing length parameter put to 1.7 in our calculations). Beyond convective zones (overshooting regions), the following relation is used instead:
(2)where vc is the average velocity of convective elements derived according to the mixing length theory and l = α × Hp is the mixing length (Hp is the pressure scale height and α is mixing length parameter put to 1.7 in our calculations). Beyond convective zones (overshooting regions), the following relation is used instead: 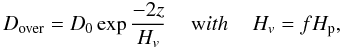 (3)where D0 is the value of Dconv at the upper radial edge of the convective core, z = | r − redge | is the radial distance from the same edge, and f is the so-called overshooting parameter, which determines the overall efficiency of convective overshooting. For z ≫ 1 (radiative regions) the diffusion coefficient is ~ 0, and abundance changes are only due to the nuclear reaction term in Eq. (1).
(3)where D0 is the value of Dconv at the upper radial edge of the convective core, z = | r − redge | is the radial distance from the same edge, and f is the so-called overshooting parameter, which determines the overall efficiency of convective overshooting. For z ≫ 1 (radiative regions) the diffusion coefficient is ~ 0, and abundance changes are only due to the nuclear reaction term in Eq. (1).
2.2. The nucleosynthesis code
The s-nucleosynthesis code, the s-process network, and the coupling of nucleosynthesis simulations with stellar evolution data are the same as described in Paper I and Paper II in detail. However, concerning the s-process network, we recall that it includes 472 nuclides (up to  ) linked by 834 reactions, and allows us to follow the nucleosynthesis of all the s-species up to
) linked by 834 reactions, and allows us to follow the nucleosynthesis of all the s-species up to 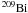 . Moreover, as for the coupling of nucleosynthesis simulations with stellar evolution data, we recall that the “post-processing” technique is used according to the prescriptions described by Prantzos et al. (1987) in addition to those reported in Kippenhahn & Weigert (1990) to take into account the inclusion of not previously mixed material into the “mixing” zones (convective plus overshooting regions) when these latter expand.
. Moreover, as for the coupling of nucleosynthesis simulations with stellar evolution data, we recall that the “post-processing” technique is used according to the prescriptions described by Prantzos et al. (1987) in addition to those reported in Kippenhahn & Weigert (1990) to take into account the inclusion of not previously mixed material into the “mixing” zones (convective plus overshooting regions) when these latter expand.
3. Models
We performed 22 s-process simulations considering two grids of stellar models (see also Table 1) with different initial (i.e. at ZAMS) masses (15 ≤ MZAMS/M⊙ ≤ 25), initial metallicities4 (10-4 ≤ Z ≤ 0.02) and overshooting parameter values (f = 10-5, 0.01, 0.02 and 0.035).
 |
Fig. 1 Overproduction factor for the six s-species |
Stellar models.
The first grid, composed of models with a given initial metallicity (see sets (a), (b), and (c) of grid (1) in Table 1), permits us to devote particular attention to the impact of convective overshooting in stellar models of different initial mass. Since a detailed study on the impact of the convective overshooting on the s-process of a Z = 0.02, M = 25 M⊙ stellar model was already performed in Paper I and Paper II, here we repeated the s-process simulations for this stellar model considering only two value of f (see set (c) of the grid (1) in Table 1), in order to study the effect of the change of the 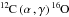 reaction rate in the stellar evolution code.
reaction rate in the stellar evolution code.
The second grid, which is composed of models with a given initial mass (see sets (a), (b), and (c) of grid (2) in Table 1), coupled with the set (b) of grid (1) in Table 1, gives us the opportunity to analyze the role of the core overshooting in stellar models of different initial metallicity.
4. Parameters describing the s-process efficiency and results
The s-process efficiency was analyzed in terms of the same s-process efficiency indicators used in Paper I and Paper II, namely:
-
the average overproduction factor F0 for the 6 s-only nuclei
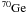 ,
, 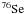 ,
, 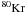 ,
, 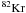 ,
, 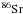 and
and 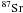 , given by
, given by 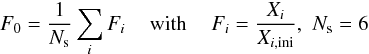 where Fi is the overproduction factor, Xi is the mass fraction (averaged over the convective He-burning core) of s-only nucleus i at the end of s-process, Xi,ini is the initial mass fraction of the same nucleus, and Ns is the number of the s-only nuclei within the mass range 60 ≤ A ≤ 87;
where Fi is the overproduction factor, Xi is the mass fraction (averaged over the convective He-burning core) of s-only nucleus i at the end of s-process, Xi,ini is the initial mass fraction of the same nucleus, and Ns is the number of the s-only nuclei within the mass range 60 ≤ A ≤ 87; -
the maximum mass number Amax for which the species in the 60 ≤ A ≤ Amax mass range are overproduced by at least a factor of about 10 and 5 (first and second value respectively in the third column of Tables 2 and 3);
-
the number of neutrons captured per initial
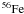 seed nucleus nc;
seed nucleus nc; -
the maximum convection zone mass extension (hereafter MCZME) during the core He-burning s-process;
-
the duration of core He-burning s-process.
The results for the first grid (i.e. grid (1) in Table 1) are summarized in terms of the previous parameters in Table 2, and the overproduction factors of the s-only nuclei within the mass range 60 ≤ A ≤ 87 as a function of nuclear mass number A are reported in Figs. 1 to 3. Results concerning the second grid (i.e. grid (2) in Table 1) are shown in Table 3 and in Figs. 4 to 6.
 |
Fig. 3 As in Fig. 1, but for Z = 0.02, M = 25 M⊙ stellar models with overshooting parameter f = 10-5 and 0.01 (see labels). Solid lines shown our results obtained with stellar models using the NACRE rate for |
Moreover, for the sake of completeness, the overproduction factors of all the s-only nuclei within the mass range 69 ≤ A ≤ 209 for all our s-process simulations are reported in Tables A.1 and A.2, in addition to a comparison with previous computations by The et al. (2007) for their stellar models with a similar mass, metallicity and input physics. Other comparisons can be found in Paper II.
5. Discussion
For all the stellar models of different initial mass and metallicity, the s-process efficiency increases when overshooting is inserted in the evolutionary computations compared with “no-overshooting” models, as found in Paper I and Paper II for simulations referring to a 25 M⊙ star model with an initial metallicity of Z = 0.02. Indeed, for all our sets of models with a fixed initial mass and metallicity, a not negligible enhancement of the s-process efficiency occurs when passing from the “no-overshooting” model (f = 10-5) of a set to any model of the same set including overshooting, with enhancements for the main s-process indicators F0 and nc until a factor ~ 6 and ~ 3, respectively.
Moreover an essentially monotonic link between the f value and the s-process efficiency is evident when overshooting is inserted in the evolutionary computations, as witnessed by the fact that both main s-process indicators F0 and nc (and all the s-process efficiency indicators more in general) gradually grow when passing from f = 0.01 to 0.035 for any set of models with a fixed initial mass and metallicity. The only exceptions to this last behavior occur for the two models with f = 0.01 having Z = 10-4 and Z = 0.01, which give birth to a more efficient s-process than the one obtained for the corresponding models with f = 0.02 (see sets (a) and (c) of Table 3, and Figs. 4 and 6). The reason of this not strictly monotonic increase of the s-process efficiency with the f value may be due to the particularly long duration of the core He-burning s-process for the two models with f = 0.01, which leads to the enhancement of the F0 and nc values and, consequently, of the s-process efficiency because of a longer neutron exposure (see also Paper II, for details). Indeed, the duration of the core He-burning s-process for the model with f = 0.01 having Z = 10-4 is almost equal to the one of the “no-overshooting” model with same initial metallicity (see set (a) of Table 3), while the duration of the core He-burning s-process for model with f = 0.01 having Z = 0.01 is the longest with respect to all the other 20 M⊙ stellar models of different initial metallicity with overshooting (see Table 3 and set (b) of Table 2).
Also evident is a clear trend with both initial mass and Z (excluding two exceptions discussed below) when setting the f value, according to which the s-process efficiency increases when we progressively increase both the mass of the models from 15 M⊙ to 25 M⊙ (see Table 2) and the Z value from 10-4 to 0.02 (see Table 3 and set (b) of Table 2), confirming the results found in other works referring to evolutionary computations without extra mixing processes owing to convective overshooting (see e.g. Prantzos et al. 1990; Rayet & Hashimoto 2000; The et al. 2000, 2007). As already mentioned in Sect. 1, the increase in s-process efficiency with the initial mass is connected to the fact that the reaction and, consequently, the production of s-nuclei is more and more efficient when the initial stellar mass is increased; instead the enhancement of the s-process efficiency with Z is linked to the fact that the source/seed ratio is constant with Z in our models, so the efficiency increases when the Z value is increased. The only exceptions to this last trend occurs for the two models with Z = 0.01 having f = 10-5 and f = 0.01 (set (b) of Table 2), which give rise to a more efficient s-process than the one obtained for the corresponding models with Z = 0.02 (set (c) of Table 3). Once again the reason for this behavior may be connected to the same previously explained effects that are related to the longer duration of the core He-burning s-process for the two models with Z = 0.01 (compared to the one of the corresponding models with Z = 0.02), which leads to the enhancement of the s-process efficiency.
In addition we find that the use of the NACRE rate for the 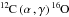 reaction gives rise to a lower s-process efficiency (see Fig. 3). This behavior seems to be connected both to the smaller lifetime of the He-burning phase in our new 25 M⊙ models – compared to those from Paper I and Paper II – which has a direct impact on the neutron exposure of the s-process seed (mainly
reaction gives rise to a lower s-process efficiency (see Fig. 3). This behavior seems to be connected both to the smaller lifetime of the He-burning phase in our new 25 M⊙ models – compared to those from Paper I and Paper II – which has a direct impact on the neutron exposure of the s-process seed (mainly 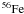 ), and to a higher availability of α particles during the late He-burning phase because less α particles are consumed by the
), and to a higher availability of α particles during the late He-burning phase because less α particles are consumed by the 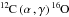 reaction because of the lower rate, as suggested by The et al. (2000). Moreover, although this reaction has only a relatively small influence on the efficiency of the s-process during the He-burning phase (see also The et al. 2007), its impact seems to be more important and, consequently, not negligible when the overshooting is inserted in stellar models. Indeed, the diminution (a factor of ~ 1.5) in the average overproduction factor F0 for the model with overshooting is higher than that (a factor of ~ 1.1, i.e. in practice unchanged) for the model without overshooting, and a similar behavior is found for all remaining s-process efficiency indicators.
reaction because of the lower rate, as suggested by The et al. (2000). Moreover, although this reaction has only a relatively small influence on the efficiency of the s-process during the He-burning phase (see also The et al. 2007), its impact seems to be more important and, consequently, not negligible when the overshooting is inserted in stellar models. Indeed, the diminution (a factor of ~ 1.5) in the average overproduction factor F0 for the model with overshooting is higher than that (a factor of ~ 1.1, i.e. in practice unchanged) for the model without overshooting, and a similar behavior is found for all remaining s-process efficiency indicators.
Furthermore, comparing Fig. 2 with Figs. 1 and 3 (see also Table 2), it appears that the s-nuclei production in the Z = 0.02 models with f ~ 0.02 − 0.035 having a given initial mass Mini seems to have a behavior similar to that of the Z = 0.02 models without convective overshoot and with an initial mass ~ Mini + 5 M⊙. This behavior could give some indication on how the convective overshooting affects the yield of a generation of stars. Indeed, the integrated yields of stellar models with convective overshooting would be, at a first approximation, simply calculated from to the integrated yield of stellar models without overshooting, but shifted appropriately in mass. For example, to give a clue about the impact on the integrated yield of stellar models with f ~ 0.02 − 0.035, the number of 15 M⊙ stars (evaluated according a given initial mass function) should be multiplied by the yields (evaluated from models without convective overshooting) of the 20 M⊙ stars and a similar shift could be used for other masses.
6. Summary and further comments
Many studies have been devoted to the s-process weak component so far, but a detailed scrutiny of the impact of the stellar evolution modeling uncertainties on this component is still missing. In the light of our preparatory studies on this topic (Paper I and Paper II), we performed a comprehensive and quantitative study on the role of convective overshooting, considering stellar models with different initial mass and metallicity (15 ≤ MZAMS/M⊙ ≤ 25; 10-4 ≤ Z ≤ 0.02).
To perform this analysis, we used the same procedure as described in Paper I and Paper II. According to this procedure, stellar models have been evolved until He exhaustion in the core, using a diffusive approach to describe the convective overshooting where a so-called overshooting parameter f determines the extension of the convectively mixed core and, consequently, the overall efficiency of convective overshooting. Then models have been used to “post-process” the stellar nuclidic composition with our s-nucleosynthesis code.
The results show that models with overshooting give a higher s-process efficiency compared with “no-overshooting” models for a given initial mass and metallicity. Less important but not negligible variations are clearly visible when changing the overshooting parameter f value in the 0.01 − 0.035 range, and the link between the f value and the s-process indicators values is essentially monotonic in all our models of different initial mass and metallicity. Also evident is the higher s-process efficiency when for a given f value we progressively increase both the mass of the models from 15 M⊙ to 25 M⊙ and the Z value from 10-4 to 0.02.
These results clearly show the level of uncertainty (up to a factor ~ 6) in the modeling of the weak s-process component due to the current lack of a self-consistent theory describing mixing processes inside the stars. Thus, prior to giving a final conclusion on the possible contribution of post-He burning phases to the s-process yields from a quantitative point of view, some additional investigation taking into account stellar evolution uncertainties in addition to the nuclear physics ones should be performed. Moreover, this additional investigation may shed light on different open questions linked, for example, to the effective existence of the LEPP process and to the model for the p-process
taking place in the type II supernovae O-Ne layers, because the relevant s-nuclei are p-process seeds (see e.g. Arnould & Goriely 2003, and references therein).
Considering that the 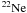 is the main neutron provider during the core He-burning phase and neglecting all the heavier
is the main neutron provider during the core He-burning phase and neglecting all the heavier 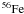 nuclei, one obtains:
nuclei, one obtains:
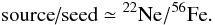 This last quantity approximately corresponds to the
This last quantity approximately corresponds to the 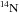 /
/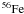 ratio at the end of the core H-burning phase which, in turn, is roughly equal to the O/
ratio at the end of the core H-burning phase which, in turn, is roughly equal to the O/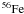 ratio at the ZAMS (see Prantzos et al. 1990; Rayet & Hashimoto 2000, for details).
ratio at the ZAMS (see Prantzos et al. 1990; Rayet & Hashimoto 2000, for details).
The s-process lifetime essentially represents the time duration where the physical conditions are suitable to synthesize s-nuclei and, more in general, to change their abundance. Following the definition adopted in Paper I and Paper II, the s-process lifetime can be evaluated according to the relation
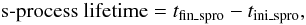 with
with 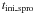 defined as the time in which the temperature at the stellar center Tc is log Tc = 8, and
defined as the time in which the temperature at the stellar center Tc is log Tc = 8, and 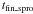 defined as the time where the extension of the convective core is reduced to zero and log Tc = 8.6.
defined as the time where the extension of the convective core is reduced to zero and log Tc = 8.6.
In some previous studies about the s-process weak component (e.g. Arcoragi et al. 1991), the approach used to model the convective overshooting is based on an artificial enhancement of the convective core extension by a quantity αov × Hp, where αov is a free parameter and Hp is the pressure scale height estimated at the upper radial edge of the convective core established through the Schwarzschild criterion. The extent of the overshooting region obtained with this instantaneous mixing approach corresponds approximately to what is expected using a diffusive approach when setting f = 0.1 × αov (see e.g. Salasnich et al. 1999; Herwig et al. 1997).
The initial mass fractions of metals for the Z = 0.02 models are taken to be equal to the values used in Papers I and II to make our results comparable to those reported in these papers. The initial mass fractions of metals for the models with Z < 0.02 are scaled from the values of the Z = 0.02 models in a way that their relative abundances are the same as in the Z = 0.02 models and, consequently, are given by the relation
where Xi(Z) is the initial mass fraction of ith metal for the models with Z < 0.02 and Xi(Z = 0.02) is the initial mass fraction of the same element for the Z = 0.02 models.
Acknowledgments
M.L.P. acknowledges the support by the Padua municipality “Padova Città delle Stelle” prize and by the Bonino-Pulejo Foundation. We also warmly thank the referee G. Meynet for his valuable suggestions to improve our manuscript.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 1, 196 [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, NuPhA, 656, 3 (NACRE) [MathSciNet] [Google Scholar]
- Arcoragi, J.-P., Langer, N., & Arnould, M. 1991, A&A, 249, 134 [NASA ADS] [Google Scholar]
- Arnould, M., & Goriely, S. 2003, Phys. Rep., 384, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, M. E., Hirschi, R., Pignatari, M., et al. 2010, Proceedings for the Nuclear Physics in Astrophysics IV conference [arXiv:1002.2788] [Google Scholar]
- Bonanno, A., Schlattl, H., & Paternò, L. 2002, A&A, 390, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, RvMP, 29, 547 [Google Scholar]
- Busso, M., Gallino, R., & Wasserburg, G. J. 1999, ARA&A, 37, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M. 1997, ApJ, 601, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Chiosi, C., Bertelli, G., & Bressan, A. 1992, ARA&A, 30, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Costa, V., Pumo, M. L., Bonanno, A., & Zappalà, R. A. 2006, A&A, 447, 641 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deng, L., & Xiong, D. R. 2008, MNRAS, 386, 1979 [NASA ADS] [CrossRef] [Google Scholar]
- El Eid, M. F., The, L.-S., & Meyer, B. S. 2009, Space Sci. Rev., 147, 1 [Google Scholar]
- Freytag, B., Ludwig, H.-G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goriely, S., & Siess, L. 2004, A&A, 421, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Blöcker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, 81 [Google Scholar]
- Hirschi, R., Meynet, G., & Maeder, A. 2004, A&A, 425, 649 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoffman, R. D., Woosley, S. E., & Weaver, T. A. 2001, ApJ, 549, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Käppeler, F. 1999, Progress in Particle and Nuclear Physics, 43, 419 [Google Scholar]
- Käppeler, F., Wiescher, M., Giesen, U., et al. 1994, ApJ, 437, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar structure and Evolution (Berlin Heidelberg: Springer-Verlag) [Google Scholar]
- Langer, N., Arcoragi, J.-P., & Arnould, M. 1989, A&A, 210, 187 [NASA ADS] [Google Scholar]
- Limongi, M., & Chieffi, A. 2003, ApJ, 592, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Herwig, F., Lattanzio, J. C., Gallino, R., & Straniero, O. 2003, ApJ, 586, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Meynet, G., & Arnould, M. 1993, in: Nuclei in the Cosmos II, ed. F. Käppeler, & K. Wisshak (Bristol: IOP), 487 [Google Scholar]
- Meynet, G., & Maeder, A. 1997, A&A, 321, 465 [NASA ADS] [Google Scholar]
- Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] [Google Scholar]
- Mowlavi, N., & Forestini, M. 1994, A&A, 282, 843 [NASA ADS] [Google Scholar]
- Pignatari, M., Gallino, R., Meynet, G., et al. 2008, ApJ, 687, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Arnould, M., & Arcoragi, J.-P. 1987, ApJ, 315, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., Hashimoto, M., & Nomoto, K. 1990, A&A, 234, 211 [NASA ADS] [Google Scholar]
- Pumo, M. L. 2007, MmSAI, 78, 689 [Google Scholar]
- Pumo, M. L., & Siess, L. 2007, ASPC, 378, 133 [NASA ADS] [Google Scholar]
- Pumo, M. L., Costa, V., Bonanno, A., et al. 2006, Mem. S.A.It. Suppl., 9, 263 (Paper I) [Google Scholar]
- Pumo, M. L., Ventura, P., D’Antona, F., & Zappalà, R. A. 2009a, MmSAI, 80, 161 [NASA ADS] [Google Scholar]
- Pumo, M. L., Turatto, M., Botticella, M. T., et al. 2009b, ApJ, 705, L138 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Gallino, R., Busso, M., Neuberger, D., & Käppeler, F. 1993, ApJ, 419, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, T., Heger, A., Hoffman, R. D., & Woosley, S. E. 2002, ApJ, 576, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Rayet, M., & Hashimoto, M. 2000, A&A, 354, 740 [NASA ADS] [Google Scholar]
- Weiss, A., & Schlattl, H. 2000, A&AS, 144, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salasnich, B., Bressan, A., & Chiosi, C. 1999, A&A, 342, 131 [NASA ADS] [Google Scholar]
- The, L.-S., El Eid, M. F., & Meyer, B. S. 2000, ApJ, 533, 998 [NASA ADS] [CrossRef] [Google Scholar]
- The, L.-S., El Eid, M. F., & Meyer, B. S. 2007, ApJ, 655, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Travaglio, C., Gallino, R., Arnone, E., et al. 2004, ApJ, 601, 864 [NASA ADS] [CrossRef] [Google Scholar]
- Tur, C., Heger, A., & Austin, S. M. 2007, ApJ, 671, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Tur, C., Heger, A., & Austin, S. M. 2009, ApJ, 702, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Heger, A., & Weaver, T. A. 2002, RvMP, 74, 1015 [NASA ADS] [Google Scholar]
- Young, P. A., Mamajek, E. E., Arnett, D., & Liebert, J. 2001, ApJ, 556, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. A., Knierman, K. A., Rigby, J. R., & Arnett, D. 2003, ApJ, 595, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Zahn, J. P. 1991, A&A, 252, 179 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Overproduction factor for the six s-species |
| In the text | |
 |
Fig. 2 As in Fig. 1, but for Z = 0.02, M = 20 M⊙ stellar models. |
| In the text | |
 |
Fig. 3 As in Fig. 1, but for Z = 0.02, M = 25 M⊙ stellar models with overshooting parameter f = 10-5 and 0.01 (see labels). Solid lines shown our results obtained with stellar models using the NACRE rate for |
| In the text | |
 |
Fig. 4 As in Fig. 1, but for Z = 10-4, M = 20 M⊙ stellar models. |
| In the text | |
 |
Fig. 5 As in Fig. 1, but for Z = 0.005, M = 20 M⊙ stellar models. |
| In the text | |
 |
Fig. 6 As in Fig. 1, but for Z = 0.01, M = 20 M⊙ stellar models. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.