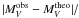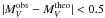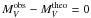| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 11 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015237 | |
| Published online | 22 November 2010 | |
Constraints on the origin of the massive, hot, and rapidly rotating magnetic white dwarf RE J 0317-853 from an HST parallax measurement⋆
1
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität
Heidelberg,
Mönchhofstr. 12-14,
69120
Heidelberg,
Germany
e-mail: bkulebi@ari.uni-heidelberg.de
2
Space Telescope Science Institute, 3700 San Martin Dr, Baltimore, MD
21218,
USA
Received: 18 June 2010
Accepted: 26 July 2010
Aims. We use the parallax measurements of RE J 0317-853 to determine its mass, radius, and cooling age and thereby constrain its evolutionary origins.
Methods. We observed RE J 0317-853 with the Hubble Space Telescope’s Fine Guidance Sensor to measure the parallax of RE J 0317-853 and its binary companion, the non-magnetic white dwarf LB 9802. In addition, we acquired spectra of comparison stars with the Boller & Chivens spectrograph of the SMARTS telescope to correct the parallax zero point. For the corrected parallax, we determine the radius, mass, and the cooling age with the help of evolutionary models from the literature.
Results. The properties of RE J 0317-853 are constrained using the parallax information. We discuss the different cases of the core composition and the uncertain effective temperature. We confirm that RE J 0317-853 is close to the Chandrasekhar’s mass limit in all cases and almost as old as its companion LB 9802.
Conclusions. The precise evolutionary history of RE J 0317-853 depends on our knowledge of its effective temperature. It is possible that it had a single star progenitor possible if we assume that the effective temperature is at the cooler end of the possible range from 30000 to 50000 K; if Teff is instead at the hotter end, a binary-merger scenario for RE J 0317-853 becomes more plausible.
Key words: white dwarfs / stars: magnetic field / binaries: visual / stars: distances / stars: individual: RE J 0317-853 / supernovae: individual: LB 9802
Based on observations made with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. The Guide Star Catalogue-II is a joint project of the Space Telescope Science Institute and the Osservatorio Astronomico di Torino.
© ESO, 2010
1. Introduction
RE J 0317-853 is a unique hydrogen-rich white dwarf, which was discovered as an EUV source by the ROSAT Wide Field Camera (Barstow et al. 1995). An analysis of follow-up spectroscopy established that the stellar surface is covered by a very strong magnetic field with a range of about 170–660 MG, implying that RE J 0317-853 has one of the strongest magnetic fields detected so far in a white dwarf.
The optical spectrum together with UV observations taken with the IUE satellite and the Hubble Space Telescope (HST) indicated that RE J 0317-853 possesses a very high effective temperatures in the range from 30 000 to 55 000 K; Barstow et al. (1995) achieved their best fit for about 49 000 K. A careful analysis of the EUVE spectrum using the interstellar medium Lyman lines to account for the interstellar extreme ultraviolet absorption implied an effective temperature of 33800 K (Vennes et al. 2003). Within these constraints, RE J 0317-853 is one of the hottest known magnetic white dwarf (MWD); in any case, it has the highest known temperature of all MWDs with a field strength above 20 MG (Kawka et al. 2007; Külebi et al. 2009).
Barstow et al. (1995) performed high-speed photometry demonstrating that the optical brightness of RE J 0317-853 varies almost sinusoidally with a period of 725.4 ± 0.9 s and an amplitude of more than 0ṃ1; these results were confirmed by Vennes et al. (2003), who inferred a period of 725.727 ± 0.001 s from the variation in the circular polarisation. The only reasonable explanation of these results is rotation, implying that RE J 0317-853 rotates more rapidly than any other known white dwarf that is not a member of a close binary. The photometric variation must be caused by differences in the brightness on various parts of the stellar surface. Since no strong absorption lines are detected in the optical, a possible explanation may be a variation in the effective temperature over the stellar surface; the reason for this temperature inhomogeneity is currently not well understood but is probably connected to stronger or weaker contributions to the magnetic pressures in the stellar atmosphere at different locations on the stellar surface with different magnetic field strengths.
To achieve a clearer insight into the evolution of RE J 0317-853, Burleigh et al. (1999) obtained phase-resolved far-UV HST Faint Object Spectrograph spectra. They found that the previous optical results could generally be confirmed, but that the splitting of the Lyman α component into subcomponents implied that the field is probably more complicated than indicated by the mean optical spectrum. By compiling a time series of spectra, a model for the magnetic field morphology across the stellar surface was produced using the radiation-transfer models through a magnetised stellar atmosphere from Jordan (1992, see paper for a basic description of the methods) and an automatic least squares procedure. The magnetic geometry could be equally well described by an offset magnetic dipole (xoff = 0.057, yoff = 0.004, and zoff = −0.220 stellar radii), which produces a surface field strength distribution in the range 140–730 MG or an expansion into spherical harmonics up to l = 3 in which the surface field strengths are constrained to be within the range 180–800 MG.
The mass of the white dwarf was constrained by estimating the absolute magnitudes (or absolute fluxes) calculated from the spectroscopic fit parameters Teff, log g and white dwarf evolutionary models (e.g. Wood 1995; Benvenuto & Althaus 1999). The determination of the mass of RE J 0317-853 is, in general not straightforward because of the effects of strong magnetic fields; the usual method of using the Stark broadening of the spectral lines to determine log g and subsequently a mass-radius relation fails in the presence of a magnetic field of several hundred MG; the reason is that the standard theory for Stark broadening assumes degenerate energy levels but the magnetic fields help remove this degeneracy.
Nevertheless, the mass determination procedure of RE J 0317-853 can be improved by the knowledge of its distance. RE J 0317-853 is inferred to be in a wide-binary double-degenerate system due from its visual companion, which is a non-magnetic DA white dwarf companion (LB 9802) 7′′ away. This object was analysed initially by Barstow et al. (1995), then later by Kawka et al. (2007) (for fit parameters see Table 1). Barstow et al. (1995) derived a distance in the range 33−37 pc with these parameters using the evolutionary models of Wood (1992). The physical companionship of LB 9802 and RE J 0317-853 has recently been confirmed by Spitzer IRAC observations (Farihi et al. 2008) that demonstrated the common proper motion nature of the system.
Spectroscopically derived parameters of LB 9802.
With an effective temperature of 50000 K and assuming a distance of 36 pc Barstow et al. (1995) concluded that the radius of RE J 0317-853 is about 0.0035 R⊙ with a corresponding extreme mass of 1.35 M⊙ (log g = 9.5). Later Vennes & Kawka (2008) derived a mass of 1.32 ± 0.03 M⊙ using Teff = 33800 K, log g = 9.4 and 27 pc for the distance. If these conclusions are true, RE J 0317-853 would not only be one of the hottest known MWD but also the most massive (≈1.35 M⊙) isolated (due to the large separation of RE J 0317-853 and LB 9802 we can assume that both stars did not interact during stellar evolution) white dwarf discovered so far; only two other white dwarfs are known with masses in excess of 1.3 M⊙: LHS 4033 with a mass in the range 1.31–1.34 M⊙ (Dahn et al. 2004) and the MWD PG 1658+441 with 1.31 ± 0.02 M⊙ (Schmidt et al. 1992).
From the theory of stellar evolution, there are two different ways to produce these massive white dwarfs: either by single-star evolution of a star with an initial mass higher than 7 or 8 M⊙ (Dobbie et al. 2006; Casewell et al. 2009; Salaris et al. 2009) or from the merger of two white dwarfs with C/O cores (see e.g. Segretain et al. 1997). The latter scenario is supported by the rapid rotation of RE J 0317-853.
Jordan & Burleigh (1999) measured the circular polarisation to have a degree of 20% at a wavelength of 5760 Å, the strongest ever found in a MWD. Together with the assumed small radius and strong gravity in the stellar photosphere, this also made RE J 0317-853 a test object for setting limits on gravitational birefringence predicted by theories of gravitation, which violate the Einstein equivalence principle (Preuss et al. 2005).
Since the mass determination of RE J 0317-853 was based entirely on the uncertain spectroscopic distance of the system, we applied for observing time with the HST to measure the trigonometric parallaxes of the white dwarf binary system to either confirm or disregard the conclusions of Barstow et al. (1995). In this paper, we present the analysis of the parallax measurement with HST’s Fine Guidance Sensor (FGS).
2. Observation
2.1. Observations with the FGS of the HST
The observations of the MWD RE J 0317-853 (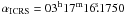 ,
, 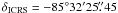 ) and its non-magnetic white dwarf companion LB 9802 (
) and its non-magnetic white dwarf companion LB 9802 (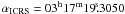 ,
, 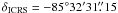 ) with the HST were performed with the Fine Guidance Sensor 1r (FGS 1r) at three epochs (March 2007, September 2007, and March 2008, see Table 2). The Fine Guidance Sensor is a two-axis, white-light shearing interferometer that measures the angle between a star and HST’s optical axis by transferring the star’s collimated and compressed light through a polarising beam splitter and a pair of orthogonal Koesters prisms (see Nelan et al. 1998; Nelan 2010, for a description of the instrument design). When FGS 1r is operated as a science instrument, HST pointing is held fixed and stabilized by FGS2 and FGS3 which operate as guiders.
) with the HST were performed with the Fine Guidance Sensor 1r (FGS 1r) at three epochs (March 2007, September 2007, and March 2008, see Table 2). The Fine Guidance Sensor is a two-axis, white-light shearing interferometer that measures the angle between a star and HST’s optical axis by transferring the star’s collimated and compressed light through a polarising beam splitter and a pair of orthogonal Koesters prisms (see Nelan et al. 1998; Nelan 2010, for a description of the instrument design). When FGS 1r is operated as a science instrument, HST pointing is held fixed and stabilized by FGS2 and FGS3 which operate as guiders.
HST orbits for HST proposal 10930 and 11300.
To derive an astrometric solution for position, proper motion, and parallaxes, RE J 0317-853, LB 9802, and the reference field stars had to be observed at a minimum of three epochs, preferably at the seasons of maximum parallax factor to allow us to cleanly separate their parallaxes from their proper motions. These seasons are separated by about six months.
Fortunately, the epochs of maximum parallax factor also resulted in HST roll angles (which are constrained by date) such that the two white dwarf stars and the optimal set of astrometric reference stars could be observed at all epochs. Figure 1 shows the parallactic ellipse and the orientations of the FGS aperture at the times of the observations (there were two March epochs, 2007 and 2008). Experience shows that a minimum of two orbits per epoch are required to achieve the highest possible accuracy in the final parallaxes. Table 2 provides the dates of the six orbits for our HST programme. Since the two white dwarfs are only ≈7′′ apart, we were able to use the same reference stars for the two white dwarfs using no more HST orbits than would be necessary for a single parallax measurement. Using identical reference stars also ensured that the parallax difference between the two putative companion stars was measured more precisely than their absolute parallaxes since the measurements share the same correction of relative to absolute parallax. In addition, their relative proper motions can be measured to provide an additional check on whether or not the two white dwarfs constitute a bound pair.
 |
Fig. 1 The parallactic ellipse of the RE J 0317-853 field and the orientation of the FGS 1r field of view at the dates of the observations. The X-axis of the FGS 1r is nearly parallel to the line connecting the circles that mark the epochs at which the observations were made. |
2.2. Spectroscopy of the astrometric reference stars
Coordinates and photometry of RE J 0317-853, LB 9802, and the reference stars.
Results of the analysis of the reference stars.
Since only relative parallaxes can be measured with HST, we had to estimate the parallaxes of a sample of reference stars in the vicinity of our target objects which comprise our local reference frame (see Fig. 2). Ref4 and Ref5 were not observed by the FGS 1r since they were not needed.
 |
Fig. 2 The field of the binary WDs RE J 0317-853 and LB 9802 and the reference stars Ref1, ..., Ref9. Ref4 and Ref5 were later omitted since they were too faint. |
Spectra of these surrounding stars of similar (or somewhat larger) brightness than RE J 0317-853 were taken in service mode with the Boller & Chivens spectrograph of the 1.5 m SMARTS telescope, located on Cerro Tololo at the Interamerican Observatory in Chile, in two nights between February 16 and 18, 2008. To ensure that the whole optical range is covered, we performed exposures with two gratings (9/Ic and 32/Ib). Both observing nights were affected by passing clouds and the relatively high airmass (>1.8) due to the large declination difference between the observatory’s zenith and the target field. Since this could not fully be corrected by flux standards, the energy distribution in the blue channel may be compromised.
The classifications for the reference stars were performed by comparing the flux-calibrated spectra to the templates of Pickles (1998). Since the Pickles library does not cover all spectral subtypes, interpolation by eye was performed where appropriate. For late G- and especially K stars, the MK class III templates were also looked at because in some cases the star actually turned out to be a giant; giants can be clearly distinguished from dwarfs, which show an indentation at 5200 Å that the giants do not or only slightly exhibit. The few metal-poor and metal-rich templates were also used, although the difference in the Pickles spectra is too small to really make a discrimination in this respect.
The absolute magnitude determination was based on an interpolation of the data taken from Lang (1992) and Allen’s astrophysical quantities (Cox 2000). It was achieved by parametrising the spectral type so that spectral type F corresponds to 0, G to 1, K to 2, and M to 3, and the spectral type subdivisions correspond to the first decimal, i.e. an G2 star would be represented by 1.2. A 5th degree polynomial is then fitted to determine the MV-spectral type relation shown in Fig. 3. This was performed for both luminosity class III and V, assuming that all our stars come from these two luminosity classes. The absolute magnitudes of the reference stars were then calculated using these two functions with their spectral class parametrised in the same way as an argument.
 |
Fig. 3 The spectrophotometric determinations of the absolute magnitude of the reference stars. The abscissa denotes the spectral type encoded in a way that F0 corresponds to 0.0, G0 to 1.0, K0 to 2.0 etc. and the spectral type subdivisions being given by the first decimal. The (red) open squares are the loci of main-sequence stars in this HR-diagram, and the (blue) open hexagons represent the giants (luminosity class III); the two curves show the resulting fits for both luminosity classes. The asterisks show the reference stars of this program. The spectral (sub)type was determined using low resolution spectra and the absolute magnitude was calculated using the fitted polynomial. |
The determination of the errors is not straightforward, since not all error sources can be easily quantified. The error in the determination of the spectral type was roughly quantified by calculating the absolute magnitude of the spectral subtypes closest to the determined ones were calculated using the same fit function (for those stars where the derived spectral type was in-between two subdivisions, i.e. in the cases of reference stars 1, 3, and 9 the second next subtype was chosen). The difference between this absolute magnitude and the absolute magnitude obtained for the star is then our estimate of the error in the absolute magnitude caused by the uncertainty in the spectral classification. This assumes that the error in the spectral type is not larger than one subdivision, which might not be true in all cases but should generally be the case. It was generally found that the difference in absolute magnitude between the measured spectral type and its neighbours is about 0.2 mag, so this value was assumed in all subsequent calculations. This error of 0.2 mag corresponds to an error of 12% in distance (see Table 4, 7th column). The corresponding error in the parallax was used for the correction of the relative parallaxes. Given the relation between parallax and distance, the error in the former is not symmetric if that of the former is. The asymmetric nature of the parallax error is represented in Col. 8 of Table 4. The errors given in Table 4 do not represent the overall error. A main source of error will most likely be the photometry, which is not of the highest precision. Moreover, our spectra do not allow us to determine the exact evolutionary status of the objects, which influences the accuracy of the absolute magnitude. For the same reason, the influence of metallicity cannot be taken into account, and all stars are assumed to be of solar abundance. Adding these uncertainties with some margin leads to an overall error in distance of 20–30%, with the stars Ref7-9 having the larger errors, since we only have one spectrum (red of Ref7, blue for the other two) for these objects. Since the parallax is the reciprocal of the distance, the stars with a large distance are the more reliable ones, especially the two giants (Ref3 and 8).
Astrometric results for RE J 0317-853, LB 9802, and the astrometric reference stars.
3. Analysis of the FGS data
Our astrometric measurements used FGS 1r in position mode to observe RE J 0317-853, LB 9802, and the associated reference field stars. At each of the three epochs, two HST orbits were used. Within each orbit, FGS 1r sequentially observed each star several times in a round-robin fashion for approximately 30 s. The standard FGS data reduction algorithms (Nelan & Makidon 2002) were employed to remove instrumental and spacecraft artifacts (such as photon shot noise, spacecraft jitter and drift, optical distortion of the FGS, differential velocity aberration, etc.). The calibrated relative positions of the stars in each of the six visits were combined using a six parameter overlapping plate technique that solves for the parallax and proper motion of each star. This process employed the least squares model GaussFit (Jefferys et al. 1988) to find the minimum χ2 best solution.
The results of the FGS measurements for RE J 0317-853, LB 9802, and the reference stars are given in Table 5. The σξ and ση are the 1σ errors of the fit of the stars onto the “master plate”. Likewise, the parallax and proper motion errors are the 1σ dispersion in those values measured for the individual observations (e.g. RE J 0317-853 and LB 9802 were observed approximately four to five times each in every HST orbit, for a total of 24 to 30 individual measurements). The errors quoted in Table 5 are typical of the performance of the FGS 1r (for comparison see e.g. Benedict et al. 2007), indicating that our observations are nominal. The best solution was obtained by directly solving for the trigonometric parallax of Ref1 and Ref6, for which we obtain values consistent with their predicted spectroscopic parallaxes. Likewise, we derive the optimal solution when we use the FGS 1r data to solve for the proper motion of Ref6 and Ref7. The bulk proper motion of the field is constrained by setting Ref6, Ref8, and Ref9 to have no proper motion. The astrometric reference star Ref2 was not used because FGS 1r resolved it to be a wide binary system, which caused an acquisition failure in the second epoch.
The parallaxes for RE J 0317-853 and LB 9802 differ by 1.101 mas, which is about four times the 1σ of their individual errors. This result includes an application of the standard “lateral colour” correction that removes the apparent shift of an object’s position in the FGS field of view due to the refractive elements in the instrument’s optical train. The correction is given as δx = (B−V)·lcx and δy = (B−V)·lcy. The coefficients lcx = −1.09 mas and lcy = −0.68 mas are derived from the observed relative positions of two calibration stars, LATCOL_A (B−V = 1.9), and LATCOL_B (B−V = 0.2), at several HST roll angles. However, RE J 0317-853 is significantly hotter and bluer than the blue calibration star LATCOL_B. It is clear from Fig. 1 that an error in the lateral colour correction (especially in this case, along the FGS X-axis, which is nearly aligned with the line connecting the two circles marking the dates of the observations) will produce an error in the measured parallax. To evaluate the validity of applying the standard lateral colour correction (which is based solely on a star’s value of B−V) to RE J 0317-853, we revisited the interpretation of the astrometric results of the lateral colour calibration observations. Details of this “plausibility” investigation will be published as an STScI FGS Instrument Scientist Report (Nelan, in preparation) but summarized here.
The spectral energy distribution (SED) of the two lateral colour calibrations stars, in addition to LB 9802, and RE J 0317-853 were convolved with the wavelength-dependent sensitivity of the FGS over its bandpass (the sensitivity decreases from ≈20% at 4000 Å to ≈2% at 7000 Å in a near linear fashion, where sensitivity refers to the probability that a photon will be detected). The number of photons observed (i.e., actually detected) by the FGS for each star at a given wavelength (Nphotons(λ)) was normalized to unity at (for the moment) an arbitrary λo. The effective FGS colour of each star was then defined to be the ratio of the wavelength weighted sum (∑ ((λo − λ) ∗ Nphotons(λ)) for all λ < λo (the “blue” sum) to the similar “red” sum (∑ ((λ − λo) ∗ Nphotons(λ)) for all λ ≥ λo over the FGS bandpass. The value of λo is the boundary between the blue and red such that for a source emitting the same number of photons at every wavelength the blue and red wavelength weighted sums are equal and the colour ratio is unity. For the FGS, we find that λo = 5092 Å.
The SEDs of both the red calibration star LATCOL_A and RE J 0317-853 were represented as black body curves with T = 2900 K and T = 50000 K, respectively, while LATCOL_B and LB 9802 were represented by stellar model atmospheres using a code based upon the Kurutz models. For LATCOL_B, a solar abundance, Teff = 8000 K, and log g = 4.1 were assumed. For LB 9802, we assumed a hydrogen-atmosphere white dwarf with Teff = 16030 K and log g = 8.2. Using these SEDs, we computed for each star the wavelength weighted blue/red ratio described above, for which we found (blue/red) = 0.13, 1.42, 1.79, and 2.54 for LATCOL_A, LATCOL_B, LB 9802, and RE J 0317-853, respectively. (A more precise estimate of the blue/red ratios for these four stars will use observed SEDs, which are currently unavailable. Here we simply evaluate the plausibility of this concept.)
If we assume that the lateral colour shift in the relative position of two stars is proportional to the difference in their blue/red ratios, we can use the the astrometric results of the lateral colour calibration, which found that the blue star LATCOL_B was shifted by –1.87 mas relative to LATCOL_A, and their blue/red ratios to determine the proportionality constant α = −1.85/(1.42−0.13) = −1.44 mas. Applying this to RE J 0317-853 and LB 9802, we find the lateral colour-induced shift in the position of RE J 0317-853 relative to LB 9802 to be –1.08 mas. The parallax result cited in Table 5 already includes a lateral colour correction of –0.25 mas in the position of RE J 0317-853 relative to LB 9802 (based solely upon the (B−V) of each star). This differs by –0.83 mas when using the difference in their blue/red ratios. If we apply this correction, the parallax difference of the two stars is reduced to 0.27 mas, which is ≈1σ of the individual measurements. We conclude that the two white dwarfs have the same parallax, and that this 0.27 mas difference is caused by the imprecise model SEDs used to construct the blue/red ratios.
The measured parallax of LB 9802 is also affected by errors in the lateral colour correction, but to a lesser extent since at (B−V) = 0.07 it is closer to the colour of the blue calibration star LATCOL_B (B−V = 0.2). Nonetheless, the parallax quoted in Table 5 may be too large by up to 0.4 mas, based on the difference in the predicted relative shift between two stars with (B−V) = 0.2 and 0.07 using the standard lateral correction and the blue/red ratio correction. Given the imprecision of the (blue/red) based correction, we take the parallax of LB 9802 to be π = 33.279 ± 0.238 mas using the standard lateral colour correction.
LB 9802 is 7′′ distant from RE J 0317-853 at a position angle PA = 145.856° as measured by FGS 1r. From the measured proper motions (Table 5), LB 9802 is moving away from RE J 0317-853 at 16.26 ± 0.86 mas yr-1 along a position angle of 133.62°, which is nearly aligned with the line of sight between the two stars. The computation of the proper motions is dominated by the observations from the first and third epochs, which were performed at the same HST orientation. Therefore the uncertainty in the lateral colour correction has no effect. At a distance of 30.05 pc (calculated from the parallax of LB 9802), this corresponds to 0.489 ± 0.026 AU yr-1, i.e. 2.33 ± 0.12 km s-1. We compare this tangential space velocity with an estimated orbital speed. If we assume that this is a bound binary system with a separation of 7′′ (210 AU at 30.05 pc), and with the total mass ranging from 2.02–2.31 M⊙ (see Sect. 4.1), a circular orbit yields a period of 2004 yr (for the higher mass estimate) to 2143 yr (for the lower mass); this corresponds to orbital speeds of 3.12–2.92 km s-1 for LB 9802 with respect to RE J 0317-853. These estimates are comparable to the tangential space velocity measured by FGS. This result and the close spatial proximity of the two stars supports the conclusion that LB 9802 and RE J 0317-853 constitute a bound system.
Although the FGS photometry shows a peak-to-peak amplitude variation between V = 14.60 and V = 14.84 (with 0.01 accuracy estimated using LB 9802 as a reference) consistent with the result from Barstow et al. (1995), the sampling was not good enough to confirm the 725 s photometric variability quantitatively by means of a Fourier analysis of this sparse data set.
4. Determination of the stellar parameters
4.1. Mass and radius determinations of RE J 0317-853 and LB 9802
 |
Fig. 4 Contour plots for |
To determine the mass of RE J 0317-853, we used synthetic bolometric colours and absolute magnitudes for carbon-oxygen (CO) core white-dwarf cooling models with thick hydrogen layers (MH/M ∗ = 10-4) (Wood 1995; Holberg & Bergeron 2006)1; when required, we used oxygen-neon (ONe) core white-dwarf cooling models with hydrogen layers of MH/M ∗ = 10-6 (Althaus et al. 2005, 2007)2.
We determined the “observed” absolute visual magnitude 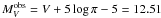 mag from V = 14.90 and π = 0.033279′′. For a given effective temperature and surface gravity, the theoretical bolometric magnitude Mbol, the bolometric correction BC = Mbol − MV, and mass m for RE J 0317-853 were calculated. The theoretical absolute visual magnitude was defined by
mag from V = 14.90 and π = 0.033279′′. For a given effective temperature and surface gravity, the theoretical bolometric magnitude Mbol, the bolometric correction BC = Mbol − MV, and mass m for RE J 0317-853 were calculated. The theoretical absolute visual magnitude was defined by 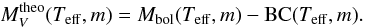 (1)The contour plots for
(1)The contour plots for 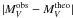 are shown in Fig. 4 for the two possible core compositions. For both compositions, a satisfactory minimum could be reached only for parts of the range of effective temperatures between 30 000 and 50 000 K because the tables were limited to an upper value of log g = 9.5 for the case of the CO cores (log g = 9.5 corresponds to a mass of 1.37 M⊙ for 30 000 K and a mass of 1.46 M⊙ for 50 000 K) and to an upper limit of 1.28 M⊙ for the ONe models.
are shown in Fig. 4 for the two possible core compositions. For both compositions, a satisfactory minimum could be reached only for parts of the range of effective temperatures between 30 000 and 50 000 K because the tables were limited to an upper value of log g = 9.5 for the case of the CO cores (log g = 9.5 corresponds to a mass of 1.37 M⊙ for 30 000 K and a mass of 1.46 M⊙ for 50 000 K) and to an upper limit of 1.28 M⊙ for the ONe models.
We calculated the minimum of 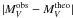 for a given mass of our range of effective temperatures; when a mass solution could not be reached inside the calculated grids, we extrapolated the theoretical magnitudes.
for a given mass of our range of effective temperatures; when a mass solution could not be reached inside the calculated grids, we extrapolated the theoretical magnitudes.
For an effective temperature of 30000 K, we estimated masses of 1.32 ± 0.02 (CO core) and 1.28 ± 0.02 (ONe core). Our CO-core calculations are consistent with the estimates of 1.31–1.37 M⊙ (Ferrario et al. 1997), who assumed a distance of 30 pc. The highest temperature for which we could obtain a solution in the 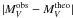 diagram is about 48000 K from which we inferred a mass of 1.46 M⊙. Any additional extrapolation may introduce substantial uncertainty because we are then approaching the Chandrasekhar limit.
diagram is about 48000 K from which we inferred a mass of 1.46 M⊙. Any additional extrapolation may introduce substantial uncertainty because we are then approaching the Chandrasekhar limit.
In the grid of theoretical values for ONe cores, we performed significant extrapolation to obtain solutions above 30 000 K (see Fig. 5). For Teff = 30000 K, we obtained a mass of 1.28 M⊙ and inferred an error of ± 0.015 from the uncertainty in the observed visual magnitude and the parallax. For an effective temperature of 50000 K, we derived 1.38 M⊙ with a slightly higher error estimate of 0.020 M⊙ due to the uncertainty of the extrapolation. The results are summarised in Table 6.
 |
Fig. 5 The mass of RE J 0317-853 versus absolute V magnitudes for an ONe white dwarf. The different curves correspond to the effective temperatures 30 000–50 000 K. Above 1.28 M⊙, we have to perform an extrapolation for Teff > 30000 K. Since we cannot strictly estimate the extrapolation error, we visually added some uncertainty to the extrapolated values, which was subsequently used to estimate the errors in Table 6. The horizontal red line denotes the “observed” MV. |
Mass and age estimations for RE J 0317-853 using different core compositions and temperatures.
We applied the same procedure to LB 9802 by using our new parallax measurements and the information from the literature outlined in Table 1. Our mass estimate for the visual magnitude given by Barstow et al. (1995) is consistent with the former results (Ferrario et al. 1997; Kawka et al. 2007, see Table 7) although we find that our calculations with the visual magnitude provided by Kawka et al. (2007) is incompatible with our mass determination if we assume that the spectroscopically determined masses for LB 9802 are correct.
With the knowledge of the Mbol for a given mass, the radius can be directly estimated at a given Teff. The radius estimates yield slightly different values when two core models are considered (see Table 6). This is caused assuming the assumption for the hydrogen layer mass to be MH/M ∗ = 10-4 in the CO cooling models (Wood 1995) versus the MH/M ∗ = 10-6 content in the ONe cooling models (Althaus et al. 2005). This produces different luminosities for a given effective temperature.
4.2. Age determination of RE J 0317-853 and LB 9802
The assessment of the cooling ages of RE J 0317-853 and LB 9802 is important to the understanding of the evolutionary history of the system. It was possible to evaluate the cooling ages of both objects with the mass estimates that we determined.
For our estimations, we used the grids of white dwarf cooling sequences for CO and ONe cores (e.g. Wood 1995; Benvenuto & Althaus 1999) for their respective range of grid parameters; for masses above the available values, we extrapolated the age values in a way similar to that for the visual magnitudes (see Figs. 5 and 6).
 |
Fig. 6 The mass of RE J 0317-853 versus logarithmic age in years for an ONe core white dwarf. The different curves correspond to the effective temperatures 30 000–50 000 K. Since we cannot strictly estimate the extrapolation error we visually added some uncertainty to the extrapolated values, which was subsequently used to estimate the errors in Table 6. |
Surprisingly, the difference in the cooling age of the two binary components is smaller than formerly estimated. For both assumed chemical compositions, the cooling age of the non-magnetic white dwarf LB 9802 is within the error bars of the cooling age of the magnetic and very massive RE J 0317-853 (see Tables 6 and 7). For the case of an ONe core with an effective temperature as high as 50 000 K, our conclusion is poorly constrained due to the extremely large uncertainties introduced by the extrapolation.
Mass and age estimations for LB 9802 using different V magnitudes in the literature and an average effective temperature of 16 000 K.
Previous age estimates were unreliable because they inferred a cooling age of RE J 0317-853 shorter than that of LB 9802, simply based on its higher effective temperature. If we use the elementary theory of cooling by Mestel (1965) assuming for a fixed effective temperature of the white dwarf, the cooling age is a function of the mass and radius tcool ∝ M/R2. This means that the cooling age for low-mass white dwarfs (<0.5 M⊙) is simply proportional to mass M5/3. As the mass of the white dwarf approaches the Chandrasekhar limit the radius asymptotically approaches zero, which means that ages for a given effective temperature depend even more strongly on the mass.
The masses estimated here are quite close to the Chandrasekhar limit (≥1.30 M⊙) where post-Newtonian corrections should be considered for the stellar equilibrium (Chandrasekhar 1964; Chandrasekhar & Tooper 1964). However, these corrections mostly affect the dynamical stability of the star, leading to collapse before reaching the Chandrasekhar limit, but induce only small corrections to mass-radius relationship. This is because the estimated radii are three orders of magnitude larger than the Schwarzschild-radius: GM/c2RWD ~ 10-3. Hence, we do not expect any effect on our mass determinations, as also noted by Koester & Chanmugam (1990).
5. The evolutionary history of the LB 9802 and RE J 0317-853 system
The projected distance of 210 AU between the two white dwarfs and their small relative proper motion suggest that they are companions and therefore share a common origin. The ages of both objects should therefore be equal or comparable within the error bars; this condition must be fulfilled for the correct evolutionary schemes of both white dwarfs.
The case of LB 9802 is straightforward because its evolutionary history is not complicated by either a strong magnetic field or an extreme mass. Therefore, the simple single-star evolution of LB 9802 places constraints on the total age of RE J 0317-853.
As mentioned above, previous analyses suggested a younger age for RE J 0317-853 than LB 9802 and for this reason the system was assumed to have an “age dilemma” (Ferrario et al. 1997). Therefore, an alternative scenario was proposed in which RE J 0317-853 is a result of the merging of two white dwarfs that have lower-mass progenitors.
5.1. Single-star origin of RE J 0317-853
With our new results, we undertook a more precise investigation. We firstly considered the single-star scenario for RE J 0317-853. To determine the total age of LB 9802 and RE J 0317-853 from the zero-age main-sequence (ZAMS) to their current stage, we used the latest semi-empirical initial-to-final-mass relations (IFMR) (Casewell et al. 2009; Salaris et al. 2009) to estimate their initial masses. By considering a diverse range of the theoretical schemes to calculateg the IFMR (metallicity, overshoot parameter, etc.), we deduced the progenitor mass of LB 9802 to be in the range 4.0–4.5 M⊙.
For the extremely high (final) mass of RE J 0317-853, the corresponding IFMR is quite uncertain. Theoretically, it was shown that 9–10 M⊙ mass stars would evolve into massive oxygen-neon (ONe) white dwarfs because of the off-centred carbon ignition in the partially degenerate conditions of their cores (Ritossa et al. 1996; García-Berro et al. 1997). With these constraints in mind, we consider more carefully a possible range of initial masses between 8 and 10 solar masses.
The total age (time on the main-sequence plus the white dwarf cooling time) of LB 9802 depends strongly on its initial mass. For the 0.84 M⊙ mass LB 9802, the initial masses in the range 4.0–4.5 M⊙ yield main-sequence lifetimes of 170–130 Myr (the progenitor ages were calculated using the evolutionary tracks from Bertelli et al. 2009, for solar metallicity). This means that the total evolutionary age of LB 9802 is in the range 410–450 Myr.
With 40–30 Myr, the pre-white-dwarf lifetime is extremely short for progenitor masses in the range between 8 and 10 M⊙, respectively. For an effective temperature of 30000 K and our resulting mass of 1.28–1.32 M⊙ for RE J 0317-853 (which would be the progeny of a 8 M⊙ star, see Casewell et al. 2009; Salaris et al. 2009), we derive total ages in the range 320–340 Myr.
If alternatively we assume an effective temperature of 50000 K for RE J 0317-853 and a CO core, we end up with a total lifetime of ≈350 Myr; for the ONe core case, the corresponding value would be ≈220 Myr. We reiterate that our estimate for the errors is rather large in the ONe case at 50000 K (see Table 6) because of the uncertainties in the extrapolation. Hence, omitting the case with ONe core at 50000 K, we can say that the total age of RE J 0317-853 is in the range 320–350 Myr.
There are additional theoretical uncertainties in the IFMR due to magnetism and rapid rotation that should be important for an extreme case such as RE J 0317-853. The effect of both of these factors on the IFMR has been the subject of some discussion. Dominguez et al. (1996) argued that rapid rotation has a positive effect on the core growth, such that a rapidly rotating star of mass 6.5 M⊙ may produce a white dwarf of mass 1.1–1.4 M⊙. Observational evidence of this was found by Catalán et al. (2008). RE J 0317-853 is the fastest rotating isolated white dwarf and this rotation may be a relic of a rapidly rotating progenitor.
The assumption of a 6.5 M⊙ mass star as the progenitor does not relieve the “age dilemma” considerably since the progenitor age for this case is ~70 Myr, which does not differ much from the 40–30 Myr estimated for 8–10 M⊙ mass stars. Catalán et al. (2008) also argued that MWDs are relatively more massive than expected on the basis of their inferred progenitors via the IFMR of non-magnetic white dwarfs. However, Wickramasinghe & Ferrario (2005) and Ferrario et al. (2005) both concluded based on their population synthesis studies this effect is of only minor importance. Since the effect of rotation and magnetism on the evolutionary age is unclear or rather small, we did not consider them in our age estimations.
Based on these considerations, we conclude that the total age of LB 9802 is 410–450 Myr at least ~100 Myr older than the respective value for RE J 0317-853 (320–350 Myr). This discrepancy implies that the single-star evolution scenario might not be applicable to RE J 0317-853.
However, the mass estimates leading to the cooling ages determined above neglected the influence of magnetism. The magnetic nature of RE J 0317-853 is likely to affect the determination of its mass because of the mass-radius relation. Ostriker & Hartwick (1968) discussed the effect of magnetism and rapid rotation on white dwarfs. Both magnetism and rotation act against the gravitation, causing an extended radius; hence, white dwarfs with strong internal magnetization have larger radii for a given mass.
To calculate the cooling tracks from synthetic colours and magnitudes of white dwarfs, mass-radius determinations are used implicitly. Hence our estimates of the masses and ages are impaired by the lack of mass-radius relations taking into account the effect of the magnetic field. For a white dwarf with 1.05 M⊙, the radius is increased by a factor 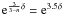 , where δ is the ratio of the magnetic energy to the gravitational energy of the star, and n is the polytropic index (Shapiro & Teukolsky 1983). In the case of RE J 0317-853, an internal magnetization of ⟨ B ⟩ = 1012–1013 G seems plausible; this would imply that δ ≈ 0.1 and therefore an increase in the radius by ~40%. Since RE J 0317-853 has an even higher mass, n is in this case close to 3 and thereby the increase in radius for a given mass is even higher.
, where δ is the ratio of the magnetic energy to the gravitational energy of the star, and n is the polytropic index (Shapiro & Teukolsky 1983). In the case of RE J 0317-853, an internal magnetization of ⟨ B ⟩ = 1012–1013 G seems plausible; this would imply that δ ≈ 0.1 and therefore an increase in the radius by ~40%. Since RE J 0317-853 has an even higher mass, n is in this case close to 3 and thereby the increase in radius for a given mass is even higher.
For an effective temperature of 30 000 K, our measured radius is 0.410 × 10-2 R⊙, whereas for 50 000 K it is 0.295 × 10-2 R⊙. When we correct the influence of the magnetic field on the radius we end up with a higher mass than determined in Sect. 4.1. If RE J 0317-853 were of higher mass the cooling time would increase so that the age dilemma no longer exists for the assumption of single-star evolution.
As an initial consideration, cooling ages of ~400 Myr, which would diminish the age inconsistency, are possible for RE J 0317-853, if it has a mass of 1.32 M⊙ rather than 1.28 M⊙ (ONe case; 0.04 M⊙ discrepancy), or 1.38 M⊙ rather than 1.32 M⊙ (CO case; 0.06 M⊙ discrepancy), for an effective temperature of 30000 K. The corrected radius of R0 = 0.32 × 10-2 R⊙ implies a mass of 1.38 M⊙ from the mass-radius relationship. This value implies that the corrections are plausibly high enough to account for the missing evolutionary age as discussed above.
If we consider Teff = 50000 K for RE J 0317-853, the mass estimates based purely on the total evolutionary age of the system would imply values well above the Chandrasekhar limit. Although it is known that strong internal magnetic field strengths also modify the Chandrasekhar limit (Ostriker & Hartwick 1968), it is still difficult to quantitatively assess the masses and their effect on cooling ages in this regime.
5.2. Binary origin of RE J 0317-853
The merger scenario for ultramassive white dwarfs was initially proposed by Bergeron et al. (1991) for GD 50, Marsh et al. (1997) proposed that this scenario could explain the properties of the hot and massive white dwarf population. For RE J 0317-853, it was similarly proposed to explain both the high angular momentum and high mass of this star (Ferrario et al. 1997). Vennes et al. (2003) also suggested that the scenario could produce a strong and non-dipolar magnetic field. They argued qualitatively that the high angular momentum is a result of the total orbital momentum of a coalescing binary and that the strong non-dipolar magnetic field can be generated by dynamo processes due to the differential rotation caused in turn by the merging.
The type of binary evolution that can lead to a double-degenerate system has been investigated in detail, since it represents a channel for producing SN Ia explosions (Webbink 1984; Iben & Tutukov 1984). In this scenario, a binary system consisting of two intermediate-mass stars (5–9 M⊙) goes through one or two phases of a common envelope (CE) and evolves to a double white dwarf system. If the final double-degenerate system has orbital periods in the range between 10 s and 10 h, it will lose angular momentum through gravitational radiation and merge in less than a Hubble time. The merging process leads to a massive central product with a surrounding Keplerian disk. Depending on the total mass of the system, the temperature in the envelope and the accretion to the merger product, the system can evolve either to a SN Ia or by an accretion-induced collapse (AIC) to a neutron star. When the total mass of the system is insufficient to create the density and the temperature to burn carbon under degenerate conditions, the system will end up as an ultra-massive white dwarf.
To test whether this scenario is indeed applicable to the case of RE J 0317-853, we have to trace back to the point in the stellar evolution where the merging could have happened, using the cooling age of RE J 0317-853 and subtracting it from the total evolutionary age of LB 9802. Using this progenitor age estimate and the theoretical constraints from the theory of binary star evolution, we can estimate the masses of the possible merging counterparts.
We begin by estimating the mass of the (secondary) binary component that needs longer to become a white dwarf. To obtain a lower limit to its mass, we assume the longest time from the main-sequence to the merging process considering the mass transfer episodes predicted by the binary scenario. After both white dwarfs are formed, the time needed for the binary to merge due to gravitational radiation depends strongly on the orbital parameters and mass of the double-degenerate system. Depending on the properties of the system, coalescence can be as fast as 0.1 Myr or as slow as 200 Myr (Iben & Tutukov 1984). To obtain a lower limit to the total evolutionary time for the system, we neglect the time needed for the double-degenerate system to coalesce.
Iben & Tutukov (1985) discussed the evolution of 3 to 12 M⊙ stars that experience two phases of mass transfer. The phase of the mass transfer can take as long or even longer than the time the star spends on the main-sequence. For a 5 M⊙ star, the main-sequence phase lasts ~90 Myr (Bertelli et al. 2009), while in the binary-evolution scenario it takes 140 Myr from the main sequence until the formation of the white dwarf. This means that 230 Myr are needed for a 5 M⊙ star to evolve into a white dwarf rather than the 100 Myr that we assumed for single-star evolution.
The possible cooling ages considered for LB 9802 (280 Myr) and RE J 0317-853 (280–320 Myr, when we assume an effective temperature of about 30 000 K) imply that the maximum time needed for binary evolution is at most the main-sequence age of LB 9802, which is 130–170 Myr (for 4.0–4.5 M⊙). The upper limit of 170 Myr is comparably short relative to the 230 Myr of binary evolution time. This provides a lower mass limit for the system. The resulting mass of a white dwarf that is a product of a 5 M⊙ star in this binary evolution scheme is 0.752 M⊙ (Iben & Tutukov 1985), which is lighter than inferred from the IFMRs determined for single-star evolution.
Since the pre-white-dwarf evolution is too long for an initial 5 M⊙, star we need a more massive progenitor hence should end up with a secondary white dwarf more massive than 0.752 M⊙. For the primary star, we assume that it has only a slightly higher mass than the secondary to deduce a lower limit to the total coalescing mass.
However, this assumption leads to serious inconsistencies, because the total mass of two components would result in more than 1.5 M⊙ being above the masses estimated for RE J 0317-853. This lower limit is also robust when we consider mass loss. Firstly, smoothed particle hydrodynamic (SPH) simulations show that only a very small mass loss is expected during merging (~10-3 M⊙, see e.g. Lorén-Aguilar et al. 2009), and secondly, we expect almost all of the Keplerian disk to be accreted on the merger product. Wind mass-loss from the Keplerian disk is assumed to be lower than 10% of the accretion rate (Mochkovitch & Livio 1990); this means that at least 90% of the disk is expected to be accreted. Lorén-Aguilar et al. (2009) also estimate 0.1–0.3 M⊙ for the disk masses, which would imply a total mass loss of ≤ 0.01–0.03 M⊙.
We note that infrared studies have detected possible disks surrounding massive white dwarfs (Hansen et al. 2006). This included RE J 0317-853 for which no convincing evidence of a disk was found in the Spitzer IRAC bands (see also Farihi et al. 2008). If RE J 0317-853 were the product of a merger of two white dwarfs, all of the matter from the Keplerian disk should have been accreted. In this scenario, total mass limits well above the estimated RE J 0317-853 mass cannot be avoided. This estimation eliminates the possibility of a binary origin for RE J 0317-853 with a current effective temperature as low as 30 000 K.
However, if the total mass of the binary system does not exceed the estimated value for RE J 0317-853, the time needed for the accretion of all the material from the disk is much longer than the evolutionary timescale. The accretion rate is expected to be ≤10-12 M⊙ yr-1 for flows with laminar viscosity (Lorén-Aguilar et al. 2009). For disk material of 0.1–0.3 M⊙, that its complete accretion time of 1–3 × 105 Myr is three orders of magnitude longer than the evolutionary timescale.
If the binary scenario were correct, the Keplerian disk should have been observed unless the accretion rate of the disk was much higher than theoretically predicted. Only accretion rates higher than 10-10 M⊙ yr-1 would lead to a total disappearance of the disk.
When two equal-mass white dwarfs merge, the symmetry of the process leads to a rotating ellipsoidal composed of CO around the white dwarf rather than a Keplerian disk. If RE J 0317-853 were still in the process of accretion we would have observed CO in the spectra but this is not the case. On the other hand, if all the material of the surrounding ellipsoid had already been accreted (mass-loss can be neglected as discussed above) the mass of RE J 0317-853 would be higher than observed (above the Chandrasekhar limit).
We also considered the possible effect on the cooling ages of additional heating of the white dwarf core due to the merging process. Recent SPH simulations indicate the possibility of heating to ~109 K in the core (Yoon & Langer 2005; Lorén-Aguilar et al. 2009). However, because of the T − 5/2 dependence of the cooling age according to the elementary theory (Mestel 1965), the effect of this extra heating on the cooling ages is expected to be small (~2 Myr) and can be neglected.
When we consider the ONe core case for an effective temperature of 50000 K, leading to an average cooling age of ~190 Myr, we end up with an upper limit to the evolution time of the secondary of 220–260 Myr; the 40 Myr spread in evolutionary time is only due to the uncertainty in the LB 9802 progenitor mass (between 4.0–4.5 M⊙). Our estimated upper limit to the total age is comparable to the evolutionary timescale of a 5 M⊙ star in a binary system as considered above. However, the cooling time estimate for RE J 0317-853 in this case is considerably uncertain (see Table 6) due to the extrapolation. Within these large error margins, we would in principle be able to obtain a sub-Chandrasekhar mass for the merger product, but this process is very unlikely when we consider the time needed for the white dwarfs to merge (10–100 Myr, Iben & Tutukov 1984). Nevertheless, the possibility of a binary origin for an ONe core RE J 0317-853 at Teff = 50000 K cannot be entirely excluded.
We note that the effect of magnetic field strength on the structure of the white dwarf, considered in Sect. 5.1 is also important to binary evolution. The implementation of this effect leads to an inference of slower cooling for RE J 0317-853 as in the single-star scenario. This would yield shorter progenitor timescales for a constant evolutionary time, leading to the lower limits on the total mass of the coalescing white dwarfs becoming even more massive. This diminishes again the probability of binary evolution for Teff = 30000 K. However, for Teff = 50000 K the uncertainties still permit the possibility of merging. Furthermore, the effect of magnetism on the stellar structure ensure that this scenario remains favourable due to the higher Chandrasekhar mass limit (Ostriker & Hartwick 1968; Shapiro & Teukolsky 1983).
6. Discussion and conclusions
RE J 0317-853 belongs to the very rare population of ultra-massive white dwarfs with masses exceeding 1.1 M⊙. The competing theoretical explanations of the origin of these white dwarfs are single-star evolution versus the merging of two degenerate stars. Without considering mass-loss during stellar evolution, we have shown that an upper limit of 1.1 M⊙ for the final white dwarf mass would exist for the white dwarfs because of the ignition of carbon in the core of the progenitor star. However, taking into account the effect of mass loss, high-mass ONe-core white dwarfs can be produced (see Weidemann 2000, for a review). Furthermore, it was proposed that even 9 to 10 M⊙ mass stars evolve into ONe core white dwarfs of mass 1.26 and 1.15 respectively, because of the off-centred carbon ignition in the partial degenerate conditions of their cores (Ritossa et al. 1996; García-Berro et al. 1997).
In the light of our current results, we have undertaken a more precise investigation of the possible evolutionary scenarios for RE J 0317-853. We have shown that the cooling ages are almost the same for the two components. The detailed analysis very much depends on a precise determination of the effective temperature; for Teff = 30000 K, we can use the calculations by Wood (1995) and Benvenuto & Althaus (1999) and conclude that within the limits of the uncertainties RE J 0317-853 is at least as old as LB 9802. For a consistent interpretation of the system, we also have to take into account the time scales of the pre-white-dwarf evolution. The more massive progenitor of RE J 0317-853 should evolve more rapidly than the progenitor of LB 9802. Taking this into account, the total age difference between LB 9802 and RE J 0317-853 amounts to ~100 Myr if single-star evolution is considered.
On the other hand, the alternative binary merger scenario proposed by Ferrario et al. (1997) and Vennes et al. (2003) as a solution to this age dilemma has severe drawbacks. When the evolutionary timescales are considered, the progenitor age of RE J 0317-853 at Teff = 30000 K yields lower limits on the mass of the merger product that is considerably higher than its estimated mass for all cases. For RE J 0317-853, we have large uncertainties in the cooling age estimate only for an effective temperature of 50000 K, so that we cannot fully exclude the binary scenario.
We have also considered the effects of the magnetic fields on both of the scenarios. Magnetic fields cause an increase in radius, hence an underestimate of the mass, which would imply longer cooling ages than estimated. For the case of Teff = 30000 K, the effect of magnetism makes the single-star scenario possible while further eliminating the binary merger origin; for the high Teff of 50000 K, even the inclusion of magnetic effects does not ensure that the single-star scenario is possible; the binary scenario remains possible within our large uncertainties.
With our measurement of the parallaxes and relative proper motion of RE J 0317-853 and LB 9802 with HST’s FGS, we have established that the wide binary system of these two stars is indeed a bound system. We have estimated the masses and ages of RE J 0317-853 and LB 9802 based on the current white dwarf cooling tracks for different core compositions and hydrogen layer masses. Owing to the magnetic nature of this object, the temperature determination of RE J 0317-853 is difficult and should be repeated in the future taking into account all available observations and including a more detailed determination of the magnetic field geometry.
For the mass and radius determination, we have considered the highest and lowest possible temperature and with these estimates we have discussed the evolutionary history and the possible origin of RE J 0317-853. Our results show that for a cooler, less massive RE J 0317-853 the binary scenario can be excluded within our uncertainties. We also proposed that the “age dilemma” might be solved when the effects of the magnetism on the structure of the white dwarf is considered. If RE J 0317-853 were hotter and more massive, then a binary origin scenario would be more plausible.
Acknowledgments
This work was supported by the Deutsches Zentrum für Luft- und Raumfahrt (DLR) under grant 50 OR 0201. B. Külebi is a student of International Max Planck School of Astronomy (IMPRS) and a part of Heidelberg Graduate School of Fundamental Physics (HGSFP). We would like thank Enrique García-Berro for providing us with the data of their SPH simulations and the anonymous referee for his valuable suggestions.
References
- Althaus, L. G., García-Berro, E., Isern, J., & Córsico, A. H. 2005, A&A, 441, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barstow, M. A., Jordan, S., O’Donoghue, D., et al. 1995, MNRAS, 277, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B. E., Feast, M. W., et al. 2007, AJ, 133, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Benvenuto, O. G., & Althaus, L. G. 1999, MNRAS, 303, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Bergeron, P., Kidder, K. M., Holberg, J. B., et al. 1991, ApJ, 372, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Bertelli, G., Nasi, E., Girardi, L., & Marigo, P. 2009, A&A, 508, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burleigh, M. R., Jordan, S., & Schweizer, W. 1999, ApJ, 510, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Casewell, S. L., Dobbie, P. D., Napiwotzki, R., et al. 2009, MNRAS, 395, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Catalán, S., Isern, J., García-Berro, E., & Ribas, I. 2008, MNRAS, 387, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1964, ApJ, 140, 417 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chandrasekhar, S., & Tooper, R. F. 1964, ApJ, 139, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, Allen’s astrophysical quantities, ed. A. N. Cox [Google Scholar]
- Dahn, C. C., Bergeron, P., Liebert, J., et al. 2004, ApJ, 605, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbie, P. D., Napiwotzki, R., Burleigh, M. R., et al. 2006, MNRAS, 369, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Dominguez, I., Straniero, O., Tornambe, A., & Isern, J. 1996, ApJ, 472, 783 [NASA ADS] [CrossRef] [Google Scholar]
- Farihi, J., Becklin, E. E., & Zuckerman, B. 2008, ApJ, 681, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrario, L., Vennes, S., Wickramasinghe, D. T., Bailey, J. A., & Christian, D. J. 1997, MNRAS, 292, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrario, L., Wickramasinghe, D., Liebert, J., & Williams, K. A. 2005, MNRAS, 361, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Ritossa, C., & Iben, Jr., I.1997, ApJ, 485, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Kulkarni, S., & Wiktorowicz, S. 2006, AJ, 131, 1106 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Kuzmin, A., Bastian, U., et al. 1998, A&A, 335, L65 [NASA ADS] [Google Scholar]
- Holberg, J. B., & Bergeron, P. 2006, AJ, 132, 1221 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1985, ApJS, 58, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Jefferys, W. H., Fitzpatrick, M. J., & McArthur, B. E. 1988, Celestial Mechanics, 41, 39 [Google Scholar]
- Jordan, S. 1992, A&A, 265, 570 [NASA ADS] [Google Scholar]
- Jordan, S., & Burleigh, M. R. 1999, in 11th European Workshop on White Dwarfs, ed. S.-E. Solheim, & E. G. Meistas, ASP Conf. Ser., 169, 235 [Google Scholar]
- Kawka, A., Vennes, S., Schmidt, G. D., Wickramasinghe, D. T., & Koch, R. 2007, ApJ, 654, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., & Chanmugam, G. 1990, Rep. Progr. Phys., 53, 837 [Google Scholar]
- Külebi, B., Jordan, S., Euchner, F., Gänsicke, B. T., & Hirsch, H. 2009, A&A, 506, 1341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lang, K. R. 1992, Astrophysical Data I. Planets and Stars, ed. K. R. Lang [Google Scholar]
- Lorén-Aguilar, P., Isern, J., & García-Berro, E. 2009, A&A, 500, 1193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, M. C., Barstow, M. A., Buckley, D. A., et al. 1997, MNRAS, 287, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1965, Stars in Stellar Systems, ed. L. H. Aller, & D. B. McLaughlin [Google Scholar]
- Mochkovitch, R., & Livio, M. 1990, A&A, 236, 378 [NASA ADS] [Google Scholar]
- Nelan, E. 2010, Fine Guidance Sensor Instrument Handbook, version 17.0 (Baltimore, MD: STScI) [Google Scholar]
- Nelan, E., & Makidon, R. 2002, HST Data Handbook: Introduction to Reducing HST Data, Vol. 1, version 4.0, ed. B. Mobasher [Google Scholar]
- Nelan, E. P., Lupie, O. L., McArthur, B., et al. 1998, in SPIE Conf. Ser. 3350, ed. R. D. Reasenberg, 237 [Google Scholar]
- Ostriker, J. P., & Hartwick, F. D. A. 1968, ApJ, 153, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Preuss, O., Solanki, S. K., Haugan, M. P., & Jordan, S. 2005, Phys. Rev. D, 72, 042001 [NASA ADS] [CrossRef] [Google Scholar]
- Ritossa, C., Garcia-Berro, E., & Iben, Jr., I. 1996, ApJ, 460, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, G. D., Bergeron, P., Liebert, J., & Saffer, R. A. 1992, ApJ, 394, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Segretain, L., Chabrier, G., & Mochkovitch, R. 1997, ApJ, 481, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., & Teukolsky, S. A. 1983, Black holes, white dwarfs, and neutron stars: The physics of compact objects, ed. S. L. Shapiro, & S. A. Teukolsky [Google Scholar]
- Vennes, S., & Kawka, A. 2008, MNRAS, 389, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Vennes, S., Schmidt, G. D., Ferrario, L., et al. 2003, ApJ, 593, 1040 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Weidemann, V. 2000, A&A, 363, 647 [NASA ADS] [Google Scholar]
- Wickramasinghe, D. T., & Ferrario, L. 2005, MNRAS, 356, 1576 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, M. A. 1992, ApJ, 386, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, M. A. 1995, in White Dwarfs, Lecture Notes in Physics (Berlin: Springer Verlag), ed. D. Koester, & K. Werner, 443, 41 [Google Scholar]
- Yoon, S., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Astrometric results for RE J 0317-853, LB 9802, and the astrometric reference stars.
Mass and age estimations for RE J 0317-853 using different core compositions and temperatures.
Mass and age estimations for LB 9802 using different V magnitudes in the literature and an average effective temperature of 16 000 K.
All Figures
 |
Fig. 1 The parallactic ellipse of the RE J 0317-853 field and the orientation of the FGS 1r field of view at the dates of the observations. The X-axis of the FGS 1r is nearly parallel to the line connecting the circles that mark the epochs at which the observations were made. |
| In the text | |
 |
Fig. 2 The field of the binary WDs RE J 0317-853 and LB 9802 and the reference stars Ref1, ..., Ref9. Ref4 and Ref5 were later omitted since they were too faint. |
| In the text | |
 |
Fig. 3 The spectrophotometric determinations of the absolute magnitude of the reference stars. The abscissa denotes the spectral type encoded in a way that F0 corresponds to 0.0, G0 to 1.0, K0 to 2.0 etc. and the spectral type subdivisions being given by the first decimal. The (red) open squares are the loci of main-sequence stars in this HR-diagram, and the (blue) open hexagons represent the giants (luminosity class III); the two curves show the resulting fits for both luminosity classes. The asterisks show the reference stars of this program. The spectral (sub)type was determined using low resolution spectra and the absolute magnitude was calculated using the fitted polynomial. |
| In the text | |
 |
Fig. 4 Contour plots for |
| In the text | |
 |
Fig. 5 The mass of RE J 0317-853 versus absolute V magnitudes for an ONe white dwarf. The different curves correspond to the effective temperatures 30 000–50 000 K. Above 1.28 M⊙, we have to perform an extrapolation for Teff > 30000 K. Since we cannot strictly estimate the extrapolation error, we visually added some uncertainty to the extrapolated values, which was subsequently used to estimate the errors in Table 6. The horizontal red line denotes the “observed” MV. |
| In the text | |
 |
Fig. 6 The mass of RE J 0317-853 versus logarithmic age in years for an ONe core white dwarf. The different curves correspond to the effective temperatures 30 000–50 000 K. Since we cannot strictly estimate the extrapolation error we visually added some uncertainty to the extrapolated values, which was subsequently used to estimate the errors in Table 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.