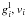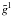| Issue |
A&A
Volume 524, December 2010
|
|
|---|---|---|
| Article Number | A41 | |
| Number of page(s) | 7 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201014784 | |
| Published online | 22 November 2010 | |
An extensive grid of mass fluxes for Galactic O stars
Astrophysics Group, Blackett LaboratoryImperial College London,
Prince Consort
Road,
London
SW7 2AZ,
UK
e-mail: l.lucy@imperial.ac.uk
Received: 13 April 2010
Accepted: 8 September 2010
A previously-described code for constructing moving reversing layers (MRL) is improved by replacing a two-parameter model for gl(v), the radiative acceleration due to lines, with a flexible non-parametric description, thus allowing a greater degree of dynamical consistency in modelling turbulent transonic flow in the outer atmospheric layers of O stars. With this new code, mass fluxes J are computed at fifty-seven points in (Teff,g)-space. Specifically, J’s are computed for all Lanz-Hubeny (2003) NLTE atmospheres with Teff(kK) ∈ (27.5,55) and log g(cms-2) ≤ 4.5. Differences with widely-used mass-loss formulae are emphasized, and opportunities for differential spectroscopic tests identified.
Key words: stars: early-type / stars: mass-loss / stars: winds, outflows
© ESO, 2010
1. Introduction
In an earlier paper (Lucy 2007, L07), the moving reversing layer (MRL) theory of Lucy & Solomon (1970, LS70) was updated by incorporating an extensive line list and improving the treatment of line formation. In addition, the models were, in effect, grafted onto the TLUSTY static NLTE O-star atmospheres of Lanz & Hubeny (2003) by imposing the TLUSTY emergent continuum flux distribution as the lower radiative boundary condition and by matching ionization fractions at T ≈ 0.75Teff.
The motivation for reviving MRL theory was the conflict between observed and predicted mass loss rates (Φ), which had led several spectroscopic groups to question the theory of radiatively-driven winds (e.g., Bouret et al. 2005; Fullerton et al. 2006). But, as emphasized in L07, the Φ’s being tested were not obtained by solving the equations governing the dynamics of radiatively-driven winds but are the values ΦV derived by Vink et al. (2000) with a refined version of the semi-empirical Monte Carlo (MC) method of Abbott & Lucy (1985). Logically, therefore, the conflict could arise from the specific assumptions of Vink et al. rather than from a failure of the radiative-driving mechanism.
In L07, MRL models were used to explore the sensitivity of the eigenvalue J = Φ/4πR2 to vt, the microturbulent velocity. Crucially, this parameter affects the flux irradiating lines as matter is driven through the sonic point; and an increase in vt from 10 to 15 km s-1 was found to decrease J by ≈ 0.3 dex. Thus, a physical effect was identified that, by reducing the predicted Φ’s, might partially contribute to resolving the conflict.
More recently (Lucy 2010, L10), MRL theory was used to investigate individual stars. This was prompted by the work of Marcolino et al. (2009) on the weak wind problem, the major discrepancy for late-type O dwarfs between their ΦV’s and observational estimates. To investigate this, a grid of 29 models was computed from which J’s for particular stars could be obtained by interpolation. The results were encouraging: although the extremely low and uncertain J’s estimated by Marcolino et al. were not matched, the predicted J’s were ≈1.4 dex lower than the JV’s. Moreover, when J’s were interpolated for the two strong-wind O4 stars analysed by Bouret et al. (2005), the results were consistent with the low values found when these authors took wind clumping into account.
In the above investigation, the L07 code was deliberately not changed, thereby avoiding any suspicion that adjustments were motivated by the observational data requiring explanation. But with the technique’s usefulness thus demonstrated, a possibly significant flaw is now addressed, namely the local departures from dynamical consistency that result from the simple two-parameter representation of line driving. This further development is especially appropriate since dynamical consistency in modelling transonic flow was identified in L10 as the key to accurate predictions of J and Φ. Accordingly, the primary purposes of this paper are first to describe how such improved models can be constructed and then to compute J’s for all TLUSTY atmospheres relevant for Galactic main-sequence O stars.
Throughout this paper J’s are in units g/s/cm2 and Φ’s in ℳ⊙/yr.
2. Improved solution technique
As in previous papers, transonic flow is assumed to be stationary, isothermal, and plane-parallel. The equation of motion can then be written as 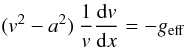 (1)here a is the isothermal speed of sound, and geff = g − ge − gl is the effective gravity, where ge = Γeg and gl are the radiative accelerations due to electron- and line scatterings, respectively.
(1)here a is the isothermal speed of sound, and geff = g − ge − gl is the effective gravity, where ge = Γeg and gl are the radiative accelerations due to electron- and line scatterings, respectively.
For given stellar parameters, we wish to find the solution of Eq. (1) such that the flow accelerates smoothly from sub- to supersonic velocities. This is achieved by finding the particular mass flux J that gives geff = 0 at the sonic point v = a, thus avoiding a singularity when integrating Eq. (1).
When approximated by a MC estimator, gl(v) is not analytic, and so solving Eq. (1) and determining its eigenvalue J is not a conventional excercise in integrating an ODE. Accordingly, in L07, a two-parameter formula was adopted for gl(v) that automatically gives geff = 0 at v = a, thus allowing the singularity-free stratification of the MRL to be obtained with a conventional integration of Eq. (1). The MC transfer calculation was then carried out in this stratified medium, resulting in estimates  for each layer of the MRL. The challenge then was to find the values of J and of the parameters δ and s that brought
for each layer of the MRL. The challenge then was to find the values of J and of the parameters δ and s that brought  into optimal agreement with gl(v;J,δ,s).
into optimal agreement with gl(v;J,δ,s).
Because of this parametric approach, the solutions obtained had noticeable residuals 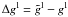 – see Fig. 3 in L10 – implying some uncertainty in the predicted J’s. Although evidence was presented that J is moderately insensitive to departures from detailed local dynamical consistency, it is nevertheless desirable to eliminate this weak point in MRL theory.
– see Fig. 3 in L10 – implying some uncertainty in the predicted J’s. Although evidence was presented that J is moderately insensitive to departures from detailed local dynamical consistency, it is nevertheless desirable to eliminate this weak point in MRL theory.
2.1. Non-parametric gl(v)
To allow the  ’s to be accurately modelled by gl(v), this function is constrained to pass through the discrete set of points
’s to be accurately modelled by gl(v), this function is constrained to pass through the discrete set of points 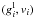 , with v1 < v2 < ... < vI. The required continuous function gl(v) is then constructed as follows: by linear logarithmic interpolation between neighbouring points for v ∈ (v1,vI); by setting
, with v1 < v2 < ... < vI. The required continuous function gl(v) is then constructed as follows: by linear logarithmic interpolation between neighbouring points for v ∈ (v1,vI); by setting  for v < v1; and by extrapolating the power law from the interval (I − 1,I) for v > vI.
for v < v1; and by extrapolating the power law from the interval (I − 1,I) for v > vI.
The discrete representation extends from a small subsonic velocity v1 to a supersonic velocity vI ≥ 2a, with spacing chosen to model the often sharply changing velocity gradient as the sonic point is approached – see Fig. 1 in L07. The kth point is located at the sonic point – i.e., vk = a – and the corresponding value of 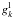 is constrained to be g∗ = g − ge, so that the regularity condition is again automatically satisfied.
is constrained to be g∗ = g − ge, so that the regularity condition is again automatically satisfied.
2.2. Stratification
With the gl(v) thus defined, the MRL’s stratification is obtained as described in Sect. 2.3 of L07, namely by two initial-value integrations of Eq. (1) starting at v = a, one for v < a and one for v > a.
To avoid a singularity at v = a, the initial velocity gradient must be such that  (2)Now, if gl(v) were an analytic function, the logarithmic derivative in Eq. (2) would be the same for both inward and outward integrations. But the adopted piecewise-linear segmented representation of log gl is not analytic: although continuous, its derivative is in general discontinuous at v = vi and thus may be so at vk = a. Accordingly, for the inward and outward integrations, the logarithmic derivatives are the slopes of the (k − 1,k) and (k,k + 1) segments, respectively.
(2)Now, if gl(v) were an analytic function, the logarithmic derivative in Eq. (2) would be the same for both inward and outward integrations. But the adopted piecewise-linear segmented representation of log gl is not analytic: although continuous, its derivative is in general discontinuous at v = vi and thus may be so at vk = a. Accordingly, for the inward and outward integrations, the logarithmic derivatives are the slopes of the (k − 1,k) and (k,k + 1) segments, respectively.
The discontinuities in the derivatives of gl(v) allow the representation to approximate curvature in (log gl − log v)-plots. Of course, as I → ∞, unlimited accuracy can be achieved, and the discontinuities then → 0.
2.3. An example
Model t400g375, with parameters Teff = 40000 K,log g = 3.75 and vt = 10 km s-1, illustrates the improved technique.
Figure 1 shows the first steps in the search for J. The starting values for 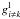 are obtained from the two-parameter formula – see Eq. (1) in L10 – with δ = 0.5 and s = 1.5 – i.e., a broken power law, with the switch to a rapidly increasing gl(v) occurring at Mach number m = v/a = 0.63. With gl(v) thus fixed, several models were computed with varying J in order to locate the root of Q1,2(J) = 0 – see Sect. 2.3 and Fig. 2 in L10. The result, J = − 5.64 dex, is then such that, as matter accelerates from m1 = 0.5 to m2 = 2.0, the work done by the gradients of gas and radiation pressures accounts for the gain in mechanical energy per g. Nevertheless, the non-vanishing residuals Δgl imply that the I − 1 values
are obtained from the two-parameter formula – see Eq. (1) in L10 – with δ = 0.5 and s = 1.5 – i.e., a broken power law, with the switch to a rapidly increasing gl(v) occurring at Mach number m = v/a = 0.63. With gl(v) thus fixed, several models were computed with varying J in order to locate the root of Q1,2(J) = 0 – see Sect. 2.3 and Fig. 2 in L10. The result, J = − 5.64 dex, is then such that, as matter accelerates from m1 = 0.5 to m2 = 2.0, the work done by the gradients of gas and radiation pressures accounts for the gain in mechanical energy per g. Nevertheless, the non-vanishing residuals Δgl imply that the I − 1 values 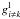 require adjustment.
require adjustment.
Ideally, corrections to 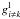 should be derived from the Δgl with an algorithm analogous to the temperature-correction procedures in stellar atmosphere theory. But here a trial-and-error procedure is followed based on inspection of plots such as Fig. 1. Thus, Fig. 1 shows that a steeper slope than s = 1.5 is required for m > 1 and that the
should be derived from the Δgl with an algorithm analogous to the temperature-correction procedures in stellar atmosphere theory. But here a trial-and-error procedure is followed based on inspection of plots such as Fig. 1. Thus, Fig. 1 shows that a steeper slope than s = 1.5 is required for m > 1 and that the 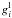 should be increased by ≈ 0.1 dex for m ∈ (0.1,0.4).
should be increased by ≈ 0.1 dex for m ∈ (0.1,0.4).
With the 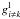 thus adjusted, a new sequence of models is computed, the modified root of Q1,2 = 0 derived, and an updated version of Fig. 1 plotted. This iterative procedure is continued until a satisfactory degree of convergence is achieved. In this case, the final model has J = − 5.72 dex and is plotted in Fig. 2. The iteratively-corrected function gl(v) now agrees closely with the
thus adjusted, a new sequence of models is computed, the modified root of Q1,2 = 0 derived, and an updated version of Fig. 1 plotted. This iterative procedure is continued until a satisfactory degree of convergence is achieved. In this case, the final model has J = − 5.72 dex and is plotted in Fig. 2. The iteratively-corrected function gl(v) now agrees closely with the  ’s. A dynamically consistent model of turbulent transonic flow has therefore been constructed.
’s. A dynamically consistent model of turbulent transonic flow has therefore been constructed.
 |
Fig. 1 Search for dynamical consistency. The open circles are the initial discrete representation ( |
 |
Fig. 2 Search for dynamical consistency. Symbols and model parameters as in Fig. 1. The interatively-corrected representation ( |
3. Microturbulence
As demonstrated in L07, the J’s predicted by MRL theory are sensitive to vt, which must therefore be included with Teff and g when comparing with observational data.
Given the importance of this sensitivity, the improved code is now applied to the model t400g375 in order to check and extend the analysis of L07. As in that investigation, when vt is varied, the b-values and incident flux distribution are from the TLUSTY model with vt = 10 km s-1.
Solutions ranging from vt = 0 – i.e., pure thermal broadening in the lines’ Doppler cores – to vt = 20 km s-1, corresponding to near sonic turbulence, are plotted in Fig. 3, together with the two solutions from L07 at 6.7 and 10 km s-1. The sensitivity to vt is confirmed.
 |
Fig. 3 Sensitivity of the eigenvalue J to microturbulent velocity vt for model t400g375. Filled circles are solutions obtained as described in Sect. 2; open circles are solutions from L07. The thermal speed of Fe ions is indicated. |
From the new results between 6.7 and 15 km s-1, the logarithmic slope at 10 km s-1 is 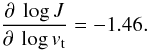 (3)This value is recommended for propagation-of-error calculations of σlog J for stars with vt’s comparable to the canonical vt = 10 km s-1.
(3)This value is recommended for propagation-of-error calculations of σlog J for stars with vt’s comparable to the canonical vt = 10 km s-1.
Figure 3 shows that, in principle, the parameter vt could bring about differences in J by ≳ 1 dex at fixed Teff,g. But as this seems not to happen for real stars, the mechanism exciting and maintaining microturbulence is presumably preventing the independent variation of this parameter, resulting perhaps in a functional dependence of vt on Teff,g.
In view of the strong damping expected for turbulence with vt/a ~ 0.5, work done by radiative forces is almost certainly required for its maintenance, in which case the phenomenon of microturbulence is not unrelated to radiatively-driven outflows. In fact, Fig. 3 suggests a direct, causal relationship as follows: given the observational evidence that wind-clumping occurs shortly after the sonic point (Bouret et al. 2005), some clumps may well lose their net outward driving and thus fall back into the photosphere (e.g., Howk et al. 2000) where their dissipated kinetic energy could excite and maintain local turbulence. If the fall-back fraction decreases with decreasing J, a feedback loop operates, so that for a given star only one pairing (J,vt) is possible.
This conjectured coupling of J and vt is supported by the difficulty of obtaining satisfactory high mass flux MRL’s when vt → 0. The J’s for vt ≲ 5 km s-1 in Fig. 3 are estimated by achieving dynamical consistency only for v/a < 1 since the extension to v/a ≳ 2 is not possible because geff becomes positive – see Fig. 4. Admittedly, this breakdown of the iterative procedure is code-specific, resulting from choosing v rather than height x as the independent variable. Nevertheless, even if the code were reconfigured to allow dynamical consistency to be extended to supersonic velocities, the resulting non-monotonic velocity law implies a density inversion at v/a ~ 2−3. Such a stratification is surely unstable and thus a possible origin of clumping and of infalling blobs.
3.1. A spectroscopic test
This sensitivity of J to vt is in stark contrast to CAK theory (Castor et al. 1975), which posits that the properties of radiatively-driven winds can be derived on the basis of the Sobolev approximation. In this approximation, gl(v) is independent of the lines’ absorption profiles and therefore independent of vt’s contribution to the width of the Doppler core.
In principle, this can be tested observationally, and is best done differentially. Thus stars differing in vt but not widely separated in (Teff,g)-space should be subjected to identical observing and diagnostic procedures to see if ΔΦ can be understood without (CAK), or only with (MRL), a contribition from Δvt.
Computed mass fluxes J.
4. Computed mass fluxes
In this section, the improved technique of Sect. 2 is used to recalculate the 29 models in Table 1 of L10 and then to add a further 28 models in order to provide a rather complete coverage of (Teff,g)-space for H-burning O stars. As before, the models’ composition is solar with NHe/NH = 0.1 (Grevess & Sauval 1998), the included metal ions are as in Table 1 of Lanz & Hubeny (2003), and vt = 10 km s-1.
4.1. O-star grid
Mass fluxes J for 57 models are given in Table 1. The grid is determined by the availability of TLUSTY atmospheres (Lanz & Hubeny 2003) and is complete for their models with log g ≤ 4.5. Because O stars on the ZAMS have log g ≈ 4.2 – see Fig. 4 in L10, J’s have not been computed for log g = 4.75.
The coverage provided by Table 1 allows J’s to be determined for all Galactic O stars by interpolation – or a slight extrapolation in a few cases. If, in addition to Teff,g and vt, a star’s distance is known, its radius can be computed and therefore also Φ = 4πR2J. Given the detailed diagnostic modelling of numerous O stars in recent years, a critical evaluation of MRL theory may be possible with existing data. This is not attempted here and is, in any case, best carried out by investigators familiar with the uncertainties of analysing circumstellar spectra.
The data in Table 1 is also relevant for investigations of stellar evolution with mass loss, for computing the latitude dependence of mass loss for rapidly-rotating stars, and for calculating its radial dependence for accretion disks.
The dependence of J(Teff,g;vt) on Teff and g is shown in Figs. 5 and 6. The most striking feature is the departure from the expected monotonic increase of J with increasing Teff that occurs when Teff ≲ 30000 K and log g ≳ 3.9. As discussed in L10, this prediction of MRL theory offers at least a partial explanation of the weak-wind phenomenon. Interestingly, the minimum at Teff ≈ 30000 K is deeper for g > gZAMS.
 |
Fig. 5 Mass flux J as a function of Teff for log g = 3.00(0.25)4.50. The data are from Table 1. The dashed line J = J ∗ defines the boundary of the weak-wind domain – see L10. |
4.2. Accuracy
The J’s in Table 1 have several sources of uncertainty. The first originates from MC sampling errors – see Appendix A. The  ’s sampling errors propagate via Q1,2 into errors in J when this quantity is determined by locating the intercept Q1,2(J) = 0 – see Fig. 2 in L10. Thus, for the final t400g375 model in Fig. 2, the least squares solution is log J = − 5.715 ± 0.014. This estimate of σlog J shows that MC noise is inconsequential since other errors are surely far greater.
’s sampling errors propagate via Q1,2 into errors in J when this quantity is determined by locating the intercept Q1,2(J) = 0 – see Fig. 2 in L10. Thus, for the final t400g375 model in Fig. 2, the least squares solution is log J = − 5.715 ± 0.014. This estimate of σlog J shows that MC noise is inconsequential since other errors are surely far greater.
The uncertainty σlog J → 0 as the number of MC quanta N → ∞, but J would still be subject to error because of residual departures from exact dynamical consistency if the continuous function gl(v) derives from only a finite number of points 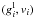 .
.
This second source of uncertainty can be estimated as follows: given that the non-parametric representation is a marked improvement over the previous model, the average | Δlog J | between the models treated both here and in L10 is a good estimate of the typical error of the previous J’s and, at the same time, a conservative error estimate for the J’s in Table 1. The 29 J’s differ on average by only 0.10 dex, with the largest difference being 0.33 dex.
A third source of uncertainty is the cumulative effect of errors in abundances, input physics and line-formation theory, many of which propagate from the TLUSTY models. A plausible guess is that these errors should rarely exceed 0.2 dex.
A fourth source of uncertainty is the derivation of J from a plane-parallel treatment of transonic flow, with back-scattering from v > 5a neglected. This is investigated in Appendix B and found to be well-justified.
A fifth and probably dominant source of uncertainty is the sensitivity to the throttling effect of turbulent line broadening (L07 and Sect. 3 above). Given our ignorance as to the source and nature of photospheric turbulence, this has perforce been investigated in the microturbulent limit, and strong sensitivity is found. Thus, from Fig. 3, we see that, with vt = 10 km s-1, photospheric turbulence reduces J by ≈ 1.3 dex from its value for laminar flow – i.e., pure thermal broadening. Within the context of the microturbulent model, an error of ± 2 km s-1 at vt ≈ 10 km s-1 implies σlog J ≈ 0.13 according to Eq. (3).
Given these uncertainties, tests of MRL theory, either spectroscopically or via stellar evolution calculations, might reasonably allow for an uncertainty of ± 0.2 dex in the J’s given in Table 1. But if a test reveals systematic discrepancies > 0.4 dex, a contradiction can be claimed.
5. Comparisons with mass-loss formulae
In this section, the MRL mass fluxes are compared to widely-used mass-loss formulae. The aim here is not a comprehensive discussion but to call attention to opportunities for differential testing, as already discussed in Sect. 3.1.
5.1. CAK
In their recent discussion of WNH stars, Smith & Conti (2008) sketch an evolutionary scenario based on an O-star mass-loss formula extracted from CAK theory. For fixed Teff, their formula gives J’s dependence on g = ge/Γe as 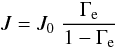 (4)where J0 is the mass flux when Γe = 0.5. Equation (4) predicts that J → ∞ as Γe → 1 – i.e., as the Eddington limit is approached – and this is basic to their claim that a feedback process results in runaway mass loss late in the core-H burning phase of massive O stars.
(4)where J0 is the mass flux when Γe = 0.5. Equation (4) predicts that J → ∞ as Γe → 1 – i.e., as the Eddington limit is approached – and this is basic to their claim that a feedback process results in runaway mass loss late in the core-H burning phase of massive O stars.
 |
Fig. 7 Comparison of MRL mass fluxes JL with scaled CAK formulae for Teff = 30,35 and 40 kK. The dashed vertical lines are the MRL-CAK offsets discussed in the text. |
In Fig. 7, the behaviour of JL as g → ge is compared to Eq. (4) when J0 is chosen to match JL at log g = 4. This comparison is carried out for Teff = 30,35 and 40 kK, for which the lowest g TLUSTY models have Γe = 0.52,0.54 and 0.52, respectively. Remarkably, MRL theory predicts greatly enhanced mass loss when a star is still well-detatched from its Eddington limit. In each of the plotted sequences, the lowest g model is offset from the scaled CAK formula by ΔJ ~ 1 dex.
If the Smith-Conti scenario were supported by actual stellar evolution tracks and accurately fitted several well-observed WNH stars, then MRL theory could be immediately dismissed as over-predicting J for evolved O stars. But neither of these circumstances obtains, and this enhanced mass loss already at Γe ≈ 0.5 will likely prove favourable to their scenario. Clearly, further work is required on the evolution of mass-losing massive stars.
In addition to its relevance for evolutionary scenarios, Fig. 7 suggests another differential test to distinguish MRL and CAK theories. In this case, pairs of stars with closely similar Teff’s but markedly different g’s should be observed and analysed identically to see which g-dependence in Fig. 7 is favoured.
5.2. Vink et al.
A model from Table 1 cannot be directly compared to the Vink et al. formula since the latter requires three fundamental stellar parameters and v∞. Accordingly, the comparison is carried out for the ZAMS models of Pols et al. (1998) with Z = 0.02. Each point on the ZAMS gives ℳ, R and L which, with the additional assumption that v∞/vesc = 2.6 (Lamers et al. 1995), allows ΦV to be computed from Eq. (12) of Vink et al. (2000). This can then be compared to ΦL = 4πR2 × J(Teff,g). Here J is obtained by simple bivariate interpolation (Abramowitz & Stegun 1965) from the four surrounding entries in Table 1, taking the independent variables to be log Teff and log g.
The two predictions for the ZAMS are plotted in Fig. 8. Throughout the entire range ΔΦ = ΦV − ΦL > 0. At Teff = 27650 K, the offset is 0.40 dex, and this increases steeply to a maximum of 1.24 dex at 30150 K. Thereafter, ΔΦ decreases – not quite monotonically – to reach a barely significant 0.27 dex at Teff = 50300 K.
The huge difference at Teff ≈ 30000 K allows MRL theory to partly explain the weak wind phenomenon, which arose when the Vink et al. predictions were compared to mass loss estimates for late-type O dwarfs. In fact, the relevant diagnostic analyses (Marcolino et al. 2009) appear still to require ΦL to be reduced by ≈ 0.8 dex – see L10.
According to Fig. 8, MRL theory predicts that a massive star’s initial Φ is markedly less than ΦV. However, when its expanding radius has reduced g by ≈1 dex, the situation reverses – see Fig. 7. Thus, for example, if a mass-losing star reaches the point (40000 K, 3.5) in (Teff,log g)-space with ℳ/ℳ⊙ = 80, then ΦV = −4.75 dex, but ΦL = −4.59 dex, a factor 1.4 larger. To put this in context, the 120 ℳ⊙ track of Limongi & Chieffi (2006) computed with Vink et al. mass loss has log g = 3.56 and 3.31 with mass 93.6 and 56.6 ℳ⊙, respectively, at its two crossings of Teff = 40000 K during core H-burning.
From the trends evident in Fig. 7, the MRL mass-loss enhancement will be even greater for g’s smaller than given in Table 1. Moreover, the Limongi-Chieffi track suggests that this part of parameter space may well be accessed by real stars. Accordingly, Table 1 needs to be extended to lower g’s, and this will require an improved theory – see Appendix B.
 |
Fig. 8 Mass-loss rates for O-stars on the zero-age main sequence (ZAMS) as a function of Teff, with masses in solar units indicated. Predictions of MRL theory (ΦL) are plotted as well as values (ΦV) derived with the formula of Vink et al. (2000). |
6. Conclusion
Motivated by the (partial) successes of MRL theory in reproducing the reduced Φ’s found by spectroscopists for O stars when wind-clumping is taken into account, the aim of this paper has been to complete the coverage of the relevant (Teff,g)-domain provided by the TLUSTY atmospheres. To this end, the MRL code has been improved by adopting a non-parametric description of gl(v), which has allowed a greater degree of dynamical consistency to be achieved for turbulent transonic flow, and thus more accurate J’s. The results of this effort are the 57 values of log J in Table 1.
Interpolation in Table 1 allows J to be derived for any O star with measured Teff and g. Moreover, a propagation-of-error calculation gives σlog J if the standard errors of these two parameters and of vt have been determined. This can be done for stars individually and independently. However, given the difficulties of diagnostic analyses, with the resulting possibility of systematic errors, there is merit in performing differential tests as suggested in Sects. 3.1 and 5.1. If vt is a slowly-varying function of Teff and g, the first test may be indecisive. But the proposed test between the MRL and CAK theories suggested by Fig. 7 is feasible. Moreover, this test is fundamental for stellar wind theory since it directly concerns the question: where in the outflow is the mass-loss rate determined?
With regard to this question, the partial success of MRL theory in explaining the weak wind phenomenon supports the LS70 argument that J and therefore Φ is determined by the regularity condition at the sonic point. This would be decisive if the observed Φ′s of the Marcolino et al. (2009) stars were convincingly revised into agreement with the predictions of MRL theory. But since only weak C IV absorption is observed, there is little or no observational basis for such improved estimates. Other tests should therefore be carried out.
Acknowledgments
I am grateful to M. Limongi and A. Chieffi for unpublished details of their evolutionary tracks and to the referee, A. de Koter, for his thoughtful comments on the proposed differential tests.
References
- Abbott, D. C., & Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowitz, M., & Stegun, I. A. 1965, in Handbook of Mathematical Functions (New York: Dover), 882 [Google Scholar]
- Bouret, J.-C., Lanz, T., & Hillier, D. J. 2005, A&A, 438, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cassinelli, J. P., & Castor, J. I. 1973, ApJ, 179, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein 1975, ApJ, 195, 157 (CAK) [NASA ADS] [CrossRef] [Google Scholar]
- Fullerton, A. W., Massa, D. L., & Prinja, R. K. 2006, ApJ, 637, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Grevess, N., & Sauval, A. J. 1998, Sp. Sci. Rev., 85, 161 [CrossRef] [Google Scholar]
- Howk, J. C., Cassinelli, J. P., Bjorkman, J. E., & Lamers, H. J. G. L. M. 2000, ApJ, 534, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 417 [Google Scholar]
- Lucy, L. B. 2007, A&A, 468, 649 (L07) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucy, L. B. 2010, A&A, 512, 33 (L10) [Google Scholar]
- Lucy, L. B. & Solomon, P. M. 1970, ApJ, 159, 879 (LS70) [NASA ADS] [CrossRef] [Google Scholar]
- Marcolino, W. L. F., Bouret, J.-C., Martins, F., et al. 2009, A&A, 498, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pols, O. R., Schroder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., & Conti, P. S. 2008, ApJ, 679, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] [Google Scholar]
Appendix A: Precision of the estimator 
The 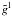 are derived from a MC simulation using estimator A, the summation over pathlengths given in Eq. (10) of L07. This is expected to be more accurate than estimator B, the summation of momentum tansfers from energy packets to matter at the discrete line-scattering events.
are derived from a MC simulation using estimator A, the summation over pathlengths given in Eq. (10) of L07. This is expected to be more accurate than estimator B, the summation of momentum tansfers from energy packets to matter at the discrete line-scattering events.
A test of the accuracy and convergence of A and B has been carried out for model t500g400. In this test, the exact gl is taken to be 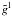 given by A when N, the number of MC quanta, is 512 × 106. Given this “exact” gl, the fractional errors of
given by A when N, the number of MC quanta, is 512 × 106. Given this “exact” gl, the fractional errors of 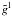 can be computed at smaller N for A and at all N for B.
can be computed at smaller N for A and at all N for B.
The mean absolute fractional errors for 0.5 < v/a < 2 are plotted against N in Fig. A.1. As expected, errors for both A and B are 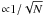 . Also as expected, A is the more accurate. From the plotted least squares fits, ϵA = 0.488 × ϵB. Thus, to achieve the same accuracy, B would have required N to be increased by the factor 4.2. The saving of computer time with A was essential in carrying out the huge modelling effort required to produce Table 1.
. Also as expected, A is the more accurate. From the plotted least squares fits, ϵA = 0.488 × ϵB. Thus, to achieve the same accuracy, B would have required N to be increased by the factor 4.2. The saving of computer time with A was essential in carrying out the huge modelling effort required to produce Table 1.
A typical simulation has N = 40 × 106 and so, according to Fig. A.1, the typical error of 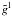 with A is 0.016 dex. But this is specific to model t500g400. At cooler Teff’s, an increasing fraction of packets propagate through the MRL without undergoing line scatterings, so that, for fixed N, the sampling error of
with A is 0.016 dex. But this is specific to model t500g400. At cooler Teff’s, an increasing fraction of packets propagate through the MRL without undergoing line scatterings, so that, for fixed N, the sampling error of 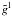 increases. Thus, for model t325g400, the above error increases to 0.20 dex.
increases. Thus, for model t325g400, the above error increases to 0.20 dex.
 |
Fig. A.1 Convergence and accuracy test of MC estimators. For model t500g400, the mean absolute fractional error ϵ of |
Appendix B: Reflection probability
When a MC quantum crosses the upper boundary of the MRL at height x1 where v/a = 5, it permanently exits the computational domain. Thus, its reflection probability p1 = 0, an assumption justified if the true p1 ≪ 1.
An estimate of p1 can be derived following the method of Abbott & Lucy (1985, Sect. III). We assume that radiative driving dominates other mechanisms beyond x1 and accelerates the wind to terminal velocity v∞. On this assumption, increases in the mechanical luminosity 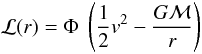 (B.1)are accounted for by a matching decrease in the radiative luminosity L(r). Thus, in the spherical shell (r,r + dr), the O(v/c) difference between the rates at which matter absorbs
(B.1)are accounted for by a matching decrease in the radiative luminosity L(r). Thus, in the spherical shell (r,r + dr), the O(v/c) difference between the rates at which matter absorbs 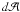 and emits dℰ radiant energy is
and emits dℰ radiant energy is 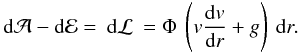 (B.2)If we now assume that the electron- and line-scatterings responsible for the energy transfer absorb from a radially-streaming radiation field and emit isotropically, then
(B.2)If we now assume that the electron- and line-scatterings responsible for the energy transfer absorb from a radially-streaming radiation field and emit isotropically, then 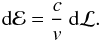 (B.3)Since this energy is radiated isotropically, the fraction propagating back through r = r1 – i.e., back into the MRL – is
(B.3)Since this energy is radiated isotropically, the fraction propagating back through r = r1 – i.e., back into the MRL – is ![\appendix \setcounter{section}{2} \begin{equation} w_{1} = \frac{1}{2} \; \left [\: 1- \sqrt{1-(z/z_{1})^{2}} \; \right ], \end{equation}](/articles/aa/full_html/2010/16/aa14784-10/aa14784-10-eq204.png) (B.4)provided that no interactions intervene. Here z = R/r, where R is the photospheric radius.
(B.4)provided that no interactions intervene. Here z = R/r, where R is the photospheric radius.
Combining the above, we find that the luminosity of inwardly-propagating radiation at r1 is 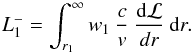 (B.5)The reflection probability is then
(B.5)The reflection probability is then 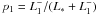 , where L∗ is the luminosity the wind-free star.
, where L∗ is the luminosity the wind-free star.
In evaluating p1, we assume 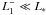 and that the supersonic wind obeys a β-velocity law with β = 1. The result is
and that the supersonic wind obeys a β-velocity law with β = 1. The result is ![\appendix \setcounter{section}{2} \begin{equation} p_{1} = \frac{\Phi}{\; \Phi_{\dagger}} \int_{0}^{z_{1}} w_{1} \: \left [\: 1+\frac{\eta}{1-z} \right ] \: {\rm d}z \end{equation}](/articles/aa/full_html/2010/16/aa14784-10/aa14784-10-eq214.png) (B.6)here Φ† = L∗/cv∞ (Cassinelli & Castor 1973) and η = (vesc/v∞)2, where vesc is the escape velocity from r = R.
(B.6)here Φ† = L∗/cv∞ (Cassinelli & Castor 1973) and η = (vesc/v∞)2, where vesc is the escape velocity from r = R.
Values of p1 have been computed for the ZAMS models in Fig. 8. Thus, at ℳ = 30 ℳ⊙ with v∞/vesc = 2.6, the ratio ΦL/Φ† = 0.044. Then, for v1 = 5a, z1 = 0.969, and we find p1 = 0.0071. The neglect of back-scattering from the exterior wind is therefore justified. Moreover, since 1 − z1 ≪ 1, the assumption of plane-parallel geometry is also justified.
But for very massive ZAMS stars, the assumption p1 = 0 is less valid. Thus, for ℳ = 80 ℳ⊙, ΦL/Φ† = 0.384, z1 = 0.972, and we find that p1 = 0.064. Accordingly, when theory and observation agree to ≲ 0.1 dex, further progress will require an improved treatment of transonic flow.
Similarly, for evolved stars, the enhanced mass loss when Γe ≈ 0.5 – see Sect. 5 – also brings about an incipient failure of the MRL model. Thus, a star with ℳ/ℳ⊙ = 80 at (40000 K, 3.5) in (Teff,log g)-space has ΦL/Φ† = 2.20 and z1 = 0.964, so that p1 = 0.348. Thus the radiative coupling of the MRL to the exterior wind ceases to be negligible.
All Tables
All Figures
 |
Fig. 1 Search for dynamical consistency. The open circles are the initial discrete representation ( |
| In the text | |
 |
Fig. 2 Search for dynamical consistency. Symbols and model parameters as in Fig. 1. The interatively-corrected representation ( |
| In the text | |
 |
Fig. 3 Sensitivity of the eigenvalue J to microturbulent velocity vt for model t400g375. Filled circles are solutions obtained as described in Sect. 2; open circles are solutions from L07. The thermal speed of Fe ions is indicated. |
| In the text | |
 |
Fig. 4 Failed search for dynamical consistency when vt = 0 for model t400g375. Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 5 Mass flux J as a function of Teff for log g = 3.00(0.25)4.50. The data are from Table 1. The dashed line J = J ∗ defines the boundary of the weak-wind domain – see L10. |
| In the text | |
 |
Fig. 6 Mass flux J as a function of g for Teff = 27.5(2.5)55.0 kK. The data are from Table 1. |
| In the text | |
 |
Fig. 7 Comparison of MRL mass fluxes JL with scaled CAK formulae for Teff = 30,35 and 40 kK. The dashed vertical lines are the MRL-CAK offsets discussed in the text. |
| In the text | |
 |
Fig. 8 Mass-loss rates for O-stars on the zero-age main sequence (ZAMS) as a function of Teff, with masses in solar units indicated. Predictions of MRL theory (ΦL) are plotted as well as values (ΦV) derived with the formula of Vink et al. (2000). |
| In the text | |
 |
Fig. A.1 Convergence and accuracy test of MC estimators. For model t500g400, the mean absolute fractional error ϵ of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.