| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201015065 | |
| Published online | 04 November 2010 | |
The impact of an updated 14N(p, γ)15O reaction rate on advanced evolutionary stages of low-mass stellar models
1
INAF - Osservatorio Astronomico di Teramo,
via M. Maggini,
64100
Teramo,
Italy
e-mail: pietrinferni@oa-teramo.inaf.it ; cassisi@oa-teramo.inaf.it
2
Astrophysics Research Institute, Liverpool John Moores University,
12 Quays House,
Birkenhead,
CH41 1LD, UK
e-mail: ms@astro.livjm.ac.uk
Received:
28
May
2010
Accepted:
25
June
2010
We investigate the impact of the 14N(p,γ)15O reaction rate as redetermined by the LUNA experiment, on the shell H-burning and core He-burning phases of low-mass, metal-poor stellar models. The new reaction rate has small but noticeable effects, the largest one being a ~7−8% reduction in the red giant branch lifetimes. To different degrees, the lifetimes and luminosities of horizontal branch models, the mass of the stellar models evolving within the RR Lyrae instability strip, the luminosity of the red giant branch luminosity function bump, the theoretical calibrations of the R-parameter, and the tip of the red giant branch luminosity are also affected. Predictions for the tip of the red giant branch luminosity, in particular, are in very good agreement with the currently available empirical constraints.
Key words: stars: interiors / stars: evolution / nuclear reactions, nucleosynthesis, abundances
© ESO, 2010
1. Introduction
The last twenty years have witnessed a significant improvement in the calculation of the relevant input physics for stellar evolution calculations, such as the equation of state of the stellar matter (i.e., Rogers et al. 1996), radiative opacities (i.e., Iglesias & Rogers 1996; Ferguson et al. 2005), nuclear cross-sections (i.e., Angulo et al. 1999), and neutrino emission rates (i.e., Haft et al. 1994). Several of these advances have been stimulated by the need to match the high-precision data from helioseismology, and an immediate consequence has been the improved accuracy of low-mass main sequence (MS) models for both Population I and II stars.
A set of key ingredients in the calculation of stellar models are the nuclear reaction rates, and much effort has been devoted to improving the measurements of rates at energies as close as possible to the Gamow peak, i.e., the energies at which nuclear reactions occur in stars. Thanks to these studies, the reaction rates involved in the p-p chain are now assumed to have a small uncertainty, and the uncertainty in the predicted age – luminosity relationship for low-mass MS stars is also negligible (< 2% – Chaboyer et al. 1998; Brocato et al. 1998). However, near the end of the MS – e.g., when the abundance of protons in the core is approaching zero – the energy supplied by the p-p chain becomes insufficient and the star reacts by contracting its core to release gravitational energy. As a consequence, according to the virial theorem, both central temperature and density increase and, when the temperature attains a value of ~15 × 106 K, the H-burning process becomes controlled by the CNO cycle, whose efficiency is critically dependent on the 14N(p,γ)15O reaction rate, the slowest reaction of the whole cycle.
Until a few years ago, the rate for the 14N(p,γ)15O reaction was uncertain by a factor of 5 at least, because all available laboratory measurements had been performed at energies well above the range of interest for astrophysical purposes (Angulo et al. 1999). The LUNA experiment (Formicola et al. 2004) has significantly improved low energy measurements by obtaining a reaction rate which is about a factor of 2 lower than previous determinations.
Because of the significant impact of the revised reaction rate on the efficiency of the CNO cycle, hence on the age – luminosity calibration during the late MS evolution, Imbriani et al. (2004) studied its effect on the age dating of Galactic globular clusters (GCs). Their analysis has shown that the new rate for the 14N(p,γ)15O reaction leads to isochrones with a brighter and hotter turn off (TO) for a fixed age, and the resulting age – TO luminosity calibration predicts on average systematically older GC ages by ~0.9 Gyr.
Weiss et al. (2005) investigated the effect of this new reaction rate on the evolution of both low- and intermediate-mass stars. They confirmed the results obtained by Imbriani et al. (2004) and extended their analysis to more advanced evolutionary stages such as the He-burning ignition at the red giant branch (RGB) tip in low-mass stars, and the core and shell He-burning stages in intermediate mass stars. Magic et al. (2010) highlighted the crucial role played by the 14N(p,γ)15O reaction rate in determining the transition mass to stars harbouring a convective core.
These studies, however, do not explore several key evolutionary properties, like the RGB bump brightness and evolutionary lifetimes during the core He-burning phase of low-mass, metal-poor stellar models, or the temperature location of models along the horizontal branch (HB).
The main aim of this paper is to fill this gap. We analyse in detail several evolutionary properties of stellar models representative of stars currently evolving along the RGB and the HB of Galactic GCs. We also investigate the impact of the new 14N(p,γ)15O reaction rate on one of the most important primary distance indicators, i.e., the I-band absolute magnitude of the tip of the RGB (TRGB), and on the R-parameter, commonly used for estimating the initial helium abundance of Galactic GCs.
The plan of this paper is as follows. In the next section, we describe briefly the set of evolutionary models employed in our analysis. Section 3 presents the impact of the new reaction rate on selected evolutionary features along the RGB stage, and provides an updated calibration of the TRGB brightness as a standard candle. Section 4 deals with the core He-burning evolutionary phase and the R-parameter calibration. Our final remarks and conclusions close the paper.
2. The models
Our calculations employed the same stellar evolutionary code used to realize the BaSTI library of stellar models (e.g., Pietrinferni et al. 2004, 2006), i.e., the same equation of state, radiative opacity, neutrino energy loss, and nuclear reaction rates, with the exception of the electron conduction opacities, which were replaced with the results of Cassisi et al. (2007, hereinafter C07). As for the 14N(p,γ)15O reaction, we performed two sets of calculations, one employing the reaction rate used in the BaSTI code (from Angulo et al. 1999 – hereinafter NACRE rate) and one with the new determination by Formicola et al. (2004; see also Imbriani et al. 2005 – hereinafter LUNA rate).
We computed stellar models in the mass range ~0.80−1.2 M⊙, from the zero age main sequence (ZAMS) to the He-ignition at the RGB tip, for the same scaled-solar heavy element mixture adopted by Pietrinferni et al. (2004 – Grevesse & Noels 1993), and the following choices of initial chemical composition (Y,Z): (0.245, 0.0001), (0.245, 0.0003), (0.246, 0.0006), (0.246, 0.001), (0.248, 0.002), (0.251, 0.004), (0.256, 0.008), (0.259, 0.01). In the course of the paper we will use also the notation [M/H] = log(Z/(1 − Z − Y)) − log(Z⊙/(1 − Z⊙ − Y⊙)), where Z⊙ = 0.0198 and Y⊙ = 0.2734, as determined in Pietrinferni et al. (2004) from the calibration of the standard solar model with the BaSTI code.
For each chemical composition, we also computed an extended set of HB stellar models, using the standard method termed “reconfiguration of pre-flash models” developed by Serenelli & Weiss (2005). In brief, we considered both the He-core mass at He-ignition of a RGB progenitor whose age at the TRGB is of the order of 13 Gyr, and modelled the accretion of the envelope with the appropriate evolutionary chemical composition until the desidered total mass along the HB was attained (see, e.g., Pietrinferni et al. 2004; Serenelli & Weiss 2005). The RGB progenitors of these additional HB models have masses equal to ~0.8 M⊙ at the lowest metallicities, increasing up to ~0.9 M⊙ for the more metal-rich compositions. We also verified that the use of the LUNA rate for the 14N(p,γ)15O reaction does not affect the solar-based mixing length calibration, hence we used the same value of the mixing length as in Pietrinferni et al. (2004).
Finally, it is relevant to mention that the 14N(p,γ)15O reaction rate was reanalysed by Marta et al. (2008) taking advantage of new laboratory measurements in the high energy regime, and an accurate analysis of the various contributions that control the final uncertainty in the total S-factor of this reaction. Their recommended value for the total S-factor is however well within 1σ of the estimate provided by Formicola et al. (2004). Adelberger et al. (2010) again studied this reaction rate by combining all available measurements. They provide a new estimate of the total S-factor that is slightly larger than the LUNA result, but still in excellent agreement within the estimated uncertainty. Because of these results, we also calculated selected stellar models (0.8 M⊙ for Z = 0.0001 and 0.002, and 0.9 M⊙ for Z = 0.01) by using alternatively the “low” and “high” rate for the 14N(p,γ)15O nuclear reaction provided by Imbriani et al. (2006) that correspond to the 1σ limits on the total S-factor of the LUNA rate.
3. The evolution along the RGB
One of the most prominent evolutionary stages in the colour − magnitude diagram of low-mass stars is the RGB, which also provides a valuable benchmark for low-mass stellar models. Star counts along the RGB can be compared with predicted evolutionary lifetimes, the brightness of the RGB bump provides constraints on the extension of the convective envelope and chemical stratification in the model interiors, and the TRGB brightness constrains the size of the He-core mass at the ignition of central He-burning (Renzini & Fusi Pecci 1988).
3.1. The RGB evolutionary lifetimes and the luminosity function bump
During the RGB evolution, the H-burning shell has a very small thickness in mass, of ≈ 0.001 M⊙ or smaller near the TRGB. When crossing the chemical discontinuity left over by the convective envelope, soon after the first dredge-up, the abrupt drop in molecular weight – related to the sudden change in the H-abundance profile – affects the H-burning efficiency and, in turn, causes a sudden change in the stellar surface luminosity. In more detail, upon encountering the H-abundance discontinuity, the matter in the shell expands and cools slightly, causing a sharp drop in the stellar surface luminosity. When thermal equilibrium is restored, the stellar luminosity begins to increase again monotonically. As a consequence, the model crosses a narrow luminosity interval three times. This occurrence produces the characteristic bump in the RGB theoretical luminosity function (Thomas 1967; Iben 1968).
Since its detection in 47 Tucanae (King et al. 1985), the RGB bump has been the target of several theoretical and observational investigations (see Di Cecco et al. 2010; and Monelli et al. 2010 for the most recent analysis, and references therein). The parameter widely adopted to study the RGB bump brightness is 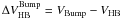 , defined as the V-magnitude difference between the RGB bump and the HB at the level of the RR Lyrae instability strip (Fusi Pecci et al. 1990). From the observational point of view,
, defined as the V-magnitude difference between the RGB bump and the HB at the level of the RR Lyrae instability strip (Fusi Pecci et al. 1990). From the observational point of view, 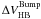 has the advantage of being independent of distance and reddening, but is difficult to evaluate when the instability strip is scarcely populated. From a theoretical point of view,
has the advantage of being independent of distance and reddening, but is difficult to evaluate when the instability strip is scarcely populated. From a theoretical point of view, 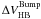 depends not only on the bump level, but also on the exact prediction of the HB luminosity, which is set by the value of the He-core mass at the He-flash (see Salaris et al. 2002, for a detailed discussion).
depends not only on the bump level, but also on the exact prediction of the HB luminosity, which is set by the value of the He-core mass at the He-flash (see Salaris et al. 2002, for a detailed discussion).
The first detailed comparison between predicted and observed measurements of 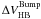 in Galactic GCs was performed by Fusi Pecci et al. (1990). By employing the theoretical models available at that time, these authors found that the observed dependence of
in Galactic GCs was performed by Fusi Pecci et al. (1990). By employing the theoretical models available at that time, these authors found that the observed dependence of 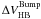 on the cluster metallicity was in good agreement with theory, but the zero point of the theoretical
on the cluster metallicity was in good agreement with theory, but the zero point of the theoretical 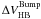 values was too small by ~0.4 mag. For some time, this result has been considered a clear drawback of standard theoretical models of low-mass RGB stars. This result was reanalysed by Cassisi & Salaris (1997), who concluded that their models provided a good match to the available observational data. This topic has been reviewed by several authors (e.g., Zoccali et al. 1999; Ferraro et al. 1999; Di Cecco et al. 2010), and from their comparisons between theory and observations one can draw the conclusion that lingering uncertainties in the HB theoretical brightness and the GC metallicity scale leave open the possibility that a discrepancy at the level of ~0.20 mag between theory and observations may exist.
values was too small by ~0.4 mag. For some time, this result has been considered a clear drawback of standard theoretical models of low-mass RGB stars. This result was reanalysed by Cassisi & Salaris (1997), who concluded that their models provided a good match to the available observational data. This topic has been reviewed by several authors (e.g., Zoccali et al. 1999; Ferraro et al. 1999; Di Cecco et al. 2010), and from their comparisons between theory and observations one can draw the conclusion that lingering uncertainties in the HB theoretical brightness and the GC metallicity scale leave open the possibility that a discrepancy at the level of ~0.20 mag between theory and observations may exist.
In the following, we investigate how the new rate for the 14N(p,γ)15O reaction affects the evolutionary lifetimes along the RGB and the brightness of the RGB bump, compared to calculations with the NACRE rate.
 |
Fig. 1 The evolution with time of the bolometric luminosity of selected stellar models (see labels), computed by using either the new LUNA 14N(p,γ)15O reaction rate, or the NACRE one. The full and open dots mark the end of the central H-burning for the the model computed with the LUNA and NACRE rate, respectively. |
Figure 1 displays the bolometric luminosity as a function of time from the end of the core H-burning stage to the TRGB, for a post-MS stellar model of a typical GC star (M = 0.8 M⊙, Y = 0.248, Z = 0.002). As expected from previous investigations (Imbriani et al. 2004; Weiss et al. 2005), the model computed with the new reaction rate reaches the end of the H-burning stage at an age older by about 120 Myr (~1% age difference) than results with the NACRE rate. The impact of this age difference on the  -age relation in GC isochrones can be estimated from Fig. 2. The
-age relation in GC isochrones can be estimated from Fig. 2. The  -age relation obtained using the LUNA rate is systematically brighter than the results with the NACRE rate. As a consequence, for a fixed observed value of
-age relation obtained using the LUNA rate is systematically brighter than the results with the NACRE rate. As a consequence, for a fixed observed value of  , LUNA isochrones infer ages older by ~0.7 Gyr than calculations with the NACRE rate.
, LUNA isochrones infer ages older by ~0.7 Gyr than calculations with the NACRE rate.
 |
Fig. 2 The absolute V-band magnitude of the TO as a function of age, for theoretical isochrones with Z = 0.0003 and Z = 0.002, as derived from stellar models computed with either the LUNA or the NACRE 14N(p,γ)15O reaction rate. |
By the time that the models displayed in Fig. 1 have reached the He-flash, the age difference between calculations with the NACRE and LUNA rate has reduced from ~120 Myr to ~20 Myr, implying that RGB evolution is slightly faster when the LUNA reaction rate is employed.
Figure 3 shows the evolution in the luminosity with time in the region of the RGB bump. The LUNA rate causes a brighter bump (by ~0.06 mag), due to a slightly shallower convective envelope at the first dredge up, as shown in Fig. 4. This is caused by the LUNA-based model having an hotter H-burning shell for a fixed He core mass.
Finally, Fig. 5 shows the trend of the absolute visual magnitude of the RGB bump as a function of the metallicity for a 12 Gyr old stellar population. The LUNA rate causes a systematically brighter RGB bump in the models than the NACRE rate, for the whole Galactic GC metallicity range. The difference from results with the NACRE rate is of the order of 0.07 mag at the lowest metallicities, becoming almost negligible in the metal-rich regime.
 |
Fig. 4 The time evolution of the He-core mass and the location of the bottom of the convective envelope, for the same models shown in Fig. 3. |
 |
Fig. 5 The V-band magnitude of the RGB bump as a function of the metallicity, for a stellar population with age equal to 12 Gyr, as derived from stellar models computed with either the LUNA or the NACRE 14N(p,γ)15O reaction rate. |
3.2. The RGB tip
The evolution along the RGB ends when the thermal conditions for igniting helium burning are attained in the electron degenerate core. A runaway nuclear burning of He in the core occurs, the so-called He-flash, after which the star contracts and starts quiescent core helium burning along the HB. The value of the He-core mass at the He-flash (McHe) controls the brightness of both the TRGB and the HB, two of the most important primary standard candles for old stellar populations (see, e.g., Lee et al. 1993; Salaris & Cassisi 1997; Caputo 1998; Catelan 2009, and references therein). Table 1 lists some relevant evolutionary properties at the TRGB for selected models computed with either the LUNA or the NACRE rate. The LUNA reaction rate leads to an higher He-core mass at the He-flash of the order of ~0.002−0.003 M⊙, than the results with the NACRE rate. The size of this difference is only slightly larger than the change due to the use of different sets of conductive opacities (Salaris et al. 2002; Cassisi et al. 2007).
Although the He-core mass is higher in the LUNA models, the surface luminosity at the TRGB is lower, the difference being Δlog (L/L⊙) ≈ 0.02 dex. This is due to the lower efficiency of the CNO cycle in the H-burning shell, which compensates for the luminosity increase expected from the higher core mass (see, e.g., the discussion in Weiss et al. 2005).
Weiss et al. (2005) obtained qualitatively similar results in terms of the variation in McHe and luminosity at the TRGB when updating their 14N(p,γ)15O reaction rate to the LUNA value and using the NACRE 3α reaction rate. Quantitatively, however, both the increase in McHe and decrease in the RGB tip luminosity are (at least for the Z = 0.0001 case tabulated in their Table 1) about a factor of 2 larger. This may be caused by their reference 14N(p,γ)15O reaction rate being the Adelberger et al. (1998) one, which is even higher than our reference NACRE rate.
We comment briefly on the results obtained with the “low” and the “high” estimates of the LUNA rate (see Sect. 2). The TRGB bolometric luminosity is affected at the level of Δlog (L/L⊙) ≈ ±0.003, while the He core mass at He-ignition is modified by only ±0.0004 M⊙. As for the evolutionary timescales, both MS and RGB lifetimes are affected at the level of at most 1%. These results show how the uncertainties in the estimates of the 14N(p,γ)15O reaction rate have only a very small impact on the properties of low-mass stellar models.
Selected properties of TRGB models, computed by adopting either the LUNA reaction rate, or the NACRE one.
3.2.1. The calibration of the TRGB method
The I-band TRGB magnitude is one of the most robust primary distance indicators. For a careful discussion of the observational advantages and drawbacks of this standard candle, we refer to Lee et al. (1993) and Madore & Freedman (1995), while an accurate analysis of the uncertainties affecting the theoretical calibration of this distance method can be found in Salaris et al. (2002) and Cassisi (2005).
On the observational side, Bellazzini et al. (2001) published an empirical calibration based on the GC ω Cen. They adopted the distance obtained by Thompson et al. (2001) from the analysis of one eclipsing binary system belonging to the cluster, and determined the TRGB apparent I-band brightness from a well populated CMD, deriving an absolute magnitude 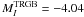 ± 0.12 in the I-Cousins filter. To date, all theoretical calibrations of the TRGB method have been within 1.5σ of this calibration as shown by Cassisi (2010). More recently, the empirical calibration of the TRGB method has been extended to higher metallicities and also to the near infrared bands by Bellazzini et al. (2004), with the inclusion of new observations for the massive GC 47 Tuc. Bellazzini et al. (2004) repeated the analysis of ω Cen with the new study of its extinction by Lub (2002), and derived an almost identical value,
± 0.12 in the I-Cousins filter. To date, all theoretical calibrations of the TRGB method have been within 1.5σ of this calibration as shown by Cassisi (2010). More recently, the empirical calibration of the TRGB method has been extended to higher metallicities and also to the near infrared bands by Bellazzini et al. (2004), with the inclusion of new observations for the massive GC 47 Tuc. Bellazzini et al. (2004) repeated the analysis of ω Cen with the new study of its extinction by Lub (2002), and derived an almost identical value, 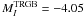 ± 0.12.
± 0.12.
 |
Fig. 6 Several calibrations of the TRGB magnitude in the I-Cousins band, as a function of the metallicity. We display results based on the LUNA and NACRE 14N(p,γ)15O reaction rate, and the semi-empirical calibration by Ferraro et al. (2000). The two filled circles with error bars correspond to the empirical estimates for ω Cen and 47 Tuc, obtained by Bellazzini et al. (2004). |
Figure 6 shows three calibrations of the TRGB magnitude in the I-Cousins band as a function of the metallicity, which are compared with the empirical estimates1 of Bellazzini et al. (2004).
When using the LUNA rate instead of the NACRE one, 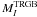 becomes fainter by about 0.05 mag at [M/H] ≤ −1.0, while at higher metallicites the differences are smaller. We note that the calibration with the LUNA rate is within ~0.5σ of the empirical estimates for both ω Cen and 47 Tuc.
becomes fainter by about 0.05 mag at [M/H] ≤ −1.0, while at higher metallicites the differences are smaller. We note that the calibration with the LUNA rate is within ~0.5σ of the empirical estimates for both ω Cen and 47 Tuc.
Figure 7 displays a similar comparison but in the near infrared. Models calculated with the LUNA rate are generally fainter by ~0.05 mag, and agree well with empirical data also in the H- and K-bands, while they are more discrepant – but still lie within the error bars – in the J-band. This may suggest a source of uncertainty in the bolometric correction to the J-band (see also the discussion in Bellazzini 2007).
The best-fit relations of our theoretical calibrations with the LUNA reaction rate are the following:
 |
Fig. 8 Upper panel: absolute visual magnitude of the ZAHB at log Teff = 3.85, as a function of the metallicity. The stellar models have been computed by adopting alternatively the NACRE or the LUNA 14N(p,γ)15O reaction rate. Lower panel: as in the upper panel, but for the bolometric luminosity of the ZAHB. |
4. The core He-burning stage
As discussed in the previous section, the use of the new LUNA reaction rate affects the mass of the He core at the RGB tip. One can therefore expect the brightness of the zero age horizontal branch (ZAHB) to also be affected. Figure 8 compares the predicted bolometric luminosity and V-band absolute magnitude of ZAHB models at log (Teff) = 3.85 – a point taken as representative of the average effective temperature of the RR Lyrae instability strip – as a function of metallicity, for various assumptions about the rate of the 14N(p,γ)15O nuclear reaction. The updated LUNA rate does not affect the brightness of the ZAHB at intermediate metallicities, while it has a modest impact, at the level of ~0.05 mag, in the high- and low-metallicity regimes: models based on the LUNA rate appears brighter at the lowest metallicity and fainter at the opposite end of the metallicity spectrum. Given that the ZAHB luminosity increases with increasing McHe and, at fixed McHe, with increasing efficiency of H-shell burning, this behaviour can be explained as follows. At low metallicites, because of the low contribution of the CNO burning to the surface luminosity in models within the instability strip, it is the increase in McHe that causes the difference in results between the LUNA and NACRE models. Increasing the initial metallicity enhances the contribution of the H-burning shell to the output luminosity, and in this case it is the lower efficiency of the CNO burning with the LUNA rate that progressively dominates the behaviour of the ZAHB luminosity, compared to NACRE results.
By comparing the results of the ZAHB and RGB calculations with LUNA and NACRE rates, one can conclude that the use of the LUNA rate leaves unaffected the theoretical calibration of the 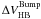 parameter for [M/H] below ~ −1.8, and decreases
parameter for [M/H] below ~ −1.8, and decreases 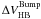 by ~0.05 mag at intermediate metallicites, and up to ~0.1 mag when [M/H] increases above ~ −1.
by ~0.05 mag at intermediate metallicites, and up to ~0.1 mag when [M/H] increases above ~ −1.
 |
Fig. 9 H-R diagram of selected HB evolutionary tracks, computed by using the LUNA reaction rate (solid line) or the NACRE one (dashed line), and for various assumptions about the metallicity and total mass. |
To monitor any change in the Teff location and morphology of HB evolutionary tracks, Fig. 9 shows the H-R diagram of selected models computed with the NACRE and LUNA rates, for three different metallicities. Given that models computed with the LUNA rate have a higher McHe at the He-flash, they also have a hotter location in the H-R diagram for a given value of the total stellar mass. As a consequence, the mean mass of models within the RR Lyrae instability strip is higher when the LUNA rate is adopted, by an amount ranging from 0.05 M⊙ for Z = 0.001, to 0.007 M⊙ for Z = 0.01.
Finally, we find that the effect of the LUNA rate on the core He-burning lifetime is small, amounting to a reduction of ~3−4% with respect to models based on the NACRE rate. This difference has been evaluated for models whose ZAHB location is within the instability strip. For lower mass HB models, the variation is even smaller (~1 Myr).
4.1. The R-parameter calibration
Values of the R-parameter as obtained for various assumptions about the 14N(p,γ)15O nuclear reaction rate and a reference age of 13 Gyr. The values obtained by the BaSTI library are also listed.
A powerful method for estimating the initial He-content in GC stars is based on the so-called R-parameter (Iben 1968; Salaris et al. 2004, and references therein). This parameter is defined as the ratio of the star counts along the HB to the number of RGB stars brighter than the HB. Theoretically, the value of the R-parameter can be obtained from the ratio of the HB lifetime of a model whose ZAHB location is within the RR Lyrae instability strip, to the time spent by its RGB progenitor at magnitudes brighter than the ZAHB brightness: R = tcHe/tRGB. Given that the lifetime during the HB phase depends on the total stellar mass, hence on the ZAHB effective temperature (see Castellani et al. 1994), it is common in the case of GCs with very blue HB morphologies, to apply a correction that takes into account the increase in tcHe with decreasing HB mass (see Cassisi et al. 2003; Sandquist et al. 2010).
As discussed before, the use of the new LUNA reaction rate affects – albeit slightly – ZAHB and TRGB brightnesses, HB and RGB evolutionary lifetimes, and it is important to verify whether the theoretical calibration of the R-parameter is influenced by the use of this updated rate. For this purpose, we compared the calibrations of the R-parameter as a function of Z and Y obtained with the LUNA and NACRE rates, keeping all other inputs unchanged. For some selected metallicities, the values of the R-parameter are listed in Table 2, where for the sake of comparison the values based on the BaSTI models are also provided. Given that dR/dY ~ 10, we find that, for a given value of R, the LUNA calibration provides helium mass fractions Y that are lower by 0.004 at Z = 0.0001, but higher by 0.001, 0.003 and 0.015 at Z = 0.0003, 0.001, and 0.01, respectively.
Overall, at fixed Z, the change in R induced by the use of the new LUNA reaction rate is smaller than the typical error bars of individual empirical estimates of R, and smaller than the theoretical uncertainty in the 12C(α,γ)16O reaction rate (Cassisi et al. 2003).
It is interesting to determine how these variations affect the estimate of the primordial He abundance based on measurements of the R-parameter in metal-poor Galactic GCs. Salaris et al. (2004) – expanding upon the work by Cassisi et al. (2003) – determined the initial He mass fraction (YGGC) of stars in a sample of 57 Galactic GCs (assuming that stars within the same cluster share the same initial He-content). They derived an average YGGC = 0.250 ± 0.006, and no significant trend with metallicity. Selected values of their theoretical calibration of R are displayed in Table 2. The model input physics is the same as in the BaSTI library, i.e., differs from the NACRE values in the table because of the different electron conduction opacities used. The BaSTI models were calculated using the Pothekin (1999) electron conduction opacities, instead of the C07 ones employed here.
The LUNA calibration displayed in Table 2 gives YGGC ~ 0.251 at the lowest and intermediate metallicities of the GC sample of Salaris et al. (2004). This value is consistent with the primordial He-content obtained from standard Big Bang nucleosynthesis calculations (see Steigman 2010). At the high metallicity end of the GC sample ([Fe/H] between −0.3 and −0.6, the exact value depending on the adopted metallicity scale), the estimated initial He mass fraction increases to YGGC ~ 0.261.
5. Summary
We have investigated the impact of the updated 14N(p,γ)15O reaction rate from the LUNA experiment on post-MS stages of low-mass stellar models. In agreement with previous work on the same subject, we have found that overall the new reaction rate has a small influence on the models, although some evolutionary properties are more sizably affected. Our results can be summarized as follows:
-
The use of the updated LUNA reaction rate leads to a slowerMS evolution but a 7−8% shorter lifetime along the RGB, than results with the NACRE rate. As a consequence, for a fixed value of the mass and initial chemical composition, LUNA low-mass stellar models attain He-ignition on the TRGB with approximately the same age as the models based on the NACRE rate.
-
For a fixed age and initial chemical composition, the bump in the RGB luminosity function predicted by theoretical isochrones is brighter by ~0.06 mag with the new rate, due to slightly shallower convective envelopes at the 1th dredge up.
-
The bolometric luminosity of the TRGB for old stellar populations is lower than in models based on the NACRE rate, despite the slightly higher He-core mass at the TRGB. The new LUNA rate provides a new theoretical calibration of the I-band TRGB magnitude as a function of [M/H] that is in good agreement with robust empirical constraints. The same result holds for near-infrared bands; only the J-band theoretical calibration seems to be slightly discrepant, although always within 1σ of the empirical data. We provide analytical calibrations of the I,J,H, and K TRGB absolute magnitudes as a function of [M/H].
-
The new LUNA rate also affects the ZAHB brightness, the size of the effect depending on the metallicity: at the lowest metallicities ZAHB models are brighter by about 0.05 mag, while they appear fainter by the same amount at high metallicities, and are unaffected in the intermediate regime. When combining this result with the effect on the RGB bump brightness, one finds that the new theoretical calibration of the
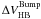 parameter is unaffected in the low metallicity regime, while it decreases by ~0.05 mag and ~0.10 mag in the intermediate- and metal-rich regime, respectively.
parameter is unaffected in the low metallicity regime, while it decreases by ~0.05 mag and ~0.10 mag in the intermediate- and metal-rich regime, respectively. -
The core He-burning lifetimes for models within the RR Lyrae instability strip are shorter by ~3−4%. The same variation is found for models located at the red side of the strip, whereas the effect is smaller for models blueward of the strip.
-
We have investigated the effect of the new rate on the calibration of R-parameter, a powerful indicator for the initial He-abundance of old stellar populations. R-parameter values based on models relying on the LUNA rate provide, for a fixed value of R, He mass fractions lower by about 0.004 at Z = 0.0001, but higher by 0.001, 0.003, and 0.015 at Z = 0.0003, 0.001, and 0.01, respectively.
Bolometric luminosities have been transformed to broadband magnitudes using the bolometric corrections described in Pietrinferni et al. (2004).
Acknowledgments
We warmly thank our referee (Achim Weiss) for very helpful comments that have helped improve the presentation of our results. This research has made use of NASA’s Astrophysics Data System Bibliographic Services, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. A.P. and S.C. acknowledge the financial support of the Ministero della Ricerca Scientifica e dell’Universita’ PRIN MIUR 2007: “Multiple stellar populations in globular clusters” (PI: G. Piotto), ASI grant ASI-INAF I/016/07/0, and the Italian Theoretical Virtual Observatory Project (PI: F. Pasian).
References
- Adelberger, E. G., Austin, S., Bahcall, J., et al. 1998, Rev. Mod. Phys., 70, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, E. G., Balantekin, A. B., Bemmerer, D., et al. 2010, Rev. Mod. Phys., submitted [arXiv:1004.2318] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nuclear Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M. 2007, A&A, 473, 171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellazzini, M., Ferraro, F. R., & Pancino, E. 2001, ApJ, 556, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Bellazzini, M., Ferraro, F. R., Sollima, A., Pancino, E., & Origlia, L. 2004, A&A, 424, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brocato, E., Castellani, V., & Villante, F. L. 1998, MNRAS, 298, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Caputo, F. 1998, A&A Rev., 9, 33 [Google Scholar]
- Cassisi, S. 2005, in Resolved Stellar Populations, Cancun, Mexico [arXiv:astro-ph/0506161] [Google Scholar]
- Cassisi, S. 2010, in Stellar Populations Planning for the Next Decade, IAU Proc., IAU Symp., 262, 13 [Google Scholar]
- Cassisi, S., & Salaris, M. 1997, MNRAS, 285, 593 [NASA ADS] [Google Scholar]
- Cassisi, S., Castellani, V., degl’ Innocenti, S., & Weiss, A. 1998, A&AS, 129, 267 [Google Scholar]
- Cassisi, S., Salaris, M., & Irwin, A. W. 2003, ApJ, 588, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Castellani, M., Castellani, V., Pulone, L., & Tornambé, A. 1994, A&A, 282, 771 [NASA ADS] [Google Scholar]
- Catelan, M. 2009, Ap&SS, 320, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Chaboyer, B., Demarque, P., Kernan, P. J., & Krauss, L. M. 1998, ApJ, 494, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cecco, A., Bono, G., Stetson, P. B., et al. 2010, ApJ, 712, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Messineo, M., Fusi Pecci, F., et al. 1999, AJ, 118, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, F. R., Montegriffo, P., Origlia, L., & Fusi Pecci, F. 2000, AJ, 119, 1282 [NASA ADS] [CrossRef] [Google Scholar]
- Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Fusi Pecci, F., Ferraro, F. R., Crocker, D. A., Rood, R. T., & Buonanno, R. 1990, A&A, 238, 95 [NASA ADS] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Origin and evolution of the elements, ed. N. Prantzos, E. Vangioni-flam, & M. Cassè (Cambridge Univ. Press), 14 [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. Jr. 1968, Nature, 220, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2004, A&A, 420, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, C. R., Da Costa, G. S., & Demarque, P. 1985, ApJ, 299, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. G., Freedman, W. L., & Madore, B. F. 1993, ApJ, 417, 553 [Google Scholar]
- Lub, J. 2002, in ω Centauri: a unique window into astrophysics, ed. F. van Leeuwen, J. Hughes, & G. Piotto (S. Francisco: ASP), ASP Conf. Ser., 265, 95 [Google Scholar]
- Madore, B. F., & Freedman, W. L. 1995, AJ, 109, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Magic, Z., Serenelli, A., Weiss, A., & Chaboyer, B. 2010, ApJ, 718, 1378 [NASA ADS] [CrossRef] [Google Scholar]
- Marta, M., Formicola, A., Gyürky, Gy., et al. 2008, Phys. Rev. C, 78, 2802 [NASA ADS] [Google Scholar]
- Monelli, M., Cassisi, S., Bernard, E. J., et al. 2010, ApJ, 718, 707 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Pothekin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
- Renzini, A., & Fusi Pecci, F. 1988, ARA&A, 26, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., & Cassisi, S. 1997, MNRAS, 289, 406 [NASA ADS] [Google Scholar]
- Salaris, M., Cassisi, S., & Weiss, A. 2002, PASP, 114, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Riello, M., Cassisi, S., & Piotto, G. 2004, A&A, 420, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Serenelli, A., & Weiss, A. 2005, A&A, 442, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandquist, E. L., Gordon, M., Levine, D., & Bolte, M. 2010, AJ, 139, 2374 [NASA ADS] [CrossRef] [Google Scholar]
- Steigman, G. 2010, J. Cosmol. Astropart. Phys., 4, 29 [Google Scholar]
- Thomas, H. C. 1967, Z. Astrophys., 67, 420 [NASA ADS] [Google Scholar]
- Thompson, I. B., Kaluzny, J., Pych, W., et al. 2001, AJ, 121, 3089 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., Serenelli, A., Kitsikis, A., Schlattl, H., & Christensen-Dalsgaard, J. 2005, A&A, 441, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Cassisi, S., Piotto, G., Bono, G., & Salaris, M. 1999, ApJ, 518, L49 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Selected properties of TRGB models, computed by adopting either the LUNA reaction rate, or the NACRE one.
Values of the R-parameter as obtained for various assumptions about the 14N(p,γ)15O nuclear reaction rate and a reference age of 13 Gyr. The values obtained by the BaSTI library are also listed.
All Figures
 |
Fig. 1 The evolution with time of the bolometric luminosity of selected stellar models (see labels), computed by using either the new LUNA 14N(p,γ)15O reaction rate, or the NACRE one. The full and open dots mark the end of the central H-burning for the the model computed with the LUNA and NACRE rate, respectively. |
| In the text | |
 |
Fig. 2 The absolute V-band magnitude of the TO as a function of age, for theoretical isochrones with Z = 0.0003 and Z = 0.002, as derived from stellar models computed with either the LUNA or the NACRE 14N(p,γ)15O reaction rate. |
| In the text | |
 |
Fig. 3 As in Fig. 1, but centred around the region of the RGB bump. |
| In the text | |
 |
Fig. 4 The time evolution of the He-core mass and the location of the bottom of the convective envelope, for the same models shown in Fig. 3. |
| In the text | |
 |
Fig. 5 The V-band magnitude of the RGB bump as a function of the metallicity, for a stellar population with age equal to 12 Gyr, as derived from stellar models computed with either the LUNA or the NACRE 14N(p,γ)15O reaction rate. |
| In the text | |
 |
Fig. 6 Several calibrations of the TRGB magnitude in the I-Cousins band, as a function of the metallicity. We display results based on the LUNA and NACRE 14N(p,γ)15O reaction rate, and the semi-empirical calibration by Ferraro et al. (2000). The two filled circles with error bars correspond to the empirical estimates for ω Cen and 47 Tuc, obtained by Bellazzini et al. (2004). |
| In the text | |
 |
Fig. 7 As in Fig. 6 but for the JHK near-infrared bands. |
| In the text | |
 |
Fig. 8 Upper panel: absolute visual magnitude of the ZAHB at log Teff = 3.85, as a function of the metallicity. The stellar models have been computed by adopting alternatively the NACRE or the LUNA 14N(p,γ)15O reaction rate. Lower panel: as in the upper panel, but for the bolometric luminosity of the ZAHB. |
| In the text | |
 |
Fig. 9 H-R diagram of selected HB evolutionary tracks, computed by using the LUNA reaction rate (solid line) or the NACRE one (dashed line), and for various assumptions about the metallicity and total mass. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{equation} % M_I= -2.912 + 2.375\cdot[{\rm M/H}] + 1.480\cdot[{\rm M/H}]^2 + 0.289\cdot[{\rm M/H}]^3 \end{equation}](/articles/aa/full_html/2010/14/aa15065-10/aa15065-10-eq62.png)
![\begin{equation} % M_K= -7.063 - 0.844\cdot[{\rm M/H}] - 0.093\cdot[{\rm M/H}]^2 \end{equation}](/articles/aa/full_html/2010/14/aa15065-10/aa15065-10-eq63.png)
![\begin{equation} % M_H= -6.638 - 0.487\cdot[{\rm M/H}] \end{equation}](/articles/aa/full_html/2010/14/aa15065-10/aa15065-10-eq64.png)
![\begin{equation} % M_J= -5.501 - 0.284\cdot[{\rm M/H}]. \end{equation}](/articles/aa/full_html/2010/14/aa15065-10/aa15065-10-eq65.png)