| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201014822 | |
| Published online | 26 October 2010 | |
Observational detection of eclipses of J5 Amalthea by the Galilean satellites
1
Armagh Observatory,
College Hill, Armagh BT61 9DG,
Northern Ireland,
UK
e-mail: aac@arm.ac.uk
2
Faulkes Telescope Project School of Physics and Astronomy, Cardiff
University, Queens Buildings, 5 The
Parade, Cardiff
CF24 3AA,
UK
3
Department of Physics and Astronomy, The Open
University, Walton
Hall, Milton Keynes
MK7 6AA,
UK
4
Division of Earth, Space and Environment, University of
Glamorgan, Pontypridd
CF37 1DL,
UK
5
Las Cumbres Observatory Global Telescope,
6740 Cortona Dr. Ste.
102, Goleta,
CA
93117,
USA
6
Department of Physics, University of California,
Santa Barbara, CA
93106,
USA
Received:
19
April
2010
Accepted:
24
June
2010
Aims. We carried out observations of the small jovian satellite Amalthea (J5) as it was being eclipsed by the Galilean satellites near the 2009 equinox of Jupiter in order to apply the technique of mutual event photometry to the astrometric determination of this satellite’s position.
Methods. The observations were carried out during the period 06/2009−09/2009 from the island of Maui, Hawaii and Siding Spring, Australia with the 2m Faulkes Telescopes North and South respectively. We observed in the near-infrared part of the spectrum using a PanStarrs-Z filter with Jupiter near the edge of the field in order to mitigate against the glare from the planet. Frames were acquired at rates > 1/min during eclipse times predicted using recent JPL ephemerides for the satellites. Following subtraction of the sky background from these frames, differential aperture photometry was carried out on Amalthea and a nearby field star.
Results. We have obtained three lightcurves which show a clear drop in the flux from Amalthea, indicating that an eclipse took place as predicted. These were model-fitted to yield best estimates of the time of maximum flux drop and the impact parameter. These are consistent with Amalthea’s ephemeris but indicate that Amalthea is slightly ahead of, and closer to Jupiter than, its predicted position by approximately half the ephemeris uncertainty in these directions. We argue that a ground-based campaign of higher-cadence photometry accurate at the 5% level or better during the next season of eclipses in 2014-15 should yield positions to within 0″̣05 and affect a corresponding improvement in Amalthea’s ephemeris.
Key words: eclipses / occultations / planets and satellites: individual: Amalthea / planets and satellites: general / methods: observational / techniques: photometric
© ESO, 2010
1. Introduction
The planet Jupiter is attended by four small satellites moving in orbits inside that of Io, the innermost Galilean moon (Thomas et al. 1998). Metis, Adrastea and Thebe were discovered during the Voyager flybys of the 1980 s (Jewitt et al. 1979; Synnott 1980a,b). Amalthea, the largest, was discovered by E. E. Barnard (Barnard 1892a,b) during a visual search for new satellites with the 36-in refractor at Lick Observatory in California, USA. The innermost pair, Metis and Adrastea, are co-located with Jupiter’s main ring system acting as both sources and shepherds of ring material. The remaining two, Amalthea and Thebe, fulfil the same function in relation to the so-called Gossamer rings (Burns et al. 1999; de Pater et al. 1999; Ockert-Bell et al. 1999; de Pater et al. 2008; Showalter et al. 2008).
The faintness of these inner moons and their proximity to the bright planet renders them difficult targets for Earth-based observers. Special techniques are often employed to mitigate against the glare from the planet. These include: utilising methane absorption bands in Jupiter’s spectrum (Karkoschka 1994), coronagraphy and post-processing (Nicholson & Matthews 1991; Kulyk et al. 2002; Kulyk & Jockers 2004; Veiga & Vieira Martins 2005; Kulyk 2008). Consequently the uncertainties in the ephemerides of these moons are large, 0″̣1−0″̣2 or several hundred km at Jupiter’s distance from Earth, compared to a few tens of km for the Galilean satellites1. On occasion, higher precision astrometry has been obtained in situ. For example, satellite positions derived from Cassini ISS NAC images during that spacecraft’s flyby of Jupiter in 2000 yielded orbit fits with O−C residuals of several tens of km for Adrastea and Metis (Evans & Porco 2001; Porco et al. 2003) and for Amalthea and Thebe (Cooper et al. 2006). Opportunities to obtain astrometry of this quality require the presence of a spacecraft in the vicinity of Jupiter; consequently, they have been quite few in number.
Predictions for the phenomena observed in this paper.
A powerful ground-based observational technique that can provide very accurate satellite positions over a long period of time and at regular intervals is that of mutual event photometry (Aksnes & Franklin 1976; Vasundhara et al. 2003; Noyelles et al. 2003; Emelyanov & Gilbert 2006). There, two satellites can be involved in several mutual eclipses or occultations when the planet is at equinox; the observable is a one-dimensional time series (a lightcurve) instead of a two dimensional Point Spread Function (PSF). Spatial precision is determined by the rate at which the brightness of the satellite can be measured and the relative speed between the two satellites involved in the event, rather than by the seeing. Aksnes & Franklin (1978) and Vachier et al. (2002) have advocated observations of mutual events between Amalthea and the Galilean satellites in order to tie its ephemeris to the significantly more accurate orbit models of those moons. Vachier et al. (2002) has pointed out the potential use of an improved ephemeris for Amalthea in understanding the dynamics of the jovian ring-moon environment.
Here we present observations and analyses of photometry of J5 Amalthea obtained as this satellite was being eclipsed by Io (J1) and Europa (J2). To our knowledge, these are the first observations of mutual events between Amalthea and the Galilean satellites. In the following Section, we describe the strategy adopted in carrying out these observations with particular emphasis on mitigating against the glare from Jupiter. In Sect. 3 we highlight the observing runs that were successfully completed and describe the procedure used to process the images from each run. Section 4 describes the model fits to the photometric data while Sect. 5 relates these fits to Amalthea’s ephemeris and discusses how our observational strategy may be improved upon. Finally, Sect. 6 summarises possible avenues for future work.
2. Observational strategy
Our observations were carried out with the Faulkes Telescopes North (FTN) and South (FTS) on the island of Maui, Hawaii and at Siding Spring, Australia respectively (cf. Table 1 of Christou et al. 2009).
In order to plan our observational campaign we generated predictions of such eclipses by incorporating SPICE Ephemeris kernel JUP230 into a prediction program previously used in Christou (2005) and Christou et al. (2009). We have only considered eclipses of Amalthea by a Galilean satellite, assuming that, in other cases, the photometric signature of the mutual event would be lost in the photon noise from the bright (Δm ~ + 9) Galilean. Moreover, to obtain a definite signature of an eclipse we have only sought to observe total or near-total eclipses. In fact, the Galilean satellites would normally saturate the CCD during the actual observations.
All observations were carried out with a PanStarrs-Z filter. This is a broadband filter (FWHM: 104 nm) centred at 870 nm; as it contains the 890 nm methane absorption feature in Jupiter’s spectrum (Karkoschka 1994), it increases the contrast of the satellite against the scattered light from Jupiter. An additional mitigation measure was to offset the telescope pointing so as to place Jupiter outside the field-of-view of the CCD keeping the planetary limb 10−15 arcsec off the edge of the chip. Finally, although use of the batch mode for telescope control would have provided a cadence of 15 s, we opted for the real time mode – where frames were acquired at the lower cadence of 40−50 s – to maintain the ability to change the observing parameters during those challenging observations. Frames were exposed for 5 s in all cases discussed below.
3. Observations and data reduction
Observations were carried out on 2009 June 23; July 21, August 9, 12 and 30; and September 3, 24, 28. Acquisition of frames on 23/06 began shortly after 15:30 UT, the predicted start of the eclipse being at 15:41 UT. A JPEG version of the most recently obtained frame is posted on the Faulkes Telescope web site within a few minutes of acquisition. This allowed near-real-time visual inspection of the telescope pointing, where it became apparent that the actual pointing offset was different than the one planned. The centre of the frame was ~2.5 s in RA further to the east bringing most of Jupiter’s disk within the field of view. As the eclipse was predicted to start at 15:41 UT it was decided to keep the telescope at its current pointing. Later examination of the FITS frames revealed a faint source at Amalthea’s predicted position. It should be noted that later observations in July and August, otherwise marred by variable weather conditions, showed this telescope pointing offset of ~37″ to be consistent. The pointing of FTN showed a similarly consistent, yet smaller, offset of ~1 s in RA. We incorporated this into the planning of our observations later in August and September by (a) allowing more time (20−30 min) between the start of the observing session and the predicted eclipse in order to “walk” the telescope to the desired pointing or (b) applying the offset directly into the initial pointing. As a result, good photometry was obtained of two eclipses by Europa on 24/09 and 28/09 using FTS and FTN respectively. The remainder of the paper concentrates on these three observing runs. Their predicted characteristics used for planning are given in Table 1 while the actual observations are summarised in Table 2.
Actual circumstances for the mutual event observations described in this work.
3.1. 23/06/2009: Io eclipses Amalthea
The image of Amalthea resided on a significant background of scattered light from Jupiter. Its gradient is quite severe near the planet and could bias photometric measurements. To mitigate against this, background pixel values within a circular annulus centred on Amalthea and several field stars were used to construct a two-dimensional model of the background within the central aperture by performing a third-degree polynomial fit. This was done through the “Patch” utility available through the Graphical Astronomy and Image Analysis (GAIA) package available through Starlink2. The templates resulting from these fits were then subtracted from the corresponding apertures leaving “differenced” images of the sources resting against a flat, zero-sum, background. Figure 1 illustrates the result of this procedure for a frame taken on 28/09. Care was taken not to place either the aperture itself, or the annular region around it used for the fit, over saturated areas of the frame. In three frames where Amalthea was not clearly visible, we were guided by their nearest neighbours in placing the aperture.
Extracting the photometry consisted of the following procedure: differenced frames where Amalthea was clearly visible were used to fit the satellite’s motion around Jupiter, modeled as a skewed ellipse on the sky plane. Jupiter’s motion was also estimated in the fitting process and a nearby star was picked as the point of origin. Aperture photometry was then carried out in each frame using the motion model to center the photometric apertures and sky-estimating annuli. In this case a radius of 2.5 pixels was used for the aperture and 5.5 and 8 pixels respectively for the inner and outer radii of the annulus. These choices minimized the measurement scatter about the mean. O−C residuals of the fit were 0.67 pixels (0″̣19) and 0.51 pixels (0″̣14) in the horizontal and vertical directions respectively. The 1σ photometric scatter (10%) was determined by considering only those measurements at least a minute before or after the predicted period of the eclipse. The seeing varied between 1″̣7 and 2″̣8.
 |
Fig. 1 Subframe of image taken during the observation of the IIEV event on 28/09/2009 from Haleakala, Maui. The circular apertures indicate the regions of the frame where the background has been subtracted out in advance of the photometric reduction. Pixel values within the apertures have been multiplied by a factor of 8 for clarity. At the centre of each aperture lie Amalthea (“A”) and the star (“S”) used for differential aperture photometry of the satellite. Jupiter is off the left edge of the frame which coincides with the edge of the detector. The bright sources saturating the detector are, from left to right, Callisto and Europa. The entire subframe spans 512 × 404 pixels or 143″ × 113″. |
3.2. 24/09/2009: Europa eclipses Amalthea
Images of Amalthea and field stars were distinctly elongated in frames acquired during this observing run. This was likely related to the pointing of the telescope near the zenith and the consequent difficulty with which the stepper motors could make subtle adjustments in the pointing of the altazimuthally-mounted telescope. Fitting Amalthea’s sky motion yielded O−C residuals of 0.64 and 0.57 pixels in the horizontal and vertical directions respectively. For the photometry we utilized elliptical apertures with a ratio of 2.0 between the major and the minor axis. Probably for this reason, the photometric scatter was similar to that for the above case (10%) despite the smaller amount of glare due to Jupiter being outside the FOV.
3.3. 28/09/2009: Europa eclipses Amalthea
This represents our highest-quality dataset. The seeing remained between 1″̣2 and 1″̣7 and the photometric scatter was 6%, smaller than in the other 2 observing runs. Fitting Amalthea’s sky motion on the images yielded O−C residuals of 0.43 and 0.34 pixels in the horizontal and vertical directions respectively.
4. Model fits
For this stage in the analysis we have used the method of Christou et al. (2009) to estimate the time tmin and distance b of closest approach between the two satellites on the impact plane. We note that, unlike the case in that paper, we are measuring the flux from the eclipsed satellite alone; hence our data is independent of the satellite albedos. During model fitting we considered the relative velocity v between the eclipsed and eclipsing satellite on the impact plane to be fixed and set to the value calculated through the HORIZONS ephemeris service (Giorgini et al. 1996). Our model cannot currently accommodate a satellite with a distinctly non-circular silhouette like Amalthea; instead we have explored the effect of several spherical approximations as explained below. For reference, Thomas et al. (1998) reported best-fit triaxal ellipsoid dimensions of 125 × 79 × 64 km. The disks of Io and Europa are assumed circular with radii of 1821.6 ± 0.5 and 1560.8 ± 0.5 km respectively. Amalthea’s 1σ ephemeris uncertainties within JUP230 as reported in the JPL Solar System Dynamics website3 are 400 km along the direction of motion, 200 km in the radial direction and 100 km in the out-of-orbit plane direction. Io’s and Europa’s are 5 km in all directions.
4.1. 23/06/2009: Io eclipses Amalthea
We have carried out fits to the data assuming circular disks for Amalthea of radius 64,
89 and 125 km. The first and third radii correspond to Amalthea’s shortest and longest
semi-axis respectively while the second radius is 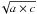 and represents Amalthea as viewed from the Earth near an ansa of its orbit. The
differences between these fits are negligible; we adopt a radius of 89 km for all
subsequent data fits in this paper. The results of all three fits are shown in Table 3 and Fig. 2. The
estimated midtime for the 23/06 event is 13 s ahead of prediction at the
4σ level of significance. Similarly, the estimated impact parameter
is 1050 km higher than the predicted value and significant at the
7σ level. A contour plot of the reduced
and represents Amalthea as viewed from the Earth near an ansa of its orbit. The
differences between these fits are negligible; we adopt a radius of 89 km for all
subsequent data fits in this paper. The results of all three fits are shown in Table 3 and Fig. 2. The
estimated midtime for the 23/06 event is 13 s ahead of prediction at the
4σ level of significance. Similarly, the estimated impact parameter
is 1050 km higher than the predicted value and significant at the
7σ level. A contour plot of the reduced 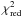 goodness-of-fit statistic
shows that, in fact, values for b as low as 700 km with corresponding
tmin 6−7 s ahead of the predictions are within the
1σ contour. The principal axis of uncertainty within the regions of
parameter space defined by these contours appears to be inclined at a negative angle to
the horizontal, an indication that the two parameters are anticorrelated. Indeed, the
linear correlation coefficient, although small, is negative. This is probably due either
(i) to the low cadence of our photometry and in particular the lack of data on the egress
phase of the eclipse and/or (ii) the relatively large photometric uncertainties. Even so,
the nominal prediction lies outside the 3-sigma contour. At that level of confidence, we
can state that (a) the actual value of b was higher than 300 km (b) if
the value of b is between 300 km and 750 km then
tmin was between 15 s and 0 s ahead of the prediction.
goodness-of-fit statistic
shows that, in fact, values for b as low as 700 km with corresponding
tmin 6−7 s ahead of the predictions are within the
1σ contour. The principal axis of uncertainty within the regions of
parameter space defined by these contours appears to be inclined at a negative angle to
the horizontal, an indication that the two parameters are anticorrelated. Indeed, the
linear correlation coefficient, although small, is negative. This is probably due either
(i) to the low cadence of our photometry and in particular the lack of data on the egress
phase of the eclipse and/or (ii) the relatively large photometric uncertainties. Even so,
the nominal prediction lies outside the 3-sigma contour. At that level of confidence, we
can state that (a) the actual value of b was higher than 300 km (b) if
the value of b is between 300 km and 750 km then
tmin was between 15 s and 0 s ahead of the prediction.
Result of the two-parameter fits to the lightcurves.
 |
Fig. 2 Model
fits to our data. Upper panels: best fit models (black curves) to
the observations (“+” signs surrounded by diamonds). Fit residuals are represented
by asterisks. Lower panels: parametric contour plots of the reduced
chi squared goodness-of-fit statistic ( |
4.2. 24/09/2009: Europa eclipses Amalthea
The parameter estimates from the fit to this lightcurve are fairly close – within
1σ – to the predicted values. Note that we have chosen not to use the
first seven data points in the fit, as they lie 2σ below Amalthea’s
average out-of-eclipse flux. The goodness-of-fit statistic is somewhat low (~0.3),
indicating that the data variances have been slightly underestimated. Evidence against
this hypothesis is that 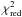 decreases if the data variances are artificially increased. As in the previous case, the
parameters are slightly anticorrelated although this is less obvious from the contour plot
of the
decreases if the data variances are artificially increased. As in the previous case, the
parameters are slightly anticorrelated although this is less obvious from the contour plot
of the 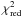 quantity. Similarly, the best estimate of tmin is slightly
(~2 s) ahead of the prediction but, since the formal uncertainty is twice this
difference, this result is not by itself significant. Finally, we note that each of the
three phases of the eclipse (ingress, totality, egress) are represented in the data,
albeit each with a single data point.
quantity. Similarly, the best estimate of tmin is slightly
(~2 s) ahead of the prediction but, since the formal uncertainty is twice this
difference, this result is not by itself significant. Finally, we note that each of the
three phases of the eclipse (ingress, totality, egress) are represented in the data,
albeit each with a single data point.
4.3. 28/09/2009: Europa eclipses Amalthea
The lightcurve of this event is of higher quality (smaller measurement scatter) than the other two cases. The fitted value of b is relatively well-determined, perhaps due to the sensitivity of grazing event lightcurves to this parameter, and in very good agreement with the prediction. The best-fit estimate for tmin is ahead of the prediction at a level of significance of between 1 and 2σ. The two parameters appear to be uncorrelated in this case.
5. Discussion
The combined results of the three data fits can be used to make statements on the state of
Amalthea’s ephemeris as inferred from these data that are stronger than those that can be
made from individual lightcurve fits. Firstly, the significantly-higher-than-predicted
estimate of the impact parameter b for the lightcurve obtained on the 23rd
June is probably spurious. Arguments in favour of this conclusion are that (a) the agreement
between the b estimates obtained for the other two lightcurves and the
predicted values is very good; and (b) the large (~1000 km) offset implied for
b is not justified given that, for the essentially planar satellite
orbits involved here, this is expected to be comparable to the out-of-plane uncertainty of
Amalthea’s position (~100 km). This assumption may, in principle, break down if Amalthea’s
speed on the impact plane becomes sufficiently small, but that is not the case in any of the
three eclipses we observed. The second major conclusion is that the observed
tmin is significantly earlier than the prediction. We have
constructed a simple model to quantify this observation in terms of position offsets in
Amalthea’s local frame. This frame is defined by the unit vectors T̂
(along-track direction), R̂ (radial direction) and N̂
(out-of-plane direction). This is, strictly speaking, an orthogonal base vector set only for
planar, circular orbits. We have extracted jovicentric positions and velocities for the Sun,
the eclipsing Galilean satellite and Amalthea at the predicted mid-eclipse time,
light-corrected for Jupiter’s distance from the Sun, and use those to relate offsets
in T, R or N to variations in
tmin or b. This enables us to calculate
numerically the partial derivatives
∂tmin/∂T,
∂tmin/∂R,
∂tmin/∂N,
∂b/∂T,
∂b/∂R,
∂b/∂N. We obtain that the partials of
tmin (b) with respect to N
are orders of magnitude smaller (larger) than the partials in the other two principal
directions. This allows us to use tmin alone to constrain likely
values of R and T offsets. From the data in Tables 1 and 3 for the
24th and 28th September events we obtain nominal offsets of
T = + 175 ± 219 km and R = −77 ± 95 km. Further, if we
replace one of the equations in this 2 × 2 linear system with the one corresponding to the
23rd June event, the two resulting systems yield ranges of ![$\left[-\mbox{131~km}, \mbox{53~km}\right]$](/articles/aa/full_html/2010/14/aa14822-10/aa14822-10-eq64.png) and
and
![$\left[\mbox{44~km}, \mbox{414~km}\right]$](/articles/aa/full_html/2010/14/aa14822-10/aa14822-10-eq65.png) for R and T respectively for a
tmin offset of ~5 s. Interestingly, one obtains a similar
value if the principal axis of uncertainty in the
for R and T respectively for a
tmin offset of ~5 s. Interestingly, one obtains a similar
value if the principal axis of uncertainty in the 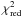 plot for that event in
Fig. 2 is extended to intersect the
b = 0 axis. We conclude that the uncertainty in our determination of
Amalthea’s position from these observations is 200 km (along-track direction) and 100 km
(radial direction) respectively and, furthermore, that Amalthea is ahead of, and slightly
closer to Jupiter than, its nominal ephemeris location. Thus, our observations yield
positional uncertainties of one half of the current 1σ ephemeris
uncertainty for Amalthea. The latter also happens to be the typical observational
uncertainty in modern conventional astrometry of this satellite. The cadence is probably at
the limit of what can be employed for useful results, given that the confidence in the
reported model fits is dependent on the distribution of the photometric points along the
lightcurve. Vachier et al. (2002) recommended a
cadence of d/v where d
is the required spatial resolution of the photometry at Jupiter’s distance from the Earth on
the plane of sky in km and v is the plane-of-sky velocity between the two
satellites in km s-1. To sample the mutual events observed here every 200 km,
half the uncertainty in conventional astrometry (~0″̣13), this criterion implies
respective cadences of 8, 6 and 11 s respectively, a factor of 4−8 higher than what was
actually used here. In general, however, the spatial resolution of the photometric sampling
would not map directly to the position uncertainty resulting from the model fit. It would
also depend eg on the quality of the photometry and the nature of the event that is
observed, for example whether it is a total or partial eclipse. Based on this work and past
experience of the authors with observations of mutual events between the major satellites of
Uranus (Christou et al. 2009) we expect that a cadence
of ~15 s and a photometric precision of 5% would achieve a position determination for
Amalthea no worse than 0″̣050 (170 km) and perhaps approaching the 0″̣010 level. For
particularly long events where v is of order 10 km s-1 an even
lower cadence may be used. Finally, the presence of a small but significant correlation
between the two parameters in the first two cases, and its absence in the third case,
indicates to us that it is linked to the uncertainties in the photometric measurement and
the low cadence. The above recommended precision of ≤5% and cadence of ≤15 s in future
observations should mitigate adequately against this.
plot for that event in
Fig. 2 is extended to intersect the
b = 0 axis. We conclude that the uncertainty in our determination of
Amalthea’s position from these observations is 200 km (along-track direction) and 100 km
(radial direction) respectively and, furthermore, that Amalthea is ahead of, and slightly
closer to Jupiter than, its nominal ephemeris location. Thus, our observations yield
positional uncertainties of one half of the current 1σ ephemeris
uncertainty for Amalthea. The latter also happens to be the typical observational
uncertainty in modern conventional astrometry of this satellite. The cadence is probably at
the limit of what can be employed for useful results, given that the confidence in the
reported model fits is dependent on the distribution of the photometric points along the
lightcurve. Vachier et al. (2002) recommended a
cadence of d/v where d
is the required spatial resolution of the photometry at Jupiter’s distance from the Earth on
the plane of sky in km and v is the plane-of-sky velocity between the two
satellites in km s-1. To sample the mutual events observed here every 200 km,
half the uncertainty in conventional astrometry (~0″̣13), this criterion implies
respective cadences of 8, 6 and 11 s respectively, a factor of 4−8 higher than what was
actually used here. In general, however, the spatial resolution of the photometric sampling
would not map directly to the position uncertainty resulting from the model fit. It would
also depend eg on the quality of the photometry and the nature of the event that is
observed, for example whether it is a total or partial eclipse. Based on this work and past
experience of the authors with observations of mutual events between the major satellites of
Uranus (Christou et al. 2009) we expect that a cadence
of ~15 s and a photometric precision of 5% would achieve a position determination for
Amalthea no worse than 0″̣050 (170 km) and perhaps approaching the 0″̣010 level. For
particularly long events where v is of order 10 km s-1 an even
lower cadence may be used. Finally, the presence of a small but significant correlation
between the two parameters in the first two cases, and its absence in the third case,
indicates to us that it is linked to the uncertainties in the photometric measurement and
the low cadence. The above recommended precision of ≤5% and cadence of ≤15 s in future
observations should mitigate adequately against this.
6. Implications for future work
This work has demonstrated the carrying out of useful mutual event photometry of Amalthea, and possibly other small satellites in the same class, with instruments that are not specifically fitted out for the purpose of observing faint sources in proximity to the giant planets. That being said, we found that our low cadence restricted our ability to exploit fully the power of this method to yield high-precision astrometry for this satellite. However, this is not an intrinsic limitation of the method or the phenomenon itself; rather a technical feature of the observing apparatus. Higher cadence observational setups should allow systematic observations of eclipses of this satellite by the Galileans with apertures smaller than the ones use here (e.g. 1 m) starting from the 2014-15 mutual event season. Indeed, sub-meter aperture instruments requiring exposure times of order a minute could be used on long-duration events.
Finally, we point out that an alternative method of accurately measuring the position of a planetary moon through CCD photometry is during its ingress in, or egress from, the planet’s shadow respectively. Generally, this method requires the precise modelling of how light is refracted away from the satellite by the planet’s atmosphere as well as accounting for albedo variegations across the satellite’s surface, phase effects and limb darkening (Mallama 1991, 1993). The reported precision of this method as applied to the Galilean satellites (Mallama et al. 2000, 2010) appears to be comparable to the corresponding figures from analysis of mutual event photometry (e.g. Emelyanov 2009). As eclipses by the planet are not limited to the periods around equinox as mutual events are, it is curious that the eclipse method has not met with more widespread use. One of the culprits may be that, for planetary satellites other than the Galileans, the eclipse condition implies proximity to the planet. For Amalthea in particular, where observable eclipses would occur 2−4 times a day, the satellite’s distance to the limb of Jupiter at either ingress or egress is always <10″ whereas it is typically ~30″ for the observations described in this paper. Hence, the scattered light problem will be more severe in the former case, requiring either a more involving reduction procedure to remove it and/or the use of specialised equipment such as a coronagraph. Observational data on such eclipses and their astrometric reduction would be useful in quantifying their suitability for orbit determination work.
JPL Ephemeris JUP230; http://ssd.jpl.nasa.gov/?sat_ephem.
Acknowledgments
The authors wish to thank the reviewer, Jean-Eudes Arlot, for his comments which improved the manuscript. The Faulkes Telescope Project is an educational and research arm of LCOGT. F.L. acknowledges support from the Dill Faulkes Educational Trust. Astronomical research at the Armagh Observatory is funded by the Northern Ireland Department of Culture, Arts and Leisure (DCAL).
References
- Aksnes, K., & Franklin, F. A. 1976, AJ, 81, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Aksnes, K., & Franklin, F. A. 1978, Icarus, 34, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Arlot, J.-E., Lainey, V., & Thuillot, W. 2006, A&A, 456, 1173 [Google Scholar]
- Barnard, E. E. 1892a, PASP, 4, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Barnard, E. E. 1892b, AJ, 12, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, J. A., Showalter, M. R., Hamilton, D. P., et al. 1999, Science, 284, 1146 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christou, A. A. 2005, Icarus, 178, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Christou, A. A., Lewis, F., Roche, P., et al. 2009, A&A, 497, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cooper, N. J., Murray, C. D., Porco, C. C., & Spitale, J. N. 2006, Icarus, 181, 223 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., Showalter, M. R., Burns, J. A., et al. 1999, Icarus, 138, 214 [NASA ADS] [CrossRef] [Google Scholar]
- de Pater, I., Showalter, M. R., & Macintosh, B. 2008, Icarus, 195, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V. 2009, MNRAS, 394, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V., & Gilbert, R. 2006, A&A, 453, 1141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, M. W., & Porco, C. C. 2001, BAAS, 33, 1036 [NASA ADS] [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, BAAS, 28, 1158 [NASA ADS] [Google Scholar]
- Jewitt, D. C., Danielson, G. E., & Synnott, S. P. 1979, Sci., 206, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Karkoschka, E. 1994, Icarus, 111, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Kulyk, I. 2008, Planet. Space Sci., 56, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Kulyk, I., & Jockers, K. 2004, Icarus, 170, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kulyk, I., Jockers, K., Karpov, N., & Sergeev, A. 2002, A&A, 383, 724 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallama, A. 1991, Icarus, 92, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Mallama, A. 1993, J. Geophys. Res., 98, 18,873 [Google Scholar]
- Mallama, A., Collins, D. F., Nelson, P., Park, J., & Krobusek, B. A. 2000, Icarus, 147, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Mallama, A., Stockdale, C., Krobusek, B. A., & Nelson, P. 2010, Icarus, in press [Google Scholar]
- Nicholson, P. D., & Matthews, K. 1991, Icarus, 93, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Noyelles, B., Vienne, A., & Descamps, P. 2003, A&A, 401, 1159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ockert-Bell, M. E., Burns, J. A., Daubar, I. J., Thomas, P. C., & Veverka, J. 1999, Icarus, 138, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Porco, C. C., West, R. A., McEwen, A., et al. 2003, Science, 299, 1541 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Showalter, M. R., de Pater, I., Verbanac, G., Hamilton, D. P., & Burns, J. A. 2008, Icarus, 195, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Synnott, S. P. 1980a, IAU Circ., 3507, 1 [NASA ADS] [Google Scholar]
- Synnott, S. P. 1980b, Science, 210, 786 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thomas, P. C., Burns, J. A., Rossier, L., et al. 1998, Icarus, 135, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Vachier, F., Arlot, J. E., & Thuillot, W. 2002, A&A, 394, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasundhara, R., Arlot, J.-E., Lainey, V., & Thuillot, W. 2003, A&A, 410, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veiga, C. H., & Vieira Martins, R. 2005, A&A, 437, 1147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Subframe of image taken during the observation of the IIEV event on 28/09/2009 from Haleakala, Maui. The circular apertures indicate the regions of the frame where the background has been subtracted out in advance of the photometric reduction. Pixel values within the apertures have been multiplied by a factor of 8 for clarity. At the centre of each aperture lie Amalthea (“A”) and the star (“S”) used for differential aperture photometry of the satellite. Jupiter is off the left edge of the frame which coincides with the edge of the detector. The bright sources saturating the detector are, from left to right, Callisto and Europa. The entire subframe spans 512 × 404 pixels or 143″ × 113″. |
| In the text | |
 |
Fig. 2 Model
fits to our data. Upper panels: best fit models (black curves) to
the observations (“+” signs surrounded by diamonds). Fit residuals are represented
by asterisks. Lower panels: parametric contour plots of the reduced
chi squared goodness-of-fit statistic ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


