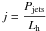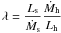| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A38 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201014753 | |
| Published online | 29 October 2010 | |
Relevance of jet emitting disc physics to microquasars: application to Cygnus X-1
1
Laboratoire d’Astrophysique, UMR 5571 Université J. Fourier/CNRS,
Observatoire de Grenoble, BP
53, 38041
Grenoble Cedex 9,
France
e-mail: pierre-olivier.petrucci@obs.ujf-grenoble.fr
2
Centre d’Étude Spatiale des Rayonnements, CESR, Université de
Toulouse [UPS], CNRS [UMR 5187], 9
Av. du Col. Roche, 31028
Toulouse,
France
Received:
8
April
2010
Accepted:
29
June
2010
Context. Interpretation of the X-ray spectra of X-ray binaries during their hard states requires a hot, optically thin medium. There are several accretion disc models that account for this aspect. However, none is designed to simultaneously explain powerful jets detected during these states.
Aims. A new quasi-Keplerian hot accretion disc solution, a jet emitting disc (JED hereafter), which is part of a global disc-jet MHD structure producing stationary super-alfvénic ejection, is investigated here. Its radiative and energetic properties are then compared to the observational constraints found in Cygnus X-1.
Methods. We solve the disc energy equation by balancing the local heating term with advection and cooling by synchrotron, bremsstrahlung, and Comptonization processes. The heating term, disc density, accretion velocity, and magnetic field amplitude were taken from published self-similar models of accretion-ejection structures. Both optically thin and thick regimes are considered in a one-temperature, gas-supported disc.
Results. Three branches of solutions are found to be possible at a given radius, but we only investigate the hot, optically thin and geometrically slim solutions. These solutions give simultaneously and consistently the radiative and energetics properties of the disc-jet system. They are able to reproduce the global accretion-ejection properties of Cygnus X-1 very well, namely its X-ray spectral emission, jet power, and jet velocity. About half of the released accretion power is used to produce two mildly relativistic (v/c ≃ 0.5) jets, and for a luminosity of about 1% of the Eddington luminosity, the JED temperature and optical depth are close to what is observed in the hard state of Cygnus X-1.
Conclusions. The accretion and ejection properties of JEDs agree with the observations of the prototypical black hole binary Cygnus X-1. The JED solutions are likely to be relevant to the whole class of microquasars.
Key words: black hole physics / accretion, accretion disks / magnetohydrodynamics (MHD) / ISM: jets and outflows / X-rays: binaries
© ESO, 2010
1. Introduction
Powerful ejections are commonly observed in galactic black holes. X-ray binaries show permanent jet radio emission during the so-called hard states (Stirling et al. 2001; Remillard & McClintock 2006; Done et al. 2007) and superluminal sporadic ejection in intermediate flaring states (Mirabel & Rodriguez 1994; Hannikainen et al. 2001; Fomalont et al. 2001; Fender et al. 2004)1.
Several models have been put forward to explain the formation of these astrophysical jets. They can be roughly classified into two categories both relying on the existence of an organized large-scale magnetic field. The first one taps the accretion energy reservoir of the disc, as first proposed by Lovelace (1976) and Blandford (1976). Since the seminal paper of Blandford & Payne (1982), it is known that jets can indeed be both accelerated and collimated by the magnetic field threading the disc. In the second category of models, jets are supposed to mainly tap the rotational energy of the black hole thanks to the so-called Blandford-Znajek process (hereafter BZ process, Blandford & Znajek 1977). In this model, accretion serves only to bring in and maintain the magnetic field in the black hole ergosphere.
That the jet power observed in some X-ray binary systems (the so-called microquasars Mirabel & Rodriguez 1998) seems remarkably independent of the nature of the compact objects, namely white dwarf, neutron star, or black hole (e.g. Kording et al. 2006; Kording et al. 2008; Tudose et al. 2009), argues for an ejection process that is also independent of the central object. This seems to be confirmed by the lack of correlation between jet power or jet velocities and measured values of black hole spins (Fender et al. 2010). Although all this evidence does not constitute definitive proof, it severely weakens the scenario where powerful jets would be powered by the BZ process.
There have been numerous 2D and 3D relativistic magnetohydrodynamic (hereafter MHD) numerical simulations of accretion flows around black holes (e.g. McKinney & Gammie 2004; Komissarov et al. 2007; Hawley & Krolik 2006; Beckwith et al. 2008; McKinney & Blandford 2009). Starting from a geometrically thick donut pervaded by its own weak poloidal or toroidal magnetic field, simulations end up with accretion onto the black hole with outflowing material along opened field lines. Accretion is caused by the onset of the magneto-rotational instability or MRI (see Balbus 2003, and references therein) that leads to formation of an almost geometrically thin disc in the innermost radii. A Poynting-dominated funnel jet is formed in the black hole polar regions in good agreement with the BZ process. This electromagnetic (no mass) funnel wind is surrounded by a mass-dominated outflow concentrated in a hollow and relatively thin cone at roughly 40 degrees inclination. Ejection is both thermally and magnetically driven and is only present if the initial magnetic field had a vertical component (Beckwith et al. 2008). Although these simulations look very promising, it is still not clear how they compare to the observed large-scale jets. Indeed, it is not clear yet whether such flows will be self-confined further out and if the mass and energy fluxes agrees with observational constraints.
On the other hand, in the footsteps of the Blandford & Payne (1982) pioneering work, it has been realized that jets could extract a significant fraction of the underlying disc angular momentum and accretion power. Under such circumstances, jets would not be a mere epiphenomenon of accretion but possibly its main driver. The whole disc structure should then be revisited by taking the disc-jet interrelation into account. This was done within a self-similar Ansatz, allowing the full set of dynamical MHD equations to be solved without neglecting any term (Ferreira & Pelletier 1995; Ferreira 1997; Casse & Ferreira 2000a,b; Ferreira & Casse 2004). It was found that the structure of these jet emitting discs (hereafter JED) is indeed deeply modified, with dynamical properties significantly different from those of a standard accretion disc or an ADAF. As a consequence, the radiative properties of a JED may also be very different. Noticeably, the main results of these self-similar, steady-state studies have been confirmed by 2D numerical MHD simulations with the VAC code (Casse & Keppens 2002, 2004), the FLASH code (Zanni et al. 2007), and the PLUTO code (Tzeferacos et al. 2009).
The purpose of this paper is to explain the dynamical, energetic, and radiative properties of JED around compact objects and to compare them with those estimated from the observations of the prototype of black hole binaries: Cygnus X-1.
The structure of the paper is as follows. We start by recalling the main characteristics of a JED in Sect. 2. We also present in Sect. 3 the method used to compute the JED thermal equilibrium. We then compare, in Sect. 4 the model expectations with the observational constraints known in Cyg X-1. Concluding remarks are discussed in Sect. 5.
2. Jet emitting discs
Jet emitting discs were originaly studied by Ferreira & Pelletier (1993) in their magnetized accretion ejection structures model (MAES herafter). This model was developed so as to treat both the accretion disc and the jet it generates consistently. The idea is the same as in earlier studies of magneto-centrifugally launched disc winds (Blandford & Payne 1982). However, in the MAES, the solution starts from the midplane of the resistive MHD disc and evolves outwards in the ideal MHD wind/jet. This differs drastically from other studies where the disc was only treated as a boundary condition, hence forbidding any precise quantication of the effect of the MHD wind on the disc.
It would be lengthy but also irrelevant to present the MAES model in great detail in this paper. Many papers have dealt with the subject from both analytical and numerical point of views, so we refer the reader to these papers for further details (e.g. Ferreira 1997; Casse & Ferreira 2000a,b; Ferreira 2002; Ferreira & Casse 2004; Casse & Keppens 2002, 2004; Zanni et al. 2007; Combet & Ferreira 2008). Instead, we give the few key assumptions and elements of the model that are important to our work.
2.1. Main assumptions
The goal of these studies was to find out the conditions for steady state jet formation and to relate jet properties (mass loss, power, kinematics, collimation) to the underlying disc properties. The MAES calculations were done under several assumptions discussed below: (1) a self-similar Ansatz; (2) an alpha-prescription for the transport coefficients; (3) the presence of a large scale, organized vertical Bz field.
-
(1)
Self-similarity enables solution of the full set of MHD equations without ignoring any term. The only simplification that must be made is in the energy equation, since microphysics (within cooling terms) is not self-similar. Thus, given some approximation (i.e. isothermal or adiabatic magnetic surfaces), a computed solution is a real solution of the full set of equations. In our case here, such a solution is obtained by crossing the MHD critical points of the flow. On the other hand, self-similarity introduces unavoidable biases in the jet collimation properties (see e.g. Ferreira 1997, for more details).
-
(2)
The disc is assumed to be turbulent so that, within our mean field approach, some prescription must be made to mimic turbulence. Following Shakura & Sunyaev (1973), an alpha prescription for the transport coefficients, namely viscosity and magnetic diffusivity, is employed. It has been shown recently that MRI gives rise to a turbulent magnetic transport that seems to behave like a resistivity, with an effective magnetic Prandtl number of order unity (Guan & Gammie 2009; Lesur & Longaretti 2009). It turns out that JED solutions are found to be close to the marginal stability limit, but always MRI unstable (Ferreira & Pelletier 1995; Ferreira 1997). Note that there is a whole range of other possible MHD instabilities when the fields are close to equipartition (Keppens et al. 2002; Blokland et al. 2005, 2007). Whether magnetically driven turbulence can indeed be described with local alpha prescriptions is still an open question (Beckwith et al. 2009). Full 3D global simulations are thus required to assess this assumption, but the huge span on space-time scales are such that this is still out of reach of modern computers.
-
(3)
The last assumption of a large-scale magnetic field in the inner regions of accretion flows is still an open and highly debated question (e.g. Lubow et al. 1994a,b; Cao & Spruit 2002; Bisnovatyi-Kogan & Lovelace 2007; Rothstein & Lovelace 2008). It has been recently argued, however, that fields could be advected inward in a standard accretion disc thanks to the quenching of the MRI at the disc upper layers (Rothstein & Lovelace 2008; Lovelace et al. 2009). This picture has been given some support from recent 2D MHD simulations of accretion-ejection structures (Murphy et al. 2010). GRMHD simulations also suggest that a vertical large-scale magnetic field is indeed needed to produce powerful jets (Beckwith et al. 2008). Thus while the controversy is certainly not closed, the assumption of a large-scale magnetic field threading the disc appears quite plausible.
2.2. Physical properties
Throughout the paper, we use R for the cylindrical radius, M for the black hole mass, and Ṁa(R) for the disc accretion rate at the radius R. The dimensionless radius will be r = R/Rg where Rg = GM / c2, mass m = M/M⊙, and disc accretion rate 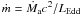 with LEdd the Eddington luminosity.
with LEdd the Eddington luminosity.
2.2.1. Radial profiles
Since a JED undergoes mass loss, the disc accretion rate is written as 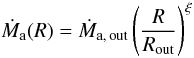 (1)where ξ measures the local disc ejection efficiency (Ferreira & Pelletier 1993) and Ṁout the accretion rate at the disc outer radius Rout. A standard accretion disc is recovered when ξ = 0. The ejection efficiency ξ is equivalent to the p exponent used in ADIOS models (Blandford & Begelman 1999). But, in strong contrast to the latter, it is not assumed but computed as a function of the disc parameters as a trans-Alfvénic regularity condition (see Ferreira 1997, for more details). For isothermal (Ferreira 1997) and adiabatic (Casse & Ferreira 2000a) magnetic surfaces, ξ is found to vary in a narrow interval around 0.01. When the disc’s upper layers are heated, mass loss can be enhanced with ξ typically reaching 0.1 or slightly more (Casse & Ferreira 2000b). Discs with more mass loss do not give rise to stationary super-Alfvénic jets.
(1)where ξ measures the local disc ejection efficiency (Ferreira & Pelletier 1993) and Ṁout the accretion rate at the disc outer radius Rout. A standard accretion disc is recovered when ξ = 0. The ejection efficiency ξ is equivalent to the p exponent used in ADIOS models (Blandford & Begelman 1999). But, in strong contrast to the latter, it is not assumed but computed as a function of the disc parameters as a trans-Alfvénic regularity condition (see Ferreira 1997, for more details). For isothermal (Ferreira 1997) and adiabatic (Casse & Ferreira 2000a) magnetic surfaces, ξ is found to vary in a narrow interval around 0.01. When the disc’s upper layers are heated, mass loss can be enhanced with ξ typically reaching 0.1 or slightly more (Casse & Ferreira 2000b). Discs with more mass loss do not give rise to stationary super-Alfvénic jets.
The disc’s vertical equilibrium depends on the balance between, on one hand, gravity and magnetic compression due to both radial and toroidal field components and, on the other, the vertical pressure (gas + radiation) gradient. We nevertheless use as a proxy for the real scale height the hydrostatic value, namely 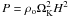 evaluated at the disc’s midplane, where P = Pgas + Prad: this greatly simplifies our expressions and produces an overestimation of at most a factor 2 (Ferreira & Pelletier 1995). With this caveat in mind, the disc’s aspect ratio in a gas supported disc is ε = H/R = cs/vK, namely the ratio of the isothermal sound speed to the Keplerian speed vK = ΩKR. Given these definitions, the radial profiles of the accretion velocity uo, particle density n = ρo / mp, gas pressure Pgas, and vertical magnetic field Bz in the JED midplane are given by
evaluated at the disc’s midplane, where P = Pgas + Prad: this greatly simplifies our expressions and produces an overestimation of at most a factor 2 (Ferreira & Pelletier 1995). With this caveat in mind, the disc’s aspect ratio in a gas supported disc is ε = H/R = cs/vK, namely the ratio of the isothermal sound speed to the Keplerian speed vK = ΩKR. Given these definitions, the radial profiles of the accretion velocity uo, particle density n = ρo / mp, gas pressure Pgas, and vertical magnetic field Bz in the JED midplane are given by 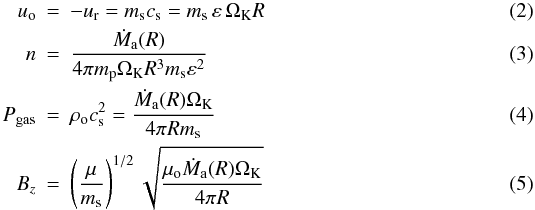 where we have introduced two dimensionless parameters, the sonic Mach number ms = uo / cs and the disc magnetization2
where we have introduced two dimensionless parameters, the sonic Mach number ms = uo / cs and the disc magnetization2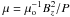 .
.
2.2.2. JED parameter space
The previous expressions (2)–(5) are common to all power-law, nearly Keplerian gas supported disc solutions. What distinguishes JEDs from other models are the values taken by the parameters ξ,ms,μ, and ε.
-
The value of ε is fixed by the resolution of the JED energy equation (see Sect. 3).
-
μ and ξ are provided by the resolution of the full set of MHD equations when properly dealing with the regularity conditions at the slow magnetosonic and Alfvénic critical points, respectively. We have already discussed the values achieved for ξ. For isothermal or adiabatic magnetic surfaces, steady-state ejection is only possible for a field smaller than but close to equipartition (Ferreira & Pelletier 1995; Ferreira 1997; Casse & Ferreira 2000a). More precisely, the range of allowed magnetizations in isothermal models goes from 0.3 to 0.8, with an average value around 0.6 (see examples of JED parameter values in Fig. A.1). This can be understood in the following way. The magnetic field is vertically pinching the accretion disc so that a quasi-static vertical equilibrium is obtained only thanks to the kinetic pressure support. As a consequence, the field cannot be too strong. But on the other hand, the field must be strong enough to accelerate the plasma efficiently at the disc surface so that the slow-magnetosonic point is crossed smoothly.
-
In a JED, the sonic Mach number can be rewritten in the form
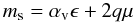 (6)where
αvϵ denotes the effect of standard
transport and 2qμ the specific contribution of the magnetic
torque. The magnetization
μ = B2/μ0P
measures the strength of the magnetic field in the disc and q = μoJrh/Bz
is the normalized radial electric current density flowing at the disc midplane.
This last parameter measures the magnetic shear as it provides an estimate of the
toroidal magnetic field component at the disc surface,
(6)where
αvϵ denotes the effect of standard
transport and 2qμ the specific contribution of the magnetic
torque. The magnetization
μ = B2/μ0P
measures the strength of the magnetic field in the disc and q = μoJrh/Bz
is the normalized radial electric current density flowing at the disc midplane.
This last parameter measures the magnetic shear as it provides an estimate of the
toroidal magnetic field component at the disc surface, 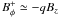 . In a standard accretion
disc,
ms = αvϵ,
with typically αv = 10-2 and
ϵ = H/R < 1, so that
the accretion velocity is largely subsonic. However, the situation in a JED is
very different since the presence of powerful jets strongly modifies the disc
angular momentum. A common feature of all solutions is that the jet torque
always dominates the local turbulent torque, as initially
proposed by Pelletier & Pudritz
(1992). This is because steady-state MAES solutions are generally found
close to equipartition (i.e. μ ≃ 1 as explained before) and
q is also of the order of unity (Ferreira & Pelletier 1995; Ferreira 1997). As a consequence, JED solutions present high
accretion velocities with ms ~ 1, which this
is verified by all isothermal and adiabatic solutions (Fig. A.1).
. In a standard accretion
disc,
ms = αvϵ,
with typically αv = 10-2 and
ϵ = H/R < 1, so that
the accretion velocity is largely subsonic. However, the situation in a JED is
very different since the presence of powerful jets strongly modifies the disc
angular momentum. A common feature of all solutions is that the jet torque
always dominates the local turbulent torque, as initially
proposed by Pelletier & Pudritz
(1992). This is because steady-state MAES solutions are generally found
close to equipartition (i.e. μ ≃ 1 as explained before) and
q is also of the order of unity (Ferreira & Pelletier 1995; Ferreira 1997). As a consequence, JED solutions present high
accretion velocities with ms ~ 1, which this
is verified by all isothermal and adiabatic solutions (Fig. A.1).
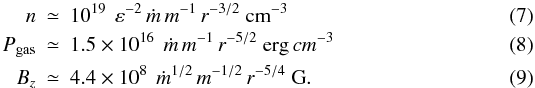 Note that the Blandford & Payne (1982) scaling for the magnetic field is recovered as we used ξ ≪ 1.
Note that the Blandford & Payne (1982) scaling for the magnetic field is recovered as we used ξ ≪ 1.
2.2.3. Global energy budget
The global energy budget in an accretion-ejection structure is 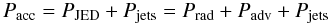 (10)where Pjets is the total power feeding the jets and PJED is the power dissipated within the JED. More precisely, PJED is the sum of the radiated Prad and advected Padv power. The disc luminosity is therefore the released accretion power minus what is advected onto the black hole and what feeds the jets.
(10)where Pjets is the total power feeding the jets and PJED is the power dissipated within the JED. More precisely, PJED is the sum of the radiated Prad and advected Padv power. The disc luminosity is therefore the released accretion power minus what is advected onto the black hole and what feeds the jets.
Given the expression (1) of the accretion rate, the total accretion power released in a quasi-Keplerian accretion disc writes as3![\begin{eqnarray} \label{paccjed} P_{\rm acc} &=& \frac{GM\dot{M}_{\rm a}(R_{\rm in})}{2 R_{\rm in}}- \frac{GM\dot{M}_{\rm a}(R_{\rm out})}{2 R_{\rm out}}\nonumber\\ &=&\frac{GM \dot M_{\rm a,\,out}}{2R_{\rm in}} \left [ \left ( \frac{R_{\rm in}}{R_{\rm out}} \right )^\xi - \frac{R_{\rm in}}{R_{\rm out}} \right ]\nonumber\\ \label{eq:pacc} &=& \frac{GM \dot M_{\rm a,\,out}}{2R_{\rm in}} (1 - g) \end{eqnarray}](/articles/aa/full_html/2010/14/aa14753-10/aa14753-10-eq52.png) (11)where
(11)where ![\begin{equation} (1-g)=\left [ \left ( \frac{R_{\rm in}}{R_{\rm out}} \right )^\xi - \frac{R_{\rm in}}{R_{\rm out}} \right ], \label{eq:f} \end{equation}](/articles/aa/full_html/2010/14/aa14753-10/aa14753-10-eq53.png) (12)namely Pacc = ηṁLEdd with an accretion efficiency η = (1 − g) / 2rin. The usual expression for the non-relativistic accretion efficiency is recovered for ξ = 0. In the following, we use rin = 6 for a Schwarzschild black hole.
(12)namely Pacc = ηṁLEdd with an accretion efficiency η = (1 − g) / 2rin. The usual expression for the non-relativistic accretion efficiency is recovered for ξ = 0. In the following, we use rin = 6 for a Schwarzschild black hole.
The power Padv that is advected onto the central object along with the accreting material scales as Padv ∝ ε2Pacc. It is thus negligible in a thin disc. Pjets is the sum of the total (kinetic, potential, and internal) energy flux advected by the outflowing plasma and the MHD Poynting flux leaving the disc surfaces. Since we are mainly interested in powerful jets, the latter contribution dominates, i.e., 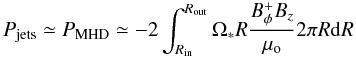 (13)where
(13)where 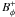 is the toroidal component of the magnetic field at the disc surface and Ω∗ the rotation speed of the magnetic surfaces4. Using the disc angular momentum conservation, one gets (see Appendix A)
is the toroidal component of the magnetic field at the disc surface and Ω∗ the rotation speed of the magnetic surfaces4. Using the disc angular momentum conservation, one gets (see Appendix A) 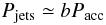 (14)where b, the jet power parameter, is known for a given MHD solution. In the above derivation, it has been assumed that the fraction of the released energy that is transferred to the jets is a constant throughout the disc. That is not necessarily true. Indeed, published self-similar models (where b is by definition a true constant) provide b ranging from ~0.5 to almost unity. It turns out that this value depends on the disc aspect ratio, but its actual dependence still needs to be looked for. As a first step and for the sake of clarity in this paper, we use it as an independent parameter.
(14)where b, the jet power parameter, is known for a given MHD solution. In the above derivation, it has been assumed that the fraction of the released energy that is transferred to the jets is a constant throughout the disc. That is not necessarily true. Indeed, published self-similar models (where b is by definition a true constant) provide b ranging from ~0.5 to almost unity. It turns out that this value depends on the disc aspect ratio, but its actual dependence still needs to be looked for. As a first step and for the sake of clarity in this paper, we use it as an independent parameter.
Consequently, given the above expressions, the total JED power PJED and JED luminosity Prad are given by 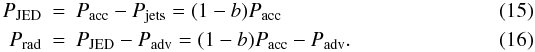 The jet power parameter b is thus a crucial parameter as it controls the power sharing between the jet and the disc. Since it is generally found in the range 0.5–0.99 (see Fig. A.1), JEDs considered here are engines converting accretion power into ejection power with high efficiency. To get the fraction of the power Prad that is actually radiated away, however we need to compute the JED thermal balance. This is explained in the next section.
The jet power parameter b is thus a crucial parameter as it controls the power sharing between the jet and the disc. Since it is generally found in the range 0.5–0.99 (see Fig. A.1), JEDs considered here are engines converting accretion power into ejection power with high efficiency. To get the fraction of the power Prad that is actually radiated away, however we need to compute the JED thermal balance. This is explained in the next section.
3. Disc thermal balance
The equation governing the internal energy of the accretion flow writes as 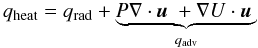 (17)where qheat is the heating power density, qrad the sum of all radiative cooling terms, P the total plasma pressure, u the flow velocity, U its internal energy and qadv the advection term. These different terms are explained below. Equation (17) is equivalent to Eq. (16) but expressed locally in the JED.
(17)where qheat is the heating power density, qrad the sum of all radiative cooling terms, P the total plasma pressure, u the flow velocity, U its internal energy and qadv the advection term. These different terms are explained below. Equation (17) is equivalent to Eq. (16) but expressed locally in the JED.
In Eq. (17) we neglect any turbulent energy transport (such as convection for instance) and assume a Maxwellian one-temperature plasma. This last point could be a crude assumption at low accretion rates (ṁ < 10-3 − 10-4). However, since we are mainly interested in this paper to apply our calculations to Cyg X-1, whose accretion rate is a few % of the Eddington rate, this assumption is expected to be quite reasonable (see e.g. Malzac & Belmont 2009).
3.1. Heating and advection terms
Equation (15) directly provides the radial JED volumetric heating rate in a disc ring of height 2H, radius R and extent dR: 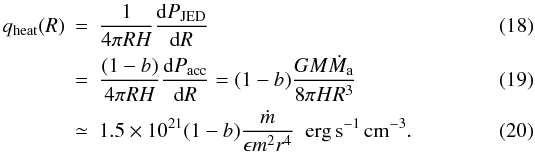 On the other hand, the advection term is identified as
On the other hand, the advection term is identified as ![\begin{equation} q_{\rm adv}=P\nabla \cdot \vecu + \nabla U\cdot\vecu = \frac{1}{\gamma-1}\left [ \gamma P\nabla \cdot \vecu+ \vecu\cdot \nabla P \right ] \label{qadvinit} \end{equation}](/articles/aa/full_html/2010/14/aa14753-10/aa14753-10-eq75.png) (21)where γ = 5 / 3 is the gas adiabatic index. Assuming that the flow poloidal velocity is dominated by its radial component ur (provided by Eq. (2)) and after some algebra, this expression becomes
(21)where γ = 5 / 3 is the gas adiabatic index. Assuming that the flow poloidal velocity is dominated by its radial component ur (provided by Eq. (2)) and after some algebra, this expression becomes 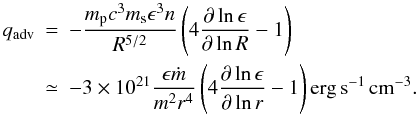 (22)The comparison between Eqs. (20) and (22) shows that advection becomes important only for large aspect ratios, namely ϵ > 0.1. As already examplified by Yuan (2001) and Yuan et al. (2003) in ADAF, the advection term may change sign and become negative, then playing the role of a heating term for the flow. Equation (22) shows that this should occur when the exponent in the radial dependency of ϵ becomes larger than 1 / 4.
(22)The comparison between Eqs. (20) and (22) shows that advection becomes important only for large aspect ratios, namely ϵ > 0.1. As already examplified by Yuan (2001) and Yuan et al. (2003) in ADAF, the advection term may change sign and become negative, then playing the role of a heating term for the flow. Equation (22) shows that this should occur when the exponent in the radial dependency of ϵ becomes larger than 1 / 4.
3.2. Radiative cooling term
We strictly follow Esin et al. (1996) for computing of the different radiative cooling rates. In the optically thin regime, the total cooling rate is simply 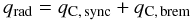 (23)where qC,sync and qC,brem correspond to the synchrotron + Comptonized synchrotron and bremsstrahlung+Comptonized bremsstrahlung cooling rates. Since JED solutions may also be optically thick, we use the generalized radiative cooling formula used by Narayan & Yi (1995) and adapted from the initial work of Hubeny (1990), which bridges the optically thin and thick cases:
(23)where qC,sync and qC,brem correspond to the synchrotron + Comptonized synchrotron and bremsstrahlung+Comptonized bremsstrahlung cooling rates. Since JED solutions may also be optically thick, we use the generalized radiative cooling formula used by Narayan & Yi (1995) and adapted from the initial work of Hubeny (1990), which bridges the optically thin and thick cases: 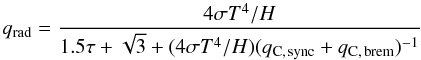 (24)where τ = τes + τabs is the disc optical depth in the vertical direction, with τes the Thomson optical depth and τabs = (H / 4σBT4)(qC,sync + qC,brem) the optical depth for absorption. At high energies, pair creation provides another means of cooling. But an a posteriori check showed that this effect always remains weak and has thus been neglected.
(24)where τ = τes + τabs is the disc optical depth in the vertical direction, with τes the Thomson optical depth and τabs = (H / 4σBT4)(qC,sync + qC,brem) the optical depth for absorption. At high energies, pair creation provides another means of cooling. But an a posteriori check showed that this effect always remains weak and has thus been neglected.
3.3. Existence of three solutions
 |
Fig. 1 Thermal balance of a jet emitting disc (JED) at r = 6 for ṁ = 0.001 and m = 10. The underlying JED structure has a jet power parameter b = 0.5 and an ejection efficiency ξ = 0.1. The dotted line is the heating term qheat, the dot-dot-dot-dashed line the radiative cooling term qrad, and the long dashed line is the advective term qadv. The Comptonized bremsstrahlung qC,brem (short dashed) and the Comptonized synchrotron qC,sync (dot-dashed) radiative terms are also shown. The solid line corresponds to qrad + qadv and the solutions of Eq. (17) are indicated by crosses. |
Figure 1 shows the different heating, cooling, and advection terms as functions of the temperature for a given black hole mass, JED radius, and accretion rate. In a gas-supported, one-temperature disc, the midplane temperature is given by 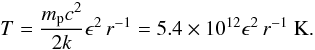 (25)The resolution of the thermal equilibrium (Eq. (17)) gives three branches of solutions, indicated by crosses on the figure The hottest one corresponds to the JED solution discussed in this paper (a more detailed discussion of the other solutions is postponed to a future work). It is a hot, optically thin, thermally and viscously stable disc solution that behaves radiatively in the same way as the LHAF solutions studied by Yuan (2001; see also Yuan et al. 2006, for a discussion on hot one-temprature accretion flows). The major difference concerns the underlying dynamics of our JED solutions, which self-consistently include the presence of powerful self-collimated jets.
(25)The resolution of the thermal equilibrium (Eq. (17)) gives three branches of solutions, indicated by crosses on the figure The hottest one corresponds to the JED solution discussed in this paper (a more detailed discussion of the other solutions is postponed to a future work). It is a hot, optically thin, thermally and viscously stable disc solution that behaves radiatively in the same way as the LHAF solutions studied by Yuan (2001; see also Yuan et al. 2006, for a discussion on hot one-temprature accretion flows). The major difference concerns the underlying dynamics of our JED solutions, which self-consistently include the presence of powerful self-collimated jets.
Figure 2 also indicates the different domains of JED solutions in the ṁ-r plane and for the two extreme values of the jet power parameter b, 0.5 and 1. In the latter case, a cold branch exists in the whole JED, regardless of the value of the accretion rate, while the hot branch is only valid below a critical accretion rate that depends on the JED radius (cf. Fig. 2). For b = 0.5, the parameter space for the cold branch is now limited to accretion rates >10-3 − 10-4, while the upper limit for the hot branch has shifted to a slightly higher accretion rate compared to b = 1, reaching ṁ of a few for JED radius greater than ~ 100 Rg.
 |
Fig. 2 JED solution domain in the ṁ-r plane. The solid line, corresponding to a jet power parameter b = 1, separates this plane into 2 regions: the top one where only the cold solution is valid and the bottom one where the 3 solutions exist. The region where only a hot solution is valid exists at very low accretion rate not shown in this figure. The limits for b = 0.5 are plotted in dashed lines. In this case the plane is divided into 3 parts with a region, for low accretion rate, where only the hot solution exists. |
 |
Fig. 3 Left: observational parameter space of |
4. Comparison to Cygnus X-1
4.1. Observational constraints
The energetics of the jets and the X-ray corona of Cygnus X-1 have been investigated recently by Malzac et al. (2009 herafter M09). It is one of the best observed black-hole X-ray binaries and is composed of a massive star and a black hole of about 10 solar masses. It is also one of the rare BHBs for which a jet has been directly observed in the hard state (Stirling et al. 2001). But more importantly, deep radio observations of the field of CygX-1 resulted in the discovery of a shell-like structure that is aligned with the resolved radio jet (Gallo et al. 2005). Assuming that this large-scale structure was inflated by the inner radio jet, its kinetic power was estimated to be near the bolometric X-ray luminosity of the binary (Gallo et al. 2005; Russell et al. 2007). With these constraints, it is possible to deduce a rough estimate of the ratio j = Pjets/Lh of the total jet kinetic power to the typical X-ray luminosity in the hard state (M09): 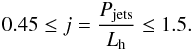 (26)Like most X-ray binaries, the bolometric luminosity of Cyg X-1 does not change dramatically during the transition to the soft state (see e.g. Frontera et al. 2001; Zdziarski et al. 2002; Malzac et al. 2006; Wilms et al. 2006). The observed luminosity jumps at most reach a factor Ls / Lh ≃ 3 − 4 (Zdziarski et al. 2002). Since the transition to soft state is likely triggered by an increase in mass accretion rate, the ratio of the soft to hard radiative efficiencies can be safely upper limited by
(26)Like most X-ray binaries, the bolometric luminosity of Cyg X-1 does not change dramatically during the transition to the soft state (see e.g. Frontera et al. 2001; Zdziarski et al. 2002; Malzac et al. 2006; Wilms et al. 2006). The observed luminosity jumps at most reach a factor Ls / Lh ≃ 3 − 4 (Zdziarski et al. 2002). Since the transition to soft state is likely triggered by an increase in mass accretion rate, the ratio of the soft to hard radiative efficiencies can be safely upper limited by 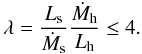 (27)It is noteworthy that there are also several estimates of the terminal jet velocity of Cyg X-1. Indeed, based on the absence of counter jet, Stirling et al. (2001) give a lower limit on the bulk velocity of the radio jet of V∞ / c > 0.6. Similar considerations and the lack of response of the radio emission on short time scales led Gleissner et al. (2004) to constrain the jet velocity in the range 0.4 < V∞ / c < 0.7. Ibragimov et al. (2007) find a similar result, 0.3 < V∞ / c < 0.5, by modelling the super-orbital modulation observed in X-ray and radio bands. This gives another independent constraint that will be very useful while comparing models to observations.
(27)It is noteworthy that there are also several estimates of the terminal jet velocity of Cyg X-1. Indeed, based on the absence of counter jet, Stirling et al. (2001) give a lower limit on the bulk velocity of the radio jet of V∞ / c > 0.6. Similar considerations and the lack of response of the radio emission on short time scales led Gleissner et al. (2004) to constrain the jet velocity in the range 0.4 < V∞ / c < 0.7. Ibragimov et al. (2007) find a similar result, 0.3 < V∞ / c < 0.5, by modelling the super-orbital modulation observed in X-ray and radio bands. This gives another independent constraint that will be very useful while comparing models to observations.
4.2. Model comparison
These observational constraints on j and λ can be easily translated into constraints on our JED parameters b and ξ. From Eqs. (14) and (16) and assuming that advection is negligible (this is verified for JEDs at ṁ of a few % of the Eddington accretion rate, as expected for Cyg X-1) we obtain 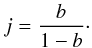 (28)The soft state is free of ejection (i.e. ξ = 0) so that
(28)The soft state is free of ejection (i.e. ξ = 0) so that 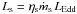 , with ηs ≃ 1 / 2rin. The hard state is characterized by
, with ηs ≃ 1 / 2rin. The hard state is characterized by 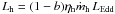 , with ηh ≡ (1 − g) / 2rin where g in the hard state is defined in Eq. (12) and then depends on ξ and the JED radial extent Rout / Rin. Within this framework, we obtain
, with ηh ≡ (1 − g) / 2rin where g in the hard state is defined in Eq. (12) and then depends on ξ and the JED radial extent Rout / Rin. Within this framework, we obtain 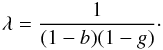 (29)The left panel of Fig. 3 displays the domain in the observed parameter space j − λ allowed by the observations. The right panel shows the same constraints but translated into our JED parameter space ξ − b, assuming Rout / Rin = 100. This value is comparable to what could be deduced from observations (e.g. Fabian et al. 1989; Young et al. 2001; Torres et al. 2005) if the standard accretion disc inner edge is directly assimilated to the JED outer radius as proposed in Ferreira et al. (2006). This figure depends only slightly on this parameter with a smooth increase in the ξ upper limit with decreasing Rout/Rin.
(29)The left panel of Fig. 3 displays the domain in the observed parameter space j − λ allowed by the observations. The right panel shows the same constraints but translated into our JED parameter space ξ − b, assuming Rout / Rin = 100. This value is comparable to what could be deduced from observations (e.g. Fabian et al. 1989; Young et al. 2001; Torres et al. 2005) if the standard accretion disc inner edge is directly assimilated to the JED outer radius as proposed in Ferreira et al. (2006). This figure depends only slightly on this parameter with a smooth increase in the ξ upper limit with decreasing Rout/Rin.
We can thus safely conclude that ξ has to be lower than ~ 0.1 and b ranging between 0.4 and 0.6 to be consistent with Cyg X-1 data.
Now, the jet terminal velocity can also be estimated. Since the jets of Cyg X-1 are not highly relativistic, we can assume that the jet power Pjets is asymptotically dominated by the kinetic energy of the ejected matter. This provides an average terminal bulk Lorentz factor 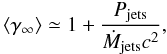 (30)where the total mass loss rate Ṁjets is such that
(30)where the total mass loss rate Ṁjets is such that 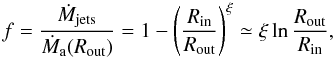 (31)with the last equality holding only for small ξ. Combining this expression with Eq. (14), we finally obtain
(31)with the last equality holding only for small ξ. Combining this expression with Eq. (14), we finally obtain 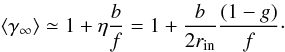 (32)The range of average jet velocities V∞ / c consistent with the values of b and ξ needed to agree with Cyg X-1 observations can then be computed from this last expression. Figure 4 shows V∞ / c as a function of the disc ejection efficiency ξ. The generally accepted values (i.e. the dark grey area in Fig. 4) provide a range in V∞ / c between 0.3 and 0.6 in good agreement with observations. This is remarkable as it arises from another independent observational constraint.
(32)The range of average jet velocities V∞ / c consistent with the values of b and ξ needed to agree with Cyg X-1 observations can then be computed from this last expression. Figure 4 shows V∞ / c as a function of the disc ejection efficiency ξ. The generally accepted values (i.e. the dark grey area in Fig. 4) provide a range in V∞ / c between 0.3 and 0.6 in good agreement with observations. This is remarkable as it arises from another independent observational constraint.
 |
Fig. 4 Average terminal jet velocity versus the disc ejection efficiency ξ in a JED, with Ṁa ∝ Rξ. The grey and dark grey areas correspond to the regions that agree with the observational constraints reported in Fig. 3. |
 |
Fig. 5 Contour plots of the JED temperature (solid lines) and optical depth (dashed lines) in the ξ − b plane at a distance of 10 RG from a 10 M⊙ black hole. The ratio of the outer to inner JED radii is taken equal to 100, and the total accretion rate for the computation of the disc thermal balance is fixed to 1% of LEdd, i.e., the typical luminosity of Cyg X-1. The grey and dark grey areas correspond to the regions that agree with the observational constraints reported in Fig. 3. |
Our treatment of the disc thermal balance allows us to estimate the expected temperature and optical depth within a JED. Contours of these two quantities at a radius of 10 RG are shown in Fig. 5. The black hole mass is taken equal to 10 M⊙ and the total luminosity is about 1% of the Eddington luminosity. This corresponds to the typical luminosity of Cyg X-1 close to the hard-to-soft state transition. The ratio of the outer to inner JED radii is fixed to 100 but Fig. 5 does not strongly depend on this parameter. Interestingly, the temperature ranges between 120 and 140 keV and the optical depth τ ≃ 0.7 − 0.9, which are not so far, given the simplicity of our thermal balance computation, from the values deduced from sophisticated fits of Cyg X-1 in the hard state (Salvo et al. 2001; Gierlinski et al. 1997; Frontera et al. 2001; Ibragimov et al. 2005; Bel et al. 2006; Wilms et al. 2006).
5. Concluding remarks
Jet emitting discs can be much less radiative than standard accretion discs fed at the same accretion rate. Indeed, JEDs redistribute the released accretion power into three outputs: radiation, advection onto the central object, and jet power. Using published self-similar calculations of JEDs that provided us with the relevant disc parameters we were able to solve the disc thermal balance around compact objects in a consistent way.
As in other studies (e.g. Chen et al. 1995), we found that there are usually three branches of solutions at a given radius: (1) a cold solution, optically thick and geometrically thin, (2) an intermediate solution, and (3) an optically thin and geometrically thicker hot solution. Only the cold and hot solutions are both thermally and viscously stable. In this paper, we focussed on the properties of the hot solution as it corresponds to the physical situation envisioned during the hard states of X-ray binaries, which are known for harbouring jets. We compared our JED model to observations by comparing the disc X-ray emission, jet power, and jet velocity with those derived in Cygnus X-1.
We found that these hot JED solutions reproduce both dynamical and radiative properties of Cygnus X-1. These solutions are characterized by a jet power parameter b ~ 0.5 and an ejection efficiency ξ < 0.1. The first condition arises from the observational fact that, in Cyg X-1, the gravitational power is apparently equally shared between the accretion flow and the jet. This requires discs with quite a large aspect ratio, ε ≃ 0.1. Such solutions, like our JED ones, are now available. On the other hand, if ξ were too large, the disc accretion rate (scaling as rξ) at the inner radius during the hard state would be much lower than at the outer radius, while they are basically the same during the soft state. This would therefore lead to a ratio of radiative efficiencies that is much higher than what is currently observed. This upper limit on the local disc ejection efficiency translates into an upper limit of the jet mass loss, namely Ṁjets / Ṁa(rout) ≃ ξln(rout / rin) < 50% (for a JED extension arbitrarily chosen to be rout / rin = 100). At first sight, this may not appear to be too constraining. However, accretion-ejection dynamics link the jet mass loss to the jet asymptotic velocity. This is why any independent measurement of the jet terminal velocity is so important. By comparing the average velocity provided by the models to the values derived from observations, we concluded that any JED model with ξ of a few percent matches all observational constraints for Cygnus X-1 jets (velocity, power, mass loss).
For the disc itself, we found JED temperatures of 120–140 keV and optical depths τ ≃ 0.7 − 0.9 for Cyg X-1 parameters. The temperature is slightly higher and the optical depth less than the values generally deduced from observations, namely Te ≃ 70 − 100 keV and τ ≃ 1 − 3 (Gierlinski et al. 1997; Frontera et al. 2001; Ibragimov et al. 2005; Bel et al. 2006; Wilms et al. 2006). However, our value for the Compton parameter 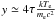 agrees closely with the observations. We thus expect an X-ray spectrum with the correct spectral index but with too high a cut-off (mainly controlled by the temperature). This could be directly linked to our overly simple treatment of the disc radiative transfer, which neglects, for example, its vertical stratification. One might also argue that the electron particle distribution is not a perfect Maxwellian. Indeed, recent computations of plasma radiative equilibria, including radiative and kinetic processes, show that a non-thermal, high-energy tail in the particle distribution is generally expected (Belmont et al. 2008; Malzac & Belmont 2009). The high-energy photons produced by these particles could create pairs, thereby increasing the particule density and decreasing the temperature. These different effects will be more precisely studied in a forthcoming paper.
agrees closely with the observations. We thus expect an X-ray spectrum with the correct spectral index but with too high a cut-off (mainly controlled by the temperature). This could be directly linked to our overly simple treatment of the disc radiative transfer, which neglects, for example, its vertical stratification. One might also argue that the electron particle distribution is not a perfect Maxwellian. Indeed, recent computations of plasma radiative equilibria, including radiative and kinetic processes, show that a non-thermal, high-energy tail in the particle distribution is generally expected (Belmont et al. 2008; Malzac & Belmont 2009). The high-energy photons produced by these particles could create pairs, thereby increasing the particule density and decreasing the temperature. These different effects will be more precisely studied in a forthcoming paper.
The presence of a non-thermal high energy tail above the thermal Comptonization cut-off in the hard state of Cygnus X-1 (McConnell et al. 2002) and GX 339-4 (Wardzinski et al. 2002; Joinet et al. 2007) suggests that the magnetic field is low in the Comptonizing region. Indeed, this excess is believed to be the signature of a population of non-thermal electrons in the corona. These high-energy electrons produce a self-absorbed synchrotron emission in the IR-optical bands. The soft photons are then Comptonized in the hot plasma. If the synchrotron luminosity is too strong then it is impossible to sustain the relatively high ( ~ 100 keV) temperature of the Maxwellian electrons. In the case of Cygnus X-1, Wardzinski & Zdziarski (2001) estimate that the non-thermal tail implies a strongly sub-equipartition magnetic field. Then based on detailed spectral modelling, Malzac & Belmont (2009) and Poutanen & Vurm (2009) infer that the ratio of magnetic to radiation energy density UB / UR < 0.3. In the framework of our model, this would imply a magnetization that is much too low to allow for the production of a jet.
However, this constraint on the magnetic field holds only if the non-thermal tail is produced inside the thermal Comptonization region. One possibility would be that the bulk of the Comptonized emission in the hard state is produced within the JED, while the non-thermal Comptonization component arises from a magnetic accretion disc corona above and below the standard outer disc. If so, the magnetic field could be strong in both JED and non-thermal corona. Then, during spectral state transitions, the non-thermal component would gradually get stronger and stronger as the transition radius between outer disc and JED moves closer to the black hole. In the soft state the JED disappears and the hard X-ray emission is dominated by non-thermal Comptonization in the corona.
A tentative summary of our knowledge of accretion-ejection phenomena can be found here http://www.issibern.ch/teams/proaccretion/
This expression neglects any input of energy from the central object at the disc’s inner edge, through turbulence or MHD Poynting flux (see for instance Casse & Ferreira 2000b).
A steady-state jet is a bunch of axisymetric magnetic surfaces nested around each other and in differential rotation. Each magnetic surface is put into rotation by the underlying disc, so that Ω∗ ≃ Ω + (r), where Ω + (r) is the angular rotation at the disc surface. This velocity can be significantly lower than that at the disc midplane.
Acknowledgments
This work has been partly supported by the French National Agency (ANR) through the project “Astro2flots” ANR-05-JCJC-0020 and the GdR PCHE in France. POP also thanks the International Space Science Institute (ISSI) for hospitality.
References
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2008, ApJ, 678, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, K., Hawley, J. F., & Krolik, J. H. 2009, ApJ, 707, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, M. C., Sizun, P., Goldwurm, A., et al. 2006, A&A, 446, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belmont, R., Malzac, J., & Marcowith, A. 2008, A&A, 491, 617 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Lovelace, R. V. E. 2007, ApJ, 667, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D. 1976, MNRAS, 176, 465 [NASA ADS] [Google Scholar]
- Blandford, R. D., & Begelman, M. C. 1999, MNRAS, 303, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Blokland, J. W. S., van der Swaluw, E., Keppens, R., & Goedbloed, J. P. 2005, A&A, 444, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blokland, J. W. S., Keppens, R., & Goedbloed, J. P. 2007, A&A, 467, 21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, X., & Spruit, H. C. 2002, A&A,385, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casse, F., & Ferreira, J. 2000a, A&A, 353, 1115 [NASA ADS] [Google Scholar]
- Casse, F., & Ferreira, J. 2000b, A&A, 361, 1178 [NASA ADS] [Google Scholar]
- Casse, F., & Keppens, R. 2002, ApJ, 581, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Casse, F., & Keppens, R. 2004, ApJ, 601, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Abramowicz, M. A., Lasota, J.-P., Narayan, R., & Yi, I. 1995, ApJ, 443, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Combet, C., & Ferreira, J. 2008, A&A, 479, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Done, C., Gierlinski, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esin, A. A., Narayan, R., Ostriker, E., & Yi, I. 1996, ApJ, 465, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R., Gallo, E., & Russell, D. 2010, MNRAS, 406, 1425 [NASA ADS] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Ferreira, J. 2002, in Star Formation and the Physics of Young Stars, ed. J. Bouvier, & J.-P. Zahn, EAS Pub. Ser., 3, 229 [Google Scholar]
- Ferreira, J., & Casse, F. 2004, ApJ, 601, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1993, A&A, 276, 625 [NASA ADS] [Google Scholar]
- Ferreira, J., & Pelletier, G. 1995, A&A, 295, 807 [NASA ADS] [Google Scholar]
- Ferreira, J., Petrucci, P.-O., Henri, G., Sauge, L., & Pelletier, G. 2006, A&A, 447, 813 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fomalont, E. B., Geldzahler, B. J., & Bradshaw, C. F. 2001, ApJ, 558, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Frontera, F., Palazzi, E., Zdziarski, A. A., et al. 2001, ApJ, 546, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Gallo, E., Fender, R., Kaiser, C., et al. 2005, Nature, 436, 819 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gierlinski, M., Zdziarski, A. A., Done, C., et al. 1997, MNRAS, 288, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Gleissner, T., Wilms, J., Pooley, G. G., et al. 2004, A&A, 425, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guan, X., & Gammie, C. F. 2009, ApJ, 697, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Hannikainen, D., Campbell-Wilson, D., Hunstead, R., et al. 2001, Ap&SS, 276, 45 [Google Scholar]
- Hawley, J. F., & Krolik, J. H. 2006, ApJ, 641, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A., Poutanen, J., Gilfanov, M., Zdziarski, A. A., & Shrader, C. R. 2005, MNRAS, 362, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A., Zdziarski, A. A., & Poutanen, J. 2007, MNRAS, 381, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Joinet, A., Jourdain, E., Malzac, J., et al. 2007, ApJ, 657, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., Casse, F., & Goedbloed, J. P. 2002, ApJ, 569, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Komissarov, S. S., Barkov, M. V., Vlahakis, N., & Konigl, A. 2007, MNRAS, 380, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Kording, E., Rupen, M., Knigge, C., et al. 2008, Science, 320, 1318 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kording, E. G., Fender, R. P., & Migliari, S. 2006, MNRAS, 369, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2009, A&A, 504, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovelace, R. V. E. 1976, Nature, 262, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E., Rothstein, D. M., & Bisnovatyi-Kogan, G. S. 2009, ApJ, 701, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994a, MNRAS, 267, 235 [NASA ADS] [Google Scholar]
- Lubow, S. H., Papaloizou, J. C. B., & Pringle, J. E. 1994b, MNRAS, 268, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Malzac, J., & Belmont, R. 2009, MNRAS, 392, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Malzac, J., Petrucci, P. O., Jourdain, E., et al. 2006, A&A, 448, 1125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malzac, J., Belmont, R., & Fabian, A. C. 2009, MNRAS, 400, 1512 [NASA ADS] [CrossRef] [Google Scholar]
- McConnell, M. L., Zdziarski, A. A., Bennett, K., et al. 2002, ApJ, 572, 984 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, J. C., & Blandford, R. D. 2009, MNRAS, L199 [Google Scholar]
- McKinney, J. C., & Gammie, C. F. 2004, ApJ, 611, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., & Rodriguez, L. F. 1994, Nature, 371, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., & Rodriguez, L. F. 1998, Nature, 392, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, G. C., Ferreira, J., & Zanni, C. 2010, A&A, 512, 82 [Google Scholar]
- Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Pelletier, G., & Pudritz, R. E. 1992, ApJ, 394, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Vurm, I. 2009, ApJ, 690, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rothstein, D. M., & Lovelace, R. V. E. 2008, ApJ, 677, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, D. M., Fender, R. P., Gallo, E., & Kaiser, C. R. 2007, MNRAS, 376, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Salvo, T. D., Done, C., Zycki, P. T., Burderi, L., & Robba, N. R. 2001, ApJ, 547, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stirling, A. M., Spencer, R. E., de la Force, C. J., et al. 2001, MNRAS, 327, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, D. F., Romero, G. E., Barcons, X., & Lu, Y. 2005, ApJ, 626, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Tudose, V., Fender, R. P., Linares, M., Maitra, D., & van der Klis, M. 2009, MNRAS, 400, 2111 [NASA ADS] [CrossRef] [Google Scholar]
- Tzeferacos, P., Ferrari, A., Mignone, A., et al. 2009, MNRAS, 1371 [Google Scholar]
- Wardzinski, G., & Zdziarski, A. A. 2001, MNRAS, 325, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Wardzinski, G., Zdziarski, A. A., Gierlinski, M., et al. 2002, MNRAS, 337, 829 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Nowak, M. A., Pottschmidt, K., Pooley, G. G., & Fritz, S. 2006, A&A, 447, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Young, A. J., Fabian, A. C., Ross, R. R., & Tanaka, Y. 2001, MNRAS, 325, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F. 2001, MNRAS, 324, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Quataert, E., & Narayan, R. 2003, ApJ, 598, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Taam, R. E., Xue, Y., & Cui, W. 2006, ApJ, 636, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Zanni, C., Ferrari, A., Rosner, R., Bodo, G., & Massaglia, S. 2007, A&A, 469, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zdziarski, A. A., Leighly, K. M., Matsuoka, M., Cappi, M., & Mihara, T. 2002, ApJ, 573, 505 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Jet power and b parameter
The power leaving the disc and carried away by the jets (from both face) is Pjets = 2∫ρupE·dS, where the integration is along one disc surface from Rin to Rout and 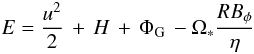 (A.1)is the well-known Bernoulli integral. It is the sum of all specific energies carried by the jet, kinetic, enthalpy, potential, and magnetic. In this last term, Ω∗ is the rotation speed of the magnetic surface and η the mass flux per magnetic flux unit.
(A.1)is the well-known Bernoulli integral. It is the sum of all specific energies carried by the jet, kinetic, enthalpy, potential, and magnetic. In this last term, Ω∗ is the rotation speed of the magnetic surface and η the mass flux per magnetic flux unit.
 |
Fig. A.1 Parameter space for the ejection efficiency ξ, the magnetization μ, the jet power parameter b and the sonic Mach number ms for the accretion-ejection solutions of Ferreira (1997) used in this paper. The lines correspond to different values of the disc aspect ratio H/R: solid lines: H/R = 0.1, dashed lines: H/R = 0.01, dot-dashed lines: H/R = 0.001. For this set of solutions, the turbulence level parameter αm is taken equal to unity. |
In the ideal MHD regime realized in jets, E is an invariant that can be evaluated at the disc surface. In a thin disc (ε ≪ 1), it writes as 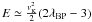 , where λBP is the Blandford & Payne (1982) magnetic lever arm parameter. For the models considered here, λBP varies between 10 and 100 so that the magnetic contribution dominates in Eq. (A.1). The jet power leaving the disc is therefore mostly in the form of an MHD Poynting flux,
, where λBP is the Blandford & Payne (1982) magnetic lever arm parameter. For the models considered here, λBP varies between 10 and 100 so that the magnetic contribution dominates in Eq. (A.1). The jet power leaving the disc is therefore mostly in the form of an MHD Poynting flux, 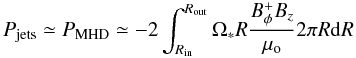 (A.2)which is exactly Eq. (13). The toroidal magnetic field at the disc surface scales as
(A.2)which is exactly Eq. (13). The toroidal magnetic field at the disc surface scales as 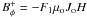 where Jo is the radial electric current density at the disc midplane, with F1 ≃ 0.4 − 0.6 for most published solutions. In a JED, where the dominant torque comes from the jets, the disc angular momentum conservation is
where Jo is the radial electric current density at the disc midplane, with F1 ≃ 0.4 − 0.6 for most published solutions. In a JED, where the dominant torque comes from the jets, the disc angular momentum conservation is 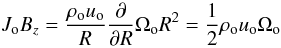 (A.3)where the subscript “o” stands for values evaluated at the disc midplane. Writing
(A.3)where the subscript “o” stands for values evaluated at the disc midplane. Writing 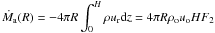 , with F2 a number of order unity found to vary between 0.4-0.6 also for most of our solutions, we obtain
, with F2 a number of order unity found to vary between 0.4-0.6 also for most of our solutions, we obtain 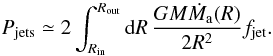 (A.4)In this expression,
(A.4)In this expression, 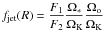 is a priori a function of the radius. However, it cannot vary much if ejection is to occur on a large radial extent. Under this assumption, our self-similar scalings apply, and we obtain Eq. (14) with
is a priori a function of the radius. However, it cannot vary much if ejection is to occur on a large radial extent. Under this assumption, our self-similar scalings apply, and we obtain Eq. (14) with 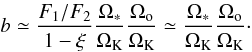 (A.5)While this quantity is nearly independent of ξ, it is clearly a function of the disc thickness, hence its temperature. The rotation of the disc material at the disc midplane scales as
(A.5)While this quantity is nearly independent of ξ, it is clearly a function of the disc thickness, hence its temperature. The rotation of the disc material at the disc midplane scales as 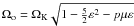 , where the second term is due to the radial pressure gradient and the third to the magnetic tension (
, where the second term is due to the radial pressure gradient and the third to the magnetic tension (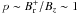 ). Thus, the thicker the disc, the greater the deviation from Keplerian and the smaller b.
). Thus, the thicker the disc, the greater the deviation from Keplerian and the smaller b.
But the dominant effect is from the rotation of the magnetic surfaces Ω∗. Indeed, Ω∗ is only defined in the upper layers of the disc once ideal MHD becomes valid. The disc density has therefore decreased significantly, thereby enhancing the outward effect of the magnetic radial tension. This tends to decrease the angular velocity Ω + of the matter and thus of the magnetic surfaces Ω∗ (see for instance the vertical profiles shown in Ferreira & Pelletier 1995). This behaviour can be also understood with the magnetic torque, which is first negative before becoming positive in the disc’s upper layers. The disc is therefore first spun down and Ω decreases.
Numerical solutions obtained with isothermal magnetic surfaces provide b ranging from 0.99 for thin discs with ε smaller than ~ 10-3 to roughly 0.5 for slim discs with ε ~ 0.1.
All Figures
 |
Fig. 1 Thermal balance of a jet emitting disc (JED) at r = 6 for ṁ = 0.001 and m = 10. The underlying JED structure has a jet power parameter b = 0.5 and an ejection efficiency ξ = 0.1. The dotted line is the heating term qheat, the dot-dot-dot-dashed line the radiative cooling term qrad, and the long dashed line is the advective term qadv. The Comptonized bremsstrahlung qC,brem (short dashed) and the Comptonized synchrotron qC,sync (dot-dashed) radiative terms are also shown. The solid line corresponds to qrad + qadv and the solutions of Eq. (17) are indicated by crosses. |
| In the text | |
 |
Fig. 2 JED solution domain in the ṁ-r plane. The solid line, corresponding to a jet power parameter b = 1, separates this plane into 2 regions: the top one where only the cold solution is valid and the bottom one where the 3 solutions exist. The region where only a hot solution is valid exists at very low accretion rate not shown in this figure. The limits for b = 0.5 are plotted in dashed lines. In this case the plane is divided into 3 parts with a region, for low accretion rate, where only the hot solution exists. |
| In the text | |
 |
Fig. 3 Left: observational parameter space of |
| In the text | |
 |
Fig. 4 Average terminal jet velocity versus the disc ejection efficiency ξ in a JED, with Ṁa ∝ Rξ. The grey and dark grey areas correspond to the regions that agree with the observational constraints reported in Fig. 3. |
| In the text | |
 |
Fig. 5 Contour plots of the JED temperature (solid lines) and optical depth (dashed lines) in the ξ − b plane at a distance of 10 RG from a 10 M⊙ black hole. The ratio of the outer to inner JED radii is taken equal to 100, and the total accretion rate for the computation of the disc thermal balance is fixed to 1% of LEdd, i.e., the typical luminosity of Cyg X-1. The grey and dark grey areas correspond to the regions that agree with the observational constraints reported in Fig. 3. |
| In the text | |
 |
Fig. A.1 Parameter space for the ejection efficiency ξ, the magnetization μ, the jet power parameter b and the sonic Mach number ms for the accretion-ejection solutions of Ferreira (1997) used in this paper. The lines correspond to different values of the disc aspect ratio H/R: solid lines: H/R = 0.1, dashed lines: H/R = 0.01, dot-dashed lines: H/R = 0.001. For this set of solutions, the turbulence level parameter αm is taken equal to unity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.