| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 19 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201014169 | |
| Published online | 27 October 2010 | |
Soft clustering analysis of galaxy morphologies: a worked example with SDSS
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: andrae@mpia-hd.mpg.de
2
Institut für Theoretische Astrophysik,
Zentrum für Astronomie, Albert-Ueberle-Str. 2,
69120
Heidelberg,
Germany
Received:
1
February
2010
Accepted:
26
May
2010
Context. The huge and still rapidly growing amount of galaxies in modern sky surveys raises the need for an automated and objective classification method. Unsupervised learning algorithms are of particular interest, since they discover classes automatically.
Aims. We briefly discuss the pitfalls of oversimplified classification methods and outline an alternative approach called “clustering analysis”.
Methods. We have categorised different classification methods according to their capabilities. Based on this categorisation, we present a probabilistic classification algorithm that automatically detects the optimal classes preferred by the data. We explored the reliability of this algorithm in systematic tests. Using a sample of 1520 bright galaxies from the SDSS, we demonstrate the performance of this algorithm in practice. We are able to disentangle the problems of classification and parametrisation of galaxy morphologies in this case.
Results. We give physical arguments that a probabilistic classification scheme is necessary. When applied to a small set of 84 galaxies visually classified as face-on discs, edge-on discs, and ellipticals, the clustering algorithm discovers precisely these classes and produces excellent object-to-class assignments. The resulting grouping of the galaxies outperforms a principal components analysis applied to the same data set. Applying the algorithm to a sample of 1520 SDSS galaxies, we find morphologically distinct classes when the number of classes are 3 and 8.
Conclusions. Although interpreting clustering results is a challenging task, the algorithm we present produces reasonable morphological classes and object-to-class assignments without any prior assumptions.
Key words: surveys / methods: data analysis / methods: statistical
© ESO, 2010
1. Introduction
Classification of objects is typically the first step towards scientific understanding, since it brings order to a previously unorganised set of observational data and provides standardised terms to describe objects. These standardised terms are usually qualitative, but they can also be quantitative, which makes them accessible for mathematical analysis. A famous example of a successful classification from the field of astrophysics is the Hertzsprung-Russell diagram, where stars exhibit distinct groups in the colour-magnitude diagram that represent their different evolutionary stages. For the same reason, galaxy classification is an important conceptual step towards understanding the physical properties, formation, and evolution scenarios of galaxies.
With the advent of modern sky surveys containing millions (e.g. SDSS, COSMOS, PanSTARRS, GAMA) or even billions (e.g. LSST) of galaxies, the classification of these galaxies is becoming more and more problematic. The vast amount of data excludes the hitherto common practice of visual classification and clearly calls for an automated classification scheme that is more efficient and more objective. Consequently, automated classification has attracted much interest: a (not exhaustive) list of previously employed classification algorithms contains, e.g., artificial neural networks (Storrie-Lombardi et al. 1992; Lahav et al. 1995, 1996; Ball et al. 2004; Banerji et al. 2010), nearest neighbours and decision trees (Humphreys et al. 2001), and support vector machines (e.g. Huertas-Company et al. 2008, 2009). More recently, Gauci et al. (2010) have demonstrated that a state-of-the-art classification algorithm called “Random Forest” outperforms decision trees and reaches accuracies of up to 97% in recovering visual classifications. Despite these efforts, the issue of morphological classification of galaxies is by no means a solved problem. A potential reason is that the morphological classes are usually defined by the scientists (“supervised” learning) and not by the data (“unsupervised” learning). The publication history of unsupervised methods, e.g., self-organising maps (Naim et al. 1997) and Gaussian mixture models (Kelly & McKay 2004, 2005), is much shorter. Unsupervised methods are very promising, since they discover the “optimal” classes automatically, thereby extending objectivity also to the definition of the classes themselves, beyond the object-to-class assignment. In this work we present an unsupervised algorithm for probabilistic classification that is competitive with the Gaussian mixture models. However, the intention of this work is not to come up with “yet another morphological classification scheme”, but rather to demonstrate an classification method to the standard practice in astrophysics. Besides, we are unable to present a full solution to the problem of morphological galaxy classification, since there is still no accepted method for parametrising arbitrary galaxy morphologies (cf. Andrae et al., in prep.). In addition, the lack of convincing classification schemes is why many experts are very sceptical about the subject of classifying galaxy morphologies as a whole. Because parametrisation of galaxy spectra is more reliable, spectral classifications have become more accepted.
In Sect. 2, we first give an overview of modern automated classification methods and work out a categorisation of these methods. We describe our parametrisation of galaxy morphologies using shapelets (Réfrégier 2003) in Sect. 3. In Sect. 4 we present the algorithm we are using, which has been introduced before by Yu et al. (2005) in the field of pattern recognition. We extensively investigate the reliability of this classification algorithm in Sect. 5. Such a study was not done by Yu et al. (2005). In Sect. 6 we present a worked example with a small sample of 1520 bright galaxies from the SDSS. The objects in this sample are selected such that no practical problems with parametrisation arise, as we want to disentangle the problems of classification and parametrisation as much as possible. The aim of this worked example is not related to science with the resulting classes or data-to-class assignments, but to demonstrate that such an algorithm indeed produces reasonable results. We conclude in Sect. 7.
2. Classification methods
2.1. Overview
In Table 1 we give an overview of different classification methods and some example algorithms, with the following two criteria.
-
1.
Is the data-to-class assignment probabilistic (soft) or not(hard)?
-
2.
Are the classes specified a priori (classification, supervised learning) or discovered automatically (clustering, unsupervised learning)?
Soft (probabilistic) algorithms are always model-based, whereas hard algorithms are not necessarily. Soft algorithms can always be turned into hard algorithms, but not vice versa. The list of example algorithms given in Table 1 is not complete. Not all algorithms fit into this categorisation, namely those that do not directly assign classes to objects (e.g. self-organising maps).
Overview of different classification and clustering algorithms with examples.
The algorithm we are going to present is a soft algorithm; i.e., the data-to-class assignment is probabilistic (cf. next section). The reason is that in the case of galaxy morphologies, it is obvious that the classes will not be clearly separable. We rather expect the galaxies to be more or less homogeneously distributed in some parameter space, with the classes appearing as local overdensities and exhibiting potentially strong overlap. As we demonstrate in Sect. 5.2, hard algorithms break down in this case, producing biased classification results. There are physical reasons to expect overlapping classes. First, the random inclination and orientation angles with respect to the line of sight induce a continuous transition of apparent axis ratios, apparent steepness of the radial light profiles and ratio of light coming from bulge and disc components. Second, observations of galaxies show that there are indeed transitional objects between different morphological types. For instance, there are transitional objects between early- and late-type galaxies in the “green valley” of the colour bimodality (e.g. Strateva et al. 2001; Baldry et al. 2004), which is also reproduced in simulations (Croton et al. 2006). We thus have to draw the conclusion that hard algorithms are generically inappropriate for analysing galaxy morphologies. This conclusion is backed up by practical experience, since even specialists usually do not agree on hard visual classifications (e.g. Lahav et al. 1996). In fact, the outcome of multi-person visual classifications becomes a probability distribution automatically (e.g. Bamford et al. 2009).
Furthermore, our algorithm is a clustering algorithm; i.e., we do not specify the morphological classes a priori, but let the algorithm discover them. This approach is called “unsupervised learning” and it is the method of choice if we are uncertain about the type of objects we will find in a given data sample. On the other hand, if we were certain about the classes, e.g., for star-galaxy classification, we should not use unsupervised methods. In the context of clustering analysis, classes are referred to as clusters, and we adopt this terminology in this article.
2.2. Probabilistic data-to-class assignment
Let O denote an object and x its parametrisation. Furthermore, let ck denote a single class out of k = 1,...,K possible classes, then prob(ck | x) denotes the probability of class ck given the object O represented by x. This conditional probability prob(ck | x) is called the class posterior and is computed using Bayes’ theorem
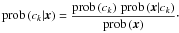 (1)The marginal probability prob(ck) is called class prior and prob(x | ck) is called class likelihood. The denominator prob(x) acts as a normalisation factor. The class prior and likelihood are obtained from a generative model (Sect. 4.3). Prior and posterior satisfy the following obvious normalisation constraints
(1)The marginal probability prob(ck) is called class prior and prob(x | ck) is called class likelihood. The denominator prob(x) acts as a normalisation factor. The class prior and likelihood are obtained from a generative model (Sect. 4.3). Prior and posterior satisfy the following obvious normalisation constraints
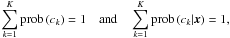 (2)which ensure that each object is definitely assigned to some class. In the case of hard assignments, both posterior prob(ck | x) and likelihood prob(x | ck) are replaced by Kronecker symbols.
(2)which ensure that each object is definitely assigned to some class. In the case of hard assignments, both posterior prob(ck | x) and likelihood prob(x | ck) are replaced by Kronecker symbols.
3. Parametrising galaxy morphologies with shapelets
3.1. Basis functions and expansion
We parametrise galaxy morphologies in terms of shapelets (Réfrégier 2003). Shapelets are a scaled version of two-dimensional Gauss-Hermite polynomials that form a set of complete basis functions that are orthonormal on the interval [ − ∞,∞ ] . A given galaxy image I(x) can be decomposed into a linear superposition of basis functions Bm,n(x / β); i.e.,
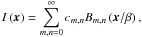 (3)where the cm,n denote the expansion coefficients that contain the morphological information and β > 0 denotes a scaling radius. In practice, the number of basis functions we can use is limited by pixel noise, such that the summation in Eq. (3) stops at a certain maximum order Nmax < ∞, which depends on the object’s signal-to-noise ratio and resolution. This means Eq. (3) is an approximation only,
(3)where the cm,n denote the expansion coefficients that contain the morphological information and β > 0 denotes a scaling radius. In practice, the number of basis functions we can use is limited by pixel noise, such that the summation in Eq. (3) stops at a certain maximum order Nmax < ∞, which depends on the object’s signal-to-noise ratio and resolution. This means Eq. (3) is an approximation only,
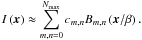 (4)We use the C++ algorithm by Melchior et al. (2007) to estimate Nmax, the scale radius and the linear coefficients, which was shown to be faster and more accurate than the IDL algorithm by Massey & Réfrégier (2005). Concerning computational feasibility, the shapelet decomposition of a typical SDSS galaxy takes a few seconds on a standard computer and is therefore feasible for very large data samples.
(4)We use the C++ algorithm by Melchior et al. (2007) to estimate Nmax, the scale radius and the linear coefficients, which was shown to be faster and more accurate than the IDL algorithm by Massey & Réfrégier (2005). Concerning computational feasibility, the shapelet decomposition of a typical SDSS galaxy takes a few seconds on a standard computer and is therefore feasible for very large data samples.
3.2. Problems with shapelet modelling
It was shown by Melchior et al. (2010) that the limitation of the number of basis functions in Eq. (4) can lead to severe modelling failures and misestimations of galaxy shapes in the case of objects with low signal-to-noise ratios. They identified two origins of these biases. First, the Gaussian profile of shapelets does not match the true profiles of galaxies, which are typically much steeper. Second, the shapelet basis functions are intrinsically spherical; i.e., they have problems in modelling highly eccentric objects. However, in this demonstration we only consider galaxies with high signal-to-noise ratios, where we can use many basis functions such that the impact of these biases is negligible. We demonstrate this in Fig. 1, where we show the shapelet reconstructions of a face-on disc, an edge-on disc, and an elliptical galaxy drawn from the sample presented in Sect. 6.1. The reconstruction of the face-on disc galaxy (top row) is excellent, leaving essentially uncorrelated noise in the residuals. However, the reconstructions of the edge-on disc galaxy (centre row) and the elliptical galaxy (bottom row) exhibit ring-like artefacts that originate in the steep light profiles of the elliptical and the edge-on disc along the minor axis. Such modelling failures appear systematically and do not introduce additional scatter into the results; i.e., similar galaxies are affected in a similar way. However, since shapelet models do not capture steep and strongly elliptical galaxies very well, we are aware that our algorithm has less dicriminatory power for galaxies of this kind.
 |
Fig. 1 Examples of shapelet models of three galaxies from SDSS (g band). Shown are the original images (left column), the shapelet models (centre column), the residuals (right column) of a face-on disc galaxy (top row), an edge-on disc galaxy (centre row), and an elliptical galaxy (bottom row). Note the different plot ranges of the residual maps. The shapelet decomposition used Nmax = 16; i.e., 153 basis functions. |
3.3. Distances in shapelet space
The coefficients form a vector space that we denote as vectors x. In a first-order approximation, these coefficient vectors are independent of the size of the object, which was encoded by the scale radius β. Moreover, we can also make x invariant against the image flux, since Eq. (3) implies that for a constant scalar α ≠ 0 the transformation x → αx changes the image flux by this same factor of α. Therefore, if we demand x·x = 1, then differing image fluxes will have no impact on the shapelet coefficients. This implies that morphologies are a direction in shapelet coefficient space and the corresponding coefficient vectors lie on the surface of a hypersphere with unit radius. We can thus measure distances between morphologies on this surface via the angle spanned by their (normalised) coefficient vectors,
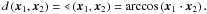 (5)Employing the polar representation of shapelets (Massey & Réfrégier 2005), we can apply rotations and parity flips to shapelet models. We can estimate the object’s orientation angle from the second moments of its light distribution (e.g. Melchior et al. 2007) and then use this estimate to align all models. This ensures invariance of the coefficients against random orientations. Additionally, we can break the degeneracy between left- and right-handed morphologies by applying parity flips such that the distance of two objects is minimised. These transformations in model space do not suffer from pixellation errors and increase the local density of similar objects in shapelet space.
(5)Employing the polar representation of shapelets (Massey & Réfrégier 2005), we can apply rotations and parity flips to shapelet models. We can estimate the object’s orientation angle from the second moments of its light distribution (e.g. Melchior et al. 2007) and then use this estimate to align all models. This ensures invariance of the coefficients against random orientations. Additionally, we can break the degeneracy between left- and right-handed morphologies by applying parity flips such that the distance of two objects is minimised. These transformations in model space do not suffer from pixellation errors and increase the local density of similar objects in shapelet space.
4. Soft clustering algorithm
We now present the soft clustering algorithm of Yu et al. (2005). Before we explain the details, we want to give a brief outline of the general method. The basic idea is to assign similarities to pairs of objects, so we first explain how to measure similarities of galaxy morphologies and what a similarity matrix is. These pairwise similarities are then interpreted by a probabilistic model, which provides our generative model. We also present the algorithm that fits the model to the similarity matrix.
4.1. Estimating similarities
Instead of analysing the data in shapelet space, we compute a similarity matrix by assigning similarities to any two data points. This approach is an alternative to working directly in the sparsely populated shapelet space or employing a method for dimensionality reduction. If we have N data points xn, then this similarity matrix will be an N × N symmetric matrix. It is this similarity matrix to which we are going to apply the soft clustering analysis.
Based on the pairwise distances in shapelet coefficient space (Eq. (5)), we estimate pairwise similarities up to a constant factor as
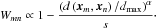 (6)Here dmax denotes the maximum distance between any two objects in the given data sample, while the exponent α > 0 and s > 1 are free parameters that tune the similarity measure. We explain how to choose α and s in Sect. 5.3. This definition ensures that 0 < Wmn ≤ 1 and that the maximum similarities are self-similarities for which d(xm,xm) = 0. This similarity measure is invariant under changes of size, flux, orientation, and parity of the galaxy morphology.
(6)Here dmax denotes the maximum distance between any two objects in the given data sample, while the exponent α > 0 and s > 1 are free parameters that tune the similarity measure. We explain how to choose α and s in Sect. 5.3. This definition ensures that 0 < Wmn ≤ 1 and that the maximum similarities are self-similarities for which d(xm,xm) = 0. This similarity measure is invariant under changes of size, flux, orientation, and parity of the galaxy morphology.
4.2. Similarity matrices and weighted undirected graphs
Square symmetric similarity matrices have a very intuitive interpretation, because they represent a weighted undirected graph. Figure 2 shows a sketch of such a graph. The data points xn are represented symbolically as nodes xn. The positions of these nodes are usually arbitrary, and it is neither necessary nor helpful to arrange them according to the true locations of the data points in parameter space. Any two data nodes xm and xn are connected by an edge, which is assigned a weight Wmn. Obviously, all the weights Wmn form an N × N matrix W, and if this matrix is symmetric; i.e., Wmn = Wnm, the edges will have no preferred direction. In this case, the weighted graph is undirected. In graph theory the matrix of weights W is called adjacency matrix, and we can interpret the similarity matrix as adjacency matrix of a weighted undirected graph.
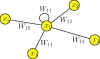 |
Fig. 2 Sketch of a weighted undirected graph. The data nodes xn are connected by edges. For the sake of visibility, only edges connecting x1 are shown. The edges are undirected and weighted by the similarity of the two connected nodes. |
After inspecting Fig. 2, we now introduce some important concepts. First, there is also an edge connecting x1 with itself. This edge is weighted by the “self-similarity” W11. These self-similarities Wnn are usually non-zero and have to be taken into account to satisfy normalisation constraints (cf. Eq. (8)). Second, we define the degree dn of a data node xn as the sum of weights of all edges connected with xn; i.e.,
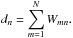 (7)We can interpret the degree dn to measure the connectivity of data node xn in the graph. For instance, we can detect outlier objects by their low degree, since they are very dissimilar to all other objects. Third, we can rescale all similarities by a constant scalar factor C > 0 without changing the pairwise relations. As a result, we acquire the normalisation constraint
(7)We can interpret the degree dn to measure the connectivity of data node xn in the graph. For instance, we can detect outlier objects by their low degree, since they are very dissimilar to all other objects. Third, we can rescale all similarities by a constant scalar factor C > 0 without changing the pairwise relations. As a result, we acquire the normalisation constraint
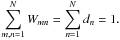 (8)This constraint ensures the normalisation of the probabilistic model we are going to set up for our soft clustering analysis of the similarity matrix.
(8)This constraint ensures the normalisation of the probabilistic model we are going to set up for our soft clustering analysis of the similarity matrix.
4.3. Bipartite-graph model
We need a probabilistic model of the similarity matrix W that can be interpreted in terms of a soft clustering analysis. Such a model was proposed by Yu et al. (2005). As similarity matrices are closely related to graphs, this model is motivated from graph theory, too. The basic idea of this model is that the similarity of two data points xm and xn is induced by both objects being members of the same clusters. This is the basic hypothesis of any classification approach: objects from the same class are more alike than objects from different classes.
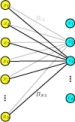 |
Fig. 3 Sketch of a bipartite graph. The bipartite graph contains two sets of nodes, X = { x1,...,xN } and C = { c1,...,cK } . Edges connect nodes from different sets only and are weighted by an adjacency matrix B. Not all edges are shown. |
In detail, we model a weighted undirected graph (Fig. 2) and its similarity matrix by a bipartite graph (Fig. 3). A bipartite graph is a graph whose nodes can be divided into two disjoint sets X = { x1,...,xN } of data nodes and C = { c1,...,cK } of cluster nodes, such that the edges in the graph only connect nodes from different sets. Again, the edges are weighted and undirected, where the weights Bnk form an N × K rectangular matrix B, the bipartite-graph adjacency matrix. The bipartite-graph model for the similarity matrix then reads
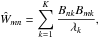 (9)with the cluster priors
(9)with the cluster priors 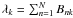 . A detailed derivation is given in the following section. This model induces the pairwise similarities via two-hop transitions X → C → X (cf. Yu et al. 2005). The numerator accounts for the strength of the connections of both data nodes to a certain cluster. The impact of the denominator is that the common membership to a cluster of small degree is considered more decisive. Obviously, the model defined by Eq. (9) is symmetric, as is the similarity matrix itself. The normalisation constraint on W as given by Eq. (8) translates via the bipartite-graph model to
. A detailed derivation is given in the following section. This model induces the pairwise similarities via two-hop transitions X → C → X (cf. Yu et al. 2005). The numerator accounts for the strength of the connections of both data nodes to a certain cluster. The impact of the denominator is that the common membership to a cluster of small degree is considered more decisive. Obviously, the model defined by Eq. (9) is symmetric, as is the similarity matrix itself. The normalisation constraint on W as given by Eq. (8) translates via the bipartite-graph model to
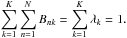 (10)These constraints need to be respected by the fit algorithm. Having fitted the bipartite-graph model to the given data similarity matrix, we compute the cluster posterior probabilities
(10)These constraints need to be respected by the fit algorithm. Having fitted the bipartite-graph model to the given data similarity matrix, we compute the cluster posterior probabilities
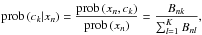 (11)which are the desired soft data-to-cluster assignments. Obviously, K cluster posteriors are assigned to each data node xn, and the normalisation constraint
(11)which are the desired soft data-to-cluster assignments. Obviously, K cluster posteriors are assigned to each data node xn, and the normalisation constraint 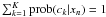 is satisfied.
is satisfied.
4.4. Mathematical derivation
Here we give a derivation of the bipartite-graph model of Eq. (9), which is more detailed than in Yu et al. (2005). The ansatz is to identify the similarity Ŵmn with the joint probability
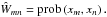 (12)This interprets Ŵmn as the probability of finding xm and xn in the same cluster. Equation (8) ensures the normalisation
(12)This interprets Ŵmn as the probability of finding xm and xn in the same cluster. Equation (8) ensures the normalisation 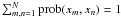 . As we do not know which particular cluster induces the similarity, we have to marginalise over all cluster nodes in Fig. 3,
. As we do not know which particular cluster induces the similarity, we have to marginalise over all cluster nodes in Fig. 3,
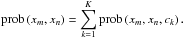 (13)With this marginalisation we have switched from the weighted undirected graph to our bipartite-graph model. Applying Bayes’ theorem yields
(13)With this marginalisation we have switched from the weighted undirected graph to our bipartite-graph model. Applying Bayes’ theorem yields
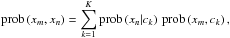 (14)where we have used
(14)where we have used
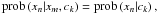 (15)since xm and xn are not directly connected in the bipartite graph; i.e., they are statistically independent. This is the only assumption in this derivation, and it implies that all statistical dependence is induced by the clusters. Using Bayes’ theorem once more yields
(15)since xm and xn are not directly connected in the bipartite graph; i.e., they are statistically independent. This is the only assumption in this derivation, and it implies that all statistical dependence is induced by the clusters. Using Bayes’ theorem once more yields
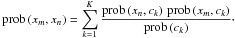 (16)We identify the bipartite-graph adjacency matrix in analogy to Eq. (12),
(16)We identify the bipartite-graph adjacency matrix in analogy to Eq. (12),
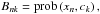 (17)with its marginalisation
(17)with its marginalisation
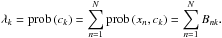 (18)The marginalised probabilities λk are the cluster priors of the cluster nodes ck in the bipartite graph. Moreover, the λk are the degrees of the nodes.
(18)The marginalised probabilities λk are the cluster priors of the cluster nodes ck in the bipartite graph. Moreover, the λk are the degrees of the nodes.
4.5. Fitting the similarity matrix
To fit the bipartite-graph model defined by Eq. (9) to a given similarity matrix, we perform some simplifications. First, we can rewrite Eq. (9) using matrix notation,
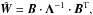 (19)where B is the N × K bipartite-graph adjacency matrix and Λ = diag(λ1,...,λk) is the K × K diagonal matrix of cluster degrees. This notation enables us to employ fast and efficient algorithms from linear algebra. We change variables by
(19)where B is the N × K bipartite-graph adjacency matrix and Λ = diag(λ1,...,λk) is the K × K diagonal matrix of cluster degrees. This notation enables us to employ fast and efficient algorithms from linear algebra. We change variables by
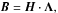 (20)where H is an N × K matrix. The elements of H can be interpreted as the cluster likelihoods, since
(20)where H is an N × K matrix. The elements of H can be interpreted as the cluster likelihoods, since 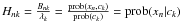 . Using these new variables H and Λ, the model
. Using these new variables H and Λ, the model 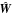 of the data similarity matrix W is given by
of the data similarity matrix W is given by
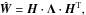 (21)where we have eliminated the matrix inversion and reduced the nonlinearity to some extent. The normalisation constraints of Eq. (10) translate to H as
(21)where we have eliminated the matrix inversion and reduced the nonlinearity to some extent. The normalisation constraints of Eq. (10) translate to H as
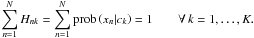 (22)The normalisation constraints on H and Λ are now decoupled, and we can treat both matrices as independent of each other. As H is an N × K matrix and Λ a K × K diagonal matrix, we have K(N + 1) model parameters. In comparison to this number, we do have
(22)The normalisation constraints on H and Λ are now decoupled, and we can treat both matrices as independent of each other. As H is an N × K matrix and Λ a K × K diagonal matrix, we have K(N + 1) model parameters. In comparison to this number, we do have 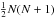 independent elements in the data similarity matrix due to its symmetry; hence, a reasonable fit situation requires
independent elements in the data similarity matrix due to its symmetry; hence, a reasonable fit situation requires 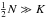 in order to constrain all model parameters.
in order to constrain all model parameters.
The data similarity matrix W is fitted by maximising the logarithmic likelihood function log ℒ of the bipartite-graph model. Yu et al. (2005) give a derivation of this function based on the theory of random walks on graphs. Their result is
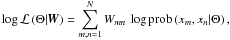 (23)where Θ = { H11,...,HNK,λ1,...,λK } denotes the set of K(N + 1) model parameters and
(23)where Θ = { H11,...,HNK,λ1,...,λK } denotes the set of K(N + 1) model parameters and 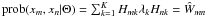 is the model. If we remember that Wmn = prob(xm,xn), then we see that log ℒ is the cross entropy of the true probability distribution Wmn = prob(xm,xn) and the modelled distribution Ŵmn = prob(xm,xn | Θ). Consequently, maximising log ℒ maximises the information our model contains about the data similarity matrix.
is the model. If we remember that Wmn = prob(xm,xn), then we see that log ℒ is the cross entropy of the true probability distribution Wmn = prob(xm,xn) and the modelled distribution Ŵmn = prob(xm,xn | Θ). Consequently, maximising log ℒ maximises the information our model contains about the data similarity matrix.
Directly maximising log ℒ is too hard, since the fit parameters are subject to the constraints given by Eqs. (10) and (22). We use an alternative approach that makes use of the expectation-maximisation (EM) algorithm, which is an iterative fit routine. Given an initial guess on the model parameters, the EM algorithm provides a set of algebraic update equations to compute an improved estimate of the optimal parameters that automatically respects the normalisation. These update equations are (Bilmes 1997; Yu et al. 2005)
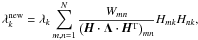 (24)
(24)
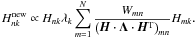 (25)The
(25)The 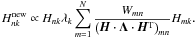 have to be normalised by hand, whereas the
have to be normalised by hand, whereas the 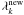 have already been normalised. Each iteration step updates all the model parameters, which has time complexity 𝒪(K·N2) for K clusters and N data nodes. We initialise all the cluster degrees to
have already been normalised. Each iteration step updates all the model parameters, which has time complexity 𝒪(K·N2) for K clusters and N data nodes. We initialise all the cluster degrees to 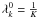 , whereby we trivially satisfy the normalisation condition and simultaneously ensure that no cluster is initialised as virtually absent. The
, whereby we trivially satisfy the normalisation condition and simultaneously ensure that no cluster is initialised as virtually absent. The 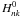 are initialised randomly and normalised “by hand”.
are initialised randomly and normalised “by hand”.
Now, we want to briefly discuss the convergence properties of the EM algorithm. It has been shown (e.g., Redner & Walker 1984) that the EM algorithm is guaranteed to converge to a local maximum of log ℒ under mild conditions. Indeed, it was shown that the EM algorithm is monotonically converging; i.e., each iteration step is guaranteed to increase log ℒ. Therefore, after each iteration step, we check how much log ℒ was increased compared to the previous step. If log ℒ changed by less than a factor of 10-9, we consider the EM algorithm to have converged. This convergence criterion was chosen based on systematic tests like those discussed in Sect. 5. Finally, the fit results are not unique, since the ordering of the clusters is purely random.
4.6. Computational feasibility
The large number of objects contained in existing and future galaxy surveys is the main reason why automated algorithms will replace visual classifications. Computational feasibility is therefore an important aspect for every algorithm. Given a certain number N of galaxies that have to be classified, classification algorithms have typical time complexities of O(N), whereas clustering algorithms never scale better than O(N2). This renders clustering analysis on extremely large data samples infeasible. We now briefly outline a combined strategy that benefits from the class discovery of an unsupervised approach and from the superior time complexity of a classifier.
The generic setup is that we have a large data set that we want to classify, but we do not know what kind of classes there are in the data. In this case, we can select a subset of T objects from the complete data set, serving as a training sample. We run a soft clustering analysis on this training sample to discover the classes. Here, we implicitly assume that the training sample is representative of the complete data set, thus it has to be sufficiently large. In this case, we can use the soft clustering results to set up a soft classifier. Let xn denote a new data point from the complete set that we want to classify into the scheme defined by the clustering algorithm. We define the posterior probability of cluster ck given the new object xn to be
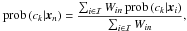 (26)where Win denotes the similarity (as estimated by Eq. (6)) of the new object xn to the object xi from the training sample, the prob(ck | xi) are the posteriors resulting from the clustering analysis on the training sample, and ℐ denotes the subset of the training sample containing the k training objects most similar to the new object. This assumes that the class assignment of the new object is only determined by those objects from the training sample that are very similar. Consequently, Eq. (26) defines a soft k-nearest-neighbour classifier. The optimal number of nearest neighbours is estimated by training the classifier on the data-to-cluster assignments of the clustering on the training sample itself. Obviously, the class posteriors defined by Eq. (26) are normalised, since the cluster posteriors satisfy
(26)where Win denotes the similarity (as estimated by Eq. (6)) of the new object xn to the object xi from the training sample, the prob(ck | xi) are the posteriors resulting from the clustering analysis on the training sample, and ℐ denotes the subset of the training sample containing the k training objects most similar to the new object. This assumes that the class assignment of the new object is only determined by those objects from the training sample that are very similar. Consequently, Eq. (26) defines a soft k-nearest-neighbour classifier. The optimal number of nearest neighbours is estimated by training the classifier on the data-to-cluster assignments of the clustering on the training sample itself. Obviously, the class posteriors defined by Eq. (26) are normalised, since the cluster posteriors satisfy 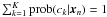 .
.
4.7. Estimating the optimal number of clusters
In this section we demonstrate how to estimate the optimal number of clusters for a given data set, which is a crucial part of any clustering analysis. It is essential to estimate the optimal number of clusters with due caution. This is a problem of assessing nonlinear models, and there are no theoretically justified methods, only heuristic approaches. Common heuristics are the Bayesian information criterion
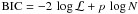 (27)and Akaike’s information criterion
(27)and Akaike’s information criterion
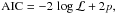 (28)where p and N denote the number of model parameters and the number of data points, respectively. As we have seen in Sect. 4.5, the bipartite-graph model involves K(N + 1) model parameters. Consequently, BIC and AIC are not applicable, since log ℒ is not able to compensate for the strong impact of the penalty terms. This inability of log ℒ is likely to originate in the sparse data population in the high-dimensional parameter space. Another tool of model assessment is cross-validation, but this is computationally infeasible in this case.
(28)where p and N denote the number of model parameters and the number of data points, respectively. As we have seen in Sect. 4.5, the bipartite-graph model involves K(N + 1) model parameters. Consequently, BIC and AIC are not applicable, since log ℒ is not able to compensate for the strong impact of the penalty terms. This inability of log ℒ is likely to originate in the sparse data population in the high-dimensional parameter space. Another tool of model assessment is cross-validation, but this is computationally infeasible in this case.
We now explain how to compare bipartite-graph models of different complexities heuristically; i.e., how to estimate the optimal number of clusters. This heuristic employs the sum of squared residuals
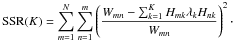 (29)The definition puts equal emphasis on all elements. If we left out the denominator in Eq. (29), the SSR would emphasise deviations of elements with high values, whereas elements with low values would be neglected. However, both high and low values of pairwise similarities are decisive. We estimate the optimal K via the position of a kink in the function SSR(K) (cf. Fig. 4). Such a kink arises if adding another cluster does not lead to a significant improvement in the similarity-matrix reconstruction.
(29)The definition puts equal emphasis on all elements. If we left out the denominator in Eq. (29), the SSR would emphasise deviations of elements with high values, whereas elements with low values would be neglected. However, both high and low values of pairwise similarities are decisive. We estimate the optimal K via the position of a kink in the function SSR(K) (cf. Fig. 4). Such a kink arises if adding another cluster does not lead to a significant improvement in the similarity-matrix reconstruction.
 |
Fig. 4 Estimating the optimal number of clusters for the data sample shown in Fig. 6. a) SSR(K) as a function of the number K of clusters. b) Mean angular changes 〈 Δ(K) 〉 averaged over ten fits. |
We demonstrate this procedure in Fig. 4 by using the toy example of Figs. 6 and 7, which is composed of six nicely separable clusters. We fit bipartite-graph models to the similarity matrix shown in Fig. 7, with K ranging from 1 to 15. The resulting SSR values are shown in panel (a) of Fig. 4. In fact, SSR(K) exhibits two prominent kinks at K = 3 and K = 6, rather than a single one. Obviously, for K = 3, the clustering algorithm groups the four nearby clusters together, thus resulting in three clusters. For K = 6, it is able to resolve this group of “subclusters”.
We can construct a more quantitative measure by computing the angular change Δ(K) of log SSR(K) at each K,
![\begin{eqnarray} % \Delta(K) &=& \arctan\left[\log\SSR(K-1) - \log\SSR(K)\right] \nonumber\\ &&- \arctan\left[\log\SSR(K) - \log\SSR(K+1)\right]. \end{eqnarray}](/articles/aa/full_html/2010/14/aa14169-10/aa14169-10-eq120.png) (30)As K is an integer, log SSR(K) is a polygonal chain and thus an angular change is well defined. A large positive angular change then indicates the presence of a kink in SSR(K)1. However, we can even do better by fitting the similarity matrix several times for each K and averaging the angular changes. The results of the fits differ slightly, since the model parameters are randomly initialised each time. These mean angular changes are shown in panel (b) of Fig. 4, averaged over 20 fits for each K. First, for large K the mean angular changes are consistent with zero; i.e., in this domain increasing K decreases SSR(K) but does not improve the fit systematically. Second, for K = 3 and K = 6, the mean angular changes deviate significantly from zero. For K = 2 and K = 4, the mean angular changes are negative, which corresponds to “opposite” kinks in the SSR spectrum and stems from K = 3 being a very good grouping of the data.
(30)As K is an integer, log SSR(K) is a polygonal chain and thus an angular change is well defined. A large positive angular change then indicates the presence of a kink in SSR(K)1. However, we can even do better by fitting the similarity matrix several times for each K and averaging the angular changes. The results of the fits differ slightly, since the model parameters are randomly initialised each time. These mean angular changes are shown in panel (b) of Fig. 4, averaged over 20 fits for each K. First, for large K the mean angular changes are consistent with zero; i.e., in this domain increasing K decreases SSR(K) but does not improve the fit systematically. Second, for K = 3 and K = 6, the mean angular changes deviate significantly from zero. For K = 2 and K = 4, the mean angular changes are negative, which corresponds to “opposite” kinks in the SSR spectrum and stems from K = 3 being a very good grouping of the data.
For large K these detections may be less definite due to the flattening of SSR(K). Therefore, we may systematically underestimate the optimal number of clusters. Moreover, this toy example also demonstrates that there may be more than a single advantageous grouping of the data and there may be disadvantageous groupings. If there are multiple detections of advantageous groupings, it may be difficult to judge which grouping is the best. In the worst case, we may even not find any signal of an advantageous grouping, which would either imply that our given sample is composed of objects of the same type or that the data does not contain enough information about the grouping. Unfortunately, this scheme of estimating the optimal number of clusters is extremely inefficient from a computational point of view. This is a severe disadvantage for very large data sets. Moreover, though this heuristic is working well, the significance of the mean angular changes is likely to be strongly influenced by the variance caused by the algorithm’s initialisation.
4.8. Comparison with previous work
As the work of Kelly & McKay (2004, 2005) is very close to our own work, we want to discuss it in some detail and work out the differences. The authors applied a soft clustering analysis to the first data release of SDSS. In Kelly & McKay (2004), they decomposed r-band images of 3037 galaxies into shapelets, using the IDL shapelet code by Massey & Réfrégier (2005). In Kelly & McKay (2005), they extended this scheme to all five photometric bands u,g,r,i,z of SDSS, thereby also taking colour information into account. Afterwards, they used a principal component analysis (PCA) to reduce the dimensionality of their parameter space. In Kelly & McKay (2004), the reduction was from 91 to 9 dimensions, and in Kelly & McKay (2005) from 455 to 2 dimensions. Then they fitted a mixture-of-Gaussians model (Bilmes 1997) to the compressed data, where each Gaussian component represents a cluster. They were able to show that the resulting clusters exhibited a reasonable correlation to the traditional Hubble classes.
Reducing the parameter space with PCA and also using a mixture-of-Gaussians model are both problematic from our point of view. First, PCA relies on the assumption that those directions in parameter space that carry the desired information also carry a large fraction of the total sample variance. This is neither guaranteed nor can it be tested in practice. Second, galaxy morphologies are not expected to be normally distributed. Therefore, using a mixture-of-Gaussians model is likely to misestimate the data distribution. Nonetheless, the work by Kelly & McKay (2004, 2005) was a landmark, both concerning their use of a probabilistic algorithm and, conceptually, by applying a clustering analysis to the first data release of SDSS.
In contrast to Kelly & McKay (2004, 2005), we do not reduce the dimensionality of the parameter space and then apply a clustering algorithm to the reduced data. We also do not try to model the data distribution in the parameter space, which would be virtually impossible owing to its high dimensionality (curse of dimensionality, cf. Bellman 1961). Rather, we use a similarity matrix, which has two major advantages. First, we do not rely on any compression technique such as PCA. Second, we cannot make any mistakes by choosing a potentially wrong model for the data distribution, since we model the similarity matrix. There are two sources of potential errors in our method:
-
1.
estimation of pairwise similarities (Eq. (6)). Thisis hampered by our lack of knowledge about the metric in themorphological space, and it is in some sense similar tomismodelling;
-
2.
modelling the similarity matrix by a bipartite-graph model. As the only assumption in the derivation of the bipartite-graph model is Eq. (15), this happens if and only if a significant part of the pairwise similarity is not induced by the clusters, but rather by observational effects among others. However, any other classification method (automated or not) will have problems in this situation, too.
5. Systematic tests
In this section we conduct systematic tests using artificial data samples that are specifically designed to investigate the impact of certain effects. First, we demonstrate that hard classification schemes cause problems with subsequent parameter estimation. Furthermore, we investigate the impact of non-optimal similarity measures, two-cluster separation, noise, and cluster cardinalities on the clustering results.
5.1. Overview
We start by describing the artificial data sets that we are going to use. Furthermore, we describe the diagnostics by which we assess the performance of the clustering algorithm. The data sets are always composed of two clusters, where the number of example objects drawn from each cluster may be different. The clusters are always designed as p-variate Gaussian distributions; i.e.,
![\begin{equation} % \prob\left(\vec x|\vec\mu,\mat\Sigma\right) = \frac{\exp\left[ -\frac{1}{2}\left(\vec x-\vec\mu\right)^{\rm T}\cdot\mat\Sigma^{-1}\cdot\left(\vec x-\vec\mu\right) \right]}{\sqrt{\left(2\pi\right)^p\,\det\mat\Sigma}}, \end{equation}](/articles/aa/full_html/2010/14/aa14169-10/aa14169-10-eq125.png) (31)where μ and Σ denote the mean vector and the covariance matrix, respectively.
(31)where μ and Σ denote the mean vector and the covariance matrix, respectively.
By knowing the true analytic form of the underlying probability distributions, we are able to assess the probabilistic data-to-cluster assignments proposed by the clustering algorithm. For two clusters, A and B, the true data-to-cluster assignment of some data point x to cluster k = A,B is given by the cluster posterior
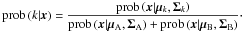 (32)The numerator prob(x | μk,Σk) is the cluster likelihood. The cluster priors
(32)The numerator prob(x | μk,Σk) is the cluster likelihood. The cluster priors 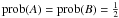 are flat and cancel out. For a given data set of N objects, these true cluster posteriors are compared to the clustering results using the expectation values of the zero-one loss function
are flat and cancel out. For a given data set of N objects, these true cluster posteriors are compared to the clustering results using the expectation values of the zero-one loss function
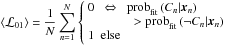 (33)and of the squared-error loss function
(33)and of the squared-error loss function
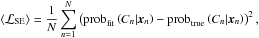 (34)where Cn denotes the correct cluster label of object xn and ¬Cn the false label. The zero-one loss function is the misclassification rate, whereas the squared-error loss function is sensitive to misestimations of the cluster posteriors that do not lead to misclassifications. As the two clusters are usually well separated in most of the following tests, the true maximum cluster posteriors are close to 100%. Therefore, misestimation means underestimation of the maximum posteriors, which is quantified by
(34)where Cn denotes the correct cluster label of object xn and ¬Cn the false label. The zero-one loss function is the misclassification rate, whereas the squared-error loss function is sensitive to misestimations of the cluster posteriors that do not lead to misclassifications. As the two clusters are usually well separated in most of the following tests, the true maximum cluster posteriors are close to 100%. Therefore, misestimation means underestimation of the maximum posteriors, which is quantified by 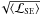 .
.
5.2. Impact of hard cuts on parameter estimation
In this first test, we want to demonstrate that hard cuts that are automatically introduced when using hard classification, or clustering algorithms can lead to systematic misestimations of parameters; i.e., biases. This is a general comment in support of our claim that hard data-to-class assignments are generically inappropriate for overlapping classes. We are not concerned yet with our soft clustering algorithm. We use two one-dimensional Gaussians with means μA and μB, variable two-cluster separation Δx = μA − μB, and constant variance σ2 = 1. We then draw N = 10000 objects from each Gaussian cluster. We estimate the means μ̂k of the two Gaussians from the resulting data sample and compare with the true means μk. The results are averaged over 1000 realisations of data samples.
 |
Fig. 5 Breakdown of hard classifications in case of overlapping clusters. Deviation μ̂A − μA of estimated and true means vs. two-cluster separation Δx for class A for hard estimator (red line), soft estimator (blue line), and predicted bias of hard estimator for Δx → 0 (dashed line). From 1000 realisations of data samples we estimated errorbars, which are shown but too small to be visible. |
 |
Fig. 6 Artificial data sample with six clusters (top) and the matrix of pairwise Euclidean distances (bottom). Each cluster has an underlying bivariate Gaussian distribution with covariance matrix Σ = diag(1,1). We sampled 50 data points from each cluster. |
 |
Fig. 7 Estimating the optimal similarity measure for the example data of Fig. 6. Top panel: modified Manhattan distance C (Eq. (39)) for s = 1.01 (cyan line), s = 1.03 (blue line), and s = 1.1 (red line). For α → 0 the matrix becomes a step matrix, which is why the constant levels depend on the scale parameter. Bottom panel: the resulting similarity matrix. |
Figure 5 shows the deviations of the estimated from the true means when using a hard cut at x = 0 (red line) and a weighted mean (blue line). A hard cut at x = 0 that assigns all data points with x < 0 to class A and those with x > 0 to class B is the most reasonable hard classification in this simple example. Once the complete sample is divided into two subsamples for classes A and B, we estimate the usual arithmetic mean
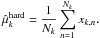 (35)As Fig. 5 shows, this estimator is strongly biased when the clusters are overlapping (Δx → 0). In the limit of Δx = 0, we can predict this bias analytically from the expectation value
(35)As Fig. 5 shows, this estimator is strongly biased when the clusters are overlapping (Δx → 0). In the limit of Δx = 0, we can predict this bias analytically from the expectation value
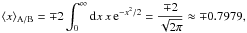 (36)where the integration is only over one half of the parameter space and the factor of 2 arises from both Gaussians contributing the same for Δx = 0. This bias is shown in Fig. 5, where for Δx = 0 also μA / B = ∓ Δx / 2 = 0. If we employ the true posteriors defined by Eq. (32) as weights and use
(36)where the integration is only over one half of the parameter space and the factor of 2 arises from both Gaussians contributing the same for Δx = 0. This bias is shown in Fig. 5, where for Δx = 0 also μA / B = ∓ Δx / 2 = 0. If we employ the true posteriors defined by Eq. (32) as weights and use
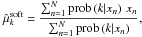 (37)then we get an unbiased estimate despite the overlap, as is evident from Fig. 5. This comparison demonstrates the breakdown of hard algorithms for overlapping clusters.
(37)then we get an unbiased estimate despite the overlap, as is evident from Fig. 5. This comparison demonstrates the breakdown of hard algorithms for overlapping clusters.
5.3. Impact of non-optimal similarity measures
We now explain how to optimise the similarity measure defined in Eq. (6) and what “optimal” means. Given the N × N symmetric matrix of pairwise distances d(xm,xn), we can tune the similarity measure by adjusting the two parameters α and s. Tuning the similarity measure has to be done with care, since there are two undesired cases: first, for α → ∞, the resulting similarity matrix approaches a constant; i.e., 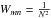 for all elements – self-similarities and off-diagonal elements – since d(xm,xn) ≤ dmax. This case prefers K = 1 clusters, independent of any grouping in the data. Second, for α → 0, the similarity matrix approaches the step matrix defined by
for all elements – self-similarities and off-diagonal elements – since d(xm,xn) ≤ dmax. This case prefers K = 1 clusters, independent of any grouping in the data. Second, for α → 0, the similarity matrix approaches the step matrix defined by
 (38)which is normalised such that
(38)which is normalised such that  . The self-similarities differ from the off-diagonal elements due to d(xm,xm) = 0. This case prefers K = N clusters. The optimal similarity measure should be as different as possible from these two worst cases. We choose α and s such that the modified Manhattan distance to the constant matrix
. The self-similarities differ from the off-diagonal elements due to d(xm,xm) = 0. This case prefers K = N clusters. The optimal similarity measure should be as different as possible from these two worst cases. We choose α and s such that the modified Manhattan distance to the constant matrix
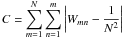 (39)is large. Figure 7 demonstrates how to tune the similarity measure using the artificial data set from the toy example of Fig. 6. The basis is the N × N symmetric distance matrix shown in the bottom panel of Fig. 6. For three different values of s, the top panel shows C as functions of α. Obviously, C(α) exhibits a maximum and can be used to choose α. For s = 1.1 the maximum is lowest and so is the distance to a constant matrix. s = 1.01 exhibits the maximum deviation from a constant matrix, but this choice of s downweights off-diagonal terms in W according to Eq. (38). Thus, we also prefer that s is not too close to 1 and s = 1.03 is the compromise of the three scale parameters shown in Fig. 7. The choice of s is not an optimisation but a heuristic. Although the artificial data set of Fig. 6 and its distance matrix are very special, we experienced that C(α) as shown in Fig. 7 is representative of the general case.
(39)is large. Figure 7 demonstrates how to tune the similarity measure using the artificial data set from the toy example of Fig. 6. The basis is the N × N symmetric distance matrix shown in the bottom panel of Fig. 6. For three different values of s, the top panel shows C as functions of α. Obviously, C(α) exhibits a maximum and can be used to choose α. For s = 1.1 the maximum is lowest and so is the distance to a constant matrix. s = 1.01 exhibits the maximum deviation from a constant matrix, but this choice of s downweights off-diagonal terms in W according to Eq. (38). Thus, we also prefer that s is not too close to 1 and s = 1.03 is the compromise of the three scale parameters shown in Fig. 7. The choice of s is not an optimisation but a heuristic. Although the artificial data set of Fig. 6 and its distance matrix are very special, we experienced that C(α) as shown in Fig. 7 is representative of the general case.
The resulting similarity matrix is shown in the right panel of Fig. 7 and exhibits a block-like structure, since we have ordered the data points in the set. This is just for the sake of visualisation and does not affect the clustering results. We clearly recognise six blocks along the diagonal, because the within-cluster similarities are always greater than the between-cluster similarities. Furthermore, we recognise a large block of four clusters in the bottom right corner that are quite similar to each other, whereas the remaining two clusters are more or less equally dissimilar to all other clusters. Consequently, the similarity matrix indeed represents all the features of the data set shown in Fig. 6.
We now demonstrate first that the optimal similarity measure indeed captures the crucial information on the data and second what happens if we do not use the optimal similarity measure. We used an artificial data set composed of two one-dimensional Gaussian clusters, both with unit variance and two-cluster separation of Δx = 3. We sampled 100 example objects from each cluster and computed the matrix of pairwise distances using the Euclidean distance measure. This data set and its distance matrix remain unchanged. For a constant parameter s = 2.25, we varied the exponent α in the similarity measure defined by Eq. (6). For each value of α, we fit bipartite-graph models with K = 1, 2 and 3 to the resulting similarity matrix, averaging the results over 15 fits each time.
Results of this test are shown in Fig. 8. Panel (a) shows the modified Manhattan distance C to a constant matrix. This curve is very similar to Fig. 7. There is a prominent peak at α ≈ 0.6, indicating the optimal similarity measure. If the similarity measure is very nonoptimal, then the similarity matrix will be close to a constant or step matrix; i.e., it constrains the bipartite-graph model poorly. In this case, we expect to observe overfitting effects; i.e., low residuals of the reconstruction and results with high variance. The computation times are longer, too, since the nonlinear model parameters can exhibit degeneracies thereby slowing down the convergence. Counter-intuitively, we seek a high value of SSR in this test, since a similarity matrix that captures the information content of the data is harder to fit. Indeed, the SSR values shown in panel (c) of Fig. 8 are significantly lower for nonoptimal α’s, and they peak near the optimal α. As expected, the mean computation times shown in panel (b) are minimal for the optimal similarity measure. Panel (d) shows how the evidence for two clusters evolves2. Near optimal α, the evidence of two clusters also shows a local maximum. The misclassification rate shown in panel (e) is insensitive to α over a broad range, but approaches a rate of 50% rather abruptly for extremely non-optimal similarity measures. The squared-error loss shown in panel (f) is more sensitive to non-optimalities. It exhibits a minimum for the optimal α and grows monotonically for non-optimal values.
 |
Fig. 8 Impact of non-optimal similarity measures on clustering results. a) Modified Manhattan distance C (Eq. (39)). b) Mean computation time per fit without errorbars. c) Mean SSR(K) values of resulting fits for K = 2. d) Mean angular change of SSR(K) at K = 2. e) Mean misclassification rate (solid line) and 50% misclassification rate (dashed line). f) Mean squared-error loss of maximum cluster posteriors. |
The most important conclusion to draw from this test is that our method of choosing α and s for the similarity measure defined in Sect. 4.1 is indeed “optimal”, in the sense that it minimises both the misclassification rate and the squared-error loss. Additionally, we see that using the optimal similarity measure can also reduce computation times by orders of magnitude.
5.4. Impact of two-cluster overlap
As we have to expect overlapping clusters in the context of galaxy morphologies, we now investigate the impact of the two-cluster overlap on the clustering results. The data sets used are always composed of 100 example objects drawn from two one-dimensional Gaussian clusters, both with unit variance. The two-cluster separation Δx is varied from 1 to 1000. For each data set, we compute the matrix of pairwise Euclidean distances and then automatically compute the optimal similarity matrix by optimising α using a constant s = 2.25 as described in Sect. 5.3. To each similarity matrix we fit bipartite-graph models with K = 1, 2, and 3 clusters. Furthermore, we fit a K-means algorithm with K = 1, 2, and 3 to each data set in order to compare the results of both clustering algorithms. For each configuration, the results are averaged over 50 fits.
Results of this test are summarised in Fig. 9. Panel (a) shows the mean evidence of two clusters, based on the angular changes in SSR(K) for the bipartite-graph model and the within-cluster scatter for the K-means algorithm. For decreasing separation Δx; i.e., increasing overlap, this evidence decreases for both algorithms, as is to be expected3. As panel (b) reveals, the misclassification rates for K-means and the bipartite-graph model both agree with the theoretical misclassification rate expected in the ideal case. For two one-dimensional Gaussians with means 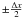 , the theoretical misclassification rate is given by
, the theoretical misclassification rate is given by
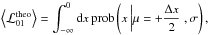 (40)which measures the overlap of both Gaussians. In the limit Δx = 0, this yields
(40)which measures the overlap of both Gaussians. In the limit Δx = 0, this yields 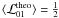 . The explanation for the excellent performance of both K-means and bipartite-graph model is that in this case the clusters have equal numbers of member objects (cf. Sect. 5.6) and are spherical. Nevertheless, the results of the K-means are biased by the hard data-to-cluster assignment. Panel (c) of Fig. 9 shows the mean squared-error loss of the bipartite-graph models4. First, the general trend is that the squared-error loss increases for decreasing two-cluster separation. This comes from the growing amount of overlap that confuses the bipartite-graph model. Second, the squared-error loss decreases significantly for Δx ≲
4. This effect can be explained as follows. For very small separations, the overlap is so strong that even the true cluster posteriors are both close to 50%. Therefore, the fitted cluster posteriors scatter around 50%, too, thereby reducing the squared error. Third, the squared error establishes a constant value of 〈 ℒSE 〉 ≈ 0.045 at large separations. In this case, the true maximum cluster posteriors are essentially 100%, so this corresponds to a systematic underestimation of the maximum posteriors of
. The explanation for the excellent performance of both K-means and bipartite-graph model is that in this case the clusters have equal numbers of member objects (cf. Sect. 5.6) and are spherical. Nevertheless, the results of the K-means are biased by the hard data-to-cluster assignment. Panel (c) of Fig. 9 shows the mean squared-error loss of the bipartite-graph models4. First, the general trend is that the squared-error loss increases for decreasing two-cluster separation. This comes from the growing amount of overlap that confuses the bipartite-graph model. Second, the squared-error loss decreases significantly for Δx ≲
4. This effect can be explained as follows. For very small separations, the overlap is so strong that even the true cluster posteriors are both close to 50%. Therefore, the fitted cluster posteriors scatter around 50%, too, thereby reducing the squared error. Third, the squared error establishes a constant value of 〈 ℒSE 〉 ≈ 0.045 at large separations. In this case, the true maximum cluster posteriors are essentially 100%, so this corresponds to a systematic underestimation of the maximum posteriors of 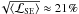 . Thanks to the large two-cluster separation, this bias does not lead to misclassifications, as is evident from panel (b) in Fig. 9. This bias originates from the fact that any two objects have a finite distance and thus a non-vanishing similarity.
. Thanks to the large two-cluster separation, this bias does not lead to misclassifications, as is evident from panel (b) in Fig. 9. This bias originates from the fact that any two objects have a finite distance and thus a non-vanishing similarity.
 |
Fig. 9 Impact of two-cluster overlap on clustering results for K-means algorithm and bipartite-graph model. a) Mean angular change of SSR(K) (bipartite-graph model) and within-cluster scatter (K-means) at K = 2. b) Mean misclassification rates of K-means and bipartite-graph model (see text) compared to theoretical prediction. All curves coincide. c) Mean squared-error loss of bipartite-graph model. |
This test further demonstrates that the bipartite-graph model yields convincing results. This is the most evident in the misclassification rate, which is in excellent agreement with the theoretical prediction of the best possible score.
5.5. Impact of noise
As observational data is subject to noise, we now investigate the response of the clustering results to noise on the similarity matrix. We simulate the noise by adding a second dimension y to the data. The two clusters are bivariate Gaussian distributions, both with 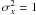 and two-cluster separation of Δx = 10 and Δy = 0. We vary the size of the variance in y-direction ranging from
and two-cluster separation of Δx = 10 and Δy = 0. We vary the size of the variance in y-direction ranging from 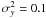 to 10 000, thereby introducing noise that translates via the Euclidean distance to the similarity matrix. From each cluster 100 example objects are drawn and we fit bipartite-graph and K-means models using K = 1, 2 and 3. The results are averaged over 50 fits for each value of
to 10 000, thereby introducing noise that translates via the Euclidean distance to the similarity matrix. From each cluster 100 example objects are drawn and we fit bipartite-graph and K-means models using K = 1, 2 and 3. The results are averaged over 50 fits for each value of 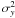 .
.
Results of this test are shown in Fig. 10. The evidence of two clusters (panel (a)) rapidly degrades for increasing variance for the bipartite-graph model, as well as for the K-means algorithm, as is to be expected. Inspecting the misclassification rate (panel (b)) reveals that both algorithms are insensitive to 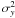 until a critical variance is reached where both misclassification rates increase abruptly. For the K-means algorithm, this breakdown happens at
until a critical variance is reached where both misclassification rates increase abruptly. For the K-means algorithm, this breakdown happens at 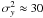 , whereas the bipartite-graph model breaks down at
, whereas the bipartite-graph model breaks down at 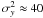 , which amounts to
, which amounts to 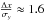 in this setup. The evidence of two clusters (panel (a)) rises again for larger variances, although both algorithms have already broken down. This is a geometric effect, because with increasing
in this setup. The evidence of two clusters (panel (a)) rises again for larger variances, although both algorithms have already broken down. This is a geometric effect, because with increasing 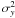 , the two clusters become more extended in the y-direction, until it is better to split the data along x = 0 rather than y = 0. This also explains why the misclassification rate is 50% in this regime. Consequently, the abrupt breakdown originates in the setup of this test. Sampling more objects from each cluster might have prevented this effect, but would have increased the computational effort drastically. Moreover, this demonstrates that isotropic distance measures are problematic. Using, e.g., a diffusion distance (e.g. Richards et al. 2009) may solve this problem. The breakdown is less abrupt in the mean squared-error loss (panel (c)), since 〈 ℒSE 〉 is also sensitive to posterior misestimation that do not lead to misclassifications.
, the two clusters become more extended in the y-direction, until it is better to split the data along x = 0 rather than y = 0. This also explains why the misclassification rate is 50% in this regime. Consequently, the abrupt breakdown originates in the setup of this test. Sampling more objects from each cluster might have prevented this effect, but would have increased the computational effort drastically. Moreover, this demonstrates that isotropic distance measures are problematic. Using, e.g., a diffusion distance (e.g. Richards et al. 2009) may solve this problem. The breakdown is less abrupt in the mean squared-error loss (panel (c)), since 〈 ℒSE 〉 is also sensitive to posterior misestimation that do not lead to misclassifications.
 |
Fig. 10 Impact of noise variance |
We conclude that the bipartite-graph model is fairly insensitive to noise of this kind over a broad range, until the setup of this test breaks down.
5.6. Impact of cluster cardinalities
Typically different types of galaxy morphologies have different abundancies in a given data sample. For instance, Bamford et al. (2009) observe different type fractions of early-type and spiral galaxies in the Galaxy Zoo project. Therefore, we now investigate how many objects of a certain kind are needed in order to detect them as a cluster. The concept of a number of objects being members of a certain cluster is poorly defined in the context of soft clustering. We generalise this concept by defining the cardinality of a cluster ck
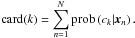 (41)This definition satisfies
(41)This definition satisfies 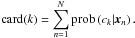 , since the cluster posteriors are normalised. In the case of hard clustering, Eq. (41) is reduced to simple number counts, where the cluster posteriors become Kronecker symbols. We use two clusters, both one-dimensional Gaussians with unit variance and a fixed two-cluster separation of Δx = 10. We then vary the number of objects drawn from each cluster such that the resulting data set always contains 200 objects. For each data set, we compute two different similarity matrices: First, we compute the similarity matrix using the optimal α for a constant s = 2.0, according to the recipe given in Sect. 5.3. This similarity measure is adapted to every data set (adaptive similarity measure). Second, we compute the similarity matrix using α = 0.6 and s = 2.0, which is the optimal similarity measure for the data set composed to equal parts of objects from both clusters. This similarity measure is the same for all data sets (constant similarity measure). To each of the two similarity matrices we fit a bipartite-graph model using K = 2 and average the results over 50 fits.
, since the cluster posteriors are normalised. In the case of hard clustering, Eq. (41) is reduced to simple number counts, where the cluster posteriors become Kronecker symbols. We use two clusters, both one-dimensional Gaussians with unit variance and a fixed two-cluster separation of Δx = 10. We then vary the number of objects drawn from each cluster such that the resulting data set always contains 200 objects. For each data set, we compute two different similarity matrices: First, we compute the similarity matrix using the optimal α for a constant s = 2.0, according to the recipe given in Sect. 5.3. This similarity measure is adapted to every data set (adaptive similarity measure). Second, we compute the similarity matrix using α = 0.6 and s = 2.0, which is the optimal similarity measure for the data set composed to equal parts of objects from both clusters. This similarity measure is the same for all data sets (constant similarity measure). To each of the two similarity matrices we fit a bipartite-graph model using K = 2 and average the results over 50 fits.
 |
Fig. 11 Impact of cardinalities on clustering results. a) Mean misclassification rate. b) Mean squared-error loss. c) Correlation of estimated and true cluster cardinality. |
The results are summarised in Fig. 11. Panel (a) shows the dependence of the misclassification rate on the cardinality of cluster A. For the adaptive similarity measure the bipartite-graph model will break down, if one cluster contributes less than 10% to the data set. For the constant similarity measure it will break down, if one cluster contributes less than 3%. The same behaviour is evident from the squared-error loss in panel (b). This problem is caused by the larger group in the data set dominating the statistics of the modified Manhattan distance C defined by Eq. (39). This is a failure of the similarity measure, not of the bipartite-graph model. The constant similarity measure stays “focussed” on the difference between the two clusters and its breakdown at 3% signals the limit where clusters are detectable with the bipartite-graph model.
Panel (c) in Fig. 11 shows the correlation of the measured cluster cardinality to the true cluster cardinality. For the constant similarity measure, both quantities correlate well. In contrast to this, the two quantities do not correlate at all for the adaptive similarity measure. Again, the adaptive similarity measure is dominated by the larger group; i.e., the similarities between the large and the small groups are systematically too high. This leads to systematic underestimation of the maximum cluster posteriors (cf. panel (b)), since for a two-cluster separation of Δx = 10 the true posteriors are essentially 100% as shown by Fig. 9c. This also affects the cluster cardinalities defined by Eq. (41). If the cluster overlap is stronger, then this bias is likely to lead to misclassifications, too.
We conclude that the optimal similarity measure defined in Sect. 5.3 fails to discover groups that contribute 10% or less to the complete data sample. A different similarity measure may solve this problem, but the optimal similarity measure has the advantage of minimising the misclassification rate and the squared-error loss for the discovered groups.
6. Worked example with SDSS galaxies
In this section we present our worked example with SDSS galaxies. First, we describe the sample of galaxies we analyse. Before applying the bipartite-graph model to the whole sample, we apply it to a small subsample of visually classified galaxies to prove that it is working not only for simple simulated data but also for real galaxy morphologies. Again, we emphasise that this is just meant as a demonstration, so parametrisation and sample selection are idealised.
6.1. The data sample by Fukugita et al. (2007)
Fukugita et al. (2007) derived a catalogue of 2253 bright galaxies with Petrosian magnitude in the r band brighter than rP = 16 from the Third Data Release of the SDSS (Abazajian et al. 2005). Furthermore, the authors provide a visual classification of galaxy morphologies based on g-band imaging, which is sensitive to HII regions and spiral arm structures. Therefore, we also analysed only g-band imaging of this sample. We expect that objects that are bright in r are also bright in the neighbouring g-band. Therefore, all these objects have a high signal-to-noise ratio; i.e., the shapelet decomposition can employ a maximum order large enough to reduce possible modelling problems.
Apart from the g-band imaging data, we also retrieved further morphological information from the SDSS database, namely Petrosian radii r50 and r90 containing 50% and 90% of the Petrosian flux, ratios of isophotal semi major and semi minor axes, and the logarithmic likelihoods of best-fitting de Vaucouleurs and exponential-disc profiles. Given the Petrosian radii r50 and r90 containing 50% and 90% of the Petrosian flux, we define the concentration index in analogy to Conselice (2003),
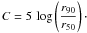 (42)For compact objects, such as elliptical galaxies, this concentration index is high, whereas it is lower for extended objects with slowly decreasing light profiles, such as disc galaxies.
(42)For compact objects, such as elliptical galaxies, this concentration index is high, whereas it is lower for extended objects with slowly decreasing light profiles, such as disc galaxies.
We then reduced the data sample in three steps, First, we sorted out peculiar objects; i.e., objects that are definitely not galaxies, blended objects, and objects that were cut in the mosaic. All these objects have no viable galaxy morphologies. This was done by visual inspection of all objects. Second, we decomposed all images into shapelets using the same maximum order Nmax = 12 (91 expansion coefficients) for all objects. The shapelet code performs several internal data processing steps, such as estimating the background noise and subtracting the potentially non-zero noise mean, image segmentation, and masking of multiple objects, estimating the object’s centroid position (cf. Melchior et al. 2007). Third, we sorted out objects for which the shapelet reconstruction does not provide reasonable models. This is done by discarding all objects whose best fits have a reduced χ2 that is not in the interval [0.9,2.0] . The lower limit is chosen very close to unity, since shapelets have the tendency to creep into the background noise and overfit objects. Setting out from the 2253 bright galaxies of Fukugita et al. (2007), the data processing leaves us with 1520 objects with acceptable χ2. We check that the morphological information contained in the original data set and the reduced data set does not differ systematically, by comparing the sample distributions of Petrosian radii, axis ratios, concentration indeces, and logarithmic likelihoods of best-fitting deVaucouleur and exponential-disc profiles. All objects are large compared to the point-spread function (PSF) of SDSS, such that a PSF deconvolution as described in Melchior et al. (2009) is not necessary. This means we analyse apparent instead of intrinsic morphologies, but both are approximately the same.
6.2. Demonstration with three clusters
In this section we apply the soft clustering algorithm by Yu et al. (2005) for the first time to real galaxies. We used a small data set of 84 galaxies, which we visually classified as edge-on disc, face-on disc or ellipticals (28 objects per type). As these 84 galaxies were very large and very bright, we decomposed them anew using a maximum order of Nmax = 16, resulting in 153 shapelet coefficients per object. Figure 1 shows one example object and its shapelet reconstruction for each type. This data set exhibits a strong grouping, and we demonstrate that the bipartite-graph model indeed discovers the edge-on discs, face-on discs, and ellipticals automatically, without any further assumptions.
The estimation of the number of clusters is shown in Fig. 12. The mean angular changes in SSR(K) averaged over 20 fits indeed reveal only one significant kink at K = 3. The lowest value of SSR at K = 3 is SSR ≈ 48, which corresponds to an rms residual (cf. Eq. (29)) of
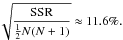 (43)The denominator
(43)The denominator 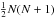 is the number of independent elements in the symmetric similarity matrix.
is the number of independent elements in the symmetric similarity matrix.
 |
Fig. 12 Mean angular changes 〈 Δ(K) 〉 of bipartite-graph model for data set composed of edge-on discs, face-on discs, and ellipticals. |
We conclude from Fig. 12 that the bipartite-graph model indeed favours three clusters. However, we still have to prove that the similarity matrix contains enough information on the data and that the bipartite-graph model discovers the correct classes. For K = 3, the cluster posteriors populate a two-dimensional plane because they are subject to a normalisation constraint. This plane is shown in Fig. 13. Indeed, the distribution of cluster posteriors exhibits an excellent grouping of ellipticals, edge-on discs, and face-on discs. The three clusters are well separated, apart from two objects labelled as edge-on discs but assigned to the cluster of ellipticals. A second visual inspection of these two “outliers” revealed that we had initially misclassified them as edge-on disc. The excellent results are particularly impressive if we remember that we analysed 84 data points distributed in a 153-dimensional parameter space. Moreover, it is very encouraging that the soft clustering analysis did indeed recover the ellipticals, face-on and edge-on discs automatically.
 |
Fig. 13 Cluster posterior space of bipartite-graph model for edge-on discs, face-on discs, and ellipticals. The triangle defines the subspace allowed by the normalisation constraint of the posteriors. The corners of the triangle mark the points of 100% posterior probability. The * indicates the point where all three posteriors are equal. Colours encode a priori classifications unknown to the algorithm. |
In order to get an impression of how good these results actually are, we compare the cluster posterior plane to results obtained from PCA; therefore, we estimate the covariance matrix Σ of the data sample in shapelet-coefficient space and diagonalise it. Only the first 83 eigenvalues of Σ are non-zero, since the 84 data objects poorly constrain the 153 × 153 covariance matrix. The first two principal components carry 66.6% of the total sample variance, and Fig. 14 displays the parameter space spanned by them. Obviously, PCA performs well in reducing the parameter space from 153 dimensions down to two, since the ellipticals, face-on, and edge-on discs exhibit a good grouping5. However, the bipartite-graph model provides much more compact and well-separated groups. This is due to the degeneracies we have broken when we computed the minimal spherical distances as described in Sect. 3. In the case of PCA, these degeneracies are unbroken and introduce additional scatter.
 |
Fig. 14 Comparing Fig. 13 with results of PCA for edge-on discs, face-on discs, and ellipticals. The parameter space is spanned by the first two principal components. The first principal component carries ≈ 45.2% and the second ≈ 21.4% of the total variance. Colours encode a priori classifications unknown to the PCA algorithm. |
In both Figs. 13 and 14, we notice that the group of ellipticals is significantly more compact than the groups of face-on and edge-on discs. This is caused by three effects. First, as discussed in Sect. 3, our parametrisation of elliptical galaxies is problematic, thereby introducing common artefacts for all objects of this type. These common features are then picked up by the soft clustering algorithm. Ironically, the problems of the parametrisation help to discriminate the types in this case. Second, we described in Sect. 3 how to make our morphological distance measure invariant against various random quantities, namely image size, image flux, orientation angle, and handedness. However, the distance measure and thus the similarity measure are not invariant against the inclination angle with respect to the line of sight, which introduces additional scatter into the clustering results. We expect that the impact of this random effect is less for ellipticals than for disc galaxies. Third, disc galaxies usually exhibit complex substructures (e.g. spiral arms or star-forming regions), whereas elliptical galaxies do not. Consequently, the intrinsic morphological scatter of disc galaxies is larger than for ellipticals.
6.3. Analysing the data set of Fukugita et al. (2007)
We now present the soft clustering results from analysing all 1520 bright galaxies from the reduced data set of Fukugita et al. (2007). We have chosen the similarity measure with s = 1.02 and corresponding optimal α ≈ 0.12, according to Sect. 5.3. The shapes of the curves of the modified Manhattan distances C(α) have the same generic form as before. Fit results of the similarity matrix for K ranging from 1 to 20 are shown in Table 2 and Fig. 15. There are significant deviations of the mean angular changes from zero for K = 3 and K = 8. The signal at K = 2 is ignored, since the SSR value is very high (cf. Table 2).
 |
Fig. 15 Estimating the number of clusters in the data set of Fukugita et al. (2007). Mean angular changes 〈 Δ(K) 〉 are averaged over 15 Fits. |
Fitting the similarity matrix of 1520 objects, with the minimal SSR value out of 15 fits and the mean angular change averaged over 15 fits.
First, we investigate the clustering results for K = 3, where we have SSR ≈ 6146 (cf. Table 2) corresponding to an rms residual of ≈ 3.7% (cf. Eq. (43)) for the similarity-matrix reconstruction. In Fig. 17 we show the top five example objects for each of the three clusters, together with a histogram of the distribution of cluster posteriors. Inspecting the example images, we clearly see that the first cluster is obviously composed of face-on disc galaxies, whereas the second cluster contains ellipticals. The third cluster is the cluster of edge-on disc galaxies or discs with high inclination angles. However, a blended object has been misclassified into this cluster, too. There are still some blended objects left that we have failed to remove, since when sorting out blended objects we visually inspected the images in reduced resolution. The cluster posteriors for K = 3 are very informative, because we first notice that objects from cluster 1 typically have very low posteriors in cluster 2 and intermediate posteriors in cluster 3; i.e., face-on discs are more similar to edge-on discs than to ellipticals. Second, objects from cluster 2 have low posteriors in all other clusters. Third, objects from cluster 3 tend to be more alike to objects in cluster 2; i.e., edge-on discs are closer to ellipticals. This is probably caused by the higher light concentration and steep light profiles. To improve our understanding of the clustering results, we compared the data-to-cluster assignments to the visual classification of Fukugita et al. (2007). The authors classified all galaxies into the types elliptical (E), S0, Sa, Sb, Sc, Sd, Im, and “unclassified” (uncl.), ignoring the difference between barred and unbarred galaxies. Results are shown in panel (a) of Fig. 16. Obviously, there are trends when moving from type E to Im: first, the fraction of objects assigned to cluster 2 decreases substantially, since we are moving from compact to loose objects. Second, the fraction of objects assigned to cluster 3 increases substantially, since elliptical galaxies usually do not exhibit pronounced elongations. Third, there is a minor increase in the fraction of objects assigned to cluster 1, which may be due to an increase in substructure while smoothness is decreasing. Apart from that, there are no obvious correlations of the results obtained from both classification schemes. We conclude that both methods roughly agree. A more detailed comparison – e.g. estimating the misclassification rate of one method with respect to the other – is conceptually impossible since both schemes use different classes, while the “truth” remains uncertain. Such a comparison would require a simulation where the “true” galaxy morphologies are known.
 |
Fig. 16 Comparing the data-to-cluster assignments for K = 3 clusters (panel a) and K = 8 clusters (panel b) to visual classifications. We show how the Fukugita types distribute over the automatically identified clusters. The cluster’s posterior distributions are estimated by summing the posteriors of all objects of this Fukugita type. |
These results demonstrate that the clustering analysis indeed yields reasonable results for realistic data sets. Furthermore, the results for three clusters are very similar to the clustering scheme of Sect. 6.2. However, three clusters are not enough to describe the data faithfully. This is evident from the much higher SSR value for K = 3 compared to K = 8 and from Fig. 18, where we show the resulting cluster posterior space for K = 3. Large parts of the available posterior space remain empty, whereas the central region is crowded. This behaviour stems from to the lack of complexity in the bipartite-graph model and strongly suggests that more clusters are necessary.
 |
Fig. 17 Top example objects for K = 3 clusters. Each row corresponds to a cluster. We also show the distribution of its cluster posteriors beneath each object. Cluster 1 seems to contain face-on discs, cluster 2 compact objects, and cluster 3 edge-on discs. |
 |
Fig. 18 Cluster posterior space for K = 3. See Fig. 13 for an explanation of the topology of this plot. |
 |
Fig. 19 Top example objects for K = 8 clusters. Each row corresponds to a cluster. For each object, we also show the histogram of the distribution of its cluster posteriors beneath it. The objects were aligned in shapelet space, not in real space. |
For K = 8 we have SSR ≈ 2254 (cf. Table 2), which corresponds to an rms residual of ≈ 2.2% for the similarity-matrix reconstruction. We show ten top example objects for each cluster in Fig. 19. First, we notice that the resulting grouping is excellent. However, it is difficult to understand the differences between some clusters. Clusters 1 and 5 are obviously objects with high ellipticities, e.g. edge-on discs, but what is the difference? Is it the bulge dominance, which is much weaker in cluster 1 than in 5? Do the clusters differ in their radial light profiles? What is the difference between clusters 2 and 7, which are both face-on discs? Of particular interest are clusters 3 and 8, where both seem to contain roundish and compact objects. However, the posterior histograms reveal a highly asymmetric relation, where objects from cluster 3 also prefer cluster 8 above all other clusters. Nevertheless, most of the top examples of cluster 8 have extremely low posteriors in cluster 3; i.e., association with cluster 3 is highly disfavoured. Although we cannot explain this result without further investigation, it is interesting that the algorithm picked up such a distinctive signal. In panel (b) of Fig. 16 we compare the data-to-cluster assignments to the visual classification of Fukugita et al. (2007). Again, there are trends when moving from types E to Im. Clusters 1 and 7 clearly prefer spiral galaxies, whereas clusters 3 and 8 prefer smooth and compact objects. Cluster 2 slightly prefers Fukugita types Sb, Sc, Sd, whereas cluster 4 does not. Irregular and unclassified objects clearly favour clusters of looser objects over clusters of smooth and compact objects. Interestingly, all curves meet at type Sa, which implies that certain features that are important for the clustering cancel out. This confirms our understanding of the clustering results being a sequence of smoothness and compactness, since Sa galaxies are the first in the sequence E, S0, Sa, Sb, Sc, Sd, Im that exhibit substructures, thereby becoming loose and less compact. We conclude that both methods also agree roughly for K = 8 clusters, though the clustering results appear to pick up more details.
As we have access to the isophotal axis ratio and the concentration index (cf. Eq. (42)) for all objects, we investigate their distributions for the clusters. Figure 20 shows the mean axis ratios and the mean concentration indices for all eight clusters averaged over the 100 top examples. The cluster with the highest mean axis ratio is cluster 1, which is the cluster of edge-on disc galaxies. The cluster with lowest concentration index is cluster 7, which is the cluster of face-on disc galaxies that exhibit extended smooth light profiles. Clusters 3, 4, 5, and 8 have the highest concentration indices. As is evident from Fig. 19, these clusters are indeed composed of rather compact objects that seem to be elliptical galaxies. However, there is no decisive distinction in Fig. 20. This is not necessarily a flaw in the clustering results, but more likely caused by concentration and axis ratio being an insufficient parametrisation scheme (cf. Andrae et al., in prep.).
 |
Fig. 20 Mean axis ratios and concentration indices for the clusters of Fig. 19. Weighted means were computed from the top 100 example objects of each cluster. We show the contours of 1σ and take possible correlations into account. |
It seems like the resulting classification scheme is essentially face-on disc, edge-on disc, and elliptical. If we increase the number of clusters, we get further diversification that may be caused by bulge dominance or inclination angles. We emphasise again that our primary goal is to demonstrate that our method discovers morphological classes and provides data-to-class assignments that are reasonable.
7. Conclusions
We briefly summarise our most important arguments and results.
-
Galaxy evolution, the process of observation, and theexperience with previous classification attempts stronglysuggest a probabilistic (“soft”) classification. Hardclassifications appear to be generically inappropriate.
-
There are two distance-based soft clustering algorithms that have been applied to galaxy morphologies so far: Gaussian mixture models by Kelly & McKay (2004, 2005) and the bipartite-graph model by Yu et al. (2005) presented in this work. The weak points of the Gaussian mixture model are the dimensionality reduction and its assumption of Gaussianity. The weakness of the bipartite-graph model is the definition of the similarity measure.
-
The shapelet formalism, our similarity measure, and the bipartite-graph model produce reasonable clusters and data-to-cluster assignments for real galaxies. The automated discovery of classes corresponding to face-on discs, edge-on discs, and elliptical galaxies without any prior assumptions is impressive and demonstrates the great potential of clustering analysis. Moreover, the automatically discovered classes have a qualitatively different meaning compared to pre-defined classes, since they represent grouping that is preferred by the given data sample itself.
-
Random effects, such as orientation angle and inclination, are a major obstacle, since they introduce additional scatter into a parametrisation of galaxy morphologies.
-
For data sets containing N galaxies, the computation times scale as 𝒪(N2). Nevertheless, we experienced that a clustering analysis is feasible for data sets containing up to N = 10000 galaxies without employing supercomputers. We conclude that a clustering analysis on a data set of one million galaxies is possible using supercomputers.
-
It is possible to enhance this method by setting up a classifier based on the classes found by the soft clustering analysis, thereby improving the time complexity from 𝒪(N2) to 𝒪(N).
-
The method presented in this paper is not limited to galaxy morphologies alone. For instance, it could possibly be applied to automated star-galaxy classification or AGN detection.
The bottom line of this paper is that automatic discovery of morphological classes and object-to-class assignments (clustering analysis) does work and is less prejudiced and time-consuming than visual classifications, though interpreting the results is still an open issue. Especially when analysing new data samples for the first time, clustering algorithms are more objective than using pre-defined classes and visual classifications. The advantages of such a sophisticated statistical algorithm justify its considerable complexity.
Acknowledgments
R.A. thanks Coryn Bailer-Jones for his comments that have been particularly useful for improving this work. Furthermore, R.A. thanks Knud Jahnke and Eric Bell for helpful discussions especially of the interpretation of the results. We also thank the anonymous referee for the constructive criticism. R.A. is funded by a Klaus-Tschira scholarship. P.M. is supported by the DFG Priority Programme 1177.
References
- Abazajian, K., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2005, AJ, 129, 1755 [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, N. M., Loveday, J., Fukugita, M., et al. 2004, MNRAS, 348, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Bamford, S. P., Nichol, R. C., Baldry, I. K., et al. 2009, MNRAS, 393, 1324 [NASA ADS] [CrossRef] [Google Scholar]
- Banerji, M., Lahav, O., Lintott, C. J., et al. 2010, MNRAS, 663 [Google Scholar]
- Bellman, R. 1961, Adaptive Control Processes: A Guided Tour (Princeton University Press) [Google Scholar]
- Bilmes, J. A. 1997, International Computer Science Institute, Technical Report TR-97-021 [Google Scholar]
- Conselice, C. J. 2003, The Relationship between Stellar Light Distributions of Galaxies and Their Formation Histories [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Nakamura, O., Okamura, S., et al. 2007, AJ, 134, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Gauci, A., Zarb Adami, K., Abela, J., & Magro, A. 2010, [arXiv:1005.0390] [Google Scholar]
- Huertas-Company, M., Rouan, D., Tasca, L., Soucail, G., & Le Fèvre, O. 2008, A&A, 478, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huertas-Company, M., Tasca, L., Rouan, D., et al. 2009, A&A, 497, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Humphreys, R. M., Karypis, G., Hasan, M., Kriessler, J., & Odewahn, S. C. 2001, in BAAS, 33, 1322 [Google Scholar]
- Kelly, B. C., & McKay, T. A. 2004, AJ, 127, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C., & McKay, T. A. 2005, AJ, 129, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O., Naim, A., Buta, R. J., et al. 1995, Science, 267, 859 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lahav, O., Naim, A., Sodré, Jr., L., & Storrie-Lombardi, M. C. 1996, MNRAS, 283, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, R., & Réfrégier, A. 2005, MNRAS, 363, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Melchior, P., Meneghetti, M., & Bartelmann, M. 2007, A&A, 463, 1215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melchior, P., Andrae, R., Maturi, M., & Bartelmann, M. 2009, A&A, 493, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melchior, P., Böhnert, A., Lombardi, M., & Bartelmann, M. 2010, A&A, 510, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naim, A., Ratnatunga, K. U., & Griffiths, R. E. 1997, ApJS, 111, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Redner, R., & Walker, H. 1984, SIAM Rev., 26, 195 [CrossRef] [MathSciNet] [Google Scholar]
- Réfrégier, A. 2003, MNRAS, 338, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, J. W., Freeman, P. E., Lee, A. B., & Schafer, C. M. 2009, ApJ, 691, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Storrie-Lombardi, M. C., Lahav, O., Sodre, Jr., L., & Storrie-Lombardi, L. J. 1992, MNRAS, 259, 8 [Google Scholar]
- Strateva, I., Ivezić, Ž., Knapp, G. R., et al. 2001, AJ, 122, 1861 [Google Scholar]
- Yu, K., Yu, S., & Tresp, V. 2005, Advances in Neural Information Processing Systems [Google Scholar]
All Tables
Fitting the similarity matrix of 1520 objects, with the minimal SSR value out of 15 fits and the mean angular change averaged over 15 fits.
All Figures
 |
Fig. 1 Examples of shapelet models of three galaxies from SDSS (g band). Shown are the original images (left column), the shapelet models (centre column), the residuals (right column) of a face-on disc galaxy (top row), an edge-on disc galaxy (centre row), and an elliptical galaxy (bottom row). Note the different plot ranges of the residual maps. The shapelet decomposition used Nmax = 16; i.e., 153 basis functions. |
| In the text | |
 |
Fig. 2 Sketch of a weighted undirected graph. The data nodes xn are connected by edges. For the sake of visibility, only edges connecting x1 are shown. The edges are undirected and weighted by the similarity of the two connected nodes. |
| In the text | |
 |
Fig. 3 Sketch of a bipartite graph. The bipartite graph contains two sets of nodes, X = { x1,...,xN } and C = { c1,...,cK } . Edges connect nodes from different sets only and are weighted by an adjacency matrix B. Not all edges are shown. |
| In the text | |
 |
Fig. 4 Estimating the optimal number of clusters for the data sample shown in Fig. 6. a) SSR(K) as a function of the number K of clusters. b) Mean angular changes 〈 Δ(K) 〉 averaged over ten fits. |
| In the text | |
 |
Fig. 5 Breakdown of hard classifications in case of overlapping clusters. Deviation μ̂A − μA of estimated and true means vs. two-cluster separation Δx for class A for hard estimator (red line), soft estimator (blue line), and predicted bias of hard estimator for Δx → 0 (dashed line). From 1000 realisations of data samples we estimated errorbars, which are shown but too small to be visible. |
| In the text | |
 |
Fig. 6 Artificial data sample with six clusters (top) and the matrix of pairwise Euclidean distances (bottom). Each cluster has an underlying bivariate Gaussian distribution with covariance matrix Σ = diag(1,1). We sampled 50 data points from each cluster. |
| In the text | |
 |
Fig. 7 Estimating the optimal similarity measure for the example data of Fig. 6. Top panel: modified Manhattan distance C (Eq. (39)) for s = 1.01 (cyan line), s = 1.03 (blue line), and s = 1.1 (red line). For α → 0 the matrix becomes a step matrix, which is why the constant levels depend on the scale parameter. Bottom panel: the resulting similarity matrix. |
| In the text | |
 |
Fig. 8 Impact of non-optimal similarity measures on clustering results. a) Modified Manhattan distance C (Eq. (39)). b) Mean computation time per fit without errorbars. c) Mean SSR(K) values of resulting fits for K = 2. d) Mean angular change of SSR(K) at K = 2. e) Mean misclassification rate (solid line) and 50% misclassification rate (dashed line). f) Mean squared-error loss of maximum cluster posteriors. |
| In the text | |
 |
Fig. 9 Impact of two-cluster overlap on clustering results for K-means algorithm and bipartite-graph model. a) Mean angular change of SSR(K) (bipartite-graph model) and within-cluster scatter (K-means) at K = 2. b) Mean misclassification rates of K-means and bipartite-graph model (see text) compared to theoretical prediction. All curves coincide. c) Mean squared-error loss of bipartite-graph model. |
| In the text | |
 |
Fig. 10 Impact of noise variance |
| In the text | |
 |
Fig. 11 Impact of cardinalities on clustering results. a) Mean misclassification rate. b) Mean squared-error loss. c) Correlation of estimated and true cluster cardinality. |
| In the text | |
 |
Fig. 12 Mean angular changes 〈 Δ(K) 〉 of bipartite-graph model for data set composed of edge-on discs, face-on discs, and ellipticals. |
| In the text | |
 |
Fig. 13 Cluster posterior space of bipartite-graph model for edge-on discs, face-on discs, and ellipticals. The triangle defines the subspace allowed by the normalisation constraint of the posteriors. The corners of the triangle mark the points of 100% posterior probability. The * indicates the point where all three posteriors are equal. Colours encode a priori classifications unknown to the algorithm. |
| In the text | |
 |
Fig. 14 Comparing Fig. 13 with results of PCA for edge-on discs, face-on discs, and ellipticals. The parameter space is spanned by the first two principal components. The first principal component carries ≈ 45.2% and the second ≈ 21.4% of the total variance. Colours encode a priori classifications unknown to the PCA algorithm. |
| In the text | |
 |
Fig. 15 Estimating the number of clusters in the data set of Fukugita et al. (2007). Mean angular changes 〈 Δ(K) 〉 are averaged over 15 Fits. |
| In the text | |
 |
Fig. 16 Comparing the data-to-cluster assignments for K = 3 clusters (panel a) and K = 8 clusters (panel b) to visual classifications. We show how the Fukugita types distribute over the automatically identified clusters. The cluster’s posterior distributions are estimated by summing the posteriors of all objects of this Fukugita type. |
| In the text | |
 |
Fig. 17 Top example objects for K = 3 clusters. Each row corresponds to a cluster. We also show the distribution of its cluster posteriors beneath each object. Cluster 1 seems to contain face-on discs, cluster 2 compact objects, and cluster 3 edge-on discs. |
| In the text | |
 |
Fig. 18 Cluster posterior space for K = 3. See Fig. 13 for an explanation of the topology of this plot. |
| In the text | |
 |
Fig. 19 Top example objects for K = 8 clusters. Each row corresponds to a cluster. For each object, we also show the histogram of the distribution of its cluster posteriors beneath it. The objects were aligned in shapelet space, not in real space. |
| In the text | |
 |
Fig. 20 Mean axis ratios and concentration indices for the clusters of Fig. 19. Weighted means were computed from the top 100 example objects of each cluster. We show the contours of 1σ and take possible correlations into account. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


