| Issue |
A&A
Volume 522, November 2010
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 18 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201014046 | |
| Published online | 04 November 2010 | |
Merging in the common envelope and the origin of early R-type stars
1
INAF-Osservatorio Astronomico di Collurania,
64100
Teramo,
Italy
e-mail: piersanti@oa-teramo.inaf.it
2
Departament de Física i Enginyeria Nuclear, Universitat
Politécnica de Catalunya, Diagonal
647, 08028
Barcelona,
Spain
3
Departamento de Física Teórica y del Cosmos, Universidad de
Granada, 18071
Granada,
Spain
Received:
12
January
2010
Accepted:
13
June
2010
Context. Binary systems experiencing one or two common envelope episodes during the red giant branch or the Hertzsprung gap phases can produce a single star, evolving along the Hayashi track, as a final outcome. Even if these objects are expected to be very common in nature, a proper description of their evolution and physical properties is still missing. Moreover, this scenario (red giant merging scenario) has been invoked as the progenitor systems of early-R stars, by assuming that the physical conditions developed as a consequence of the cores merging could produce the mixing into the convective envelope of fresh carbon that was synthesized during the He-flash.
Aims. We analyze in detail the red giant merging scenario to verify if the resulting star develops the physical conditions suitable for a dredge-up of C-enriched material from the core to the envelope.
Methods. We performed 3D simulations of the merging stars, to check whether He is burnt efficiently during the formation of a self-sustained disk. We therefore did 1D computations of the accretion phase occurring after the merging and of the following evolution up to the settling of quiescent He-burning in the center. We adopted different assumptions on the amount of angular momentum transferred from the disk to the core and on the angular momentum transport.
Results. Efficient He-burning does not occur during the merging, because a very high temperature (T > 108 K) at the disk/He-core interface develops only for a few minutes. Our computations show that the accretion process is the leading parameter in determining the final properties of the merged object. In particular, the thermal energy delivered by the accreted matter determines the heating of the whole newborn core, thus preventing the developing of highly degenerate physical conditions. This occurrence determines the onset of the He-burning with an He-flash milder and closer to the center, as compared to standard RGB stars. Rotation and different angular momentum transport efficiency plays a secondary role by determining the exact location of the first He-flash. In none of the computed models is material formed in the He-core mixed into the convective envelope, because the H-burning shell, which always active during the He-flashes and later on, acts as a barrier.
Conclusions. In the red giant merging scenario, the physical conditions suitable for both a peculiar He-flash and the dredging-up of C-enriched material never occur. Our results speak against the possibility that such an evolutionary scenario could represent the progenitor system of early R-stars.
Key words: stars: evolution / binaries: close / stars: rotation / stars: chemically peculiar / hydrodynamics / accretion: accretion disks
© ESO, 2010
1. Introduction
R-type stars are carbon stars, chemically characterized by C/O > 1 (by number) in their envelopes. They are further classified into two groups (Shane 1928): R0-4 (hot or early-R stars), equivalent to K-type giants, and R5-8 (cool or late-R stars) equivalent to M stars. While it has been shown that late-R stars are very probably normal (N-type) asymptotic giant branch (AGB) carbon stars, as their s-element abundance pattern is reproduced well by low-mass AGB nucleosynthesis models (e.g. see Zamora et al. 2009), up to now no consistent evolutionary scenario has been found for early-R stars. Strong constraints can be obtained by the observed properties of these stars. In particular, they have near solar metallicity and show enhanced nitrogen ([N/Fe] ~ 0.5), a low 12C/13C ratio (<15) and no s-element enhancements (Dominy 1984; Zamora et al. 2009). Moreover, they are located in the H-R diagram at the same place as red clump stars (Knapp et al. 2001; Perryman & ESA 1997). Finally, it is surprising that no R-star has been found so far in a binary system (McClure 1997), although a minimum of ~30% binary systems is expected in any G/K giant (or similar) populations.
The observed luminosities and the lack of s-elements in the spectra is at odds with the possibility that hot R-stars could be related to AGB stars. Moreover, carbon stars are unlikely to form by mass transfer at near solar metallicity mainly because of the high solar oxygen abundance to be surpassed (Abia et al. 2003), although a few exceptions seem to exist (e.g. BD +57° 2161, see Začs et al. 2005). On the other hand, if the primordial cloud were initially polluted in C, one should also find near solar metallicity carbon-rich stars at an early evolutionary phase (e.g., in the main sequence – MS), as for metal-poor carbon-rich stars in the galactic halo (e.g. Aoki et al. 2007), but up to now not a single star has ever been found.
Based on this evidence, it has been proposed that the enhancement of carbon in the external layers could occur during a peculiar He-flash in a red giant (RG) star with a mass ~1.0 M⊙. This scenario would account for the chemical peculiarities of early-R stars with respect to both MS and AGB stars belonging to the same population. In this case, it is argued that carbon produced during He-flashes is dredged-up by surface convection, which deeply penetrates throughout the H-shell into the He-core.
The first suggestion of a possible mixing during the He-flash at the tip of the red giant branch (RGB) was proposed by Schwarzschild & Härm (1962) for Population II low mass stars. Nevertheless, in successive studies, the same authors concluded that the flash was weaker than less accurate calculations had shown before, and claimed that the star survives the helium flash without any mixing (Härm & Schwarzschild 1966). Then a lively discussion about the physical properties and numerical treatment of the He-flash started and it is still going on today. Despain (1982) concluded that hydrostatic models do not produce mixing at the He-flash, while recent 3D hydrodynamical simulations (Dearborn et al. 2006; Lattanzio et al. 2006; Mocák et al. 2008, 2009; Mocák 2009) show that the properties of the He-flash do not significantly differ from the 1D hydrostatic calculations. Note that 3D numerical simulations can only follow a few hours of evolution after the He-flash, while the time between the first He-ignition and quiescent He-burning ranges from 105 to 106 yr. It has to be pointed out that these results agree fairly good with observations, which show that the majority of the low-mass stars passes the He-flash phase without substantially altering their physical structure and surface chemical composition. However, 3D models by Mocák (2009) exhibit turbulent entrainment at both the inner and outer edges of the convective shell powered by the He-flash. This determines the growth of the convective unstable zone toward H-rich layers on a dynamical timescale, an effect usually neglected in 1D hydrostatic simulations, even if the mixing of the He-burning ashes into the convective envelope does not necessarily take place (Mocák 2009).
Paczynski & Tremaine (1977) were the first authors to obtain the mixing of carbon produced during the He-flash into the stellar envelope. In this work, the authors artificially shifted out the mass coordinate at which the first He-flash occurs toward the border of the He-core. In this way, owing to the large energy released, the overlying H-burning shell is pushed outward and it dies down, so that, after the He-flash episode is extinguished, surface convection deeply penetrates regions enriched in carbon produced by 3α reactions. Such an occurrence could be caused, for example, by the cooling effects of axions or by “super” neutrinos. In the first case, as shown in Domínguez et al. (1999), for axion mass close to the current estimated values, the location where He-flash is ignited moves outward, close to the He/H interface. Similarly, Angelou & Lattanzio (2008) increase the neutrino cooling efficiency by hand until He-ignition occurs close enough to the edge of the He-core to produce carbon dredge-up. We want to point out that the latter is just an artifact and it does not have to be regarded as a possible physical mechanism because, otherwise, the whole evolutionary scenario for post-RGB low-mass stars would be completely altered. In this scenario, even if one could envision a selective physical mechanism able to produce such a mixing, the dredged-up material could have the right C/O ratio, but very high 12C/13C ratio, in total disagreement with that observed in early-R stars.
On the other hand, the enhancement of carbon abundance in the envelope of a RG star has been obtained by standard evolutionary calculations of extremely metal-poor stars (Z ~ 0 – see Hollowell et al. 1990; Picardi et al. 2004). At variance with higher metallicity stars, in this case He-burning is ignited closer to the He/H interface, where H-burning is active at a very reduced level owing to the lack of CNO catalysts. As a consequence, the flash-driven convective shell erodes the tail of the H profile, carrying down fresh protons into high temperature zones enriched in carbon. This determines the formation of two convective shells, the inner one powered by 3α reactions and the outer one powered by p-captures on 12C. Later on, when the convective shell related to He-burning dies down, the external convective zone enriched in H, as well as CNO isotopes, merges with the convective envelope, thus determining the chemical pollution of the surface layers. However, this peculiar He-flash occurs only in very low metallicity stars, while hot R-stars have almost solar metallicity, so that such an evolutionary scenario has to be ruled out.
Based on the evolutionary calculations by Mengel & Gross (1976), Dominy (1984) suggested that the carbon dredge-up could occur during the He-flash in stars having very rapidly rotating He-cores. However, even if the computations performed by Mengel & Gross (1976) clearly show that the mass coordinate of He-ignition depends on the angular velocity in the He-core (faster rotators ignite He farther from the center), no carbon dredge-up is found at all. In fact, even if, by increasing the rotational velocity, the mass location of He-flash ignition moves outward, the total mass of the He-core increases faster, so that the He-flash occurs farther from the He/H discontinuity, as compared to non rotating models.
As a matter of fact, the existing detailed numerical simulations of RGB low mass stars, obtained under different physical assumptions, seem to rule out the possibility that the chemical peculiarities of hot R-stars could be brought back to the He-flash. However, McClure (1997) interpreted the “statistically improbable finding” of no hot R-stars in binary systems as evidence that their progenitors were initially all binaries, which coalesced into a single object during their evolution.
By assuming that such a merger could produce the physical conditions needed to give rise to a peculiar He-flash and a consequent dredge-up of carbon into the external layers, Izzard et al. (2007) explore statistically different binary scenarios. They discuss different evolutionary channels and conclude that the most favorable one is the merger of an He white dwarf (He-WD) with an RG star. In this case, the primary component of the initial binary system undergoes a stable mass transfer episode, thereby determining the formation of an intermediate system made by an He WD, the daughter of the Roche lobe-filling star, and a normal star, which corresponds to the initial secondary component. The secondary has been rejuvenated by the accretion from the companion so that its mass is higher.
Finally, when the secondary evolves out of the main sequence phase, it undergoes a common envelope episode, during which the He-WD and the He-core merge. The final outcome is a single star having an He-core given by the sum of the He-WD and the initial He-core of the secondary, and an H-rich mantle, corresponding to the residual mass of the initial envelope of the secondary.
Other possible scenarios are related to the merging of a star crossing the Hertzsprung gap with an He-WD or an RG star. In both these cases one faces with a binary systems, whose components have already developed a partially degenerate He-core.
The statistical analysis by Izzard et al. (2007) produces ten times more stars than required to match the observed early-R to red clump star ratio. This discrepancy becomes more severe after the analysis by Zamora et al. (2009), although this may not be a problem at all since only a few of these systems would finally reach the peculiar (and still unknown) conditions that lead to carbon mixing into the envelope. Moreover, the physical properties of the common envelope phase, as well as the parameters distribution of initial binaries, are affected by large uncertainties so that the expected frequency of the merging scenario could be overestimated.
In principle, the previously discussed scenario is very interesting because the merging of two degenerate structures not only leads to the formation of a rapidly rotating core, a condition which, as discussed before, is not enough to induce an anomalous He-flash, but it also determines very different physical conditions (mainly temperature distribution) than standard single RGB stars. This scenario, interesting in its own right, has never been investigated in detail. The final outcome of two He-WDs merging has been computed, but without including the effects of rotation (e.g. Iben 1990), while, to our knowledge, the physical structure resulting by a merging during a common envelope episode has never been determined.
In this work we investigate the RGB merging scenario to verify that it can be regarded as the progenitor system of early R-stars. We explore in detail the physical properties of these systems as a function of the orbital parameters of the initial binary systems and perform fully evolutionary calculations of the He-flash phase of the merged objects. On general grounds, it has been argued that, during the merging of two degenerate components, the less massive one disrupts to form an accretion disk from which matter flows onto the companion (e.g. Benz et al. 1990; Rasio & Shapiro 1995). This implies that, in the merging scenario for early-R stars progenitors, three different phases have to be distinguished:
-
1)
the coalescence, during the common envelope phase, when thetwo degenerate components spiral in;
-
2)
the merging itself, corresponding to the formation of an accretion disk around one of the degenerate cores; and
-
3)
the accretion, i.e. the transfer of mass from the disk to the surviving He-core.
2. Selection of the models and the coalescence phase
Following the statistical analysis by Izzard et al. (2007), we focus attention on the merging of an He-WD with an RG star (their R3 channel). For this choice of parameters, the primary evolves toward the RGB after H exhausts at the center and overfills its own Roche lobe. The corresponding mass transfer process is conservative, so that the envelope of the primary is completely removed, leaving a degenerate He-core (He-WD) as a remnant, while the secondary accretes the matter lost by the companion to become a blue straggler. Later on, when the secondary exhausts H at the center, it ascends the Hayashi track and a common envelope (CE) episode occurs. Among all the possible systems representing this subtype in Izzard et al. (2007), we select three systems that span the whole range of possible values for MWD and MRG in the R3a evolutionary channel by Izzard et al. (2007, see their Fig. 2).
We do not follow the evolution of these systems from the beginning, but we derive the properties of the intermediate configuration, i.e. after the first mass transfer episode, from the analysis of Izzard et al. (2007, see their Fig. 2 and the discussion in Sect. 3.1.1). The adopted values are listed in Table 1, where we report, from left to right, the mass of the secondary at the onset of the CE episode (MRG), the He-WD mass (MWD), the mass of the He-core of the secondary (Mcore), the separation at the onset of the CE (A), and the residual mass of the secondary (core plus envelope mass) at the merging time (Mf).
Summary of the orbital parameter before the merging of the He-WD and the He-core of the RG star (see text for more details).
The coalescence of the two He-cores can be described as follows. The high rate at which mass is transferred from the RG star to the WD determines the formation of an expanded common envelope, which heats up from the conversion of orbital energy of the very compact degenerate cores into thermal energy via viscous braking. The loss of orbital energy determines the shrinking of the orbits up to the moment the WD overfills its own Roche lobe, giving rise to a dynamical mass transfer. This occurrence marks the beginning of the merging phase, during which the He-WD completely disrupts and forms a self-sustained accretion disk around the He-core of the secondary. Thus, one can envision the final system as a very expanded H envelope that represents the residual mass of the original secondary convective envelope surrounding a very compact structure: the original He-core plus the accretion disk.
To properly describe this sequence of events, we followed the evolution of the accreted secondary from the main sequence phase in detail up to the onset of the CE phase. For the selected parameters, at each time step we computed the value of the separation as determined by the angular momentum loss via gravitational wave radiation and the corresponding Roche lobe radius1. These models were computed by means of the Lagrangian 1D hydrostatic code FRANEC (Chieffi & Straniero 1989). In all the computed models we adopted Z = 0.02 − Y = 0.280 (solar composition) as the initial chemical composition and used the metal distribution derived by Piersanti et al. (2007) for the Grevesse & Sauval (1998) mixture. Consistently, we adopted the value α = 2.25 for the mixing length parameter. All the input physics (namely, equation of state and radiative opacity coefficients) are the same as in Piersanti et al. (2007). The contribution of electron conduction to the opacity was evaluated according to Potekhin et al. (1999).
 |
Fig. 1 Projection in the orbital plane depicting the evolution of Model C in Table 2, from the initial Roche-lobe contact until the formation of a single object composed by the core of the red giant surrounded by a Keplerian disk made of the debris of the former He white dwarf. The scale along the sequence represents the logarithm of temperature in Kelvin degrees. Each snapshot is a 1011 by 1011 cm box centered on the center of mass of the system. |
When the stellar radius becomes larger than the corresponding Roche lobe radius, we
determined the final configuration at the merging (i.e. the residual mass of the envelope)
according to Nelemans et al. (2001, see their
Appendix A.2.4)![\begin{eqnarray} \frac{M_{\rm RG}M_f}{R_{\rm RG}}\!+\!\frac{M_{\rm WD}^2}{R_{\rm WD}}=\lambda\cdot\alpha_{\rm CE} \left[\frac{(M_{\rm RG}-M_f)M_{\rm WD}}{2 a_{\rm RLOF}}\!-\!\frac{M_{\rm RG}M_{\rm WD}}{2A}\right], \end{eqnarray}](/articles/aa/full_html/2010/14/aa14046-10/aa14046-10-eq25.png) (1)where
aRLOF is the value of the separation at the merging time of
the two cores, while RRG and RWD are
the radii of the accreted secondary and of the He WD, respectively, at the onset of the CE
episode. In the previous equation we set
λαCE = 1.
(1)where
aRLOF is the value of the separation at the merging time of
the two cores, while RRG and RWD are
the radii of the accreted secondary and of the He WD, respectively, at the onset of the CE
episode. In the previous equation we set
λαCE = 1.
3. The dynamical merging phase: 3D SPH simulations
To simulate the dynamical stages of the merging of the RG star and the He-WD, we used the SPH technique. This method decomposes the star into several interpolation points (called particles, as they have an associated mass) that follow the Euler fluid equations. The physical properties at the location of particles was retrieved by averaging them locally over neighbor particles (see Monaghan 2005, for more details).
The SPH method has been extensively used in the past to simulate merging and collision processes between MS stars (Lombardi et al. 2006) or compact stars of different types (Guerrero et al. 2004; Rosswog 2005; Lorén-Aguilar et al. 2005). It is a very flexible method that conserves angular momentum to a large extent, an important feature when handling these scenarios. To carry out the simulation we adopted the standard formulation given by Monaghan (2005) to the problem of tidal interaction and further destruction of the He-WD under the gravitational field of the giant. The basic fluid equations include mass, momentum, and energy conservation. Details of the mathematical formulations of these equations can be found in Monaghan (1992), Monaghan (2005), or Rosswog (2009).
Main properties of the calculated 3D models.
Gravity is calculated by dividing the system in clusters of different size and using a multipolar expansion (up to quadrupole) to approximate the force exerted by each cluster onto a particle (Hernquist 1987). In addition, shocks are usually handled in SPH with an artificial viscosity formalism. Including artificial viscosity in the scheme is necessary for several reasons: 1) to handle shocks that could appear during the dynamical phases of the merging, in particular mildly strong internal shocks in the accreted material exists during the making of the spiral arms seen in Fig. 1; 2) to avoid the penetration and mixing of particles in the absence of hydrodynamical instabilities; 3) to have the necessary minimum amount of viscosity in SPH to stabilize the system, reducing the oscillations of physical magnitudes due to numerical noise. The use of artificial viscosity has the negative side introducing an unphysical shear stress that can lead, for instance, to an excess of viscous coupling through the disk, which in turn may lead to spurious entropy generation. Nevertheless, this term is needed in any hydrodynamical simulation in order to transform bulk motion into thermal energy. In our calculations we used the standard Monaghan-Lattanzio artificial viscosity (Monaghan 1992), which depends on two parameters (α and β) that control the strength of this term. The equation of state includes the contribution of radiation, of ions, that are treated as an ideal gas including Coulomb, polarization and other minor corrections, and of partially degenerate electrons. A simple nuclear network of 14 isotopes was included in the code although the amount of nuclear combustion observed during the merging was negligible.
Owing to the strong restriction of the time step imposed by the Courant time, simulations were limited to the dynamical stages of the coalescence. We take model M1 in Table 1 as our initial model. Once the He-WD radius is equal to the Roche-lobe radius, the mass transfer increases and evolution becomes very dynamical. To follow that phase with SPH, both stars were first mapped to a 3D distribution of mass-particles. Such mapping was performed in two steps. In the first one the particles were radially distributed following the 1D density profile, while their angular position was chosen at random. During the second step, we let the system of particles of each star evolve in isolation towards equilibrium under gravity and pressure forces. Once stability of each component was reached, both stars were put in a compact orbit around their common center of mass with a major semi-axis chosen so that the surface of the He-WD was in (or close to) contact with the inner Lagrangian point of the Roche lobe. Each model shown in Table 2 was settled in corotation at the beginning of the coalescence process. We used N1 = 50000 particles and N2 = 36833 particles to describe the RG and the He-WD, respectively. With that choice we were able to resolve four orders of magnitude in density, although, working in 3D, resolution is insufficient to resolve the envelope of the giant, except a really tiny region above the core. Figure 2 depicts the density profile of the giant in 1- and 3Ds versus mass and radial coordinates. It is clear that the 3D initial model of the giant star only extends a little farther than the core owing to the steep density gradient. However, as mentioned in the previous section, the evolutionary timescale of the envelope is much longer than the characteristic time of the merging of the cores, so we assume that no interaction with the envelope takes place during the merging. The relevant features of the calculated models are given in Table 2, where we report, from left to right the initial orbital distance, the artificial viscosity parameters, the maximum temperature achieved during the merging, the local density and the time corresponding to the maximum temperature, the total time of the simulation, the angular velocity of the central remnant and the maximum relative variation of total energy and angular momentum for the whole calculation. Models A, B, C, and D differ in the initial orbital distance, while model A1 was performed to explore the influence of the artificial viscosity, compared to model A.
 |
Fig. 2 Density profile of the RG star in front of the radius (top axis) and the mass coordinate (bottom axis). The symbols denote the region that is actually simulated in the 3D calculations. |
3.1. Hydrodynamics of the merging
We use model C in Table 2, an intermediate case, that describes the evolution of the compact system from the beginning of the merging until the formation of a centrifugally sustained disk.
The state of the system at different times is depicted in Fig. 1. In each snapshot all particles are projected onto the X-Y plane. Initially both stars are situated in a synchronized circular orbit with an initial orbital distance a0 = 1.1 RL. From the very beginning, mass from the outer layers of the He-WD star is accreted by the RG-core, producing a positive feedback between two processes. First, the gravitational potential of the RG-core increases, thereby producing stronger gravitational tides that tighten the system and deform the He-WD, hence sustaining a continuous mass transfer. Secondly, as WDs are degenerate systems, the mass lost by the He-WD produces an expansion of its radii that favors the mass transfer. Within approximately eight orbits, diluted spiral arms are formed as mass is shed from the He-WD. Angular momentum is transported outward and transferred to these spiral arms. When the He-WD has lost about 0.02 M⊙ (half accreted and half in the spiral arms), a fast decompression occurs, leading to a rapid merger of the system, which happens within one orbit (t ≈ 3400–3600 s). Figure 3 depicts the evolution of the accreted mass onto the RG core for Models A and C. It can be seen that the mass accretion rate changes drastically from approximately 3.2 × 10-6 to 9.8 × 10-5 M⊙/s, to fall again to 2.1 × 10-6 M⊙/s after the merger, denoting a very dynamical process. In the moment of disruption, the accreted mass achieves its maximum temperature and lower density (see Fig. 4). The consequences of such a temperature increase on He combustion is discussed later.
 |
Fig. 3 Evolution of mass transfer during the last two hours of the merging process. The picture corresponds to models A and C in Table 2. |
After the merger a self-sustained disk is formed rapidly, in about 1000 s. Within this time, mass has been shed from the equatorial plane of the newly born remnant, forming narrow and long spiral arms. At late times these spiral arms will eventually fall again onto the remnant; nevertheless, the ultimate fate of these spiral arms is not clear because their interaction with the envelope is a complicated issue that cannot be addressed with the resolution of present simulations. Probably for moderate elapsed times, the spiral arms will be able to survive because their density is at least five orders of magnitude higher than the density of the innermost part of the envelope, but their long-term evolution is unknown. The spiral arm is shorter for those models where the initial orbital distance is shorter because decompression happens closer to the RG-core, thereby inducing a faster recapture of the spiral arm. As matter is accreted, the disk is monotonically heated by dynamical friction and by the slow increase in density.
At the end of the simulation (t = 6490 s), the remnant is a 0.25 M⊙ WD with angular velocity ω = 0.036 rad s-1. As can be seen in Fig. 1, most of the debris of the He-WD forms a Keplerian disk around the RG-core. On the other hand, around 0.05 M⊙ were accreted by the former He-core of the RG star. The accreted material transfers angular momentum to the He-core, which increases its angular velocity, therefore the angular velocity profile tends to be flat within the core of the RG, turning to Keplerian beyond a critical radius (Rcrit ≃ 3 × 109 cm). As mentioned before, using the artificial viscosity formalism to handle shocks introduces some amount of artificial shear stress that can affect the angular momentum distribution along the disk. To check the sensitivity of the model against artificial viscosity, we carried out a calculation (model A1 in Table 2), using a much lower value for the α and β parameters, which control the amount of viscosity. As seen in Table 2 the main results of the simulation do not strongly depend on the particular value adopted for these parameters. On the other hand, there is a dependence of Tmax and ρTmax on aorb. Both magnitudes decrease as aorb increases, and the merger is smoother for longer initial distances, making the He-ignition even more unlikely to happen. The dependence of Tmax and ρTmax on aorb in fact reflects the outcome of different initial conditions. When the initial distance of the stars increases, a gentler mass transfer affects the further evolution. As said, we cannot simulate the interaction of the envelope with the secondary star. Thus it was impossible to calculate the detailed evolution of the orbital parameters leading to the merger and set precise values for Tmax and ρTmax. Nevertheless, although these peak magnitudes change when different initial separations were considered, the change is hardly big enough to alter the main conclusions of this section concerning the prompt He-ignition.
 |
Fig. 4 Maximum values of temperature and corresponding density reached in the He-WD during the merging as a function of time for model C. |
3.2. Helium ignition?
An accretion disk composed basically by He is formed as a consequence of the merging
process. At the innermost part of that disk, the temperature is high because of the
combination of compression, internal shocks, and viscous dissipation. In the simulations,
shocks were spread over a distance of several times the smoothing length parameter. On the
other hand, viscous dissipation occurs on a scale that cannot be resolved by the
hydrodynamical code. Therefore the evolution of maximum temperature depicted in Fig. 4 is merely qualitative and must be taken with caution.
However, the trend shown by temperature in Fig. 4
indicates that there is a temperature peak in the accretion disk lasting several minutes.
As the disk is composed mainly of ionized He where electrons are partially degenerate, it
is interesting to explore to what extent He-burning affects the chemical composition of
the disk material or even if it could lead to a thermal runaway. Figure 5 shows the characteristic nuclear time as a function of
temperature at ρ = 5.28 × 103 g cm-3 (the density
of the particle that had the maximum temperature in Fig. 4). The characteristic nuclear time for He-burning, defined as
τnuc = Eint/Ṡ3α
(where Eint is the internal energy and
Ṡ3α the energy generation rate of the
triple alpha reaction), is then compared to the free-fall time 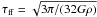 ,
to the sonic time
τsonic = h/cs
(here h is the smoothing length parameter and
cs the local sound speed), as well as to the time for the
disk to complete one revolution, τorb ≃ 200 s. As can be seen,
none of these times are close enough to the characteristic nuclear time to ensure
combustion. In fact, even the time needed to complete one orbit is many orders of
magnitude below τnuc at Tpeak. We
conclude that very little combustion, if any, will take place during the merging process.
,
to the sonic time
τsonic = h/cs
(here h is the smoothing length parameter and
cs the local sound speed), as well as to the time for the
disk to complete one revolution, τorb ≃ 200 s. As can be seen,
none of these times are close enough to the characteristic nuclear time to ensure
combustion. In fact, even the time needed to complete one orbit is many orders of
magnitude below τnuc at Tpeak. We
conclude that very little combustion, if any, will take place during the merging process.
 |
Fig. 5 Characteristic combustion time for helium, τnuc, as a function of temperature for ρ = 5.28 × 103 g cm-3. Also shown are the free-fall time, τff, the sound-crossing time (over the smoothing length h), τsonic, and the time spent by the disk to complete one orbit, τorb. The curves correspond to model C in Table 2. |
4. The post-merging configuration and the accretion phase
In the hydrostatic simulation of the accretion phase, we assumed that the inner structure (He-core plus accretion disk) evolves on a much shorter timescale than the evolutionary timescale of the extended envelope. Moreover, the accretion disk can be regarded as a sort of discontinuity in the system, insulating the accreting core from the H-rich envelope. On this basis, we computed the accretion phase under the reasonable assumption that no direct interaction of the envelope with the inner structure occurs at all.
The existing 3D simulations of the merging of two degenerate components clearly indicate that the mass flow from the newborn accretion disk to the surviving component occurs at a rate close to the Eddington value2, so that we set Ṁ = 10-5 M⊙ yr-1 in all our computations. This represents a rough estimate of the real value of the Eddington limit, which depends on the radius of the accreting core according to the equation: ṀEdd ≃ 10-4Racc/κe (in M⊙ yr-1), where Racc is the radius of the accreting core (in solar units) and κe the opacity.
However, the result of the accretion process onto a degenerate object mainly depends on the ratio between the accretion timescale, which in our case is τacc ≃ 0.2 M⊙/Ṁ = 2 × 105 yr, and the thermal diffusion timescale, which is much longer (on the order of 107 yr – see the discussion in Piersanti et al. 2003b). The final results of our computations therefore do not depend on the adopted Ṁ.
To determine the post-merging situation, we follow the evolution of the accreted secondary (MRG in Table 1) from the main sequence up to the onset of the common envelope phase. We let the star lose mass at a very high rate (Ṁ = 10-2 M⊙ yr-1) up to the momentum when MRG reduces down to Mf. The accretion phase is computed by depositing He-rich matter directly onto the He-core of the remaining secondary, with mass equal to Mf. We assume that the accreted matter has the same specific entropy as the underlying core. When an amount of matter equal to the mass of the original He-WD (MWD in Table 1) has been accreted, we stop the accretion and let the model evolve.
It is worth noticing that matter falling onto the He-core deposits angular momentum and delivers thermal energy by compression. The compression produces an increase in the local temperature, while rotation lifts the structure, thus causing cooling. As a consequence the final outcome of the merging will be determined by the interplay of these two processes. To disentangle the effects of compressional heating and rotation, we computed two sets of models, by neglecting and by including the transfer of angular momentum from the disk to the He-core, respectively.
5. Nonrotating models
5.1. The accretion phase
When matter falls onto the surface of the He-core, it delivers thermal energy that remains locally stored. As discussed in Piersanti et al. (2003b), this is related to the fact that, for the adopted Ṁ, the accretion timescale is shorter than the thermal diffusion timescale, so that the energy released by compression cannot be efficiently transferred inward. Thus, the local temperature largely increases, as shown in Fig. 6, where we report the temperature profile for some selected structures during the accretion phase for all the considered models. The number attached to each curve represents the evolutionary sequence throughout the accretion phase. As can be noticed, while the temperature increases at the mass coordinate of the original He-core border, it remains almost constant in the inner zones. Moreover, this figure discloses the differences in the initial thermal content of the computed models. In fact, in the M1 and M2 cases, the temperature is almost constant in the whole He-core, while for M3 it has a maximum at the center. The isothermal profile clearly indicates the onset of electron degeneracy, typical of low-mass stars climbing the RGB. On the other hand, the M3 model has an MS mass close to the lower limit for intermediate mass stars (e.g. see Domínguez et al. 1999), so the He-core is never fully degenerate. The temperature run outside the original He-core clearly indicates that the overlying structure (both the accreted layers and the H-rich convective envelope survived the CE episode) is expanding thanks to thermal energy flowing from the point where mass is deposited outward. During the accretion phase, the temperature outside the accreting core is so low that H-burning is extinguished.
 |
Fig. 6 Temperature profiles for selected models during the accretion phase of all the computed sequences, as shown inside each panel (top to bottom panel M1, M2, and M3 cases, respectively). The number attached to each curve traces the time evolution. |
During the whole accretion phase, none of the considered models ignites He. This is because the amount of accreted matter is too low to attain the ignition conditions. This finding is in good agreement with the results of Iben (1990), who computed the accretion of He-rich matter onto an He-WD as a consequence of the merging of two He-WDs, with masses equal to 0.25 and 0.13 M⊙.
 |
Fig. 7 As in Fig. 6, but for the evolution after the accretion phase up to the He-ignition. The shaded zone in the right portion of the upper panel represents the location of the H-burning shell, as labeled (see text for details). |
 |
Fig. 8 Time evolution for the M1 model of H- and He-burning luminosities (upper panel) and mass coordinate of the H-shell, of the inner border of the convective envelope, of the mass extension of the flash-driven convective shell, and of the convective core during central He-burning (lower panel). We set t = 0 at the end of the accretion phase. |
5.2. The evolution up to the He-flash and beyond
After accretion has halted, thermal energy is diffused inward in the M1 model while the whole structure contracts. As a consequence the H-burning shell resumes. However, the temperature in the core does not increase enough to allow the He-ignition, so that the following evolution is driven by the H-burning shell, which determines the growth in mass of the underlying He-rich zones. This produces the compressional heating of the core up to the moment when He-burning is ignited very close to the center (at the mass coordinate 4.5 × 10-3 M⊙) via a mild flash. In the upper panel of Fig. 7, the mass location of the H-burning shell is marked by the vertical drop of the temperature profile in the range 0.36–0.39 M⊙ (the shaded zone on the right part of the panel), while the onset of the He-flash corresponds to the sudden increase in the temperature near the center (curves labeled 8 and 9).
In contrast, the thermal energy diffused inward is high enough in the M2 model (central panel in Fig. 7) to determine the ignition of He-burning at the mass coordinate ~0.12 M⊙, well before the thermal wave could attain the center. For the M3 model (lower panel in Fig. 7), the heating of the inner zone is so efficient that He-burning is ignited directly at the center.
The He-flash ignition in the M1 model occurs under not highly degenerate physical conditions, so that the delivered energy is less than the typical value attained in low-mass stars, as shown in the upper panel of Fig. 8, where we report the luminosity related to H-burning (dashed line) and He-burning (solid line). The flash triggers a convective shell that extends over almost the whole He-core, as shown in the lower panel of Fig. 8, where we plot the mass coordinate of the inner border of the convective envelope (solid line), the mass coordinate of the H-shell3 (dashed line), the mass extension of the flash-driven convective shell (light-shaded region) and of the convective core in central He-burning (heavy-shaded region). A further inspection of this figure discloses that, after the first episode, three flashes occur on a very short timescale, even if their strength is greatly reduced. When each flash dies down, the outer border of the convective shell recedes, while it remains constant in mass when the new flash is ignited. On the other hand, the convective envelope has the opposite behavior: when the flash is dying down convection penetrates downward, while it recedes when the new flash is ignited. Because the delivered energy is not very high and the He-flash is ignited very close to the center, the H-shell does not expand very much, so H-burning does not extinguish, thus avoiding any mixing of material from the He-core into the overlying H-rich envelope.
Similar considerations can also be made for the M2 model, the properties of which are summarized in Fig. 9. In this case, because the He-core is less degenerate than the M1 case, the energy delivered by the first He-flash is lower. Moreover, it is ignited more externally, so that the total evolutionary time up to the onset of quiescent He-burning at the center is different. In particular, after the first flash, a convective shell forms, redistributing the energy excess in the zones of the He-core overlying the He-ignition point. After the flash-driven convective shell dies down, the whole star expands to dissipate the energy excess produced by the flash. As a consequence, both the He- and H-burning efficiency largely reduce and the whole then star contracts. This determines the heating up of more inner zones in the core for both contraction-induced compression and thermal diffusion, so that a second flash is ignited. This sequence of events repeats up to the moment when the third flash (the last one) determines the physical conditions suitable for He-burning at the center. As in the previous case, no mixing of the core material with the overlying H-rich envelope occurs because the H-burning shell, which represents an entropy barrier for convection, never extinguishes.
Finally, the M3 model fully ignites He-burning at the center with a very mild flash, so that the corresponding convective zone remains well confined in the inner part of the He-core (see Fig. 10).
In Table 3 we summarize our results and report some selected quantities for the three computed models: Mc1 the He-core mass at the merging time, Mc2 the He-core mass at the end of the accretion phase, Mc3 the He-core mass at the onset of the first He-flash, Mfl the mass coordinate where the first He-flash is ignited, and ΔMfl the maximum extension of the flash-driven convective shell.
6. Rotating models
Our 3D simulations show that the merging process is more complex than an accretion of matter at a very high rate onto a degenerate component. In fact, at the merging time, the two cores are rotating around the center of mass of the system, so that it can be safely assumed that after the disruption of the less massive component, the newborn self-sustained disk is rotating around the remaining core, in such a way that the total angular momentum is conserved. This situation is unstable because the angular momentum diffusion throughout the disk makes the angular velocity of the disk at the interface core/disk become smaller than the Keplerian critical value (ωcr). As a consequence, mass previously belonging to the disk fills the gravitational potential of the underlying core. Such a situation cannot be considered a real accretion process, but an outward movement of the mass coordinate of the core, through the disk. Moreover, the matter engulfed in the core is rapidly rotating, with an angular velocity close to the critical value, so that the core itself acquires angular momentum.
In order to properly model this evolution, we modified our code by including the effects of rotation. For this aim, we followed Piersanti et al. (2003b, see their Sect. 4). We included the effect of rotation in the hydrostatic equilibrium equation, but we ignored the corrective term in the expression of the radiative gradient (but see the discussion in Endal & Sofia 1976). At variance with Piersanti et al. (2003b), we considered differential rotation and, following Endal & Sofia (1978), we describe the evolution of angular momentum through the star via a nonlinear diffusion equation (see their Eq. (3)). Such an approach is equivalent to assuming that zones, where the diffusion timescale is shorter then the time needed for a structural change, rotate rigidly (constant angular velocity). We evaluated the efficiency of both dynamical (convection, semiconvection, Solberg-Hoiland, and dynamical shear) and secular (Eddington-Sweet circulation, Goldreich-Shubert-Fricke, secular shear) instabilities by computing the corresponding diffusion coefficients as described in Heger et al. (2000). The angular momentum transport equation is solved with the chemical evolution equations (Eq. (4) in Endal & Sofia 1978) to take into account the feedback of chemical mixing on molecular weight profile, which could inhibit secular instabilities (μ-current).
In solving the angular momentum transport and chemical mixing equations, we computed the effective diffusion coefficient as the sum of the convective one and those related to secular and dynamical rotationally instabilities.
In our computations, we assumed that matter falling onto the He-core deposits angular
momentum at a rate given by 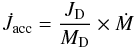 (2)where
JD is the total angular momentum of the disk,
MD the disk total mass, and Ṁ the adopted
accretion rate. We neglected the spin angular momentum of the two cores and, following Izzard et al. (2007), we assumed that
JD is equal to the total angular momentum of the system just
before the merging time, according to the formula:
(2)where
JD is the total angular momentum of the disk,
MD the disk total mass, and Ṁ the adopted
accretion rate. We neglected the spin angular momentum of the two cores and, following Izzard et al. (2007), we assumed that
JD is equal to the total angular momentum of the system just
before the merging time, according to the formula:
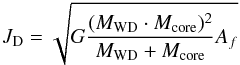 (3)where
Af is the value of the separation at the
merging time.
(3)where
Af is the value of the separation at the
merging time.
As is well known (e.g. see Piersanti et al. 2003b;
Saio & Nomoto 2004), the deposit of angular
momentum onto the degenerate core, coupled with the expansion triggered by the thermal
energy excess released by the accreted matter, determines the expansion of the external
layers of the core itself. As a consequence, the local value of
ωcr decreases, so that the accreting core experiences the
Roche instability. Up to now no clear consensus exists concerning the further evolution of
the accreting degenerate structure after the critical conditions are attained. Piersanti et al. (2003a) suggest that rotation acts as a
fine-tuning mechanism of the accretion process, in such a way that the mass effectively
deposited onto the core is determined by the condition that the core itself remains
gravitationally bound. On the other hand, Saio &
Nomoto (2004) follow Paczynski (1991) and
Popham & Narayan (1991) by assuming that
under critical conditions angular momentum is transferred back from the core to disk. In the
former scenario, the rate at which matter is effectively accreted onto the core decreases
and the specific angular momentum transferred remains constant, while in the latter,
Ṁ remains constant and 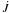 decreases. An accurate analysis of this topic
is far beyond the scope of the present work, so we just point out that the physics of a
thick accretion disk is very poorly known. In the following, we assume that, when the Roche
instability occurs, the angular momentum excess is returned to the disk and then transferred
from the outer border of the disk itself to the extended envelope.
decreases. An accurate analysis of this topic
is far beyond the scope of the present work, so we just point out that the physics of a
thick accretion disk is very poorly known. In the following, we assume that, when the Roche
instability occurs, the angular momentum excess is returned to the disk and then transferred
from the outer border of the disk itself to the extended envelope.
6.1. The accretion phase
In general, rotation has a lifting effect in the evolution of stars, reducing the local gravity, hence the local pressure. As a consequence, rotating stars are cooler and less dense than non rotating ones. Such an occurrence makes it difficult to foresee the effect of rotation on the ignition conditions of accreting degenerate cores, which in turn depend on a complex interplay of cooling and expansion. In fact, on one hand the rotational-induced cooling would point toward more degenerate physical conditions at the onset of the He-flash, while the reduced density would act in an opposite way.
 |
Fig. 11 Profiles of the angular velocity normalized to the local critical value (ωcr) for selected models during the accretion phase of all computed sequences, as labeled in each panel. |
 |
Fig. 12 Angular momentum evolution during the accretion phase of all the computed sequences, as labeled inside each panel. Jdep is the total angular momentum transferred during the accretion process, while Jcore and Jenv represent the amount of angular momentum stored in the core and in the envelope, respectively. |
To illustrate the effects of rotation, in Fig. 11 we report profiles of the angular velocity normalized to the local critical value of some selected models during the accretion phase for all the cases listed in Table 1. As can be noticed, owing to the transfer of angular momentum, the external layers of the He-core acquire very high angular velocity (the pronounced local maximum at the mass coordinate ~0.2 M⊙, the exact value depending on the considered evolutionary sequence). As a consequence of the reduced local gravity and of the thermal energy excess determined by the mass deposition, these layers expand, and the accreting core experiences very soon the Roche instability4. Such an occurrence is clearly marked in the figure by the progressive increase in the ratio ω/ωcr in the expanded envelope (right portion of each panel in the figure), where we assume that the angular momentum excess in the core is redistributed (see above). From this moment up to the end of the accretion phase, angular momentum is constantly returned from the He-core to the disk, hence dissipated into the fully convective extended envelope. This occurrence is displayed clearly in Fig. 12, where we report the total angular momentum transferred during the accretion process (Jdep – solid line), the amount of angular momentum stored in the core (Jcore – dashed line) and the amount of angular momentum in the envelope (Jenv – dotted line) as a function of the accreted mass normalized to MWD (M ∗ = Ṁ·t/MWD).
However, the angular momentum remains stored in the external zone of the original He-core and in the accreted layers, because the angular momentum transport inward is not efficient at all. It is worthwhile noticing that the whole He-core is unstable for the Eddington-Sweet criterion5, but the corresponding angular momentum redistribution occurs on a much longer timescale (τES ~ 108 −109 yr) than the evolutionary time (accretion timescale). Similar considerations are valid also for the secular shear instability, whose characteristic timescale for the physical situation considered in the present work is on the order of τSS ~ 107 yr.
The effects of rotation on the temperature profiles are shown in Fig. 13. As for nonrotating models, the mass accretion at a high rate determines the release of thermal energy via compressional heating, but, because of the gravitational lifting triggered by the spinning-up of the core, the external layers of the core itself expand, and these zones rapidly cool down. Later on, when angular momentum is transferred back to the disk, hence to the H-rich envelope, the layers accreted during the previous evolution begin to contract, and thermal energy is delivered so that a new local maximum forms close to the mass coordinate of the original He-core. Below this point, the core is supported by the pressure of degenerate electrons, so that the thermal diffusion timescale remains much longer than the evolutionary time. As a consequence, the inner region of the core remains largely unaffected by the compressional heating in the accreted zones.
6.2. The evolution up the He-flash and beyond
When accretion comes to a halt, the external zones of the He-core begin to contract, thus
determining once again the onset of the Roche instability. To explain such an occurrence,
we consider two models, characterized by
ωi, ωcr,i, Ri,
and
ωf, ωcr,f, Rf,
where the subscripts i and f refer to the initial and final configurations, respectively.
The initial structure is rotating with angular velocity close to the critical value
(ωi ≃ ωcr,i),
so that by applying the local conservation of angular momentum we get:
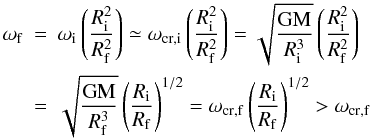 (4)where
we have simplified the form factor related to the momentum of inertia. In this condition
we assume that angular momentum is transferred from the core to the extended envelope, as
shown in Fig. 14, depicting the evolution of the
angular momentum fraction stored in the core (Jcore) and in
the envelope (Jenv).
(4)where
we have simplified the form factor related to the momentum of inertia. In this condition
we assume that angular momentum is transferred from the core to the extended envelope, as
shown in Fig. 14, depicting the evolution of the
angular momentum fraction stored in the core (Jcore) and in
the envelope (Jenv).
When the evolutionary timescale is long enough, thermal energy is efficiently transferred inward, while the whole structure continues to contract. In this condition angular momentum is also transferred toward the center via the secular shear mechanism. As a consequence, the angular momentum in the outermost zones of the He-core decreases, and the core itself recedes from the critical condition.
These events are clearly shown in Figs. 15 and 16 where we report the profiles of temperature and angular velocity normalized to the local critical value, respectively, for some selected structures after the accretion phase and up to the He-ignition. By comparing these two figures, it turns out that in all the computed sequences the thermal diffusion timescale in the He-core is less than the timescale for the secular shear instability, τSS; as a consequence, the thermal wave rapidly reaches the center of the star while angular momentum increases only in the more external zone of the initial He-core (let say up to ~0.15 M⊙ ).
 |
Fig. 14 Evolution after the end of the accretion phase of the fraction of the angular momentum fraction stored in the core (Jcore – solid line) and in the envelope (Jenv – dashed line). Each panel refers to a different model, as labeled. |
Figure 15 shows that, because of the contraction of the whole structure, H-burning resumes in a shell, as indicated by the sharp decrease in the temperature profile in the right portion of the figure. Moreover, this figure shows that in the M1 and M2 cases the heating of the innermost zones determined by the thermal wave is not high enough for He-ignition; therefore, as for non rotating models, the following evolution is driven by the H-burning shell, which determines the growth in mass of the He-core. In contrast, in the M3 model the thermal energy diffused inward is high enough to directly determine the physical conditions suitable for He-ignition at the center.
In all the computed models, He-burning is ignited at the center. In Fig. 17 and in Table 4, we summarize the results obtained for rotating models. By inspecting the upper panels in Fig. 17, it turns out that the M1 and M2 rotating models undergo a stronger He-flash than the nonrotating ones, and, as a consequence, the mass extension of the flash-driven convective zone is larger. This is explained by the accreted layers rotating very rapidly at the end of the accretion phase in rotating models because of the transfer of angular momentum. This determines the reduction of both the local temperature and density. As a consequence, a smaller amount of thermal energy can be diffused inward, so that the whole He-core heats up at a lower level than nonrotating models. Moreover, the angular momentum transport from the accreted layers toward the center spins the whole core up. This determines the reduction of the local compressibility, so that the compressional heating of the core due to the mass deposited by the H-burning shell is less efficient. As a consequence, the He-core mass has to be increased, with respect to nonrotating models, in order to attain the physical conditions suitable for He-ignition (see the differences in the Mc3 value reported in Tables 3 and 4).
Similar considerations can be made for the M3 model, for which the He-flash in the rotating case is not as strong as the nonrotating case. In fact, in this case, when angular momentum begins to be transferred inward, the whole core undergoes a homologous compression that determines the heating up of the inner zones, hence the He-ignition.
6.3. The effect of different angular momentum transport in the He-core
In the computation of 1D rotating models, it has to be taken into account that the angular momentum transport and the rotationally-induced mixing are included based on the estimated efficiencies of rotational instabilities, which in some cases are affected by large uncertainties. For example, as shown in a series of papers (Maeder & Meynet 1996; Maeder 1997; Maeder & Zahn 1998), the secular shear instability might not be suppressed by μ-gradients due to the turbulence produced by the barioclinic instability. As a consequence, the corresponding angular momentum transport and the resulting chemical mixing could result more efficient than usually assumed (see the discussion in Saio & Nomoto 2004).
 |
Fig. 17 Upper panel: time evolution, for all the computed rotating models (as labeled inside the upper panels), of H- and He-burning luminosities. In the lower panel, the mass coordinate of the H-shell, of the inner border of the convective envelope, of the mass extension of the convective core (heavy-shaded) are plotted. In the lower panel of M3 model, the mass coordinate of the inner border of the convective envelope has been artificially lowered by 0.1 M⊙. |
To check the sensitivity of our results on the efficiency of the angular momentum transport in the He-core, we computed an additional set of models, by assuming that the secular shear instability occurs on a much shorter timescale than the evolutionary time, so that the He-core behaves as a rigidly rotating body (constant angular velocity in the core). The obtained results are summarized in Table 5 and in Fig. 18. As can be noticed, the behavior of models with rigidly rotating cores is intermediate between nonrotating and differentially rotating ones. In particular, the He-flash is ignited at the center in the M1 and M3 cases, while it is ignited at 0.0375 M⊙ from the center in the M2 case. The same considerations also apply to the strength of the main flash episode, hence to the mass extension of the flash-driven convective episode.
7. Summary and discussion
We have investigated the physical properties of an He-WD undergoing a merging with the He-core of an RG companion in a binary system during a common envelope episode. Detailed computation of the merging phase by means of an SPH code shows that, even if the temperature at the disk/He-core interface becomes higher than 108 K, the physical conditions suitable for an efficient He-burning are available for a very short time, so that it can be safely concluded that no combustion at all takes place.
 |
Fig. 18 The same as in Fig. 17, but for the models computed by assuming rigid body rotation in the He-core. In the lower panel of the M3 model, the mass coordinate of the inner border of the convective envelope has been artificially lowered by 0.07 M⊙. |
By means of a 1D hydrostatic code, we followed in detail the accretion phase and the following evolution up to the full ignition of He-burning at the center (horizontal branch phase), under different assumptions on the amount of angular momentum deposited by the accreted matter, as well as on the angular momentum transport efficiency in the accreting He-core. Our analysis shows that the main physical process driving the evolution of the star arisen from the merging is accretion. In fact, owing to the high value of Ṁ typical of a post-merging situation, thermal energy is delivered for compression by the matter falling onto the He-core on a timescale shorter than the thermal diffusion timescale; as a consequence, the local temperature increases, while the inner zone of the core remains largely unaffected. All the computed models do not ignite He-burning during the accretion phase because the amount of the accreted mass is too small to produce the physical conditions suitable for the ignition of 3α reactions. During this phase, due to the flow of thermal energy outward from the disk/core, the H-rich envelope hugely expands, making the H-burning shell die down. However, surface convection does not bypass the H/He discontinuity, since the expanded envelope and the compact inner structure are completely decoupled.
Later on, when the disk extinguishes and the accretion process comes to a halt, the evolutionary timescale becomes longer and the thermal energy excess localized at the original disk/He-core interface is smeared off via thermal diffusion toward the center. This occurrence completely modifies the physical properties of the inner zones, determining, in particular, an increase in the temperature level along the whole He-core. At the same time, the contraction of the external layers determines the reignition of H-burning shell. As a result, He-burning is ignited very soon after the thermal adjustment, in some cases well before the thermal wave could attain the center, in some others after a few mass has been deposited by the H-burning shell onto the He-core. At variance with standard models of RGB stars, the ignition of He-burning occurs very close to the center (in the majority of the cases, exactly at the center).
Rotation modulates the behavior just discussed, without altering the general properties of the evolution up to the full He-ignition at the center. In particular, our models show that rotating cores ignite He-burning in inner zones, as compared to nonrotating cores; moreover, for a fixed total mass of the post-merging star, differentially rotating structures attain higher total He-core masses than do nonrotating ones, while rigidly rotating cores have intermediate values.
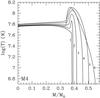 |
Fig. 19 Temperature profiles of some selected models during the accretion phase for the M4 model (see text). |
In all the considered cases, the flash-driven convective shell at its maximum remains well confined inside the He-core. Moreover, during the following evolution, surface convection does not penetrate zones enriched in carbon during the flash episodes. Such an occurrence is related to the fact that in all the models, independently of both the rotational level of the core and the total amount of thermal energy delivered by the accreted matter, the H-burning shell again becomes active after the end of the accretion phase, thus preventing any mixing of material between the core and the envelope.
As a consequence, when considering the problem of early-R stars progenitors, our results rule out the scenario of an He-WD merging with the He-core of an RG star. Moreover, our findings can be also applied to the merging of a star crossing the Hertzsprung gap with an He-WD or an RG star. In fact, for both these cases the mass extension of the He-cores and/or of the He-WD are comparable to the values we consider in the present paper.
Among all the evolutionary channels proposed by Izzard et al. (2007), the only one we cannot rule out on the basis of the previously discussed models is the merging scenario of a massive He-WD (MWD ~ 0.38−0.48 M⊙) with the He-core of an RG star. In this case, since the He-WD is definitively more massive than the RG core, the latter will disrupt forming the accretion disk. Moreover, the total mass of the initial He-WD plus the He-core is higher than the canonical mass limit for He-ignition in degenerate physical condition for a typical low-mass solar metallicity star (MHe ~ 0.49 M⊙), so one can suspect that in this case the ignition of the He-flash will occur very close to the border of the He-core, thus creating a favorable situation for the convective coupling of He- and H-rich zones.
 |
Fig. 20 Upper panel: time evolution of H- and He-burning luminosities for the M4 model. Lower panel: mass coordinate of the H-shell (dashed line) and of the inner border of the convective envelope (solid line). The grey zones represent the mass extension of flash-driven convective shell (light-shaded) and the convective core during central He-burning (heavy-shade). |
To explore such a possibility, we considered an additional system (M4 case) with
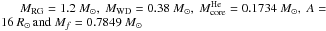 . We computed the evolution of the
post-merging configuration by assuming very high efficiency of angular momentum transport in
the He-core (rigid rotation case). As can be noticed by inspecting Fig. 19, also in this case the deposition of matter determines the release of
thermal energy and, consequently, the formation of a pronounced peak in the temperature
profile. When accretion comes to a halt, the temperature at the original interface
He-WD/disk is very high (T = 1.28 × 108 K), but
3α reactions are not fully ignited since the corresponding density is
relatively low (ρ ~ 6500 gcm-3). After that, the structure
begins to contract, the H-burning shell resumes, and an He-flash is ignited at the base of
the accreted layers. Because of the non degenerate physical conditions, the flash itself is
mild (see Fig. 20), and the corresponding convective
shell remains well confined inside the He-rich region. After the first episode, twelve
He-flashes occur, the last one determining the full ignition of He-burning at the center.
Also in this case, the entropy barrier represented by the active H-burning shell prevents
the mixing of material from the core to the envelope. One can guess that for a slightly
higher value for the mass of the original He-core, He-burning would be ignited during the
accretion process when the H-shell is switched off. In this case, the resulting He-flash
would be milder and the remaining disk would prevent any penetration of the convective
envelope. On the other hand, for a lower value of
. We computed the evolution of the
post-merging configuration by assuming very high efficiency of angular momentum transport in
the He-core (rigid rotation case). As can be noticed by inspecting Fig. 19, also in this case the deposition of matter determines the release of
thermal energy and, consequently, the formation of a pronounced peak in the temperature
profile. When accretion comes to a halt, the temperature at the original interface
He-WD/disk is very high (T = 1.28 × 108 K), but
3α reactions are not fully ignited since the corresponding density is
relatively low (ρ ~ 6500 gcm-3). After that, the structure
begins to contract, the H-burning shell resumes, and an He-flash is ignited at the base of
the accreted layers. Because of the non degenerate physical conditions, the flash itself is
mild (see Fig. 20), and the corresponding convective
shell remains well confined inside the He-rich region. After the first episode, twelve
He-flashes occur, the last one determining the full ignition of He-burning at the center.
Also in this case, the entropy barrier represented by the active H-burning shell prevents
the mixing of material from the core to the envelope. One can guess that for a slightly
higher value for the mass of the original He-core, He-burning would be ignited during the
accretion process when the H-shell is switched off. In this case, the resulting He-flash
would be milder and the remaining disk would prevent any penetration of the convective
envelope. On the other hand, for a lower value of 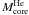 , He-burning would be ignited at
the base of the accreted layers or in the external zones of the original He-WD, in more
degenerate physical conditions. But, the H-burning shell would be fully active in this case,
thus once again preventing any mixing of core and envelope material.
, He-burning would be ignited at
the base of the accreted layers or in the external zones of the original He-WD, in more
degenerate physical conditions. But, the H-burning shell would be fully active in this case,
thus once again preventing any mixing of core and envelope material.
When considering the general picture of the early R-stars progenitors, our results allow us to draw some important conclusions. According to the current accepted evolutionary scenario, the chemical peculiarities of these stars have to be brought back to a peculiar He-flash that triggers the dredge-up of freshly synthesized carbon from the He-core into the H-rich envelope (Dominy 1984). The existing theoretical models show that such a mixing occurs if the He-flash is ignited in highly degenerate physical conditions very close to the border of the He-core, as happens in the case of extremely metal-poor stars (e.g. Picardi et al. 2004) or in models with neutrino cooling efficiency increased by hand (Paczynski & Tremaine 1977; Angelou & Lattanzio 2008). A rapidly rotating core, as is often invoked, cannot by itself produce the peculiar conditions for the He-ignition, because, as shown in the pioneer work by Mengel & Gross (1976), they rotate as a rigid body, thus leaving the temperature profile unaltered.
In this respect, the binary origin of hot R-stars, particularly the RG-merging scenario, is promising in many regards. In fact, the accretion process naturally leads to the increase in the local temperature and angular velocity in the outer region of the core. In the present work we have studied the post merging properties of RG-mergers and find that in none of the computed models does the dredge-up of freshly synthesized carbon occur from the core into the envelope. Moreover, on the basis of evolutionary and/or statistical arguments (see the discussion in Sects. 4.1 and 4.2 of Izzard et al.2007), other possible merged objects that arise by different evolutionary channels do not appear to be suitable candidates as R-stars progenitors.
In summary, our analysis of the most probable evolutionary path of single stars and in binary systems fails to find the peculiar He-flash that is currently considered the source of the early R-stars’ chemical anomalies. New ideas and more investigations are needed.
The value of the Roche lobe radius is evaluated according to Eggleton (1983).
Acknowledgments
We would like to thank the referee (R.G. Izzard) for his valuable comments and suggestions. This work was partially supported by the Spanish Ministerio de Ciencia e Innovación project AYA2008-04211-C02-02 and by the ASI-INAF I/016/07/0.
References
- Abia, C., Domínguez, I., Gallino, R., et al. 2003, PASA, 20, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Angelou, G., & Lattanzio, J. 2008, PASA, 25, 155 [NASA ADS] [Google Scholar]
- Aoki, W., Beers, T. C., Christlieb, N., et al. 2007, ApJ, 655, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Cameron, A. G. W., Press, W. H., & Bowers, R. L. 1990, ApJ, 348, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Chieffi, A., & Straniero, O. 1989, ApJS, 71, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Dearborn, D. S. P., Lattanzio, J. C., & Eggleton, P. P. 2006, ApJ, 639, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Despain, K. H. 1982, ApJ, 253, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Chieffi, A., Limongi, M., & Straniero, O. 1999, ApJ, 524, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Dominy, J. F. 1984, ApJS, 55, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Guerrero, J., García-Berro, E., & Isern, J. 2004, A&A, 413, 257 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Härm, R., & Schwarzschild, M. 1966, ApJ, 145, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Hernquist, L. 1987, ApJS, 64, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Hollowell, D., Iben, I. J., & Fujimoto, M. Y. 1990, ApJ, 351, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I. J. 1990, ApJ, 353, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Izzard, R. G., Jeffery, C. S., & Lattanzio, J. 2007, A&A, 470, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knapp, G., Pourbaix, D., & Jorissen, A. 2001, A&A, 371, 222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lattanzio, J., Dearborn, D., Eggleton, P., & Dossa, D. 2006, in International Symposium on Nuclear Astrophysics – Nuclei in the Cosmos [Google Scholar]
- Lombardi, Jr., J. C.,Proulx, Z. F., Dooley, K. L., et al. 2006, ApJ, 640, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Lorén-Aguilar, P., Guerrero, J., Isern, J., Lobo, J. A., & García-Berro, E. 2005, MNRAS, 356, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1997, A&A, 321, 134 [NASA ADS] [Google Scholar]
- Maeder, A., & Meynet, G. 1996, A&A, 313, 140 [NASA ADS] [Google Scholar]
- Maeder, A., & Zahn, J. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
- McClure, R. D. 1997, PASP, 109, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Mengel, J. G., & Gross, P. G. 1976, Ap&SS, 41, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Mocák, M. 2009, Ph.D. Thesis, Max-Planck-Institut für Astrophysik, Garching bei München [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2008, A&A, 490, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocák, M., Müller, E., Weiss, A., & Kifonidis, K. 2009, A&A, 501, 659 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monaghan, J. J. 1992, ARA&A, 30, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J. 2005, Rep. Prog. Phys., 68, 1703 [Google Scholar]
- Nelemans, G., Yungelson, L. R., Portegies Zwart, S. F., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1991, ApJ, 370, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B., & Tremaine, S. D. 1977, ApJ, 216, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues, Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Picardi, I., Chieffi, A., Limongi, M., et al. 2004, ApJ, 609, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Gagliardi, S., Iben, I. J., & Tornambé, A. 2003a, ApJ, 598, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Gagliardi, S., Iben, I. J., & Tornambé, A. 2003b, ApJ, 583, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Straniero, O., & Cristallo, S. 2007, A&A, 462, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popham, R., & Narayan, R. 1991, ApJ, 370, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Baiko, D. A., Haensel, P., & Yakovlev, D. G. 1999, A&A, 346, 345 [NASA ADS] [Google Scholar]
- Rasio, F. A., & Shapiro, S. L. 1995, ApJ, 438, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S. 2005, ApJ, 634, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Rosswog, S. 2009, New Astron. Rev., 53, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Nomoto, K. 2004, ApJ, 615, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarzschild, M., & Härm, R. 1962, ApJ, 136, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Shane, C. D. 1928, Lick Observatory Bulletin, 13, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Zamora, O., Abia, C., Plez, B., Domínguez, I., & Cristallo, S. 2009, A&A, 508, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Začs, L., Schmidt, M. R., Musaev, F. A., Galazutdinov, G. A., & Sperauskas, J. 2005, A&A, 441, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Summary of the orbital parameter before the merging of the He-WD and the He-core of the RG star (see text for more details).
All Figures
 |
Fig. 1 Projection in the orbital plane depicting the evolution of Model C in Table 2, from the initial Roche-lobe contact until the formation of a single object composed by the core of the red giant surrounded by a Keplerian disk made of the debris of the former He white dwarf. The scale along the sequence represents the logarithm of temperature in Kelvin degrees. Each snapshot is a 1011 by 1011 cm box centered on the center of mass of the system. |
| In the text | |
 |
Fig. 2 Density profile of the RG star in front of the radius (top axis) and the mass coordinate (bottom axis). The symbols denote the region that is actually simulated in the 3D calculations. |
| In the text | |
 |
Fig. 3 Evolution of mass transfer during the last two hours of the merging process. The picture corresponds to models A and C in Table 2. |
| In the text | |
 |
Fig. 4 Maximum values of temperature and corresponding density reached in the He-WD during the merging as a function of time for model C. |
| In the text | |
 |
Fig. 5 Characteristic combustion time for helium, τnuc, as a function of temperature for ρ = 5.28 × 103 g cm-3. Also shown are the free-fall time, τff, the sound-crossing time (over the smoothing length h), τsonic, and the time spent by the disk to complete one orbit, τorb. The curves correspond to model C in Table 2. |
| In the text | |
 |
Fig. 6 Temperature profiles for selected models during the accretion phase of all the computed sequences, as shown inside each panel (top to bottom panel M1, M2, and M3 cases, respectively). The number attached to each curve traces the time evolution. |
| In the text | |
 |
Fig. 7 As in Fig. 6, but for the evolution after the accretion phase up to the He-ignition. The shaded zone in the right portion of the upper panel represents the location of the H-burning shell, as labeled (see text for details). |
| In the text | |
 |
Fig. 8 Time evolution for the M1 model of H- and He-burning luminosities (upper panel) and mass coordinate of the H-shell, of the inner border of the convective envelope, of the mass extension of the flash-driven convective shell, and of the convective core during central He-burning (lower panel). We set t = 0 at the end of the accretion phase. |
| In the text | |
 |
Fig. 9 The same as in Fig. 8, but for the M2 model. |
| In the text | |
 |
Fig. 10 As in Fig. 8, but for the M3 model. |
| In the text | |
 |
Fig. 11 Profiles of the angular velocity normalized to the local critical value (ωcr) for selected models during the accretion phase of all computed sequences, as labeled in each panel. |
| In the text | |
 |
Fig. 12 Angular momentum evolution during the accretion phase of all the computed sequences, as labeled inside each panel. Jdep is the total angular momentum transferred during the accretion process, while Jcore and Jenv represent the amount of angular momentum stored in the core and in the envelope, respectively. |
| In the text | |
 |
Fig. 13 Temperature profiles for the same models as in Fig. 11. |
| In the text | |
 |
Fig. 14 Evolution after the end of the accretion phase of the fraction of the angular momentum fraction stored in the core (Jcore – solid line) and in the envelope (Jenv – dashed line). Each panel refers to a different model, as labeled. |
| In the text | |
 |
Fig. 15 As in Fig. 13, but for the evolution after the accretion phase up to the He-ignition. |
| In the text | |
 |
Fig. 16 As in Fig. 11, but for the evolution after the accretion phase up to the He-ignition. |
| In the text | |
 |
Fig. 17 Upper panel: time evolution, for all the computed rotating models (as labeled inside the upper panels), of H- and He-burning luminosities. In the lower panel, the mass coordinate of the H-shell, of the inner border of the convective envelope, of the mass extension of the convective core (heavy-shaded) are plotted. In the lower panel of M3 model, the mass coordinate of the inner border of the convective envelope has been artificially lowered by 0.1 M⊙. |
| In the text | |
 |
Fig. 18 The same as in Fig. 17, but for the models computed by assuming rigid body rotation in the He-core. In the lower panel of the M3 model, the mass coordinate of the inner border of the convective envelope has been artificially lowered by 0.07 M⊙. |
| In the text | |
 |
Fig. 19 Temperature profiles of some selected models during the accretion phase for the M4 model (see text). |
| In the text | |
 |
Fig. 20 Upper panel: time evolution of H- and He-burning luminosities for the M4 model. Lower panel: mass coordinate of the H-shell (dashed line) and of the inner border of the convective envelope (solid line). The grey zones represent the mass extension of flash-driven convective shell (light-shaded) and the convective core during central He-burning (heavy-shade). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


