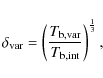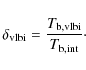| Issue |
A&A
Volume 521, October 2010
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 6 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014957 | |
| Published online | 13 October 2010 | |
Physical parameters of a relativistic jet at very high redshift: the case of the blazar J1430+4204
P. Veres1,2 - S. Frey3,5 - Z. Paragi4,5 - L. I. Gurvits4
1 - Dept. of Physics of Complex Systems, Eötvös University, Pázmány P. s. 1/A, 1117 Budapest, Hungary
2 -
Dept. of Physics, Bolyai Military University, PO Box 15, Budapest, 1581, Hungary
3 -
FÖMI Satellite Geodetic Observatory, PO Box 585, 1592 Budapest, Hungary
4 -
Joint Institute for VLBI in Europe, PO Box 2, 7990 AA Dwingeloo, The Netherlands
5 -
MTA Research Group for Physical Geodesy and Geodynamics, PO Box 91, 1521 Budapest, Hungary
Received 8 May 2010 / Accepted 23 June 2010
Abstract
Context. The high-redshift (z=4.72) blazar J1430+4204
produced a major radio outburst in 2005. Such outbursts are usually
associated with the emergence of a new component in the inner radio
jet.
Aims. We searched for possible changes in the radio structure on
milli-arcsecond angular scales, to determine physical parameters that
characterise the relativistic jet ejected from the centre of this
source.
Methods. We analysed 15-GHz radio interferometric images
obtained with the Very Long Baseline Array (VLBA) before and after the
peak of the outburst.
Results. We did not identify any significant new jet component
over a period of 569 days. We estimated the Doppler factor, the Lorentz
factor, and the apparent transverse speed of a putative jet component
using three different methods. The likely small jet angle to the line
of sight and our values of the apparent transverse speed are consistent
with not detecting a new jet feature.
Key words: radio continuum: galaxies - galaxies: active - galaxies: jets - galaxies: individual: J1430+4204 - techniques: interferometric
1 Introduction
Active galactic nuclei (AGNs) are thought to harbour supermassive (up to
![]()
![]() )
black holes. Accretion onto these black holes is
responsible for the extreme luminosity of AGNs over the whole
electromagnetic
spectrum. Part of the infalling matter may be transformed into jets
ejected
with relativistic speeds. The radio emission in radio-loud AGNs
originates in these jets via synchrotron process. The appearance of the
source strongly depends on the orientation of the jet axis with respect
to viewing direction.
If a jet points close to the line of sight
toward the observer, its brightness is significantly enhanced. For a
review of
the unified schemes for radio-loud AGNs, see Urry & Padovani (1995).
)
black holes. Accretion onto these black holes is
responsible for the extreme luminosity of AGNs over the whole
electromagnetic
spectrum. Part of the infalling matter may be transformed into jets
ejected
with relativistic speeds. The radio emission in radio-loud AGNs
originates in these jets via synchrotron process. The appearance of the
source strongly depends on the orientation of the jet axis with respect
to viewing direction.
If a jet points close to the line of sight
toward the observer, its brightness is significantly enhanced. For a
review of
the unified schemes for radio-loud AGNs, see Urry & Padovani (1995).
A particular class of AGNs are blazars. They show large and rapid brightness variations, from the radio to the gamma-ray regime. Among them, the BL Lac objects have no strong emission lines characteristic of other AGNs in the optical spectrum. The radio polarisation of the blazars could be high and variable. According to the models of AGNs (Urry & Padovani 1995), we look at these objects from almost exactly the direction of their relativistic jets.
![\begin{figure}
\par\includegraphics[width=150mm]{14957fg1.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg7.png)
|
Figure 1: The 15-GHz total flux density vs. time for J1430+4204 from the Ryle Telescope monitoring (G. Pooley, priv. comm.). The points are connected in the flaring phase for clarity. Solid vertical lines mark the times of the two VLBA observations. The filled circles correspond to the measured VLBI flux densities. Dashed lines mark calendar years as indicated. The typical flux density error bars are smaller or comparable in size with the symbols. |
| Open with DEXTER | |
J1430+4204 (B1428+4217) is a blazar with a flat radio spectrum, at an extremely
high redshift, z=4.72 (Hook & McMahon 1998).
Long-term radio flux density monitoring at 15 GHz revealed a
significant brightening of J1430+4204, starting in 2004 and reaching
its peak in 2005 (Worsley et al. 2006).
The object increased its flux density by a factor of 3 in about 4
months (in the source rest frame). At the same time, a corresponding
outburst was not detected in X-rays with the XMM-Newton satellite,
although a long-term X-ray spectral variability is evident in the
source (Worsley et al. 2006).
The X-ray spectrum of J1430+4204 suggests a large amount of intrinsic absorption with neutral hydrogen column density
![]() cm-2(Worsley et al. 2004,2006).
cm-2(Worsley et al. 2004,2006).
The radio structure of J1430+4204 at the milli-arcsecond (mas) scale is
mainly compact as revealed by Very Long Baseline Interferometry (VLBI)
imaging observations at 5 GHz (Helmboldt et al. 2007; Paragi et al. 1999),
and 2.3 and 8.4 GHz (US Naval Observatory Radio Reference Frame Image Database,
USNO RRFID![]() ). A weak
extension to the bright compact core is also seen in the W-SW direction. On
scales three orders of magnitude larger, the central emission region is
dominant as well, but there is also a jet component at a
). A weak
extension to the bright compact core is also seen in the W-SW direction. On
scales three orders of magnitude larger, the central emission region is
dominant as well, but there is also a jet component at a ![]() 4
4
![]() angular distance from the brightness peak, in the W-NW direction (Fig. 2
of Cheung et al. 2008). The pc- and kpc-scale structures are therefore
misaligned by
angular distance from the brightness peak, in the W-NW direction (Fig. 2
of Cheung et al. 2008). The pc- and kpc-scale structures are therefore
misaligned by ![]() 50
50
![]() .
Imaging with the Chandra satellite revealed
X-ray emission also at the position of the kpc-scale radio jet component. This
source has currently the highest redshift kpc-scale radio and X-ray jet known
(Cheung et al. 2008).
.
Imaging with the Chandra satellite revealed
X-ray emission also at the position of the kpc-scale radio jet component. This
source has currently the highest redshift kpc-scale radio and X-ray jet known
(Cheung et al. 2008).
Total flux density outbursts are usually followed by an emergence of a new jet
component in the VLBI images of radio AGNs (e.g. Savolainen et al. 2002).
By observing J1430+4204 after the brightening, we aimed at detecting a new
component in a hope to have a zero-epoch point for a later measurement of its
apparent proper motion. Due to the uniquely high redshift, the source
J1430+4204 would provide an important observational information for studies of
jet kinematics otherwise supported by the best-observed sample in the 15-GHz
MOJAVE (Monitoring of Jets in Active Galactic Nuclei with VLBA Experiments)
survey (Lister et al. 2009) restricted mainly to z<2.5. Reliable jet
proper motion measurements could not yet be made at redshifts as high as
![]() .
Information on the jet kinematics of J1430+4204 and other
high-redshift sources would eventually be an important contribution for
supplementing the apparent proper motion-redshift statistics as a cosmological
test (e.g. Kellermann et al. 2004; Cohen et al. 1988; Vermeulen & Cohen 1994)
with measurements at the extreme tail of the redshift distribution.
.
Information on the jet kinematics of J1430+4204 and other
high-redshift sources would eventually be an important contribution for
supplementing the apparent proper motion-redshift statistics as a cosmological
test (e.g. Kellermann et al. 2004; Cohen et al. 1988; Vermeulen & Cohen 1994)
with measurements at the extreme tail of the redshift distribution.
In this study, we report on our high-resolution radio interferometric observations of J1430+4204 (Sect. 2). We analyse the mas-scale radio structure of the source, and determine the Doppler boosting factor and the bulk Lorentz factor of the jet. We estimate the apparent proper motion of a possibly emerging new jet component and conclude that it is below the detection limit in our observations (Sect. 3). Finally, we put J1430+4204 in context by comparing it with other similar AGNs at lower redshifts (Sect. 4).
2 Observations and data analysis
We observed J1430+4204 at 15 GHz with the ten 25-m diameter radio telescopes of the US National Radio Astronomy Observatory (NRAO) Very Long Baseline Array (VLBA) on 2006 September 15. The total observing time was 8 h. The data were recorded in full circular polarisation with a bandwidth of 32 MHz. We also obtained data taken earlier in a similar 15-GHz VLBA experiment (code BY019) from the NRAO data archive. These observations were done on 2005 February 23, prior to the peak of the total flux density curve (Fig. 1) of J1430+4204. The observing time was 5.8 h. Both data sets were correlated at the NRAO VLBA correlator in Socorro (New Mexico, USA).
We performed the standard VLBI calibration procedures for both experiments using the NRAO Astronomical Image Processing System (AIPS, Diamond 1995). The visibility amplitudes were calibrated using system temperatures and antenna gains measured at the antennas. Instrumental delays were corrected using phase-calibration information provided along with the data. Fringe-fitting was performed over 2-min solution intervals. Additional calibrator and fringe-finder sources (J0854+2006, J0927+3902, J1256-0547, J1407+2827, J1426+3625 and J1642+3948) were also observed.
The calibrated visibility data were exported to and imaged with the Caltech
Difmap package (Shepherd et al. 1994). The conventional hybrid mapping
procedure with several iterations of CLEANing and phase (then amplitude)
self-calibration was applied. Our uniformly-weighted total intensity images of
J1430+4204 are displayed in Figs. 2a (2005 February 23) and 2b (2006 September 15).
Uniform weighting was applied to maximise the angular resolution.
Naturally-weighted images did not reveal any other low surface brightness structure.
Identical coordinate scales and contour
levels are used in both images. The fractional linear polarisation of the VLBI
``core'' was ![]() 1% and 2% at the first and second epochs, respectively. We
detected no polarised emission from outside the core.
1% and 2% at the first and second epochs, respectively. We
detected no polarised emission from outside the core.
The source total flux density at 15 GHz was monitored at the Ryle Telescope (Fabian et al. 1999). The light curve is shown in Fig. 1, where the epochs of the two VLBA experiments, as well as the flux densities measured with the VLBA are marked for comparison.
![\begin{figure}
\par\includegraphics[width=62mm,angle=270,bb=50 80 520 770]{14957...
...ncludegraphics[width=62mm,angle=270,bb=50 80 520 770]{14957fg3.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg14.png)
|
Figure 2:
15-GHz VLBA images of J1430+4204 on 2005 February 23 a), top) and 2006 September 15 b), bottom). In the top image, the peak brightness is 200 mJy/beam, the restoring beam is
1.17 mas |
| Open with DEXTER | |
3 Results
3.1 The compact radio structure of J1430+4204
The mas-scale radio structure of J1430+4204 is dominated by a compact, nearly
unresolved core in the 15-GHz VLBA images, at both epochs (Fig. 2).
Additionally, a diffuse emission region is seen with a low surface brightness,
out to ![]() 4 mas from the brightness peak, in the position angles between
about
4 mas from the brightness peak, in the position angles between
about
![]() and
and
![]() .
(Position angles are conventionally
measured from north through east.) This is most likely a steep-spectrum radio
emission from optically thin plasma along the jet. But we do not have spectral
information on the source at this spatial resolution, since our measurements
were taken at the single frequency of 15 GHz. Notably, the position angle of
the faint emission region is consistent with the source extension observed with
VLBI at lower frequencies and lower resolution (USNO
RRFID, Helmboldt et al. 2007; Paragi et al. 1999).
.
(Position angles are conventionally
measured from north through east.) This is most likely a steep-spectrum radio
emission from optically thin plasma along the jet. But we do not have spectral
information on the source at this spatial resolution, since our measurements
were taken at the single frequency of 15 GHz. Notably, the position angle of
the faint emission region is consistent with the source extension observed with
VLBI at lower frequencies and lower resolution (USNO
RRFID, Helmboldt et al. 2007; Paragi et al. 1999).
Apart from the compact core, we did not detect any significant jet component of which the proper motion could be reliably measured between the two observing epochs separated by 569 days.
We fitted elliptical Gaussian brightness distribution models to the radio core,
using the self-calibrated visibility data in Difmap. The resulting model
parameters are S1=209 mJy flux density,
![]() mas major
axis,
mas major
axis,
![]() mas minor axis (full width at half maximum, FWHM)
at the first epoch, and S2=166 mJy,
mas minor axis (full width at half maximum, FWHM)
at the first epoch, and S2=166 mJy,
![]() mas,
mas,
![]() mas at the second epoch. The fitted major axis position
angles (
mas at the second epoch. The fitted major axis position
angles (
![]() and
and
![]() )
indicate a W-SW extension of the innermost radio structure, quite consistently with the weak mas-scale radio emission
(Fig. 2).
)
indicate a W-SW extension of the innermost radio structure, quite consistently with the weak mas-scale radio emission
(Fig. 2).
The comparison of the total and VLBI flux densities at the first epoch
(Fig. 1) indicates that ![]() 50 mJy is completely resolved
out by the VLBA. Although total flux density monitoring data were not
available, by extrapolating the descending light curve, it is reasonable to
assume a similar difference at the second VLBA epoch.
50 mJy is completely resolved
out by the VLBA. Although total flux density monitoring data were not
available, by extrapolating the descending light curve, it is reasonable to
assume a similar difference at the second VLBA epoch.
3.2 Determination of the source parameters
We used three methods for determining the following parameters of
J1430+4204: the apparent transverse speed of a possible blob in the jet
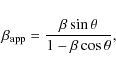
|
(1) |
the Doppler boosting factor
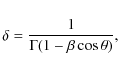
|
(2) |
and the bulk Lorentz factor
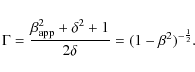
|
(3) |
Here
The most important physical parameter characterizing the jet flow is the bulk
Lorentz factor (![]() ). We are also interested in the apparent tangential
velocity of the putative blob in the jet which we translate into proper motion.
The distance scale at this redshift is 6.497 pc mas-1. We assume a flat
cosmological model with
). We are also interested in the apparent tangential
velocity of the putative blob in the jet which we translate into proper motion.
The distance scale at this redshift is 6.497 pc mas-1. We assume a flat
cosmological model with
![]() km s-1 Mpc-1,
km s-1 Mpc-1,
![]() and
and
![]() throughout this paper.
throughout this paper.
Usually the Lorentz factor and the jet angle to the line of sight (![]() )
are determined from the measured Doppler factor, and the proper motion of jet
component(s) inferred from multi-epoch VLBI monitoring of radio AGNs. Since the
latter measurement is not available in our case, we took a different approach.
For the jet angle to the line of sight,
)
are determined from the measured Doppler factor, and the proper motion of jet
component(s) inferred from multi-epoch VLBI monitoring of radio AGNs. Since the
latter measurement is not available in our case, we took a different approach.
For the jet angle to the line of sight,
![]() ,
we assumed
,
we assumed
![]() as found from bulk Comptonization modelling of the observed X-ray spectrum of
J1430+4204 (Celotti et al. 2007). We determined the Doppler factor using
three different methods, calculated the corresponding Lorentz factor, and
estimated the amount of possible jet component proper motion. The
inferred proper motion is indeed consistent with our non-detection. This in
turn supports the initial assumption that
as found from bulk Comptonization modelling of the observed X-ray spectrum of
J1430+4204 (Celotti et al. 2007). We determined the Doppler factor using
three different methods, calculated the corresponding Lorentz factor, and
estimated the amount of possible jet component proper motion. The
inferred proper motion is indeed consistent with our non-detection. This in
turn supports the initial assumption that ![]() has a small value and
therefore this blazar is viewed nearly ``pole-on''.
has a small value and
therefore this blazar is viewed nearly ``pole-on''.
3.2.1 Parameters from the radio variability
Hovatta et al. (2009) describe a method to determine the Doppler factor
(
![]() )
from the total flux density variability of the source.
Following this method, we fitted an exponential function to the brightest flare
in the flux density curve (Fig. 1) as
)
from the total flux density variability of the source.
Following this method, we fitted an exponential function to the brightest flare
in the flux density curve (Fig. 1) as
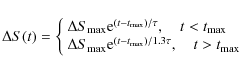
|
(4) |
where t is the time,
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14957fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg41.png)
|
Figure 3: The rising phase of the flare in the 15-GHz total flux density light curve (crosses) of J1430+4204, fitted with a three-component exponential model (solid curve). Dotted curves show the individual components. |
| Open with DEXTER | |
We then determined the variability brightness temperature
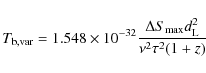
|
(5) |
where
For calculating the Doppler factor from variability
we assume that energy equipartition holds between the particles and the magnetic field in the radio-emitting region (Readhead 1994). In this case the intrinsic brightness temperature is
We obtained the variability brightness temperature
![]() K, and the Doppler factor
K, and the Doppler factor
![]() .
The implied
apparent transverse speed is
.
The implied
apparent transverse speed is
![]() and thus the Lorentz
factor is
and thus the Lorentz
factor is
![]() .
.
The apparent proper motion of a possible new jet component is
![]() mas yr-1. This means that during the time between the two VLBA
observations (
mas yr-1. This means that during the time between the two VLBA
observations (
![]() )
the blob could have moved by
)
the blob could have moved by
![]() 0.03 mas. This angular displacement is just below the limit which we
can possibly detect with the VLBA at this wavelength, about 10% of the
restoring beam size (cf. Lister et al. 2009). Such a detection is
further complicated by the fact that the absolute astrometric position of the
core in our VLBA images is not known. Should the flare result in a slight
displacement of the source brightness distribution peak (well within the
restoring beam), the change remains unnoticed because self-calibration
effectively shifts the brightness peak of the VLBA image into the phase centre,
to the a priori source position that was assumed for the correlation of the
interferometric measurements. Accurate relative astrometric registration of
the brightness peak could have been possible via phase-referencing observations
to an external radio source. Alternatively, a well-defined stationary feature
further along the jet could have served as a positional reference, but there
seems no suitable component in our images (Fig. 2).
0.03 mas. This angular displacement is just below the limit which we
can possibly detect with the VLBA at this wavelength, about 10% of the
restoring beam size (cf. Lister et al. 2009). Such a detection is
further complicated by the fact that the absolute astrometric position of the
core in our VLBA images is not known. Should the flare result in a slight
displacement of the source brightness distribution peak (well within the
restoring beam), the change remains unnoticed because self-calibration
effectively shifts the brightness peak of the VLBA image into the phase centre,
to the a priori source position that was assumed for the correlation of the
interferometric measurements. Accurate relative astrometric registration of
the brightness peak could have been possible via phase-referencing observations
to an external radio source. Alternatively, a well-defined stationary feature
further along the jet could have served as a positional reference, but there
seems no suitable component in our images (Fig. 2).
3.2.2 Parameters from the brightness temperature measured with VLBI
The brightness temperature of a component in the radio source can be measured from
our VLBI data, using the following formula (e.g. Condon et al. 1982):
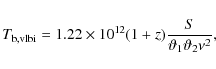
|
(7) |
where S is the flux density (Jy),
We again assume that the intrinsic brightness temperature is the
equipartition brightness temperature (Readhead 1994; Lähteenmäki et al. 1999),
![]() K. We will call the Doppler boosting factor derived
this way as the VLBI Doppler factor:
K. We will call the Doppler boosting factor derived
this way as the VLBI Doppler factor:
This is valid if the brightness temperature is measured at the turnover frequency. In our case, the turnover frequency in the broad-band radio spectrum of is J1430+4204 is around 15 GHz (Worsley et al. 2006), close to our VLBA observing frequency.
Our fitted elliptical Gaussian brightness distribution models to the core
suggest
![]() K and
K and
![]() K at the two VLBA epochs. These values correspond to
Lorentz factors of
K at the two VLBA epochs. These values correspond to
Lorentz factors of
![]() and
and
![]() for the two epochs.
Consistently with the first method based on variability, this one also predicts
a proper motion of
for the two epochs.
Consistently with the first method based on variability, this one also predicts
a proper motion of
![]() mas yr-1.
mas yr-1.
3.2.3 Estimating the intrinsic brightness temperature
So far we assumed that the intrinsic brightness temperature of the source was equal to the equipartition value,
![]() K (Readhead 1994).
However, with two independent measurements of the apparent brightness
temperature (from the variability and from the VLBI structure), and
with the assumption that the underlying Doppler factors are the same,
we can calculate the intrinsic brightness temperature (Lähteenmäki et al. 1999). Using Eqs. (6) and (8),
K (Readhead 1994).
However, with two independent measurements of the apparent brightness
temperature (from the variability and from the VLBI structure), and
with the assumption that the underlying Doppler factors are the same,
we can calculate the intrinsic brightness temperature (Lähteenmäki et al. 1999). Using Eqs. (6) and (8),
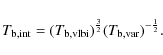
|
(9) |
At our two VLBI epochs, we get
3.2.4 Parameters from the inverse Compton process
By assuming that the X-ray radiation of the source results from inverse-Compton
scattered photons of the radio synchrotron radiation, one can estimate the
Doppler factor (Ghisellini et al. 1993; Güijosa & Daly 1996) as
![\begin{displaymath}\delta_{\rm IC} = f(\alpha) (1+z) S_{\rm m} \times\left[\frac...
...}^{6-4\alpha}\nu_{\rm op}^{5-3\alpha}}\right]^{1/(4-2\alpha)}
\end{displaymath}](/articles/aa/full_html/2010/13/aa14957-10/img68.png)
|
(10) |
where
Here we also need to assume that the VLBI observations were carried out at the
turnover frequency, which holds for our case. We find the value of the
inverse-Compton Doppler factor to be
![]() and
and
![]() for the first and second VLBA epochs,
respectively. Assuming again
for the first and second VLBA epochs,
respectively. Assuming again
![]() (Celotti et al. 2007),
the Lorentz factor and the apparent transverse speed for the two epochs are:
(Celotti et al. 2007),
the Lorentz factor and the apparent transverse speed for the two epochs are:
![]() and
and
![]() ;
;
![]() and
and
![]() .
At the distance of the source, this
translates to an apparent proper motion of
.
At the distance of the source, this
translates to an apparent proper motion of
![]() mas yr-1and
mas yr-1and
![]() mas yr-1. In 569 days, the putative jet
component would have moved by
mas yr-1. In 569 days, the putative jet
component would have moved by ![]() 0.04 - 0.1 mas.
0.04 - 0.1 mas.
4 Discussion
We estimated the Doppler factor in the blazar J1430+4204 using different methods based on radio variability (
![]() ), VLBI imaging assuming equipartition (
), VLBI imaging assuming equipartition (
![]() ), and the inverse Compton process (
), and the inverse Compton process (
![]() ). These estimates are summarised in
Table 1, along with the other source parameters derived.
). These estimates are summarised in
Table 1, along with the other source parameters derived.
Table 1: Parameters of J1430+4204 estimated from radio variability, VLBI imaging and the inverse Compton process.
While the mean
![]() ratio is in the order of unity
for the AGN sample of Güijosa & Daly (1996), there are differences up to
a factor of
ratio is in the order of unity
for the AGN sample of Güijosa & Daly (1996), there are differences up to
a factor of ![]() 4 in the Doppler boosting factors derived by the two
independent methods. Errors come from the uncertainties of the input
parameters, and larger inconsistencies may reflect deviations from the
equipartition in certain sources. In the case of J1430+4204, our three
estimates of the Doppler factor are remarkably similar, the values agree within
a factor of
4 in the Doppler boosting factors derived by the two
independent methods. Errors come from the uncertainties of the input
parameters, and larger inconsistencies may reflect deviations from the
equipartition in certain sources. In the case of J1430+4204, our three
estimates of the Doppler factor are remarkably similar, the values agree within
a factor of ![]() 2.
2.
To estimate the bulk speed of the jet material (![]() )
and the corresponding
Lorentz factor (
)
and the corresponding
Lorentz factor (![]() ), we assumed
), we assumed
![]() for the jet angle to the
line of sight, found from bulk Comptonisation modelling of the X-ray spectrum by
Celotti et al. (2007). At a given Doppler factor,
for the jet angle to the
line of sight, found from bulk Comptonisation modelling of the X-ray spectrum by
Celotti et al. (2007). At a given Doppler factor,
![]() (e.g. Urry & Padovani 1995), which in our case constrains the allowed range of the viewing angles to
(e.g. Urry & Padovani 1995), which in our case constrains the allowed range of the viewing angles to
![]() .
The value of
.
The value of ![]() is quite insensitive to the actual
is quite insensitive to the actual ![]() in most of the possible range of viewing angles. Therefore our
conclusions remain valid even if we allow for somewhat different values
of
in most of the possible range of viewing angles. Therefore our
conclusions remain valid even if we allow for somewhat different values
of ![]() .
.
From measuring the source variability and from imaging the mas-scale
radio structure at nearly the same time, we could determine the
intrinsic brightness temperature of J1430+4204. Our values (
![]() K and
K and
![]() K at two different epochs)
are consistent with those obtained for a larger sample of lower-redshift AGNs
(Lähteenmäki et al. 1999), suggesting that
K at two different epochs)
are consistent with those obtained for a larger sample of lower-redshift AGNs
(Lähteenmäki et al. 1999), suggesting that
![]() K
in compact extragalactic radio sources.
K
in compact extragalactic radio sources.
How is the other intrinsic parameter, the Lorentz factor of the jet in
J1430+4204 (
![]() )
compared to those values measured in other
AGNs? The systematic multi-epoch 15-GHz VLBA monitoring of a large
flux-density-limited sample of radio-loud AGNs in the 2-cm VLBA Survey and the
MOJAVE survey (Lister et al. 2009; Kellermann et al. 2004; Cohen et al. 2007) revealed that Lorentz factors can be as high as
)
compared to those values measured in other
AGNs? The systematic multi-epoch 15-GHz VLBA monitoring of a large
flux-density-limited sample of radio-loud AGNs in the 2-cm VLBA Survey and the
MOJAVE survey (Lister et al. 2009; Kellermann et al. 2004; Cohen et al. 2007) revealed that Lorentz factors can be as high as
![]() ,
but the sources typically have values between 5 and 10. The
overwhelming majority of the MOJAVE sources are at z<2.5; the most distant
object in the sample is J0646+4451 at z=3.4. As far as the Lorentz factor is
concerned, our high-redshift object is therefore similar to those studied in
the MOJAVE survey.
,
but the sources typically have values between 5 and 10. The
overwhelming majority of the MOJAVE sources are at z<2.5; the most distant
object in the sample is J0646+4451 at z=3.4. As far as the Lorentz factor is
concerned, our high-redshift object is therefore similar to those studied in
the MOJAVE survey.
The maximum apparent speed vs. redshift plot for the MOJAVE quasars
(Fig. 8 of Lister et al. 2009) shows that most of the values are found
in the range
![]() .
The estimated apparent speed of
J1430+4204 fits well in this picture and is closer to the low values.
.
The estimated apparent speed of
J1430+4204 fits well in this picture and is closer to the low values.
The estimate for the jet apparent proper motion (
![]() mas yr-1)
obtained from our analysis for J1430+4204 is small compared to other sources at
lower redshifts. This result fits the observed angular velocity-redshift
relation and is consistent with the cosmological interpretation of the
redshifts (Kellermann et al. 2004).
mas yr-1)
obtained from our analysis for J1430+4204 is small compared to other sources at
lower redshifts. This result fits the observed angular velocity-redshift
relation and is consistent with the cosmological interpretation of the
redshifts (Kellermann et al. 2004).
5 Conclusion
The high-redshift (z=4.72) blazar J1430+4204 produced a major radio flux density outburst in 2005 (Fig. 1). About a year after the peak of the 15-GHz flux density curve, we imaged the source with the VLBA at this frequency. We also analysed similar archive VLBA data taken during the rise of radio light curve. At both epochs separated by 569 days, the mas-scale radio structure of the source was remarkably similar: a compact optically thick ``core'' and a weak extension to W-SW (Fig. 2). The core could be fitted with elliptical Gaussian model components.
We searched for a new emerging component usually observable after large radio outbursts in AGNs. Based on our VLBA imaging, we did not detect any new jet component to be associated with the event. Assuming a small jet angle to the line of sight, we used three different methods to estimate the expected proper motion of such a component. These gave consistently small values for the proper motion. We found that our time base and angular resolution were insufficient to distinguish any new blob in the jet. Supposing that the jet was launched in 2004, the elapsed time until the second VLBA observation is 950days. During this time the putative blob should have moved by 0.05 mas.
Our estimates for the intrinsic physical parameter describing the jet, the bulk
Lorentz factor (
![]() )
are comparable to the typical values
found for other well-studied samples of blazars
(e.g. Lister et al. 2009; Hovatta et al. 2009).
The intrinsic brightness temperature is close to the equipartition value
and is fully consistent with brightness temperatures measured in
other sources (
)
are comparable to the typical values
found for other well-studied samples of blazars
(e.g. Lister et al. 2009; Hovatta et al. 2009).
The intrinsic brightness temperature is close to the equipartition value
and is fully consistent with brightness temperatures measured in
other sources (
![]() K, Lähteenmäki et al. 1999)
K, Lähteenmäki et al. 1999)
According to our estimates of the apparent proper motion, the emergence of a
new jet component associated with the major 2005 outburst in J1430+4204 could
possibly be detected with the angular resolution of ground-based VLBI at 15 GHz
over a time span of ![]() 10 years.
10 years.
The National Radio Astronomy Observatory (NRAO) is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. We are grateful to Guy Pooley for sharing the Ryle Telescope data with us. We thank the referee, Esko Valtaoja for his comments. This work was supported by the Hungarian Scientific Research Fund (OTKA grants K077795 and K72515). This research has made use of the United States Naval Observatory (USNO) Radio Reference Frame Image Database (RRFID), and the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Celotti, A., Ghisellini, G., & Fabian, A. C. 2007, MNRAS, 375, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, C. C., Stawarz, L., Siemiginowska, A., et al. 2008, in Extragalactic Jets: Theory and Observation from Radio to Gamma Ray, ed. T. A. Rector, & D. S. De Young, ASP Conf. Ser., 386, 462 [Google Scholar]
- Cohen, M. H., Barthel, P. D., Pearson, T. J., & Zensus, J. A. 1988, ApJ, 329, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M. H., Lister, M. L., Homan, D. C., et al. 2007, ApJ, 658, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Condon, M. A., Gisler, G., & Puschell, J. J. 1982, ApJ, 252, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond, P. J. 1995, in Very Long Baseline Interferometry and the VLBA, ed. J. A. Zensus, P. J. Diamond, & P. J. Napier, ASP Conf. Ser., 82, 227 [Google Scholar]
- Fabian, A. C., Celotti, A., Pooley, G., et al. 1999, MNRAS, 308, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Güijosa, A., & Daly, R. A. 1996, ApJ, 461, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Helmboldt, J. F., Taylor, G. B., Tremblay, S., et al. 2007, ApJ, 658, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I. M., & McMahon, R. G. 1998, MNRAS, 294, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Hovatta, T., Valtaoja, E., Tornikoski, M., & Lähteenmäki, A. 2009, A&A, 494, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kellermann, K. I., Lister, M. L., Homan, D. C., et al. 2004, ApJ, 609, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Lähteenmäki, A., Valtaoja, E., & Wiik, K. 1999, ApJ, 511, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Paragi, Z., Frey, S., Gurvits, L. I., et al. 1999, A&A, 344, 51 [NASA ADS] [Google Scholar]
- Readhead, A. C. S. 1994, ApJ, 426, 51 [Google Scholar]
- Savolainen, T., Wiik, K., Valtaoja, E., Jorstad, S. G., & Marscher, A. P. 2002, A&A, 394, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shepherd, M. C., Pearson, T. J., & Taylor, G. B. 1994, BAAS, 26, 987 [NASA ADS] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vermeulen, R. C., & Cohen, M. H. 1994, ApJ, 430, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Celotti, A., & Iwasawa, K. 2004, MNRAS, 350, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Worsley, M. A., Fabian, A. C., Pooley, G. G., & Chandler, C. J. 2006, MNRAS, 368, 844 [NASA ADS] [CrossRef] [Google Scholar]
Footnotes
- ... RRFID
![[*]](/icons/foot_motif.png)
- http://rorf.usno.navy.mil/rrfid.shtml
All Tables
Table 1: Parameters of J1430+4204 estimated from radio variability, VLBI imaging and the inverse Compton process.
All Figures
![\begin{figure}
\par\includegraphics[width=150mm]{14957fg1.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg7.png)
|
Figure 1: The 15-GHz total flux density vs. time for J1430+4204 from the Ryle Telescope monitoring (G. Pooley, priv. comm.). The points are connected in the flaring phase for clarity. Solid vertical lines mark the times of the two VLBA observations. The filled circles correspond to the measured VLBI flux densities. Dashed lines mark calendar years as indicated. The typical flux density error bars are smaller or comparable in size with the symbols. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=62mm,angle=270,bb=50 80 520 770]{14957...
...ncludegraphics[width=62mm,angle=270,bb=50 80 520 770]{14957fg3.ps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg14.png)
|
Figure 2:
15-GHz VLBA images of J1430+4204 on 2005 February 23 a), top) and 2006 September 15 b), bottom). In the top image, the peak brightness is 200 mJy/beam, the restoring beam is
1.17 mas |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{14957fg4.eps}
\end{figure}](/articles/aa/full_html/2010/13/aa14957-10/Timg41.png)
|
Figure 3: The rising phase of the flare in the 15-GHz total flux density light curve (crosses) of J1430+4204, fitted with a three-component exponential model (solid curve). Dotted curves show the individual components. |
| Open with DEXTER | |
| In the text | |
Copyright ESO 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.